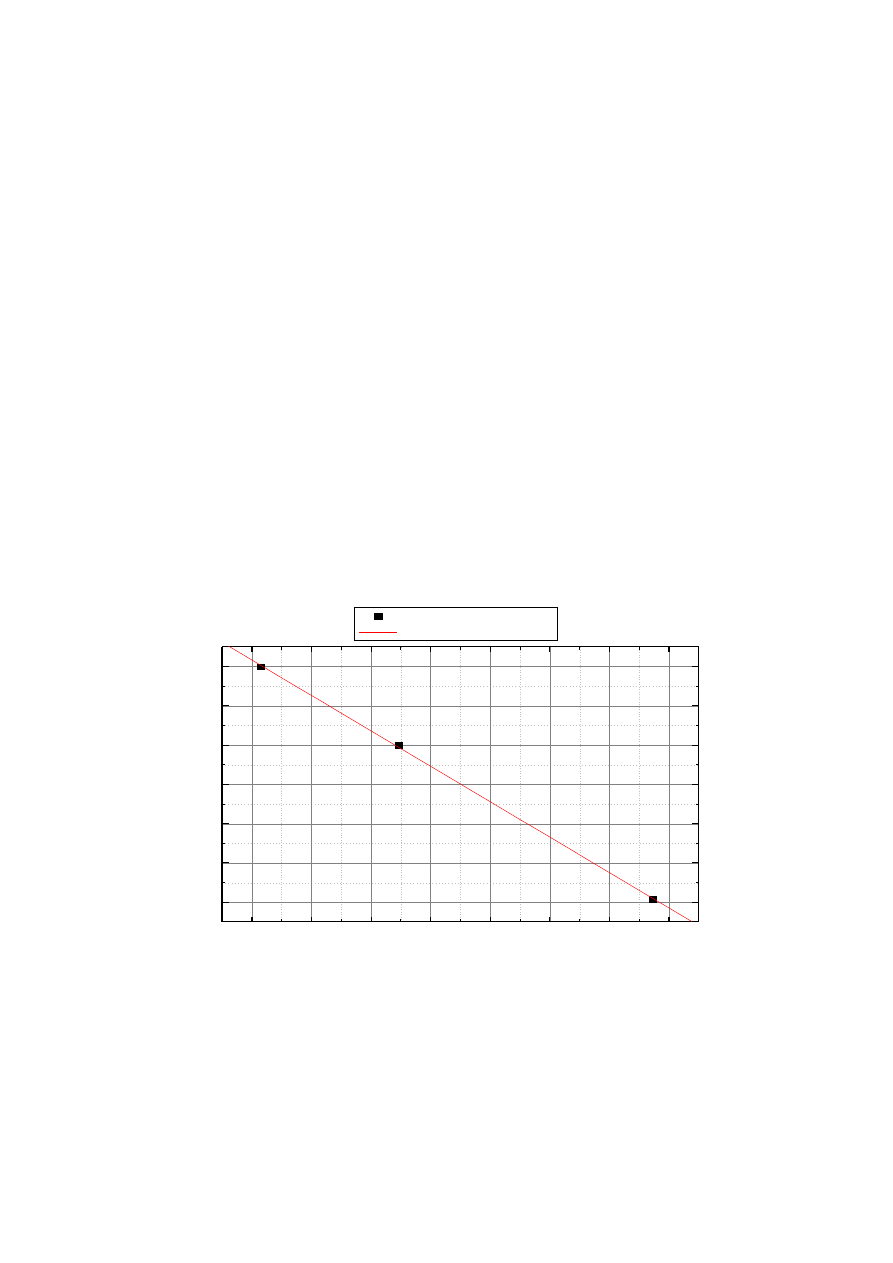
Konrad Pawlak 233633

ĆWICZENIE 8

POMIAR OPORNOŚCI W FUNKCJI TEMPERATURY

1. Cel ćwiczenia.
Celem ćwiczenia było wyznaczenie charakterystyki temperaturowej elementów
oporowych takich jak rezystor oraz termistor typu Ntc (czyli o ujemnym
współczynniku temperaturowym). Za układ pomiarowy służyły trzy karty w
sterowniku Eurodriver – karta RBR przeznaczona do pomiaru oporności, karta TRM1
służąca jako termometr cyfrowy i druga karta TRM1 wykorzystywana jako
przetwornik ADC. Po podłączeniu aparatury pomiarowej zgodnie z instrukcją
przystąpiono do kalibracji układu.

2. Kalibracja.
W celu kalibracji dokonano pomiaru kilku charakterystycznych temperatur w
jednostkach pomiarowych przetwornika (ciekłego azotu, lodu i wrzątku), następnie
przypisano im wartości w stopniach Celsjusza i wyznaczono współczynniki prostej A
i B w programie Origin.

Wyk.1. Kalibracja.

A=-0,04511 B=-26,91238

-3000

-2000

-1000

0

1000

2000

3000

4000

-200

-150

-100

-50

0

50

100

wartosc temperatury
doasowanie liniowe

te

m

p

e

ra

tu

ra

[

0

C

]

wartosc przetwornika w j.p.

3. Wyznaczenie charakterystyki rezystancji rezystora w funkcji temperatury.

W celu wyznaczenia charakterystyki rezystancji w funkcji temperatury należało
skorzystać ze wzoru zamieszczonego w instrukcji:

Wzór 1:

Z

N

N

X

R

U

U

U

U

R

⋅

−

+

=

2

2

gdzie:

Rz

- opornik zakresowy (tu 100k lub 1M)

Rx

- mierzona oporność

U

- napięcie stałe zasilające mostek 10V

UN - napięcie nierównowagi mostka

Ustawiono dla rezystora zakres 100k, zanurzono termometr wraz z rezystorem w
ciekłym azocie, odczekano na ustabilizowanie się wskazań termometru i rozpoczęto
pomiary. Wyjęto rezystor z azotu i odczekano do jego ocieplenia się do temperatury
zbliżonej do pokojowej. Z zebranych danych wartości napięcia nierównowagi
mostka wyliczono oporności, a następnie przedstawiono je na Wykresie 2.

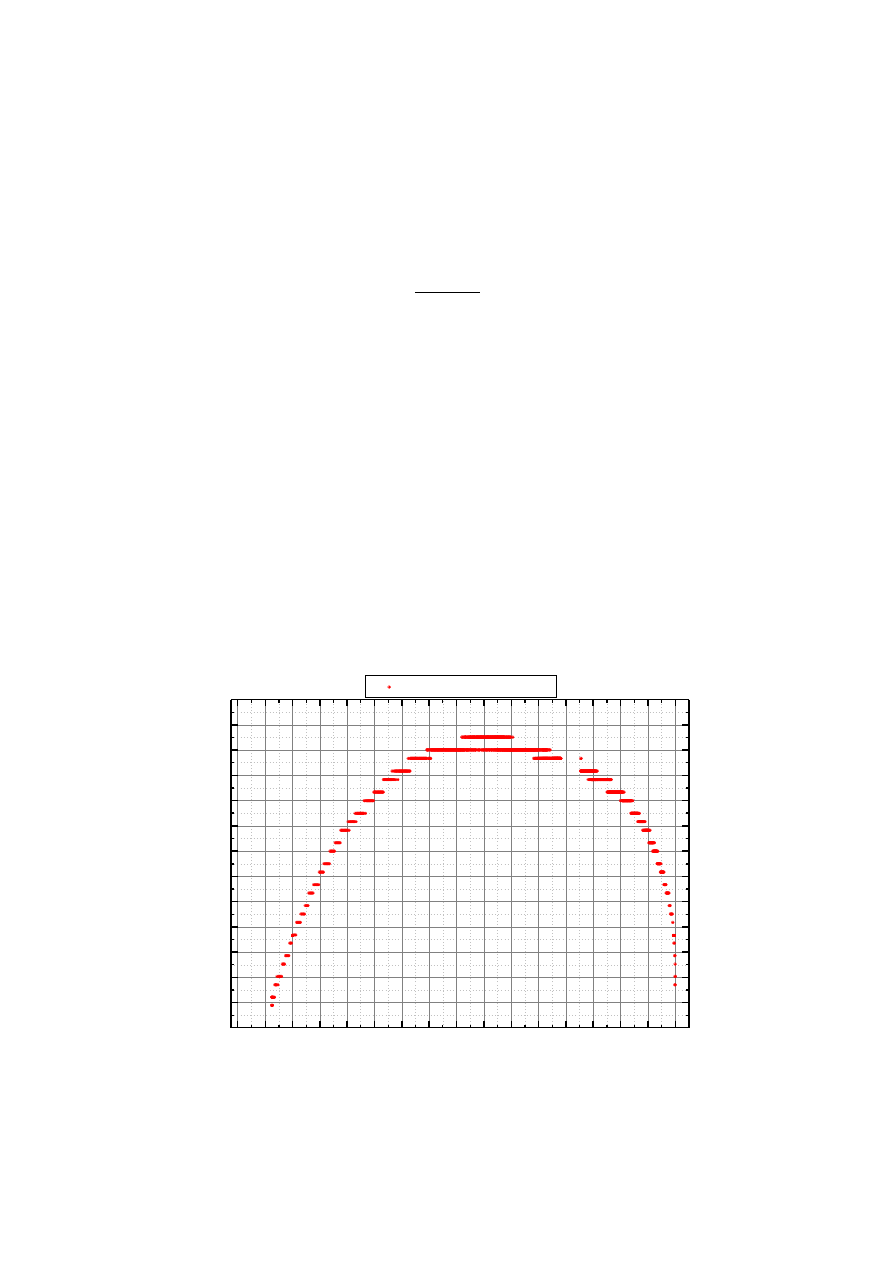
Wyk.2 Rezystancja rezystora w funkcji temperatury, ocieplanie i ochładzanie.

Następnie przeprowadzono analogiczne pomiary, tym razem jednak najpierw

-220-200-180-160-140-120-100 -80 -60 -40 -20 0

20 40 60 80 100

102250

102500

102750

103000

103250

103500

103750

104000

104250

104500

104750

105000

105250

105500

Punkty pomiarowe

R

e

zy

st

a

n

cj

a

[

Ω

]

Temperatura [

o

C]

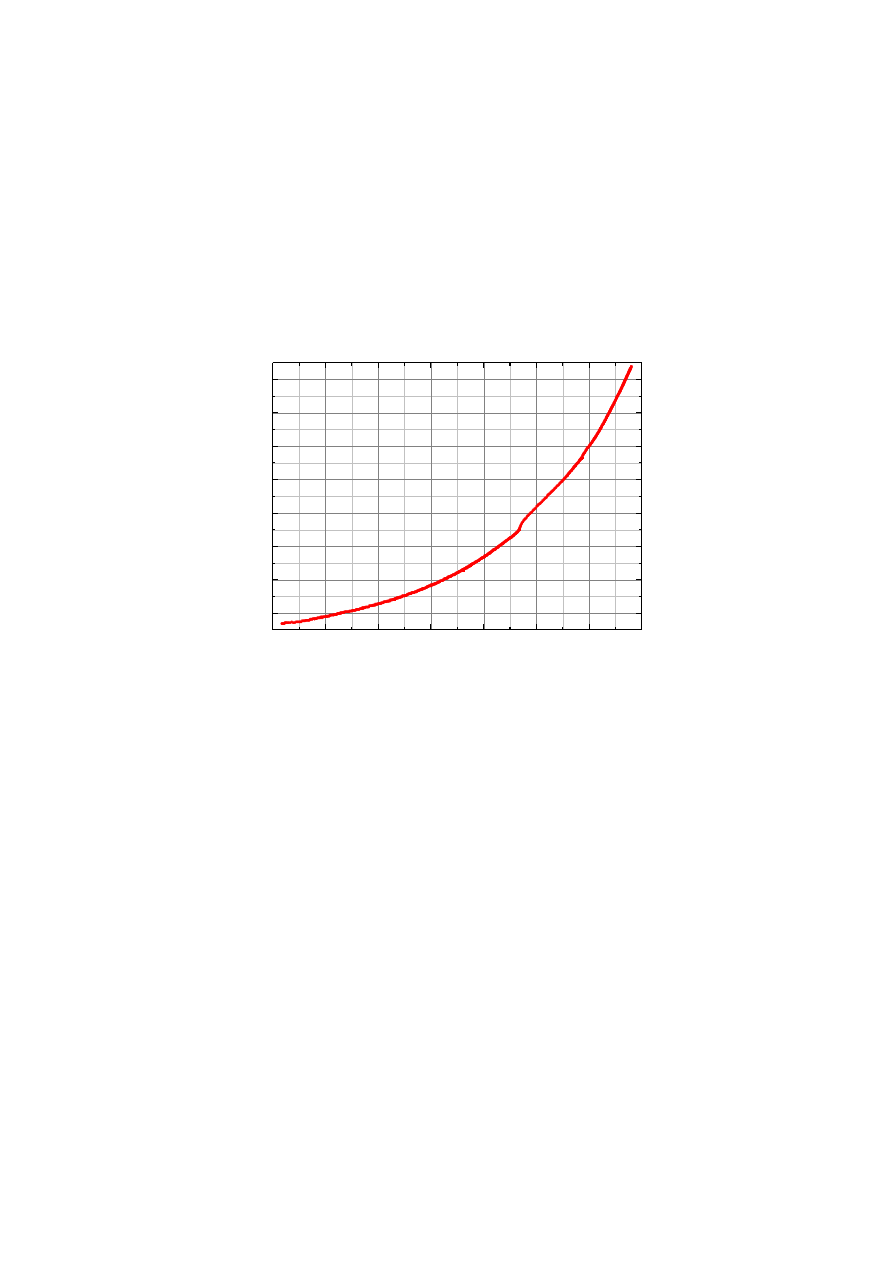
zanurzono termometr z rezystorem w czajniku z wrzątkiem, odczekano aż wskazania
temperatury się ustabilizują, wyciągnięto termometr w rezystorem z czajnika i
zaczęto pomiar aż do osiągnięcia temperatury zbliżonej do pokojowej.
Charakterystykę ochładzania rezystora w funkcji temperatury przedstawia Wykres 3.

Kolejnym punktem pomiarów było zbadanie zmiany właściwości termistora NTC w
zależności od temperatury. Pomiary były analogiczne do tych dla rezystora, z tą
różnicą, że wykonano je na zakresie 1M. Wykres 4 przedstawia ilustruje zmianę
oporności po wyjęciu termistora z wrzątku.

Wyk.3. Rezystancja termistora w funkcji temperatury, ochładzanie.

Następnie zanurzono termometr wraz z termistorem w ciekłym azocie, wyciągnięto
po ustabilizowaniu się temperatury i rozpoczęto pomiar. Wykres 5 ilustruje zmianę
rezystancji w funkcji temperatury.

1 0 0

9 0

8 0

7 0

6 0

5 0

4 0

3 0

1 0 0 0 0

2 0 0 0 0

3 0 0 0 0

4 0 0 0 0

5 0 0 0 0

6 0 0 0 0

7 0 0 0 0

8 0 0 0 0

O

p

o

rn

o

s

c

[

O

h

m

]

T e m p e r a t u r a [ 0 C ]

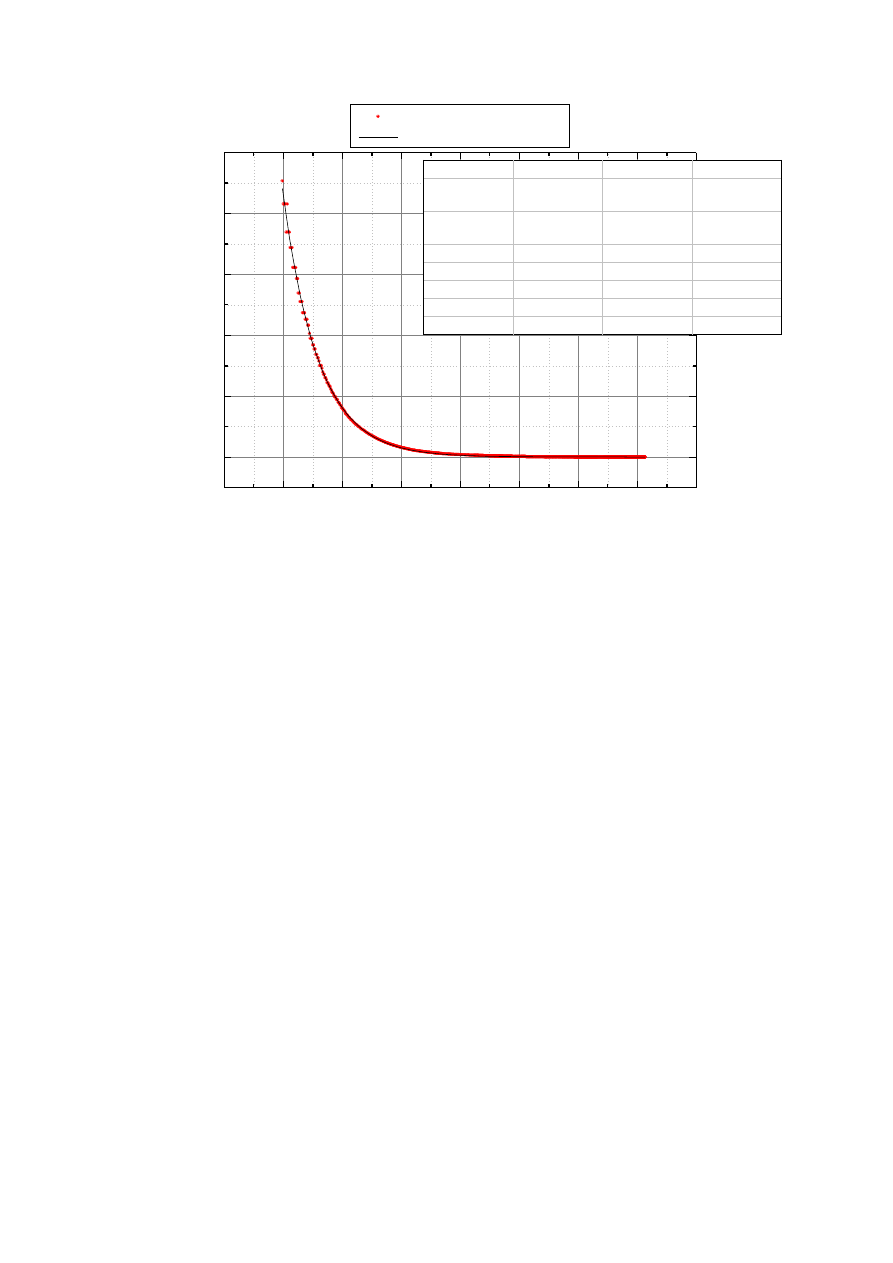
Wyk.4. Rezystancja termistora w funkcji temperatury, ocieplanie

4.Wnioski.
Pierwszym wnioskiem jest to, że wraz z temperaturą oporność elementów ulega
zmianie, dla rezystora jest to dość niewielka zmiana, natomiast dla termistora skok
jest duży, wynoszący kilka rzędów wielkości. Charakterystyczne również dla
termistora typu NTC okazało się to, że wraz ze wzrostem temperatury, oporność tego
elementu maleje. Kalibracja w trzech punktach zapewniła dość dużą precyzję
pomiaru, dlatego można je uznać za dość dokładne.

Z nieznanych przyczyn, rezystancja przy nagrzewaniu rezystora do temperatur od 0
do bliskich 100 stopni Celsjusza spada, zamiast rosnąć, co jest niezgodne ze wzorem
R=R

0

[1+a(T-T0)+b(T-T0)

2

+1........]. Nie wiem co jest tego powodem, ale powtarza

się to przy każdym pomiarze, więc przyczyna musi tkwić w wadzie sprzętu.

-120

-100

-80

-60

-40

-20

0

20

40

0,00E+000

1,00E+008

2,00E+008

3,00E+008

4,00E+008

5,00E+008

punkty pomiarowe
dopasowanie liniowe

O

p

o

rn

o

sc

[

O

m

y]

Temperatura [stopnie Celsjusza]

Model

Exponential

Equation

y=y0+Aexp(r0/

x)

Reduced Chi-

Sqr

1,8234E12

Adj. R-Square

0,99904

Value

Standard Error

Book4_D

y0

312372,69638

32225,2864

Book4_D

A

101267,11858

1041,60303

Book4_D

R0

-0,08349

1,08883E-4