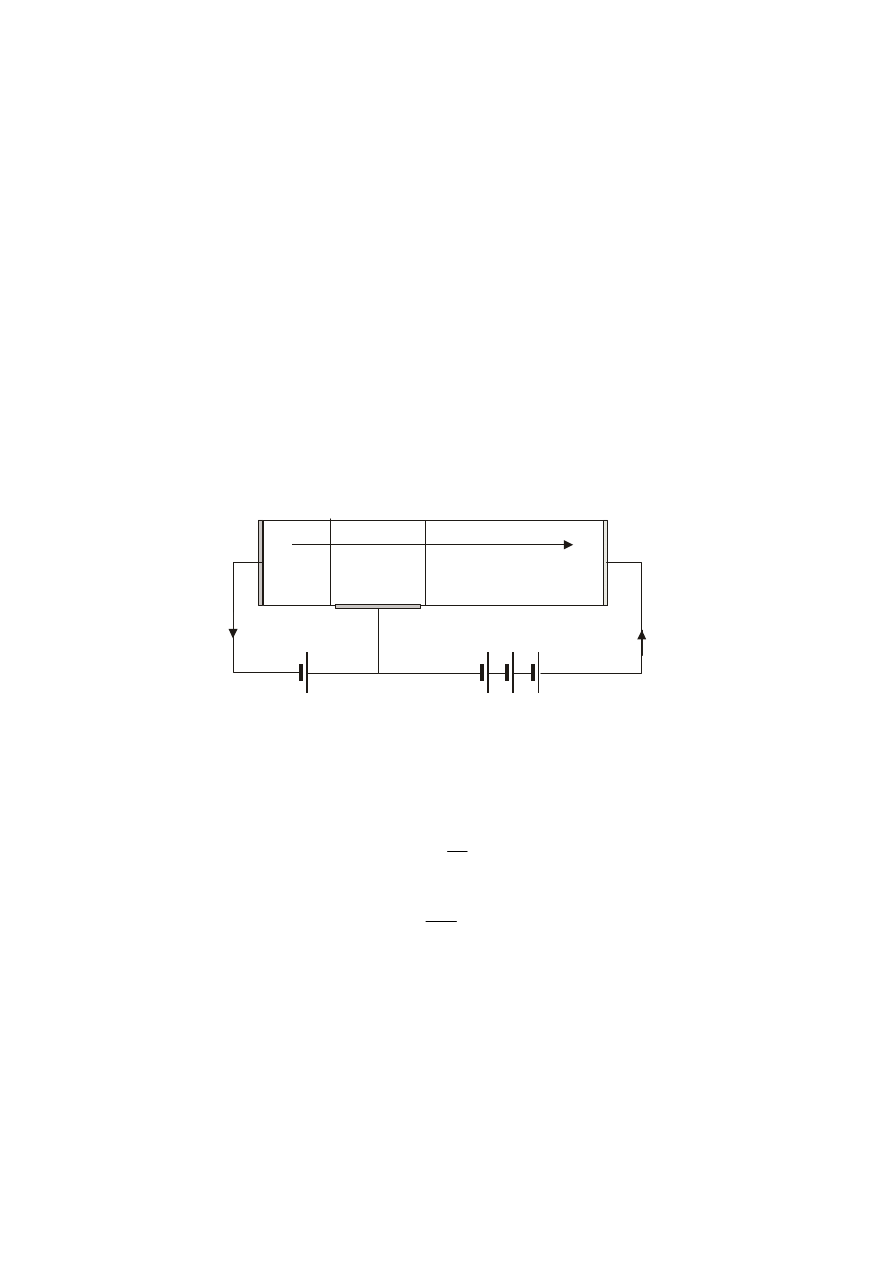
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

1

7.TRANZYSTOR BIPOLARNY - szkic do wykładu

7.1. Efekt tranzystorowy

Rozpływ prądów w strukturze n-p-n, przy polaryzacji złącza E-B w kierunku
przewodzenia a złącza B-C w kierunku zaporowym:
-

z emitera do bazy są wstrzykiwane elektrony

-

w obszarze bazy elektrony dyfundują w kierunku złącza B-C

-

po przejściu przez bazę, elektrony zostają uniesione przez przez pole
elektroczne złącza (wymiecione z obszaru złącza) B-C do obszaru kolektora.

Strumień elektronów wstrzykniętych z emitera do bazy tworzy prąd emitera w
obwodzie wejściowym. Strumień elektronów odbieranych przez kolektor tworzy
prąd kolektora i jednocześnie jest prądem wyjściowym

Rys.7.1.

Przy przyjętych uproszczeniach prąd kolektora jest równy prądowi emitera. Zależy
on wyłącznie od napięcia polaryzującego złącze B-E. Można zapisać:

I

C

= I

E

Zatem współczynnik wzmocnienia prądowego dla prądu stałego wynosi:

1

=

=

α

E

C

N

I

I

(7.1)

podobnie wzmocnienie dla małych przyrostów wynosi

1

=

Δ

Δ

=

α

E

C

N

I

I

(7.2)

Skoro prąd wejściowy jest taki sam jak prąd wyjściowy, to jak to się ma do
wzmacniania mocy?

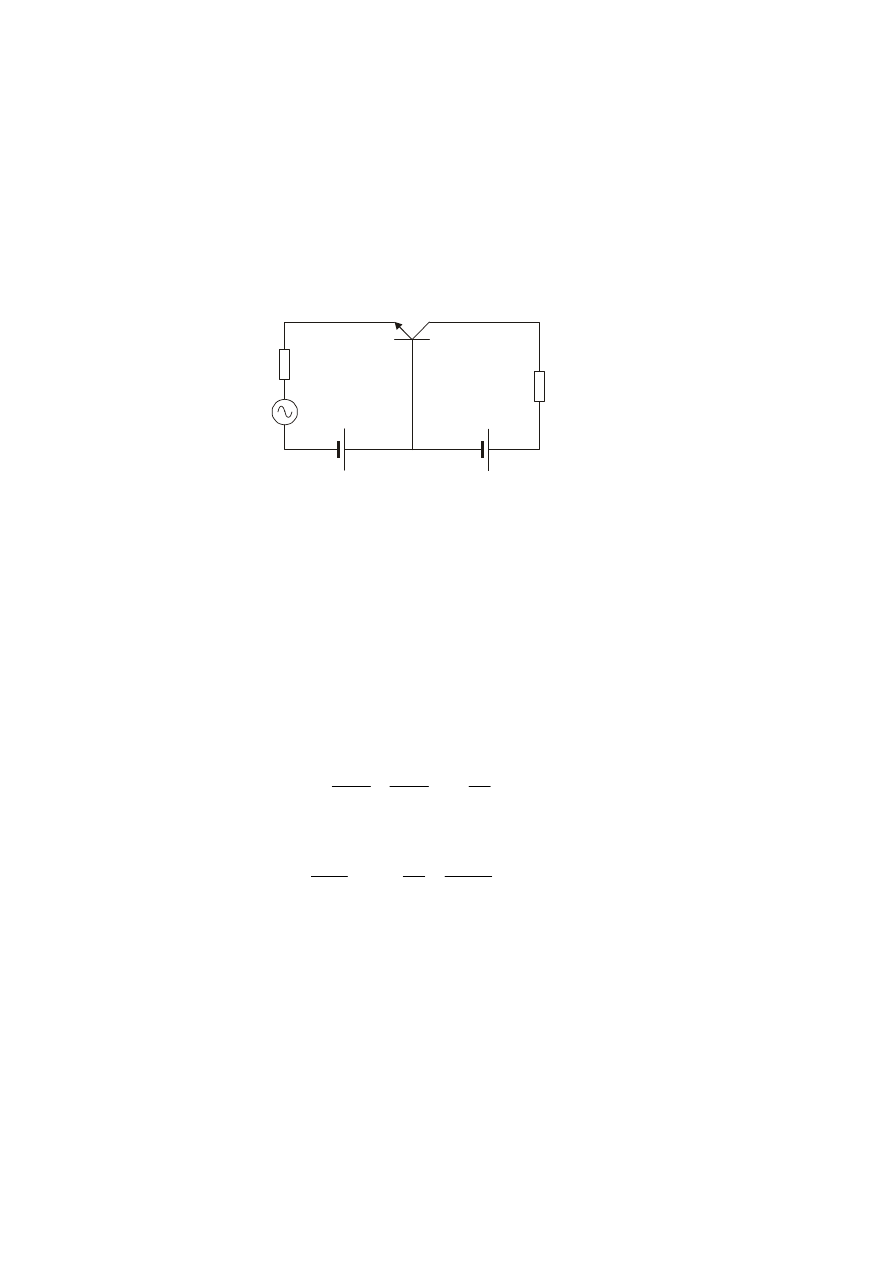
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

2

7.2. Tranzystor jako wzmacniacz mocy.

Rys.7.2.

Obydwa złącza tranzystora są spolaryzowane napięciem stałym: emiterowe -
dodatnim a kolektorowe ujemnym; w obwodzie wejściowym jest źródło małego
sygnału sinusoidalnego e

g

Wartość chwilowa mocy dostarczanej na wejściu tranzystora:

we

em

we

r

i

P

2

=

(7.3)

Moc odbierana przez odbiornik R

L

L

cm

wy

R

i

P

2

=

(7.4)

Spełnienie warunku dopasowania (równości) rezystancji wyjściowej r

wy

z

rezystancją odbiornika R

L

daje maksymalną moc oddaną do odbiornika

r

wy

= R

L

Współczynnik wzmocnienia mocy wynosi:

we

wy

we

em

wy

cm

we

em

L

cm

P

r

r

r

i

r

i

r

i

R

i

k

2

2

2

2

2

α

=

=

=

(7.5)

Gdy α=1, k

P

= r

wy

/ r

we

Rezystancja wejściowa r

we

jest mała i równa rezystancji diody (patrz: ):

Ω

=

≈

≈

+

=

25

1

26

mA

mV

I

R

I

m

r

r

T

s

T

d

we

ϕ

ϕ

a

∞

→

wy

r

,

Rezystancja wyjściowa r

wy

, którą stanowi wstecznie spolaryzowane złącze jest

bardzo duża i wynosi od kilkuset do kilku tysięcy omów. Stosunek r

wy

/ r

we

we

wzorze (7.5) wynosi kilka tysięcy, zatem wzmocnienie mocy tranzystora a tym
samym także wzmocnienie napięciowe, przy

α

N

≈

1 jest duże. Tranzystor jest

rzeczywiście transformatorem rezystancji trans-re-sistorem i wzmacniaczem
mocy. Tranzystor spełnia funkcje elementu czynnego i może służyć do liniowego
wzmacniania sygnałów elektrycznych. Rys.7.2.

D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

3

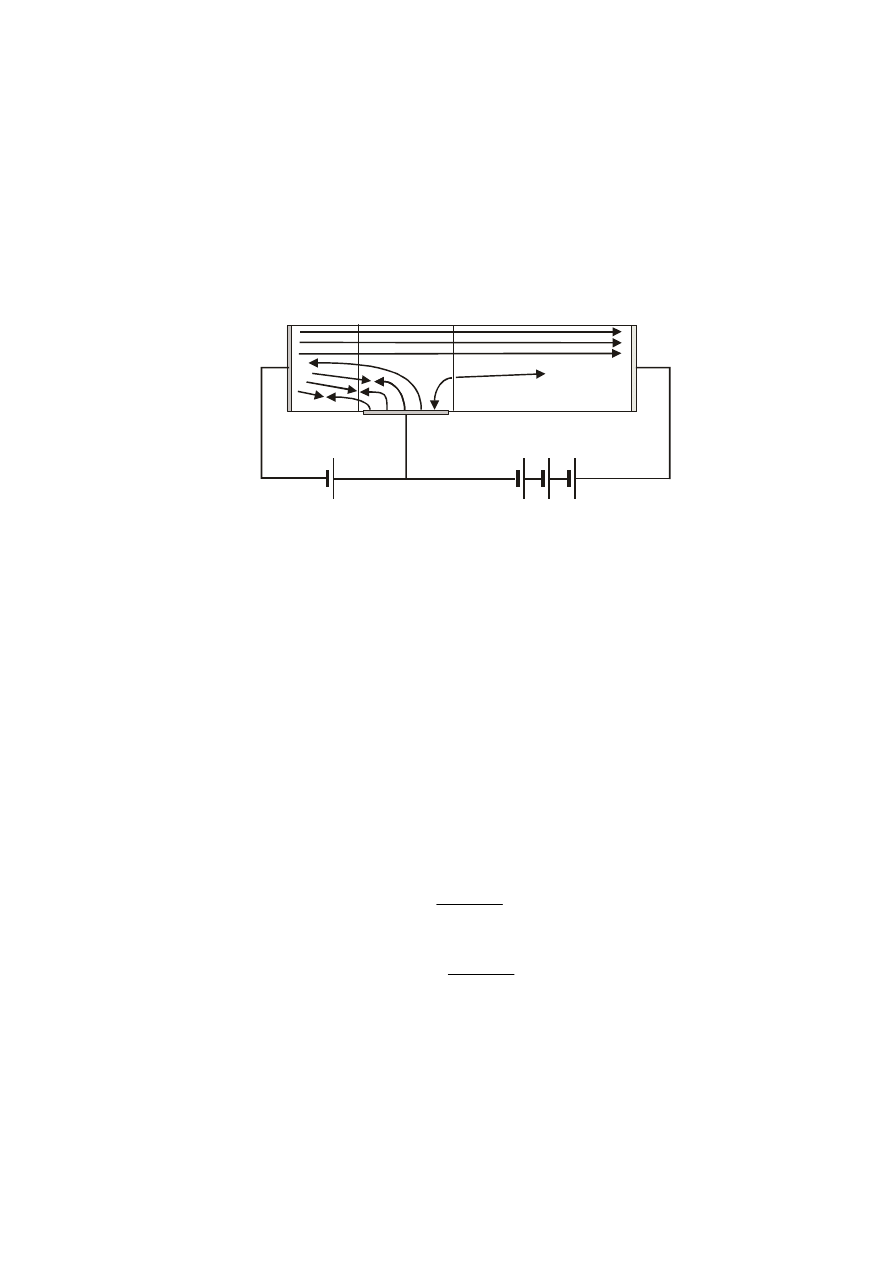
7.3. Dokładny model zjawisk w tranzystorze bipolarnym.

Rys.7.3.

Rzeczywisty prąd kolektora zawiera składową generowaną w złączu C-B.
Generowane termicznie pary elektron-dziura, w wyniku silnego pola są wymiatane:
elektrony w kierunku kolektora, tworząc prąd zerowy, natomiast dziury w kierunku
bazy. (Na zacisku kolektora prąd jest większy o składową termiczną I

CB0

generowaną w złączu.)

0

+

α

=

CB

E

N

C

I

I

I

(7.6)

Prąd w obwodzie bazy wynosi:

0

CB

pE

rEB

rB

B

I

I

I

I

I

−

+

+

=

(7.7)

I

rB

-

prąd rekombinacyjny w bazie,

I

rEB

-

prąd rekombinacyjny w warstwie zaporowej złacza E-B,

I

pE

-

prąd dyfuzyjny dziur z bazy do emitera.

I

CB0

-

prąd złącza kolektorowego zależny silnie od temperatury; powstaje w
wyniku termicznej generacji nośników w pobliżu złącza i jest rzędu 10

-15

–

10

-14

;

większy w tranzystorach germanowych.

Skorygowane współczynniki wzmocnienia wynoszą odpowiednio:

E

CB

C

N

I

I

I

0

−

=

α

,

(7.8)

0

0

CB

B

CB

C

N

I

I

I

I

+

−

=

β

(7.9)

D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

4

Współczynnik wzmocnienia prądowego α

N

b

e

E

nE

nE

C

E

C

N

I

I

I

I

I

I

α

α

α

⋅

=

⋅

=

=

(7.10)

rEB

pE

nE

nE

E

nE

e

I

I

I

I

I

I

+

+

=

=

α

(7.11)

b

r

r

rB

C

C

nE

C

b

t

I

I

I

I

I

+

τ

τ

=

+

=

=

α

(7.12)

α

e

-

współczynnik sprawności wstrzykiwania emitera określający jaka część
całkowitego prądu emitera stanowi strumień nośników wstrzykniętych do
bazy; po przejściu przez złącze wstrzykujące, prąd I

E

zostaje zmniejszony

α

e

razy.

α

b

-

współczynnik transportu (współczynnik rekombinacji w bazie)
określający, jaka część strumienia elektronów wstrzykniętych do bazy
dochodzi do kolektora (jest zbierana przez kolektor); po przejściu przez
obszar bazy, prąd I

nE

jest mniejszy α

b

razy.

τ

r

-

parametr materiałowy,

t

b

-

czas przelotu

D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

5

7.4. Elementarny model tranzystora jako wzmacniacza dużych sygnałów

Model ma odzwierciedlić poznaną dotychczas, podstawową właściwość
tranzystora jaką jest wzmacnianie. Wspólną końcówką dla schematu typu T (rys.)
dla wejścia i wyjścia jest końcówka bazy.

E

C

I

I

⋅

=

α

(7.13a)

C

B

E

I

I

I

+

=

(7.13b)

Rys.7.4.


Podstawiając

B

C

I

I

⋅

=

β

we wzorach ( 7.13a) i (7.13b), otrzymamy:

E

B

I

I

⋅

=

⋅

α

β

(7.14a)

B

E

I

I

⋅

=

⋅

β

α

(7.15a)

B

B

E

I

I

I

⋅

+

=

β

(7.14b)

(

)

B

E

I

I

⋅

+

=

β

1

(7.15b)

a stąd związek między współczynnikami wzmocnienia prądowego

α

i

β

β

β

α

+

=

1

(7.16)

α

α

β

−

=

1

(7.17)

Podstawiając (7.16) do wzoru (7.13a) otrzymamy po uporządkowaniu równania
opisujące tranzystor w układzie w którym wspólna końcówką jest emiter.

B

C

I

I

⋅

=

β

(7.18a)

C

B

E

I

I

I

+

=

(7.18b)

(7.19)

Rys.7.5. Schemat zastępczy modelu tranzystora bipolarnego dla dużych sygnałów

(Wprowadzić przykład z ALLEY’a str 71)

D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

6

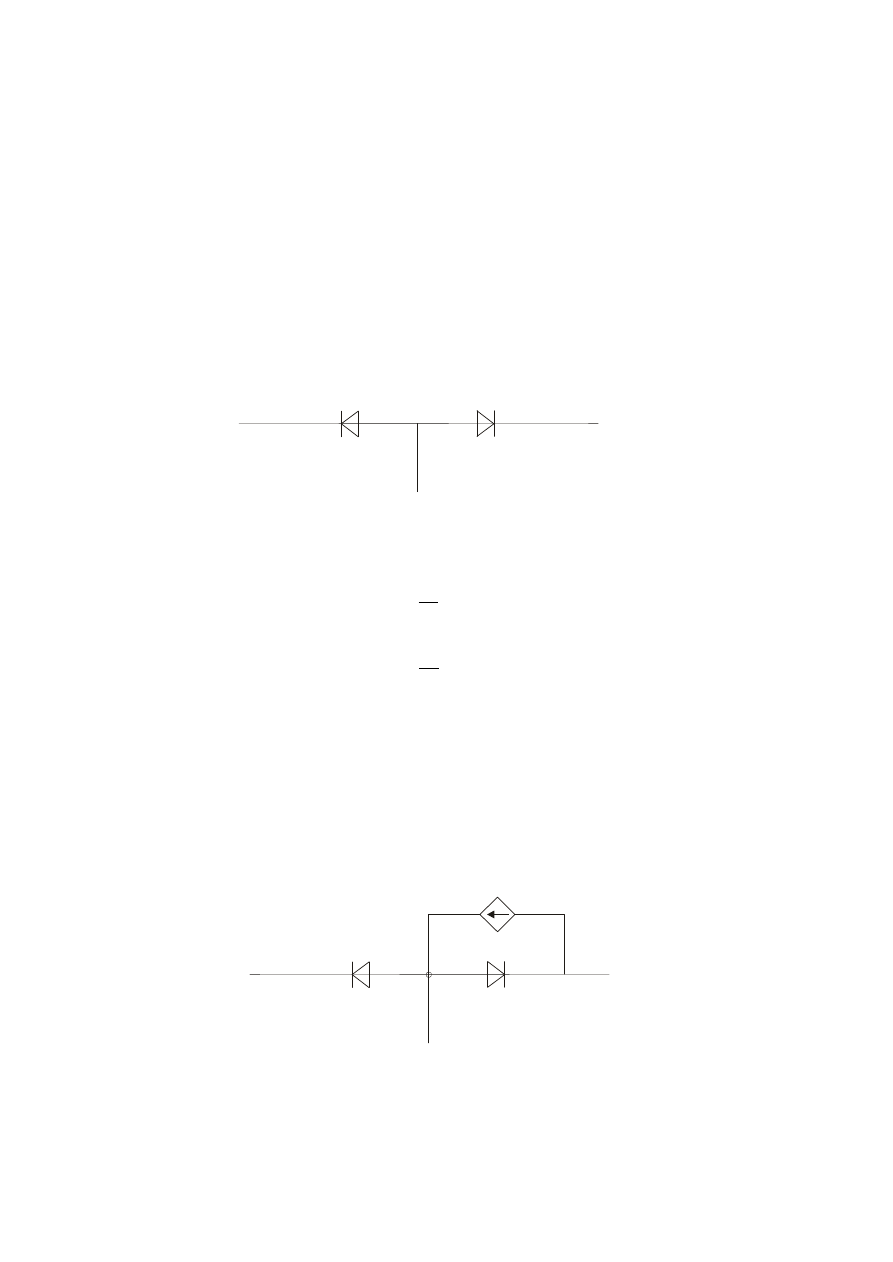
7.5. Modele nieliniowe tranzystora dla dużych sygnałów (wg podstawowych
równań)

Model EBERSA – MOLLA – wariant injekcyjny

Zakres zatkania charakteryzuje brakiem oddziaływania wzajemnego złączy
spolaryzowanych napięciem ujemnym. Przez złącza płyną tylko prądy upływu

DC

C

I

I

−

=

(7.20b)

DE

E

I

I

=

(7.20a)

Rys. 7.6.

Prądy złączy wynoszą odpowiednio:















−

=

1

T

EB

U

ES

DE

e

I

I

ϕ

(7.21a)















−

=

1

T

CB

U

CS

DC

e

I

I

ϕ

(7.21b)

gdzie:

ES

I

,

CS

I

- prądy nasycenia złączy,

EB

U

,

CB

U

- napięcia na złączach.

W zakresie aktywnym normalnym, przez złącze baza-kolektor płynie dodatkowo
prąd nośników wstrzykiwanych przez złącze emiterowe, reprezentowany przez
źródło prądowe, który wynosi:

DE

N

I

⋅

α

,

Rys. 7.7.

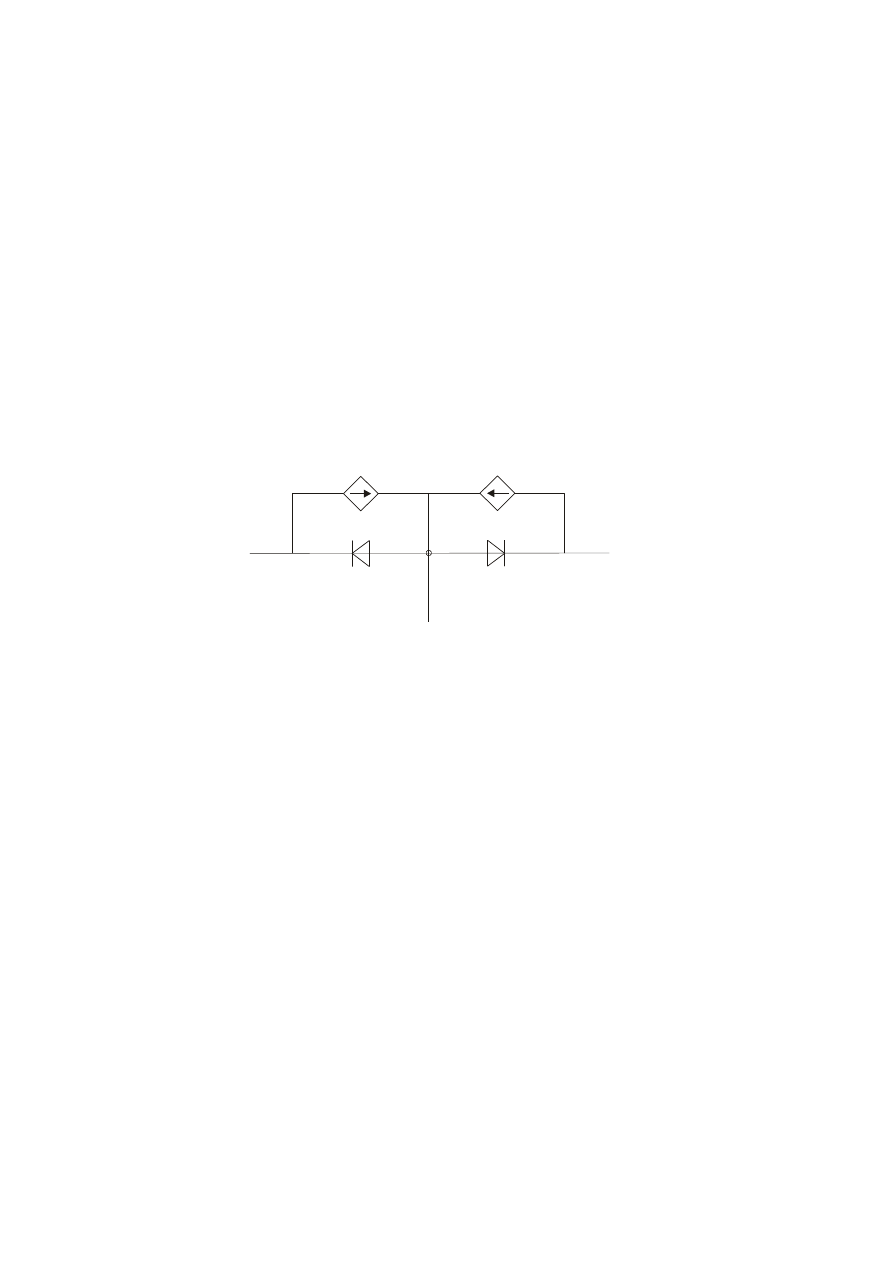
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

7

DE

E

I

I

=

(7.22a),

DC

DE

N

C

I

I

I

−

⋅

=

α

(7.22b)

W zakresie aktywnym nasycenia obydwa złącza mają charakter wstrzykujący.
Oprócz składowych unoszenia, w każdym złączu płynie prąd wstrzykniętych
nośników przez przeciwne złącze. W schemacie zastępczym prądy są
reprezentowane jako źródła prądowe. Ze względu na niesymetrię budowy
tranzystora, rozróżnia się dwa współczynniki wzmocnienia prądowego: w kierunku
normalnym –

N

α

, oraz w kierunku inwersyjnym

I

α

(znacznie mniejsza wartość).

Schemat modelu przedstawiono na rys. 7.8. a opisujące go równania są następujące

Rys.7.8.

DC

I

DE

E

I

I

I

⋅

−

=

α

(7.23a),

DC

DE

N

C

I

I

I

−

⋅

=

α

(7.23b)

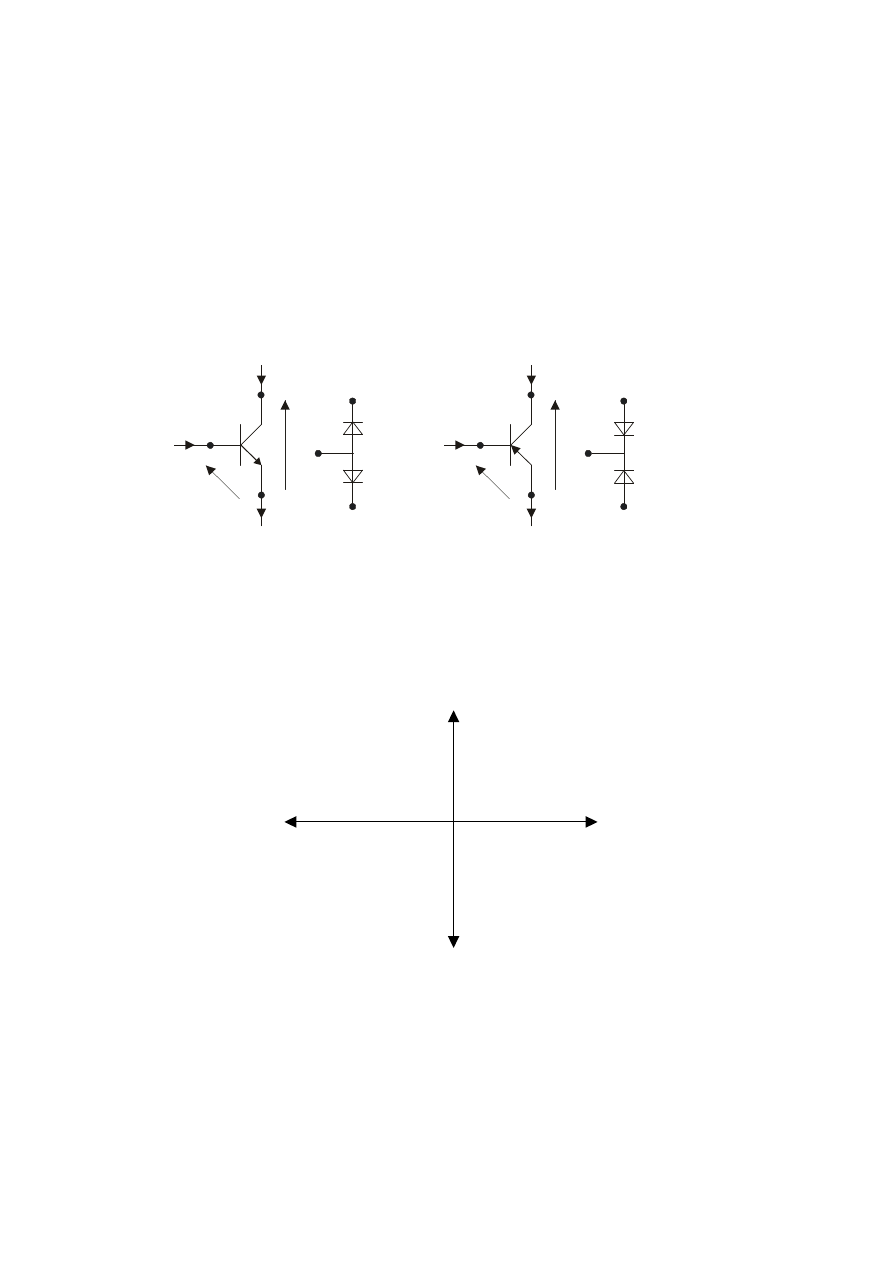
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

8

7.6. Budowa tranzystora

Tranzystor bipolarny (działanie oparte na przewodnictwie obu rodzajów nośników:
elektronów i dziur) jest zbudowany z dwóch złączy PN tworzących strukturę PNP
lub NPN (rys.)











Rys.7.9.



7.7. Zakresy pracy

Rys.7.10.

U

BE

U

BE

U

BC

U

BC

Zakres aktywny

normalny

Zakres

zatkania

Zakres aktywny

nasycenia

Zakres aktywny

inwersyjny

polaryzacja zaporowa

polaryzacja przewodzenia

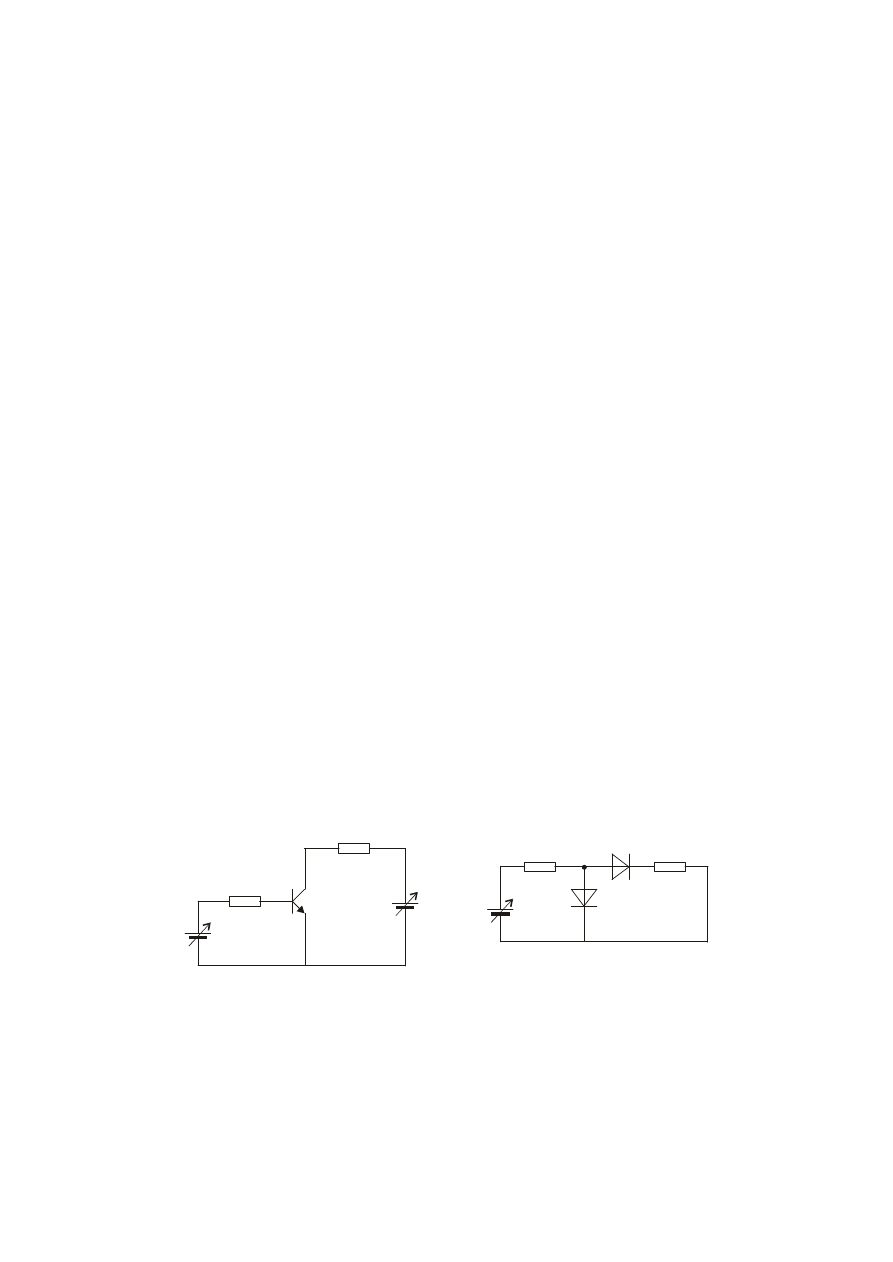
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

9

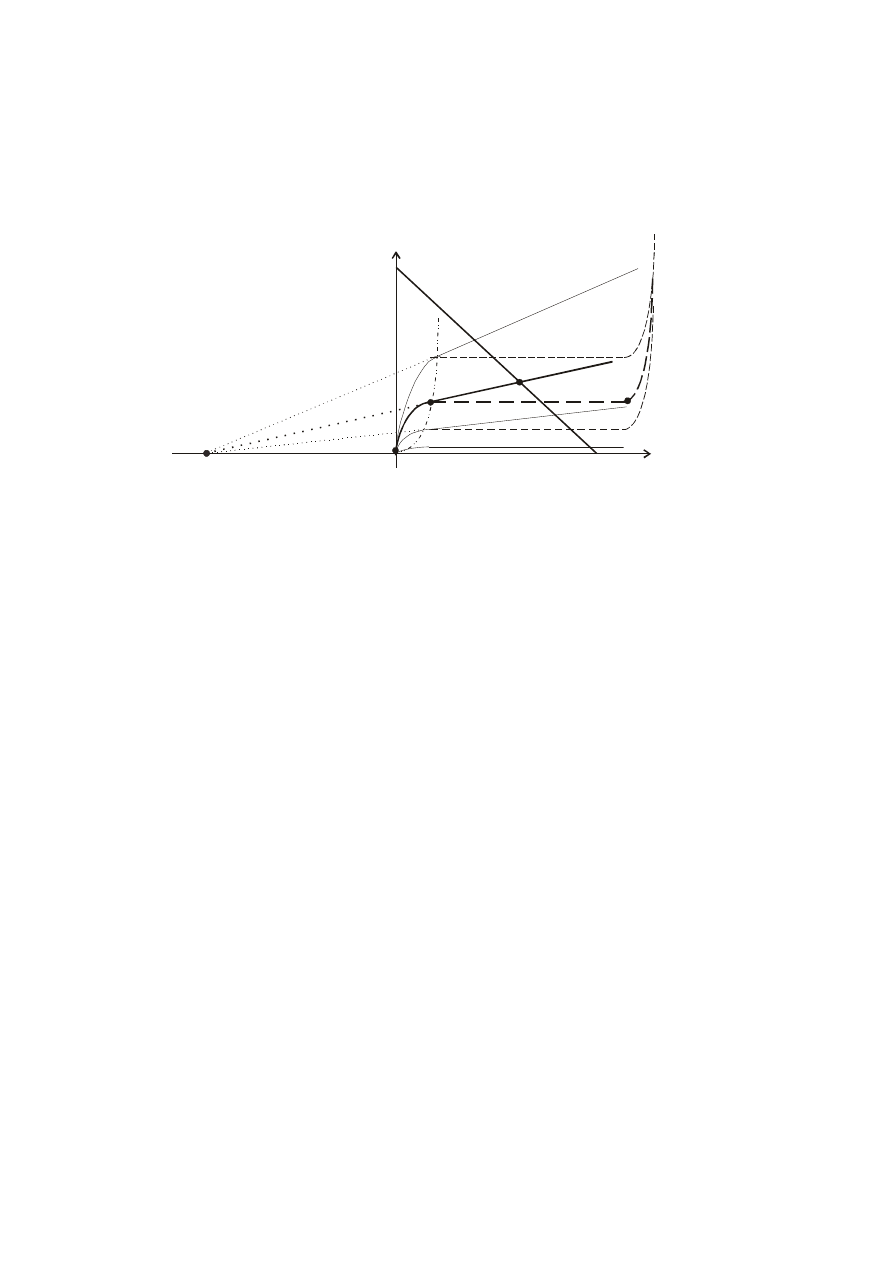
7.8. Charakterystyki statyczne tranzystora

Charakterystyka wyjściowa. Napięcie Earley’a.

Charakterystyki statyczne wejściowa i wyjściowa opisują powiązania
odpowiednich wielkości na wejściu i wyjściu tranzystora.

Prześledźmy drogę punktu pracy Q po charakterystyce wyjściowej.

Zwiększając od zera napięcie U

CC

zasilania tranzystora w układzie przedstawionym

na rys. , przy stałej, dodatniej wartości prądu bazy Q przemieszcza się od A do B.
Obydwa złącza są w stanie przewodzenia (przy potencjale wynoszącym ok. 0,7V i
większym prądzie złącza emiterowego) co oznacza stanie nasycenia tranzystora.

Nasycenie może mieć miejsce przy różnych wartościach prądu

C

I

,

regulowanych wartością prądu bazy zgodnie z poniższą przyczynowością:

↑

B

I

,

↑

C

I

,

↑

C

C

I

R

,

↓

−

=

)

(

C

C

CC

CE

I

R

U

u

gdy

CEsat

CE

U

u

<

( 7.24 )

Powyżej wartości napięcia

V

u

CE

7

,

0

≈

, złącze kolektorowe zostaje

spolaryzowanym wstecznie i następuje przejście tranzystora do pracy aktywnej.
Punkt pracy przemieszcza się od B do C. Jest to zakres pracy aktywnej-normalnej
lub inaczej zakres liniowy. Odcinek B-C powinien leżeć poziomo nad osią
napięcia, opisując stałą wartość prądu kolektora zgodnie z wzorem modelu
idealnego

B

DC

C

I

I

⋅

=

β

. W rzeczywistości ta część charakterystyki jest nachylona

pod kątem, którego wierzchołek wyznacza napięcie Earley’a VA

.

(rys. ).

Dalsze zwiększanie napięcia zasilania obwodu kolektora (punkt Q

przemieszcza się poza odcinkiem B-C) prowadzi do gwałtownego wzrostu prądu i
w konsekwencji przebicia złącza.

Rys.7.11.

D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

10

Rys.7.12.

Charakterystyki prądowo- napięciowe odpowiadające typowym charakterystykom
teoretycznym tranzystora:
-

prąd I

C

zasadniczo nie zależy od napięcia u

CB

, dla ustalonej wartości i

E

, (OB),

-

prąd I

C

zasadniczo nie zależy od napięcia u

CE,

dla ustalonej wartości I

B.

(OE).

Odstępy między krzywymi teoretycznymi na w/w rysunkach są jednakowe dla
jednakowych przyrostów wielkości będącej parametrem ( β ma wartość stałą) co
nie zachodzi w rzeczywistości. W rzeczywistych ch-kach tranzystora obserwujemy
niejednakowe odstępy między charakterystykami; β - nie jest stałe, prąd i

C

nie jest

stały dla ustalonej wartości i

B

lecz wzrasta ze wzrostem napięcia u

CE

.

Charakterystyka wejściowa

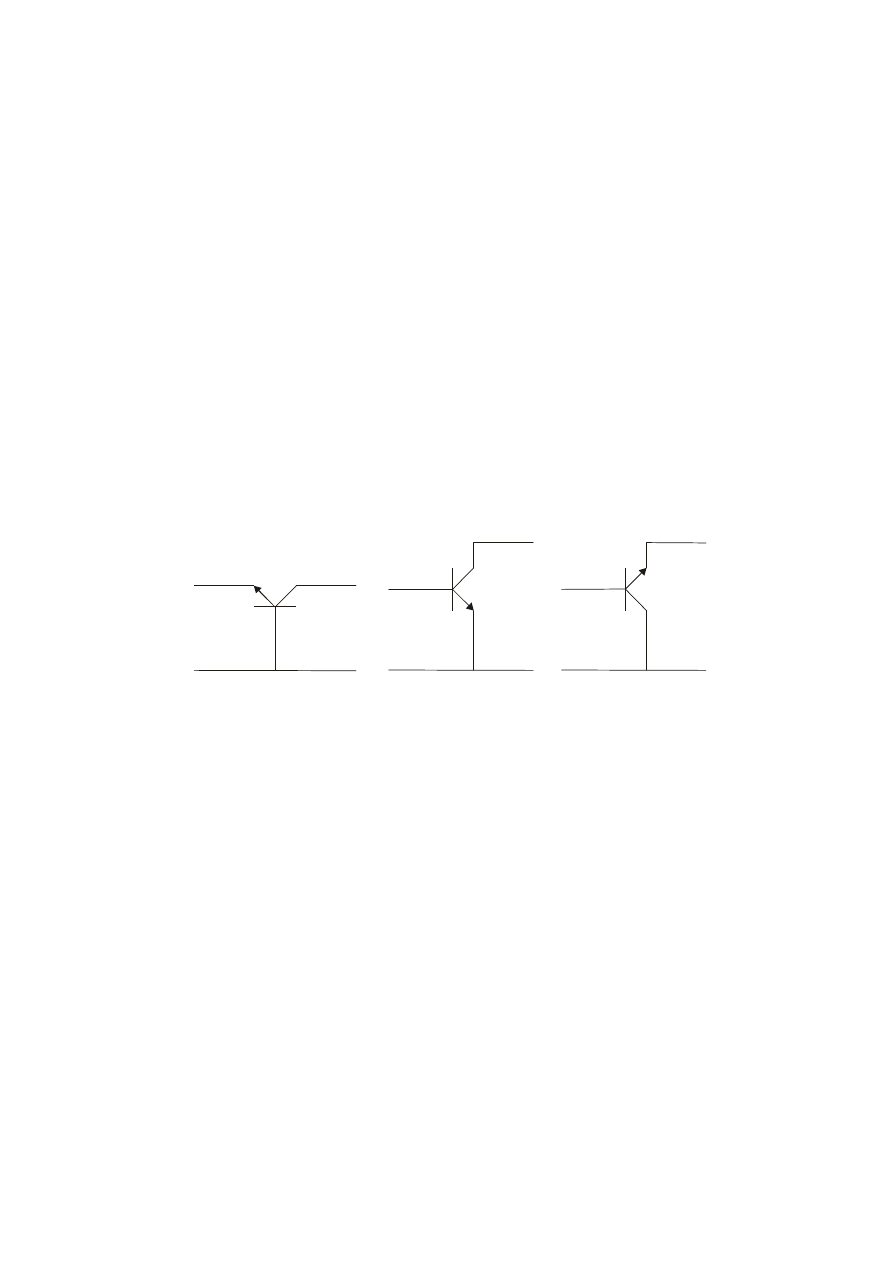
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

11

7.9. Parametry katalogowe tranzystora bipolarnego



7.10. Podstawowe konfiguracje pracy tranzystora jako wzmacniacza

Tranzystor jest elementem trójkońcówkowym. Traktowany jako czwórnik musi
mieć jedną z końcówek wspólną dla wejścia i wyjścia. Dla uzyskania wzmocnienia
mocy jest wymagane by końcówka bazy była jedną z wejściowych a końcówka
kolektora jedną z wyjściowych. Mamy stąd 3 racjonalne konfiguracje o
odmiennych właściwościach i różnych zastosowaniach.











Rys.7.13. Konfiguracje tranzystora jako wzmacniacza

We wszystkich jednak tranzystor na czas trwania sygnału znajduje się w
normalnych warunkach polaryzacji, tj. złącze emiter-baza jest spolaryzowane w
kierunku przewodzenia a złącze kolektor-baza – w kierunku wstecznym (Linv.21)




Podobnie jak dla złącza p-n, rozróżnia się pracę tranzystora:
-

nieliniową: statyczną i dynamiczną,

-

liniową: dla małych sygnałów, małej i dużej częstotliwości

WB
OB

WE
OE

WC
OC

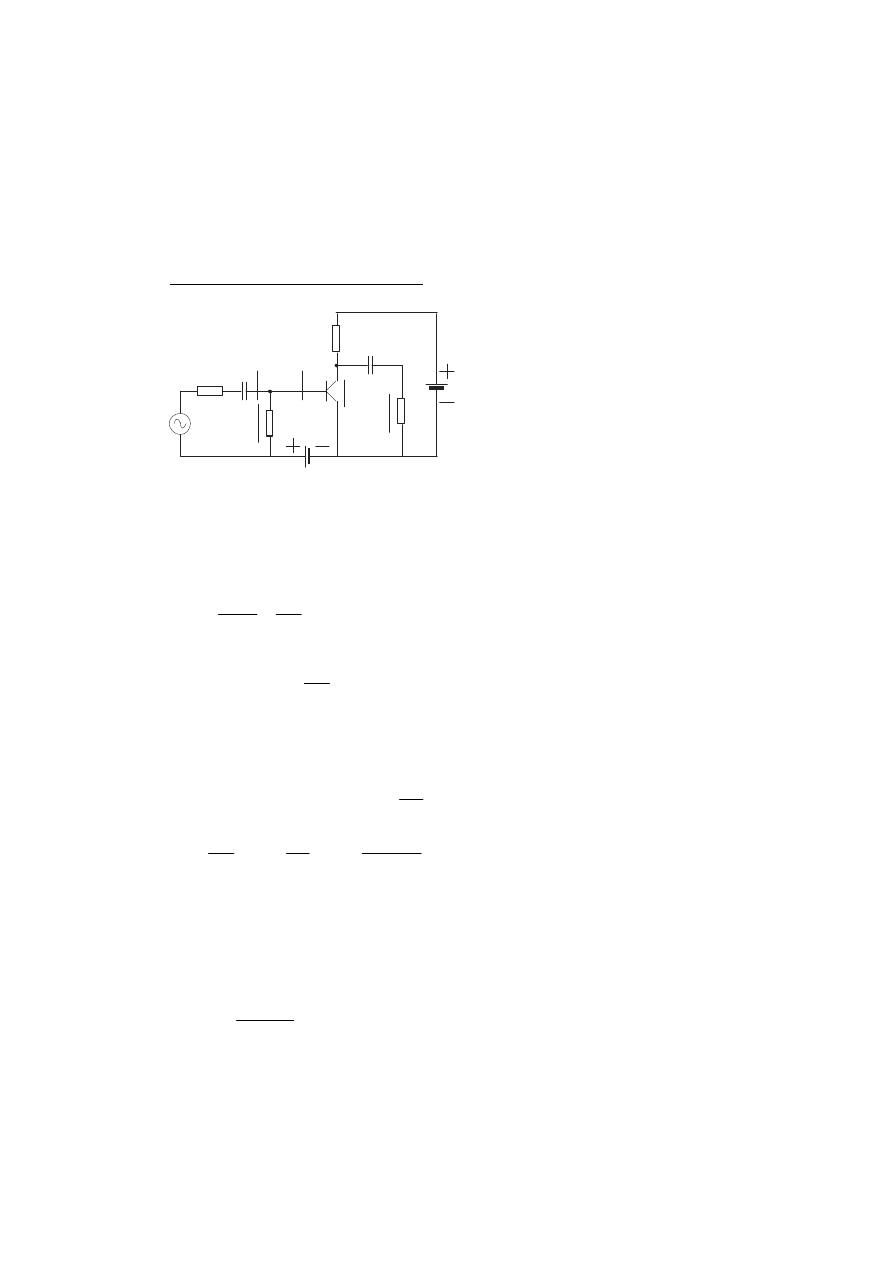
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

12

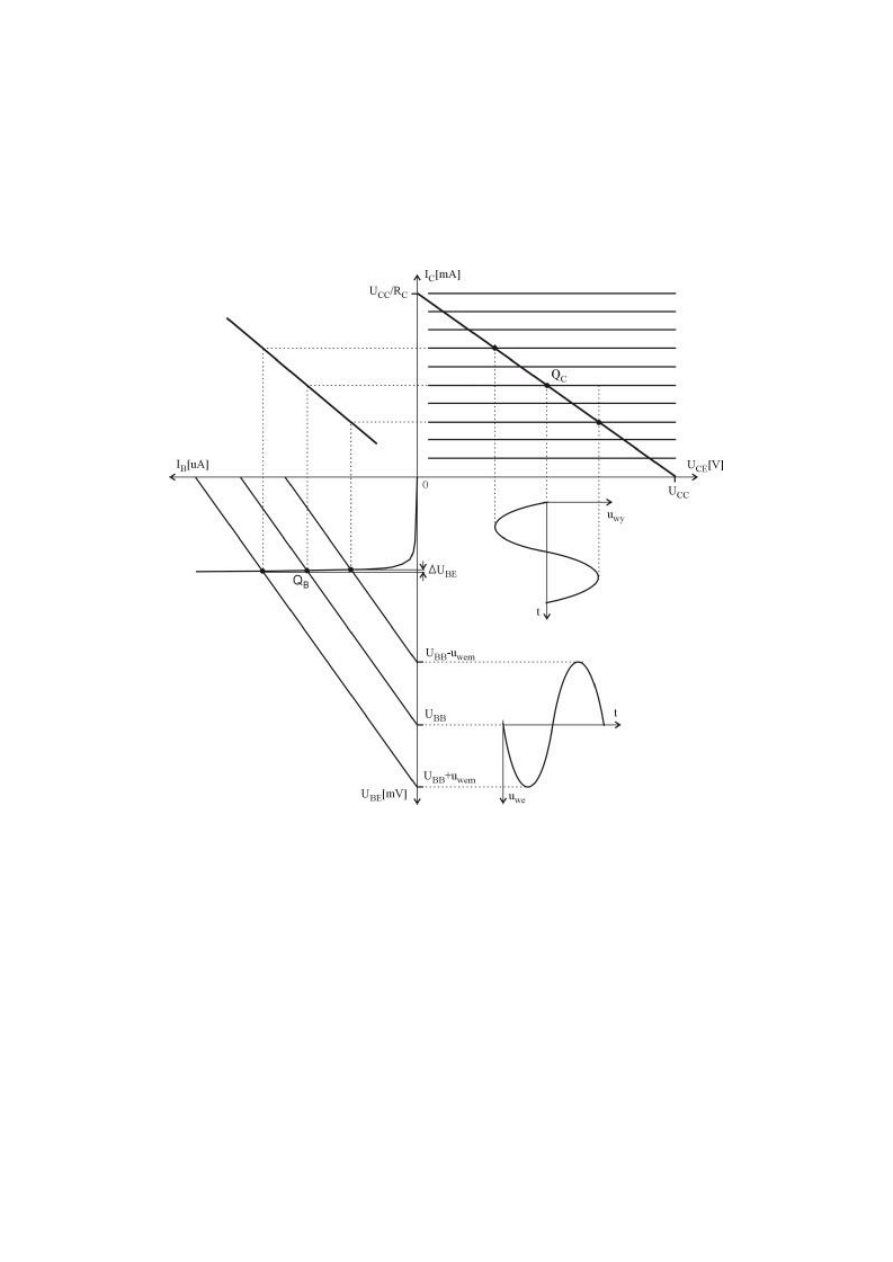
Analiza tranzystora układzie OE

Układ o wspólnym emiterze WE (OE)

Źródła U

CC

, U

BB

polaryzują złącza

tranzystora aby znajdował się on w
stanie aktywnym.
Na wejściu jest podany sygnał
napięciowy (sygnał wzbudzenia) u

we

o małej w wartości w stosunku do
napięcia U

BE

polaryzacji bazy. Sygnał

ten powoduje zmianę prądu bazy.
Zmiana tego prądu (bazy) sprawi

zmianę prądu kolektora a w konsekwencji zmianę sygnału wyjściowego jakim jest
napięcie na zaciskach kolektor-emiter.

Wszystkie te zmiany dzieją się w określonych warunkach pracy tranzystora

zdeterminowanych przez napięcia polaryzacji (zasilania) obwodu wejściowego i
obwodu wyjściowego, tj. w punkcie pracy tranzystora.

be

we

be

BE

B

r

u

r

u

I

=

∆

=

∆

be

we

B

C

r

u

I

I

0

0

β

β

=

∆

=

∆

Równanie obwodu wyjściowego, na podstawie II prawa Kirchhoffa, ma postać:

C

C

C

CE

R

I

E

u

−

=

be

C

we

C

C

CE

wy

r

R

u

R

I

u

u

0

β

−

=

∆

−

=

∆

=

be

CE

C

be

C

we

wy

u

r

r

R

r

R

u

u

k

||

0

0

β

β

−

=

−

=

=

Rezystancja wejściowa

B

be

we

R

r

r

||

=

Rezystancja wyjściowa

C

ce

wy

R

r

r

||

=

Wzmocnienie prądowe

0

0

R

r

r

k

wy

wy

i

+

−

=

β

u

BE

r

be

r

we

u

we

u

wy

u

CE

I

B

I

C

R

B

R

C

R

L

D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

13

Właściwości:

- układ odwraca fazę sygnału wejściowego
- dość duże wzmocnienie: napięciowe, prądowe i mocy
- rezystancja wejściowa umiarkowanie mała
- rezystancja wyjściowa umiarkowanie duża

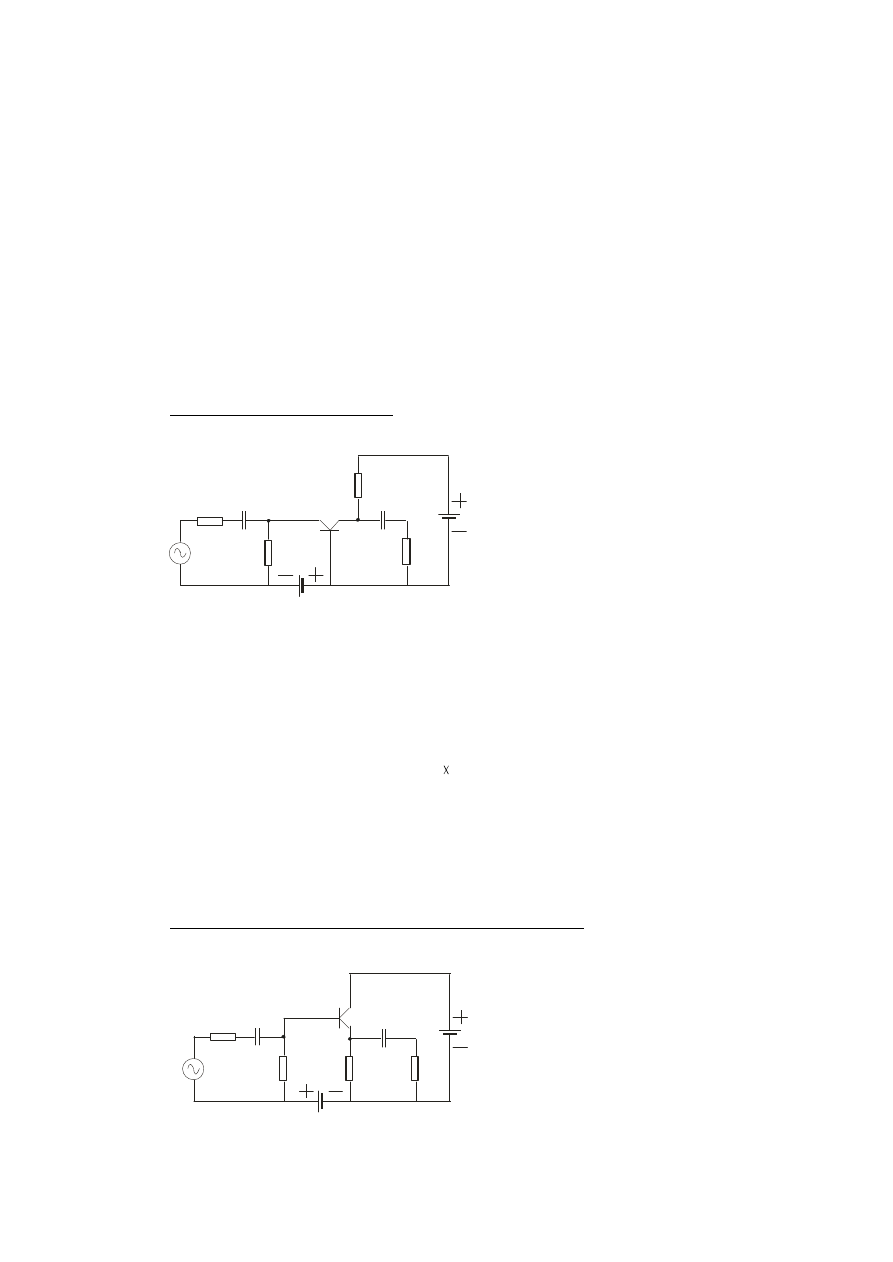
Układ o wspólnej bazie WB (OB)

Prądy i napięcia zawierają składowe
stałe związane z polaryzacją i
nałożone na nie – dużo mniejsze –
składowe

zmienne:

sygnały

użyteczne przenoszone za pomocą
kondensatorów

sprzęgających

(jednocześnie

separujących

składowe stałe od zmiennych). Na
wejściu

jest

podany

sygnał

napięciowy u

we

o małej w wartości w stosunku do napięcia U

EB

polaryzacji bazy

Właściwości:

- układ nie odwraca fazy sygnału wejściowego
- wzmocnienie prądowe nieco mniejsze od 1
- wzmocnienie napięciowe dość duże (podobne jak OE)
- rezystancja wejściowa b. mała; r

we(WE)

/(β+1)

- rezystancja wyjściowa b. duża; (β+1) r

wy(WE)

Stabilność pracy, korzystne właściwości w zakresie w.cz., wada- mała
wartość rezystancji wejściowej
Zastosowanie:

wzmacniacze w.cz.

Układ o wspólnym kolektorze WC (OC) – wtórnik emiterowy

Na wejściu jest podany sygnał
napięciowy u

we

o małej w wartości

w stosunku do napięcia U

BE

polaryzacji bazy Napięcie U

BE

D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

14

baza-emiter zmienia się nieznacznie przy zmianach prądu kolektora i
stąd

WY

BE

WE

u

U

u

=

∆

≈

Właściwości:

- nie odwraca fazy sygnału wejściowego,
- wzmocnienie napięciowe =1 (potencjał emitera nadąża , „wtóruje” za
potencjałem bazy i stąd wtórnik emiterowy)
- wzmocnienie prądowe podobne jak dla OE
- rezystancje wejściowa – duża
- rezystancja wyjściowa - mała
- układ transformuje (przenosi) rezystancję z obwodu emitera do obwodu bazy
jako (β+1) razy większą, natomiast rezystancję z obwodu bazy przenosi do
obwodu emitera jako rezystancję (β+1) razy mniejszą – transformator
rezystancji.

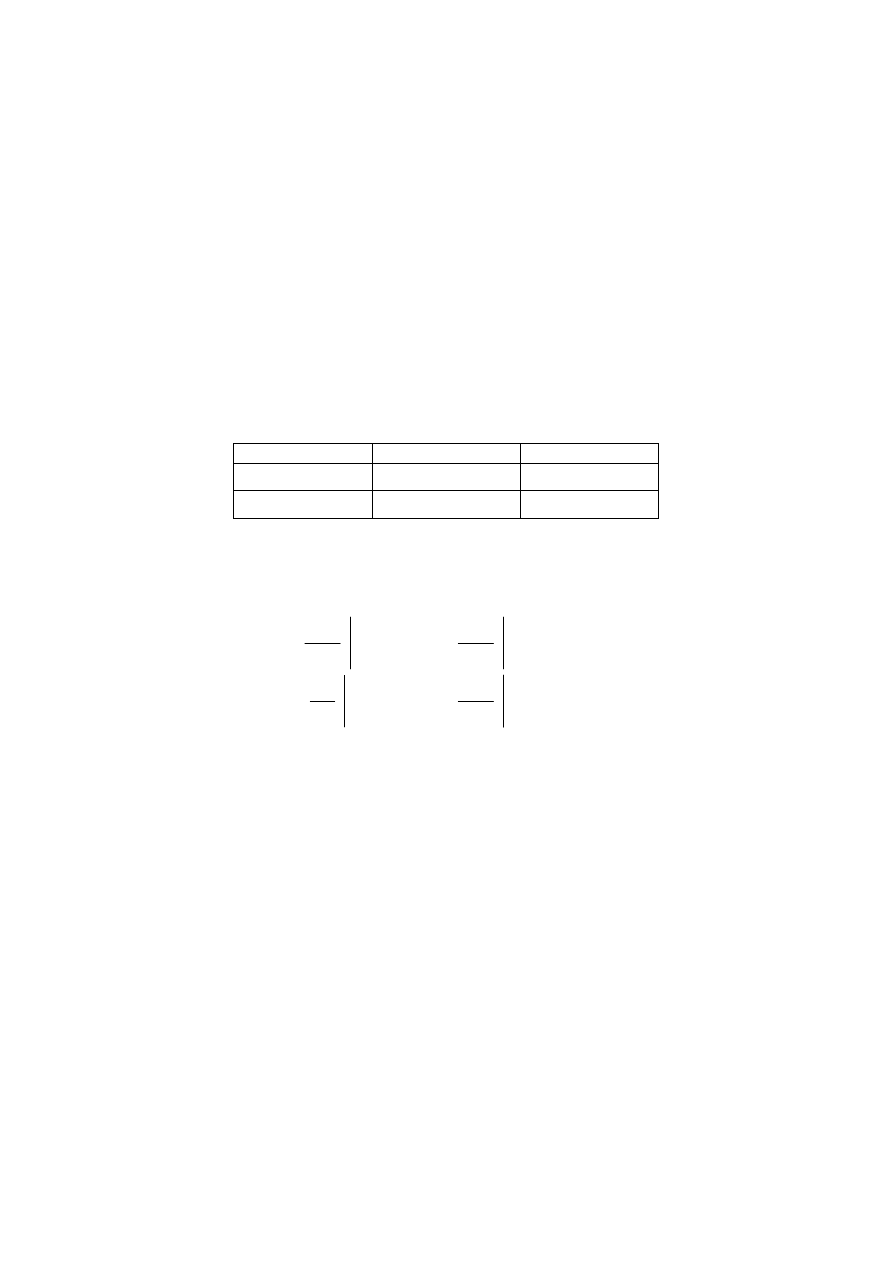
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

15

7.11. Modele liniowe tranzystora dla małych sygnałów

Model opisujący właściwości tranzystora przy niewielkich zmianach punktu pracy,
oznaczających małe sygnały wymuszające - jest liniowy. Spośród parametrów
zaciskowych czwórnika reprezentującego taki model tranzystora, wybiera się dwie
wielkości wyjściowe jako funkcje pozostałych dwóch wielkości tj. wejściowych.

Modele o parametrach mieszanych

Czwórnik o parametrach mieszanych będzie opisany układem równań stosownym
do układu pracy tranzystora jak podano w tablicy.

OB

OE

OC

)

,

(

CB

E

EB

u

i

f

u

=

)

,

(

CE

B

BE

u

i

f

u

=

)

,

(

EC

B

BC

u

i

f

u

=

)

,

(

CB

E

C

u

i

f

i

=

)

,

(

CE

B

C

u

i

f

i

=

)

,

(

EC

B

E

u

i

f

i

=

Rozpatrując niewielkie (przyrostowe) zmiany wielkości wyjściowych w wyniku
określonych zmian wielkości wejściowych, dla układu OE otrzymuje się
następujący układ równań:

CE

i

CE

C

B

u

B

C

C

CE

i

CE

BE

B

u

B

BE

BE

u

u

i

i

i

i

i

u

u

u

i

i

u

u

B

CE

B

CE

∆

⋅









∂

∂

+

∆

⋅









∂

∂

=

∆

∆

⋅









∂

∂

+

∆

⋅









∂

∂

=

∆

(7.25)

Zastępując przyrosty niewielkimi sygnałami

be

BE

u

u

=

∆

,

ce

CE

u

u

=

∆

,

b

B

i

i

=

∆

,

c

C

i

i

=

∆

,

Otrzymuje się następujący układ równań opisujący czwórnik o parametrach
mieszanych:

ce

e

b

e

c

ce

e

b

e

be

u

h

i

h

i

u

h

i

h

u

⋅

+

⋅

=

⋅

+

⋅

=

22

21

12

11

(7.26)

którego parametry oznaczają odpowiednio:

D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

16

CE

u

B

BE

e

i

u

h









∂

∂

=

11

,

B

i

CE

BE

e

u

u

h









∂

∂

=

12

,

CE

u

B

C

e

i

i

h









∂

∂

=

21

,

B

i

CE

C

e

u

i

h









∂

∂

=

22

.

Opis czwórnikowy tranzystora dla pozostałych układów pracy OB i OC
wyprowadza się w sposób analogiczny jak przedstawiony wyżej dla OE.




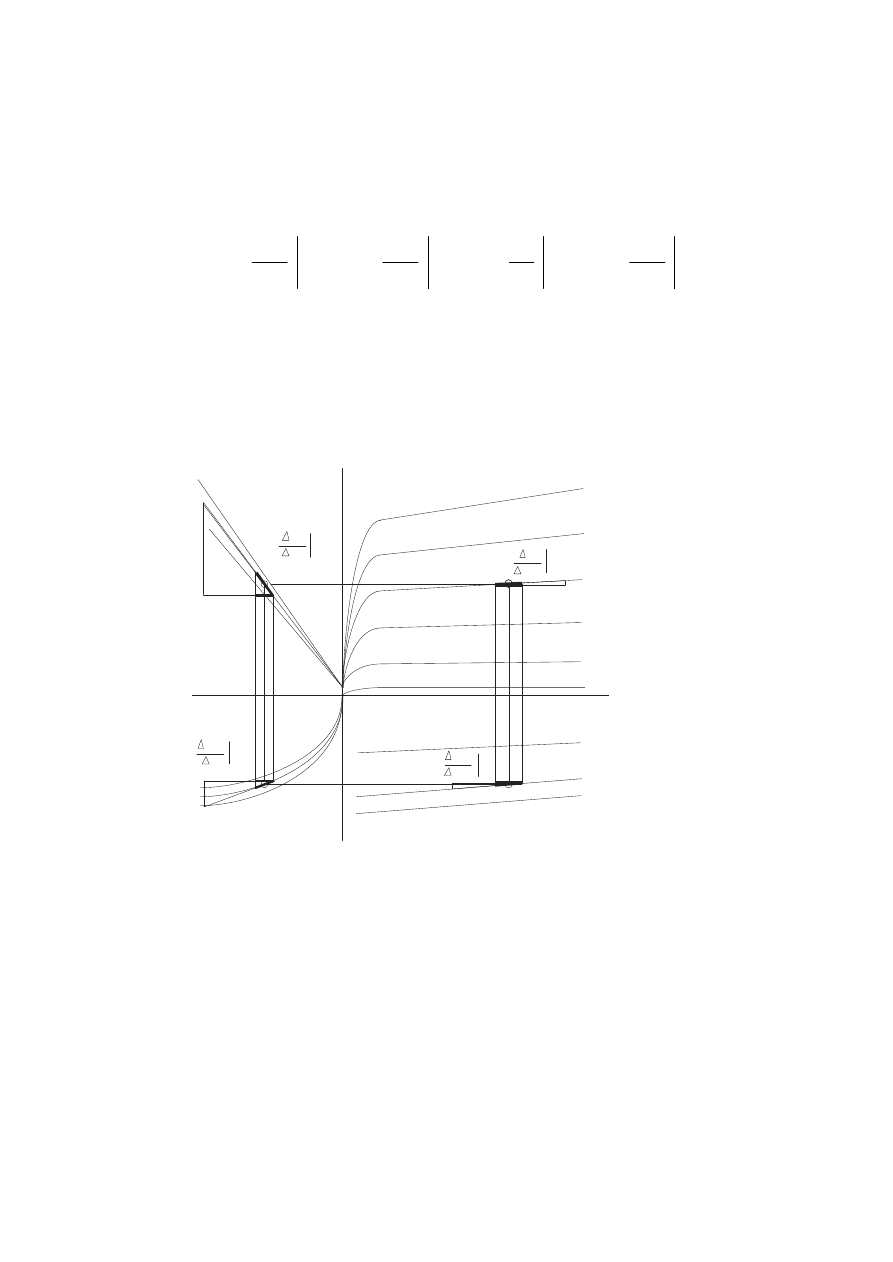
7.12. Wyznaczanie parametrów czwórnikowych, mieszanych, na podstawie
charakterystyk statycznych

I

C

U

CE

U

BE

I

B

h =

21

I

B

I

C

U

CE

U

CE

I

B

U

BE

h =

11

I

B

U

BE

U

CE

h =

12

I

C

U

CE

h =

22

I

B

Rys. 7.14.

Schemat modelu

D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

17

Parametry mieszane w różnych konfiguracjach

Parametr

OE

OB

OC

11

h

e

h

11

e

e

e

e

h

h

h

h

12

21

11

1

−

∆

+

+

e

h

11

12

h

e

h

12

e

e

e

e

e

h

h

h

h

h

12

21

12

1

−

∆

+

+

−

∆

e

h

12

1

−

21

h

e

h

21

(

)

e

e

e

e

e

h

h

h

h

h

12

21

21

1

−

∆

+

+

+

∆

−

)

1

(

21e

h

+

−

22

h

e

h

22

e

e

e

e

h

h

h

h

12

21

22

1

−

∆

+

+

e

h

22

e

h

∆

e

e

e

e

h

h

h

h

21

12

22

11

−

ez

h

e

e

e

h

h

h

12

21

1

−

∆

+

+

b

h

∆

b

b

b

b

h

h

h

h

21

12

22

11

−

11

h

- rezystancja wejściowa,

12

h

- wsp. sprzężenia napięciowego

21

h

- wsp. wzmocnienia prądowego,

22

h

- konduktancja wyjściowa

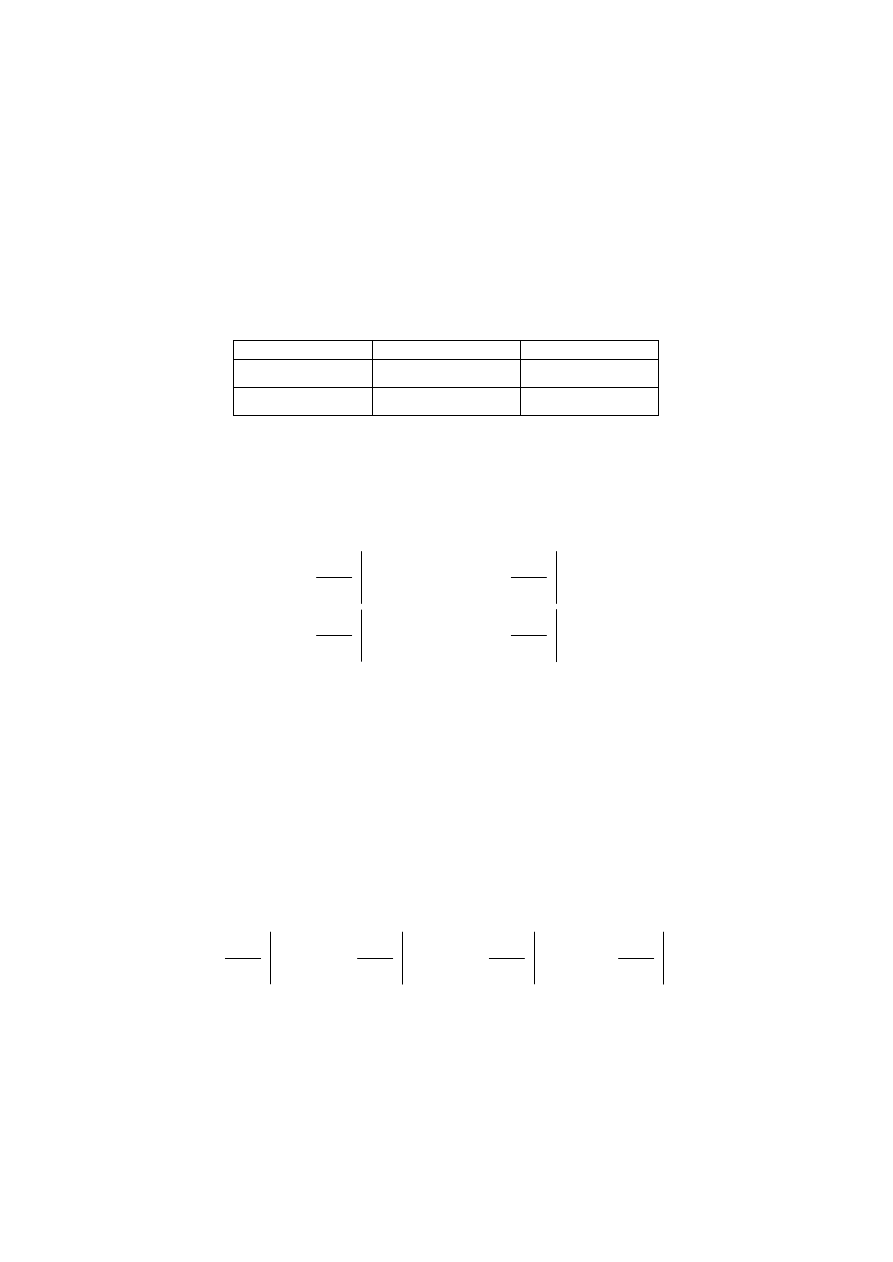
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

18

7.13.Modele o parametrach admitancyjnych

OB

OE

OC

)

,

(

CB

BE

B

u

u

f

i

=

)

,

(

CE

BE

B

u

u

f

i

=

)

,

(

EC

BC

B

u

u

f

i

=

)

,

(

CB

BE

C

u

u

f

i

=

)

,

(

CE

BE

C

u

u

f

i

=

)

,

(

EC

BC

C

u

u

f

i

=

Rozpatrując niewielkie (przyrostowe) zmiany wielkości wyjściowych w wyniku
określonych zmian wielkości wejściowych, dla układu OE otrzymuje się
następujący układ równań:

CE

const

u

CE

C

BE

const

u

BE

C

C

CE

const

u

CE

B

BE

const

u

BE

B

B

u

u

i

u

u

i

i

u

u

i

u

u

i

i

BE

CE

BE

CE

∆

⋅









∂

∂

+

∆

⋅









∂

∂

=

∆

∆

⋅









∂

∂

+

∆

⋅









∂

∂

=

∆

=

=

=

=

Zastępując przyrosty niewielkimi sygnałami

b

B

i

i

=

∆

,

c

C

i

i

=

∆

,

be

BE

u

u

=

∆

,

ce

CE

u

u

=

∆

,

Otrzymuje się następujący układ równań opisujący czwórnik o parametrach
mieszanych:

ce

e

be

e

c

ce

e

be

e

b

u

y

u

y

i

u

y

u

y

i

⋅

+

⋅

=

⋅

+

⋅

=

22

21

12

11

( )

którego parametry oznaczają odpowiednio:

CE

u

BE

B

e

u

i

y









∂

∂

=

11

,

BE

u

CE

B

e

u

i

y









∂

∂

=

12

,

CE

u

BE

C

e

u

i

y









∂

∂

=

21

,

BE

u

CE

C

e

u

i

y









∂

∂

=

22

.

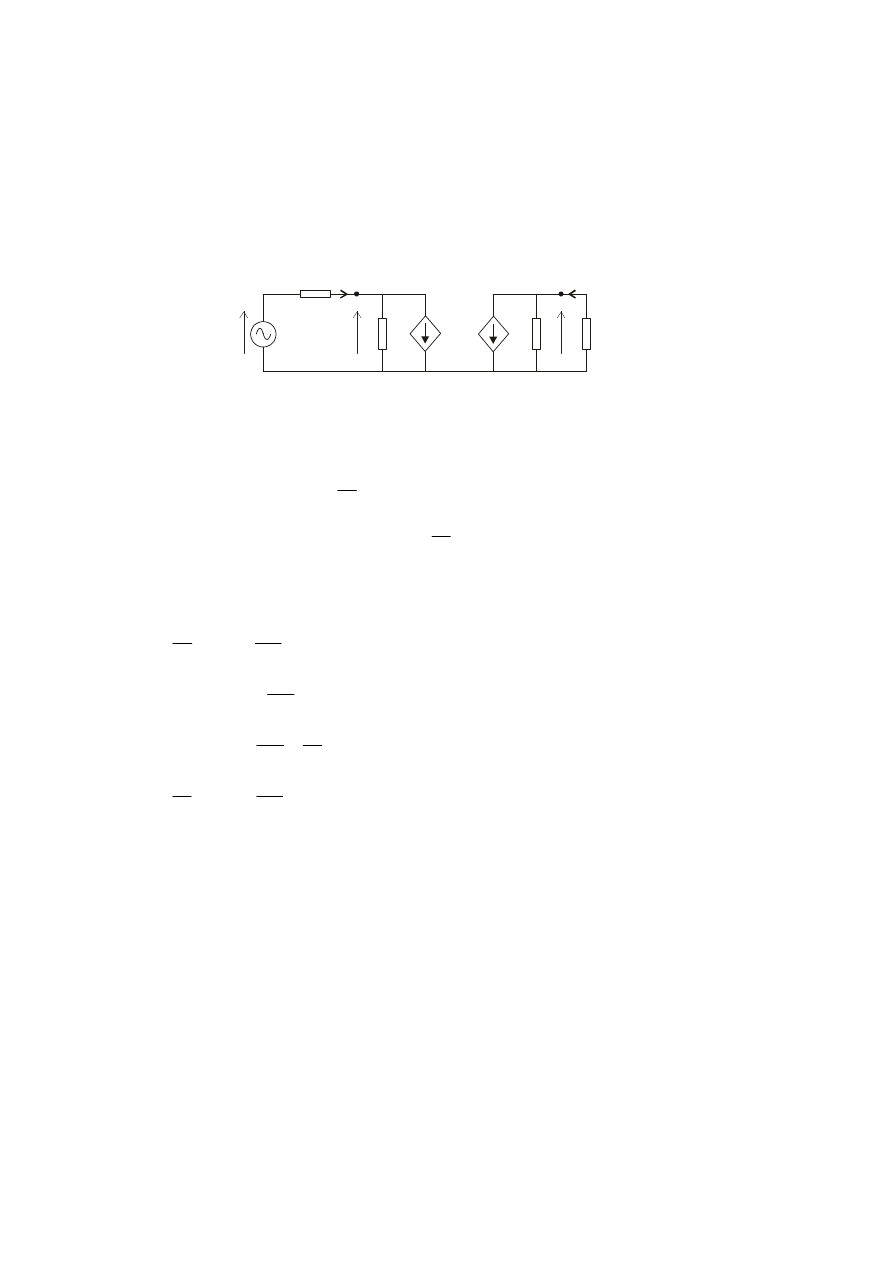
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

19

ce

ce

be

m

c

ce

w

be

be

b

u

r

u

g

i

u

g

u

r

i

⋅

+

⋅

=

⋅

+

⋅

=

1

1

( )

e

e

be

h

y

r

11

11

1

1

=

=

0

11

12

12

≈

−

=

=

e

e

e

w

h

h

y

g

(oddziaływanie zwrotne często pomijane w obliczeniach)

be

e

e

e

m

r

h

h

y

g

β

=

=

=

11

21

21

- transkonduktancja lub konduktancja wprzód,

e

e

e

e

e

e

e

ce

h

h

h

h

h

h

y

r

22

12

21

22

11

11

22

)

(

1

1

≈

−

=

=

D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

20

Pomiary parametrów modelu liniowego

•

g

m

– transkonduktancja - najważniejszy parametr modelu - można wyznaczyć na

podstawie ch-ki przejściowej; parametr w zasadzie nie zależy od indywidualnych
właściwości tranzystora









≈

T

BE

CS

C

u

I

i

ϕ

exp

mV

i

i

u

I

u

i

g

C

T

C

T

BE

CS

T

u

BE

C

m

CE

25

exp

1

|

≈

=









⋅

=

∂

∂

=

ϕ

ϕ

ϕ

•

rezystancja wyjściowa na schemacie zastępczym reprezentuje rezystancję
zastępczą dla małych sygnałów, którą można wyznaczyć na podstawie
charakterystyk statycznych wyjściowych; jest odwrotnościa przewodności
wyjściowej

C

CE

Y

C

C

u

C

CE

ce

ce

I

u

U

I

U

i

u

g

r

BE

+

=

∆

∆

=

∂

∂

=

=

|

1

gdzie U

Y

– jest tzw. napięciem Early’ego.

Wyznaczane z pomiarów r

ce

typowe wartości U

Y

≈ 80....200V (dla NPN) i

40....150V (dla PNP)

•

Rezystancja wejściowa dla małych sygnałów widziana z zacisków
wejściowych.

Praktycznie wyznacza się na podstawie znanej transkonduktancji g

m

.

C

T

m

C

BE

U

B

BE

be

I

g

i

u

i

u

r

const

CE

ϕ

β

β

β

⋅

=

=









∂

∂

=

∂

∂

=

=

|

•

transkonduktancja zwrotna (oddziaływanie zwrotne )

BE

u

CE

B

w

u

i

g

|

∂

∂

=

0

>

w

g

- przy małych prądach;

0

<

w

g

- przy dużych prądach;

4

10

−

<

w

g

Przy małych częstotliwościach oddziaływanie wsteczne jest do pominięcia.

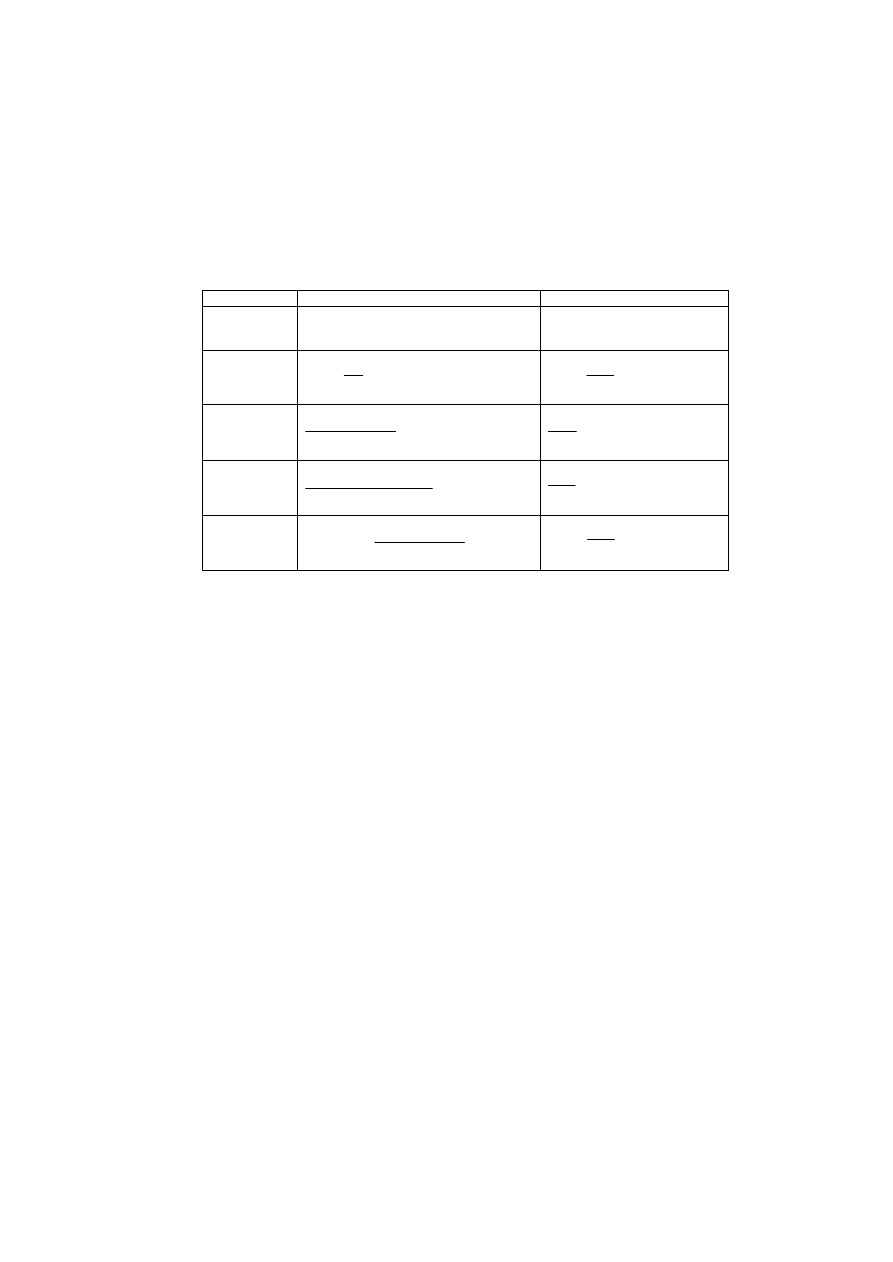
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

21

Ze zwiększaniem się częstotliwości natomiast – rośnie.

Dokładne (słuszne dla w.cz.)

Przybliżone (słuszne dla m.cz.

oraz gdy

e

b

cb

g

g

'

'

<<

)

e

h

11

w

bb

Y

r

1

'

+

e

b

bb

g

r

'

'

1

+

e

h

12

w

jc

cb

Y

C

j

g

ω

+

'

0

'

'

≈

e

b

cb

g

g

e

h

21

w

jc

cb

m

Y

C

j

g

g

ω

−

−

'

β

=

e

b

m

g

g

'

e

h

22

w

jc

cb

m

ce

Y

C

j

g

g

g

ω

+

⋅

+

'

'

'

cb

e

b

m

ce

g

g

g

g

⋅

+

)

(

'

'

jc

je

de

cb

e

b

w

C

C

C

j

g

g

Y

+

+

+

+

=

ω

D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

22

Małosygnałowe właściwości podstawowych układów pracy tranzystora






Sposób wyznaczania parametrów h tranzystora w punkcie pracy Q

11

α

=

11

tg

h

12

α

=

12

tg

h

21

α

=

21

tg

h

22

α

=

22

tg

h

6

B

4

B

6

BE

4

BE

0

U

B

BE

)

6

,

4

(

e

11

I

I

U

U

I

U

h

CE

-

-

=

=

=

∆

∆

∆

5

CE

4

CE

5

BE

4

BE

0

I

CE

BE

)

5

,

4

(

e

12

U

U

U

U

U

U

h

B

−

−

=

=

=

∆

∆

∆

1

B

2

B

1

C

2

C

0

U

B

C

)

1

,

2

(

e

21

I

I

I

I

I

I

h

CE

−

−

=

=

=

∆

∆

∆

1

CE

3

CE

1

C

3

C

0

I

CE

C

)

1

,

3

(

e

22

U

U

I

I

U

I

h

B

−

−

=

=

=

∆

∆

∆

D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY

BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic

J.Piłaciński: Elektronika – materiały pomocnicze do wykładu

23