D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
7.TRANZYSTOR BIPOLARNY - szkic do wykładu
7.1. Efekt tranzystorowy
Rozpływ prądów w strukturze n-p-n, przy polaryzacji złącza E-B w kierunku przewodzenia a złącza B-C w kierunku zaporowym:
-
z emitera do bazy są wstrzykiwane elektrony
-
w obszarze bazy elektrony dyfundują w kierunku złącza B-C
-
po przejściu przez bazę, elektrony zostają uniesione przez przez pole
elektroczne złącza (wymiecione z obszaru złącza) B-C do obszaru kolektora.
Strumień elektronów wstrzykniętych z emitera do bazy tworzy prąd emitera w obwodzie wejściowym. Strumień elektronów odbieranych przez kolektor tworzy prąd kolektora i jednocześnie jest prądem wyjściowym
Rys.7.1.
Przy przyjętych uproszczeniach prąd kolektora jest równy prądowi emitera. Zależy on wyłącznie od napięcia polaryzującego złącze B-E. Można zapisać:
IC = IE
Zatem współczynnik wzmocnienia prądowego dla prądu stałego wynosi:
I
α = C = 1
(7.1)
N
IE
podobnie wzmocnienie dla małych przyrostów wynosi
Δ I
α =
C = 1
(7.2)
N
Δ IE
Skoro prąd wejściowy jest taki sam jak prąd wyjściowy, to jak to się ma do wzmacniania mocy?
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
1
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
7.2. Tranzystor jako wzmacniacz mocy.
Rys.7.2.
Obydwa złącza tranzystora są spolaryzowane napięciem stałym: emiterowe -
dodatnim a kolektorowe ujemnym; w obwodzie wejściowym jest źródło małego sygnału sinusoidalnego eg
Wartość chwilowa mocy dostarczanej na wejściu tranzystora:
P
i 2
= r
(7.3)
we
em we
Moc odbierana przez odbiornik RL
P
i 2
= R
(7.4)
wy
cm
L
Spełnienie warunku dopasowania (równości) rezystancji wyjściowej rwy z
rezystancją odbiornika RL daje maksymalną moc oddaną do odbiornika
rwy = RL
Współczynnik wzmocnienia mocy wynosi:
2
2
i R
i r
r
cm
L
cm wy
wy
k
2
=
=
= α
(7.5)
P
i 2 r
i 2 r
r
em we
em we
we
Gdy α=1, kP = rwy / rwe
Rezystancja wejściowa rwe jest mała i równa rezystancji diody (patrz: ):
ϕ
ϕ
r
a r
,
wy → ∞
we =
m
r
T
d
+ R ≈ T
s
≈ 26 mV = Ω
25
I
I
1 mA
Rezystancja wyjściowa rwy, którą stanowi wstecznie spolaryzowane złącze jest bardzo duża i wynosi od kilkuset do kilku tysięcy omów. Stosunek rwy / rwe we wzorze (7.5) wynosi kilka tysięcy, zatem wzmocnienie mocy tranzystora a tym samym także wzmocnienie napięciowe, przy α ≈
N
1 jest duże. Tranzystor jest
rzeczywiście transformatorem rezystancji trans-re-sistorem i wzmacniaczem mocy. Tranzystor spełnia funkcje elementu czynnego i może służyć do liniowego
wzmacniania sygnałów elektrycznych. Rys.7.2.
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
2
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
7.3. Dokładny model zjawisk w tranzystorze bipolarnym.
Rys.7.3.
Rzeczywisty prąd kolektora zawiera składową generowaną w złączu C-B.
Generowane termicznie pary elektron-dziura, w wyniku silnego pola są wymiatane: elektrony w kierunku kolektora, tworząc prąd zerowy, natomiast dziury w kierunku bazy. (Na zacisku kolektora prąd jest większy o składową termiczną ICB0
generowaną w złączu.)
I = α I + I
(7.6)
C
N E
CB 0
Prąd w obwodzie bazy wynosi:
I = I
+ I
+ I − I
(7.7)
B
rB
rEB
pE
CB 0
IrB -
prąd rekombinacyjny w bazie,
IrEB -
prąd rekombinacyjny w warstwie zaporowej złacza E-B,
IpE -
prąd dyfuzyjny dziur z bazy do emitera.
ICB0-
prąd złącza kolektorowego zależny silnie od temperatury; powstaje w
wyniku termicznej generacji nośników w pobliżu złącza i jest rzędu 10-15 –
10-14;
większy w tranzystorach germanowych.
Skorygowane współczynniki wzmocnienia wynoszą odpowiednio:
I − I
C
CB 0
α =
,
(7.8)
N
IE
I − I
C
CB 0
β =
(7.9)
N
I + I
B
CB 0
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
3
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
Współczynnik wzmocnienia prądowego αN
I
I
I
C
C
nE
α =
=
⋅
= α ⋅ α
(7.10)
N
e
b
I
I
I
E
nE
E
I
I
nE
nE
α =
=
(7.11)
e
I
I
+ I
+ I
E
nE
pE
rEB
I
I
τ
C
C
r
α =
=
=
(7.12)
b
I
I + I
τ + t
nE
C
rB
r
b
αe -
współczynnik sprawności wstrzykiwania emitera określający jaka część
całkowitego prądu emitera stanowi strumień nośników wstrzykniętych do
bazy; po przejściu przez złącze wstrzykujące, prąd IE zostaje zmniejszony αe razy.
αb -
współczynnik transportu (współczynnik rekombinacji w bazie)
określający, jaka część strumienia elektronów wstrzykniętych do bazy
dochodzi do kolektora (jest zbierana przez kolektor); po przejściu przez obszar bazy, prąd InE jest mniejszy αb razy.
τr -
parametr materiałowy,
tb -
czas przelotu
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
4
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
7.4. Elementarny model tranzystora jako wzmacniacza dużych sygnałów
Model ma odzwierciedlić poznaną dotychczas, podstawową właściwość
tranzystora jaką jest wzmacnianie. Wspólną końcówką dla schematu typu T (rys.) dla wejścia i wyjścia jest końcówka bazy.
I
= α ⋅ I
(7.13a)
C
E
I
= I + I
(7.13b)
E
B
C
Rys.7.4.
Podstawiając I = β ⋅ I we wzorach ( 7.13a) i (7.13b), otrzymamy: C
B
β ⋅ I = α ⋅ I
(7.14a)
α ⋅ I = β ⋅ I
(7.15a)
B
E
E
B
I = I + β ⋅ I
(7.14b)
I = 1 + β ⋅ I
(7.15b)
E
(
)
E
B
B
B
a stąd związek między współczynnikami wzmocnienia prądowego α i β
β
α =
α
(7.16)
β =
(7.17)
1 + β
1 − α
Podstawiając (7.16) do wzoru (7.13a) otrzymamy po uporządkowaniu równania opisujące tranzystor w układzie w którym wspólna końcówką jest emiter.
I
= β ⋅ I
(7.18a)
C
B
I
= I + I
(7.18b)
E
B
C
(7.19)
Rys.7.5. Schemat zastępczy modelu tranzystora bipolarnego dla dużych sygnałów
(Wprowadzić przykład z ALLEY’a str 71)
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
5
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
7.5. Modele nieliniowe tranzystora dla dużych sygnałów (wg podstawowych równań)
Model EBERSA – MOLLA – wariant injekcyjny
Zakres zatkania charakteryzuje brakiem oddziaływania wzajemnego złączy
spolaryzowanych napięciem ujemnym. Przez złącza płyną tylko prądy upływu
I
= − I
(7.20b)
I
= I
(7.20a)
C
DC
E
DE
Rys. 7.6.
Prądy złączy wynoszą odpowiednio:
U
EB
ϕT
I
I
e
(7.21a)
DE =
ES
− 1
U
CB
ϕT
I
I
e
(7.21b)
DC =
CS
− 1
gdzie: I
, I
- prądy nasycenia złączy,
ES
CS
U
, U
- napięcia na złączach.
EB
CB
W zakresie aktywnym normalnym, przez złącze baza-kolektor płynie dodatkowo prąd nośników wstrzykiwanych przez złącze emiterowe, reprezentowany przez źródło prądowe, który wynosi: α ⋅ I ,
N
DE
Rys. 7.7.
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
6
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
I
= I
(7.22a),
I
= α ⋅ I − I
(7.22b)
E
DE
C
N
DE
DC
W zakresie aktywnym nasycenia obydwa złącza mają charakter wstrzykujący.
Oprócz składowych unoszenia, w każdym złączu płynie prąd wstrzykniętych nośników przez przeciwne złącze. W schemacie zastępczym prądy są
reprezentowane jako źródła prądowe. Ze względu na niesymetrię budowy
tranzystora, rozróżnia się dwa współczynniki wzmocnienia prądowego: w kierunku
normalnym – α , oraz w kierunku inwersyjnym α (znacznie mniejsza wartość).
N
I
Schemat modelu przedstawiono na rys. 7.8. a opisujące go równania są następujące Rys.7.8.
I
= I − α ⋅ I (7.23a),
I
= α ⋅ I − I (7.23b)
E
DE
I
DC
C
N
DE
DC
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
7
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
7.6. Budowa tranzystora
Tranzystor bipolarny (działanie oparte na przewodnictwie obu rodzajów nośników: elektronów i dziur) jest zbudowany z dwóch złączy PN tworzących strukturę PNP
lub NPN (rys.)
Rys.7.9.
7.7. Zakresy pracy
UBC
Zakres aktywny
Zakres aktywny
inwersyjny
nasycenia
UBE
UBE
polaryzacja zaporowa
polaryzacja przewodzenia
Zakres
Zakres aktywny
zatkania
normalny
UBC
Rys.7.10.
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
8
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
7.8. Charakterystyki statyczne tranzystora
Charakterystyka wyjściowa. Napięcie Earley’a.
Charakterystyki statyczne wejściowa i wyjściowa opisują powiązania
odpowiednich wielkości na wejściu i wyjściu tranzystora.
Prześledźmy drogę punktu pracy Q po charakterystyce wyjściowej.
Zwiększając od zera napięcie UCC zasilania tranzystora w układzie przedstawionym na rys. , przy stałej, dodatniej wartości prądu bazy Q przemieszcza się od A do B.
Obydwa złącza są w stanie przewodzenia (przy potencjale wynoszącym ok. 0,7V i
większym prądzie złącza emiterowego) co oznacza stanie nasycenia tranzystora.
Nasycenie może mieć miejsce przy różnych wartościach prądu I ,
C
regulowanych wartością prądu bazy zgodnie z poniższą przyczynowością:
I
, I
, R I
, u
U
R I
gdy u
< U
( 7.24 )
CE = (
CC −
)
C C
↓
C C ↑
C ↑
B ↑
CE
CEsat
Powyżej wartości napięcia u
≈
V
7
,
0
, złącze kolektorowe zostaje
CE
spolaryzowanym wstecznie i następuje przejście tranzystora do pracy aktywnej.
Punkt pracy przemieszcza się od B do C. Jest to zakres pracy aktywnej-normalnej lub inaczej zakres liniowy. Odcinek B-C powinien leżeć poziomo nad osią napięcia, opisując stałą wartość prądu kolektora zgodnie z wzorem modelu idealnego I = β
⋅ I . W rzeczywistości ta część charakterystyki jest nachylona
C
DC
B
pod kątem, którego wierzchołek wyznacza napięcie Earley’a VA. (rys. ).
Dalsze zwiększanie napięcia zasilania obwodu kolektora (punkt Q
przemieszcza się poza odcinkiem B-C) prowadzi do gwałtownego wzrostu prądu i
w konsekwencji przebicia złącza.
Rys.7.11.
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
9
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
Rys.7.12.
Charakterystyki prądowo- napięciowe odpowiadające typowym charakterystykom teoretycznym tranzystora:
-
prąd IC zasadniczo nie zależy od napięcia uCB, dla ustalonej wartości iE, (OB),
-
prąd IC zasadniczo nie zależy od napięcia uCE, dla ustalonej wartości IB. (OE).
Odstępy między krzywymi teoretycznymi na w/w rysunkach są jednakowe dla jednakowych przyrostów wielkości będącej parametrem ( β ma wartość stałą) co nie zachodzi w rzeczywistości. W rzeczywistych ch-kach tranzystora obserwujemy
niejednakowe odstępy między charakterystykami; β - nie jest stałe, prąd iC nie jest stały dla ustalonej wartości iB lecz wzrasta ze wzrostem napięcia uCE .
Charakterystyka wejściowa
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
10
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
7.9. Parametry katalogowe tranzystora bipolarnego
7.10. Podstawowe konfiguracje pracy tranzystora jako wzmacniacza
Tranzystor jest elementem trójkońcówkowym. Traktowany jako czwórnik musi mieć jedną z końcówek wspólną dla wejścia i wyjścia. Dla uzyskania wzmocnienia
mocy jest wymagane by końcówka bazy była jedną z wejściowych a końcówka kolektora jedną z wyjściowych. Mamy stąd 3 racjonalne konfiguracje o
odmiennych właściwościach i różnych zastosowaniach.
WB
WE
WC
OB
OE
OC
Rys.7.13. Konfiguracje tranzystora jako wzmacniacza
We wszystkich jednak tranzystor na czas trwania sygnału znajduje się w normalnych warunkach polaryzacji, tj. złącze emiter-baza jest spolaryzowane w kierunku przewodzenia a złącze kolektor-baza – w kierunku wstecznym (Linv.21)
Podobnie jak dla złącza p-n, rozróżnia się pracę tranzystora:
-
nieliniową: statyczną i dynamiczną,
-
liniową: dla małych sygnałów, małej i dużej częstotliwości
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
11
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
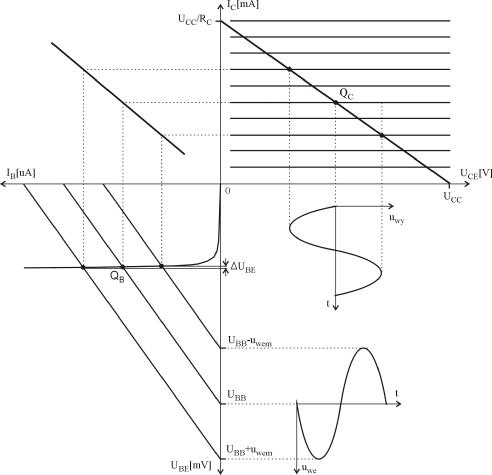
Analiza tranzystora układzie OE
Układ o wspólnym emiterze WE (OE)
Źródła UCC , UBB polaryzują złącza
tranzystora aby znajdował się on w
RC
stanie aktywnym.
r
r
we
be
IC
Na wejściu jest podany sygnał
IB
uCE
napięciowy (sygnał wzbudzenia) uwe
uBE
u
R
o małej w wartości w stosunku do
u
wy
L
we
RB
napięcia UBE polaryzacji bazy. Sygnał
ten powoduje zmianę prądu bazy.
Zmiana tego prądu (bazy) sprawi
zmianę prądu kolektora a w konsekwencji zmianę sygnału wyjściowego jakim jest
napięcie na zaciskach kolektor-emiter.
Wszystkie te zmiany dzieją się w określonych warunkach pracy tranzystora
zdeterminowanych przez napięcia polaryzacji (zasilania) obwodu wejściowego i
obwodu wyjściowego, tj. w punkcie pracy tranzystora.
∆ u
u
BE
we
I
∆ =
=
B
r
r
be
be
uwe
I
∆ = β ∆ I = β
C
0
B
0 rbe
Równanie obwodu wyjściowego, na podstawie II prawa Kirchhoffa, ma postać:
u
= E − I R
CE
C
C
C
RC
u
= ∆ u = − I
∆ R = − u β
wy
CE
C
C
we
0 rbe
uwy
R
R || r
C
C
CE
k =
= − β
= − β
u
u
0 r
0
r
we
be
be
Rezystancja wejściowa
r
= r || R
we
be
B
Rezystancja wyjściowa
r
= r || R
wy
ce
C
Wzmocnienie prądowe
r
k
wy
= − β
i
0 r + R
wy
0
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
12
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
Właściwości:
- układ odwraca fazę sygnału wejściowego
- dość duże wzmocnienie: napięciowe, prądowe i mocy
- rezystancja wejściowa umiarkowanie mała
- rezystancja wyjściowa umiarkowanie duża
Układ o wspólnej bazie WB (OB)
Prądy i napięcia zawierają składowe
stałe związane z polaryzacją i
nałożone na nie – dużo mniejsze –
składowe
zmienne:
sygnały
użyteczne przenoszone za pomocą
kondensatorów
sprzęgających
(jednocześnie
separujących
składowe stałe od zmiennych). Na
wejściu
jest
podany
sygnał
napięciowy uwe o małej w wartości w stosunku do napięcia UEB polaryzacji bazy Właściwości:
- układ nie odwraca fazy sygnału wejściowego
- wzmocnienie prądowe nieco mniejsze od 1
- wzmocnienie napięciowe dość duże (podobne jak OE)
- rezystancja wejściowa b. mała; rwe(WE)/(β+1)
- rezystancja wyjściowa b. duża; (β+1) rwy(WE)
Stabilność pracy, korzystne właściwości w zakresie w.cz., wada- mała
wartość rezystancji wejściowej
Zastosowanie:
wzmacniacze w.cz.
Układ o wspólnym kolektorze WC (OC) – wtórnik emiterowy
Na wejściu jest podany sygnał
napięciowy uwe o małej w wartości
w stosunku do napięcia UBE
polaryzacji bazy Napięcie UBE
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
13
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
baza-emiter zmienia się nieznacznie przy zmianach prądu kolektora i
stąd u
≈ ∆ U = u
WE
BE
WY
Właściwości:
- nie odwraca fazy sygnału wejściowego,
- wzmocnienie napięciowe =1 (potencjał emitera nadąża , „wtóruje” za
potencjałem bazy i stąd wtórnik emiterowy)
- wzmocnienie prądowe podobne jak dla OE
- rezystancje wejściowa – duża
- rezystancja wyjściowa - mała
- układ transformuje (przenosi) rezystancję z obwodu emitera do obwodu bazy
jako (β+1) razy większą, natomiast rezystancję z obwodu bazy przenosi do
obwodu emitera jako rezystancję (β+1) razy mniejszą – transformator
rezystancji.
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
14
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
7.11. Modele liniowe tranzystora dla małych sygnałów
Model opisujący właściwości tranzystora przy niewielkich zmianach punktu pracy, oznaczających małe sygnały wymuszające - jest liniowy. Spośród parametrów zaciskowych czwórnika reprezentującego taki model tranzystora, wybiera się dwie wielkości wyjściowe jako funkcje pozostałych dwóch wielkości tj. wejściowych.
Modele o parametrach mieszanych
Czwórnik o parametrach mieszanych będzie opisany układem równań stosownym
do układu pracy tranzystora jak podano w tablicy.
OB
OE
OC
u
= f ( i , u ) u = f ( i , u ) u
= f ( i , u )
EB
E
CB
BE
B
CE
BC
B
EC
i = f ( i , u )
i = f ( i , u )
i = f ( i , u )
C
E
CB
C
B
CE
E
B
EC
Rozpatrując niewielkie (przyrostowe) zmiany wielkości wyjściowych w wyniku określonych zmian wielkości wejściowych, dla układu OE otrzymuje się
następujący układ równań:
u
∂
u
∂
BE
BE
u
∆
=
⋅ i
∆
+
⋅ u
∆
BE
B
CE
i
∂
u
∂
B
CE
u
i
CE
B
i
∂
i
∂
(7.25)
C
C
i
∆
=
⋅ i
∆
+
⋅ u
∆
C
B
CE
i
∂
u
∂
B
CE
u
i
CE
B
Zastępując przyrosty niewielkimi sygnałami
u
∆
= u ,
u
∆
= u ,
i
∆ = i ,
i
∆ = i ,
BE
be
CE
ce
B
b
C
c
Otrzymuje się następujący układ równań opisujący czwórnik o parametrach mieszanych:
u
= h 11 ⋅ i + h 12 ⋅ u
be
e
b
e
ce
(7.26)
i
= h 21 ⋅ i + h 22 ⋅ u
c
e
b
e
ce
którego parametry oznaczają odpowiednio:
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
15
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
u
∂
u
∂
i
∂
i
∂
BE
h
,
BE
h
,
C
h
,
C
h
.
22
=
21
=
12
=
11
=
e
i
∂
e
u
∂
e
∂ i
e
∂ u
B
u
CE
B
CE
CE
iB
uCE
iB
Opis czwórnikowy tranzystora dla pozostałych układów pracy OB i OC
wyprowadza się w sposób analogiczny jak przedstawiony wyżej dla OE.
7.12. Wyznaczanie parametrów czwórnikowych, mieszanych, na podstawie
charakterystyk statycznych
IC
I
h =
C
21
I
U
I
B
CE
C
h =
22
U
I
CE
B
I
U
B
CE
UBE
h =
11
U
I
U
BE
B
CE
h =
12
U
I
CE
B
UBE
Rys. 7.14.
Schemat modelu
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
16
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
Parametry mieszane w różnych konfiguracjach
Parametr
OE
OB
OC
h
e
11
h
h
h
11
11 e
1 +
h
+ ∆ h − h
11 e
e
21
e
12 e
h
∆ − h
e
12 e
h
h
1 − h
12
12 e
1 + h
+ ∆ h − h
12 e
e
21
e
12 e
− (∆ h + h
e
e
21 )
h
h
− 1
( + h )
21
21 e
1 + h
+ h
∆ − h
21 e
e
21
e
12 e
h
22 e
h
h
h
22
22 e
1 +
h
+ h
∆ − h
22 e
e
21
e
12 e
h
∆
h h
− h h
e
11 e
22 e
12 e
e
21
h
1 + h
+ ∆ h − h
ez
e
21
e
12 e
h
∆
h h
− h h
b
b
11
22 b
12 b
b
21
h - rezystancja wejściowa, h - wsp. sprzężenia napięciowego
11
12
h - wsp. wzmocnienia prądowego, h - konduktancja wyjściowa
21
22
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
17
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
7.13.Modele o parametrach admitancyjnych
OB
OE
OC
i = f ( u , u )
i = f ( u , u )
i = f ( u , u )
B
BE
CB
B
BE
CE
B
BC
EC
i = f ( u , u ) i = f ( u , u ) i = f ( u , u
)
C
BE
CB
C
BE
CE
C
BC
EC
Rozpatrując niewielkie (przyrostowe) zmiany wielkości wyjściowych w wyniku określonych zmian wielkości wejściowych, dla układu OE otrzymuje się
następujący układ równań:
i
∂
∂ i
B
B
∆ i
=
⋅ ∆ u
+
⋅ u
∆
B
BE
CE
u
∂
u
∂
BE
=
CE
u
const
u
= const
CE
BE
i
∂
i
∂
C
C
i
∆
=
⋅ ∆ u
+
⋅ u
∆
C
BE
CE
u
∂
u
∂
BE
=
CE
u
const
u
= const
CE
BE
Zastępując przyrosty niewielkimi sygnałami
i
∆ = i ,
i
∆ = i ,
u
∆
= u ,
u
∆
= u ,
B
b
C
c
BE
be
CE
ce
Otrzymuje się następujący układ równań opisujący czwórnik o parametrach mieszanych:
i
= y 11 ⋅ u
+ y 12 ⋅ u
b
e
be
e
ce
( )
i
= y 21 ⋅ u
+ y 22 ⋅ u
c
e
be
e
ce
którego parametry oznaczają odpowiednio:
i
∂
i
∂
i
∂
∂ i
B
y
,
B
y
,
C
y
,
C
y
.
22
=
21
=
12
=
11
=
e
u
∂
e
u
∂
e
u
∂
e
u
∂
BE
u
CE
BE
CE
CE
uBE
uCE
uBE
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
18
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
1
i
=
⋅ u
+ g ⋅ u
b
be
w
ce
rbe
( )
1
i
= g ⋅ u
+
⋅ u
c
m
be
ce
rce
1
1
= y =
11 e
r
h
be
e
11
h 12
g
y
(oddziaływanie zwrotne często pomijane w obliczeniach)
w =
= − e
e
≈ 0
12
h 11 e
h 21
β
e
g = y
- transkonduktancja lub konduktancja wprzód,
21
=
=
m
e
h
r
11 e
be
1
1
= y =
( h h
− h h ) ≈ h
22 e
e
11
22 e
21 e 12 e
22 e
r
h
ce
e
11
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
19
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
Pomiary parametrów modelu liniowego
• gm – transkonduktancja - najważniejszy parametr modelu - można wyznaczyć na podstawie ch-ki przejściowej; parametr w zasadzie nie zależy od indywidualnych właściwości tranzystora
u
i
I
exp
C ≈
BE
CS
ϕT
∂ i
1
u i
i
g
C
=
|
=
⋅ I
BE
C
C
exp
=
≈
m
∂ u u
CS
CE
ϕ
ϕ
ϕ
25 mV
BE
T
T
T
• rezystancja wyjściowa na schemacie zastępczym reprezentuje rezystancję zastępczą dla małych sygnałów, którą można wyznaczyć na podstawie
charakterystyk statycznych wyjściowych; jest odwrotnościa przewodności
wyjściowej
1
u
∂
U
∆
U + u
CE
C
Y
CE
r =
=
|
=
=
ce
u
g
i
BE
∂
I
∆
I
ce
C
C
C
gdzie UY – jest tzw. napięciem Early’ego.
Wyznaczane z pomiarów rce typowe wartości UY ≈ 80....200V (dla NPN) i 40....150V (dla PNP)
• Rezystancja wejściowa dla małych sygnałów widziana z zacisków
wejściowych. Praktycznie wyznacza się na podstawie znanej transkonduktancji gm.
∂ u
u
∂
β
ϕ
BE
BE
T
r =
|
=
=
= β ⋅
be
U
i
CE = const
∂
i g
I
B
C
m
C
∂ β
• transkonduktancja zwrotna (oddziaływanie zwrotne )
∂ iB
g =
|
w
uBE
u
∂ CE
g
- przy małych prądach;
w > 0
g
- przy dużych prądach;
4
g
10−
w <
w < 0
Przy małych częstotliwościach oddziaływanie wsteczne jest do pominięcia.
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
20
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
Ze zwiększaniem się częstotliwości natomiast – rośnie.
Dokładne (słuszne dla w.cz.)
Przybliżone (słuszne dla m.cz.
oraz gdy g
<<
)
'
g
cb
b' e
h
1
1
11 e
r
+
r
+
bb'
'
Y
bb
g
w
b' e
h
g
g
' + j
C
ω
12 e
jc
cb
'
cb
≈ 0
Y
g
w
'
b e
h
g − g
g
' − jωC
21 e
m
jc
cb
m
= β
Y
g '
w
b e
h
g
+ j C
ω
g
22 e
jc
cb
g +
'
g ⋅
m
g +
⋅ g '
ce
m
ce
cb
Y
g '
w
b e
Y = g
+ g + jω C + C + C
'
'
(
)
w
de
je
jc
b e
cb
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
21
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
Małosygnałowe właściwości podstawowych układów pracy tranzystora
Sposób wyznaczania parametrów h tranzystora w punkcie pracy Q
h = tg 11
α
11
h = tg 12
α
12
h = tg α21
21
h
= tg α22
22
U
∆
U
- U
BE
BE 4
BE 6
h
=
=
11e( 4 6
, )
I
∆
I
- I
B
B4
B6
∆U = 0
CE
∆U
U
− U
BE
BE 4
BE 5
h
=
=
12e( 4 5
, )
∆U
U
− U
CE
CE 4
CE 5
∆I = 0
B
I
∆
I
− I
C
C 2
C 1
h
=
=
21e( 2 1
, )
∆I
I
− I
B
B 2
B1
U
∆
= 0
CE
I
∆
I
− I
C
C 3
C 1
h
=
=
22e( 3 1
, )
∆U
U
− U
CE
CE 3
CE 1
∆I = 0
B
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
22
D:\DYD\2012 - 2013\materialy dla stud Niest 1_st_sem 3\TRANZYSTORY
BIPOLARNE szkic.docTRANZYSTORY BIPOLARNE szkic
J.Piłaciński: Elektronika – materiały pomocnicze do wykładu
23
Wyszukiwarka
Podobne podstrony:
TRANZYSTORY BIPOLARNE szkic unlocked
TRANZYSTORY POLOWE szkic unlocked
F 1 Zasada działania tranzystora bipolarnego
90 Tranzystor bipolarny jako wzmacniacz
cw5 Tranzystor bipolarny
etr2 lab odpowiedzi na pytania do laborek z tranzystora bipolarnego, Mechatronika, 2 Rok
Układ zasilania tranzystorów bipolarnych
126 Budowa tranzystora bipolarnego
Tranzystor bipolarny-gac, Szkoła, Politechnika 1- 5 sem, SEM IV, Elektronika i Energoelektronika. La
Tranzystory Bipolarne, elektronika, stodia czyjeś
Badanie tranzystora bipolarnego
Omówić zakresy i konfiguracje pracy tranzystora bipolarnego bjt
Badanie wzmacniacza szerokopasmowego, Ćwiczenie nr 23: -Badanie tranzystora bipolarnego -
Tranzystor bipolarny?135 oraz unipolarny czasy
Sprawozdanie Tranzystor bipolarny Sprawozdanie Tranzystory bipolarne
Tranzystory bipolarne
Katalog tranzystorów bipolarnych
więcej podobnych podstron