3UDZGRSRGRELHVWZR L VWDW\VW\ND

5.04.1997 r.

___________________________________________________________________________

1

Zadanie 1.

: SLHUZV]HM XUQLH ]QDMGXM VL NXOH SRQXPHURZDQH OLF]EDPL

]D Z GUXJLHM XUQLH ± NXOH SRQXPHURZDQH OLF]EDPL :\FLJDP\ ORVRZR SR

MHGQHM NXOL ] ND*GHM XUQ\ 3UDZGRSRGRELHVWZR *H RELH NXOH PDM WHQ VDP QXPHU MHVW
równe:

(A)

2

1

(B)

5

1

(C)

10

1

(D)

40

1

(E)

50

1

3UDZGRSRGRELHVWZR L VWDW\VW\ND

5.04.1997 r.

___________________________________________________________________________

2

Zadanie 2.

: SLHUZV]HM VNU]\QFH MHVW MDEáHN ]GURZ\FK L ]HSVXW\FK : GUXJLHM

VNU]\QFH MHVW MDEáHN ]GURZ\FK L ]HSVXW\FK :\ELHUDP\ ORVRZR ]

SUDZGRSRGRELHVWZHP MHGQD GUXJD MHGQ ]H VNU]\QHN L Z\FLJDP\ ] QLHM Uy*QH

MDEáND -DNLH MHVW SUDZGRSRGRELHVWZR *H Z\EUDOLP\ GUXJ VNU]\QN MHOL ZLHP\ *H

ZV]\VWNLH MDEáND RND]Dá\ VL ]GURZH"

(A)

2

1

(B)

9

4

(C)

















3

40

3

29

(D)

29

14

(E)

29

28

3UDZGRSRGRELHVWZR L VWDW\VW\ND

5.04.1997 r.

___________________________________________________________________________

3

Zadanie 3. Niech X i Y

EG ]PLHQQ\PL ORVRZ\PL WDNLPL *H

X

PD JVWRü

( )







≤

=

−

przypadku

przeciwnym

w

x

dla

e

x

f

x

0

0

(

)

x

k

e

k

x

x

X

k

Y

−

⋅

=

=

=

!

Pr

dla

,

2

,

1

,

0

=

k

(A)

X i Y

V ]PLHQQ\PL QLH]DOH*Q\PL

(B)

X i Y

V ]PLHQQ\PL nieskorelowanymi

(C)

(

)

[

]

( )

( )

Y

VAR

X

VAR

Y

X

COV

⋅

=

2

,

(D)

X oraz

X

Y

−

V ]PLHQQ\PL nieskorelowanymi

(E)

(

)

1

,

=

−

X

Y

X

COV

3UDZGRSRGRELHVWZR L VWDW\VW\ND

5.04.1997 r.

___________________________________________________________________________

4

Zadanie 4.

0DFLHU] SU]HMFLD áDFXFKD 0DUNRZD R VWDQDFK

4

3

2

1

,

,

,

E

E

E

E

jest

równa:

























=

1

0

0

0

0

0

0

0

0

0

1

3

1

3

1

3

1

2

1

2

1

P

Niech

( )

1

,

2

n

P

EG]LH SUDZGRSRGRELHVWZHP *H áDFXFK SR Z\NRQDQLX n kroków

]QDMG]LH VL Z VWDQLH

1

E

MHOL Z FKZLOL SRF]WNRZHM ]QDMGRZDá VL Z VWDQLH

2

E .

(A)

( )

3

2

1

,

2

lim

=

∞

→

n

n

P

(B)

( )

2

1

1

,

2

lim

=

∞

→

n

n

P

(C)

( )

1

1

,

2

lim

=

∞

→

n

n

P

(D)

( )

1

,

2

lim

n

n

P

∞

→

nie istnieje

(E)

( )

6

5

1

,

2

lim

=

∞

→

n

n

P

3UDZGRSRGRELHVWZR L VWDW\VW\ND

5.04.1997 r.

___________________________________________________________________________

5

Zadanie 5. Zmienne losowe X i Y

PDM áF]Q\ UR]NáDG SUDZGRSRGRELHVWZD R

JVWRFL

( )

(

)







≤

≤

>

⋅

=

−

⋅

−

przypadku

przeciwnym

w

x

x

y

dla

e

x

y

x

f

x

y

x

0

1

0

,

,

-H*HOL

( )

( )

X

Y

E

X

=

µ

to

( )

(

)

X

Y

µ

>

Pr

wynosi:

(A)

2

1

(B)

1

−

e

(C)

1

(D)

e

+

1

1

(E)

e

+

1

2

3UDZGRSRGRELHVWZR L VWDW\VW\ND

5.04.1997 r.

___________________________________________________________________________

6

Zadanie 6.

n

x

x

x

,

,

,

2

1

MHVW SUyE ORVRZ ] UR]NáDGX R JVWRFL

( )

(

)







≥

=

−

⋅

−

przypadku

przeciwnym

w

x

dla

e

x

f

x

0

θ

θ

θ

(VW\PDWRU QDMZLNV]HM ZLDURJRGQRFL QLH]QDQHJR SDUDPHWUX

θ

PD SRVWDü

(A)

{

}

n

x

x

x

n

−

=

,

,

,

max

ˆ

2

1

θ

(B)

{

}

n

x

x

x

,

,

,

min

ˆ

2

1

=

θ

(C)

1

1

ˆ

1

−

⋅

=

∑

=

n

i

i

x

n

θ

(D)

( )













−

⋅

=

∑

=

n

i

i

x

n

1

exp

ln

1

ˆ

θ

(E)

{

}

2

ln

,

,

,

ˆ

2

1

+

=

n

x

x

x

med

θ

3UDZGRSRGRELHVWZR L VWDW\VW\ND

5.04.1997 r.

___________________________________________________________________________

7

Zadanie 7.

:\NRQDQR SRPLDUyZ SHZQHM QLH]QDQHM ZLHONRFL

µ

jednym

SU]\U]GHP SRPLDURZ\P D QDVWSQLH SRPLDUyZ LQQ\P SU]\U]GHP =DNáDGDP\ *H
wyniki pomiarów

15

11

10

2

1

,

,

,

,

,

,

X

X

X

X

X

V QLH]DOH*Q\PL ]PLHQQ\PL

ORVRZ\PL SU]\ F]\P ND*GD ]H ]PLHQQ\FK

10

2

1

,

,

,

X

X

X

PD UR]NáDG QRUPDOQ\ R

parametrach

(

)

2

1

.

0

,

µ

SRGF]DV JG\ ND*GD ]H ]PLHQQ\FK

15

11

,

,

X

X

PD UR]NáDG QRUPDOQ\ R SDUDPHWUDFK

(

)

2

2

.

0

,

µ

1DOH*\ WDN GREUDü ZVSyáF]\QQLNL

15

2

1

,

,

,

c

c

c

*HE\ HVW\PDWRU

∑

=

=

n

i

i

i

X

c

1

ˆ

µ

E\á QLHREFL*RQ\P HVW\PDWRUHP R PLQLPDOQHM ZDULDQFML

(A)

15

1

15

1

=

=

=

c

c

(B)

20

1

10

1

=

=

=

c

c

i

10

1

15

11

=

=

=

c

c

(C)

10

1

10

1

=

=

=

c

c

i

0

15

11

=

=

=

c

c

(D)

90

8

10

1

=

=

=

c

c

i

45

1

15

11

=

=

=

c

c

(E)

90

8

10

1

=

=

=

c

c

i

90

1

15

11

=

=

=

c

c

3UDZGRSRGRELHVWZR L VWDW\VW\ND

5.04.1997 r.

___________________________________________________________________________

8

Zadanie 8.

=DNáDGDP\ *H OLF]ED URV]F]H Z FLJX URNX GOD SHZQHJR SRUWIHOD U\]\N

MHVW ]PLHQQ ORVRZ X R UR]NáDG]LH 3RLVVRQD =DREVHUZRZDQR ZDUWRü

2600

=

X

.

Czy test hipotezy:

( )

2500

:

0

=

X

E

H

przeciwko alternatywie:

( )

2500

:

1

>

X

E

H

prowadzi do odrzucenia

0

H

QD SR]LRPLH LVWRWQRFL

α

?

7HVW ]EXGRZDQR Z RSDUFLX R SU]\EOL*HQLH UR]NáDGX 3RLVVRQD UR]NáDGHP QRUPDOQ\P L
ma obszar krytyczny postaci

c

X

>

.

(A)

TAK, dla

005

.

0

=

α

(B)

NIE, dla

005

.

0

=

α

; TAK, dla

01

.

0

=

α

(C)

NIE, dla

01

.

0

=

α

; TAK, dla

05

.

0

=

α

(D)

NIE, dla

05

.

0

=

α

; TAK, dla

1

.

0

=

α

(E)

NIE, dla

1

.

0

=

α

3UDZGRSRGRELHVWZR L VWDW\VW\ND

5.04.1997 r.

___________________________________________________________________________

9

Zadanie 9.

20

2

1

,

,

,

X

X

X

MHVW SUyE ORVRZ ] UR]NáDGX QRUPDOQHJR R SDUDPHWUDFK

(

)

2

,

0

σ

5R]ZD*P\ QDMPRFQLHMV]\ WHVW KLSRWH]\

1

:

2

0

=

σ

H

przeciwko alternatywie:

3

:

2

1

=

σ

H

1D SR]LRPLH LVWRWQRFL 0RF WHVWX Z\QRVL

(A)

RNRáR

(B)

RNRáR

(C)

RNRáR

(D)

RNRáR

(E)

RNRáR

3UDZGRSRGRELHVWZR L VWDW\VW\ND

5.04.1997 r.

___________________________________________________________________________

10

Zadanie 10.

1LHFK ; EG]LH ]PLHQQ ORVRZ R UR]NáDG]LH Z\NáDGQLF]\P R JVWRFL

( )







≥

=

⋅

−

przypadku

przeciwnym

w

x

dla

e

x

f

x

0

θ

)XQNFMD WZRU]FD PRPHQW\ ]PLHQQHM ORVRZHM

{

}

m

X

Y

,

min

=

, gdzie

0

>

m

MHVW GDQ

OLF]E Z\UD*D VL Z]RUHP

(A)

( )

( )

[

]

1

1

1

1

1

≠

⋅

−

⋅

−

=

−

−

t

dla

e

t

t

t

M

t

m

Y

;

( )

1

1

+

=

m

M

Y

(B)

( )

1

,

1

1

min

<













−

=

t

dla

e

t

t

M

mt

Y

;

( )

1

≥

=

t

dla

e

t

M

mt

Y

(C)

( )

mt

Y

e

t

t

M

⋅

−

=

1

1

(D)

( )

m

t

dla

e

t

m

m

t

M

mt

Y

<

⋅

−

=

;

( )

m

t

dla

t

M

Y

≥

∞

=

(E)

( )

( )

[

]

1

1

1

1

1

<

⋅

−

⋅

−

=

−

−

t

dla

e

t

t

t

M

t

m

Y

;

( )

1

≥

∞

=

t

dla

t

M

Y

3UDZGRSRGRELHVWZR L VWDW\VW\ND

5.04.1997 r.

___________________________________________________________________________

11

Egzamin dla Aktuariuszy z 5 kwietnia 1997 r.

3UDZGRSRGRELHVWZR L VWDW\VW\ND

Arkusz odpowiedzi

*

,PL L QD]ZLVNR ./8&= 2'32:,('=,

Pesel ...........................................

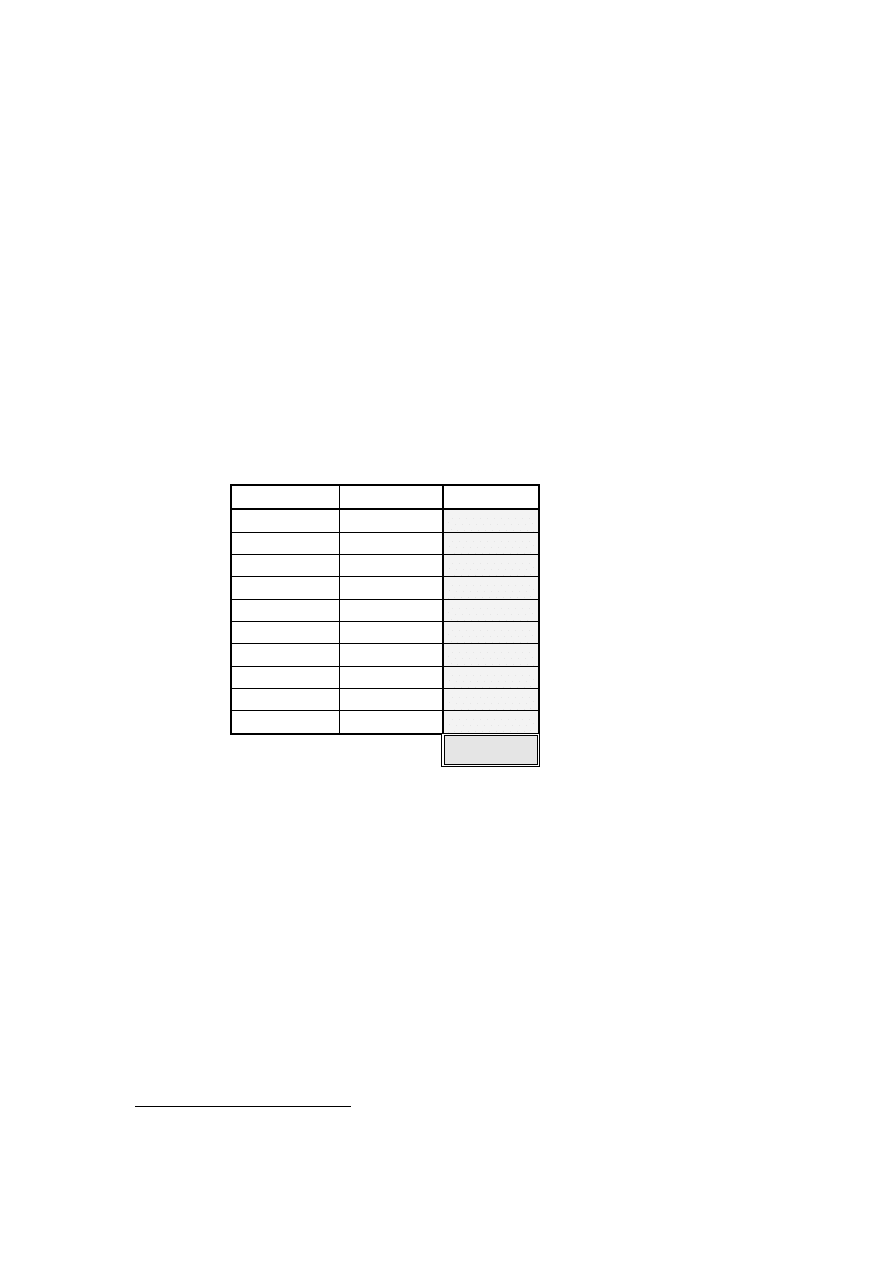
Zadanie nr

2GSRZLHG( Punktacja

♦

1

D

2

B

3

D

4

A

5

B

6

B

7

D

8

C

9

D

10

A

*

2FHQLDQH V Z\áF]QLH RGSRZLHG]L XPLHV]F]RQH Z Arkuszu odpowiedzi.

♦

:\SHáQLD .RPLVMD (J]DPLQDF\MQD