1.0. DANE.
Dłudośc mostu:
L=
105
m
Wysokośc mostu w przęśle:
H=
17,5
m
Obciążenie kolejowe:
+ 3
Stal:
18G2A
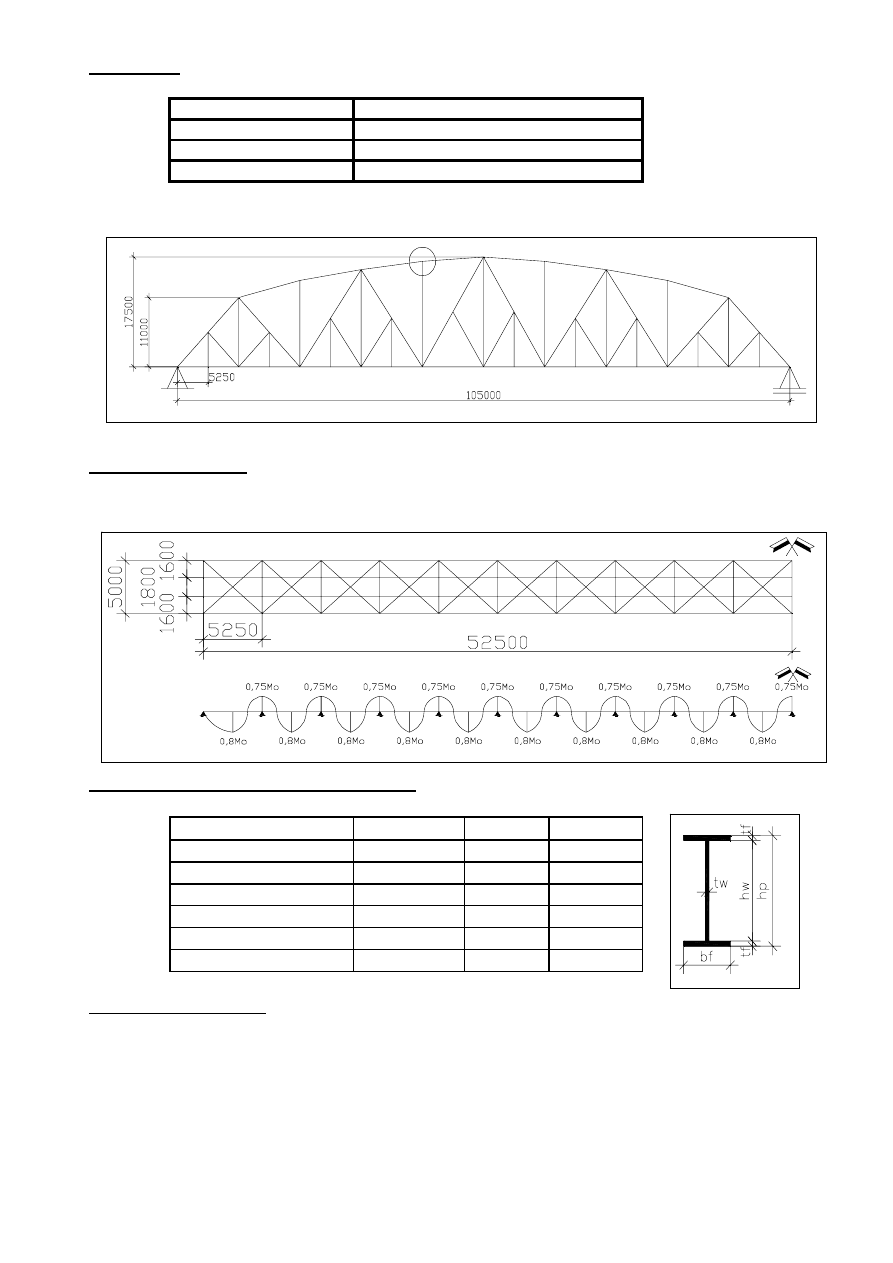
SCHEMAT STATYCZNY
2.0. PODŁUŻNICA.
SCHEMAT STATYCZNY
2.1. Przyjęte wstępne wymiary podłużnicy.
Nazwa elementu
Symbol
Wymiar
Jednostka
Długość podłużnicy
l
p
5,25
m
Szerokośc pasów
b
f
0,22
m
Grubość pasów
t
f
0,03
m
Grubość środnika
t
w
0,018
m
Wysokość środnika
h
w
0,4
m
Wysokośc podłużnicy
h
p
= h
w
+ 2* t
f
0,46
m
2.2. Zebranie obciążeń.
2.2.1. Obciążenia stałe.
- Ciężar własny podłużnicy - wartości charakterystyczne
A = 2 * b
f
* t
f
+ h
w
*n t
w
=
0,0204
m
²
g
p
= A * (78,5 + 2) =
1,642
kN/m
- Ciężar nawierzchni kolejowej typu: S60 - wartości charakterystyczne
1
g
s60
=
3,5
kN/m
- Ciężar własny podłużnicy - wartości obliczeniowe
gf =
1,2
g
p,o
= g
p
* gf =
1,971
kN/m
- Ciężar nawierzchni kolejowej typu: S60 - wartości obliczeniowe
gf =
1,2
g
s60,o
= g
s60
* gf =
4,200
kN/m
- Wartości sumaryczne obciążenia stałego:
q = g
p
+ g
s60
=
5,142
kN/m
q
o
= g
p,o
+ g
s60,o
=
6,171
kN/m
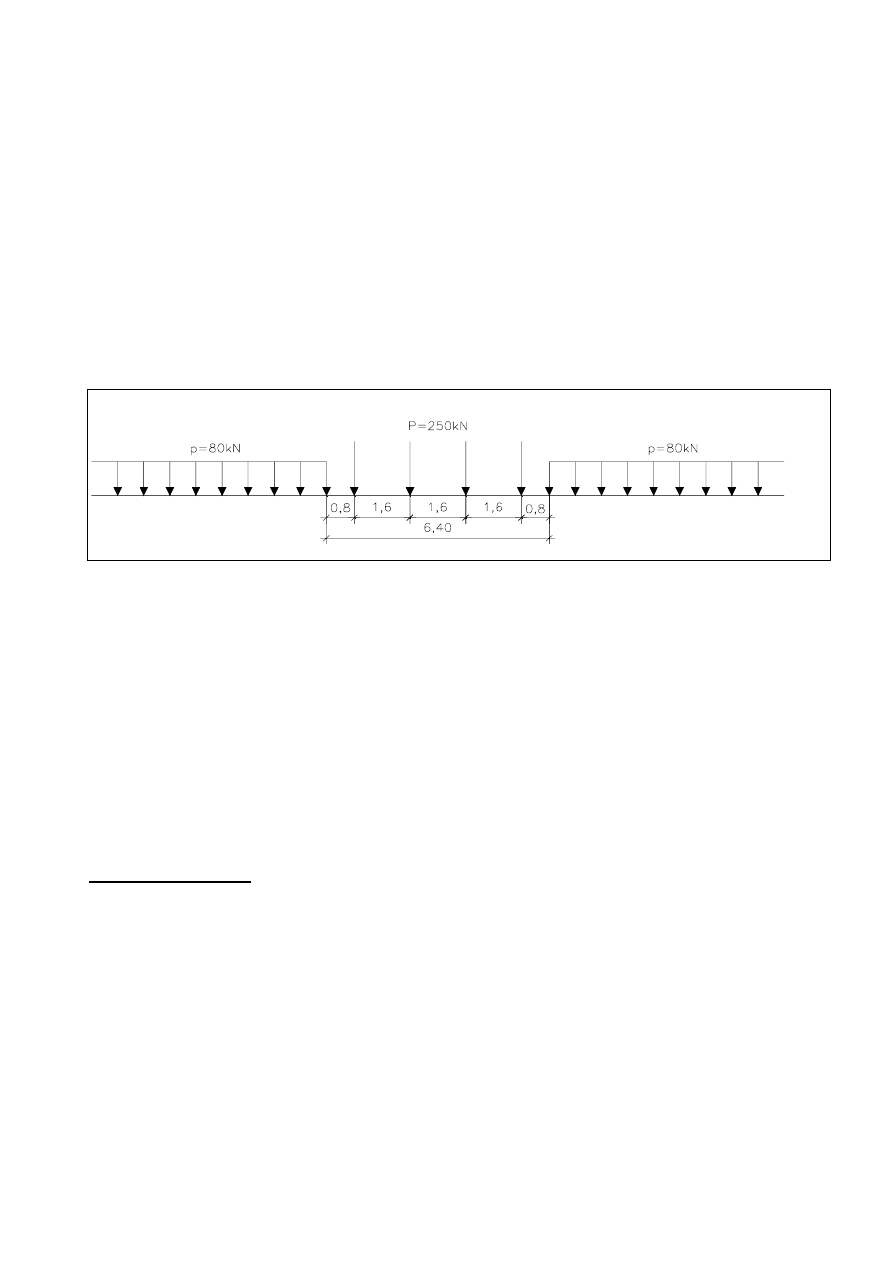
2.2.2. Obciążenia ruchome.
SCHEMAT OBCIĄŻENIA RUCHOMEGO
ak =
1,33
- mnożnik klasy obciążenia
P = 250kN * a
k
=
332,5
kN
- obciążenie skupione - wartości charakterystyczne
p = 80kN/m * a
k
=
106,4
kN/m
- obciążenie równ. roz. - wartości charakterystyczne
gf =
1,5
P
o
= P * gf =
498,75
kN
- obciążenie skupione - wartości charakterystyczne
p
o
= p * gf =
159,6
kN/m
- obciążenie równ. roz. - wartości charakterystyczne
2.2.2.1. Wspólczynnik dynamiczny podłużnicy.
L = L
p
+ 3m =
8,25
m
f = 1,44 / (L^0,5 - 0,2) + 0,2
1,359
2.3. Siły wewnętrzne.
Siły dla przekroju przęsłowego i podporowego:
- przekrój przęsłowy M = 0,8 * Mo
- przekrój podporowy M = 0,75 * Mo, Q = 1,2 * Qo"
- gdzie Mo, Qo - max wartości sił wewnętrznych dla belki wolnopopdpartej o Lo
- długość podłużnicy
l
p
=
5,25
m
- wartości charakterystyczne
q =
5,142
kN/m
2.3.1. Obciążenia stałe wartości charakterystyczne.
M
o,q
= 0,125 * q * l
p
² =
17,716
kNm
Q
o,q
= 0,5 * q * l
p
=
13,498
kN
2
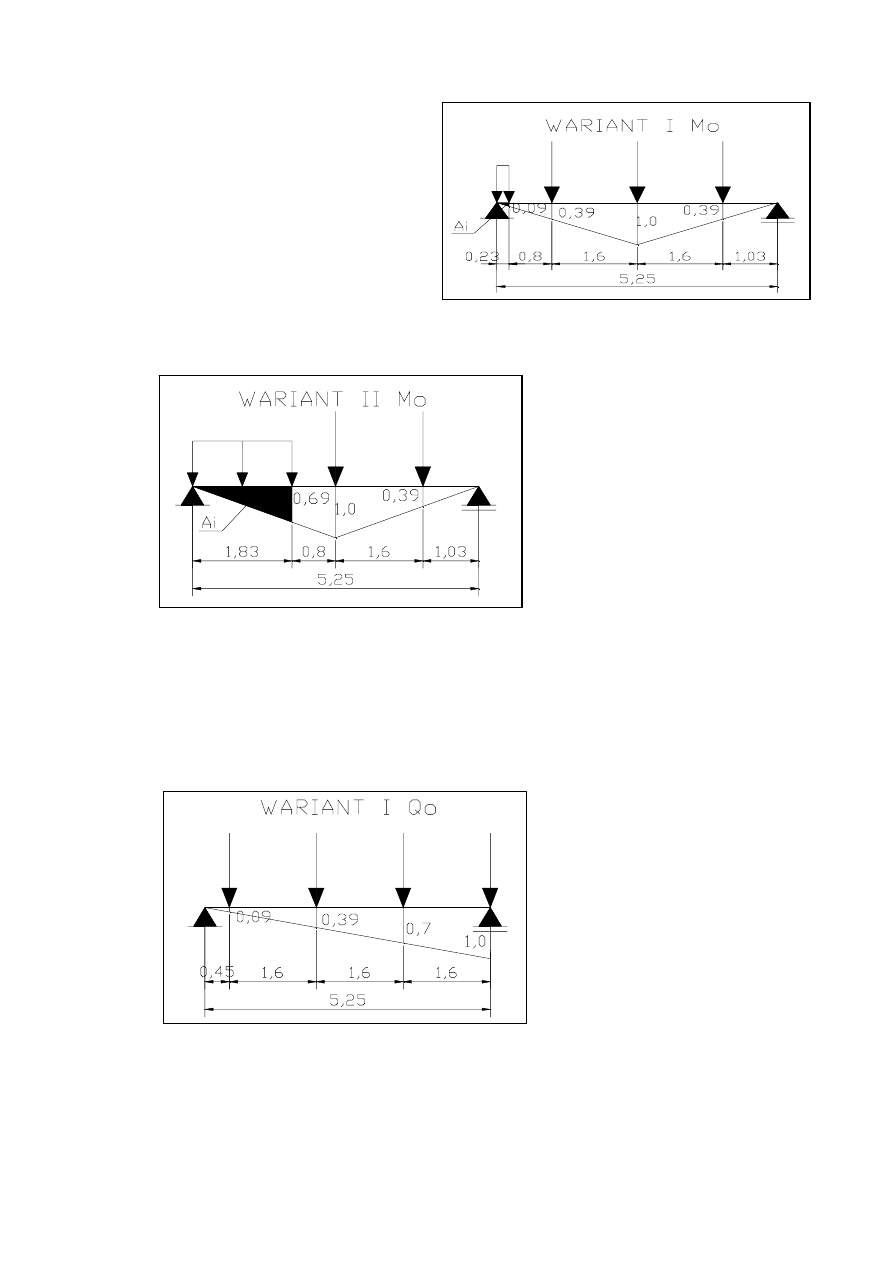
2.3.2.Obciążenia ruchome wartości charakterystyczne.
q
i
= 0,5 * q =
2,571
kN/m
P
i
= 0,5 * P =
166,250
kN
h
1
=
0,390
h
2
=
1,000
h
3
=
0,390
A
i
=
0,010
m
M
o1
= (S h
i
*P
i
+A
i
*q
i
)*0,25*l
p
=
388,436
kNm
P
i
= 0,5 * P =
166,250
kN
q
i
= 0,5 * q =
2,571
kN/m
h
1
=
1,000
h
2
=
0,390
A
i
=
0,631
m
M
o2
= (S h
i
*P
i
+A
i
*q
i
)*0,25*l
p
=
305,433
kNm
P
i
= 0,5 * P =
166,250
kN
h
1
=
0,090
h
2
=
0,390
h
3
=
0,700
h
4
=
1,000
3
Qo1
= S h
i
* P
i
* 0,25 * l
p
=
475,683
kNm
P
i
= 0,5 * P =
166,250
kN
q
i
= 0,5 * q =
2,571
kN/m
h
1
=
0,390
h
2
=
0,700
h
3
=
1,000
A
i
=
0,150
m
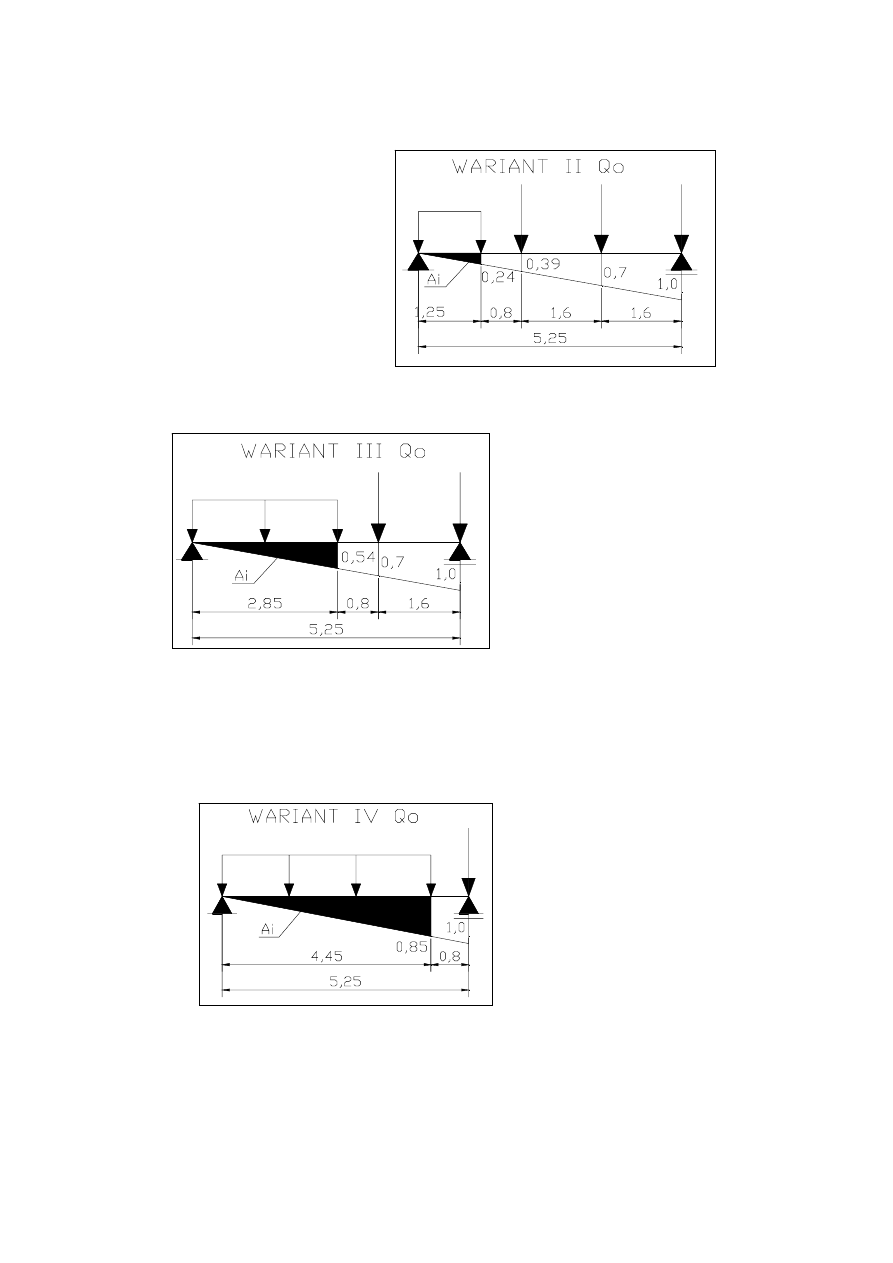
Q
o2
= (S h
i
*P
i
+A
i
*q
i
) =
347,848
kNm
P
i
= 0,5 * P =
166,250
kN
q
i
= 0,5 * q =
2,571
kN/m
h
1
=
0,700
h
2
=
1,000
A
i
=
0,770
m
Q
o3
= (S h
i
*P
i
+A
i
*q
i
) =
284,603
kNm
P
i
= 0,5 * P =
166,250
kN
q
i
= 0,5 * q =
2,571
kN/m
h
1
=
1,000
A
i
=
1,891
m
Q
o4
= (S h
i
*P
i
+A
i
*q
i
) =
171,113
kNm
4

2.3.3.Końcowe wartości Mo i Qo.
- wartości charakterystyczne bez współczynnika dynamicznego:
M
o,q
=
17,716 kNm
Q
o,q
=
13,498 kN
M
o,p
= max( Mo,
1
; M
o,2
) =
388,436
kNm
Q
o,p
= max( Qo,
1
; Q
o,2
; Q
o,3;
Q
o,4
) =
475,683
kN
M
o
= M
o,p
+ M
o,q
=
406,153
kNm
Q
o
= Q
o,p
+ Q
o,q
=
489,181
kN
- wartości charakterystyczne ze współczynnikiem dynamicznym:
f =
1,359
Mo,q =
17,716
kNm
Qo,q =
13,498
kN
M
o,p,f
= max( Mo,
1
; M
o,2
) * f =
527,833
kNm
Q
o,p,f
= max( Qo,
1
; Q
o,2
; Q
o,3
) * f =
646,389
kN
M
o,f
= M
o,p,f
+ M
o,q
=
545,549
kNm
Q
o,f
= Q
o,p,f
+ Q
o,q
=
659,887
kN
- wartości obliczeniowe ze współczynnikiem dynamicznym:
l
p
=
5,250
m
f =
1,359
g =
1,500
q
o
= g
p,o
+ g
s60,o
=
6,171
kN/m
M
o,qo
= 0,125 * q
o
* l
p
² =
21,260
kNm
Q
o,qo
= 0,5 * q
o
* l
p
=
16,198
kN
M
o,p,f,g
= max(Mo,
1
; M
o,2
)*f*g=
818,324
kNm
Q
o,p,f,g
=max(Qo,
1
;Q
o,2
;Q
o,3
)*f*g=
969,583
kN
M
o,f,g
= M
o,p,f,g
+ M
o,q,g
=
839,584
kNm
Q
o,f,g
= Q
o,p,f,g
+ Q
o,q,g
=
985,781
kN
2.3.4. Siły wewnętrzne w przekroju przęsłowym.
- wartości charakterystyczne bez wspólczynnika dynamicznego:
M
A,k
= 0,8 * M
o
=
324,922
kNm
- wartości charakterystyczne ze współczynnikiem dynamicznym:
M
A,k,f
= 0,8 * M
o,f
=
436,440
kNm
- wartości obliczeniowa ze współczynnikiem dynamicznym:
M
A,f,g
= 0,8 * M
o,
671,667
kNm
2.3.5. Siły wewnętrzne w przekroju podporowym.
- wartości charakterystyczne bez wspólczynnika dynamicznego:
M
B,k
= 0,75 * M
o
=
304,615
kNm
Q
B,k
= 1,2 * Q
o
=
587,017
kN
- wartości charakterystyczne ze współczynnikiem dynamicznym:
M
B,k,f
= 0,75 * M
o,f
=
409,162
kNm
QB,k,f
= 1,2 * Q
o,f
=
791,865
kN
- wartości obliczeniowa ze współczynnikiem dynamicznym:
M
B,f,g
= 0,75 * M
o,f,g
=
629,688
kNm
Q
B,f,g
= 1,2 * Q
o,f,g
=
1182,938
kN
5

2.4.0. Cechy geometryczne przekroju.
2.4.1.Moment bezwładności przekroju.
J
x
= t
w
* h
w
³ / 12 + 2 * b
f
* t
f
³ / 12 + b
f
* t
f
* (h
w
/ 2 + t
f
/ 2)
² * 2
J
x
=
0,000700
m
4
2.4.2. Wskaźnik wytrzymałości przekroju.
Wx
= J
x
/ (0,5 * h
p
) =
0,003043
m³
2.4.3. Moment statyczny części odciętej osią x-x.
S
x
= t
w
* h
w
* 0,5 * 0,25 *h
w
+ b
f
* t
f
(h
w
* 0,5 + t
f
* 0,5)
S
x
=
0,001779
m³
Wx1
= J
x
/ (0,5 * (h
p
- 2 * t
f
) =
0,003499
m³
2.4.4. Moment statyczny części odciętej osią 1-1.
S
x1
=b
f
* t
f
* 0,5 * (h
p
+ t
f
)
S
x1
=
0,001419
m³
2.5.0. Stan graniczny nośności.
2.5.1. Przekrój przęsłowy.
- maksymalne naprężenia normalne:
M
A,f,g
=
671,667
kNm
W
x
=
0,003043 m³
s
max
= M
A,f,g
/ W
x
=
220761,458
kN/m
²
s
max
=
221
MPa
R =
280
MPa
- sprawdzenie warunku wytrzymałościowego:
s
max
=
221
<
1,05 * R =
294
MPa
Warunek został spełniony!
2.5.2. Przekrój podporowy.
- maksymalne naprężenia normalne:
M
B,f,g
=
629,688
kNm
W
x
=
0,003043
m³
s
max
= M
B,f,g
/ W
x
=
206963,867
kN/m
²
s
max
=
207
MPa
R =
280
MPa
- sprawdzenie warunku wytrzymałościowego:
s
max
=
207
<
1,05 * R =
294
MPa
Warunek został spełniony!
6

2.5.3. Naprężenia normalne na wysokości połączenia pasa ze środnikiem.
M
B,f,g
=
629,688
kNm
W
x1
=
0,00349888 m³
s
max
= M
B,f,g
/ W
x1
=
179968,580
kN/m
²
s
max
=
180
MPa
R =
280
MPa
- sprawdzenie warunku wytrzymałościowego:
s
max
=
180
<
1,05 * R =
294
MPa
Warunek został spełniony!
2.5.4. Maksymalne naprężenia styczne na poziomie osi X-X.
Q
B,f,g
=
1182,938
kN
S
x
=
0,001779
m³
J
x
=
0,000700
m
4
t
w
=
0,018
m
t
max
= Q
B,f,g
* S
x
/ (J
x
* t
w
) =
167073,131
kN/m
²
t
max
=
167
MPa
R
t
=
170
MPa
- sprawdzenie warunku wytrzymałościowego:
t
max
=
167
<
R
t
=
170
MPa
Warunek został spełniony!
2.5.5. Maksymalne naprężenia styczne na poziomie osi 1-1.
Q
B,f,g
=
1182,938
kN
J
x
=
0,000700
m
4
S
x1
=
0,001419
m³
t
w
=
0,018 m
t
max
= Q
B,f,g
* S
x
/ (J
x
* t
w
) =
133264,065
kN/m
²
t
max
=
133
MPa
R
t
=
170
MPa
- sprawdzenie warunku wytrzymałościowego:
t
max
=
133
<
R
t
=
170
MPa
2.5.6. Złożony stan naprężeń na poziomie osi 1-1.
s
1
=
180
MPa
t
1
=
133
MPa
s
z
= (s
1
² + 3 * t
1
²)^0,5 =
293
MPa
R =
280
MPa
- sprawdzenie warunku wytrzymałościowego:
s
z
=
293
<
1,1 * R =
308
MPa
Warunek został spełniony!
2.6.0. Stan graniczny użytkowania - ugięcie.
M =
324,922
kNm
l
p
=
5,250
m
E =
205000000
kN/m
²
J
x
=
0,000700
m
4
f = 5 * M * l
p
² / (48 * E * J
x
) =
0,007 m
f
dop
= l
p
/ 600 =
0,009 m
- sprawdzenie warunku wytrzymałościowego:
f =
0,007
<
f
dop
=
0,009 Warunek został spełniony!
7
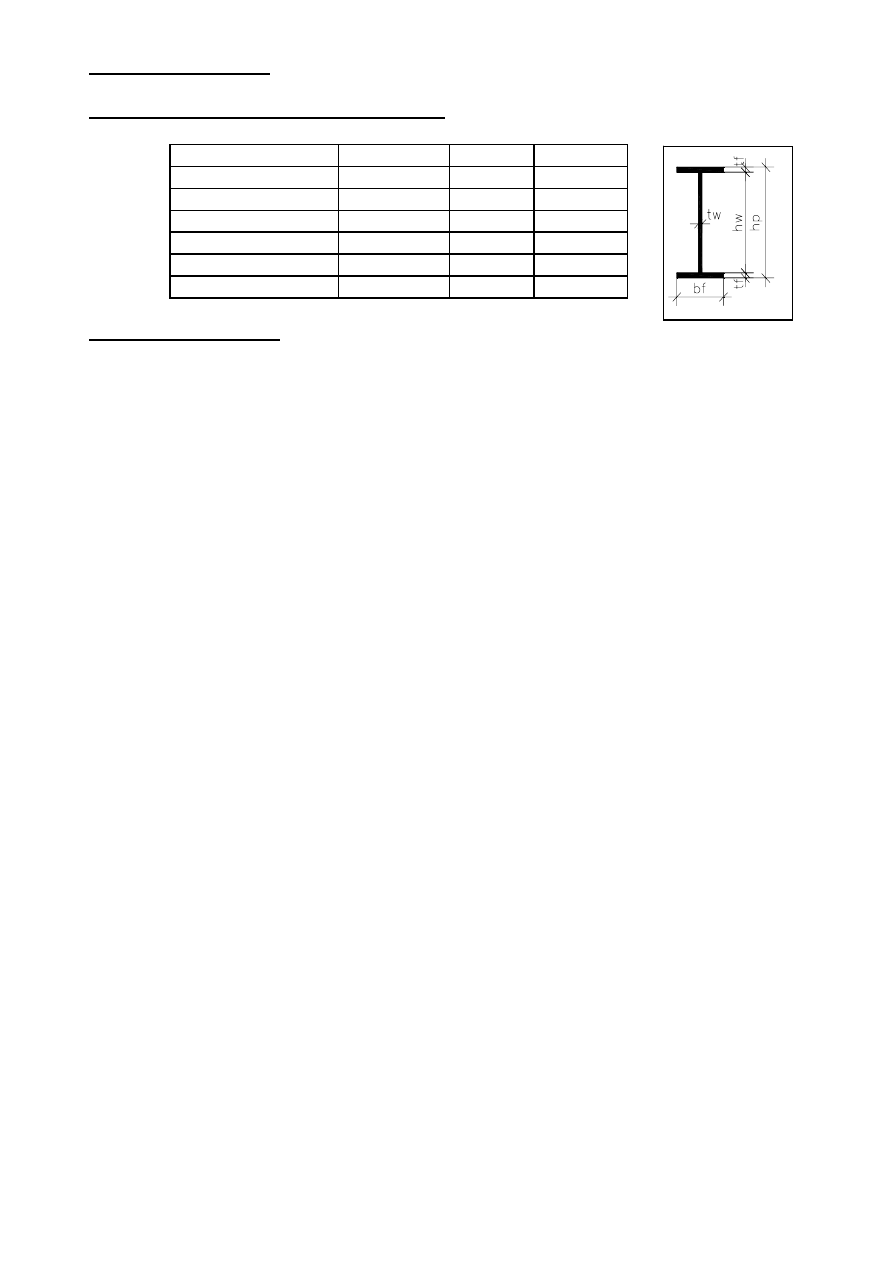
3.0. POPRZECZNICA.
3.1.0. Przyjęte wymiary wstępne poprzecznicy.
Nazwa elementu
Symbol
Wymiar
Jednostka
Dłogośc poprzecznicy
l
po
5
m
Szerokośc pasów
b
f
0,36
m
Grubośc pasów
t
f
0,03
m
Grubośc środnika
t
w
0,018
m
Wysokośc środnika
h
w
0,5
m
Wysokośc poprzecznicy
h
p
= h
w
+ 2* t
f
0,56
m
3.2.0. Zebranie obciążeń.
3.2.1. Obciążenia stałe.
- Ciężar własny poprzecznicy - wartości charakterystyczne
A = 2 * b
f
* t
f
+ h
w
*n t
w
=
0,0306
m
²
g
po
= A * (78,5 + 2) =
2,463
kN/m
- Ciężar nawierzchni kolejowej typu: S60 - wartości charakterystyczne
g
s60
=
3,5
kN/m
l
p
=
5,25
m
- długość podłużnicy
R
s60
= 0,5 * g
s60
* l
p
=
9,188
kN
- Reakcje z podłużnicy od ciężaru własnego - wartości charakterystyczne
g
p
=
1,642
kN/m
l
p
=
5,25
m
- długość podłużnicy
R
p
= 0,5 * g
p
* l
p
=
4,311
kN
- Ciężar własny poprzecznicy - wartości obliczeniowe
gf =
1,2
g
po,o
= g
po
* gf =
2,956
kN/m
- Reakcja z podłużnicy od ciężaru własnego - wartości obliczeniowe
gf =
1,2
R
p,o
= R
p
* gf =
5,173
kN
- Reakcje z poprzecznicy od nawierzchni kolejowej typu: S60 - wartości obliczeniowe
gf =
1,2
R
s60,o
= R
s60
* g
f
=
11,025
kN
- Wartości sumaryczne obciążenia stałego:
q = g
po
=
2,463
kN/m
q
o
= g
po,o
=
2,956
kN/m
R = R
p
+ R
s60
=
13,498
kN
R
o
= R
p,o
+ R
s60,o
=
16,198
kN
3.2.2. Obciążenia ruchome.
ak =
1,33
- mnożnik klasy obciążenia
P = 250kN * a
k
=
332,5
kN
- obciążenie skupione - wartości charakterystyczne
p = 80kN/m * a
k
=
106,4
kN/m
- obciążenie równ. roz. - wartości charakterystyczne
gf =
1,5
P
o
= P * gf =
498,75
kN
- obciążenie skupione - wartości charakterystyczne
8
p
o
= p * gf =
159,6
kN/m
- obciążenie równ. roz. - wartości charakterystyczne
3.2.2.1. Wspólczynnik dynamiczny poprzecznicy.
L = 2 * l
p
+ 3m =
13,5
m
f = 1,44 / (L^0,5 - 0,2) + 0,2 =
1,234
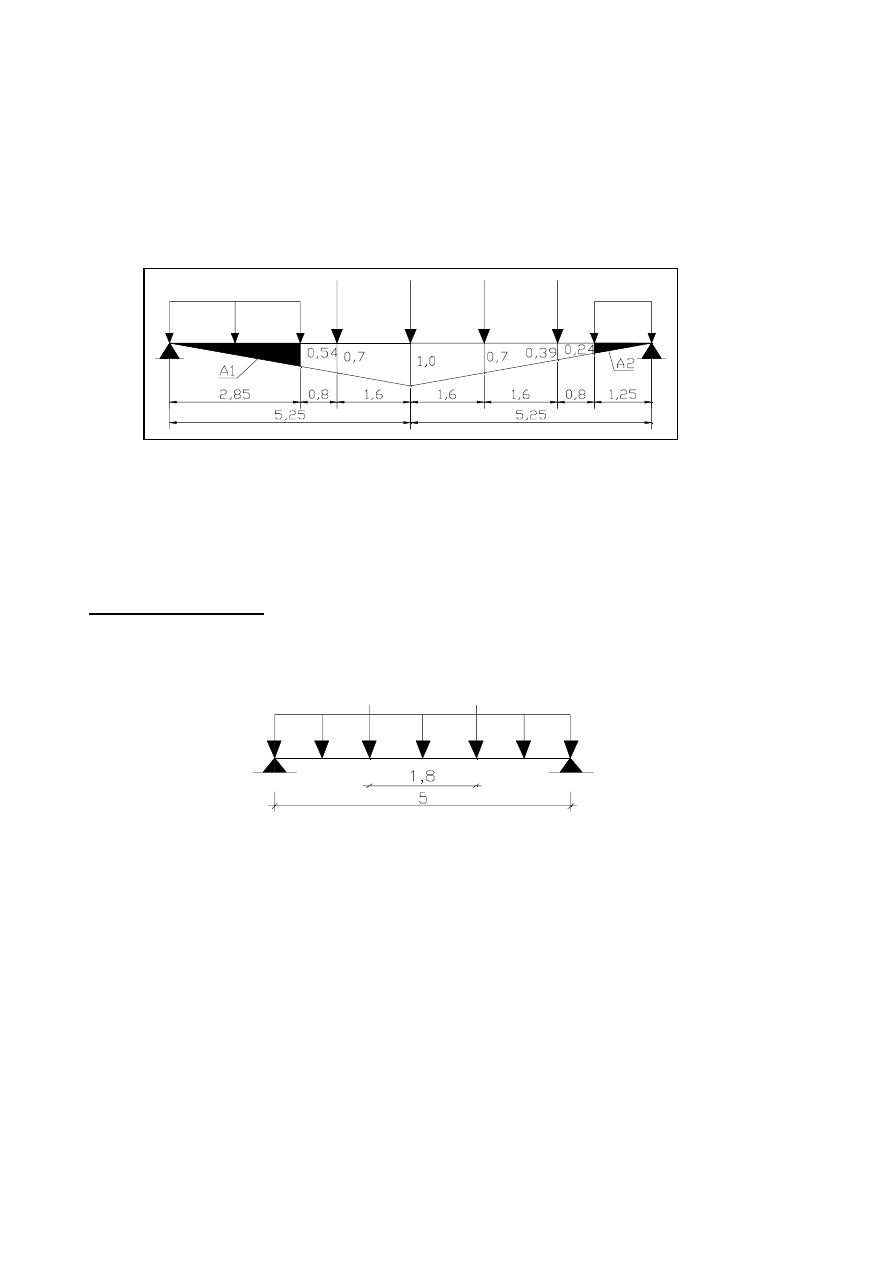
SCHEMAT OBCIĄŻENIA RUCHOMEGO DZIALAJACEGO
DZIALAJACEGO NA POPRZECZNICĘ
P
i
= 0,5 * P =
166,250
kN
p
i
= 0,5 * p =
53,200
kN/m
h
1
=
0,700
h
3
=
0,700
A
1
=
0,7695
m
h
2
=
1,000
h
4
=
0,39
A
2
=
0,15
m
R
r,k
= (S h
i
*P
i
+A
i
*p
i
) =
512,755
kN
3.3.0. Siły wewnętrzne.
SCHEMAT PRACY POPRZECZNICY
3.3.1. Reakcja podporowa wartości charakterystyczne.
R
A,k
= R
r,k
+ R + q * l
po
/ 2
=
532,411
kN
3.3.2. Moment w miejscu przyłożenia siły pionowej wartości charakterystyczne.
M
B,k=
R
A,k
*(l
po
/2-0,9)-q*(l
po
/2-0,9)²=
845,552
kNm
QB,k =
R
A,k
- q * (l
po
/2 - 0,9) =
522,312
kN
3.3.3. Reakcja podporowa wartości charakterystyczne ze współczynnikiem dynamicznym.
f =
1,234
R
A,k,f
= R
r,k
* f + R + q * l
po
/ 2
=
676,908
kN
9

3.3.4. Moment wartości charakterystyczne ze współczynnikiem dynamicznym.
f =
1,234
M
B,k,f =
R
A,k,f
* (l
po
/2 - 0,9) - q * (l
po
/2 - 0,9)²
M
B,k,f =
1076,746 kNm
QB,k,f =
R
A,k,f
- q * (l
po
/2 - 0,9) =
672,966
kN
3.3.5. Reakcja podporowa wartości obliczeniowe ze współczynnikiem dynamicznym.
f =
1,234
g =
1,2
g =
1,5
R
A,o,f,g
= R
r,k
*f*g+R*g+q*l
po
/2*g
R
A,o,f,g
=
1009,465 kN
3.3.6. Moment w miejscu przyłożenia siły pionowej wartości charakterystyczne.
f =
1,200
g =
1,2
g =
1,5
M
B,o,f,g =
R
A,o,f,g
* (l
po
/2 - 0,9) - q * (l
po
/2-0,9)² * g
M
B,o,f,g =
1607,576 kNm
QB,o,g,f=
R
A,o,f,g
-q*(l
po
/2-0,9)*g=
1005,523
kN
3.4.0. Cechy geometryczne przekroju.
3.4.1. Moment bezwładności przekroju.
J
x
= t
w
* h
w
³ / 12 + 2 * b
f
* t
f
³ / 12 + b
f
* t
f
* (h
w
/ 2 + t
f
/ 2)
² * 2
J
x
=
0,001692 m
4
3.4.2. Wskaźnik wytrzymałości przekroju.
Wx
= J
x
/ (0,5 * h
p
) =
0,006041
m³
3.4.3. Moment statyczny części odciętej osią x-x.
S
x
= t
w
* h
w
* 0,5 * 0,25 *h
w
+ b
f
* t
f
(h
w
* 0,5 + t
f
* 0,5)
S
x
= 0,0034245 m³
Wx1
= J
x
/ (0,5 * (h
p
- 2 * t
f
) =
0,006766
m³
3.4.4. Moment statyczny części odciętej osią 1-1.
S
x1
=b
f
* t
f
* 0,5 * (h
p
+ t
f
)
S
x1
=
0,002862 m³
10

3.5.0. Stan graniczny nośności - przekrój przęsłowy.
3.5.1. Maksymalne naprężenia normalne.
M
B,o,f,g =
1607,576 kNm
W
x
=
0,006041 m³
s
max
= M
B,o,f,g
/ W
x
=
266098,808
kN/m
²
s
max
=
266
MPa
R =
280
MPa
3.5.2. Sprawdzenie warunku wytrzymałościowego.
s
max
=
266
<
1,05 * R =
294
MPa
Warunek został spełniony!
3.5.3. Naprężenia normalne na wysokości połączenia pasa ze środnikiem.
M
B,o,f,g =
1607,576 kNm
W
x1
=
0,006766 m³
s
max
= M
B,o,f,g
/ W
x1
=
237588,222
kN/m
²
s
max
=
238
MPa
R =
280
MPa
3.5.4. Sprawdzenie warunku wytrzymałościowego.
s
max
=
238
<
1,05 * R =
294
MPa
Warunek został spełniony!
3.5.5. Maksymalne naprężenia styczne na poziomie osi X-X.
QB,o,g,f =
1005,523 kN
S
x
= 0,0034245 m³
J
x
=
0,001692 m
4
t
w
=
0,018
m
t
max
= Q
B,o,f,g
* S
x
/ (J
x
* t
w
) =
113091,553
kN/m
²
t
max
=
113
MPa
R
t
=
170
MPa
3.5.6. Sprawdzenie warunku wytrzymałościowego.
t
max
=
113
<
R
t
=
170
MPa
Warunek został spełniony!
3.5.7. Maksymalne naprężenia styczne na poziomie osi 1-1.
QB,o,g,f =
1005,523 kN
S
x1
=
0,002862 m³
J
x
=
0,001692 m
4
t
w
=
0,018
m
t
max
= Q
B,o,f,g
* S
x1
/ (J
x
* t
w
) =
94515,411
kN/m
²
t
max
=
95
MPa
11
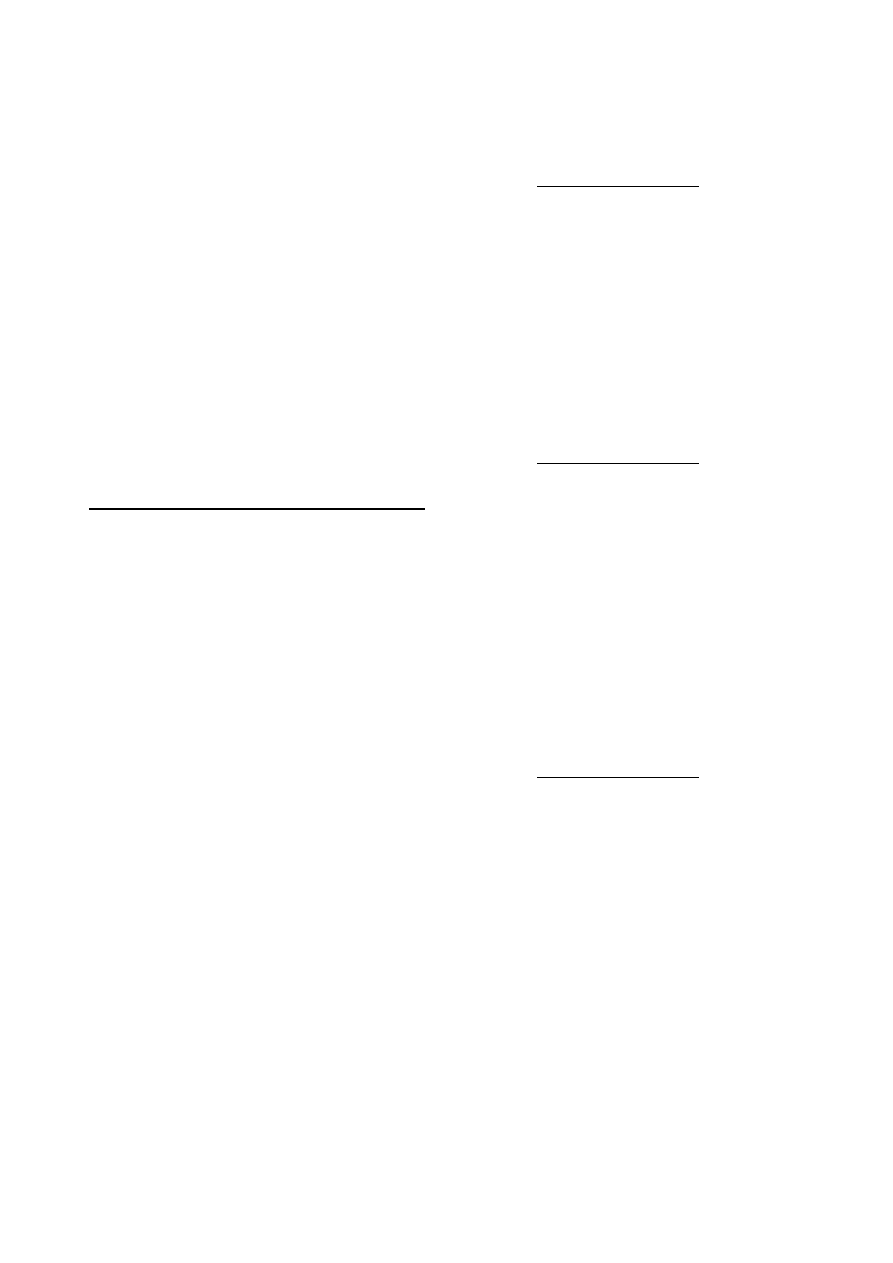
R
t
=
170
MPa
3.5.8. Sprawdzenie warunku wytrzymałościowego.
t
max
=
95
<
R
t
=
170
MPa
Warunek został spełniony!
3.5.9. Złożony stan naprężeń na poziomie osi 1-1.
s
1
=
238
MPa
t
1
=
95
MPa
s
z
= (s
1
² + 3 * t
1
²)^0,5 =
289
MPa
R =
280
MPa
3.5.10. Sprawdzenie warunku wytrzymałościowego.
s
z
=
289
<
1,1 * R =
308
MPa
Warunek został spełniony!
3.6.0. Stan graniczny użytkowania - ugięcie.
M =
845,552
kNm
E = 205000000 kN/m
²
l
po
=
5,000
m
J
x
=
0,001692 m
4
f = 5 * M * l
p
² / (48 * E * J
x
) =
0,006
m
f
dop
= l
p
/ 600 =
0,008
m
3.6.1. Sprawdzenie warunku wytrzymałościowego.
f =
0,006
<
f
dop
=
0,008
Warunek został spełniony!
12
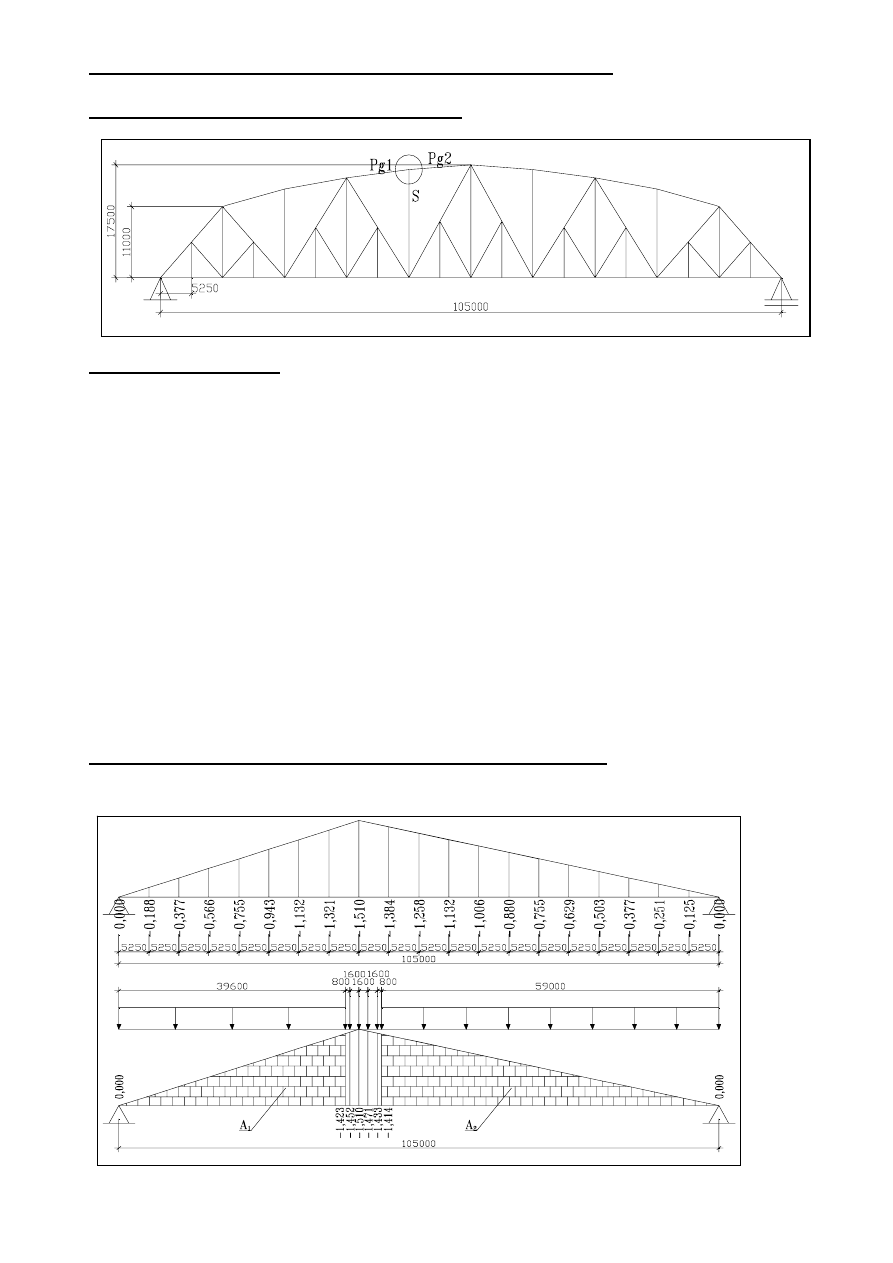
4.0. SIŁY WEWNĘTRZNE W PRĘTACH WYBRANEGO WĘZŁA.
4.1.0. Schemat statyczny mostu - wybrany węzeł.
4.2.0. Zebranie obciążeń.
4.2.1. Zebranie obciążeń stałych działających na dżwigar kratowy.
- Długość podłużnicy
l
p
=
5,25
m
- Długość poprzecznicy
l
po
=
5
m
- Ciężar własny podłużnicy - wartości charakterystyczne
g
p
=
1,642
kN/m
- Ciężar nawierzchni kolejowej typu: S60 - wartości charakterystyczne
g
s60
=
3,5
kN/m
- Ciężar własny poprzecznicy - wartości charakterystyczne
g
po
=
2,463
kN/m
- Reakcje od ciężaru stałego - wartość charakterystyczna
R
g,k
=0,5*((g
p
+g
s60
)*l
p
+g
po
*l
po
) =
19,657
kN
- Reakcje od ciężaru stałego - wartość obliczeniowa
gf =
1,2
R
g,k
=0,5*((g
p
+g
s60
)*l
p
+g
po
*l
po
)*g
f
=
23,588
kN
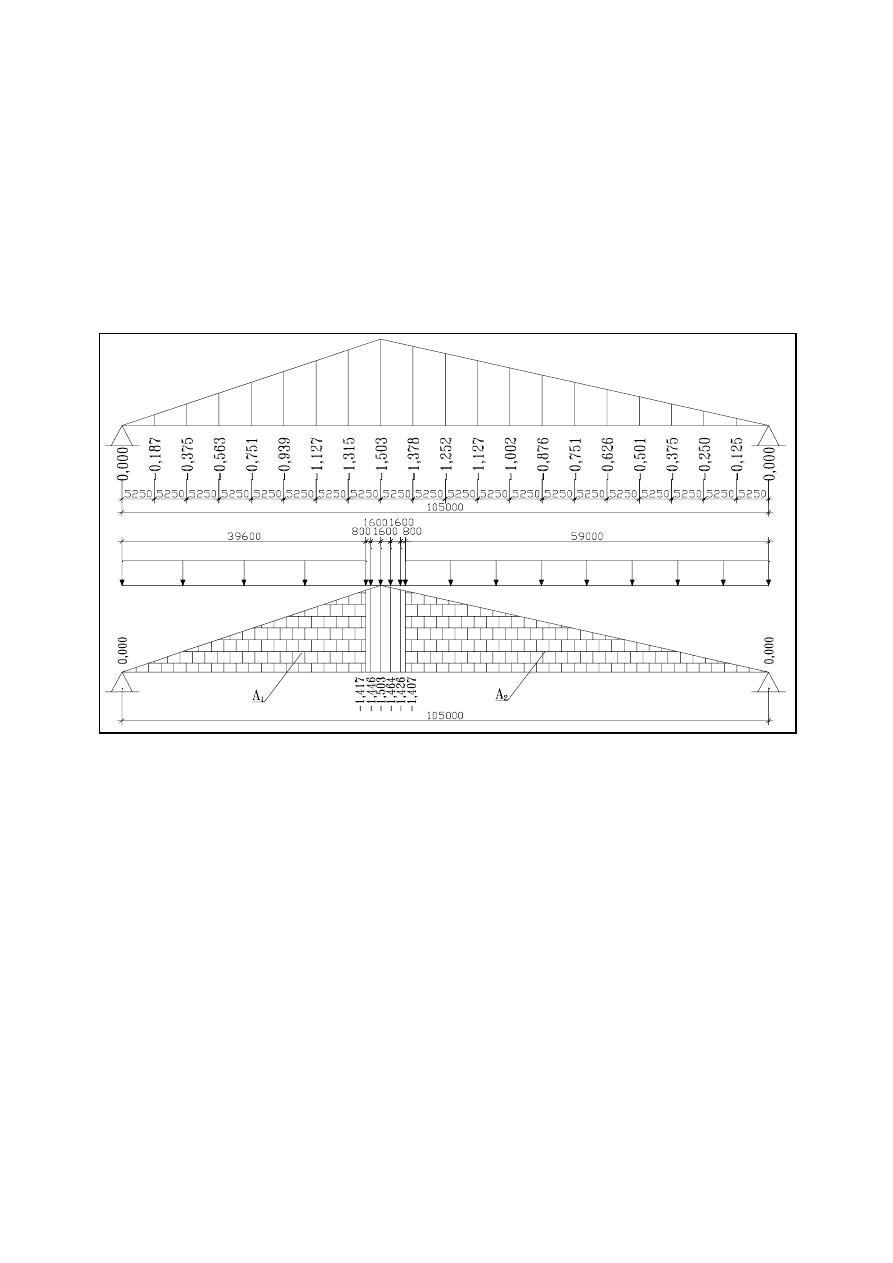
4.2.0. Wyznaczenie lini wpływowych oraz sił statycznych w prętach.
4.2.1. Wykres lini wpływowej dla pręta Pg1.
13

4.2.1.1. Siła w pręcie Pg1 od obciążenia stałego - wartość charakterystyczna.
R
i
= R
g,k
=
19,657
kN
h
1
= -0,188
h
7
= -1,321
h
13
= -0,880
h
19
= -0,125
h
2
= -0,377
h
8
= -1,510
h
14
= -0,755
h
3
= -0,566
h
9
= -1,384
h
15
= -0,629
h
4
= -0,755
h
10
= -1,258
h
16
= -0,503
h
5
= -0,943
h
11
= -1,132
h
17
= -0,377
h
6
= -1,132
h
12
= -1,006
h
18
= -0,251
N
g,k
= S h
i
*R
i
=
-296,656 kN
4.2.1.2. Siła w pręcie Pg1 od obciążenia stałego - wartość obliczeniowa.
gf =
1,2
N
g,o
= N
g,k
g
f
=
-355,988
kN
4.2.1.3. Siła w pręcie Pg1 od obciążenia ruchomego - wartość charakterystyczna.
Obciążenia ruchome:
ak =
1,33
- mnożnik klasy obciążenia
P = 250kN * a
k
=
332,5
kN
- obciążenie skupione - wartości charakterystyczne
p = 80kN/m * a
k
=
106,4
kN/m
- obciążenie równ. roz. - wartości charakterystyczne
gf =
1,5
P
o
= P * gf =
498,75
kN
- obciążenie skupione - wartości charakterystyczne
p
o
= p * gf =
159,6
kN/m
- obciążenie równ. roz. - wartości charakterystyczne
- Wspólczynnik dynamiczny dla pręta Pg:
L
o
=
10,58
m
f = 1,44 / (L^0,5 - 0,2) + 0,2 =
1,292
4.2.1.4. Wyznaczenie maksymalnej siły ściskającej dla pręta Pg1.
P
i
= 0,5 * P =
166,250
kN
p
i
= 0,5 * p =
53,200
kN/m
h
1
=
-1,4520
h
2
=
-1,5100
h
3
=
-1,4710
h
4
=
-1,433
A
1
=
-28,175
m
A
2
=
-41,713
m
N
p,k
= (S h
i
*P
i
+A
i
*p
i
) =
-4693,285
kN
4.2.1.4. Siła w pręcie Pg1 od obciążenia ruchomego - wartość charakterystyczna ze
wsp. dynamicznym.
N
p.k,f
= N
p,k *
f =
-6062,387 kN
4.2.1.5. Siła w pręcie Pg1 od obciążenia ruchomego - wartość obliczeniowa .
gf =
1,5
14
N
p.o,f,g
= N
p,k,f
* gf = -9093,580 kN
4.2.1.6. Sumaryczne wartości siły w pręcie Pg1.
- Wartości charakterystyczne bez współczynnika dynamicznego:
N
k
= N
p,k
+ N
g,k
= -4989,942 kN
- Wartości charakterystyczne wraz ze współczynnikiem dynamicznym:
N
k,f
= N
p,k,f
+ N
g,k
= -6359,043 kN
- Wartości obliczeniowe:
N
o
= N
p,o,f,g
+ N
g,o
= -9449,568 kN
4.2.2. Wykres lini wpływowej dla pręta Pg2.
4.2.2.1. Siła w pręcie Pg2 od obciążenia stałego - wartość charakterystyczna.
R
i
= R
g,k
=
19,657
kN
h
1
= -0,187
h
7
= -1,315
h
13
= -0,876
h
19
= -0,125
h
2
= -0,375
h
8
= -1,503
h
14
= -0,751
h
3
= -0,563
h
9
= -1,378
h
15
= -0,626
h
4
= -0,751
h
10
= -1,252
h
16
= -0,501
h
5
= -0,939
h
11
= -1,127
h
17
= -0,375
h
6
= -1,127
h
12
= -1,002
h
18
= -0,250
N
g,k
= S h
i
*R
i
=
-295,300 kN
4.2.2.2. Siła w pręcie Pg2 od obciążenia stałego - wartość obliczeniowa.
gf =
1,2
N
g,o
= N
g,k
g
f
=
-354,360
kN
15
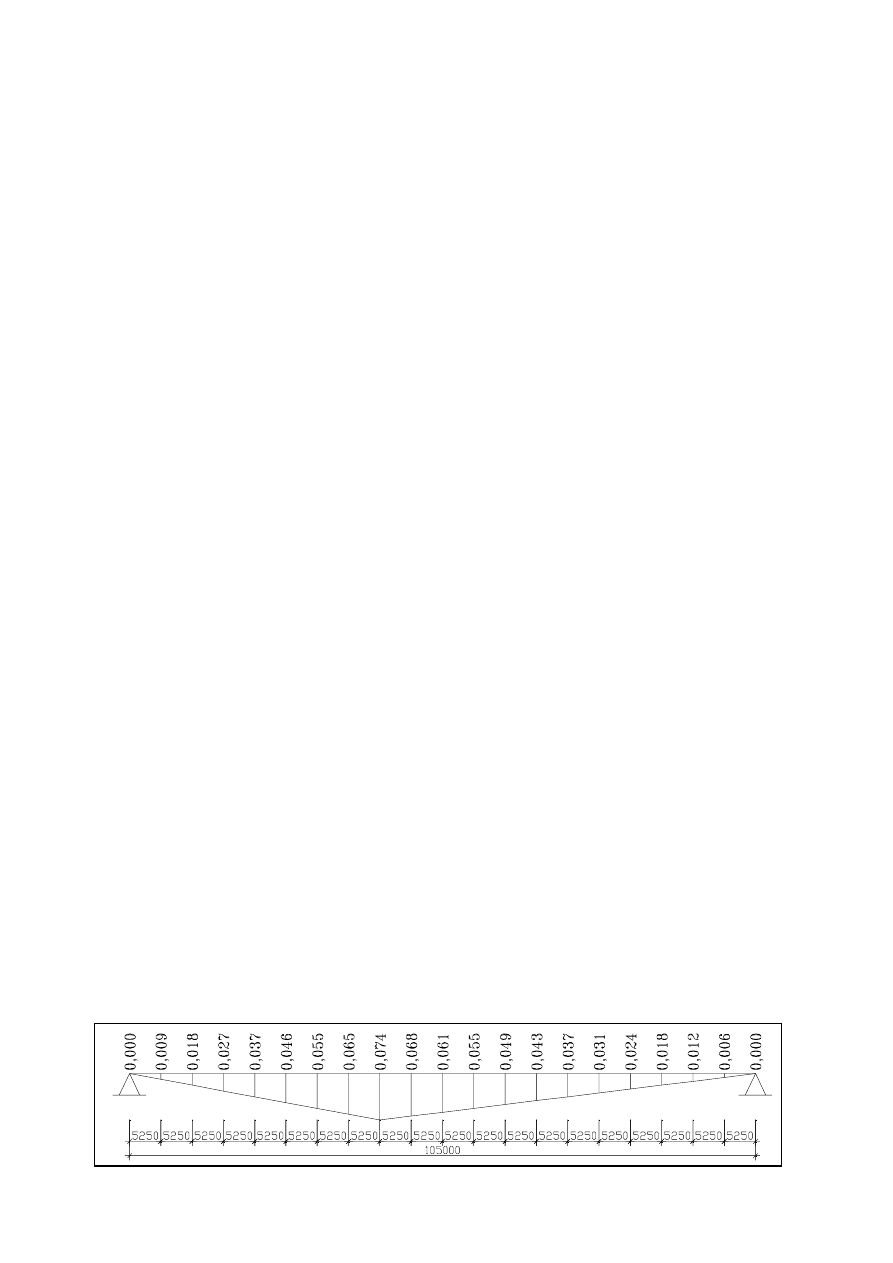
4.2.2.3. Siła w pręcie K1 od obciążenia ruchomego - wartość charakterystyczna.
Obciążenia ruchome:
ak =
1,33
- mnożnik klasy obciążenia
P = 250kN * a
k
=
332,5
kN
- obciążenie skupione - wartości charakterystyczne
p = 80kN/m * a
k
=
106,4
kN/m
- obciążenie równ. roz. - wartości charakterystyczne
gf =
1,5
P
o
= P * gf =
498,75
kN
- obciążenie skupione - wartości charakterystyczne
p
o
= p * gf =
159,6
kN/m
- obciążenie równ. roz. - wartości charakterystyczne
- Wspólczynnik dynamiczny dla pręta K1:
L
o
=
10,523
m
f = 1,44 / (L^0,5 - 0,2) + 0,2 =
1,293
4.2.2.4. Wyznaczenie maksymalnej siły ściskającej dla pręta Pg2.
P
i
= 0,5 * P =
166,250
kN
p
i
= 0,5 * p =
53,200
kN/m
h
1
=
-1,4460
h
4
=
-1,426
h
2
=
-1,5030
A
1
=
-28,057
m
h
3
=
-1,4640
A
2
=
-41,507
m
N
p,k
= (S h
i
*P
i
+A
i
*p
i
) =
-4671,491
kN
4.2.2.4.1. Siła w pręcie Pg2 od obciążenia ruchomego - wartość charakterystyczna,
ze wsp. dynamicznym.
N
p.k,f
= N
p,k *
f =
-6040,586 kN
4.2.2.5. Siła w pręcie Pg2 od obciążenia ruchomego - wartość obliczeniowa.
gf =
1,5
N
p.o,f,g
= N
p,k,f
* gf =
-9060,879
kN
4.2.2.6. Sumaryczne wartości siły ściskającej w pręcie Pg2.
- Wartości charakterystyczne bez współczynnika dynamicznego:
N
k
= N
p,k
+ N
g,k
=
-4966,791 kN
- Wartości charakterystyczne wraz ze współczynnikiem dynamicznym:
N
k,f
= N
p,k,f
+ N
g,k
= -6335,886 kN
- wartości obliczeniowe:
N
o
= N
p,o,f,g
+ N
g,o
= -9415,239 kN
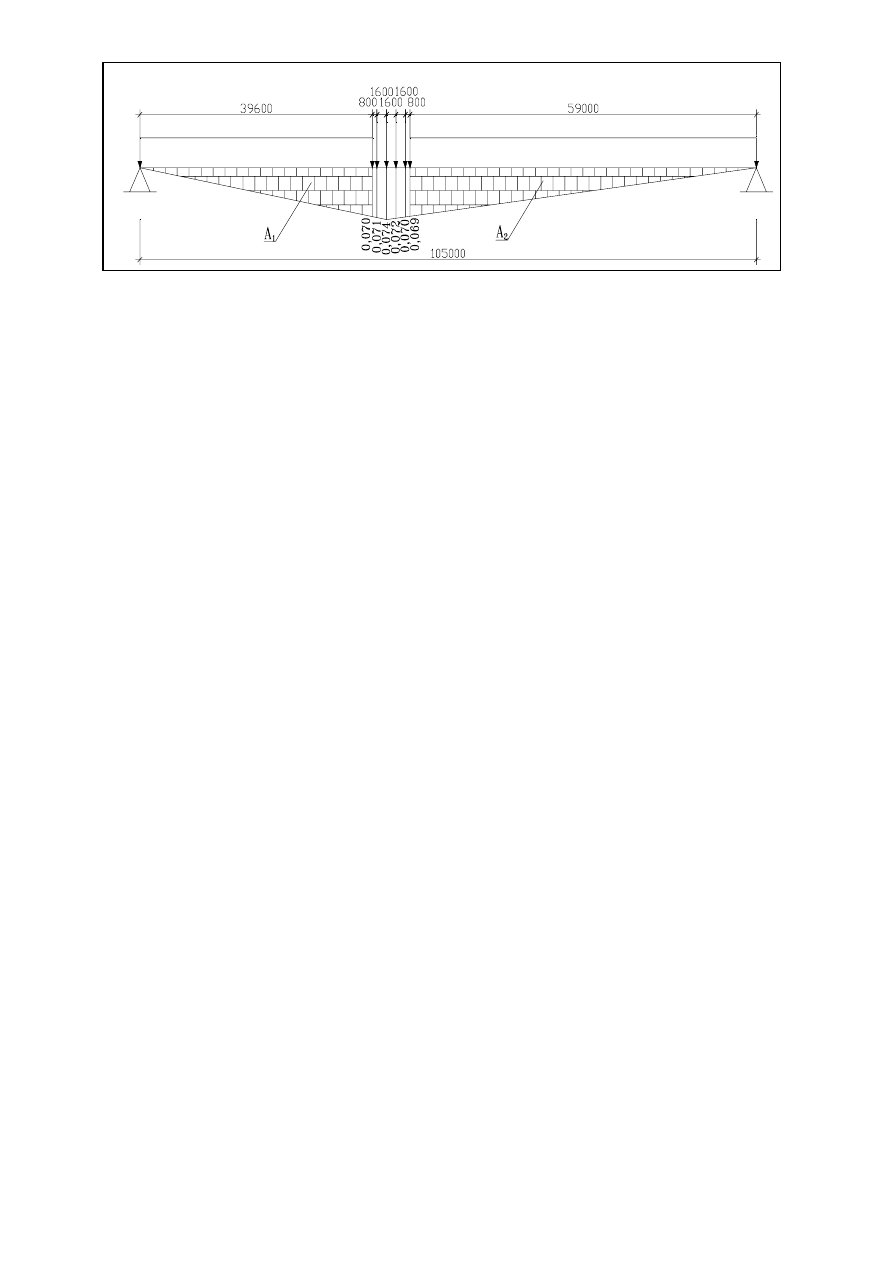
4.2.3. Wykres lini wpływowej dla pręta S - słupek.
16
4.2.3.1. Siła w pręcie S od obciążenia stałego - wartość charakterystyczna.
R
i
= R
g,k
=
19,657
kN
h
1
= 0,009
h
7
= 0,065
h
13
= 0,043
h
19
= 0,006
h
2
= 0,018
h
8
= 0,074
h
14
= 0,037
h
3
= 0,027
h
9
= 0,068
h
15
= 0,031
h
4
= 0,037
h
10
= 0,061
h
16
= 0,024
h
5
= 0,046
h
11
= 0,055
h
17
= 0,018
h
6
= 0,055
h
12
= 0,049
h
18
= 0,012
N
g,k
= S h
i
*R
i
=
14,448 kN
4.2.3.2. Siła w pręcie S od obciążenia stałego - wartość obliczeniowa.
gf =
1,2
N
g,o
= N
g,k
g
f
=
17,337
kN
4.2.3.3. Siła w pręcie S od obciążenia ruchomego - wartość charakterystyczna.
Obciążenia ruchome:
ak =
1,33
- mnożnik klasy obciążenia
P = 250kN * a
k
=
332,5
kN
- obciążenie skupione - wartości charakterystyczne
p = 80kN/m * a
k
=
106,4
kN/m
- obciążenie równ. roz. - wartości charakterystyczne
gf =
1,5
P
o
= P * gf =
498,75
kN
- obciążenie skupione - wartości charakterystyczne
p
o
= p * gf =
159,6
kN/m
- obciążenie równ. roz. - wartości charakterystyczne
- Wspólczynnik dynamiczny dla pręta K1:
L
o
=
16,8
m
f = 1,44 / (L^0,5 - 0,2) + 0,2 =
1,189
4.2.3.4. Wyznaczenie maksymalnej siły rozciągającej dla pręta S.
P
i
= 0,5 * P =
166,250
kN
p
i
= 0,5 * p =
53,200
kN/m
h
1
=
0,071
h
2
=
0,074
h
3
=
0,072
h
4
=
0,07
A
1
=
1,386
m
17

A
2
=
2,036
m
N
p,k
= (S h
i
*P
i
+A
i
*p
i
) =
229,738
kN
4.2.3.4.1. Siła w pręcie S od obciążenia ruchomego - wartość charakterystyczna,
ze wsp dynamicznym.
N
p.k,f
= N
p,k *
f =
273,238
kN
4.2.3.5. Siła w pręcie S od obciążenia ruchomego - wartość obliczeniowa.
gf =
1,5
N
p.o,f,g
= N
p,k,f
* gf =
409,856
kN
4.2.3.6. Sumaryczne wartości siły rozciągającej w pręcie S.
- Wartości charakterystyczne bez współczynnika dynamicznego:
N
k
= N
p,k
+ N
g,k
=
244,185
kN
- Wartości charakterystyczne wraz ze współczynnikiem dynamicznym:
N
k,f
= N
p,k,f
+ N
g,k
=
287,685
kN
- Wartości obliczeniowe:
N
o
= N
p,o,f,g
+ N
g,o
=
427,193
kN
18
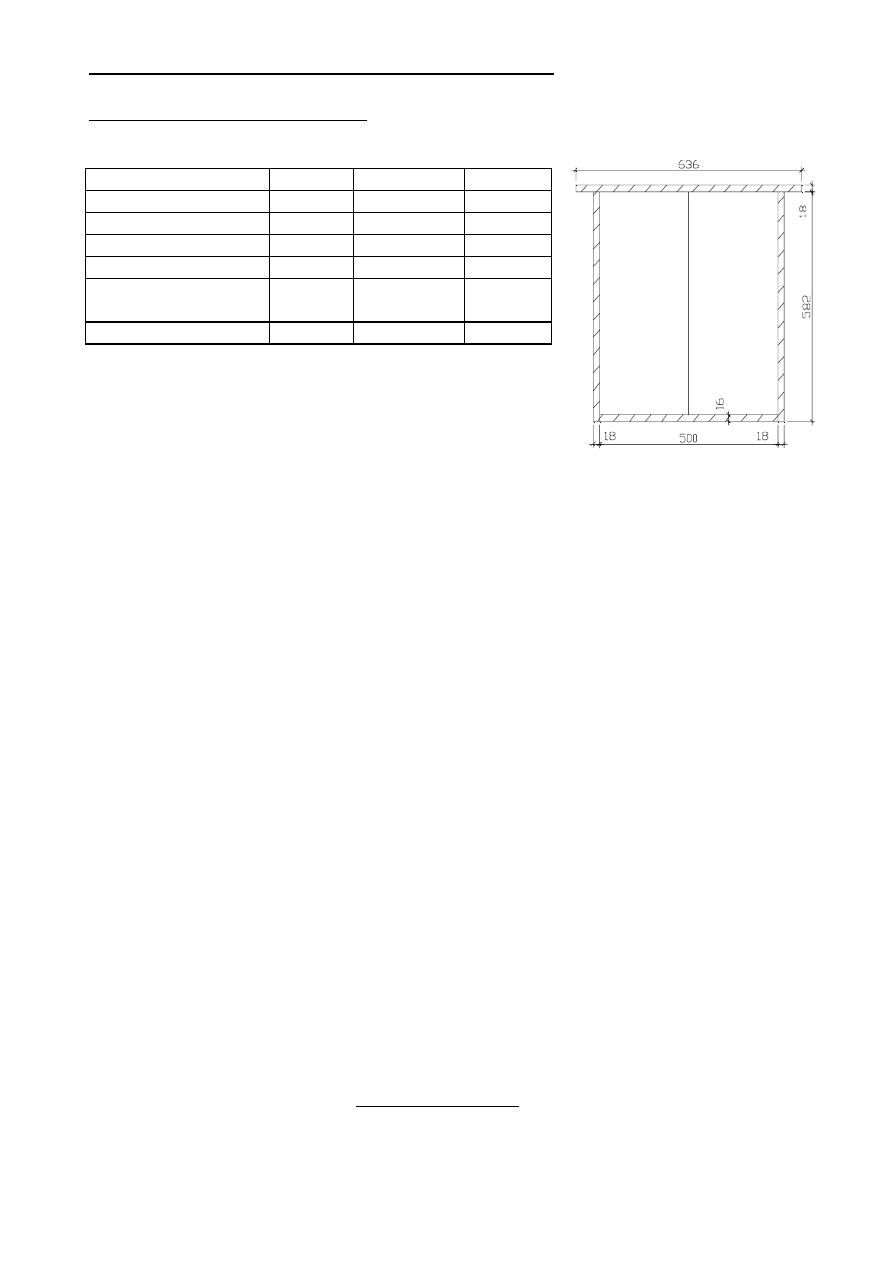
5.0. WYMIAROWANIE PRĘTÓW WYBRANEGO WĘZŁA.
5.1. Pręt Pg1 - wymiary wstępne.
Nazwa elementu
Symbol
Wymiar
Jednostka
Wysokośc Pd1
h
0,6
m
Szerokośc pasa dolnego
b
1
0,5
m
Szerokośc pasa górnego
b
2
0,636
m
Grubośc pasa dolnego
t
1
0,016
m
Grubośc środników i
t
2
0,018
m
pasa górnego
Pole przekroju
A
0,040472
m²
5.1.1. Zestawienie max sił obliczeniowych w pręcie.
N
obl
=
9449,568
kN
ściskanie
N
maxk
=
4989,942
kN
ściskanie
N
mink
=
296,656
kN
ściskanie
5.1.2.0. Środek ciężkości przekroju.
5.1.2.1. Moment statyczny przekroju względem zewnętrznej krawędzi dolnej półki:
S= b
1
*t
1
*0,5*t
1
+2*t
2
*(h-t
1
)*(h/2+t
1
)+b
2
*t
2
*(h-t
2
/2)
S= 0,01347335 m³
y= S/A=
0,33
m
x= b
1
/2=
0,25
m
5.1.2.2. Promieni bezwładności przekroju.
I
x
= t
1
³*b
1
/12+ t
1
*b
1
*(y-t
1
/2)²+ 2*[(h-t
1
)³*t
2
/12+(h-t
1
)*t
2
*((h-t
1
)/2+t
1
-y))²]+t
2
³*b
2
/12+t
2
*b
2
*(h-y-t
2
/2)²
I
x
=
0,002218 m
4
- Promień bezwładności przekroju w płaszczyźnie ramy
i
x
= (I
x
/A)^0,5=
0,234
m
I
y
= b
1
³*t
1
/12+b
2
³*t
2
/12+2*(h-t
1
)*t
2
³/12+ 2*(h-t
1
)*t
2
*(b
2
/2+t
2
/2)²
I
y
= 0,002801 m
4
- Promień bezwładności przekroju z płaszczyzny ramy
i
y
= (I
y
/A)^0,5=
0,263
m
5.1.3.0. Sprawdzenie warunku smukłości.
5.1.3.1. Smukłośc pasa dolnego w płaszczyźnie ramy.
l<150
l=l
w
/i
x
=
45,19
< 150
Warunek został spełniony!
l
w
=µ*l
o
=
10,58
m
l
o
=
10,58
m
µ=
1,0
19

5.1.3.2. Smukłośc pasa dolnego z płaszczyzny ramy.
l<150
l=l
w
/i
y
=
40,22
< 150
l
w
=µ*l
o
=
10,58
m
l
o
=
10,58
m
µ=
1,0
5.1.4.0. Nośnośc dla elementu ściskanego osiowo.
Smukłość porównawcza:
l=
45,19
R=
280
MPa
l
p
=118*(200/R)^0.5= 99,728202
l/l
p
=
0,45
Współczynnik wyboczeniowy.
m
w
=
1,15
s= (P*m
w
)/F
w
≤ R
P=
9,449568 MN
F
w
=
0,04
σ=
268,51
MPa
≤ R =
280
MPa
σ
/R=
0,96
Warunek został spełniony!
5.1.4.1. Nośnośc z uwzględnieniem zmęczenia.
Rodzaje karbów:
nr1 stal poza złączem o powierzchni surowej oraz krawędziach po cieciu gazowym automatycznym β=1,4;
nr2 stal poza złączami o powierzchni surowej, w miejscu zmiany przekroju z wyokrągleniem promieni r>50mm β=1,8;
nr3 złącze spawane spoiną czołową z podpawaniem spoiną nie sprawdzoną defektoskopowo na całej dlugości β=2,9;
nr4 złącze spawane spoiną czołową, podpawaną dwuch elementów o różnej szerokości lub grubości β=1,4;
nr5 złącza spawane spoinami równoległymi do kierunku działania siły, obrobionymi mechanicznie przy zastosowaniu
spawania ręcznego β=1,4;
nr6 stal w pobliżu żeber i przepon przyspawanych do pasów spoinami pachwinowymi poprzecznie do kierunku działania
siły przy przejściu nie obrobionym β=2,2;
nr7 połączenie spoinami pachwinowymi podłużnymi elementu pręta kratownicy β=3,4;
nr8 stal pręta kratownicy z przyspawanymi poprzecznymi żebrami lub przeponami z wykrojami w narożach, przez które
przeprowadzone są spoiny pachwinowe jeśli pręt jest ściskany β=1,8;
nr9 złącze na śruby pracujące na ścinanie i stal części łączonych pracujących na docisk β=1,8.
Do obliczeń przyjmuję najbardziej niekożystną warośc β=3,4.
σ
k
≤ R*m
zm
R=
280
MPa
m
zm
= c/[(a*β- b)- (a*β+ b)* ρ]
ρ= σ
min
/ σ
max
=
0,059
A=
0,040472 m²
σ
max
= N
maxk
/ A=
123,29
MPa
σ
min
= N
mink
/A=
7,33
MPa
20
c=
1,1
b=
0,3
a=
0,8
β=
3,4
m
zm
= 0,49
R*m
zm
=
137,47
MPa
123,29
MPa
≤
137,47
MPa
Warunek został spełniony!
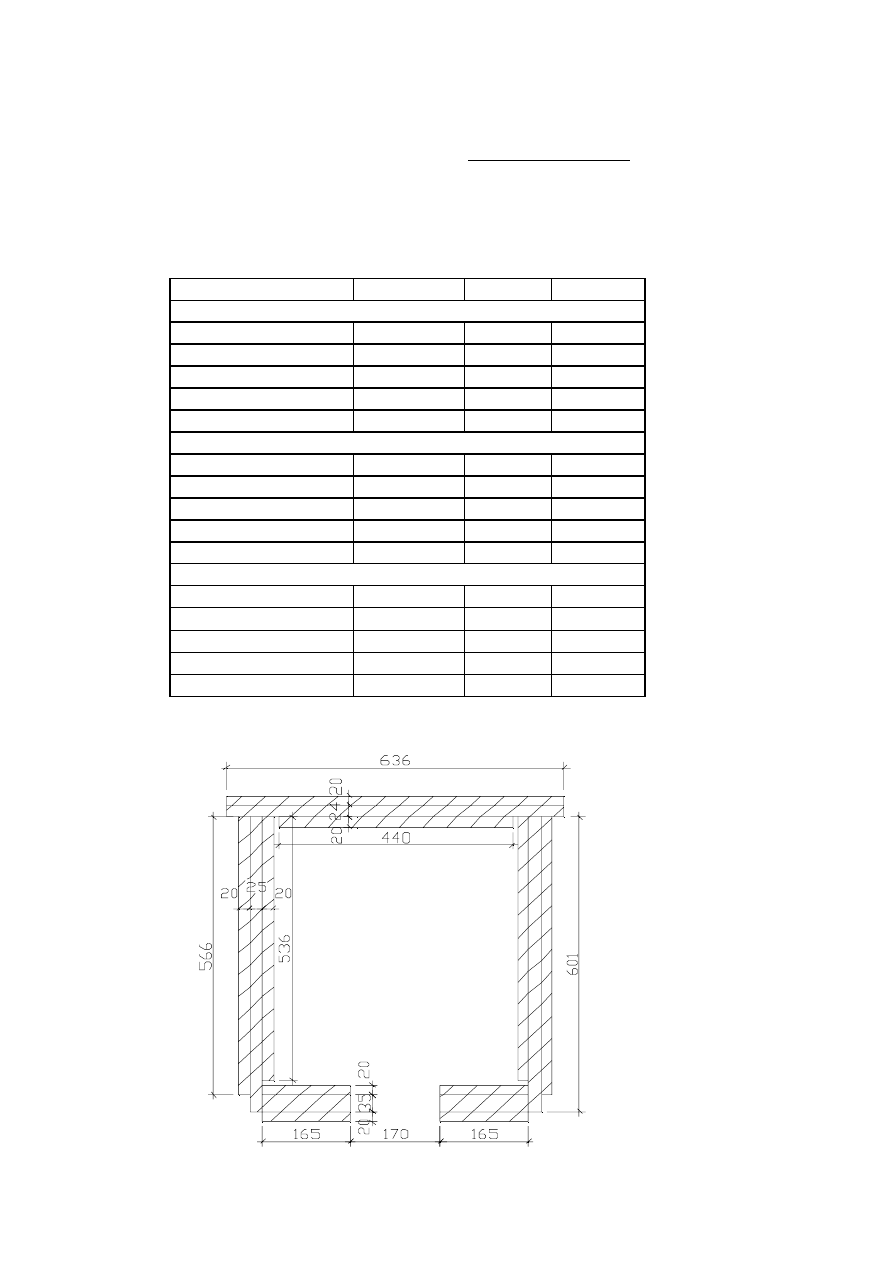
5.1.5.0. Styk pasa górnego.
5.1.5.1. Wymiary wstępne.
Nazwa elementu
Symbol
Wymiar
Jednostka
PAS DOLNY
Szerokośc pasa dolnego
bd
0,165
m
Grubośc pasa dolnego
t
d
0,035
m
Szerokośc podkładki 1
b
pd1
0,165
m
Szerokośc podkładki 2
b
d2
0,165
m
Grubośc podkładek
t
pd
0,020
m
PAS GÓRNY
Szerokośc pasa górnego
b
g
0,636
m
Grubośc pasa górnego
tg
0,024
m
Szerokośc podkładki 1
b
pg1
0,636
m
Grubosc podkładek
t
pg
0,020
m
Szerokośc podkładki 2
b
pg2
0,440
m
ŚRODNIK
Wysokośc środnika
hs
0,601
m
Grubośc środnika
ts
0,025
m
Wysokośc podkładki 1
hps1
0,536
m
Wysokosc podkładki 2
hps2
0,566
m
Grubośc podkładek
tps
0,020
m
21

5.1.5.2. Połączenie pasa dolnego.
Przyjęto połączenia na śruby sprężające.
Średnica śrub sprężających:
d=(50*t
pd
)^0,5-2= 29,622777 mm
Przyjęto:
d=
30
mm
Średnica otworu:
d
o
=d+2=
32
mm
5.1.5.2.1. Sprawdzennie warunków połączenia.
F
npasa
≤ F
nnak
F
npasa
= b
d
*t
d
-1*t
d
*d
o
=
0,004655
m²
F
nnak
= t
pd
*(b
p1d
+ b
p2d
)- 1* 2*t
pd
* d
o
=
0,00532
m²
0,00466 m²
≤
0,00532
m²
Warunek został spełniony!
5.1.5.2.2. Nośność pojedyńczej śruby.
N'= n*µ*P
s
n=
2
- ilość powierzchni tarcia
P
s
= 0,8* R
02
* F
s
/1,25=
478,39
kN
- siła napinająca dla śrub M30 kl. 12.9
R
02
=
1058
MPa
F
s
=π*d²/4=
0,000707 m²
µ=
0,45
- współczynnik tarcia
N'=
430,55
kN
5.1.5.2.3. Ilości śrub w połączeniu.
N'* n ≥ N
pasa
R=
280
MPa
N
pasa
= b
g
* t
g
* R=
1617
kN
n= N
pasa
/ N'=
3,755690
Przyjęto
n= 4
śrub po jednej stronie połączenia
5.1.5.3. Połączenie pasa górnego.
Średnica śrub sprężających:
d=(50*t
pg
)^0,5-2= 29,622777 mm
Przyjęto :
d=
30
mm
Średnica otworu:
d
o
=d+2=
32
mm
5.1.5.3.1. Sprawdzennie warunków połączenia.
F
npasa
≤ F
nnak
F
npasa
= b
g
*t
g
-3*t
g
*d
o
=
0,01296
m²
F
nnak
= 2*t
pg
*b
pg
- 3* 2*t
pg
* d
o
=
0,021600
m²
0,01296 m²
≤
0,0216 m²
Warunek został spełniony!
22

5.1.5.3.2. Nośność pojedyńczej śruby.
N'= n*µ*P
s
n=
2
- ilość powierzchni tarcia
P
s
= 0,8* R
02
* F
s
/1,25=
478,39
kN
- siła napinająca dla śrub M30 kl. 12.9
R
02
=
1058
MPa
F
s
=π*d²/4=
0,000707 m²
µ=
0,45
- współczynnik tarcia
N'=
430,55
kN
5.1.5.3.3. Ilości śrub w połączeniu.
N'* n ≥ N
pasa
R=
280
MPa
N
pasa
= b
d
* t
d
* R=
4273,92
kN
n= N
pasa
/ N'=
9,926727
Przyjęto
n= 10
śrub po jednej stronie połączenia
5.1.5.4. Połączenie pasa środników.
Średnica śrub sprężających:
d=(50*t
s
)^0,5-2= 33,355339 mm
Przyjęto :
d=
34
mm
Średnica otworu:
d
o
=d+2=
36
mm
5.1.5.4.1. Sprawdzennie warunków połączenia.
I
nśr
≤ I
nnak
I
śr
= h
s
³
* t
s
/12
=
0,000452 m
2
I
nnak
= t
ps
* h
ps2
³
/ 12 + t
ps
*h
ps1
³/12=
0,000559
m
2
0,00045
m²
≤
0,00056
m²
Warunek został spełniony!
5.1.5.4.2. Nośność pojedyńczej śruby.
N'= n*µ*P
s
n=
2
- ilość powierzchni tarcia
P
s
= 0,8* R
02
* F
s
/1,25=
591,38
kN
- siła napinająca dla śrub M34 kl. 12.9
R
02
=
1058
MPa
F
s
=π*d²/4=
0,000873 m²
µ=
0,45
- współczynnik tarcia
N'=
532,24
kN
5.1.5.4.3. Ilości śrub w połączeniu.
N'* n ≥ N
pasa
R=
280
MPa
N
pasa
= b
d
* t
d
* R=
4207
kN
n= N
pasa
/ N'=
7,904
Przyjęto
n= 8
śrub po jednej stronie połączenia
23
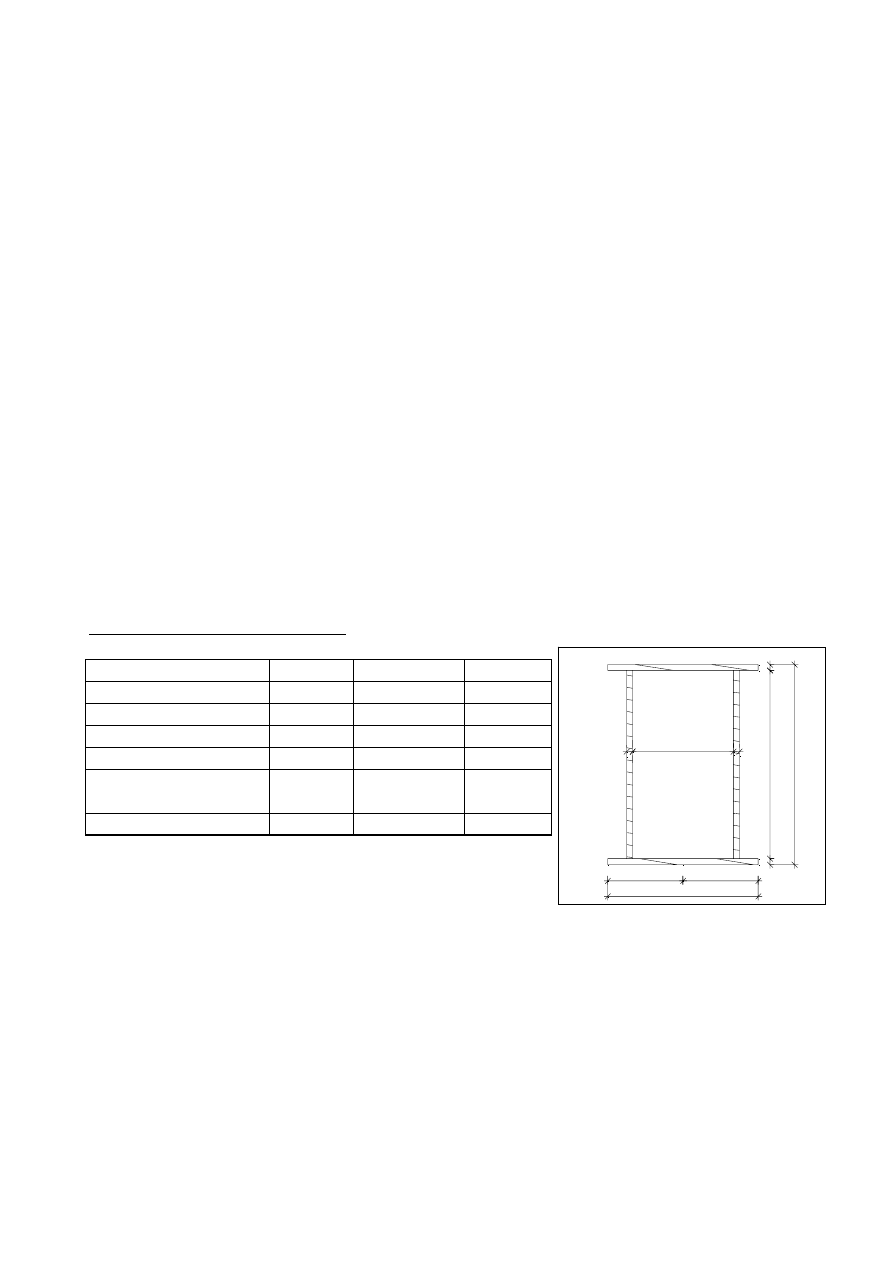
5.1.5.5.4.4. Rozstaw śrub w połączeniu.
(t-d
1
)* t
s
* R ≥ n* N'
R=
280
MPa
n=
2
N'=
532,24
kN
t
max
= (n* N')/ (t
s
* R)+ d
1
=
0,19
m
5.1.5.4.5. Warunki konstrukcyjne rozmieszczenia śrub.
5.1.5.4.5.1. Odległość środka otworu od krawedzi elementu w kierunku
zgodnym z kierunkiem działania siły.
e
1
≥ =2*30 =
60
mm (pas dolny)
e
1
≥ =2*30 =
60
mm (pas górny)
e
1
≥ =2*34 =
68
mm (środnik)
5.1.5.4.5.2.2. Rozmieszczenie śrub w nośnych połączeniach elementów rozciaganych.
pas dolny 3,5*d≤t ≤ 8*d
105
mm
≤ t ≤
240
mm
t ≤ 16*t
pd
t ≤
240
mm
pas górny 3,5*d≤t ≤ 8*d
105
mm
≤ t ≤
240
mm
t ≤ 16*t
pg
t ≤
240
mm
środnik 3,5*d≤t ≤ 8*d
119
mm
≤ t ≤
272
mm
t ≤ 16*t
ps
t ≤
320
mm
5.2. Pręt S - wymiary wstępne.
Nazwa elementu
Symbol
Wymiar
Jednostka
Wysokość h
0,500
m
Szerokość pasa dolnego
b
1
0,400
m
Szerokość pasa górnego
b
2
0,400
m
Grubość pasa dolnego
t
1
0,016
m
Grubość środników i
t
2
0,016
m
pasa górnego
Pole przekroju
A
0,029
m²
5.2.1. Zestawienie max sił obliczeniowych w prętach.
N
obl
=
427,193
kN
N
maxk
=
244,185
kN
N
mink
=
14,448
kN
5.2.2.0. Środek ciężkości przekroju.
y= h/ 2=
0,25
m
x= b
1
/ 2=
0,20
m
16
268
16
200
200
400
16
50
0
16
53
2
24

5.2.2.1. Promieni bezwładności przekroju.
I
x
= t
1
³*b
1
/12+ t
1
*b
1
*(0,275-(0,05+t
1
/2))²+ 2*[(h)³*t
2
/12]+t
2
³*b
2
/12+t
2
*b
2
*(h-y-t
2
/2)²
I
x
=
0,001010 m
4
- Promień bezwładności przekroju w płaszczyźnie ramy
i
x
= (I
x
/A)^0,5=
0,187
m
I
y
= b
1
³*t
1
/12+b
2
³*t
2
/12+2*(h-t
1
)*t
2
³/12+ 2*(h-t
1
)*t
2
*(b
2
/2+t
2
/2)²
Iy= 0,000841 m
4
- Promień bezwładności przekroju z płaszczyzny ramy
i
y
= (I
y
/A)^0,5=
0,171 m
5.2.3.0. Sprawdzenie warunku smukłości.
5.2.3.1. Smukłośc pasa górnego z plaszczyzny ramy.
l<200
l
o
=
16,8
m
µ=
1,0
l
w
=µ*l
o
=
16,8
m
l=l
w
/i
x
=
89,72
< 200
Warunek został spełniony!
5.2.3.2. Smukłośc pasa dolnego w płaszczyźnie ramy.
l<200
l
o
=
16,8
m
µ=
1,0
l
w
=µ*l
o
=
16,8
m
l=l
w
/i
y
=
98,31
< 200
Warunek został spełniony!
5.2.4.0. Nośnośc dla elementu rozciaganego osiowo.
s= (P)/F
w
≤ R
R=
280
Mpa
P=
0,427193
MN
l=
98,31
s= (P*m
w
)/F
w
≤ R
F
w
=
0,029
m²
σ =
14,83
MPa
≤ R =
280
Mpa
σ
/R=
0,05
Warunek został spełniony!
5.2.4.1. Nośnośc z uwzględnieniem zmęczenia.
Rodzaje karbów:
nr1 stal poza złączem o powierzchni surowej oraz krawędziach po cieciu gazowym automatycznym β=1,4;
nr2 stal poza złączami o powierzchni surowej, w miejscu zmiany przekroju z wyokrągleniem promieni r>50mm β=1,8;
nr3 złącze spawane spoiną czołową z podpawaniem spoiną nie sprawdzoną defektoskopowo na całej dlugości β=2,9;
nr4 złącze spawane spoiną czołową, podpawaną dwuch elementów o różnej szerokości lub grubości β=1,4;
nr5 złącza spawane spoinami równoległymi do kierunku działania siły, obrobionymi mechanicznie przy zastosowaniu
spawania ręcznego β=1,4;
nr6 stal w pobliżu żeber i przepon przyspawanych do pasów spoinami pachwinowymi poprzecznie do kierunku działania
siły przy przejściu nie obrobionym β=2,2;
nr7 stal pasa rozciąganego belki pełnościennej w pobliżu spoiny pachwinowej poprzecznej nieobrobionej β=2,2;
25
nr8 połączenie spoinami pachwinowymi podłużnymi elementu pręta kratownicy β=3,4;
nr9 stal pręta kratownicy z przyspawanymi poprzecznymi żebrami lub przeponami z wykrojami w narożach, przez które
przeprowadzone są spoiny pachwinowe jeśli pręt jest rozciągany β=2,2;
nr10 złącze na śruby pracujące na ścinanie i stal części łączonych pracujących na docisk β=1,8.
Do obliczeń przyjmuję najbardziej niekożystną warośc β=3,4.
σ
k
≤ R*m
zm
R=
280
MPa
m
zm
= c/[(a*β+ b)- (a*β- b)* ρ]
ρ= σ
min
/ σ
max
=
0,059
c= 1,1
A=
0,00
m²
a= 0,8
σ
max
= N
maxk
/ A=
8,48
MPa
b= 0,3
σ
min
= N
mink
/A=
0,50
MPa
β= 3,4
m
zm
= 0,53
R*m
zm
=
147,98
MPa
8,48
MPa
≤
147,9794
MPa
Warunek został spełniony!
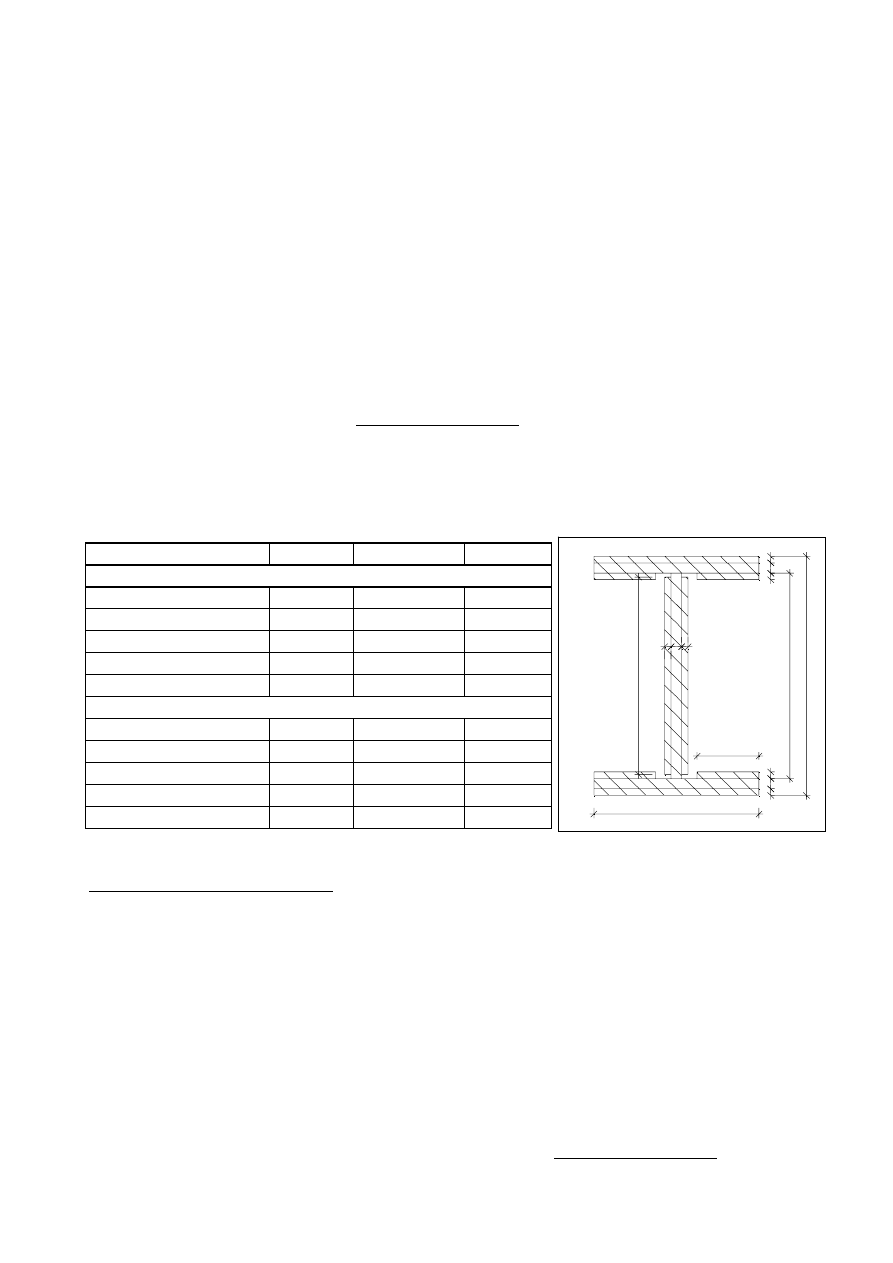
5.2.5.0. Styk w węźle S.
5.2.5.1. Wymiary wstępne.
Nazwa elementu
Symbol
Wymiar
Jednostka
ŚRODNIK
Szerokośc środnika
b
s
0,5
m
Grubośc środnika
t
s
0,025
m
Szerokośc podkładki 1
b
ps1
0,48
m
Szerokośc podkładki 2
b
ps2
0,48
m
Grubośc podkładek
t
sd
0,016
m
PÓŁKI
Wysokośc półek
hs
0,4
m
Grubośc półk
ts
0,025
m
Wysokosc podkładki
h
ps1
0,40
m
Wysokośc podkładki
h
ps2
0,150
m
Grubośc podkładek
t
ps
0,016
m
5.2.5.2. Połączenie środnika.
Przyjęto połączenia na śruby sprężające.
Średnica śrub sprężających:
d=(50*t
sd
)^0,5-2= 26,284271 mm
Przyjęto:
d=
27
mm
Średnica otworu:
d
o
=d+2=
29
mm
5.2.5.2.1. Sprawdzennie warunków połączenia.
F
npasa
≤ F
nnak
F
npasa
= b
s
*t
s
-2*t
s
*d
o
=
0,01105
m²
F
nnak
= t
sd
*(b
ps2
+ b
ps1
)- 2* 2*t
sd
* d
o
=
0,013504
m²
0,01105
m²
≤
0,013504
m²
Warunek został spełniony!
400
150
480
16
25
16
16
25
16
500
582
16
25
16
26

5.2.5.2.2. Nośność pojedyńczej śruby.
N'= n*µ*P
s
n=
2
- ilość powierzchni tarcia
P
s
= 0,8* R
02
* F
s
/1,25=
387,49
kN
- siła napinająca dla śrub M27 kl. 12.9
R
02
=
1058
MPa
F
s
=π*d²/4=
0,000572 m²
µ=
0,45
N'=
348,74
kN
- współczynnik tarcia
5.2.5.2.3. Ilości śrub w połączeniu.
N'* n ≥ N
pasa
R=
280
MPa
N
pasa
= b
s
* t
s
* R=
3500
kN
n= N
pasa
/ N'=
10,0360
Przyjęto
n= 11
-
ilość śrub po jednej stronie połączenia
5.2.5.3. Połączenie półek.
Średnica śrub sprężających:
d
1
=(50*t
ps
)^0,5-2= 26,284271 mm
Przyjęto :
d
1
=
27
mm
Średnica otworu:
d
o
=d+2=
29
mm
5.2.5.3.1. Sprawdzennie warunków połączenia dla pojedyńczej półki.
I
npł
≤ I
npł
I
npł
= h
s
* t
s
³/12
=
0,000133 m
2
I
npł
= t
ps
* h
ps1
³/ 12+ 2*(t
ps
* h
ps2
³/12+t
ps
*h
ps2
*(h/2-h
ps2
/2)²=
0,000169
m
2
0,000133
m²
≤
0,000169
m²
Warunek został spełniony!
5.2.5.3.2. Nośność pojedyńczej śruby.
N'= n*µ*P
s
n=
2
- ilość powierzchni tarcia
P
s
= 0,8* R
02
* F
s
/1,25=
387,49
kN
- siła napinająca dla śrub M27 kl. 12.9
R
02
=
1058
MPa
F
s
=π*d²/4=
0,000572 m²
µ=
0,45
- współczynnik tarcia
N'=
348,74
kN
5.2.5.3.3. Ilości śrub w połączeniu.
N'* n ≥ N
pasa
R=
280
MPa
N
pasa
= b
s
* t
s
* R=
2800
kN
n= N
pasa
/ N'=
8,0288
Przyjęto
n= 9
-
ilość śrub po jednej stronie połączenia
27
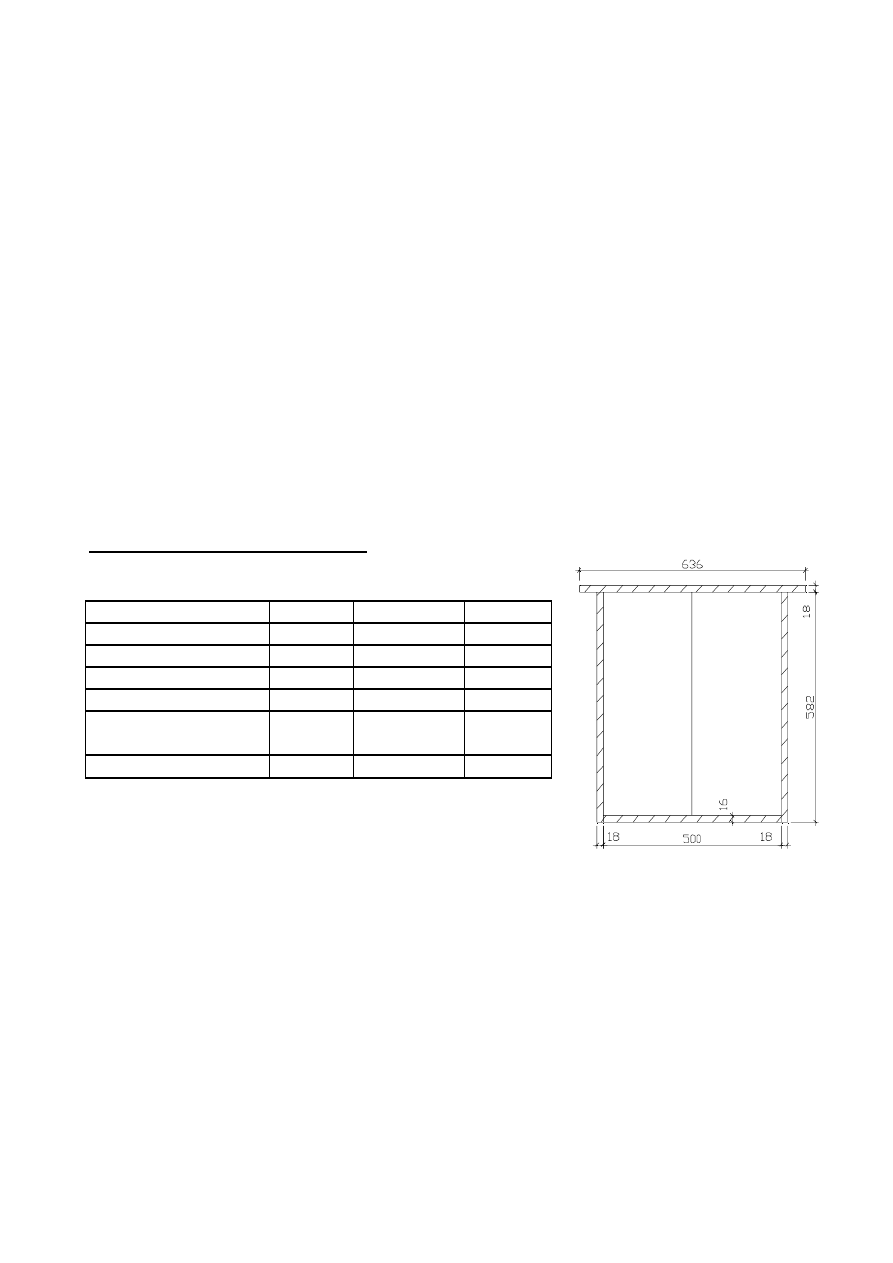
5.2.5.3.4. Rozstaw śrub w połączeniu.
(t-d
1
)* t
s
* R ≥ n* N'
R=
280
MPa
n=
2
N'=
348,74
kN
t
max
= (n* N')/ (t
s
* R)+ d
1
=
0,13
m
5.2.5.4. Warunki konstrukcyjne rozmieszczenia śrub.
5.2.5.4.1. Odległość środka otworu od krawedzi elementu w kierunku
zgodnym z kierunkiem działania siły.
e1≥ =2*27 =
54
mm
(półki)
e1≥ =2*27 =
54
mm
(środnk)
5.2.5.4.2. Rozmieszczenie śrub w nośnych połączeniach elementów ściskanych.
środniki 3,5*d ≤ t ≤ 6*d
94,5
mm
≤ t ≤
162
mm
t ≤ 12*t
sd
t ≤
192
mm
półki 3,5*d ≤ t ≤ 6*d
94,5
mm
≤ t ≤
162
mm
t ≤ 12*t
ps
t ≤
192
mm
5.3. Pręt Pg2 - wymiary wstępne.
Nazwa elementu
Symbol
Wymiar
Jednostka
Wysokośc Pd1
h
0,600
m
Szerokośc pasa dolnego
b
1
0,500
m
Szerokośc pasa górnego
b
2
0,636
m
Grubośc pasa dolnego
t
1
0,016
m
Grubośc środników i
t
2
0,018
m
pasa górnego
Pole przekroju
A
0,040
m²
5.3.1. Zestawienie max sił obliczeniowych w pręcie.
N
obl
=
9415,239
kN
ściskanie
N
maxk
=
4966,791
kN
ściskanie
N
mink
=
259,3
kN
ściskanie
5.3.2.0. Środek ciężkości przekroju.
5.3.2.1. Moment statyczny przekroju względem zewnętrznej krawędzi dolnej półki:
S= b
1
*t
1
*0,5*t
1
+2*t
2
*(h-t
1
)*(h/2+t
1
)+b
2
*t
2
*(h-t
2
/2)
S=
0,0135
m³
y= S/A=
0,33
m
x= b
1
/2=
0,25
m
5.3.2.2. Promieni bezwładności przekroju.
I
x
= t
1
³*b
1
/12+ t
1
*b
1
*(y-t
1
/2)²+ 2*[(h-t
1
)³*t
2
/12+(h-t
1
)*t
2
*((h-t
1
)/2+t
1
-y))²]+t
2
³*b
2
/12+t
2
*b
2
*(h-y-t
2
/2)²
28

I
x
=
0,002218 m
4
- Promień bezwładności przekroju w płaszczyźnie ramy
i
x
= (I
x
/A)^0,5=
0,234
m
I
y
= b
1
³*t
1
/12+b
2
³*t
2
/12+2*(h-t
1
)*t
2
³/12+ 2*(h-t
1
)*t
2
*(b
2
/2+t
2
/2)²
I
y
= 0,002801 m
4
- Promień bezwładności przekroju z płaszczyzny ramy
i
y
= (I
y
/A)^0,5=
0,263
m
5.3.3.0. Sprawdzenie warunku smukłości.
5.3.3.1. Smukłośc pasa dolnego w płaszczyźnie ramy.
l<150
l=l
w
/i
x
=
44,95
< 150
Warunek został spełniony!
l
w
=µ*l
o
=
10,523
m
l
o
=
10,523
m
µ=
1,0
5.3.3.2. Smukłośc pasa dolnego z płaszczyzny ramy.
l<150
l=l
w
/i
y
=
40,00
< 150
l
w
=µ*l
o
=
10,523
m
l
o
=
10,523
m
µ=
1,0
5.3.4.0. Nośnośc dla elementu ściskanego osiowo.
Smukłość porównawcza:
l=
44,95
R=
280
MPa
l
p
=118*(200/R)^0.5= 99,728202
l/l
p
=
0,45
Współczynnik wyboczeniowy.
m
w
=
1,15
s= (P*m
w
)/F
w
≤ R
P=
9,415239 MN
F
w
=
0,04
σ=
267,53
MPa
≤ R =
280
MPa
σ
/R=
0,96
Warunek został spełniony!
5.3.4.1. Nośnośc z uwzględnieniem zmęczenia.
Rodzaje karbów:
nr1 stal poza złączem o powierzchni surowej oraz krawędziach po cieciu gazowym automatycznym β=1,4;
nr2 stal poza złączami o powierzchni surowej, w miejscu zmiany przekroju z wyokrągleniem promieni r>50mm β=1,8;
nr3 złącze spawane spoiną czołową z podpawaniem spoiną nie sprawdzoną defektoskopowo na całej dlugości β=2,9;
nr4 złącze spawane spoiną czołową, podpawaną dwuch elementów o różnej szerokości lub grubości β=1,4;
nr5 złącza spawane spoinami równoległymi do kierunku działania siły, obrobionymi mechanicznie przy zastosowaniu
spawania ręcznego β=1,4;
nr6 stal w pobliżu żeber i przepon przyspawanych do pasów spoinami pachwinowymi poprzecznie do kierunku działania
siły przy przejściu nie obrobionym β=2,2;
nr7 połączenie spoinami pachwinowymi podłużnymi elementu pręta kratownicy β=3,4;
29
nr8 stal pręta kratownicy z przyspawanymi poprzecznymi żebrami lub przeponami z wykrojami w narożach, przez które
przeprowadzone są spoiny pachwinowe jeśli pręt jest ściskany β=1,8;
nr9 złącze na śruby pracujące na ścinanie i stal części łączonych pracujących na docisk β=1,8.
Do obliczeń przyjmuję najbardziej niekożystną warośc β=3,4.
σ
k
≤ R*m
zm
R=
280
MPa
m
zm
= c/[(a*β- b)- (a*β + b)* ρ]
c=
1,1
ρ= σ
min
/ σ
max
=
0,052
a=
0,8
A=
0,040472 m²
b=
0,3
σ
max
= N
maxk
/ A=
122,72
MPa
β=
3,4
σ
min
= N
mink
/A=
6,41
MPa
m
zm
= 0,49
R*m
zm
=
136,14
MPa
122,72
MPa
≤
136,14
MPa Warunek
został spełniony!
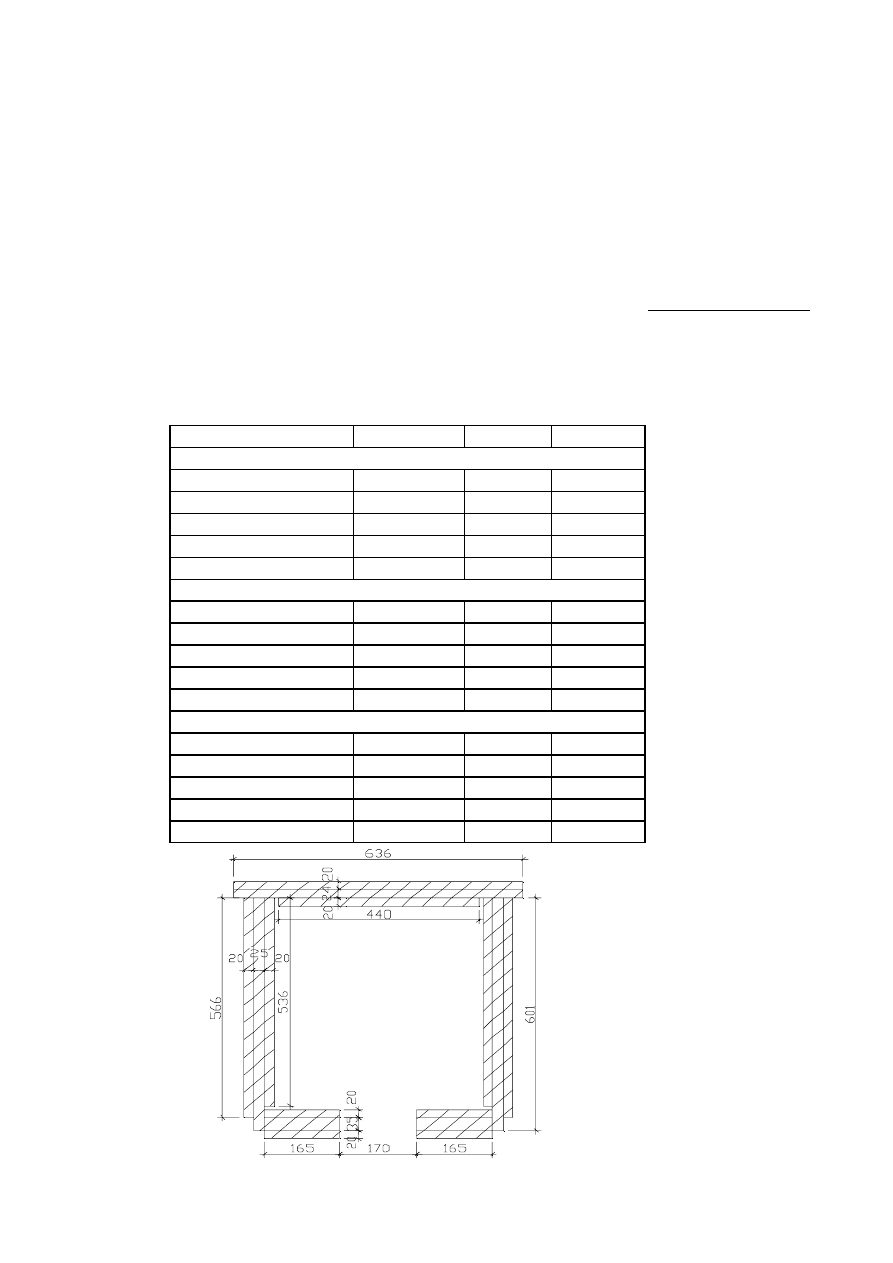
5.3.5.0. Styk pasa dolnego.
5.3.5.1. Wymiary wstępne.
Nazwa elementu
Symbol
Wymiar
Jednostka
PAS DOLNY
Szerokośc pasa dolnego
bd
0,165
m
Grubośc pasa dolnego
t
d
0,035
m
Szerokośc podkładki 1
b
pd1
0,165
m
Szerokośc podkładki 2
b
d2
0,165
m
Grubośc podkładek
t
pd
0,020
m
PAS GÓRNY
Szerokośc pasa górnego
b
g
0,636
m
Grubośc pasa górnego
tg
0,024
m
Szerokośc podkładki 1
b
pg1
0,636
m
Grubosc podkładek
t
pg
0,020
m
Szerokośc podkładki 2
b
pg2
0,440
m
ŚRODNIK
Wysokośc środnika
hs
0,601
m
Grubośc środnika
ts
0,025
m
Wysokośc podkładki 1
hps1
0,536
m
Wysokosc podkładki 2
hps2
0,566
m
Grubośc podkładek
tps
0,020
m
30

5.3.5.2. Połączenie pasa dolnego.
Przyjęto połączenia na śruby sprężające.
Średnica śrub sprężających:
d=(50*t
pd
)^0,5-2=
29,6228
mm
Przyjęto:
d=
30
mm
Średnica otworu:
d
o
=d+2=
32
mm
5.3.5.2.1. Sprawdzennie warunków połączenia.
F
npasa
≤ F
nnak
F
npasa
= b
d
*t
d
-1*t
d
*d
o
=
0,004655
m²
F
nnak
= t
pd
*(b
p1d
+ b
p2d
)- 1* 2*t
pd
* d
o
=
0,00532
m²
0,00466 m²
≤
0,00532
m²
Warunek został spełniony!
5.3.5.2.2. Nośność pojedyńczej śruby.
N'= n*µ*P
s
n=
2
- ilość powierzchni tarcia
P
s
= 0,8* R
02
* F
s
/1,25=
478,39
kN
- siła napinająca dla śrub M30 kl. 12.9
R
02
=
1058
MPa
F
s
=π*d²/4=
0,000707 m²
µ=
0,45
- współczynnik tarcia
N'=
430,55
kN
5.3.5.2.3. Ilości śrub w połączeniu.
N'* n ≥ N
pasa
R=
280
MPa
N
pasa
= b
g
* t
g
* R=
1617
kN
n= N
pasa
/ N'=
3,755690
Przyjęto
n= 4
śrub po jednej stronie połączenia
5.3.5.3. Połączenie pasa górnego.
Średnica śrub sprężających:
d=(50*t
pg
)^0,5-2= 29,622777 mm
Przyjęto :
d=
30
mm
Średnica otworu:
d
o
=d+2=
32
mm
5.3.5.3.1. Sprawdzennie warunków połączenia.
F
npasa
≤ F
nnak
F
npasa
= b
g
*t
g
-3*t
g
*d
o
=
0,01296
m²
F
nnak
= 2*t
pg
*b
pg
- 3* 2*t
pg
* d
o
=
0,021600
m²
0,01296 m²
≤
0,0216 m²
Warunek został spełniony!
31

5.3.5.3.2. Nośność pojedyńczej śruby.
N'= n*µ*P
s
n=
2
- ilość powierzchni tarcia
P
s
= 0,8* R
02
* F
s
/1,25=
478,39
kN
- siła napinająca dla śrub M30 kl. 12.9
R
02
=
1058
MPa
F
s
=π*d²/4=
0,000707 m²
µ=
0,45
- współczynnik tarcia
N'=
430,55
kN
5.3.5.3.3. Ilości śrub w połączeniu.
N'* n ≥ N
pasa
R=
280
MPa
N
pasa
= b
d
* t
d
* R=
4273,92
kN
n= N
pasa
/ N'=
9,926727
Przyjęto
n= 10
śrub po jednej stronie połączenia
5.3.5.4. Połączenie pasa środników.
Średnica śrub sprężających:
d=(50*t
s
)^0,5-2= 33,355339 mm
Przyjęto :
d=
34
mm
Średnica otworu:
d
o
=d+2=
36
mm
5.3.5.4.1. Sprawdzennie warunków połączenia.
I
nśr
≤ I
nnak
I
śr
= h
s
³
* t
s
/12
=
0,000452 m
2
I
nnak
= t
ps
* h
ps2
³
/ 12 + t
ps
*h
ps1
³/12=
0,000559
m
2
0,00045
m²
≤
0,00056
m²
Warunek został spełniony!
5.3.5.4.2. Nośność pojedyńczej śruby.
N'= n*µ*P
s
n=
2
- ilość powierzchni tarcia
P
s
= 0,8* R
02
* F
s
/1,25=
591,38
kN
- siła napinająca dla śrub M34 kl. 12.9
R
02
=
1058
MPa
F
s
=π*d²/4=
0,000873 m²
µ=
0,45
- współczynnik tarcia
N'=
532,24
kN
5.3.5.4.3. Ilości śrub w połączeniu.
N'* n ≥ N
pasa
R=
280
MPa
N
pasa
= b
d
* t
d
* R=
4207
kN
n= N
pasa
/ N'=
7,9043
Przyjęto
n= 8
śrub po jednej stronie połączenia
32

5.3.5.4.4. Rozstaw śrub w połączeniu.
(t-d
1
)* t
s
* R ≥ n* N'
R=
280
MPa
n=
2
N'=
532,24
kN
t
max
= (n* N')/ (t
s
* R)+ d
1
=
0,19
m
5.3.5.4.5. Warunki konstrukcyjne rozmieszczenia śrub.
5.3.5.4.5.1. Odległość środka otworu od krawedzi elementu w kierunku
zgodnym z kierunkiem działania siły.
e
1
≥ =2*30 =
60
mm (pas dolny)
e
1
≥ =2*30 =
60
mm (pas górny)
e
1
≥ =2*34 =
68
mm (środnik)
5.3.5.4.4.2.2. Rozmieszczenie śrub w nośnych połączeniach elementów rozciaganych.
pas dolny 3,5*d≤t ≤ 8*d
105
mm
≤ t ≤
240
mm
t ≤ 16*t
pd
t ≤
240
mm
pas górny 3,5*d≤t ≤ 8*d
105
mm
≤ t ≤
240
mm
t ≤ 16*t
pg
t ≤
240
mm
środnik 3,5*d≤t ≤ 8*d
119
mm
≤ t ≤
272
mm
t ≤ 16*t
ps
t ≤
320
mm
33
Wyszukiwarka
Podobne podstrony:
kratownica obliczenia
kratownica obliczenie sił
Kratownica obliczanie sposoby
Projekt Inzynierski Obliczenia wiązara kratowego G3 mitek
projekt 2 obliczenia, PKM projekty, PROJEKTY - Oceloot, Projekt II kratownica PKM, Inne, Obliczenia
Obliczenia(1), + Szkoła +, Budownictwo komunikacyjne, Mosty
Obliczenia2, AGH, Semestr 5, PKM całość, PKM akademiki I, PKM, Projekt nr 2
Obliczenia węzła kratownicy
obliczenia mosty podstawy
Obliczenia4, AGH, Semestr 5, PKM całość, PKM akademiki I, PKM, Projekt nr 2
Obliczenie kratownicy przy pomocy programu RMWin
Całość Obliczenie zasobów gazu ziemnego złoża Bosusław
Obliczenia węzła kratownicy
Obliczenie kratownicy przy pomocy programu RMWin
kratownica projekt obliczenia i Nieznany
Obliczenia, AGH, Semestr 5, PKM całość, PKM akademiki I, PKM, Projekt nr 2, projekt rafal
Cwiczenie 5 -Obliczanie pr¦Ödko+Ťci krytycznej, studia calosc, studia całość, 3 semestr, inig, Wiert
SF028a Schemat blokowy Model obliczeniowy spawanych węzłów kratownic rurowych
Obliczenia mosty Kasia, Mosty - projekty
więcej podobnych podstron