Matematyka A, egzamin, 19 czerwca 2008, rozwia

֒

zania

1.

Znale´z´c promie´

n i ´srodek okre

֒

gu, kt´

ora zawiera zbi´or z lo˙zony ze wszystkich tych liczb zes-

polonych z , dla kt´

orych

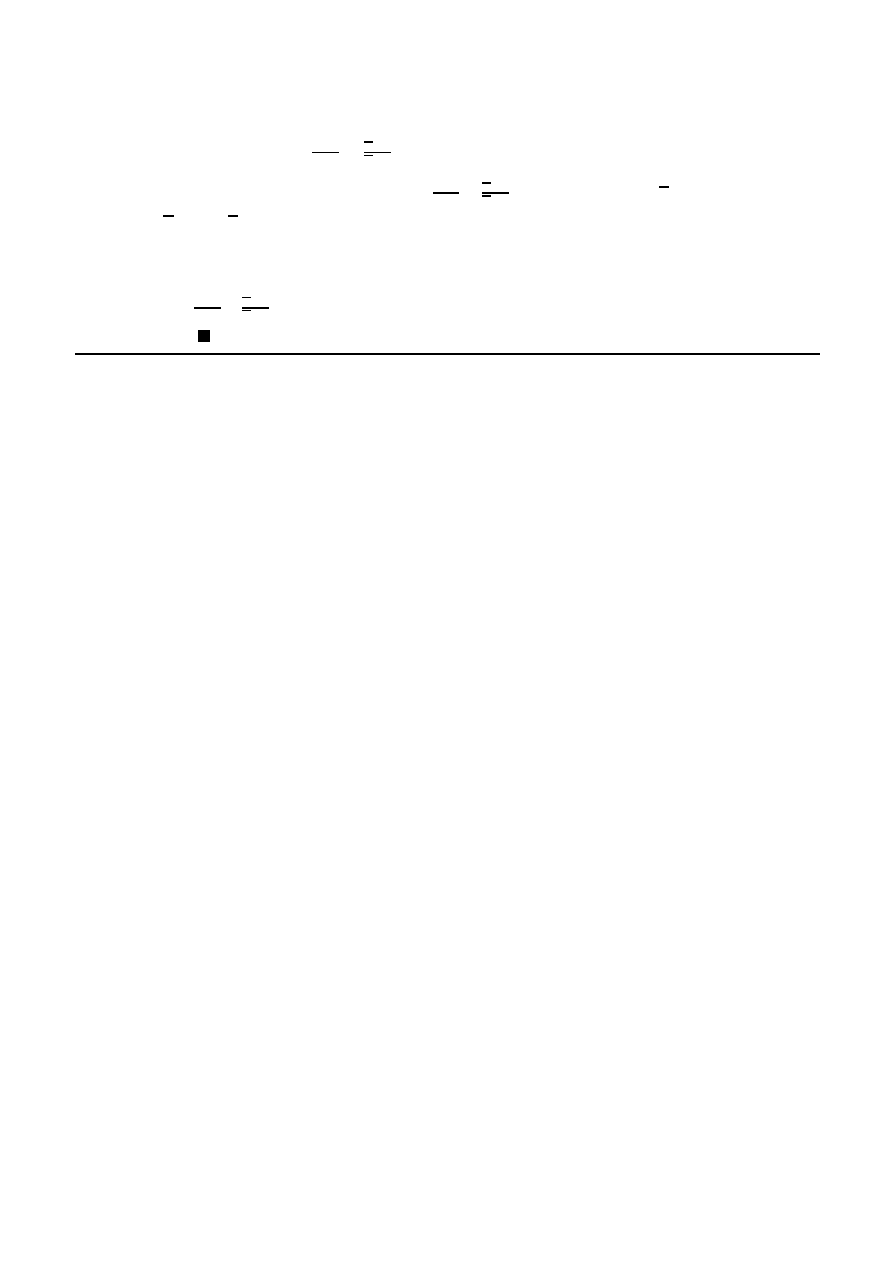
z+1
z−1

+

z+1
z−1

= 0 .

Rozwia

֒

zanie:

Mno˙za

֒

c stronami r´

owno´s´c

z+1
z−1

+

z+1
z−1

= 0 przez (z − 1)(z − 1) otrzymujemy:

0 = (z +1)(z −1)+(z +1)(z −1) = 2|z|

2

−2 = 2(|z|

2

−1) , zatem |z| = 1 . Otrzymali´smy r´ownanie

okre

֒

gu, kt´

orego ´srodkiem jest punkt 0 , a promieniem jest liczba 1 . Oczywi´scie wyj´sciowe

r´

ownanie nie jest spe lnione dla z = 1 , bo w mianowniku liczba 0 pojawi´c sie

֒

nie mo˙ze. Wobec

tego r´

ownanie

z+1
z−1

+

z+1
z−1

= 0 opisuje okra

֒

g o ´srodku w punkcie 0 i promieniu 1 z wy la

֒

czeniem

punktu z = 1 .

2.

Znale´z´c warto´sci i wektory w lasne macierzy A =






1

0

0

1

0

1

1

1

1 −1

1

0

−1

0

0

1






w tym zespolone.

Rozwia

֒

zanie:

R´

ownanie charakterystyczne tej macierzy to:

0 =

1 − λ

0

0

1

0

1 − λ

1

1

1

−1

1 − λ

0

−1

0

0

1 − λ

pierwszy

======

wiersz

(1 − λ)

1 − λ

1

1

−1

1 − λ

0

0

0

1 − λ

−

−

0

1 − λ

1

1

−1

1 − λ

−1

0

0

trzeci

======

wiersz

(1 − λ)

2

1 − λ

1

−1

1 − λ

+

1 − λ

1

−1

1 − λ

=

= (1 − λ)

1

+ 1

1 − λ

1

−1

1 − λ

= (1 − λ)

2

+ 1

2

.

Wynika sta

֒

d, ˙ze je´sli λ jest warto´scia

֒

w lasna

֒

, to (1 − λ)

2

= −1 , zatem 1 − λ = ±i , wie

֒

c

λ

= 1∓i . Mamy wie

֒

c (1−λ)

2

+1

2

= λ−(1−i)

2

λ

−(1+i)

2

, wie

֒

c obie te warto´sci w lasne sa

֒

podw´

ojne, a to oznacza, ˙ze odpowiadaja

֒

ce im podprzestrzenie w lasne moga

֒

by´c jednowymiarowe

lub dwuwymiarowe. Zajmiemy sie

֒

warto´scia

֒

w lasna

֒

1 + i . Za l´o˙zmy, ˙ze kolejnymi wsp´o lrze

֒

dnymi

jej wektora w lasnego sa

֒

liczby x

1

, x

2

, x

3

, x

4

. Z definicji wektora w lasnego wynika, ˙ze spe lnione sa

֒

naste

֒

puja

֒

ce cztery r´

owno´sci x

1

+x

4

= (1+i)x

1

, x

2

+x

3

+x

4

= (1+i)x

2

, x

1

−x

2

+x

3

= (1+i)x

3

oraz −x

1

+ x

4

= (1 + i)x

4

. Po uproszczeniu pierwsza z nich wygla

֒

da tak x

4

= ix

1

, a czwarta

−x

1

= ix

4

. Sa

֒

one wie

֒

c r´

ownowa˙zne, po druga z nich to pierwsza pomno˙zona stronami przez i .

Podstawiaja

֒

c x

4

= ix

1

do drugiego r´

ownania wyj´sciowego uk ladu otrzymujemy x

3

+ ix

1

= ix

2

,

Trzecie r´

ownanie przybiera posta´c x

1

− x

2

= ix

3

. Wida´c, ˙ze te dwa r´ownania sa

֒

r´ownowa˙zne,

wystarczy przenie´s´c wszystko na jedna

֒

strone

֒

i pomno˙zy´c jedno z nich przez i . Mo˙zemy zatem

przyja

֒

´c np. x

1

= 1 oraz x

2

= 0 . Wtedy x

3

= i(x

2

− x

1

) = −i oraz x

4

= i . Znale´zli´smy jeden z

wektor´ow w lasnych: ~v =

−−−−−−−→

(1, 0, −i, i) . W taki sam spos´ob stwierdzamy, ˙ze wektor ~

w

=

−−−−−−→

(0, 1, i, 0)

jest te˙z wektorem w lasnym odpowiadaja

֒

cym warto´sci w lasnej 1 + i . Jasne jest, ˙ze nie istnieje

taka liczba zespolona c , ˙ze ~v = c~

w

lub ~

w

= c~v , a to oznacza, ˙ze ka˙zdy inny wektor w lasny

odpowiadaja

֒

cy warto´sci w lasnej 1 + i mo˙zna zapisa´c w postaci c

1

~

v

+ c

2

~

w

, gdzie c

1

, c

2

∈ C

(bo zbi´

or wektor´

ow w lasnych jest podprzestrzenia

֒

wymiaru > 1 i jednocze´snie ≤ 2 , wie

֒

c

wymiaru 2 ).

Poniewa˙z wszystkie wyrazy macierzy sa

֒

rzeczywiste oraz 1 − i = 1 + i , wie

֒

c wektorami

w lasnymi odpowiadaja

֒

cym warto´sci w lasnej sa

֒

−−−−−−−→

(1, 0, i, −i) oraz

−−−−−−−→

(0, 1, −i, 0) — zasta

֒

pili´smy

wszystkie wsp´o lrze

֒

dne liczbami sprze

֒

˙zonymi. Pozosta le wektory w lasne odpowiadaja

֒

ce tej warto´sci

w lasnej to c

1

−−−−−−−→

(1, 0, i, −i) + c

2

−−−−−−−→

(0, 1, −i, 0) , gdzie c

1

, c

2

∈ C .

3.

Szybko´s´c stygnie

֒

cia cia la jest wprost proporcjonalna do r´o˙znicy temperatur cia la i otaczaja

֒

-

cego go powietrza. W cia

֒

gu 10 minut temperatura cia la zmala la ze 100

◦

C do 60

◦

C.

Temperatura powietrza r´

owna jest 20

◦

C. Po jakim czasie temperatura cia la zmniejszy sie

֒

do 25

◦

C?

Rozwia

֒

zanie:

Oznaczmy przez T (t) temperature

֒

stygna

֒

cego cia la w chwili t , przy czym

spe lnione sa

֒

r´

owno´sci T (0) = 100 i T (10) = 60 . Niech k oznacza wsp´o lczynnik proporcjo-

nalno´sci, kt´

ora wyste

֒

puje w tre´sci zadania. Dla dostatecznie ma lej liczby ∆t zachodzi przy-

bli ˙zona

r´

owno´s´c

T (t+∆t)−T (t)

∆t

≈ k T (t) − 20

. Po przej´sciu do granicy przy ∆t −→ 0 otrzy-

mujemy r´

ownanie T

′

(t) = k T (t) − 20

, czyli

kt

+ C =

R k dt = R

T

′

(t)

T (t)−20

dt

=

R

dT

T −20

= ln |T − 20| .

Z tre´sci zadania wynika od razu, ˙ze T > 20 . Wobec tego T − 20 = T (t) − 20 = e

C

· e

kt

. Mamy

60 = T (10) = 20 + e

C

· e

10k

oraz 100 = T (0) = 20 + e

C

· e

k·0

= 20 + e

C

. Wynika sta

֒

d, ˙ze

T

(t) = 20 + 80e

kt

= 20 + 80 e

10k

t/10

= 20 + 80

40
80

t/10

= 20 + 80

1
2

t/10

.

Mamy znale´z´c taka

֒

liczbe

֒

t

, ˙ze 25 = T (t) = 20 + 80

1
2

t/10

, czyli 5 = 80

1
2

t/10

, a to oznacza,

˙ze

1

16

=

1
2

t/10

. Wynika sta

֒

d, ˙ze

t

10

= 4 , zatem t = 40 .

4.

Rozwia

֒

za´c r´

ownanie r´

o˙zniczkowe tx

′

+ (t + 1)x = 3t

2

e

−t

.

Znale´z´c rozwia

֒

zanie tego r´

ownania spe lniaja

֒

ce warunek x(1) = 0 .

Rozwia

֒

zanie:

Rozwia

֒

˙zemy najpierw r´

ownanie jednorodne tx

′

+ (t + 1)x = 0 . Mo˙zna je

przepisa´c w postaci

x

′

x

= −

t+1

t

= −1 −

1

t

. Po sca lkowaniu tej r´owno´sci stronami otrzymujemy

ln |x(t)| = −t−ln |t|+C . Sta

֒

d x(t) = ±e

C

·e

−t

·

1

t

. Oznaczaja

֒

c K = ±e

C

otrzymujemy r´owno´s´c

x

(t) =

K

t

e

−t

.

Teraz znajdziemy rozwia

֒

zanie r´

ownania niejednorodnego uzmienniaja

֒

c sta la

֒

K

, czyli przyj-

muja

֒

c, ˙ze K = K(t) jest funkcja

֒

zmiennej t . Szukamy zatem rozwia

֒

zania w postaci K(t)

1

t

e

−t

.

Podstawiaja

֒

c to wyra˙zenie do r´

ownania tx

′

+ (t + 1)x = 3t

2

e

−t

w miejsce x(t) otrzymujemy

3t

2

e

−t

= K

′

(t)e

−t

+ K(t)

1

t

e

−t

′

+ (t + 1)K(t)

1

t

e

−t

= K

′

(t)e

−t

+ K(t)

1

t

e

−t

′

+ (t + 1)

1

t

e

−t

=

= K

′

(t)e

−t

— ostatnia r´owno´s´c jest konsekwencja

֒

tego, ˙ze funkcja

1

t

e

−t

jest rozwia

֒

zaniem r´ownania jedno-

rodnego. Upraszczaja

֒

c otrzymujemy K

′

(t) = 3t

2

, zatem K(t) = t

3

+ c , gdzie c oznacza pewna

֒

sta la

֒

. Wobec tego x(t) = t

3

+ c

1

t

e

−t

.

Mamy znale´z´c rozwia

֒

zanie spe lniaja

֒

ce warunek pocza

֒

tkowy 0 = x(1) = (1 + c)e

−1

. Sta

֒

d

wynika, ˙ze c = −1 , zatem poszukiwana funkcja to t

3

− 1

1

t

e

−t

. Jej dziedzina

֒

jest p´o lprosta

(0, ∞) , bo dziedzina

֒

rozwia

֒

zania r´

ownania r´

o˙zniczkowego ma by´c przedzia l, w tym przypadku

zawieraja

֒

cy liczbe

֒

1 .

Uwaga:

Rozwia

֒

zanie mo˙zna skr´

oci´c wprowadzaja

֒

c pomocnicza

֒

funkcje

֒

y

(t) = tx(t) . Wtedy

wyj´sciowe r´

ownanie przyjmuje posta´c y

′

(t) + y = 3t

2

e

−t

. Na taki pomys l wpadaja

֒

z latwo´scia

֒

te osoby, kt´

ore rozwia

֒

za ly troche

֒

zada´

n samodzielnie, bo widza

֒

, ˙ze tx

′

+ x = (tx)

′

.

5.

Znale´z´c rozwia

֒

zanie og´

olne r´

ownania

x

′′

(t)−2x

′

(t)+5x(t) = 4e

t

+17 cos(2t)−12e

t

sin(2t) .

Rozwia

֒

zanie:

Mamy do czynienia z r´

ownaniem liniowym niejednorodnym o sta lych wsp´o l-

czynnikach. R´

ownanie charakterystyczne to 0 = λ

2

− 2λ + 5 = (λ − 1)

2

+ 4 . Jego pierwiastkami

sa

֒

wie

֒

c liczby 1 ± 2i . Wynika sta

֒

d, ˙ze rozwia

֒

zanie og´

olne r´ownania jednorodnego ma posta´c

c

1

e

(1+2i)t

+ c

2

e

(1−2i)t

, gdzie c

1

, c

2

oznaczaja

֒

liczby zespolone.

Po prawej stronie wyste

֒

puja

֒

quasiwielomiany ( e

t

) lub ich cze

֒

´sci rzeczywiste ( 17 cos(2t) )

ba

֒

d´z urojone ( −12e

t

sin(2t) ). Liczba 1 nie jest pierwiastkiem r´ownania charakterystycznego,

wie

֒

c istnieje taka liczba c , ˙ze funkcja ce

t

jest rozwia

֒

zaniem r´ownania

x

′′

(t) − 2x

′

(t) + 5x(t) = 4e

t

.

By tak by lo musi by´c spe lniona r´

owno´s´c c − 2c + 5c = 4 , czyli c = 1 . Poszukiwanym roz-

wia

֒

zaniem jest funkcja e

t

.

Kolej na r´ownanie x

′′

(t) − 2x

′

(t) + 5x(t) = 17 cos(2t) = Re 17e

2it

. Rozwia

֒

˙zemy r´ownanie

x

′′

(t) − 2x

′

(t) + 5x(t) = 17e

2it

. Poniewa˙z liczba 2i nie jest pierwiastkiem r´ownania charakte-

rystycznego, wie

֒

c istnieje taka liczba zespolona c , ˙ze funkcja ce

2it

jest rozwia

֒

zaniem r´ownania

x

′′

(t) − 2x

′

(t) + 5x(t) = 17e

2it

. Podstawiaja

֒

c ce

2it

w miejsce x w tym r´ownaniu otrzymujemy

−4ce

2it

− 4cie

2it

+ 5ce

2it

= 17e

2it

, czyli c(1 − 4i)e

2it

= 17e

2it

. Wobec tego c =

17

1−4i

= 1 + 4i .

Wobec tego funkcja (1 + 4i)e

2it

jest rozwia

֒

zaniem r´

ownania x

′′

(t) − 2x

′

(t) + 5x(t) = 17e

2it

,

a poniewa˙z wszystkie wsp´

o lczynniki z lewej jego strony sa

֒

liczbami rzeczywistymi, wie

֒

c funk-

cja Re (1 + 4i)e

2it

= Re (1 + 4i)(cos(2t) + i sin(2t)) = cos(2t) − 4 sin(2t) jest rozwia

֒

zaniem

r´ownania x

′′

(t) − 2x

′

(t) + 5x(t) = 17 cos(2t) .

Wreszcie r´

ownanie x

′′

(t) − 2x

′

(t) + 5x(t) = −12e

t

sin(2t) = Im − 12e

(1+2i)t

. Tym razem

liczba 1+2i jest pierwiastkiem jednokrotnym r´

ownania charakterystycznego, wie

֒

c rozwia

֒

zaniem

r´ownania c

1

e

(1+2i)t

be

֒

dzie quasiwielomian stopnia pierwszego z wyk ladnikiem 1+2i , czyli funk-

cja postaci (ct + d)e

(1+2i)t

, gdzie symbole c, d oznaczaja

֒

liczby zespolone. Z tego, jak wygla

֒

da

rozwia

֒

zanie r´ownania jednorodnego, jasno wynika, ˙ze nie ma ˙zadnych ogranicze´

n na liczbe

֒

d

(w rozwia

֒

zaniu wyste

֒

puje sk ladnik c

1

e

(1+2i)t

, wie

֒

c mo˙zna uzna´c, ˙ze d = c

1

). Znajdziemy c .

Podstawiamy do r´ownania x

′′

(t) −2x

′

(t) +5x(t) = −12e

(1+2i)t

funkcje

֒

cte

(1+2i)t

. Otrzymujemy

−12e

(1+2i)t

= 2c(1+2i)e

(1+2i)t

+ct(1+2i)

2

e

(1+2i)t

−2ce

(1+2i)t

−2ct(1+2i)e

(1+2i)t

+5cte

(1+2i)t

=

= 4ice

(1+2i)t

,

zatem c = 3i . Wobec tego, ˙ze wszystkie wsp´o lczynniki po lewej stronie r´ownania sa

֒

rzeczywi-

ste, funkcja Im 3ite

(1+2i)t

= 3te

t

cos(2t) jest rozwia

֒

zaniem szczeg´olnym ostatniego r´ownania

pomocniczego x

′′

(t) − 2x

′

(t) + 5x(t) = −12e

t

sin(2t) .

Wobec tego rozwia

֒

zaniem og´

olnym r´

ownania

x

′′

(t) − 2x

′

(t) + 5x(t) = 4e

t

+ 17 cos(2t) − 12e

t

sin(2t)

jest funkcja e

t

+ cos(2t) − 4 sin(2t) + 3te

t

cos(2t) + c

1

e

(1+2i)t

+ c

2

e

(1−2i)t

, gdzie c

1

, c

2

oznaczaja

֒

dowolne liczby zespolone. Mo˙zna bez trudu zauwa˙zy´c, ˙ze je´sli c

2

= c

1

, to warto´sci tej funkcji

sa

֒

rzeczywiste. Mo˙zna te˙z zapisa´c to samo rozwia

֒

zanie w postaci

e

t

+ cos(2t) − 4 sin(2t) + 3te

t

cos(2t) + d

1

e

t

cos(2t) + d

2

e

t

sin(2t) .

W tym przypadku rozwia

֒

zania rzeczywiste otrzymujemy dla rzeczywistych d

1

, d

2

.

6.

Niech f (x, y) = x

2

y

+ xy

2

− 3xy . Znale´z´c najmniejsza

֒

i najwie

֒

ksza

֒

warto´s´c funkcji f

w kwadracie Q = {(x, y):

−1 ≤ x ≤ 13 i

− 1 ≤ y ≤ 13} .

Rozwia

֒

zanie:

Wielomian jest funkcja

֒

cia

֒

g la

֒

w ca lej p laszczy´znie, wie

֒

c r´ownie˙z w ka˙zdym

punkcie kwadratu Q , kt´

ory jest zbiorem domknie

֒

tym i ograniczonym. Twierdzenie Weier-

strassa o osia

֒

ganiu kres´

ow m´

owi, ˙ze w pewnym punkcie kwadratu przyjmowana jest najwie

֒

ksza

spo´sr´

od wszystkich warto´sci przyjmowanych w punktach kwadratu. Mo˙ze ona by´c przyjmo-

wana w punkcie brzegu kwadratu lub w punkcie wewne

֒

trznym. W drugim przypadku obie

pochodne cza

֒

stkowe musza

֒

by´c r´

owne 0 . To samo dotyczy najmniejszej warto´sci tej funkcji.

Mamy

∂f
∂x

(x, y) = 2xy + y

2

− 3y = y(2x + y − 3) i

∂f
∂y

(x, y) = x

2

+ 2xy − 3x = x(x + 2y − 3) .

Latwo mo˙zna zauwa˙zy´c, ˙ze uk lad r´

owna´

n

∂f
∂x

(x, y) = 0 =

∂f
∂y

(x, y) r´ownowa˙zny jest temu, ˙ze

spe lniony jest co najmniej jeden z naste

֒

puja

֒

cych uk lad´

ow:

x

= 0 = y ,

x

= 0 = 2x + y − 3 ,

y

= 0 = x + 2y − 3

i

2x + y − 3 = 0 = x + 2y − 3 .

Mamy wie

֒

c cztery punkty krytyczne: (0, 0) , (0, 3) , (3, 0) i (1, 1) . Poniewa˙z f (0, 0) = 0 ,

f

(3, 0) = f (0, 3) = 0 i f (1, 1) = −1 , wie

֒

c −1 nie jest najwie

֒

ksza

֒

warto´scia

֒

funkcji f na kwa-

dracie Q , a 0 nie jest jej najmniejsza

֒

warto´scia

֒

. Przyjrzymy sie

֒

punktom brzegu kwadratu Q .

Mamy f (−1, y) = y − y

2

+ 3y = y(4 − y) ≤ 2(4 − 2) = 4 przy czym r´owno´s´c zachodzi jedynie dla

y

= 2 (w lasno´sci paraboli!). Mamy te˙z f (−1, −1) = −5 i f (−1, 13) = −13 · 9 = −117 , zatem

je´sli −1 ≤ y ≤ 13 , to −117 ≤ f (−1, y) ≤ 4 . W taki sam spos´ob stwierdzi´c mo˙zna, ˙ze je´sli

−1 ≤ x ≤ 13 , to −117 ≤ f (x, −1) ≤ 4 . Dalej f (13, y) = 169y + 13y

2

− 39y = 13y(y + 10) ≥

≥13(−1)(−1 + 10) = −117 — ca ly przedzia l [−1, 13] le˙zy po prawej stronie punktu −5 ,

w kt´

orym funkcja kwadratowa przyjmuje swa

֒

najmniejsza

֒

warto´s´c, wie

֒

c na przedziale [−1, 13]

funkcja 13y(y + 10) jest ´sci´sle rosna

֒

ca. Sta

֒

d −117 ≤ f (13, y) ≤ f (13, 13) = 13 · 13 · 23 dla

y

∈ [−1, 13] . Analogicznie −117 ≤ f (x, 13) ≤ 13

2

· 23 dla x ∈ [−1, 13] . Wynika sta

֒

d, ˙ze

najmniejsza

֒

warto´scia

֒

funkcji f na kwadracie Q jest liczba −117 = f (−1, 13) = f (13, −1) , a

najwie

֒

ksza

֒

— liczba f (13, 13) = 13

2

· 23 = 3887 .

Uwaga: mo˙zna sprawdzi´

c, ˙ze w punkcie

(1, 1) funkcja f ma lokalne minimum w la´sciwe;

jest to najmniejsza warto´s´

c funkcji spo´sr´

od przyjmowanych w punktach tr´

ojka

֒

ta o wierzcho lkach

(0, 0) , (3, 0) i (0, 3) .