The demand for high-quality ceramics is increasing in
many fields. The applications are spreading to highly
functional materials known as the ‘‘fine ceramics’’
as well as materials for houseware and buildings.
Although

material

science

for

ceramics

has

advanced significantly during the last few decades,
the production processes still rely on old methods.
Particularly, R&D has not addressed the drying
process, and drying is usually carried out slowly in
order to avoid undesirable cracks and deformations.
The reason is often attributed to the fact that ceramic
drying involves maintaining a molded configuration.
Although ceramics are sensitive to the surrounding
atmosphere during drying, it is very

difficult to

predict the heat- and mass-transfer rates and the air
flow pattern in dryers with sufficient accuracy and
generalize the results to the wide variety of ceramics.
Many ceramic manufacturers are small companies,
and they may not wish to invest much effort in cer-
amic drying R&D as drying occurs only at the pre-
treatment stage in ceramic production. However,

drying is important for precisely designing the mold-
ing, determining the high-efficient heating rate in a
dryer, and completing the drying so as to reduce the
ratio of failure during sintering and yielding the quali-
fied productions.

The objective of this chapter is to outline the R&D

problems of the ceramic-drying process in order to
promote its R&D. Industrial drying technology is
almost kept as a confidential issue by each manufac-
turer and the available publications are quite limited.
The research on the problem of drying shrinkage
under these circumstances is reviewed here briefly as
well. Future directions are also considered for improv-
ing the drying process for shortening drying time,
energy saving, the precise design of molding, and
high quality ceramic production.

31.2 ROLES OF DRYING IN

PRODUCTION PROCESS

Ceramics are produced industrially by various pro-
cesses. The typical processes for the production of

2006 by Taylor & Francis Group, LLC.

refractor y are diagra mmed in Figure 31.1. D r y i n g i s
always involved in any process but sometimes takes
place during t he preparation processes such as
grinding, c lassification, purification, mixing, and
granulation. F or s uch drying, the c onventional
technology for powders or granules may be avail-
able although t here might be problems t hat are yet
to be solved. The other drying phases after molding
or pressing must be performed to r emove w ater in
order t o m aintain t he molded configuration. Some
of the m ajor difficulties t hat arise during ceramic
drying are a s f ollows: ( 1) the r ise in the drying rate
must be naturally limited because the faster rate in
the beginning of drying results i n rapid attainment
of the critical m oisture c ontent and then the r e-
markable reduction of the rate in the falling rate
period; (2) f ailures and irregular deformation may
be generated due to drying shrinkage and internal
st ress it induces; ( 3) molding m ust be designed with
predicting the de f ormati on; (4) uniform drying is
difficult to perform because temperature and hu-
midity, as w ell as local heat- and mass-trans fer
coefficients, are often highly dependent upon the
location in the industrial dryers. T he quality of the
ceramic produced is seriously af fected by these
problems. The ceramic drying described in this

chapter is mainly confined to the drying of this
step after molding.

Typical kinds of molding or pressing and their

charact eristics are summa rized in

Table 31.1

. The uni-

axial pressing is a common pressing method and is
available for relatively flat ceramics like tiles. This
pressing can be classified into two categories: dry and
wet pressings. Slip casting is mold from slurry. In the
injection molding, the cake of clay is injected into the
mold through a nozzle from the cylinder. It is easy to
supply a constant volume of cake into the mold that is
appropriate for the mass production of complicated
molding. The doctor-blade process is used for very
thin-ceramic production, and a continuous operation
is possible. The extrusion method involves extruding
the cake through the dice screw. Pipes and honey-
combs are produced by this method. We can see that
some methods do not involve any drying process.
However, the size and shape of ceramics are limited
because molding with a uniform density distribution in
the ceramics is difficult. Therefore, the wet methods
are still required for the production of complicated
shapes or large sizes. The drying process would thus
become more important for the precise design of
molds and the accomplishment of highly quality-con-
trolled efficient drying.

Raw material

Compounding

Ball mill

Sieving

Mixing

Spray drying

Kneading

Sieving

Lubricant

Dry press

Sintering

Products

Raw material

Compounding

Ball mill

Sieving

Mixing

Drying

Casting

Products

Deflocculant

FIGURE 31.1 Typical flow of ceramic production.

2006 by Taylor & Francis Group, LLC.

TABLE 31.1
Classification of Molding Methods in Ceramic Production Process

Method

Product Shape

Merit

Demerit

Drying

Pressing

Dry press

Uniaxial

pressing

Flat (container of electronic

parts, brick for mill’s wall)

The cheapest cost

Easy to automate factories

Direct sintering after pressing

Limitation of size and shape

Wet press

Flat (container of electronic

parts, brick for mill’s wall)

The cheapest cost

Easy to automate factories

Limitation of size and shape

Yes

Isostatic press (hydrostatic

press or rubber press)

Cylinder, pillar, sphere (mill’s

ball, plug, vacuum bulb tube)

Uniform density distribution

Less distortion

Mass production

Frequent reformation of mold

Hot press

Ceramics with high density

and strength

Low porosity and high strength

Sintering at low temperature

Limitation of shape

Difficult in mass production

Casting

Slip casting

Thin and complicated (melting

pot, yarn guide of spinning or
weavening, blade)

Simple equipments

Available for very

complicated–shape products

Easy to cause distortion

Taking long term for the

production of casts

Yes

Wide space for storage of casts

Molding

Injection molding

Complicated (yarn

guide of spinning
or weavening,
bulb, turbine blade)

Complicated shape with large size

High accuracy of size

Expensive metal molds

Not appropriate

for small ceramics

Yes

Smooth surface

Difficult to remove waxes

Doctor-blade process

Thin plate less than 1.5 mm thick

(laminate package, multifilm
slab, thick slab)

Good productivity

High accuracy of size

Expensive equipment

Wide space for installation

Large equipment for the molding

of large products

Yes

Uniform shrinkage

Extraction

Long tube and pillar (insulation

tube, protection tube)

Unlimited length of products

Continuous production

Yes

ß
2006

by
Taylor

&
Francis

Group,

LLC.

31.3 DRYING SHRINKAGE

Shrinkage during drying is one of the most impor tant
factors for the quality con trol of molded produ cts. It
is not only related to the de formati on and the gener-
ation of crack, war p, and saggi ng but also influenc es
the drying pr ocess its elf. Hence the drying of ceram ics
cannot be discus sed wi thout taking into accou nt the
shrinka ge problem .

W ater in mate rials exists with a potenti al for oc -

cupying voids, i.e., a sucti on potential for granula r
beds like sand , powd er, clay, and brick, an ab sorption
potenti al for activated alumi na and activated carbo n,
and a chemi cal bond for organic mate rials. The gra-
dient of these potentials , corres pondin g to that of
moisture co ntent, be comes the driving force for the
moisture movem en t in wet material s. The suction po-
tential can be classified into: (1) capillary suction poten-
tial and (2) osmotic suction potential, and it is known
that the shrinkage due to drying generally arises par-
ticularly for materials including water by the osmot ic
suction poten tial wi thin their intern al voids as clay.
while the cap illary sucti on potenti al is affe cted by the
capillary force in the mate rials consis ting of pa rticles
larger than 50- mm or der, the osmotic suctio n pot en-
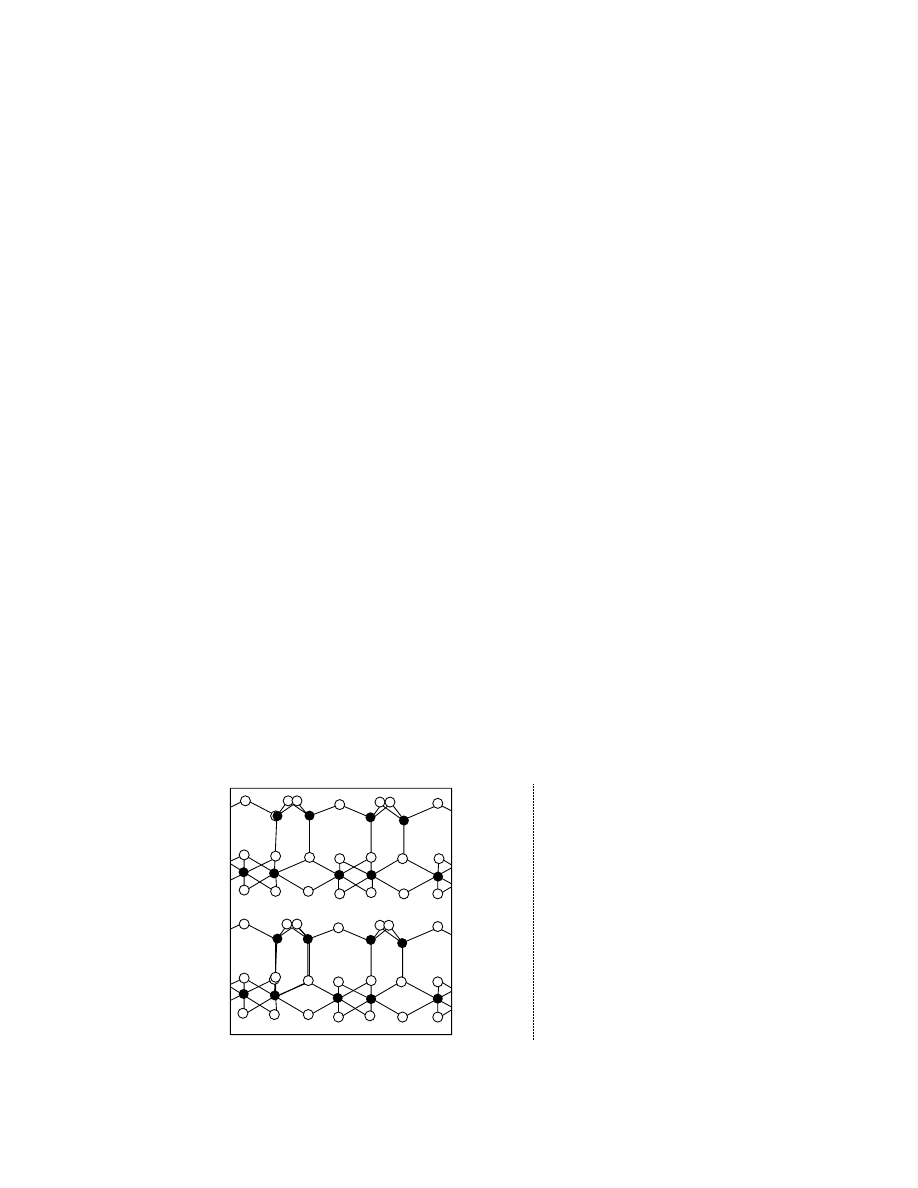
tial is brou ght a bout owing to an elect rochemi cal
effect between the wat er and the surfac e of pa rticles
smaller than micromet ers or submi cron order. The
surface of the pa rticles at the interface between clay
and water is gene rally negatively charged because
positive ions are dissoc iated from the surfa ce into
the water and ne gative ions are exposed on the sur-
face unless the other pos itive ions are also displ aced
so as to keep it electrica lly ne utral. Then the hydrogen
ions in the water are gather ed in the vicin ity of the
surface as illustrated in Figu re 31.2. Hence it is wel l

underst ood that wate r mo lecules woul d be su bjected
to osmot ic force arou nd the particles and the par-
ticles exist ap art from each oth er forming a wat er film
in wet clay. Nort on and Joh nson [1] predicted the
water- film thickne ss of Florida kaolin, fully water
based, on the data of pressure vs. linear shrinkage
using the pressing chamber. They reported that the
thickness varied between 3 and 30 nm for particles
0.32 mm in diameter depending upon the pressure
(<4 MPa).

The osmotic suction potential for clay was meas-

ured against the moisture content by Newitt and
Coleman [2] and Ohtani et al. [3] in comparison with
the capillary suction potential for granular materials.

Figure 31.3

[2] shows the relation be tween the osmot ic

suction potential and the moisture content for china
clay. The potential was observed to be proportional
to the exponential of the moisture content. The cor-
relation was influenced significantly by the additives
due to electrochemical interactions. The capillary suc-
tion potential for the bed of glass spheres of 40 mm in
diameter was much lower than the osmotic suction
potential for clay, and it was between 0 and 2500 mm
H

O depending upon the moisture content [3].

The shrinkage of clay is affected by the reduced

thickness of the water films formed on the particles due
to the osmotic suction potential and particles ap-
proaching closer to one another as water is removed
during drying. If all the clay particles are separated
from one another by water films and the void among
particles of clay is sufficiently filled up with osmotic
water, the volume of the shrinkage may be equal to
the volume of the removed water until particles con-
tact with the neighbor particles and the removed
water begins to be replaced in the void by air [2].
When the drying proceeds beyond this stage, the

+ +

−
−

−

Water film

Free water

FIGURE 31.2 The electrochemical effect on a fine particle in clay–water system.

2006 by Taylor & Francis Group, LLC.

shrinkage would be considered completed. The pat-
tern of this shrinkage is shown in Figure 31.4. How-
ever, the actual behaviors of shrinkage of clay are not
always idealized because it is not possible that all the
particles are perfectly separated from one another at
initial moisture content and begin to contact with
neighboring particles at the same time.

The first quantitative studies on the behavior of

clay shrinkage during drying were conducted by
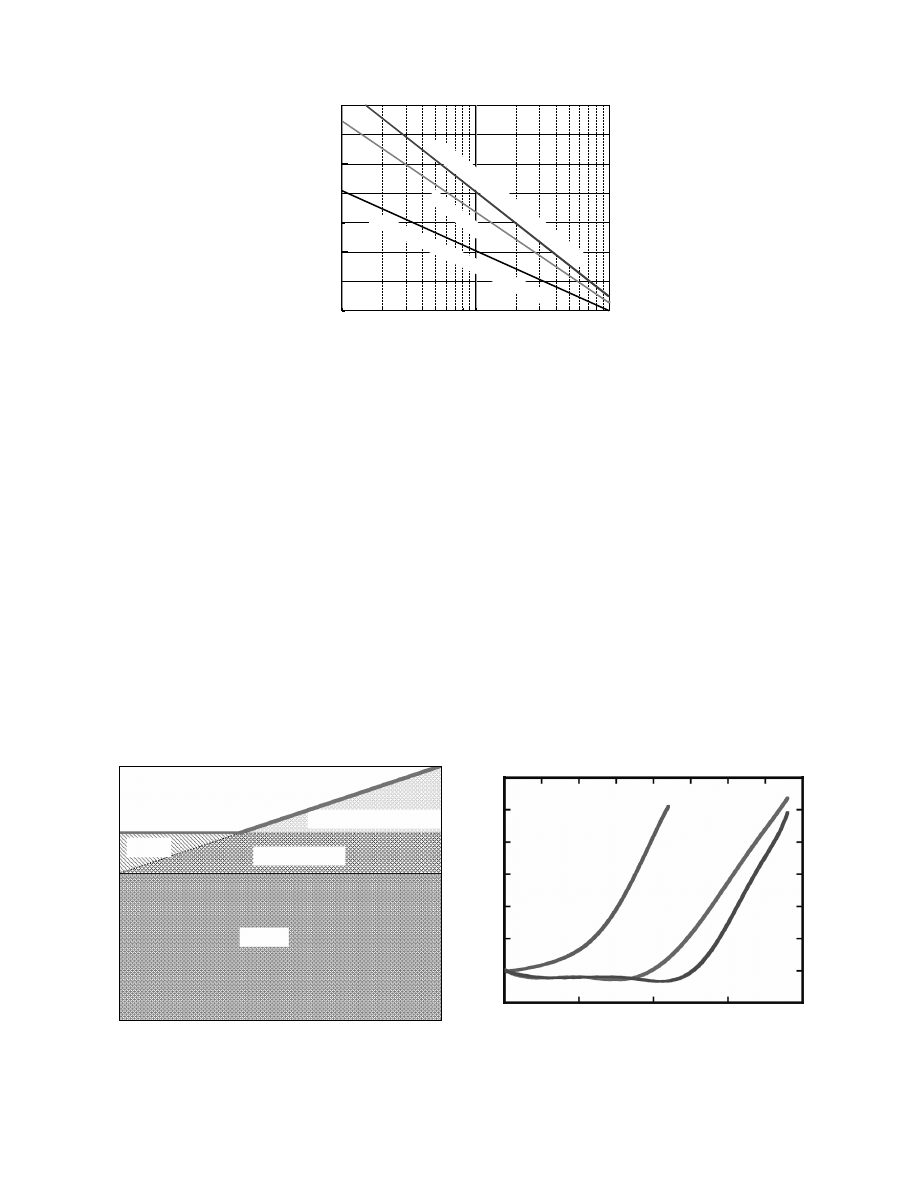
Norton [4], Macey [5], and Kamei and Toei [6]. Fig-
ure 31.5 [7] shows typical shrinkage curves. The
feature of the curves was dependent upon the kind
of the clay. Williamson [8] and Cox and Williamson
[9] studied the effect of orientation of the particle’s
crystal in ball clays produced by casting on the drying
shrinkage. The total shrinkage and the shrinkage rate
in the perpendicular direction to the major face of
particles were greater than those in the parallel direc-

tion. According to Noble et al. [10] if the molding
pressure for consolidation before drying is increased,
not only the minimum specific volumes of clay
achieved by drying can be decreased but also the
strength of the ceramics after sintering can be desir-
ably improved.

Most of these shrinking behaviors have been de-

termined under the conditions of normal atmospheric
drying or during slow drying rate. Hasatani et al. [11]
studied the impact of drying conditions on the shrink-
ing behavior of clay molded into sphere or slab. The
shrinking behaviors were influenced considerably by
the air temperature and the drying rate since the
moisture distributions and strain–stress due to the
gradient of moisture in the clay might be related to
the total volume. The shrinked volume was not al-
ways equal to the volume of water removed except
during the early period of drying. These results

0.30

0.34

0.38

0.42

0.46

0.50

0.54

0.58

0.1

Moisture content (kg-H

O/kg-dry solid)

Osmotic suction potential/101.3 (kPa/kPa)

Addition of sodium silicate (0.2%)

No additive

Addition of hydrochloric acid (0.2%)

FIGURE 31.3 Relation between osmotic suction potential and moisture content for china clay.

Shrinkage water

Pore water

Pore

Solid

Moisture content

Volume

FIGURE 31.4 Shrinking pattern of clay.

−1

0.1

(a) Fire clay

(b) Ball clay

0.2

Moisture content (kg-H

O/kg-dry soild)

Linear shrinkage (%-dry base)

0.3

0.4

FIGURE 31.5 Typical shrinking curves for some sorts of clay.

2006 by Taylor & Francis Group, LLC.

suggest that it is not possible to precisely predict the
shrinking behavior of molded clay only from the aver-
age moisture content and more accurate investiga-
tions are required to study its behavior.

31.4 MOISTURE MOVEMENT AND DRYING

BEHAVIOR

Several researches have been carried out to under-
stand the mechanism of moisture movement in clay
during drying. Newitt et al. [12] and Wakabayashi
[13] investigated the moisture movement in clay by
liquid diffusion and vapor diffusion, which affect the
drying characteristics particularly the falling rate.
They concluded that the liquid diffusion dominates
the movement until about 20%-dry basis in moisture
content for stoneware clay and 30% for the mixture of
80% Kibushi clay and 20% feldspar. Wakabayashi
[14] also evaluated the effective moisture diffusion
coefficient of some sorts of clay such as Kibushi,
Gairome, stoneware, feldspar, and their mixtures.
The effective diffusion coefficient is available for the
brief description of the moisture movement behavior.
The effective diffusion coefficient D can be defined by

(31:1)

They correlated D as

aKg

exp(

Kw)

kmS

þ gw)

(31:2)

where k is Carman’s constant (

¼ 5), N is the mass flux

of moisture, S is the specific surface area of clay, v

the specific volume of dry clay, w is the moisture
content with dry base, g is the specific gravity of a
clay particle, r

is the density of a clay particle, and m

is the viscosity of liquid water. Constants a and K are
given empirically by 2.02

Pa and 24.9 kg-solid/

kg-water, respectively.

To understand the mechanism further, a micro-

scopic investigation on the moisture content in clay is
required. The osmotic suction potential was intro-
duced as the driving force of moisture movement,
describ ed in

Se ction 31.3

, an d was success ively a p-

plied to the prediction of moisture movement in wet
clay [15,16]. The theoretical analysis on the two-
dimensional moisture transfer of cylindrical clay
was performed taking into account the effects of
both osmotic suction and strain–stress caused by
the shrinkage [17,18]. However, only the transient
mass-transfer equation was analyzed, assuming a
constant drying rate on the external surface of the

clay. Comini and Lewis [19] developed the finite
element method to solve simultaneous heat and mois-
ture transfer for noncompressible porous media for a
complicated geometry of the axial symmetry such as
electric insulators. The three-dimensional problem on
heat and moisture transfer, involving the drying
shrinkage, was analyzed by Hasatani et al. [20].
Their model was not only limited to surface evapor-
ation period but also applied to geometries more
complicated than a simple slab shape. In the future,
it is expected that drying kinetics would be experi-
mentally studied and the simple analysis be made
available for the entire drying periods.

Drying is a macroscopical phenomenon involving

simultaneous heat and mass transfer. Suppose that heat
conduction and moisture diffusion are dominant dur-
ing the overall transfer process in a homogeneous med-
ium. The multidimensional conservation equations for
an anisotropic medium can then be expressed as

¼ rJ

þ _q

þ DH

(31:3)

¼ rJ

(31:4)

The heat flux J

and mass flux J

in Equation 31.3

and Equation 31.4 are given by

¼ k

rT k

rC k

(31:5)

¼ D

rC D

rT D

(31:6)

The motion of water is influenced by the water pres-
sure, which is induced by the capillary or osmotic
suction resulting from evaporation in porous media.
The water flows in the relatively larger pores satur-
ated with water rather than by diffusion process. In
such a case, the pressure diffusion term dominates the
mass-transfer rate in Equation 31.6. The Soret effect
described by the temperature diffusion term is gener-
ally considered small compared with other terms.
Then Equation 31.6 can be simplified as

¼ D

(31:7)

The liquid flow rate in the porous media is given by
Darcy’s law:

(31:8)

where k

denotes the permeability. As the mass-trans-

fer rate should equal the water-flow rate if the vapor
flow is ignored, the pressure diffusivity D

is derived

from both Equation 31.8 and Equation 31.7:

2006 by Taylor & Francis Group, LLC.

(31 : 9)

Hence

Equat ion 31.4

can be rew ritten from

Equation

31.7

a nd Equation 31.9, assuming unifor m propert ies

in the body ,

@ C

@ t

p (31 : 10)

The capillary pressur e of water is determ ined by a
balance of the interfacia l energi es among the three
phases: solid , liquid, an d vap or, the wetti ng angle of
liquid– solid, an d the radii of the pores, whi ch are
depend ent on the pore struc ture in the med ium and
the amoun t of water exist ing in the pores. The os-
motic pressur e is dependen t on the por e structure and
the liqui d–solid interface. Ther efore, one must predict
the pressur e p statistica lly from the pore structure
distribut ion model.

In order to simp lify the model, alternati vely, the

mass-tr ansfer equatio n is often express ed by introd u-
cing the mois ture co ntent w as the driving force for
moisture trans fer,

@ w

@ t

¼ r

r w

(31 : 11)

The initial an d bounda ry cond itions must be specified
depend ing on the drying syst em an d the surround ing
atmosp here to whi ch a medium is expo sed.

31.5 DESIGNING PROCEDURE OF DRYERS

Dryers are class ified briefly into three types: parall el
current , countercur rent, an d crossc urrent , by the dir-
ection of hot airstrea m and mate rials movem ent. The
parallel- current type is intro duced when fast dry ing
rate is necessa ry in the e arlier drying pe riod. The
countercur rent type is avail able for the case where
drying ope ration is co nducted to maint ain a slow
rate in the earli er period an d sequen tially increa sing
the drying rate at a later period. Bat ch dryers in a
broader sense can be co nsidere d essential ly as one of
the c rosscurrent type. In this secti on, the outli ne of
the dryer-de signing proced ure is descri bed for the
most popul ar hot air he ating.

31.5.1 H

EAT AND

ASS

ALANCE

The fir st step toward any dryer design is the consid-
eration of heat and mass ba lance within the dryer.
Consid er the heat and mass balance when wet mate r-
ials with the mois ture con tent w

(kg-wat er/kg-dry

solid) and tempe ratur e T

(K) are dried in a dr yer

and the dry produ cts with the mois ture content w

(kg-wat er/kg-dry soli d) and tempe ratur e T

(K) a re

obtaine d. Suppos e that the heat loss is negli gibly
small, the total heat balance equ ation is express ed by

þ F

( c

þ c

) T

¼ G

þ F

( c

þ c

) T

(31 : 12)

where G

(kg-dry air/s) is the hot air mass -flow rate

with dry base, i (J/kg-dry air) is the wet air enthalp y,
F

(kg-dr y so lid/s) is the treatment rate of dry mate r-

ials, c

(J/(kg/ K)) is the specific he at of dry soli d, an d c

(J/(kg/K) ) is the specific heat of water. The subscrip ts 0
and 1 deno te the cond itions at inlet an d outlet of dryer,
respectivel y. F

is given by F

¼ F

/(1

þ w

) from

the treatment rate of wet mate rials F

(kg-wet soli d/

s). The wet air enthal py is correlated by

¼ c

þ ( l þ c

) H (31 : 13)

where c

(J/(kg/K)) is the specific heat of dry air, T

(K)

is the air temperature, l (J/kg) is the latent heat of water
evaporation, c

(J/(kg

K)) is the specific heat of steam,

and H (kg-water/kg-dry air) is the humidity.

The mass balance de duces the foll owing e quation:

)

¼ F

) (31 : 14)

If air temperatur es at the inlet an d outlet of the dry er
and humidi ty at the inlet are known as operatin g co n-
ditions, G

and H

can be solved simultaneously from

Equation 31.12 and Equation 31.14. The air tempera-
ture at the outlet T

should be chosen such that the

humidity obtained at the outlet, H

, does not exceed

the saturated humidity at T

. The flow rate of hot air

necessary at the normal standard state (101.3 kPa,
298.15 K), V

-wet air/s), is obtained by

298:15G

101:3

air

water

(31:15)

where R is the gas constant (8.314

J/(kmol/K)),

air

is the average molecular weight of air (28.97 kg/

kmol), and m

water

is the molecular weight of water

(18.02 kg/kmol).

31.5.2 D

ETERMINATION OF

RYER

IZE

AND

RYING

IME

A typical dryer used for continuous drying of ceram-
ics is a tunnel dryer seen in

Figure 31.6

. The length of

tunnel-type dryers and drying time are estimated fun-
damentally by the following procedures.

Now consider the countercurrent dryer modeled

as sh own in

Figure 31.7

. In the dryer, there are two

2006 by Taylor & Francis Group, LLC.

zones of the constant drying rate period and falling
rate period. In the zone of the constant rate period,
the mass balance between z, where z is equal to 0, and
z

becomes

)

¼ G

)

(31:16)

The mass balance between z, where z is equal to 0,
and z is

w) ¼ G

(31:17)

The differential expression of Equation 31.17 is
written by

¼ G

¼ R

a dz

(31:18)

where w

and H

denote the critical moisture content

and humidity at z

¼ z

, R

is the constant drying rate,

and a is the surface area of materials existing per unit
length of dryer. The constant drying rate is expressed as

¼ k

H) ¼

)

(31:19)

where k

and h are the mass- and heat-transfer coef-

ficients, respectively; H

is the saturated humidity;

and T

is the saturated temperature. Substituting

Equation 31.19 into Equation 31.18, integration
of Equation 31.18 deduces the length of the constant
rate period zone.

(31:20)

When H

is assumed to be constant in the constant

rate period zone, Equation 31.20 becomes

(31:21)

The mass-transfer coefficient k

can be approximated

analogically with the Lewis relation from the heat-
transfer coefficient h and specific heat of wet air c

for the water–air system.

(31:22)

In the zone of the falling drying rate, similar to the
constant rate period zone, the following balance
equations are obtained:

)

¼ G

)

(31:23)

w) ¼ G

(31:24)

¼ G

¼ R

a dz

(31:25)

The reducing drying rate R

is often correlated from

the drying characteristic curves determined experi-
mentally for wet materials in the following form:

¼ R

(31:26)

where w

is the equilibrium moisture content. Then

the length of the reducing rate period zone is given by

(31:27)

If the function f is approximated by the linear of the
first order, the length z

for a constant saturated

humidity is derived as

Trucks

Fresh air

Wet materials

Dry materials

Heater

Fan

Exhaust air

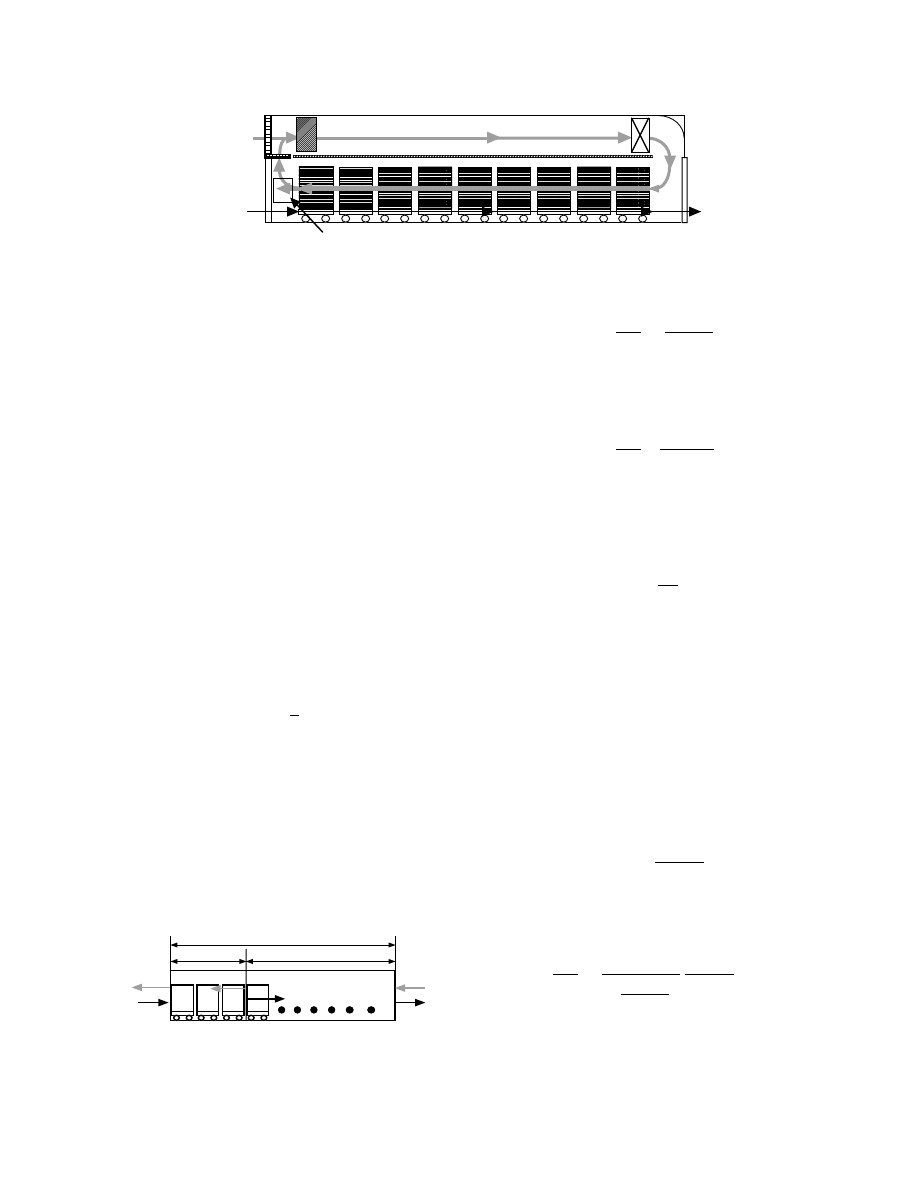
FIGURE 31.6 Configuration of typical tunnel dryers.

FIGURE 31.7 Model of hot air countercurrent flow for
design of continuous tunnel dryer.

2006 by Taylor & Francis Group, LLC.

)

(31 : 28)

As the prehe ating period is consider ably shorte r than
other periods , the total length of the dryer Z is deter-
mined by

¼ z

þ z

(31 : 29)

When the surfa ce area and the dry weig ht of each
molded mate rial are a

and m

, the drying time t

given by the foll owing equati on is requ ired to get dry
material s wi th mois ture co ntent w

(31 : 30)

31.6 DRYERS

31.6.1 T

UNNEL

RYERS

The varie ty of dryers used for drying process es of
molded ceramics is limited. A typic al continuous
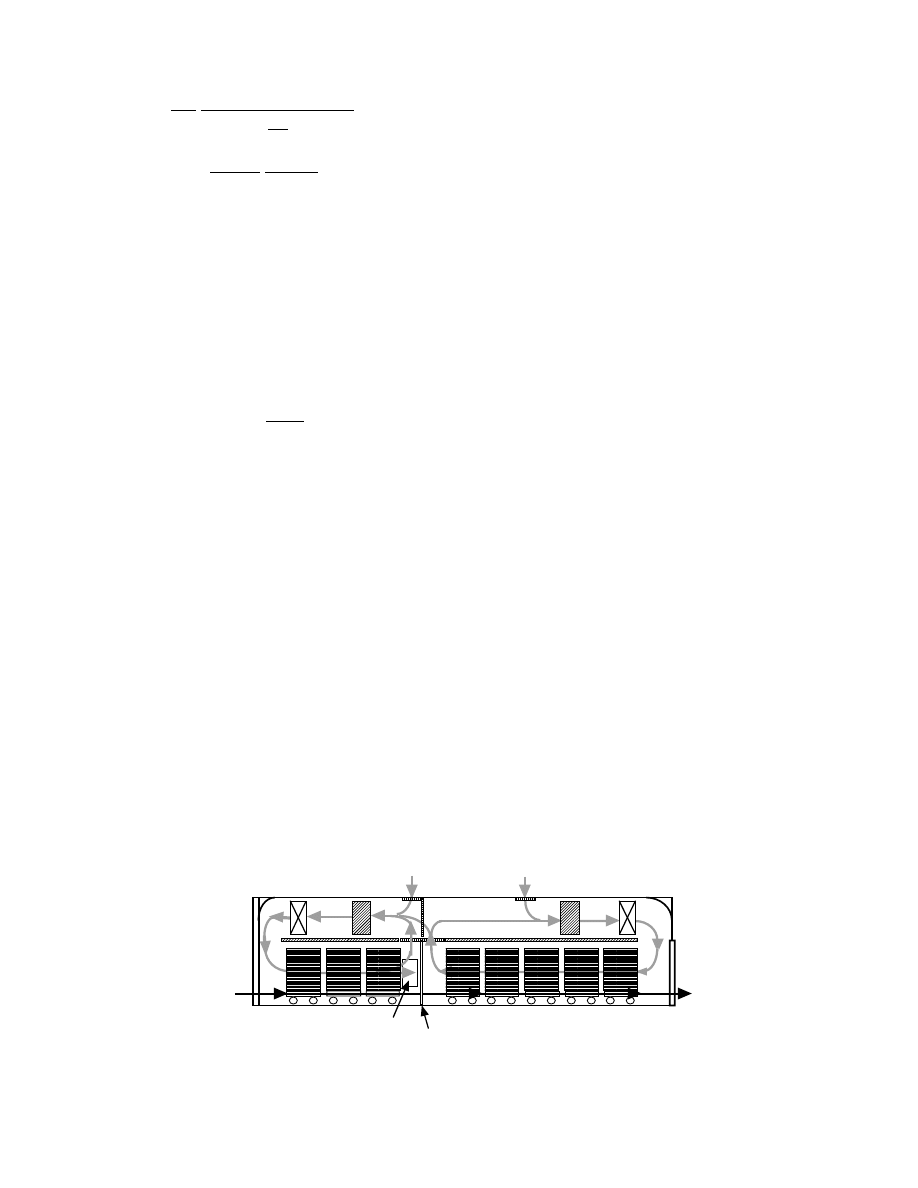
type of ceram ic drying is the tunn el dr yer whose
repres entative confi guration is shown in

Figure 31.6

Tunnel dryers are adaptabl e for drying req uiring
longer pe riods and are mass -produc ing, but they re-
quire a large installa tion space. Cerami cs put
on trucks are moved through the tunnel. M ultiway
flow of hot air is often intro duced to control the
drying rate independ ently during the co nstant and
falling rate periods other than the co untercur rent,
parallel current , or cro sscurrent agains t the mov ing
direction of ceram ics. In the exa mple sho wn in Figu re
31.8, the constant rate pe riod is operate d by a parall el
flow to he at up rapidl y and enha nce the drying rate,
and the co unter flow is employ ed during the falling

rate pe riod. Humi d air during flowi ng in wet mate r-
ials recir culat es partly to co ntrol the humidi ty by
mixing wi th fresh air. Hot air temperatur e sup plied
to the dryer is ge nerally 370 to 470 K. Then the loga-
rithmic mean of tempe ratur e difference between air
and ceramics in the constant rate period becomes 30
to 70 K. The prod uct of the heat- transfer coefficie nt
and the specific surfa ce area, ha , is between 230 and
350 W /(K

-dryer vo lume). In the truck carrier type,

a number of ceram ics are placed on a truck and the
hot air flow rate is set usually to pass through among
the ceram ics at 1 to 5 m/s. If the clear ance among the
ceram ics is not suffici ent, it results in nonuni form
drying and drifting the air flow between trucks and
the wall of tunn el. Hence, the arrange ment of ceram -
ics on trucks and ventilat ion of air by blow ers shou ld
take place caref ully.

31.6.2 B

AND

RYERS

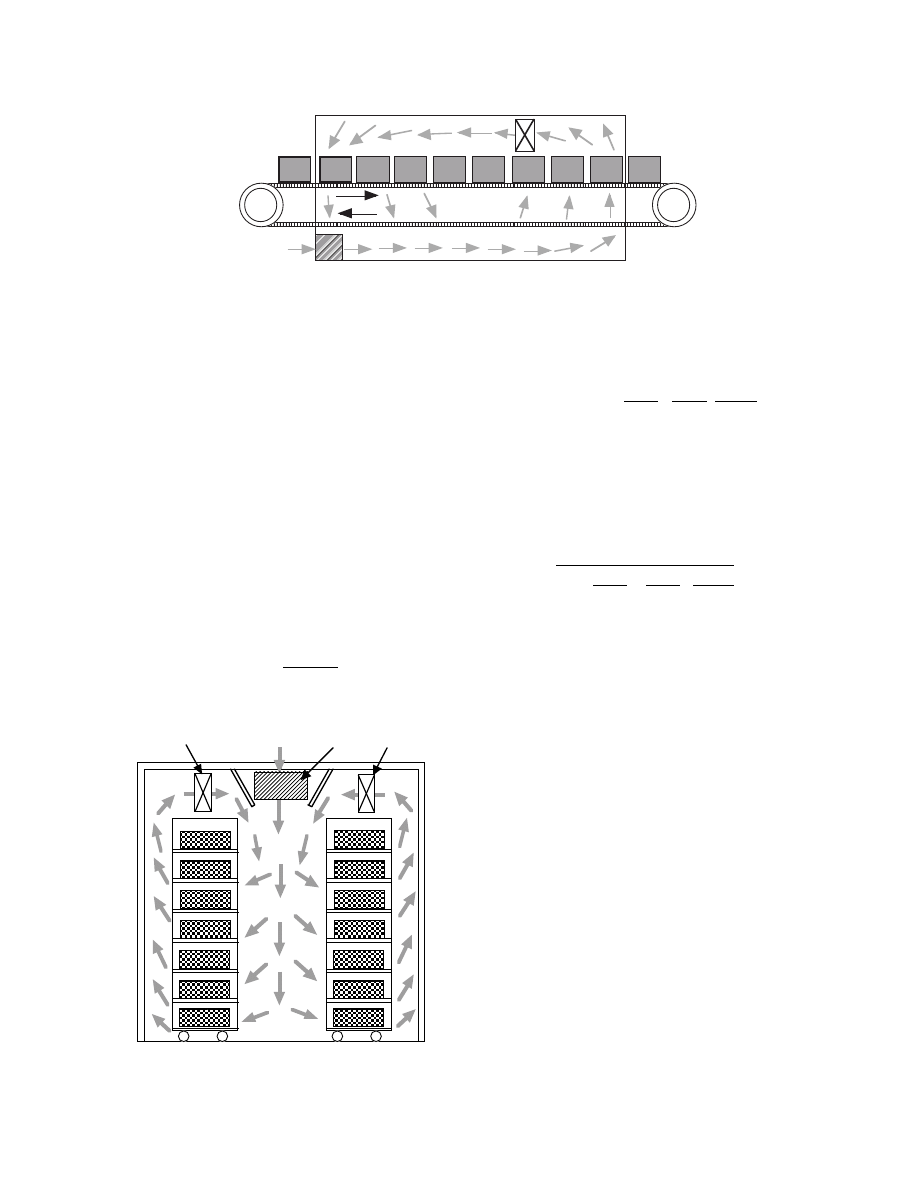
Band dryers are also of continuous ope ration type.
Mater ials are conveyed on ba nds rotating in the dry-
ing ch amber as shown in

Figu re 31.9

. Band consis ts

of a net or a perforated plate . Hot air flows crossing
the ba nd upwar d or downw ard because heat- and
mass-tr ansfer rates are greater than that from parall el
flow. It is pos sible to control the tempe ratur e, humid-
ity, and flow rate of air at each optimu m state in some
zones separated in the dryer. Alth ough the ope ration
tempe ratures are almos t the same as the tunnel
dryers , ha is 45 to 9 5 W /(K

-dryer volume ) for the

parallel flow.

31.6.3 B

ATCH

RYERS

A typical configuration of batch dryers is shown in

Figure 31.10

. We t material s are placed on trays or

shelves, which are set in a dryer’s room. Hot air
circulates among the shelves in the room by a blower.
These dryers are available for drying of various types

Trucks

Fresh air

Wet materials

Dry materials

Heater

Fan

Exhaust air

Fresh air

Heater

Partition

Fan

FIGURE 31.8 Concept of the combined-flow pattern of hot air in continuous tunnel dryer.

2006 by Taylor & Francis Group, LLC.

of ceram ics as drying c ondition s, i.e., time, tempe ra-
ture, air rate, etc. , in eac h batch operati on, can easily
be ch anged an d control led. In most cases, howeve r,
manpow er is required to pack, install, and remove the
material s from the shelve s. The dr ying time must be
determ ined preli minarily from the drying charact er-
istics obtaine d from a laborat ory scale of experi ment.
As the drying charact eristic and the critical mois ture
content are depen dent upon tempe rature, humidi ty,
and air rate, the prelimina ry experi mental test shou ld
be perfor med wi th care to ad just to the atmosp heric
conditi ons in the drye rs. When a pa rt of the hot air
recirculat es to impro ve the effective energy utilization
and con trol the humidi ty in the dryers , the recir cula-
tion ratio X is determined to maint ain a co nstant
humidi ty by the followin g eq uation:

¼ 1

R =G

(31 : 31)

For the exhaust air, V

/s) becomes

¼ G

X ) 22:4

28 : 97

18 : 02

273 : 15

(31 : 32)

where R (kg/ s) is the evap oration rate; H

an d H

(kg-

water/k g-dry air) are the humidi ty of fresh air and
exhaust air, respect ively; and T

(K) is the tempe ra-

ture of exhau st air. Dry air mass-flo w rate circul ating
in dryers G

(kg/ s) is given by

22 : 4

28 : 97

18 : 02

273 : 15

(31 : 33)

where V

/s) is the air flow rate in the drye rs, H

the hum idity of air in the dryers , and T

is the tem-

peratur e in the dryers.

Hot air tempe ratur e suppli ed to the dryers is ge n-

erally between 370 and 420 K for batch dryers , and
the logarithm ic mean of tempe ratur e difference be -
tween air and c eramics in the constant rate period is
approxim ately 30 and 100 K. The operati ng range of
ha lies betw een 230 and 350 W/(K

-dryer volume ).

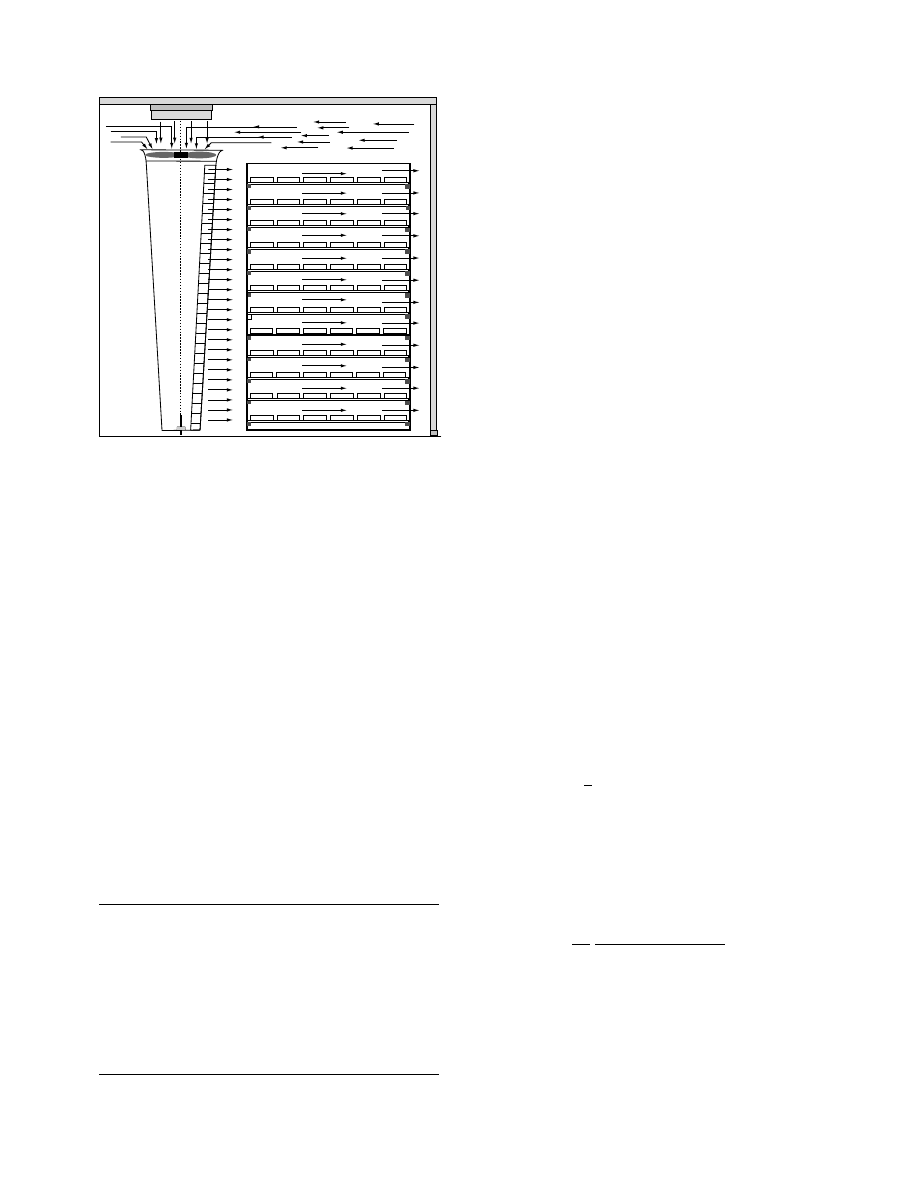
A dr yer assem bled with an air chambe r, often

known as the air-cir culating unit, is sho wn in

Figure

31.11

. It is de signed to impr ove the mixi ng of fresh

hot air an d recircu lating air an d ensure unifor m air
flow throu gh the dryer chamber.

31.6.4 D

RYING BY

NFRARED

EATING

Mater ials are heated directly by infrared irradiat ion.
Infrared lamps as well as hot rods and plates with
efficient emission performance can be used as infrared
sources. When wet materials are heated in the con-
stant drying rate period by infrared radiation, the
surface temperature increases to a temperature higher
than the wet bulb temperature and the drying rate is
enhanced. However, the drying operation must be

Heater

Fan

Conveyer

Wet materials

Dry materials

Fresh air

FIGURE 31.9 Configuration of typical band dryers.

Fresh air

Heater

Fan

FIGURE 31.10 Configuration of typical batch dryers.

2006 by Taylor & Francis Group, LLC.

perfor med carefu lly as a rapid drying rate may resul t
in the failure of ceram ics due to shrinka g e. An
applic ation of infrared heatin g and combined infr a-
red-conv ecti ve he ating in the falling drying rate
period is effe ctive in enhan cing the drying rate. It is
easy to control the power of infrared sou rces. Thus ,
infrared heati ng is often applie d to a comp lex con fig-
uration of ceram ics with fins or waves avo iding the
generat ion of cracks in a sho rter time. It is necessa ry
to control the power so that the sou rces facing a
simple su rface of ceramics are strong whereas tho se
to a comp lex surfa ce are weak [21].

Infra red heati ng syste ms are class ified as open

type, tunne l type, an d closed type. The open type is
the simplest syst em to co mplemen t, but its energy loss
is the large st. The tun nel type inst alls infrared so urces
in tunnel dryers and is operate d continuou sly. The
closed type is operate d in a closed roo m, and usually
has the highest energy efficien cy, as lis ted in
Table 31.2, beca use the mate rials are not only he ated

by direct irradiat ion of radiat ive energy from infrared
sources but also by the convecti ve heatin g of air
heated by the sources.

31.6.5 D

RYING BY

ICROWAVE

EATING

The frequency of the microwave used for industrial
heating comprises two bands of 2450 and 915 MHz in
the broad countries. These frequencies are greatly
effecti ve for he ating of water.

Figu re 31.12

sho ws a

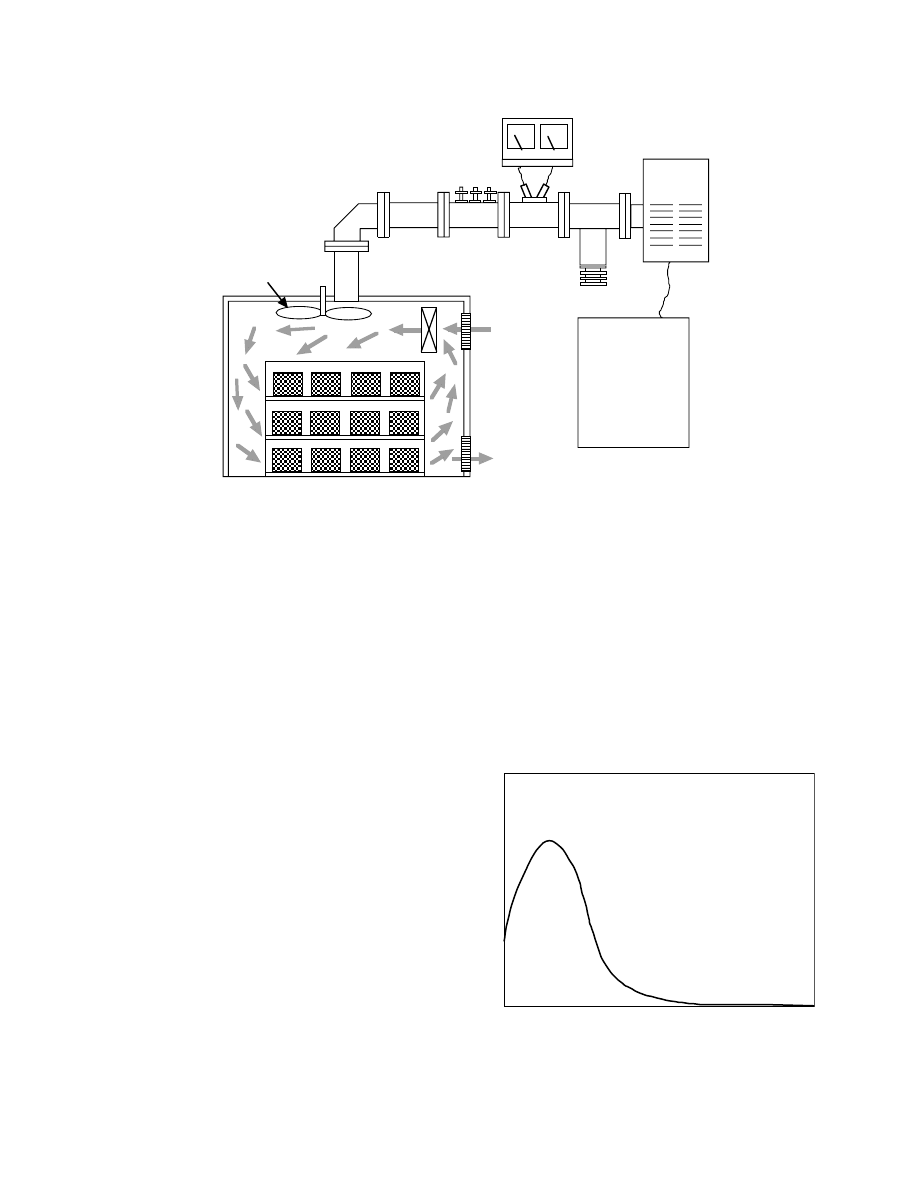
typical system of drying by microwave heating.
Microwaves are generated in a magnetron, which is
introduced into an applicator where the wet materials
are heated via transmission through a waveguide.
Using the waveguide, an isolator that is an absorber
of reflection wave prevents the wave from returning
to the generator and breaking it. A power monitor for
measuring the output power and a tuner that adjusts
to inhibit the reflection of microwave from the appli-
cator are also installed. The merits of microwave
heating can be summarized as follows:

Wet materials are heated internally because
microwave energy can penetrate the inside of
the body.

Only wet materials are heated selectively and
high energy efficiency is expected.

Rapid heating is possible.

The operation and control processes are easy,
and drying is possible in any atmosphere includ-
ing a vacuum.

When a material whose relative dielectric constant is
«

is placed in the electric field E (V/m) and frequency

f (Hz), the heating rate per unit volume P (W/m

) is

correlated to the equation

5
9

f E

tan d

(31:34)

where tan d is the dielectric loss tangent. The product
«

tan d is called as loss the factor. The half power

depth D (m) represents the length penetrating the
materials from the surface until the power dissipates
to half, and is given by

¼ 0:347

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ tan

(31:35)

where l (m) is the wavelength.

Uniform drying of molded ceramics such as

honeycombs is performed without deformation by
controlling the microwave profile along the material
length. In the drying of thick ceramics by microwave

ACU

FIGURE 31.11 Advanced batch dryer with the air-circulating
unit. (From catalogue of Novokeram.)

TABLE 31.2
Energy Efficiency of Infrared Heating for
Various Types

Type

Energy Efficiency

Open

25–35

Tunnel

45–50

Closed

50–65

2006 by Taylor & Francis Group, LLC.

heating, the material internal temperature may rise
rapidly to a temperature higher than the surface tem-
perature. This results in explosive expansion due to
the internal vapor pressure. The microwave power
should, therefore, be controlled appropriately to pre-
vent overheating the inside of the body.

31.6.6 D

RYING BY

LECTRIC

URRENT

EATING

Electric current heating is applied to the drying of
cylindrically symmetric ceramics such as insulators.
This heating method enhances the drying rate while
controlling the crack formation by the effect of in-
ternal heating. In general, parts of fins or hoods of
insulators dry up remarkably faster than the body,
resulting in the formation of cracks due to drying-
induced stress. As the electric current selectively heats
the body rather than the hoods, drying up of hoods
may be inhibited in comparison with the drying by
hot air heating. If defects are still found, wrapping
around ceramics is further introduced to control the
drying rate. The operation takes place usually in
charging the voltage of 100 to 400 V between both
the edges depending on the size of insulators. The
temperature of rods should be increased slowly in
order to be maintained almost uniformly throughout
the drying period until the maximum temperature is
less than approximately 320 K. The typical electric
current pattern changes in a drying process are

shown in Figure 31.13. In the earlier period, the cur-
rent rises gradually due to shrinkage whereas it falls
down in the later period because of the reduction of
the moisture content. The peak current density is in
the order of a few milliamperes per square centimeter.
In this method, a special structure for adjusting the
electrodes on the insulators may be necessary to en-
sure a good contact throughout the entire drying
period even if the ceramics shrink.

Power controller

Generator

Power monitor

Isolator

Tuner

Waveguide

Fan

Fresh air

Exhaust air

FIGURE 31.12 A standard assembly of microwave drying and batch dryer with the chamber of air-circulating unit.

Time

Electric current

FIGURE 31.13 A typical pattern of current during electric
current drying of insulators.

2006 by Taylor & Francis Group, LLC.

31.7 STUDIES ON FAILURE AND

DEFORMATION OF CERAMICS

The generation of failure and deformation of molded
clay are the undesirable problems requiring quality
control during ceramic production. The mechanical
properties of wet clay are important parameters to
understand the mechanism of the drying phenomena.
Many experimental data are available for a variety of
clays [22–26]. The mechanical behavior of clay is
generally described by the viscoelasticity or plasticity,
which is dependent on the moisture content. In add-
ition to the simulation of heat and moisture transfer,
the strain–stress analysis is simultaneously required
not only to predict the deformation and the failure of
molded ceramics during drying but also to precisely
design the mold in order to develop an effective
process. Recently, theoretical studies have been con-
ducted for one of the problems including the shrink-
age of clay [17,18,20] while numerically simulating the
clay-drying problem. However, research taking into
account the failure generation and development of an
effective drying process to improve the drying rate
has been quite minimal. If the drying of molded clay
is conducted too quickly, it may result in rapid surface
dry-up while keeping a wet state in the inside. A fall in
the fast-drying rate often causes the failure or the
generation of deformation. These phenomena appear
during the low moisture-migration rate in the clay.

Figure 31.14 shows an analytical result of the

maximum tensile stress generated within a slab of
drying clay with a physical length of 60 mm, width
of 60 mm, and thickness of 24 mm [27]. The param-
eters of drying operation and ceramic properties are

represented by dimensionless parameters such as the
Biot number (Bi) and Lewis number (Le). Assuming
constant properties of the slab, the former number
corresponds to the heating rate and the latter to the
internal diffusion rate of moisture. Thus a higher Bi
applies rapid heating rate whereas a higher 1/Le
means larger effective diffusion coefficient of mois-
ture in the body. W

denotes average moisture content

normalized by initial content. The absolute magnitude
of the maximum tensile stress should be considered on
an arbitrary scale as it depends largely on the mechan-
ical properties of the slab, but the dimensionless
parameters of these properties are not available.
Although a higher Bi results in remarkably stronger
stress, the stress falls down with a larger 1/Le. Hence,
heat-transfer enhancement in the dryer and uniform
drying are not possible during ceramic drying unless
the moisture-migration rate in the clay is actively or
passively enhanced by an auxiliary drying method
such as the superheated steam drying. Therefore
both

experimental

and

theoretical

studies

are

expected to make significant contributions to R&D
of noble drying methods.

31.8 CONCLUSIONS

The R&D for the ceramic production utilizing ad-
vanced drying technology has been proposed. The
drying of ceramics must be carefully carried out in
order to keep their own molded configuration. If the
drying process is hastened, it will result in serious
problems such as drying up of the surface, undesir-
able deformation, and crack generation. Several re-
searchers have studied the mechanism of moisture
movement and shrinkage of clay. Some molding pro-
cesses using the dry method have been developed. It
may seem that the research works on the drying of
ceramics have been almost complete. However, there
are few systematic investigations on the quality con-
trol of ceramics during drying and on the develop-
ment of the precise prediction method for the design
of the molding and the dryers. Furthermore, the qual-
ity problems arising from drying have not been
solved. It should be pointed out that there are still
many R&D programs required to improve the drying
process of ceramics.

REFERENCES

1. Norton, F.H. and Johnson, A.L., 1944, Fundamental

Study of Clay. V-Nature of Water Film in Plastic Clay,
Journal of the American Ceramic Society, 27(3), pp. 77–80.

2. Newitt, D.M. and Coleman, M., 1952, The Mech-

anism of Drying of Solids. Part III—The Drying

500

1000

1500

0.80

0.85

0.90

[-]

0.95

Maximum tensile stress

0.4,1/Le

0.1

0.1,0.05

0.2,0.1

0.1,0.1

0.05,0.1

0.1,0.2

FIGURE 31.14 Maximum tensile stress analyzed during
convective heat drying for a slab of 60

60 24 mm.

2006 by Taylor & Francis Group, LLC.

Characteristics of China Clay, Transactions of the
Institution of Chemical Engineers, 30, pp. 28–45.

3. Ohtani, S., Suzuki, M., and Maeda, S., 1963, On the

Suction Potential of Granular Material, Kagaku
Kogaku, 27(9), pp. 638–645.

4. Norton, F.H., 1939, Precise Measurement of Drying

Shrinkage, Ceramic Age, 33, pp. 7–8.

5. Macey, H.H., 1942, Clay–Water Relationships and the

Internal Mechanism of Drying, Transactions of the Brit-
ish Ceramic Society, 41, pp. 73–121.

6. Kamei, S. and Toei, R., 1952, Studies on Drying

Shrinkage, Kagaku Kikai, 16(11), pp. 372–377.

7. Shiraki, Y., 1980, Ceramic Seizou Process (Ceramic

production Process), in Japanese, Gihodo, Tokyo.

8. Williamson, W.O., 1955, Oriented Aggregation, Differ-

ential Drying-Shrinkage and Recovery from Deform-
ation of a Kaolinite–Illite Clay, Transactions of the
British Ceramic Society, 54(7), pp. 413–442.

9. Cox, R.W. and Williamson, W.O., 1958, Differential

Shrinkage of Clays and Bodies Caused by Particle-
Orientation and Its Significance in Testing-Procedure,
Transactions of the British Ceramic Society, 57(2)
pp. 85–101.

10. Noble, W., Williams, A.N., and Clews, F.H., 1958,

Influence of Moisture Content and Forming-Pressure
on the Properties of Heavy Clay Products, Transactions
of the British Ceramic Society, 57(7), pp. 414–461.

11. Hasatani, M., Itaya, Y., and Muroie, K., 1993. Con-

traction Characteristics of Molded Ceramics during
Drying, Drying Technology, 11(14), pp. 815–830.

12. Newitt, D.M., Nagara, P.N., and Papadopoulos, A.L.,

1960, The Deposition of Solute Material in Porous
Beds during Convection and Conduction Drying,
Transactions of the Institution of Chemical Engineers,
38, pp. 273–278.

13. Wakabayashi, K., 1964, Moving-Moisture in the

Drying of Clay, Kagaku Kogaku, 28(1), pp. 12–18.

14. Wakabayashi, K., 1964, Moisture Diffusion Coeffi-

cients of Solid during Drying Process, Kagaku Kogaku,
28(1), pp. 33–38.

15. Wakabayashi, K., 1965, On Liquid Moisture Move-

ment in Particle Bed, Funtai Kogaku, 2(5), pp. 1153–
1156.

16. Wakabayashi, K., Yamaguchi, S., Matsumoto, T., and

Mita, T., 1977, Liquid Moisture Movement in a Fine

Particle Bed during Drying Process, Kagaku Kogaku
Ronbunshu, 3(2), pp. 189–194.

17. Shishido, I., Maruyama, T., Funaki, M., and Ohtani,

S., 1987, On the Drying Mechanism of Shrinkage
Material, Kagaku Kogaku Ronbunshu, 13(1), pp. 78–85.

18. Shishido, I. Muramatsu, T., and Ohtani, S., 1988, Local

Moisture Content and Stress Distributions within Clay
during Drying Shrinkage, Kagaku Kogaku Ronbunshu,
14(1), pp. 87–94.

19. Comini, G. and Lewis, R.W., 1976, A Numerical Solu-

tion of Two-Dimensional Problems Involving Heat and
Mass Transfer, International Journal of Heat and Mass
Transfer, 19, pp. 1387–1392.

20. Hasatani, M., Itaya, Y., and Hayakawa, K., 1991,

Strain–Stress Formation and Heat and Moisture Trans-
fer of Clay during Drying, Proceedings of the Seventh
Polish Drying Symposium, Lodz (Poland).

21. Sato, T., 1998, Drying Method and Equipment of

Molded Ceramics (in Japanese), Patent in Japan, No.
10–325676.

22. Shiraki, Y. and Komaki, T., 1955, Studies on Clay–

Water System. (I-12) Visco-Elastic Properties of Clay
Paste, Journal of the Ceramic Association of Japan,
63(708), pp. 194–197.

23. Shiraki, Y., 1955, Studies on Clay–Water System. (II-1)

Plasticity of Clay, Journal of the Ceramic Association of
Japan, 63(709), pp. 233–243.

24. Shiraki, Y. and Fukuura, Y., 1955, Studies on Clay–

Water System. (II-4) Plastic Deformation of Nearly
Dry Clay, and Relations between Water Content and
Modulus of Rupture and Modulus of Elasticity,
Journal of the Ceramic Association of Japan, 63(714),
pp. 527–532.

25. Shiraki, Y., 1955, Studies on Clay–Water System. (II-3)

Theoretical Consideration to the Visco-Elastic Property
of Clay–Water Masses, Journal of the Ceramic Associ-
ation of Japan, 63(712), pp. 421–429.

26. Shishido, I., Iida, K., Muramatsu, T., and Ohtani, S.,

1987, Measurement of Mechanical and Transport
Properties in Drying Shrinkage Materials, Kagaku
Kogaku Ronbunshu, 13(4), pp. 522–525.

27. Itaya, Y., Taniguchi, S., and Hasatani, M., 1997, A

Numerical Study of Transient Deformation and Stress
Behavior of a Clay Slab during Drying, Drying Tech-
nology, 15(1), pp. 1–21.

2006 by Taylor & Francis Group, LLC.

Document Outline

Table of Contents
Chapter 031: Drying of Ceramics

Wyszukiwarka

Podobne podstrony:
Modeling with shrinkage during the vacuum drying of carrot (daucus carota) (Arévalo Pinedo, Xidieh M
Influence of drying methods on drying of bell pepper (Tunde Akintunde, Afolabi, Akintunde)
Far infrared and microwave drying of peach (Jun Wang, Kuichuan Sheng)
Microwave Application in Vacuum Drying of Fruits (Drouzaf, H SchuberP)
Microwave vacuum drying of model fruit gels (Drouzas, Tsami, Saravacos)
041 Drying of Polymers
039 Drying of Biotechnological Products
042 Drying of Enzymes
Modeling and minimizing process time of combined convective and vacuum drying of mushrooms and parsl
022 Drying of Fish and Seafood
026 Drying of Herbal Medicines and Tea
Characterization of microwave vacuum drying and hot air drying of mint leaves (Mentha cordifolia Opi
Microwave Application in Vacuum Drying of Fruits (Drouzaf, H SchuberP)
040 Drying of Coated Webs
Microwave Drying of Parsley Modelling, Kinetics, and Energy Aspects
Microwave Finish Drying of Diced Apples in a Spouted Bed
043 Drying of Coal

więcej podobnych podstron

031 Drying of Ceramics

Document Outline