VII. ANALIZA KONSTRUKCJI NAWIERZCHNI- NAPRĘŻENIA I UGIĘCIA W PÓŁPRZESTRZENI
SPRĘŻYSTEJ, UKŁAD DWUWARSTWOWY, WIELOWARSTWOWY
(wg Boussinesq’a) Ośrodek gruntowy można uważać za półprzestrzeń, która jest ograniczona od góry
płaszczyzną poziomą (powierzchnią terenu) i rozprzestrzenia się nieskończenie głęboko i szeroko.
Przyjmuje się, że ośrodek gruntowy jest sprężysty(liniowo odkształcalny), izotropowy (takie same właściwości
fizyczne w każdym punkcie) i jednorodny. Takie założenie ułatwia wyznaczenie wartości naprężeń i odkształceń,
a wartości błędu popełnionego przy obliczeniach zależą od tego, jak dalece rzeczywista zależność odkształceń
od naprężeń gruntu w rozpatrywanych warunkach różni się od prawa Hoocke’a.
W granicach stosowanych w praktyce obciążeń można przyjąć, że odkształcenia ośrodka gruntowego są liniowo
zależne od naprężeń (ośrodek liniowo- odkształcalny). [Wiłun]
Naprężenie jest to graniczna wartość stosunku siły działającej na nieskończenie mały element pola przekroju
ciała do wymiaru tego pola:
=limΔ /Δ (A-> 0)
1. Naprężenia- notacja
Układ wsp. radialny:
σz- naprężenia pionowe
σr- n. poziome radialne
σϕ- n. poziome obwodowe
Układ wsp. prostokątny:
σx- n. poziome w kierunku ‘x’
σy- n. poziome w kierunku ‘y’
σz- n. pionowe
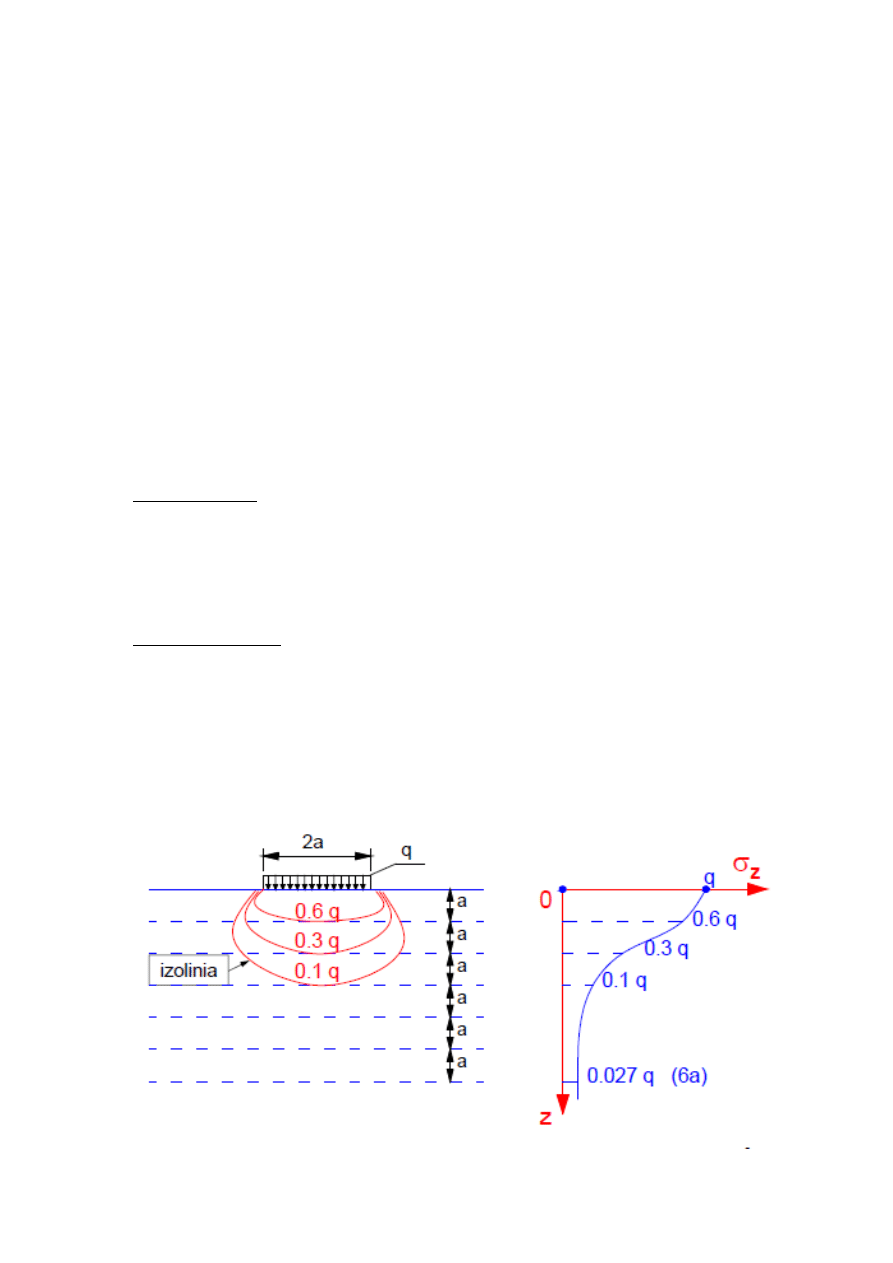
2. Interpetacja naprężeń pionowych nawierzchni
Z powyższego wynikają wnioski:
- informacja o maksymalnych naprężeniach gwarantuje projektowanie w taki sposób by naprężenia nie
powodowały uszkodzeń
- im większa głębokość tym naprężenia są mniejsze, można stosować słabszy grunt (tym, samym słaby
grunt może przenieść naprężenia o ile będzie wystarczająco daleko).
Naprężenia można obliczyć:
, gdzie
Nz wyznaczamy z nomogramu. Jest to wielkość zależna od stosunku r/a oraz z/a.
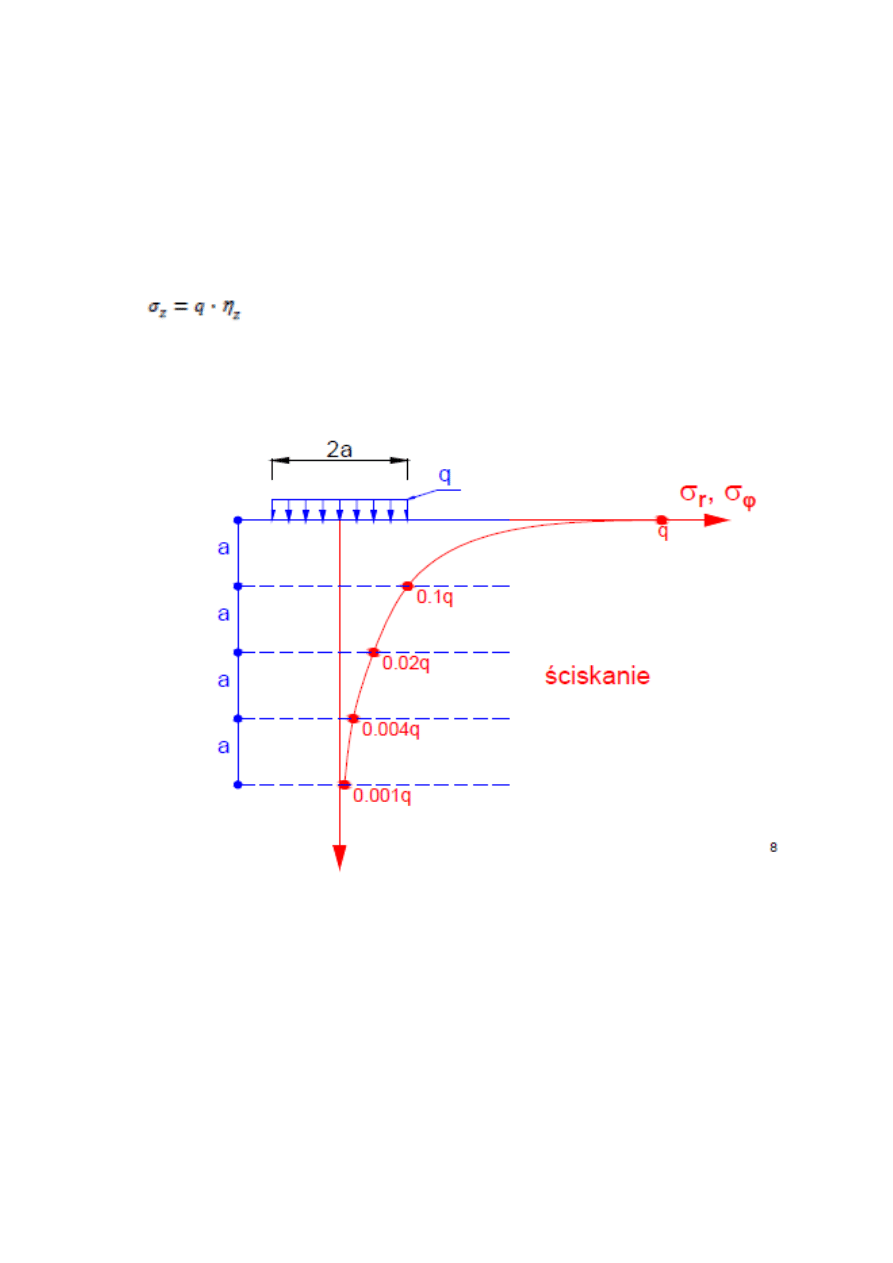
3. Interpretacja naprężeń radialnych i obwodowych
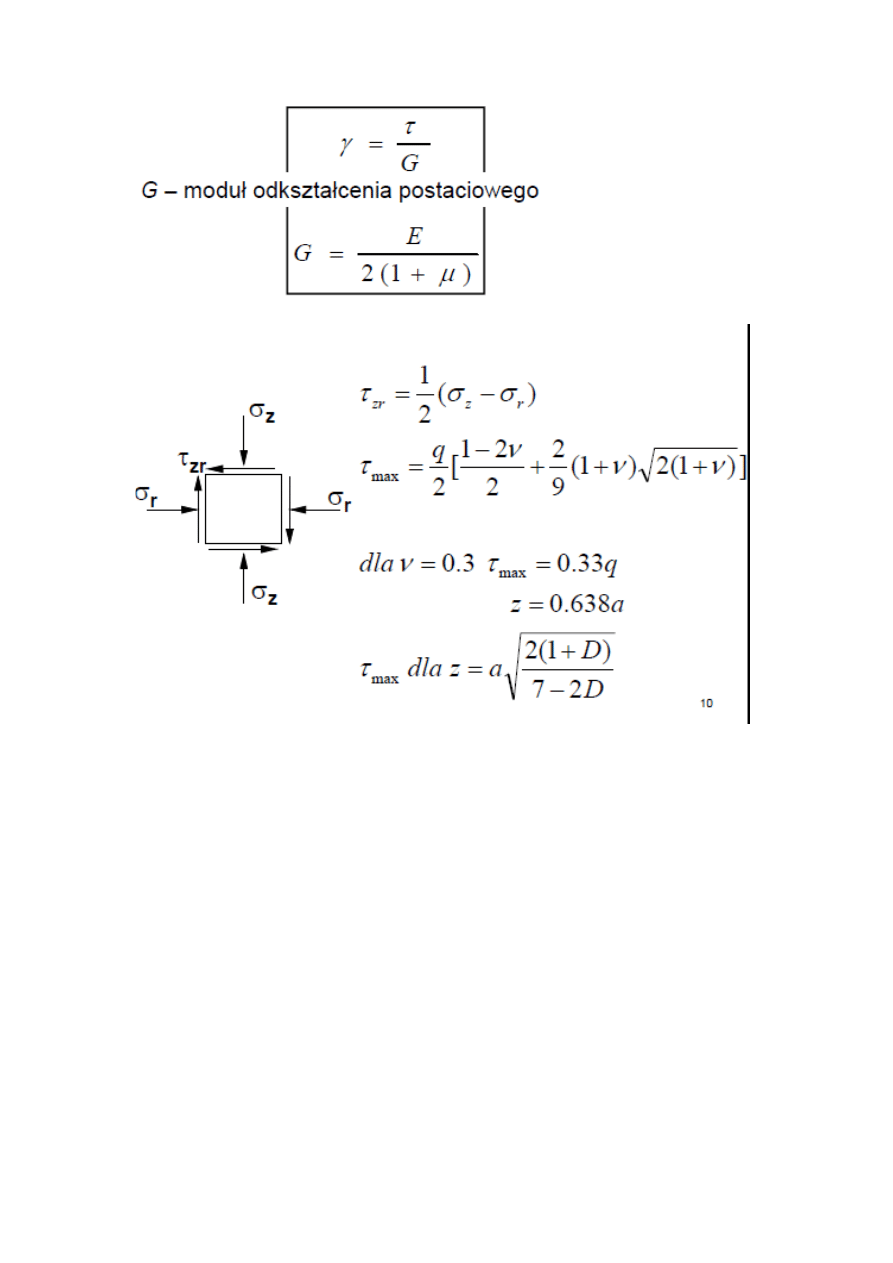
4. Naprężenia styczne w nawierzchni
Wyraża się wzorem:
Interpretacja graficzna naprężeń stycznych w półprzestrzeni:
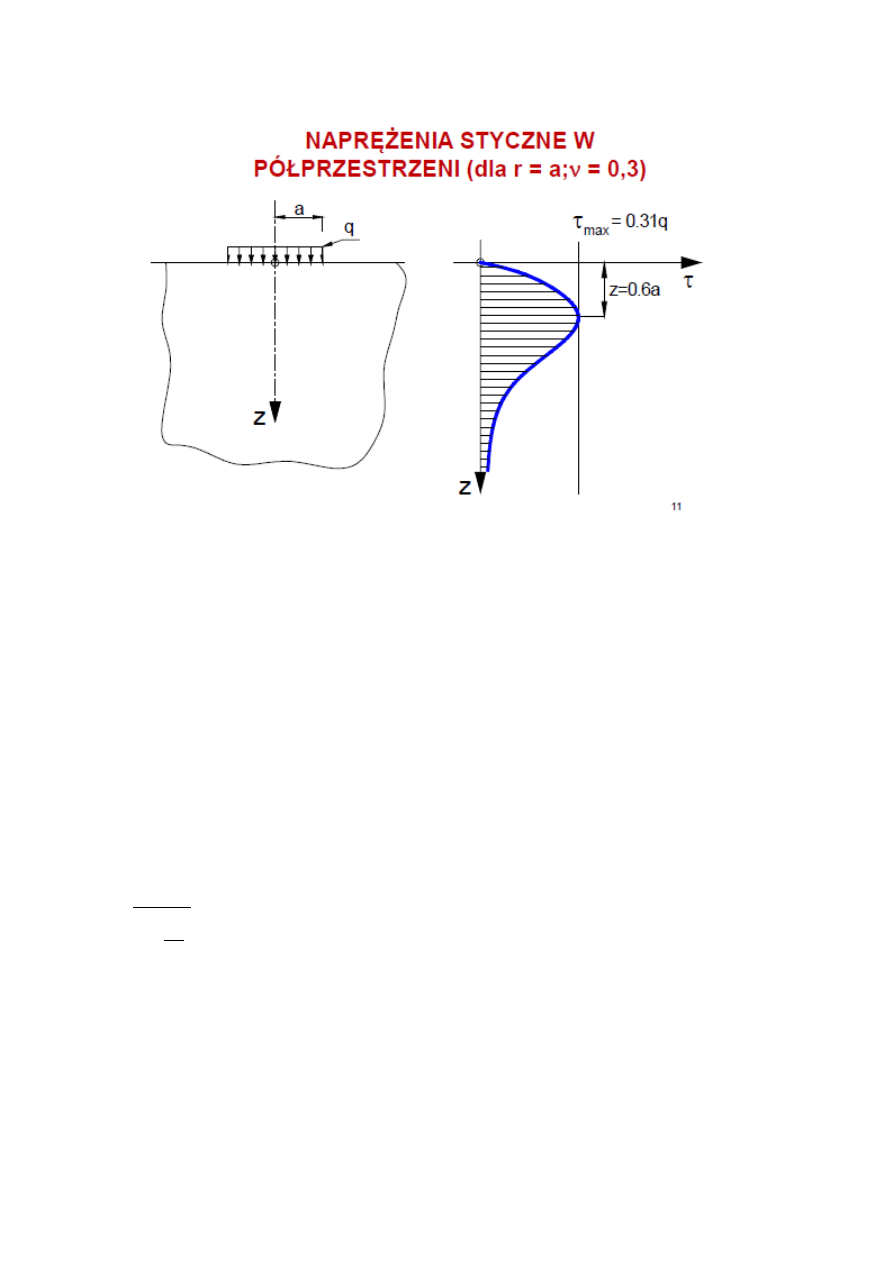
5. Modele obliczeniowe w półprzestrzeni sprężystej (ugięcia poniżej dotyczą ‘płyty’ naciskowej, jaka
obciąża półprzestrzeń) UGIĘCIA
Ugięcia pionowe nawierzchni występują wskutek:
- ściśliwości nawierzchni, podsypki i podłoża;
-przemieszczeń, występujących w materiale poszczególnych warstw.
W warunkach małej wilgotności podłoża nawierzchnia pracuje dobrze. Ugięcia nawierzchni można uważać
za sprężyste, a rozkład naprężeń i odkształceń można obliczać metodami teorii sprężystości.
W warunkach dużej wilgotności podłoża (na wiosnę), gdy podsypka nie nadąża odsączać nadmiaru wody z
podłoża, tłuczniowa warstwa nośna staje się również zawilgocona. Nawierzchnia ma zmniejszoną
sztywność i wytrzymałość na zginanie. Wskutek tego ma miejsce koncentracja naprężeń bezpośrednio pod
kołem. Zwiększają się naprężenia w podłożu gruntowym, które ulega większym ugięciom. W pierwszym
okresie zwiększają się ugięcia nawierzchni w dół, czemu towarzyszy powstawanie naprężeń rozciągających
w dolnej części nawierzchni. W miarę zwiększenia się wypierania podłoża i podnoszenia się nawierzchni
obok koła powstają naprężenia rozciągające również i w jej górnej części.
5.1. Płyta podatna (obciążenie kołem ogumionym)
Założenie: Naprężenie kontaktowe jest stałe na całej powierzchni.
, gdzie q- ciśnienie w ogumieniu
v- wsp. Poissona
E- moduł sprężystości
a- promień powierzchni zastępczej koła
5.2. Płyta sztywna (płyta stalowa o dużej grubości (nieodkształcalna))
Założenie: Naprężenie kontaktowe od obciążenia ma kształt paraboliczny
W uproszczeniu można przyjąć, że naprężenia od obciążenia kołem pojazdu rozkładają się pod kątem 35-
45 stopni, w zależności od sztywności danych warste. Im sztywniejsze warstwy, tym naprężenia rozkładają
się na większym obszarze.
6. Układ dwuwarstwowy
Rozwiązania dla ośrodków dwuwarstwowych, w odróżnieniu od powszechnie stosowanego w wielu
modelach projektowania i diagnozowania nawierzchni – ośrodka jako półprzestrzeni sprężystej, daje lepszą
możliwość oceny rzeczywistych ugięć nawierzchni ze względu na wyraźnie występującą warstwowość
konstrukcji (warstwy nawierzchni – podłoże gruntowe).
Burmister opracował zagadnienie rozkładu naprężeń dla ośrodka dwuwarstwowego przy następujących
założeniach i warunkach brzegowych i całości:
- Materiał w każdej warstwie jest JEDNORODNY, SPRĘŻYSTY I IZOTROPOWY;
- Górna warstwa ma ograniczoną grubość – h, ale nieograniczoną rozciągłość poziomą;
- Dolna warstwa jest nieograniczona w poziomie i pionie;
- Warstwa górna spoczywa na warstwie dolnej i warstwy znajdują się w ciągłym między sobą kontakcie
(pełna szczepność);
- Wartość współczynnika Poissona przyjęto: v1=v2=0,5,
- W górnej warstwie poza obszarem obciążonym nie występują dodatkowe naprężenia
styczne i normalne.
Naprężenia i odkształcenia wyznacza Burmister w zależności od stosunku modułów sprężystości E1 i E2
górnej i dolnej warstwy.
Naprężenia pionowe normalne w punkach leżących na osi pionowej obszaru obciążonego można obliczyć:
=
Gdzie:
− [%] wyznaczany z nomogramu (zależny od 1 2 , ) [nomogram wyklad4/slajd17]
q- obc na powierzchni warstwy pierwszej, działające na obszarze kołowym o promieniu a.
W przypadku układu dwuwarstwowego ugięcia oblicza się ze wzoru:
, przy czym wartość modułu E2 wyznacza się
z pomocą nomogramu:
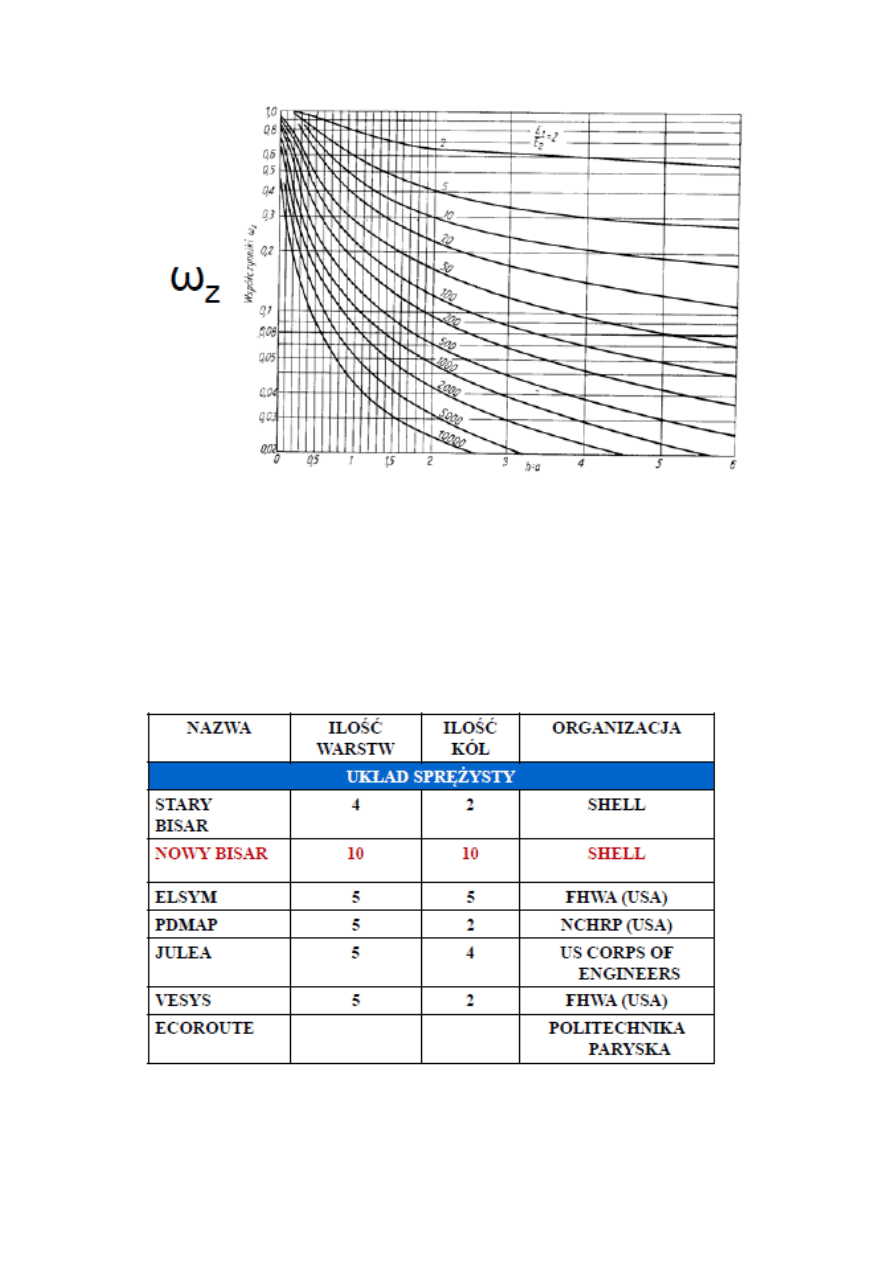
W porównaniu z układem jednowarstwowym w przypadku układu dwuwarstwowego ugięcia są mniejsze.
7. Model trójwarstwowy i wielowarstwowy
Najczęściej stosowany jest model teoretyczny nawierzchni, który rozwiązuje się metodami:
- analitycznymi
- elementów skończonych.
Konieczne założenia: materiały warstw są jednorodne, sprężyste i izotropowe. Obciążenie natomiast jest
przyłożone równomiernie na śladzie zastępczym kołowym, eliptycznym lub innym.
Przykładowe programy komputerowe do analizy naprężeń w układach wielowarstwowych:
8. Szczepność międzywarstwowa
Niewystarczające powiązanie międzywarstwowe (sczepność) powoduje zwiększone ugięcia nawierzchni, te
zaś generują zwiększone odkształcenia i naprężenia rozciągające na spodzie poszczególnych warstw. Przy
nałożeniu się niekorzystnych warunków obciążenia i stanu konstrukcji mogą wystąpić przedwczesne
deformacje (np. koleiny), wybrzuszenia, boczne przesunięcia lub też strukturalne uszkodzenia w postaci
spękań, wyłomów lub odprysków.
Przykład:
Oblicz ugięcie nawierzchni pod kołem pojedynczym o ciężarze 50kN, ciś. Kontaktowym 850kPa ,gdy:
Moduł odkształcenia gruntu: 40MPa
Ułożono dwie warstwy licząc od góry: 200mm o E=250MPa i 200mm o E=150MPa