19.12.2011
Filtry cyfrowe do analizy na egzamin zerowy z Przetwarzania Sygnałów
Swiss Army Knife of Digital Networks
– czyli wielofunkcyjny filtr cyfrowy –
– agregat filtru grzebieniowego FIR (ang. comb filter) i ogniwa bikwadratowego IIR
(ang. biquad)
Transmitancja
wielofunkcyjnego filtru cyfrowego (FC), na podstawie którego
można wygenerować filtry pokazane na następnych stronach, o numerach od 1.1 do 1.22
)
(z
H
2
2
1
1
0
2
2
1
1
0
1
/
1
)
1
(
)
(
−
−
−
−
−
−
−
+
+
×
−
=
z
a
z
a
a
z
b
z
b
b
z
c
z
H
N
1
−
z
]
[n
y
1
−
z
•
•
•
1
−
z
]
[n
y
1
−
z
0
a
⊗
⊗
⊗
1
a
2
a
⊗
⊗
⊗
0
b
1
b
2
b
⊕
⊕
⊕
⊕
⊕
]
[n
x
⊗
N
z
−
1
c
+ −
•
]
1
[
−
n
w
]
2
[
−
n
w
]
[n
w
Literatura
[1]
R. Lyons and A. Bell: The Swiss Army Knife of Digital Networks, IEEE Signal Processing
Magazine, dsp tips & trics, vol. 21, May 2004, pp. 90-100. Dostęp: czytelnia WETI w wersji
papierowej lub elektronicznie via Biblioteka Główna PG, baza IEEEXplore.
[2]
C. Turner: Recursive discrete-time sinusoidal oscillators, IEEE Signal Processing Magazine,
vol. 20, May 2003, pp. 103-111.
[3]
http://ccrma-www.stanford.edu/~jos/waveguide/Comb-Filters.html
[4]
Texas Instruments: How can comb filters be used to synthesize musical instruments on a
TMS320 DSP?, TMS320 DSP Designers Notebook, No 56, 1995.
[5]
J. Proakis and D. Manolakis: Digital Signal Processing – Principles, Algorithms and
Applications. 3
rd
edition, Upper Saddle River, NJ, Prentice-Hall, 1996, Comb Filters pp. 345-
350.
[6]
C. Dick and F. Harris: FPGA signal processing using sigma-delta modulation, IEEE Signal
Processing Magazine, vol. 17, Jan. 2000, pp. 20-35.
[7] Materiały firmy Xilinx w Internecie: w Google wpisujemy
“Cascaded Integrator Comb (CIC)” +”March 14, 2002”
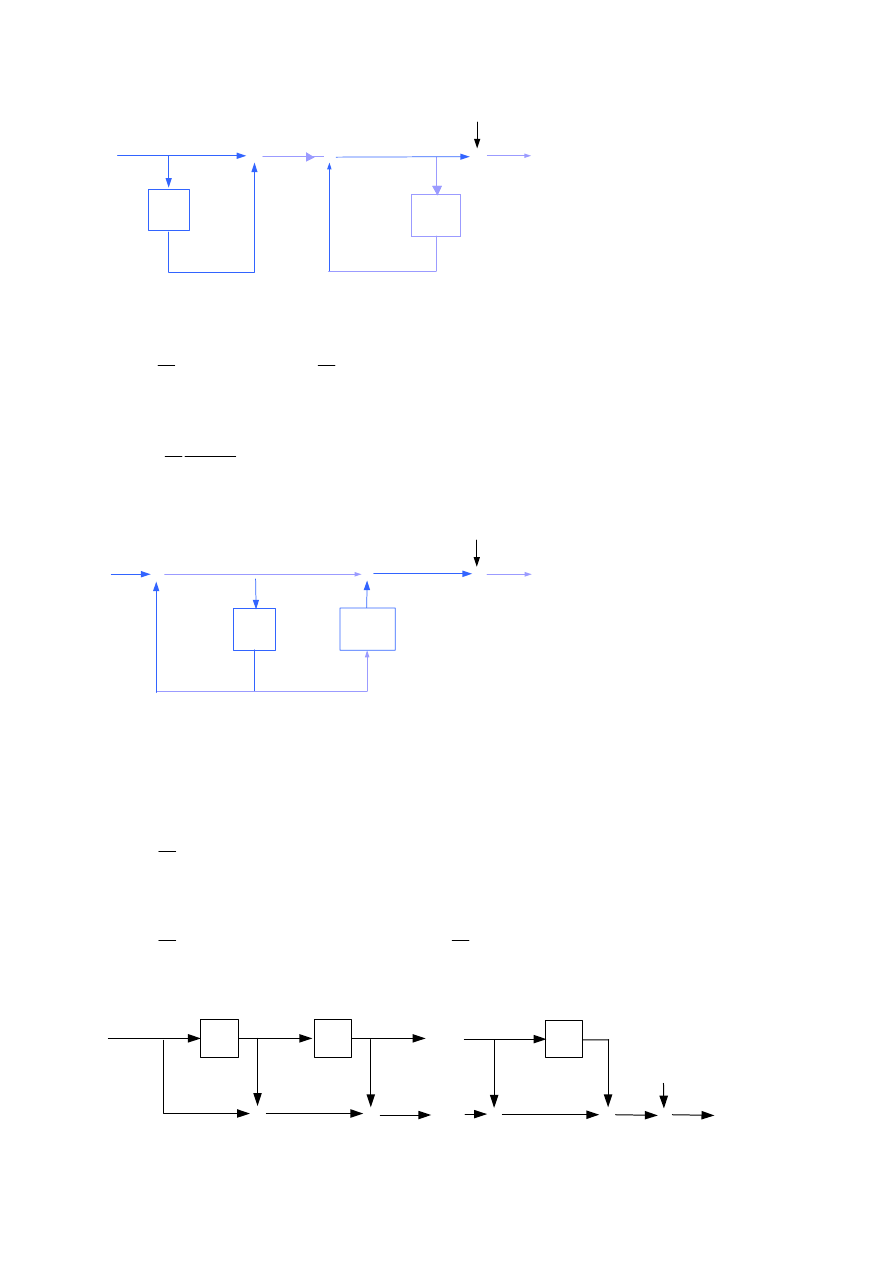
1.1. System średniej ruchomej
1
−
z
•
1
−
z
⊗
]
[n
x
N
/
1
]
[n
y
]
[n
v
⊕
⊕
N
z
−
+ −
•
Algorytm
]
1
[
]
[
1
])
1
[
]
[
(
1
]
[
]
[
]
[
]
[
−
+
=
−
+
=
−
−
=
n
y
n
v
N
n
Ny
n
v
N
n
y
N
n
x
n
x
n
v
Transmitancja
1
1
1
1
)
(
−
−
−
−
=
z
z
N
z
H
N
Powyższy filtr można też zrealizować jak niżej.
•
⊗
]
[n
x
N
/
1
]
[n
y
]
[n
v
⊕
⊕
)
1
(
−
− N
z
+
−
•
1
−
z
Tę strukturę znajdujemy pod nazwą RRS od ang. Recursive Running Sum i jest ona stosowana
m.in. jako pierwszy stopień filtru antyaliasingowego w konwerterach A/C np. firmy Analog
Devices. Algorytmem tej struktury jest
)])
1
(
[
]
[
(
1
]
[
]
1
[
]
[
]
[
−
−
−
=
−
+
=
N
n
v
n
v
N
n
y
n
v
n
x
n
v
Taką samą transmitancję ma filtr FIR o długości N, o strukturze transwersalnej i algorytmie
∑
−
=
−
=
−
−
+
+
−
+
=
1
0
]
[
1
)])
1
(
[
]
1
[
]
[
(
1
]
[
N
k
k
n
x
N
N
n
x
n
x
n
x
N
n
y
L
gdzie współczynniki są jednostkowe.
⊕
1
−
z
⊗
1
−
z
⊕
L
L ⊕
⊕
1
−
z
]
[n
y
]
[n
x
N
/
1
•
]
2
[
−
n
x
]
1
[
−
n
x
•
•
•
)]
1
(
[
−
− N
n
x
2
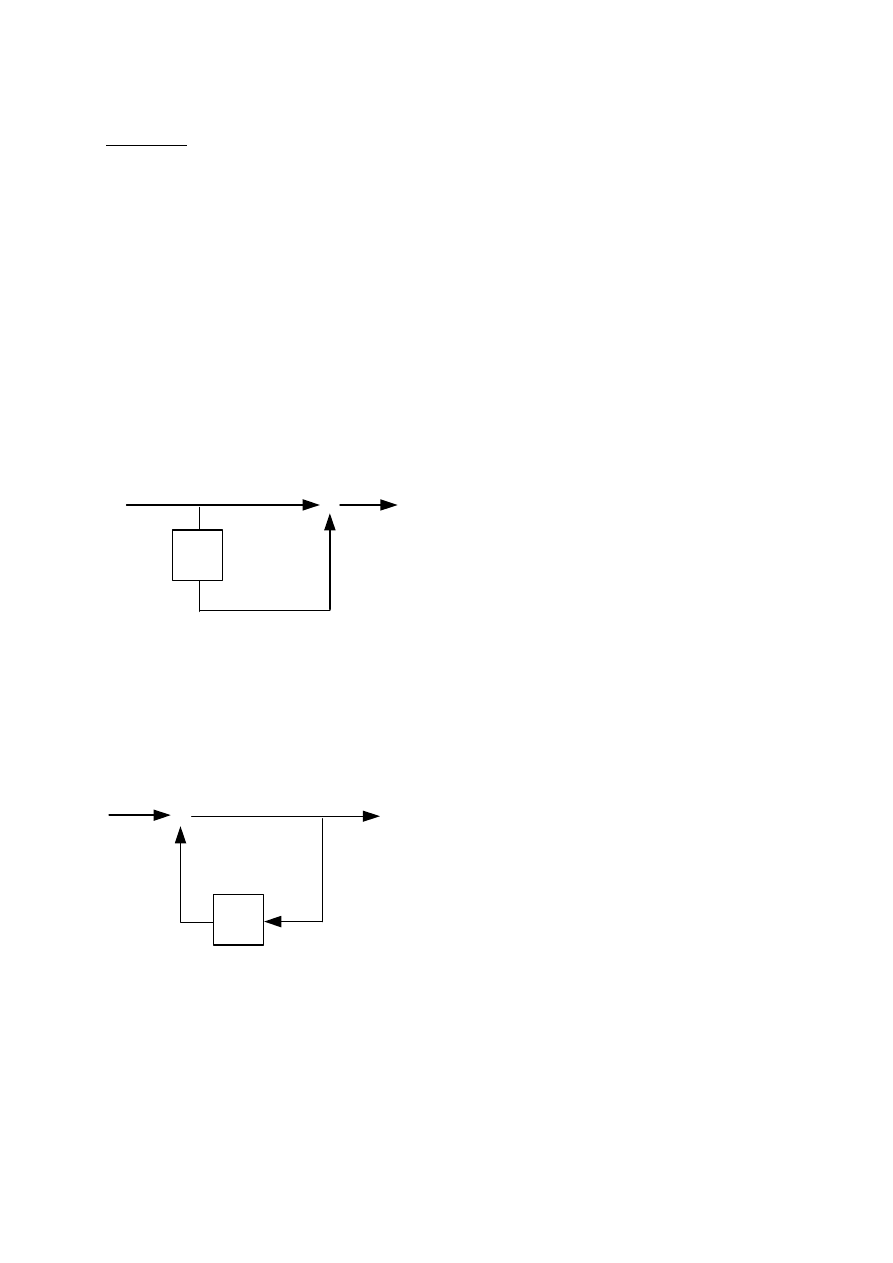
Struktura rekursywna (IIR – RRS) jest bardziej efektywna, bo wymaga tylko jednego
dodawania i jednego odejmowania na jedną próbkę wyjściową (pomijając skalowanie)
niezależnie od wartości N, podczas gdy filtr FIR musi wykonać
1
−
N
dodawań na próbkę
wyjściową. Zauważmy też, że ma tu N zer równomiernie rozłożonych na okręgu
jednostkowym, dla
)
(z
H
)
/ N
k
2
exp( j
z
k
π
=
,
N
k
<
≤
0
i jeden biegun dla
1
=
z
, który kasuje zero
na tej pozycji.
1.2. System różnicujący – dyskretna wersja systemu różniczkującego. Tu transmitancja
. Ten system jedynie przybliża idealną charakterystykę dla m.cz.
względem
. A idealny system różniczkujący ma liniową charakterystykę amplitudową
w funkcji częstotliwości.
1
1
)
(
−
−
=
z
z
H
s
F
⊕
1
−
z
]
[n
y
]
[n
x
•
+
−
1.3. Integrator. Ten system realizuje sumę bieżącą wejściowych próbek
, stanowiąc
dyskretno-czasowy równoważnik integratora (układu całkującego) czasu ciągłego.
]
[n
x
⊕
1
−
z
]
[n
y
]
[n
x
•
3
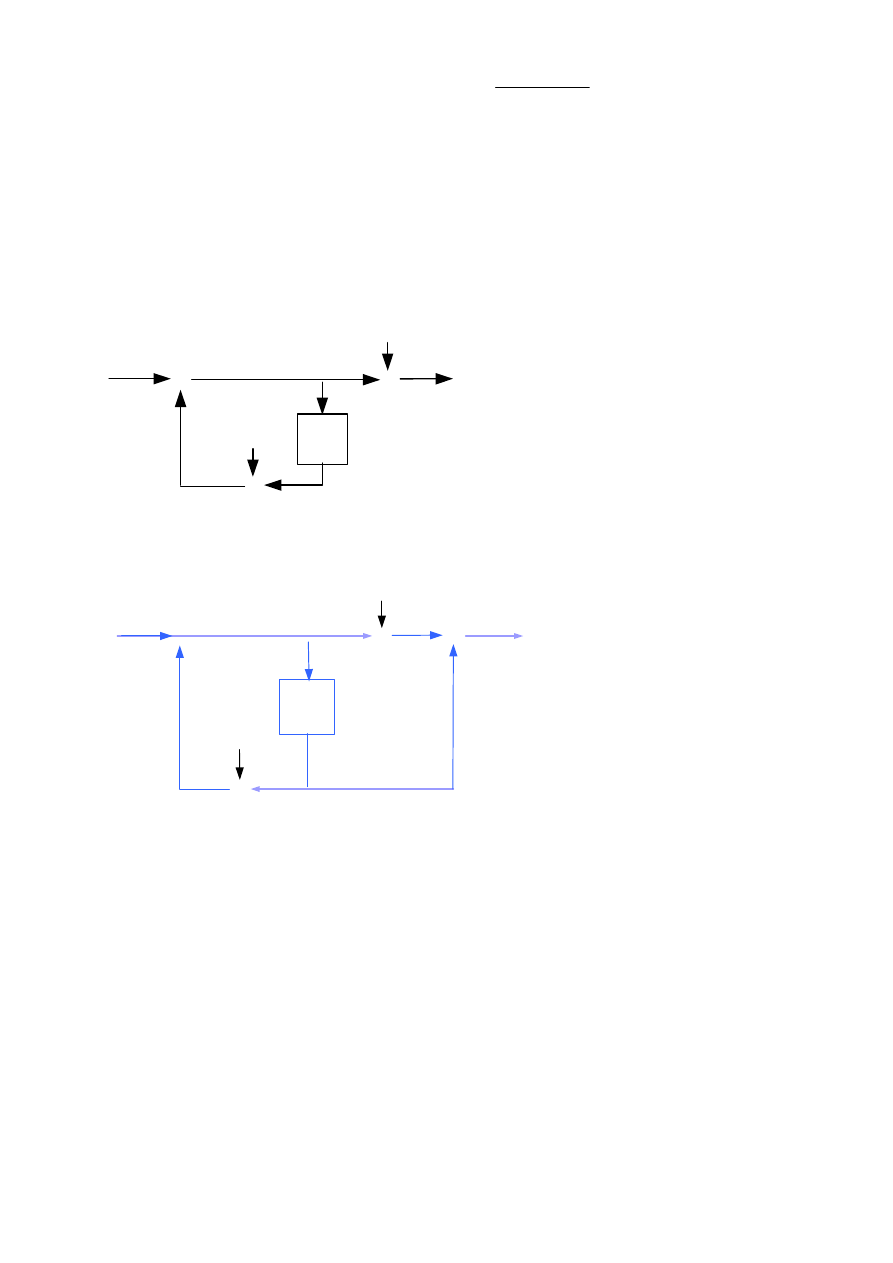
1.4. Integrator z przeciekiem. Transmitancja
1
)
1
(
1
)
(
−
−
−
=
z
z
H
α
α
. Ten integrator nazywany
jest również uśredniającym eksponencjalnie (ang. exponential averager). Stosowany jest
w implementacjach LP (ang. lowpass) do redukcji szumu losowego. Jest to filtr IIR
pierwszego rzędu, gdzie, dla stabilnej pracy, stała
α musi leżeć w zakresie
0
1
<
<
α
.
Jest to filtr o nieliniowej charakterystyce fazowej, z pojedynczym biegunem dla
α
−
= 1
z
. Dla małych wartości
α charakterystyka amplitudowa jest wąska, kosztem
wydłużenia odpowiedzi impulsowej filtru, a więc odpowiedzi na pobudzenie
]
n
[
δ
.
⊕
1
−
z
]
[n
x
•
⊗
]
[n
y
α
α
−
1
⊗
1.5. System opóźniający pierwszego rzędu
•
⊗
]
[n
x
R
]
[n
y
]
[n
v
⊕
⊕
•
1
−
z
⊗
R
−
]
1
[
−
n
v
Jest to system wszechprzepustowy (podklasa IIR) pierwszego rzędu, który ma względnie stałą
charakterystykę opóźnienia grupowego dla małych częstotliwości. Opóźnienie systemu
wynosi
delay
total
1
∆
+
=
D
próbek, gdzie typowo
leży w zakresie od
delay
∆
5
.
0
−
do 0.5 i jest ułamkiem okresu
próbkowania
. Przykładowo, gdy
s
F
T
/
1
=
delay
∆
jest równe 0.2, to opóźnienie systemu dla
małych częstotliwości wynosi 1.2 okresu próbkowania. Współczynnik R o wartości
rzeczywistej to
4
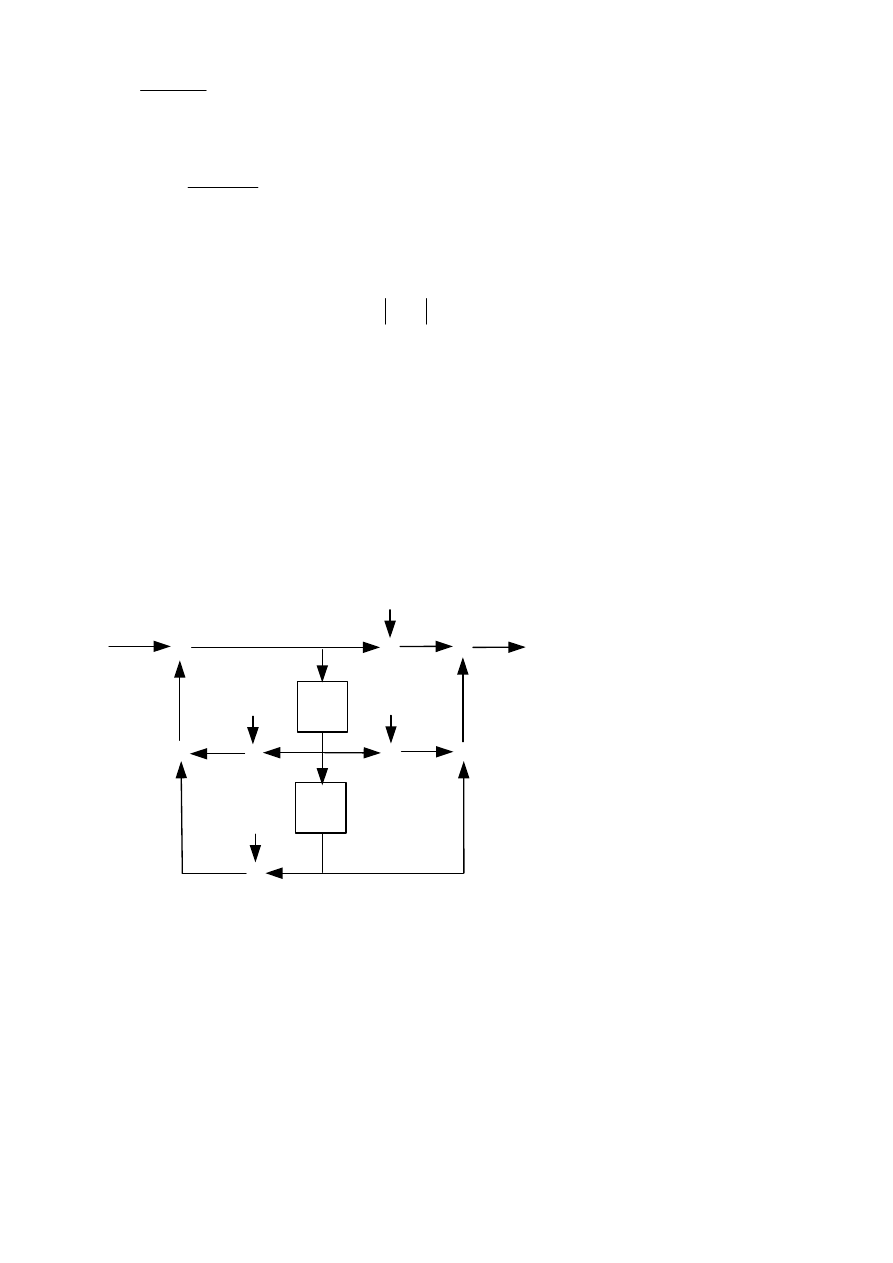
2
delay
delay
+
∆
∆
−
=
R
A transmitancja systemu
)
1
(
)
(
)
(
1
1
del
1,
−
−
+
+
=
Rz
z
R
z
H
ma biegun dla
R
z
−
=
i zero dla
R
z
/
1
−
=
. Charakterystyka amplitudowa dla
=0.2
(R=0.91) jest stała. Pasmo skupione jest wokół składowej stałej (dc), w którym opóźnienie
grupowe zmienia się o nie więcej niż
delay
∆
10
/
delay
∆
względem wyspecyfikowanej wartości
(pozioma „belka” na wykresie w tablicy 1 [1]) obejmując z grubsza przedział o szerokości od
o
dla systemów pierwszego rzędu. System ten okazuje się użyteczny, gdy
sygnał wejściowy jest nadpróbkowany, tzn. gdy jego widmo jest w zakresie częstotliwości
małych względem
.
total
D
s
F
1
.
0
d
s
F
s
F
2
.
0
1.6. System opóźniający drugiego rzędu
⊕
1
−
z
]
[n
x
•
⊗
]
[n
y
2
R
1
R
−
⊗
z
1
−
⊗
⊕
⊗
•
1
R
2
R
−
⊕
⊕
•
]
[n
v
]
2
[
−
n
v
]
1
[
−
n
v
Jest to system wszechprzepustowy (podklasa IIR) drugiego rzędu, który ma względnie stałą
charakterystykę opóźnienia grupowego dla małych częstotliwości, ale w szerszym zakresie
częstotliwości niż dla systemu pierwszego rzędu. Opóźnienie systemu wynosi
delay
total
2
∆
+
=
D
próbek, gdzie typowo
leży w zakresie od
delay
∆
5
.
0
−
do 0.5 i jest ułamkiem okresu
próbkowania
. Przykładowo, gdy
s
F
T
/
1
=
delay
∆
jest równe 0.3, to opóźnienie systemu dla
5
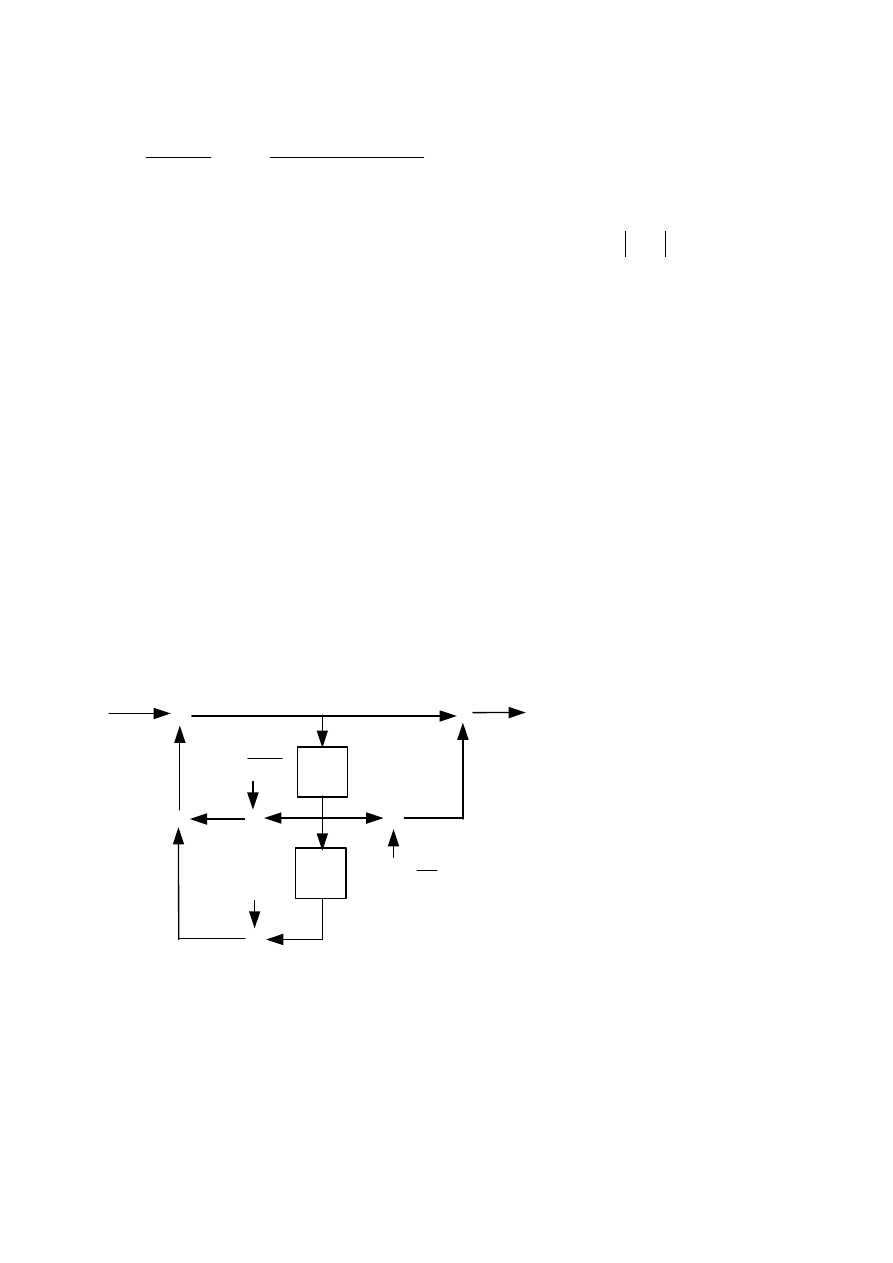
małych częstotliwości wynosi 2.3 okresu próbkowania. Współczynniki
i
o wartościach
rzeczywistych to
1
R
2
R
10
/
∆
3
2
delay
delay
1
+
∆
∆
−
=
R
i
)
4
)(
3
(
)
1
)(
(
delay
delay
delay
delay
2
+
∆
+
∆
+
∆
∆
=
R
Charakterystyka amplitudowa jest stała. Pasmo skupione jest wokół składowej stałej (dc), w
którym opóźnienie grupowe zmienia się o nie więcej niż
delay
względem
wyspecyfikowanej wartości
(pozioma „belka” na wykresie w tablicy 1 [1]) obejmując z
grubsza przedział o szerokości od
do
dla tego systemu drugiego rzędu.
total
D
s
F
26
.
0
s
F
38
.
0
Performancja dla
=0.3 (
= – 0.182 i
=0.28) jest pokazana w tablicy 1 [1].
Pasmo płaskiej charakterystyki opóźnienia grupowego jest szersze dla ujemnych
niż
gdy
jest dodatnie. Przykładowo, to oznacza, że gdy potrzebujemy mieć opóźnienie
grupowe
=2.5 odstępów próbkowania, to lepiej użyć zewnętrznego opóźnienia
jednostkowego i ustawić
na – 0.5 niż pozwolić na to, by
delay
∆
delay
∆
1
R
2
R
delay
∆
delay
∆
total
D
delay
∆
było równe 0.5. Aby
zapewnić stabilność,
delay
∆
musi być większe od – 1.
1.7. Obwód (filtr) Goertzela
⊕
1
−
z
•
]
[n
y
N
k
π
2
cos
2
⊗
z
1
−
⊗
⊕
⊗
•
N
k
j
e
π
2
−
1
−
]
[n
x
]
[n
v
]
2
[
−
n
v
⊕
]
1
[
−
n
v
Ten tradycyjny obwód Goertzela jest wykorzystywany do detekcji pojedynczego tonu
(sinusoidy) ponieważ oblicza on N-punktową, tzw. „single-bin”, dyskretną transformatę
Fouriera (DFT) scentrowaną na kącie
N
k /
2
π
θ
=
w radianach na próbkę (rad/Sa)
odpowiadającym częstotliwości
Hz. Zmienna częstotliwościowa k, z zakresu
, nie musi być całkowita. W tablicy 2 linią ciągłą pokazano zachowanie się tego
N
kF
s
/
N
k
<
≤
0
6
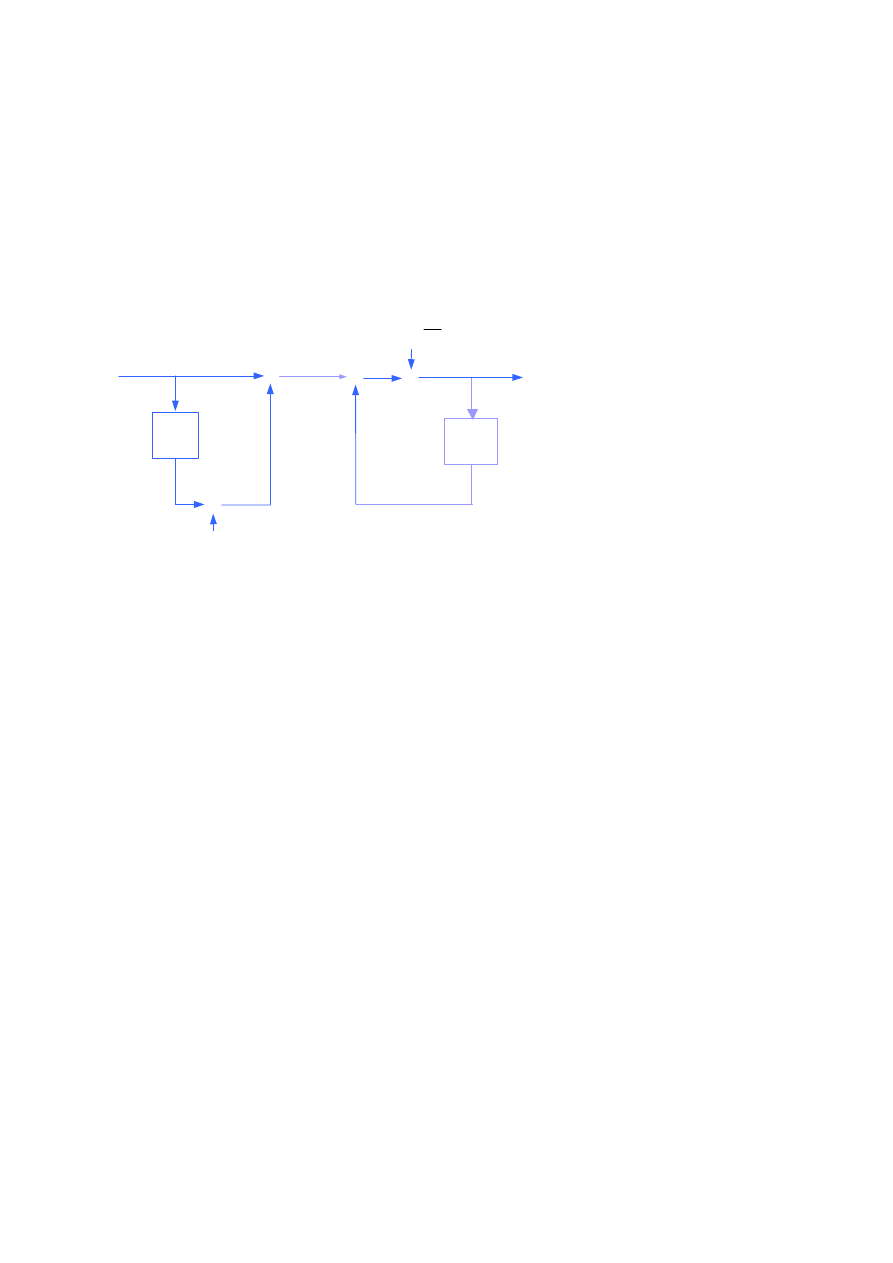
obwodu. Natomiast charakterystykę amplitudową algorytmu Goertzela dla N=8 i k=1
pokazano linią przerywaną.
Po zaaplikowaniu na wejściu N+1 próbek, na wyjściu otrzymamy wynik: y[n] w postaci
„single-bin DFT”. Nakład obliczeniowy na DFT wynosi tu N+2 rzeczywistych mnożeń i
2N+1 dodawań. Obwód jest typowo stabilny ponieważ w praktyce bierze się stosunkowo
małe N (rzędu setek) przed ponowną jego inicjacją.
1.8. Przesuwna DFT (ang. sliding DFT)
1
−
z
•
1
−
z
⊗
]
[n
x
N
k
j
re
π
2
]
[n
y
]
[n
v
⊕
⊕
N
z
−
+
−
•
⊗
N
r
W tej strukturze obliczana jest N-punktowa, tzw. „single-bin”, dyskretna transformata
Fouriera (DFT) scentrowana na kącie
N
k /
2
π
θ
=
w radianach na próbkę (rad/Sa) na okręgu
jednostkowym, odpowiadającym częstotliwości
Hz. N to rozmiar DFT, a zmienna
częstotliwościowa k, z zakresu
N
s
/
kF
N
k
<
≤
0
, jest całkowita. Aby zapewnić stabilność tego
obwodu, współczynnik tłumienia r (ang. damping factor) powinien być możliwie bliski, na
ile to możliwe, ale mniejszy od jedności. Po zaaplikowaniu N próbek wejściowych, ten
obwód obliczy nowy wynik kolejnej DFT dla każdej nowej próbki wejściowej (stąd
nazwa „przesuwna DFT”) przy nakładzie numerycznym (ang. computational workload)
wynoszącym jedynie cztery mnożenia rzeczywiste i cztery dodawania rzeczywiste na próbkę
wejściową. Jeżeli podstawimy
to pasmo analizowanych częstotliwości będzie
scentrowane na kącie
]
[n
x
N
r
−
N
/
)
2
/
1
c
=
1
k
(
2
+
=
π
θ
w rad/Sa, co odpowiada częstotliwości
Hz.
N
F
k
s
/
)
2
/
1
(
+
7
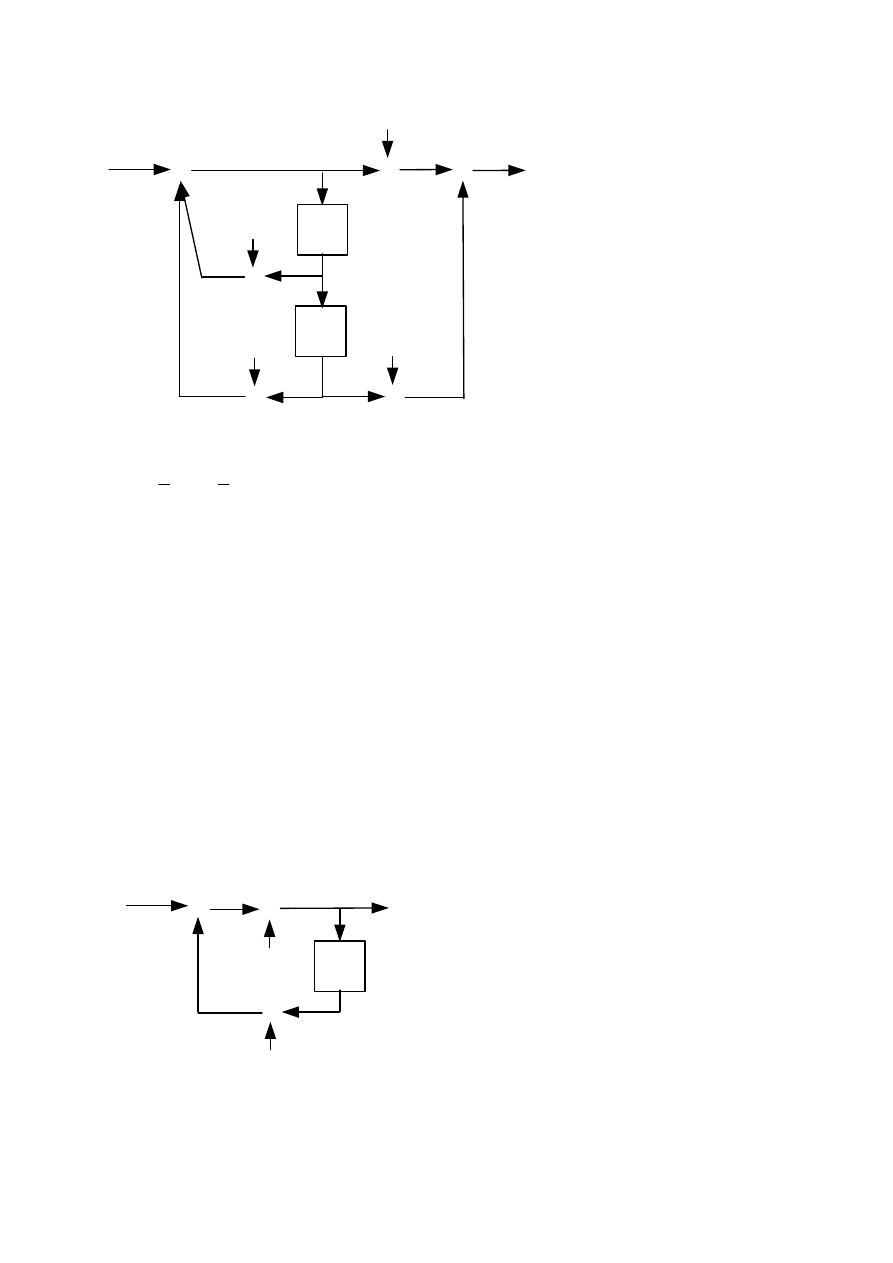
1.9. Oscylator sinusoidy o wartościach rzeczywistych.
⊕
1
−
z
]
[n
x
•
⊗
]
[n
y
2
/
1
ϑ
cos
2
⊗
z
1
−
⊗
⊕
⊗
•
•
2
/
1
−
1
−
Algorytm
]
2
[
]
1
[
cos
2
]
[
]
[
]
2
[
2
1
]
[
2
1
]
[
−
−
−
⋅
+
=
−
−
=
n
v
n
v
n
x
n
v
n
v
n
v
n
y
ϑ
generuje sygnał sinusoidy
o wartościach rzeczywistych, której amplituda nie jest
funkcją częstotliwości wyjściowej. Wartość
]
[n
y
s
t
F
F
/
2
π
ϑ
=
w rad na próbkę, gdzie to
częstotliwość generowana, w Hz. By zastartować oscylator należy zadać próbkę
t
F
]
1
[
−
n
y
,
poprzez wymuszenie wartości mnożnika
ϑ
cos
2
1
=
a
równej 1, a następnie obliczamy nowe
próbki wyjściowe dla rosnącej wartości n. Dla implementacji stałoprzecinkowej
współczynniki filtru mogą wymagać skalowania tak, aby wszystkie wyniki pośrednie
znajdowały się we właściwym zakresie numerycznym.
1.10. Oscylator kwadraturowy
⊕
1
−
z
]
[n
x
•
⊗
]
[n
y
]
[n
G
ϑ
j
e
⊗
]
1
[
−
n
y
Oscylator zwany z ang. „coupled” – połączony – generuje sygnał wyjściowy zespolony
)
exp(
)
sin(
)
cos(
]
[
ϑ
ϑ
ϑ
jn
n
j
n
n
y
=
+
=
(tzw. zespoloną sinusoidę) nastrojoną na
8
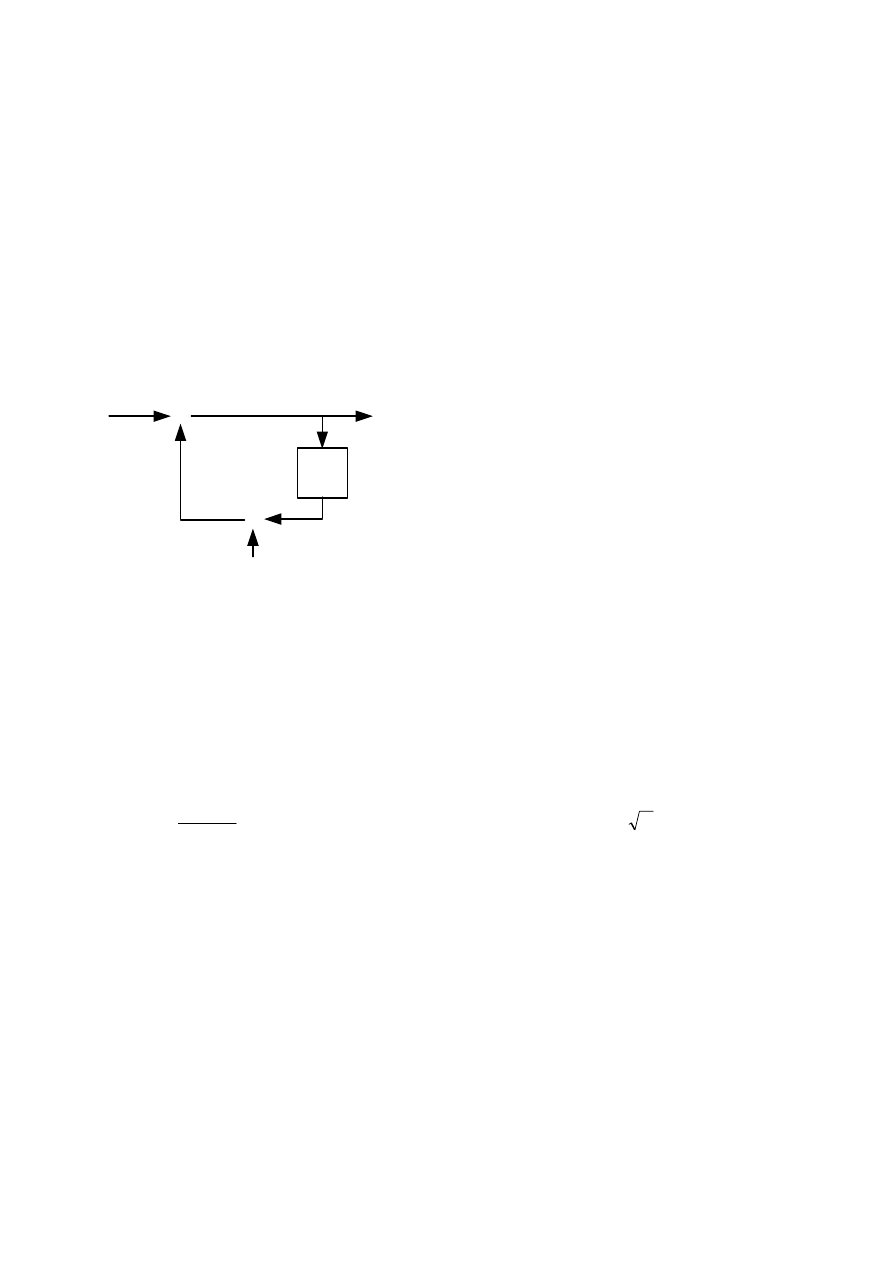
częstotliwość
Hz. Eksponenta dla w tablicy 2 [1] wynosi
t
F
1
a
s
t
F
F
/
2
π
ϑ
=
rad/Sa. Aby
zastartować ten oscylator, zadajemy wartość zespolonej próbki
, sterującej
mnożnikiem
, wynoszącą
0 , i zaczynamy obliczać próbki wyjściowe z rosnącą
wartością n. Ażeby zapewnić stabilność sygnału na wyjściu oscylatora w implementacjach z
arytmetyką stałoprzecinkową, należy obliczyć korektę wzmocnienia
dla każdej próbki
wyjściowej. Wartości będą bardzo bliskie jedności [2].
]
1
[
−
n
y
]
[n
G
1
a
1 j
+
]
[n
G
2
−
]
[n
y
[
−
n
y
2
−
z
1
α
α
±
=
z
α
α
α
=
1
a
1.11. Akustyczny filtr grzebieniowy
⊕
z
]
[n
x
•
α
⊗
]
2
Ta struktura to system IIR drugiego rzędu (najprostsza wersja) wykorzystywana przez fanów
audio do syntetyzowania dźwięku instrumentu szarpanej struny (ang. plucked string
instrument
). Sygnałem wejściowym są próbki szumu losowego. Filtr ten ma piki (maksima)
charakterystyki amplitudowej dla składowej stałej (dc) i dla częstotliwości , co
powoduje „dołki” (ang. dips) dla częstotliwości
2
/
s
F
±
4
/
s
F
±
. Transmitancją filtru jest
1
)
(
−
=
z
H
ac
, która ma dwa bieguny zlokalizowane dla
na płaszczyźnie
zespolonej. Ażeby zapewnić stabilność, wartość rzeczywistej musi być mniejsza od
jedności, a im jest bliższa jedności, tym węższe są piki na charakterystyce amplitudowej.
Bardziej realistyczną syntezę dźwięku otrzymamy np. biorąc
i górny element
biquadu na rysunku ze strony 1 o opóźnieniu zwiększonym do, powiedzmy, ośmiu zamiast
jednostkowego, to uzyskamy więcej pików na charakterystyce amplitudowej pomiędzy 0 i
Hz. W tej muzycznej aplikacji sygnałem wejściowym dla filtru są próbki białego
szumu gaussowskiego. Inne obwody syntetyzujące z sukcesem instrumenty szarpanej struny
(ang. plucked string instrument) omówiono m.in. w [3], [4] i [5].
2
/
s
F
9
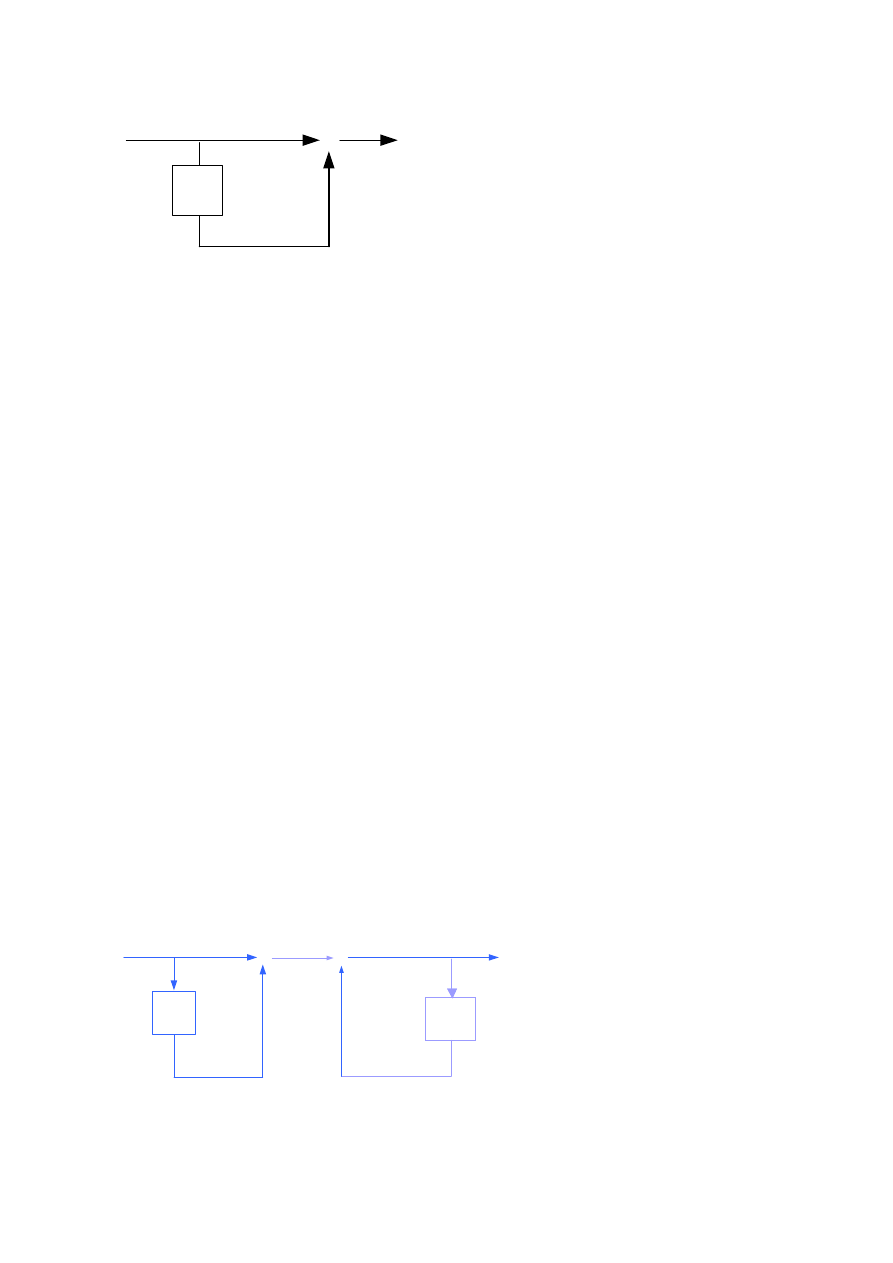
1.12. Filtr grzebieniowy
⊕
N
z
−
]
[n
y
]
[n
x
•
+
−
W tablicy 3 [1] na samym początku występuje standardowy filtr FIR – kluczowy element w
wielu aplikacjach filtracji. Jego transmitancja
zawiera N zer równomiernie
rozłożonych na okręgu jednostkowym na płaszczyźnie z, ulokowanych w
,
gdzie k jest liczbą całkowitą
N
z
z
H
−
−
= 1
)
(
comb
N
k
j
e
k
z
/
2
]
[
π
=
N
k
<
≤
0
)
(
comb
z
H
. Te wartości to N pierwiastków o wartości
jednostkowej, gdy weźmiemy równe zero co daje
]
[k
z
(
)
]
/
2
=
N
k
j
N
e
π
1
=
N
[k
z
2
/
N
m
. N zer na
okręgu jednostkowym powoduje powstanie miejsc zerowych na charakterystyce
amplitudowej (nieskończone tłumienie) dla okresowo powtarzających się częstotliwości
, gdzie m jest liczbą całkowitą
N
mF
s
/
0
≤
≤
. Maksymalne wzmocnienie tego
liniowo-fazowego filtru wynosi dwa.
Jeżeli podstawimy w filtrze grzebieniowym
1
1
−
=
c
otrzymując transmitancję
, to mamy tu alternatywny liniowo-fazowy filtr grzebieniowy z zerami
obróconymi (zrotowanymi) wokół okręgu jednostkowego w kierunku przeciwnym do ruchu
wskazówek zegara o kąt
N
z
z
H
−
+
= 1
)
(
comb
alt
N
/
π
rad/Sa, co pozycjonuje zera dla kątów
N
k
/
)
2
/
1
(
2
+
π
rad/Sa
na okręgu jednostkowym płaszczyzny z. Te obrócone zera spowodują występowanie miejsc
zerowych na charakterystyce amplitudowej dla okresowo powtarzających się częstotliwości
. Dla tego filtru pik na charakterystyce amplitudowej jest zlokalizowany na
częstotliwości 0 Hz (dc).
N
F
m
s
/
)
2
/
1
(
+
1.13. Filtr pasmowy na
4
/
s
F
•
]
[n
x
]
[n
y
⊕
⊕
+
−
•
16
−
z
]
16
[
−
n
x
+
−
2
−
z
]
2
[
−
n
y
10

Jest to filtr pasmowy (ang. bandpass) scentrowany wokół częstotliwości , liniowo-
fazowy w paśmie przenoszenia, o charakterystyce amplitudowej opisanej funkcją typu
. Ma on bieguny w
4
/
s
F
x
x /
)
sin(
j
z
±
=
, a zatem aby nastąpiło zerowanie bieguna/zera,
opóźnienie (N) filtru grzebieniowego musi być całkowitą wielokrotnością liczby cztery.
Transmitancja tego bezmnożnikowego filtru pasmowego o gwarantowanej stabilności wynosi
)
1
/(
)
1
(
)
(
2
pb
−
−
+
−
=
z
z
z
H
N
.
1.14. Filtr IIR pierwszego rzędu
•
⊗
]
[n
x
z
j
z
e
R
θ
]
[n
y
]
[n
v
⊕
⊕
•
1
−
z
⊗
p
j
p
e
R
θ
]
1
[
−
n
v
Ten filtr ma strukturę 2D (ang. direct form) z pojedynczym biegunem ulokowanym na
promieniu
względem początku układu współrzędnych na płaszczyźnie z pod kątem
p
R
p
θ
rad/Sa i pojedynczym zerem na promieniu
względem początku układu współrzędnych na
płaszczyźnie z pod kątem
z
R
z
θ
π
+
. Dla współczynników rzeczywistych (
0
=
=
z
p
θ
θ
) ten filtr
może mieć charakterystykę amplitudową jedynie dolnoprzepustową albo górno-przepustową,
ale nie jest możliwe zrealizowanie charakterystyk: pasmowo-przepustowej ani pasmowo-
zaporowej. Transmitancją filtru jest
.
)
1
−
z
1
/(
)
1
(
(
1
iir
1,
−
−
+
e
R
z
e
R
z
H
p
z
j
p
j
z
θ
θ
)
=
Charakterystyka amplitudowa tego filtru ma szerokie pasma przejściowe tak, że trudno
tu wyróżnić pasma: przepustowe i zaporowe. Oczywiście, aby zapewnić stabilność należy
lokować biegun wewnątrz okręgu jednostkowego na płaszczyźnie z, a im
jest bliższe
jedności, tym filtr jest bardziej wąskopasmowy.
p
R
11

1.15. Korektor (ang. equalizer) fazy pierwszego rzędu
•
⊗
]
[n
x
∗
− R
]
[n
y
]
[n
v
⊕
⊕
•
1
−
z
⊗
R
]
1
[
−
n
v
Ta struktura ma charakterystykę amplitudową, która jest stała w całym paśmie częstotliwości
(filtr wszech-przepustowy). Ma ona biegun dla
R
z
= na płaszczyźnie z i zero ulokowane dla
, gdzie gwiazdka oznacza sprzężenie. Wartość R, która może być rzeczywista lub
zespolona, ale której moduł (wartość bezwzględna) musi być mniejsza od jedności by
zapewnić stabilność, kontroluje nieliniową charakterystykę fazową. Ten korektor ma
transmitancję
.
∗
R
/
1
∗
(
=
)
1
/(
)
)
(
1
1
eq
1,
−
−
∗
−
+
−
Rz
z
R
z
H
Takie obwody mogą być użyte jako korektory fazowe przez skaskadowanie za filtrem
lub obwodem, którego nieliniowa charakterystyka fazowa wymaga zgrubnej linearyzacji.
Celem jest tu uczynienie docelowej charakterystyki fazowej tak bliskiej liniowej, jak jest to
tylko możliwe. W tablicy 3 [1] pokazano ciągłą linią charakterystykę fazową filtru dla
, a dla porównania linią przerywaną przedstawiono charakterystykę fazową dla
. Ten filtr wszech-przepustowy pierwszego rzędu może być również użyty do
interpolacji i uzyskania audio rewerberacji dla sygnałów o małych częstotliwościach.
7
.
0
=
R
3
.
0
−
=
R
12
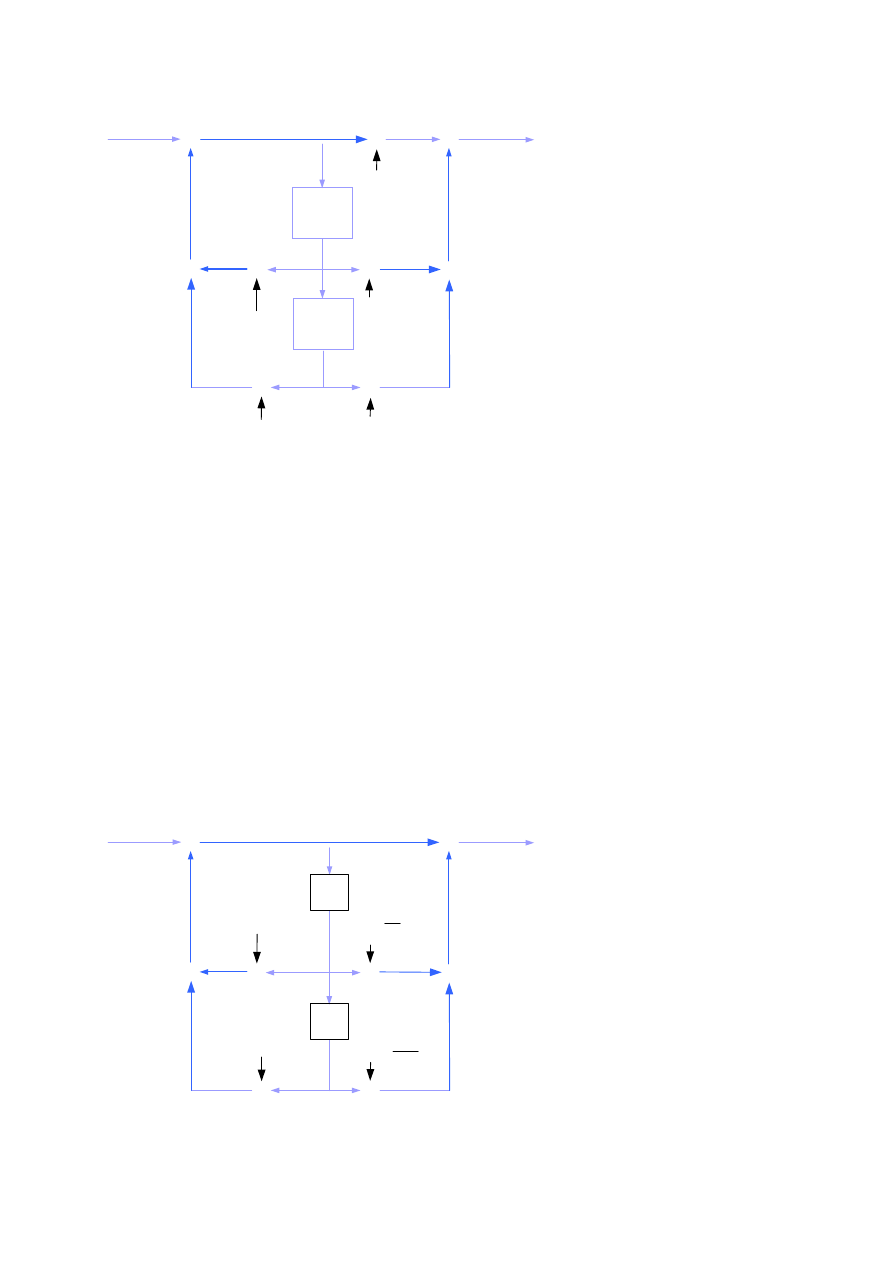
1.16. Filtr IIR drugiego rzędu
1
−
z
]
1
−
z
•
•
]
[n
w
•
1
−
z
[n
y
1
−
z
]
[n
w
⊗
⊗
194
.
1
1
=
a
436
.
0
2
−
=
a
⊗
⊗
⊗
0605
.
0
0
=
b
121
.
0
1
=
b
0605
.
0
2
=
b
⊕
⊕
⊕
⊕
]
[n
x
Ten filtr drugiego rzędu o strukturze 2D (ang. direct form) zwany jest koniem roboczym (ang.
workhorse) implementacji filtru IIR. Zespolone sprzężone pary biegunów i zer sterujące
charakterystyką amplitudowo-fazową, mogą być ulokowane gdziekolwiek na płaszczyźnie z.
Z powodu tego, że filtry IIR wysokiego rzędu są bardzo wrażliwe na efekty kwantyzacji i
problemy związane z potencjalnym przepełnieniem rejestrów (ang. overflow), praktycy
typowo implementują filtry IIR przez kaskadowanie kopii tego filtru IIR drugiego rzędu
celem zapewnienia stabilności i uniknięcia cykli granicznych. Transmitancja filtru jest taka,
jak na pierwszej stronie tego opracowania, ale przy
0
1
=
c
. Można tu zrealizować filtry
dolnoprzepustowe, górno-przepustowe, pasmowo-przepustowe i pasmowo-zaporowe.
1.17. Korektor fazy (ang. equalizer) drugiego rzędu
]
•
•
]
[n
w
•
[n
y
]
[n
w
⊗
θ
cos
2
1
R
a
=
2
2
R
a
−
=
⊗
⊗
⊗
θ
cos
2
1
R
b
−
=
2
2
1
R
b
=
⊕
⊕
⊕
⊕
]
[n
x
1
−
z
1
−
z
13
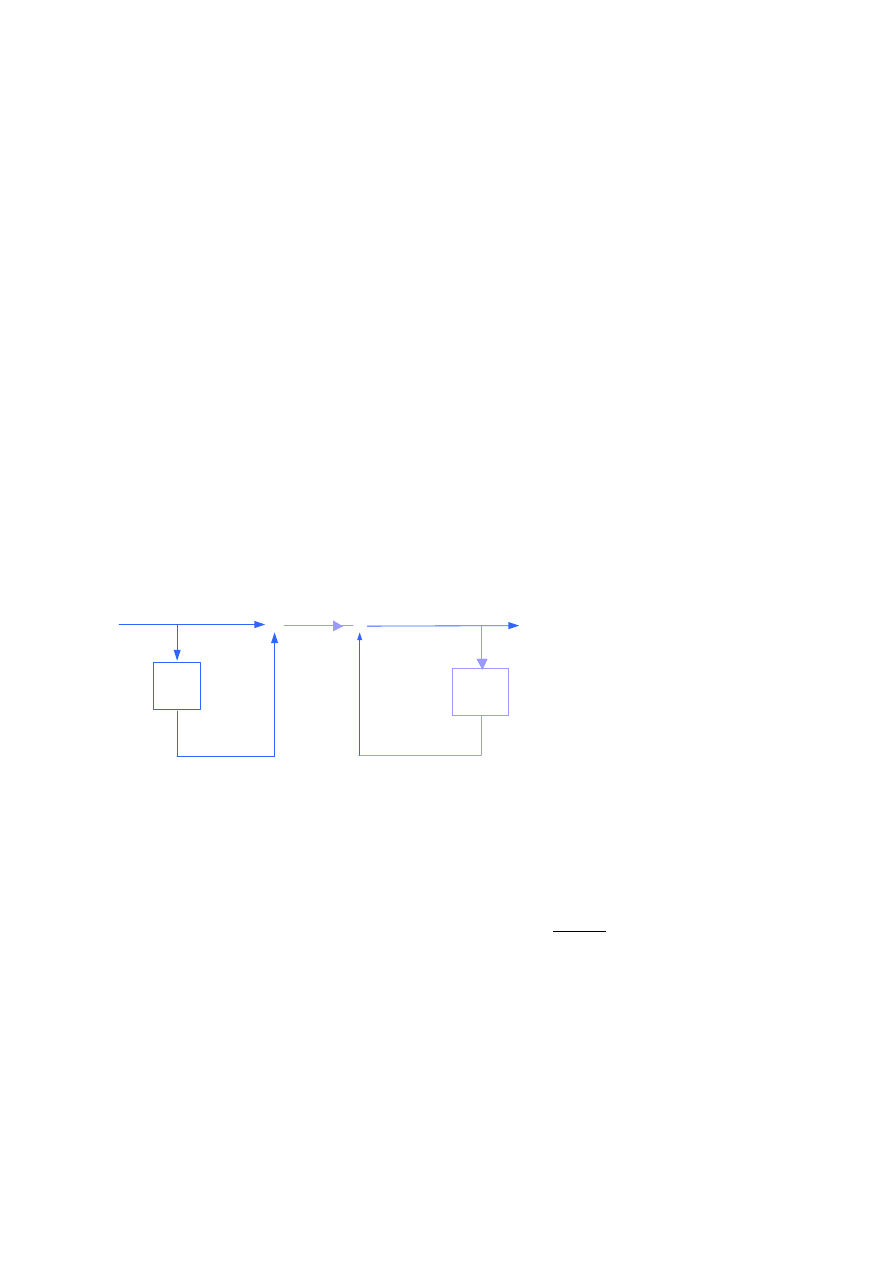
Ta struktura (ang. biquad) ma charakterystykę amplitudową, która jest stała w całym paśmie
częstotliwości (filtr wszech-przepustowy). Ma ona dwa bieguny zespolone sprzężone
ulokowane na promieniu R na płaszczyźnie z, z kątami
θ
±
rad/Sa i dwa zespolone sprzężone
zera ulokowane dla promienia odwrotnego,
1
, z kątami
R
/
θ
±
rad/Sa. Położenie biegunów i
zer, kontrolowane za pomocą rzeczywistej wartości R, steruje kształtem nieliniowej
charakterystyki fazowej.
W tablicy 3 [1] pokazano ciągłą linią charakterystyki: amplitudową i fazową, filtru dla
i
6
.
0
=
R
3
/
π
θ
=
7
.
0
, a dla porównania linią przerywaną przedstawiono charakterystykę fazową
dla
i
−
=
R
3
/
π
θ
=
. Takie obwody mogą być w pierwszym rzędzie użyte jako korektory
fazowe przez skaskadowanie za filtrem lub obwodem, którego nieliniowa charakterystyka
fazowa wymaga linearyzacji. Celem jest tu uczynienie docelowej charakterystyki fazowej tak
bliskiej liniowej, jak jest to tylko możliwe. Wielokrotnie skaskadowane biquady mogą mieć
akceptowalnie skorygowane charakterystyki fazowe.
1.18. Filtr interpolacyjny CIC (od ang. cascaded integrator-comb) jednostopniowy
wykorzystywany do interpolacji w dziedzinie czasu dyskretnego
1
−
z
•
1
−
z
]
[n
x
]
[n
y
⊕
⊕
+ −
•
8
−
z
Jeżeli sygnał dyskretny jest przepróbkowywany w górę, za pomocą ekspandera o krotności
N, (przez wtrącenie
próbek o wartości 0 pomiędzy każdą parę próbek danych) i
następnie przetworzymy go przez filtr dolnoprzepustowy, to na wyjściu filtru otrzymamy
interpolowany przez N wariant sygnału oryginalnego. Transmitancją filtru
dolnoprzepustowego z powyższego rysunku jest
1
−
N
1
1
1
)
(
−
−
−
−
=
z
z
z
H
N
, gdzie
. Celem
zwiększenia tłumienia obrazów widma, możemy skaskadować (połączyć szeregowo – w
łańcuszek) M kopii filtru grzebieniowego, a po nim skaskadować M ogniw bikwadratowych.
Takie skaskadowane filtry będą również miały węższe pasmo przenoszenia wokół
częstotliwości 0 Hz.
8
=
N
W praktyce operacja ekspansji (wtrącania zer) jest wykonywana za filtrem
grzebieniowym, a przed bikwadem. Korzystne tu jest, że opóźnienie filtru grzebieniowego
14
jest wówczas równe
, co redukuje potrzeby pamięciowe dla filtru grzebieniowego do
jedynki.
1
=
N
Filtry CIC są typowo wykorzystywane jako pierwszy stopień wielostopniowej filtracji
dolnoprzepustowej [7] w sprzętowej (ang. hardware) interpolacji z krotnością N z powodu
tego, że nie potrzeba tu żadnych mnożeń.
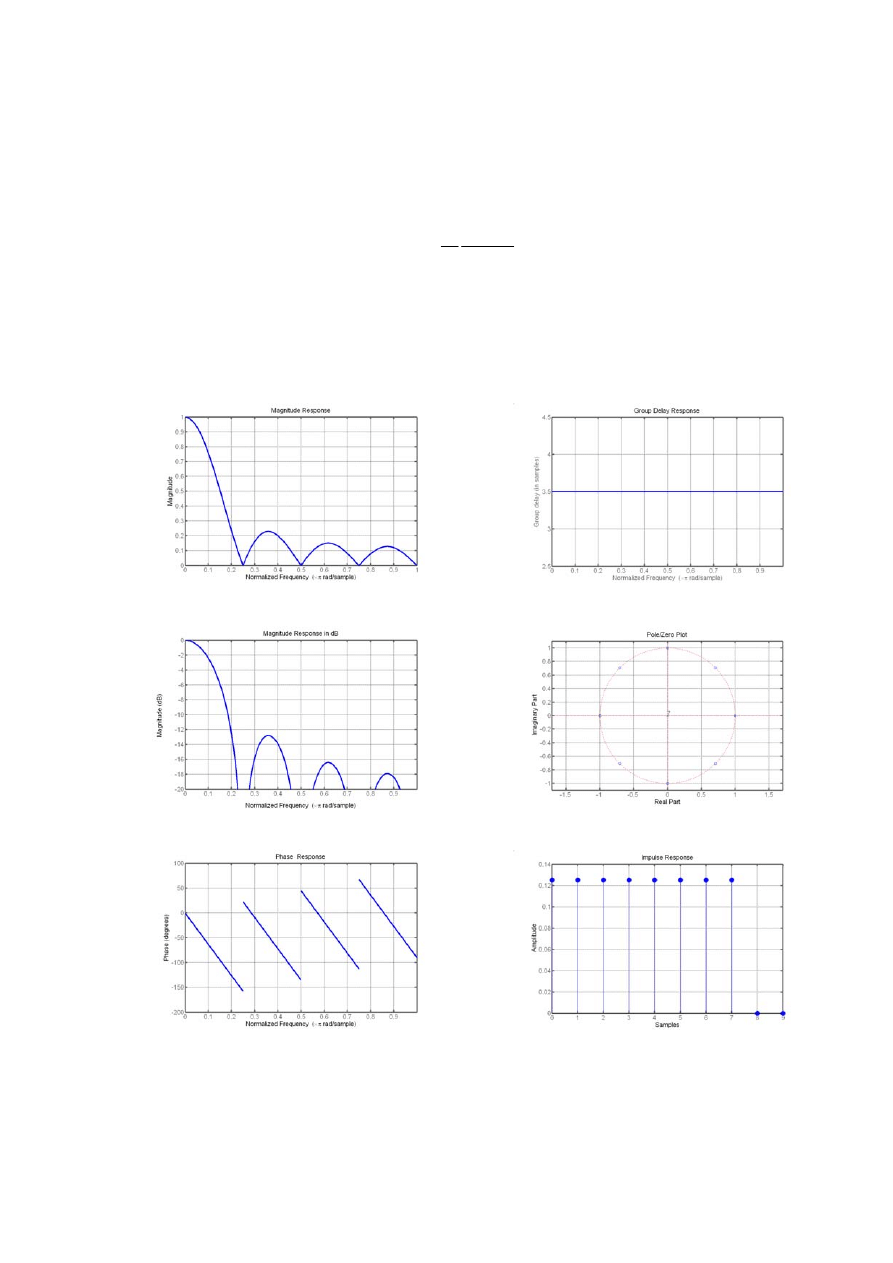
Rysunki poniżej wykonano dla
8
dla
,
1
1
1
)
(
1
=
−
−
=
−
−
N
z
z
N
z
H
N
, a wówczas
1
)
0
(
=
=
z
H
co oznacza, że charakterystyka amplitudowa jest równa 1 dla składowej stałej.
Te rysunki otrzymano w MATLABie za pomocą GUI: fvtool([
/8,
]
1
0
0
0
0
0
0
0
1
−
])
1
1
[
−
z
parametrami – wielkość fontów 16 pkt, grubość ramki 3 pkt, grubość krzywej niebieskiej 3
pkt.
15
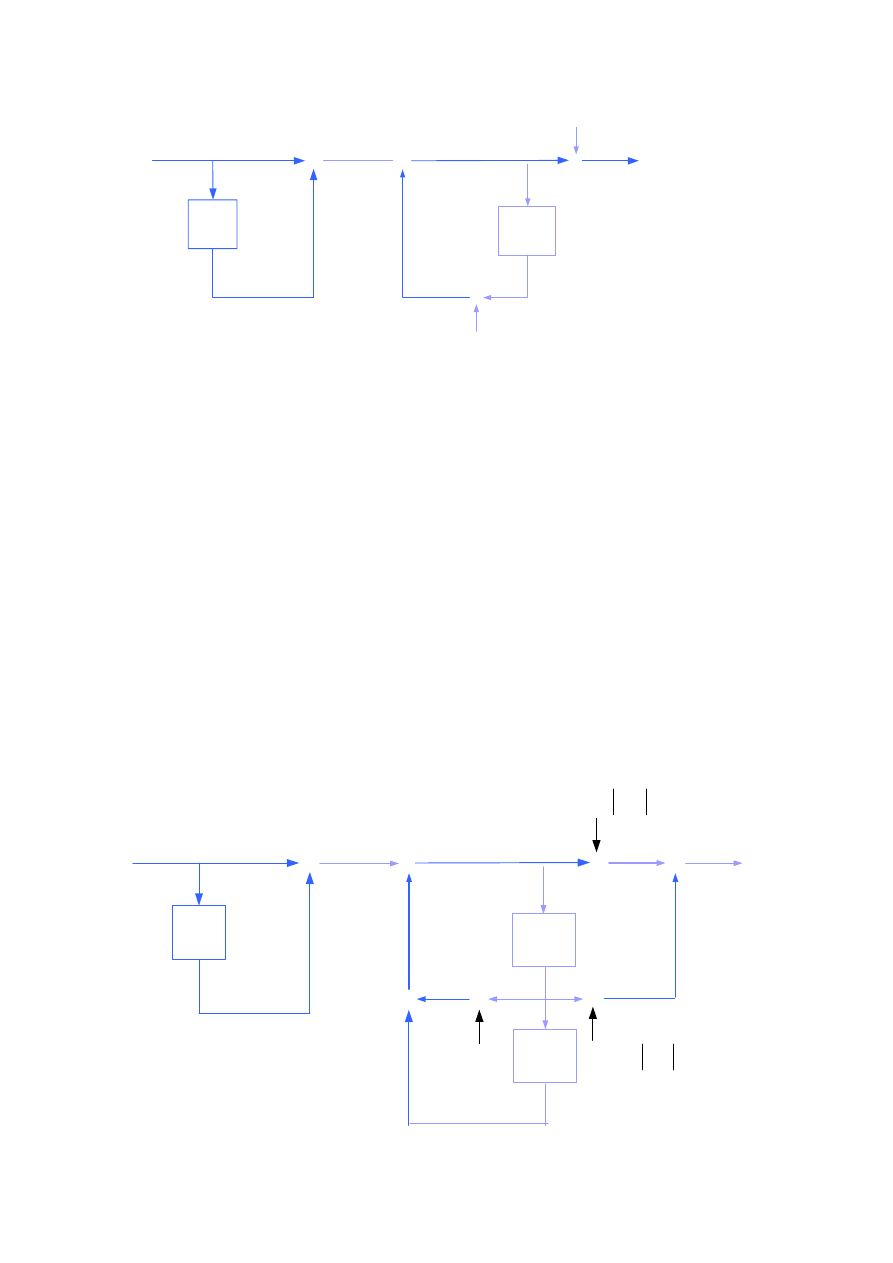
1.19. Zespolony FSF
1
−
z
•
1
−
z
]
[n
x
]
[n
y
⊕
⊕
+ −
•
N
z
−
⊗
⊗
k
j
e
a
θ
=
1
k
b
)
1
(
0
−
=
Ta struktura to pojedyncza sekcja zespolonego częstotliwościowo próbkującego filtru FSF
(ang. frequency sampling filter) o amplitudowej charakterystyce częstotliwościowej opisanej
funkcją typu
, scentrowanej na kącie
x
x /
)
sin(
N
k
k
/
2
π
θ
=
rad na próbkę na okręgu
jednostkowym, odpowiadającemu częstotliwości
Hz. N i k to liczby całkowite, a k
należy do przedziału
N
kF
s
/
N
k
<
≤
0
. Im większe N, tym węższy jest listek główny charakterystyki
amplitudowej filtru.
Jeżeli połączymy równolegle wiele biquadów (wszystkie sterowane za pomocą
pojedynczego filtru grzebieniowego) z sąsiadującymi ze sobą częstotliwościami środkowymi,
to możemy zbudować filtry pasmowo-przepustowe o niemal liniowej charakterystyce
fazowej. Tablica 4 [1] pokazuje charakterystyki potrójnego zespolonego filtru pasmowego o
trzech biquadach scentrowanych, odpowiednio, na
2
i
,
1
,
0
=
k
.
1.20. Rzeczywisty FSF, Typ I
1
−
z
]
[n
y
1
−
z
•
•
1
−
z
]
[n
y
1
−
z
⊗
⊗
k
a
θ
cos
2
1
=
⊗
k
k
H
b
φ
cos
0
=
)
cos(
1
k
k
k
H
b
θ
φ
−
−
=
⊕
⊕
⊕
⊕
]
[n
x
N
z
−
+ −
•
]
1
[
−
n
w
]
2
[
−
n
w
]
[n
w
N
k
k
/
2
π
θ
=
+
−
16
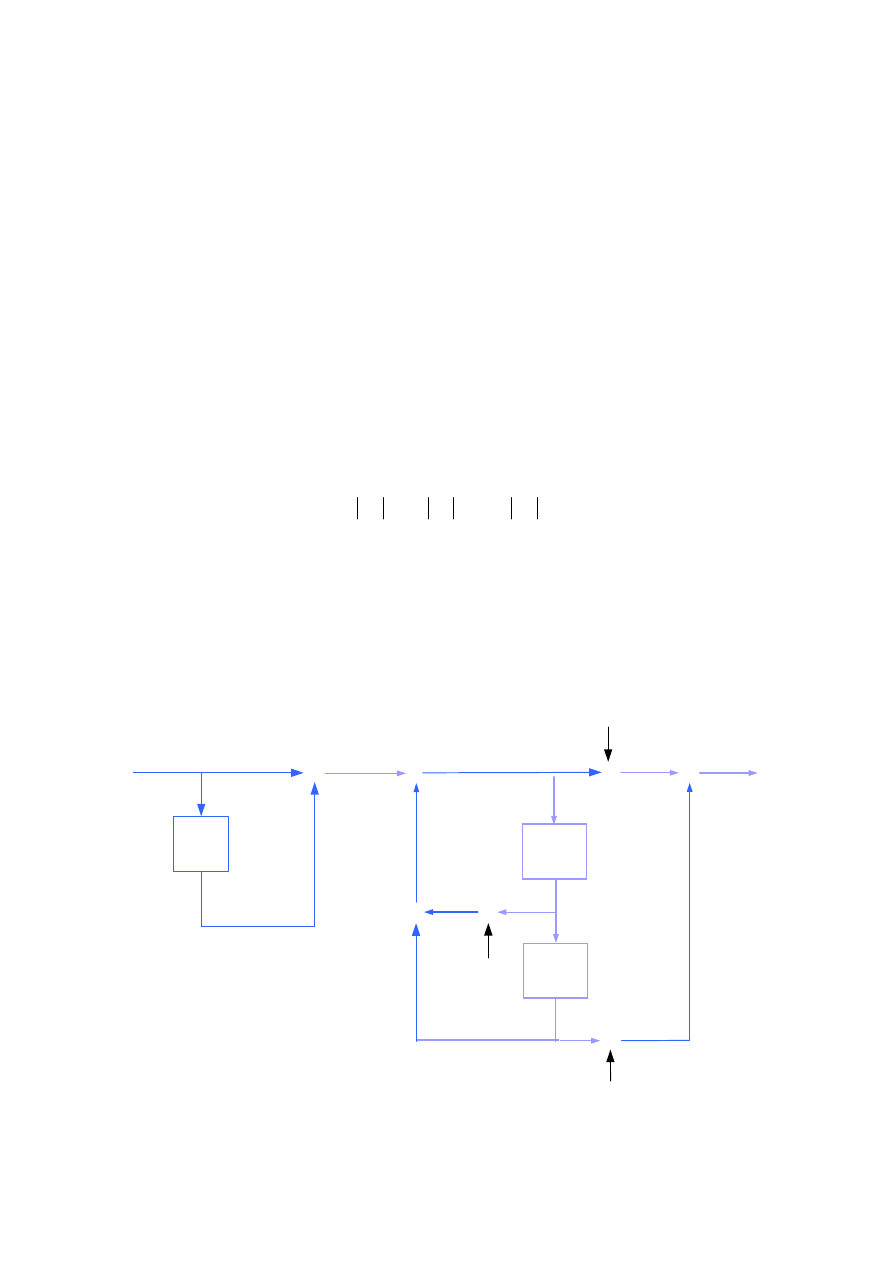
Ta struktura to pojedyncza sekcja częstotliwościowo próbkującego filtru FSF (ang. frequency
sampling filter) o współczynnikach rzeczywistych, o amplitudowej charakterystyce
częstotliwościowej opisanej funkcją typu sin(
, scentrowanej na kątach
x
x /
)
N
k
k
/
2
π
θ
±
=
±
rad na próbkę na okręgu jednostkowym, gdzie N jest liczbą całkowitą, a k należy do
przedziału
. Im większe N, tym węższy jest listek główny charakterystyki
amplitudowej filtru.
N
k
<
≤
0
Jeżeli połączymy równolegle wiele biquadów (wszystkie sterowane za pomocą
pojedynczego filtru grzebieniowego) z sąsiadującymi ze sobą częstotliwościami środkowymi,
to możemy zbudować filtry dolnoprzepustowe o niemal liniowej charakterystyce fazowej. W
tym przypadku zespolone czynniki wzmocnienia
są pożądanymi wartościami pików
charakterystyk amplitudowych dla k-tego biquadu. Parametr
k
H
k
φ
w rad to pożądane względne
przesunięcie fazy
. Tablica 4 [1] pokazuje charakterystyki potrójnego zespolonego filtru
dolnoprzepustowego z N=22, o trzech biquadach, scentrowanych, odpowiednio, na
. W tym przykładzie
k
H
2
i
,
1
,
0
=
k
1
0
=
H
,
2
1
=
H
i
74
2
=
H
.
0
. Te filtry mogą mieć, w
paśmie przepustowym, fluktuacje charakterystyki grupowego opóźnienia tak duże jak
Ten filtr rekursywny FSF (FIR) jest najczęściej spotykany w podręcznikach z DSP (ang.
digital signal processing), np. [5].
s
F
/
2
.
1.21. Rzeczywisty FSF, Typ IV
1
−
z
]
[n
y
1
−
z
•
•
1
−
z
]
[n
y
1
−
z
⊗
⊗
k
a
θ
cos
2
1
=
⊗
k
k
M
b
)
1
(
0
−
=
)
(
)
1
(
2
k
k
M
b
−
−
=
⊕
⊕
⊕
⊕
]
[n
x
N
z
−
+ −
•
]
1
[
−
n
w
]
2
[
−
n
w
]
[n
w
N
k
k
/
2
π
θ
=
+
−
•
17
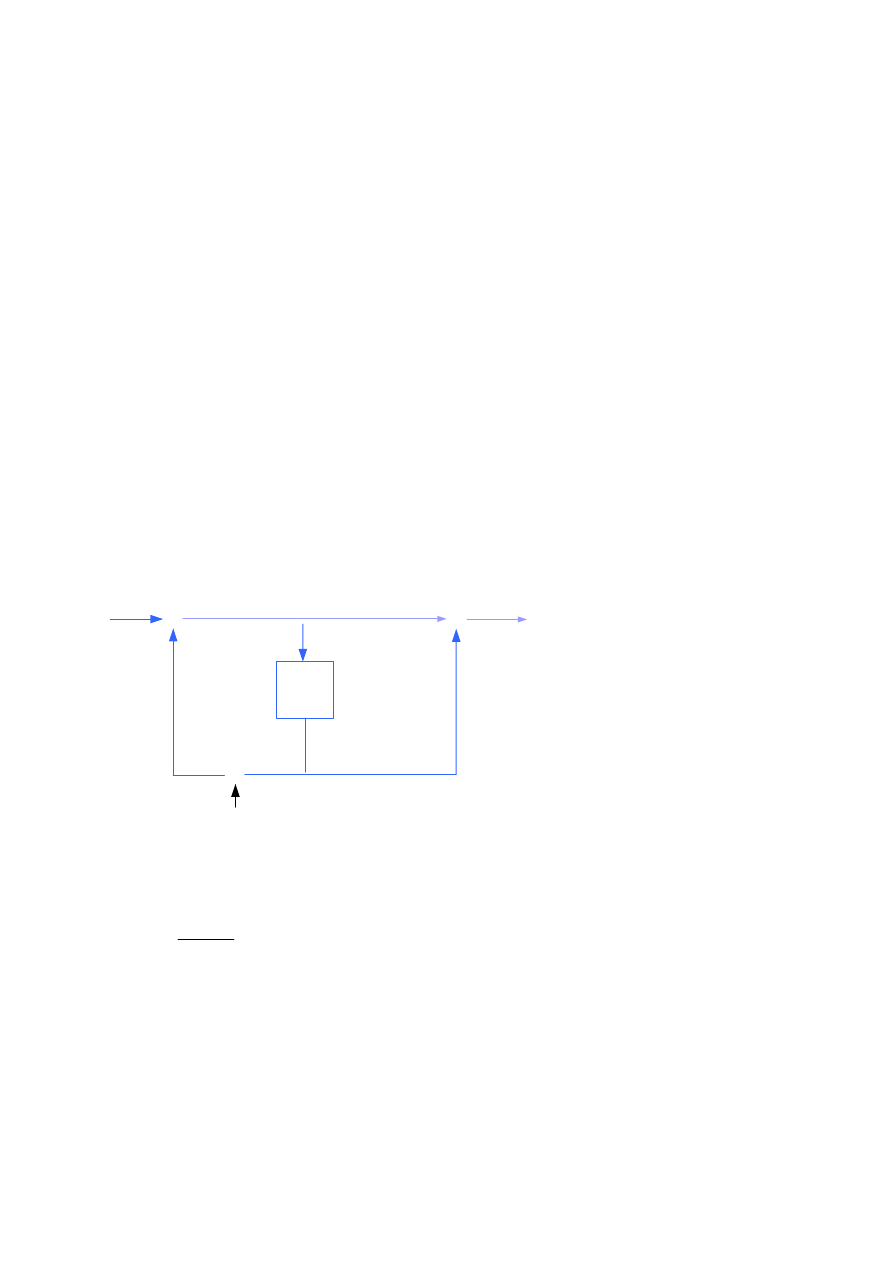
Ta struktura zachowuje się podobnie jak poprzedni filtr FSF, typu I, ale z istotnymi
wyjątkami. Po pierwsze, w implementacjach dolnoprzepustowych z wieloma biquadami (ang.
multibiquad) ten filtr ma dokładnie liniową charakterystykę fazową. Również, ten filtr ma
większe tłumienie zaporowe niż filtr typu I.
Współczynniki wzmocnienia
to pożądane wartości pików charakterystyki
amplitudowej k-tego biquadu. Tablica 4 [1] pokazuje charakterystyki dla potrójnego
zespolonego filtru dolnoprzepustowego z N=22, o trzech biquadach, scentrowanych,
odpowiednio, na k
. W tym przykładzie mamy
k
M
2
i
,
1
,
0
=
1
0
=
M
,
i
M
. O
tym filtrze warto wiedzieć, że: przy roztropnym wyborze współczynników wzmocnienia
,
można zbudować wąskopasmowe dolnoprzepustowe liniowo-fazowe filtry FIR, które w
pewnych przypadkach mogą wymagać mniejszych nakładów obliczeniowych (ang.
computational workload) niż słynne filtry FIR optymalne w sensie Czebyszewa [5],
wykorzystywane często jako odniesienie do porównań z innymi, nowymi filtrami.
2
1
=
M
74
.
0
2
=
M
k
1.22. System usuwania składowej stałej
•
]
[n
x
+
]
[n
y
]
[n
v
⊕
⊕
•
1
−
z
⊗
α
=
1
a
]
1
[
−
n
v
−
Ten system usuwa składową stałą (dc) z sygnału wejściowego . Transmitancja systemu
]
[n
x
1
1
dc
1
1
)
(
−
−
−
−
=
z
z
z
H
α
ma biegun zlokalizowany dla
α
=
z
i zero dla
1
=
z
. Ostrość wycinania
(ang. notch) jest determinowana przez
α
=
z
. Wycinana jest częstotliwość 0 Hz (dc).
Stabilność zapewnia spełnienie warunku
1
0
<
<
α
. Im
α
jest bliższa jedności, tym ostrzejsza
jest charakterystyka wycinania. (Przykładowa wartość
α
to 0.8 w tablicy 4 [1].) Filtr ten ma
nieliniową charakterystykę fazową.
W tych implementacjach stałoprzecinkowych, gdzie ciąg wyjściowy musi mieć
obcięte wartości próbek aby uniknąć przepełnienia (ang. data overflow), tzn.
musi mieć
]
[n
y
]
[n
y
18

mniej bitów niż ciąg wejściowy , można użyć metodę kształtowania szumu ze
sprzężeniem zwrotnym (ang. feedback noise shaping) aby zredukować szum kwantyzacji
spowodowany powyższym obcięciem bitów [6].
]
[n
x
b
1
Ażeby uniknąć przepełnienia, alternatywą do obcinania bitów jest ograniczenie
wzmocnienia filtru. Przykładowo, możemy poprzedzić nasz system usuwania składowej stałej
o dodatnim wzmocnieniu, obwodem, którego wzmocnienie jest mniejsze od jedności. Jeszcze
innym sposobem jest wzięcie b
i
G
=
0
G
−
=
, gdzie
2
/
)
1
(
α
+
=
G
w naszej implementacji
dla tego celu, przy czym uzyskamy transmitancję
1
1
−
−
dc
alt,
1
)
(
−
−
=
G
z
H
z
Gz
α
o zredukowanym
wzmocnieniu.
19
Wyszukiwarka
Podobne podstrony:
Zaproszenie do sklepu na prezen Nieznany
FutureMap 1 terminarz wydarzeń do 40r na Planecie Ziemia (ang )
Portrety Żydów na kartach szkolnych lektur Przedstaw różne sposoby kreacji Żydów, odwołując się do a
Czerniak, Adam Pozyskiwanie i interpretowanie danych do analiz ilościowych Potrzeby pracodawców a k
tablice do analizy konkur
DO TEL! 5= Genetyka nadci nieni Nieznany
(W7a Stale do kszta t na zimno cz I [tryb zgodno ci])
instrukcja bhp na stanowisku ko Nieznany
1 2510 do pracy na zimno
MATERIALY DO WYKLADU CZ IV id Nieznany
FW14 fale na granicy osrodkow 0 Nieznany
2009 EGZ WSTEPNY NA AM ODP(2) Nieznany
więcej podobnych podstron