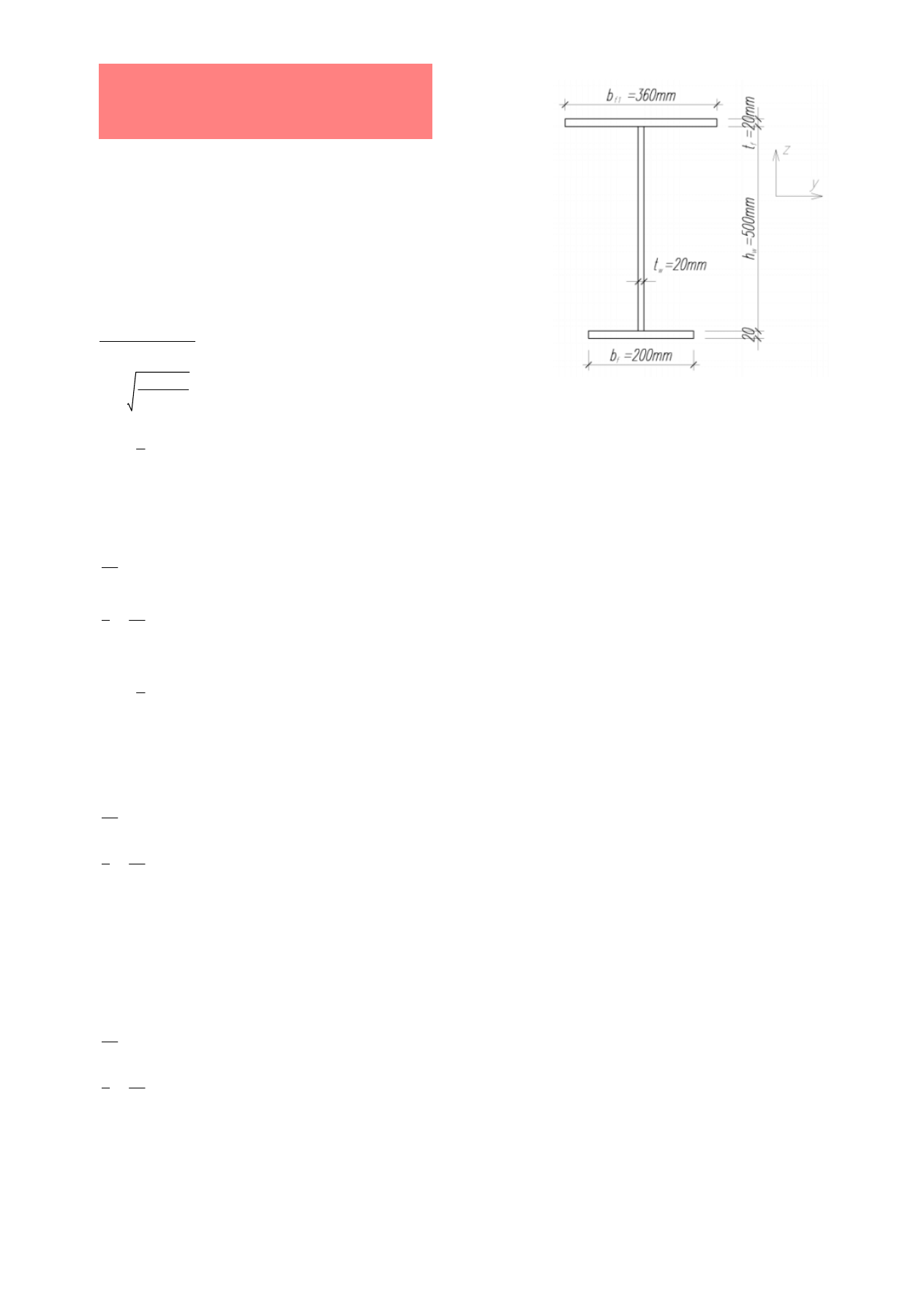
1. Dla przekroju jak na rysunku i fy=235 MPa określić:

− klasę przekroju (Załącznik 1)
− nośność na ściskanie NRc
− nośność na zginanie względem osi z - MRz.

bf

200mm



bf1 360mm



tf

20mm



hw

500mm



tw

20mm



fy

235MPa



ROZWIĄZANIE:
klasa przekroju:

ε

235MPa

fy

1





półka górna:



b1

1
2

bf1 tw









170 mm







n

9



c

b1 170 mm







t

tf 20 mm







b1

tf

8.5



c

t

b1

tf

n ε





=

1



półka górna w 1 klasie

półka dolna:



b1

1
2

bf tw









90 mm







n

9



c

b1 90 mm







t

tf 20 mm







b1

tf

4.5



c

t

b1

tf

n ε





=

1



półka dolna w 1 klasie

środnik:



h1

hw 500 mm







t

tw 20 mm







c

h1 500 mm







n

72



h1

tw

25



c

t

h1

tw

n ε





=

1



środnik w 1 klasie

Cały przekrój w 1 klasie.

Nośność na ściskanie

A

bf1 tf



bf tf





hw tw





21200 mm

2







γM0

1.0



NRc

A fy



γM0

4982 kN







Nośność na zginanie

Wpl 2

bf1

2

tf



bf1

4



tw

2

hw



tw

4





bf

2

tf



bf

4



















898000 mm

3







MRz

Wpl fy



γM0

211.03 kN m









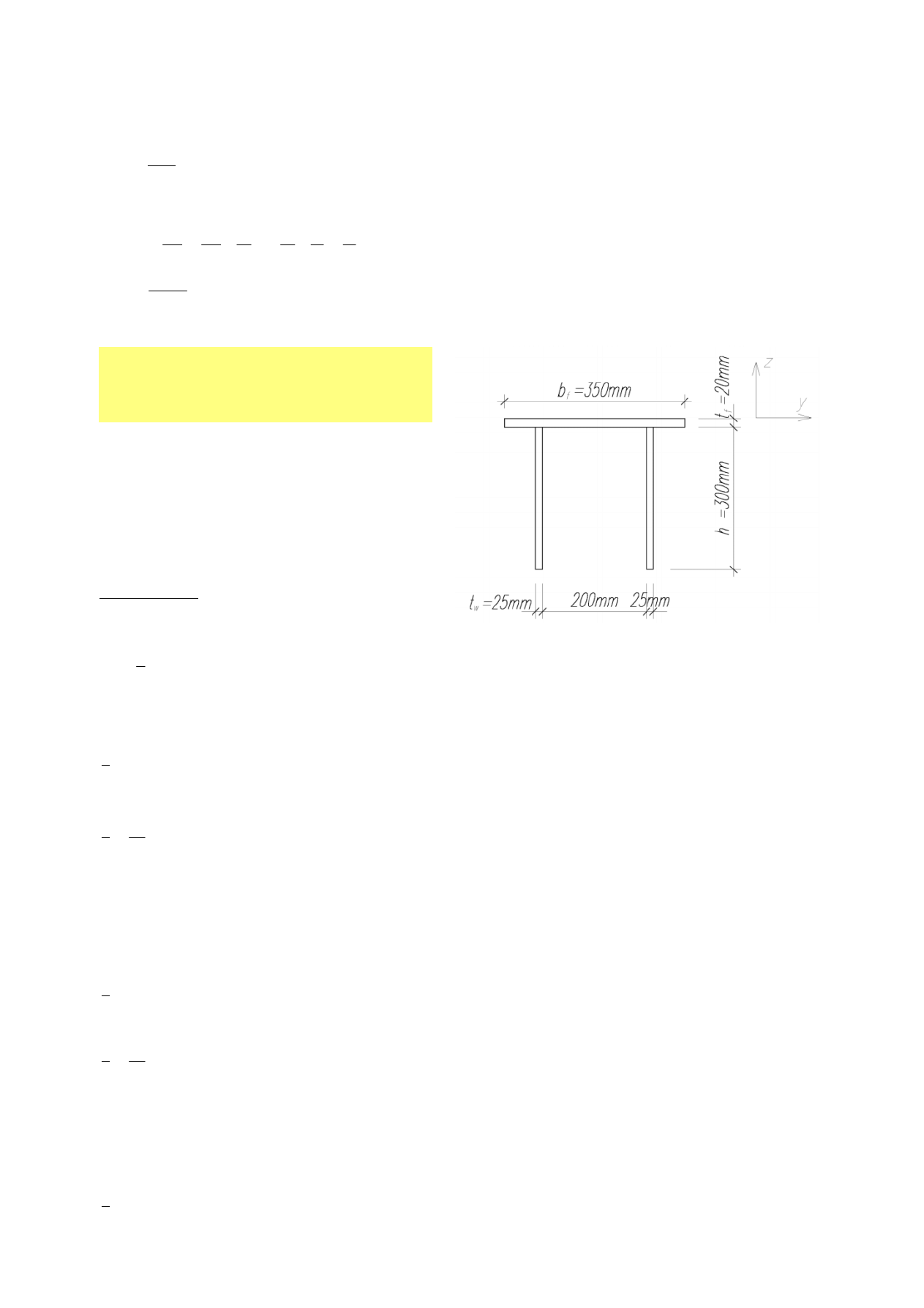
2. Dla przekroju jak na rysunku i fy=235 MPa określić:

− klasę przekroju (Załącznik 1)
− nośność na ściskanie NRc
− nośność na zginanie względem osi y - MRy

bf

350mm



tw

25mm



tf

20mm



h

300mm



fy

235MPa



ROZWIĄZANIE:
Klasa przekroju

pas część wspornikowa



b1

1
2

bf 2 tw





200mm









50 mm







t

tf 20 mm







c

b1 50 mm







c

t

2.5



n

9



c

t

b1

tf

n ε





=

1



Pas część wspornikowa w 1 klasie

pas część środkowa



b1

200mm



t

tf 20 mm







c

b1 200 mm







c

t

10



n

33



c

t

b1

tf

n ε





=

1



Pas część środkowa w 1 klasie

wspornik (środnik pionowy)



h1

h

300 mm







t

tw 25 mm







c

h1 300 mm







c

t

12



n

9



c

t

h1

tw

n ε





=

0



n

10



c

t

h1

tw

n ε





=

0



n

14



c

t

h1

tw

n ε





=

1



Wspornik (środnik pionowy) klasy 3

Cały przekrój klasy 3

Nośność na ściskanie

A

2 h

 tw



bf tf





22000 mm

2







γM0

1.0



NRc

A fy



γM0

5170 kN







Nośność na zginanie
moment statyczny

S

2 h

 tw



h
2



bf tf



h

tf
2



















4420000 mm

3







środek ciężkości

z0

S
A

200.909 mm







klasa przekroju wspornika zginanego

α

z0

h

0.67





n

9



c

h

300 mm







t

tw 25 mm







c

t

h

tw

n ε



α



=

1



Wspornik zginany klasy 1

momenty statyczne

S1

2 tw



z0



z0

2



1009111.57 mm

3







S2

bf tf



h

tf
2



z0

















2 h z0









tw



h z0



2





1009111.57 mm

3







wskaźnik oporu plastycznego

Wpl1 S1 S2



2018223.14 mm

3







nośność

MRy

Wpl1 fy



γM0

474.282 kN m









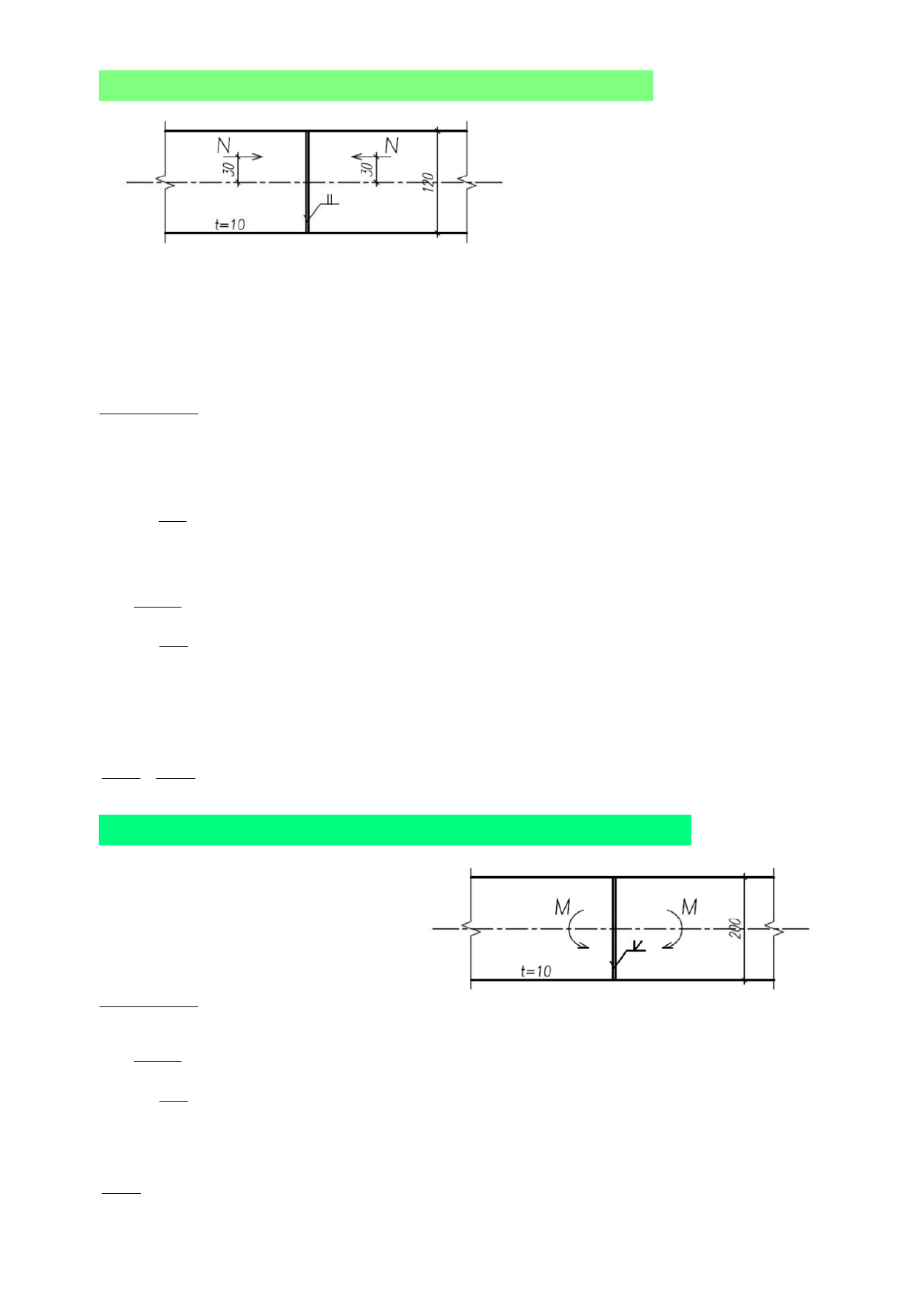
3. Określić nośność ściskanego mimośrodowo styku stalowego płaskownika 120x10.
Styk wykonano spoiną czołową. N = 100 kN; S235, fy = 235 MPa, fu = 360 MPa

N

100kN



fy

235MPa



fu

360MPa



aw

10mm



Lw

120mm



e

30mm



ROZWIĄZANIE:
Nośność na ściskanie

A

aw Lw



1200 mm

2







γM0

1



Nc.Rd

A fy



γM0

282 kN







Nośność na zginanie

W

aw Lw

2



6

24000 mm

3







Mc.Rd

W fy



γM0

5.64 kN m









Warunek na zginanie

NEd

N

100 kN







MEd

NEd e



3 kN m









NEd

Nc.Rd

MEd

Mc.Rd



1.0



1



warunek spełniony

4. Sprawdzić nośność zginanego styku stalowego płaskownika 200x10, zginanego momentem
M=500kNm; Styk wykonano spoiną czołową. S235, fy = 235 MPa, fu = 360 MPa

aw

10mm



Lw

200mm



fy

235MPa



fu

360MPa



M

500kN m





ROZWIĄZANIE:
Nośność na zginanie

W

aw Lw

2



6

66666.667 mm

3







Mc.Rd

W fy



γM0

15.667 kN m









Warunek na zginanie

MEd

M

500 kN m









MEd

Mc.Rd

1.0



0



Warunek niespełniony

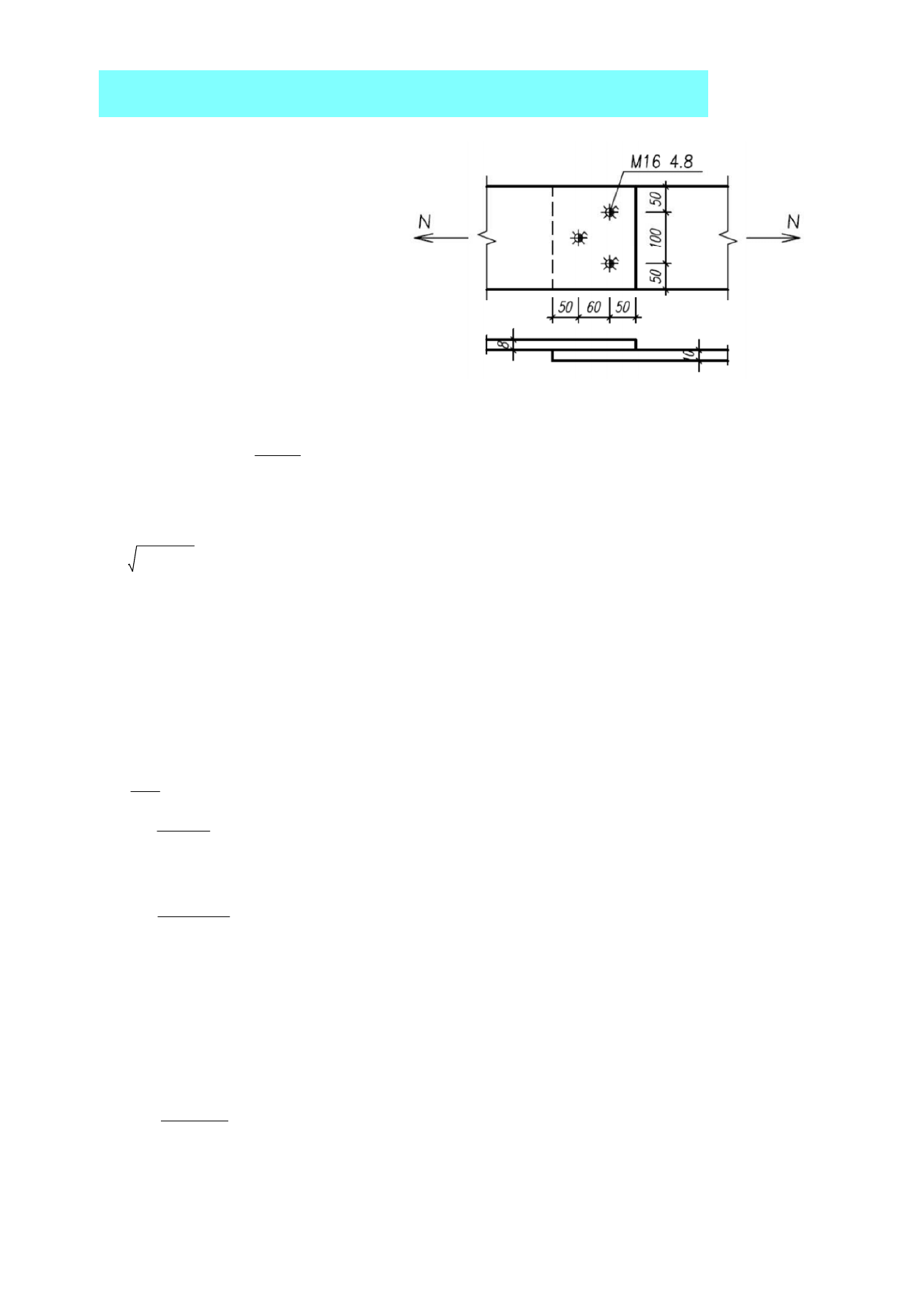
5. Określić nośność połączenia.
Śruby M16 kl.4.8. Sprawdzić poprawność rozmieszczenia łączników fy=235 MPa, fu = 360 MPa,
fub =400 MPa, fyb = 320 MPa, αv = 0,5, k1 = 2,5, αb = 1,0, d0 = 18 mm

fy

235MPa



d

16mm



fu

360MPa



t1

8mm



fub

400MPa



t2

10mm



fyb

320MPa



t

min t1 t2







8 mm







αv

0.5



γM2

1.25



k1

2.5



αb

1.0



d0

18mm



ROZWIĄZANIE:
Rozmieszczenie łączników

e1

50mm



p1

60mm



e2

50mm



p2

100mm

2

50 mm







e1 1.2 d0





1



p1 2.2 d0





1



e2 1.2 d0





1



p2 2.4 d0





1



L

p1

2

p2

2



78.102 mm







L

2.4 d0





1



e1 max 8 t 125mm



(

)



1



e2 max 8 t 125mm



(

)



1



p1 min 14 t 175mm



(

)



1



p2 min 14 t 175mm



(

)



1



Łączniki prawidłowo rozmieszczone

Nośność na ścinanie

A

π d

2


4

201.062 mm

2







Fv.Rd

αv fub



A



γM2

32.17 kN







Nośność na docisk

Fb.Rd

k1 αb



fu



d

 t

γM2

92.16 kN







FRd min Fv.Rd Fb.Rd







32.17 kN







liczba śrub

n

3



FRd FRd n



96.51 kN







Nośność blachy na rozerwanie

Anet

2 e2



2 p2





2 d0









t



1312 mm

2







NV.Rd

0.9 Anet



fu



γM2

340.07 kN







Nośnośćpołączenia FRd 96.51 kN







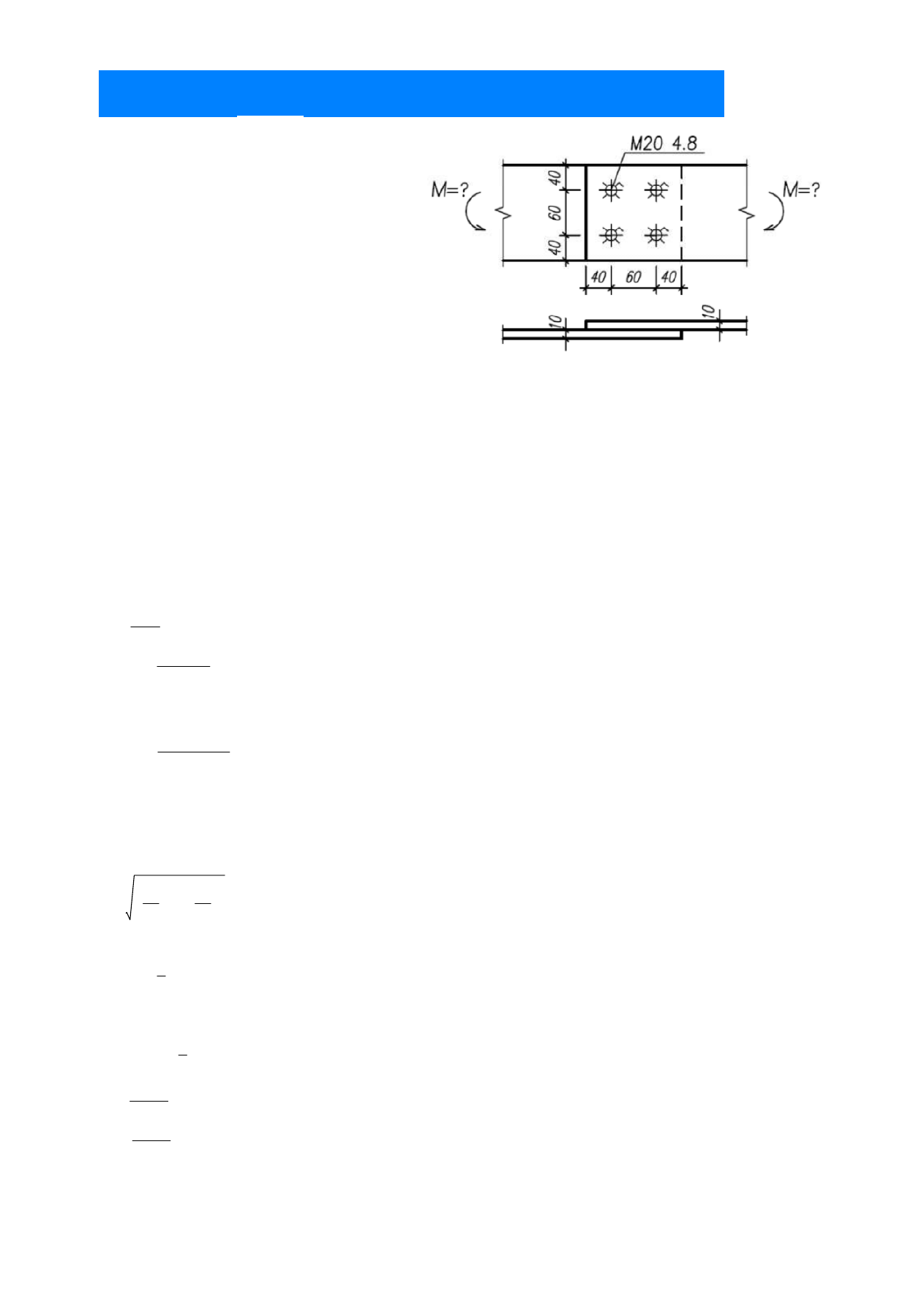
6. Określić nośność połączenia z uwagi na nośność śrub. Śruby M20 kl.4.8 . Sprawdzić poprawność
rozmieszczenia łączników. fy=235MPa, fu=360 MPa, fub = 400 MPa, fyb = 320 MPa, αv = 0,5, k1 = 2,5,
αb = 1,0, d0 = 22 mm

d

20mm



fy 235 MPa





e1

40mm



fu 360 MPa





e2

40mm



fub 400 MPa





p2

60mm



fyb 320 MPa





p1

60mm



αv

0.5



t

10mm



k1 2.5



γM2

1.25



αb

1



d0

22mm



ROZWIĄZANIE:
Rozmieszczenie łączników

e1 1.2 d0





1



p1 2.2 d0





1



e2 1.2 d0





1



p2 2.4 d0





1



e1 max 8 t 125mm



(

)



1



e2 max 8 t 125mm



(

)



1



p1 min 14 t 175mm



(

)



1



p2 min 14 t 175mm



(

)



1



Łączniki prawidłowo rozmieszczone

Nośność śrub na ścinanie

A

π d

2


4

314.159 mm

2







Fv.Rd

αv fub



A



γM2

50.265 kN







Nośność śrub na docisk

Fb.Rd

k1 αb



fu



d

 t

γM2

144 kN







FRd min Fv.Rd Fb.Rd







50.265 kN







liczba śrub

n

4



FRd FRd n



201.062 kN







Siły w śrubie

r

p1

2













2

p2

2













2



42.426 mm







ri

4 r

2



7200 mm

2







FiM M

r

ri



=

FRd 4 FiM





FRd 4 M

r

ri



















M

FRd ri



4 r





M

FRd ri



4 r



8.53 kN m









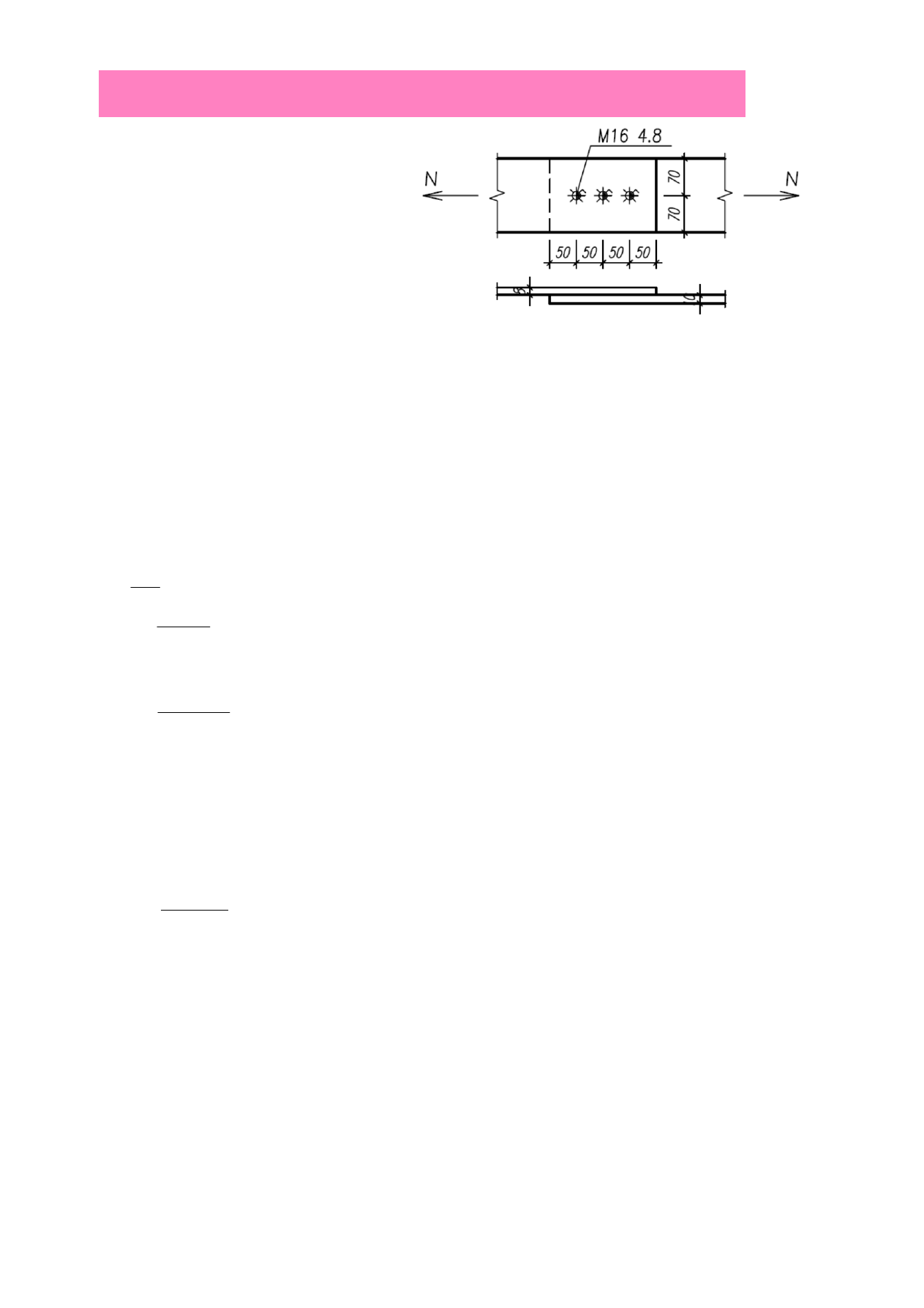
7. Jaką maksymalną siłę może przenieść połączenie płaskowników? Śruby M16 kl.4.8. Sprawdzić
poprawność rozmieszczenia łączników fy=235 MPa,fu = 360 MPa, fub = 400 MPa, fyb = 320MPa, αv = 0,5,
k1 = 2,5, αb = 1,0, do = 18 mm.

fy 235 MPa





d

16mm



fu 360 MPa





t1

8mm



fub 400 MPa





t2

10mm



fyb 320 MPa





t

min t1 t2







8 mm







αv

0.5



e1

50mm



γM2

1.25



k1 2.5



αb

1



p1

50mm



d0

18mm



e2

70mm



ROZWIĄZANIE:
Rozmieszczenie łączników

e1 1.2 d0





1



p1 2.2 d0





1



e2 1.2 d0





1



e1 max 8 t 125mm



(

)



1



e2 max 8 t 125mm



(

)



1



p1 min 14 t 175mm



(

)



1



Łączniki prawidłowo rozmieszczone

Nośność śrub na ścinanie

A

π d

2


4

201.062 mm

2







Fv.Rd

αv fub



A



γM2

32.17 kN







Nośność śrub na docisk

Fb.Rd

k1 αb



fu



d

 t

γM2

92.16 kN







FRd min Fv.Rd Fb.Rd







32.17 kN







liczba śrub

n

3



FRd FRd n



96.51 kN







Nośność blachy na rozerwanie

Anet t 2 e2



d0









976 mm

2







NV.Rd

0.9 Anet



fu



γM2

252.979 kN







Nośnośćpołączenia FRd 96.51 kN







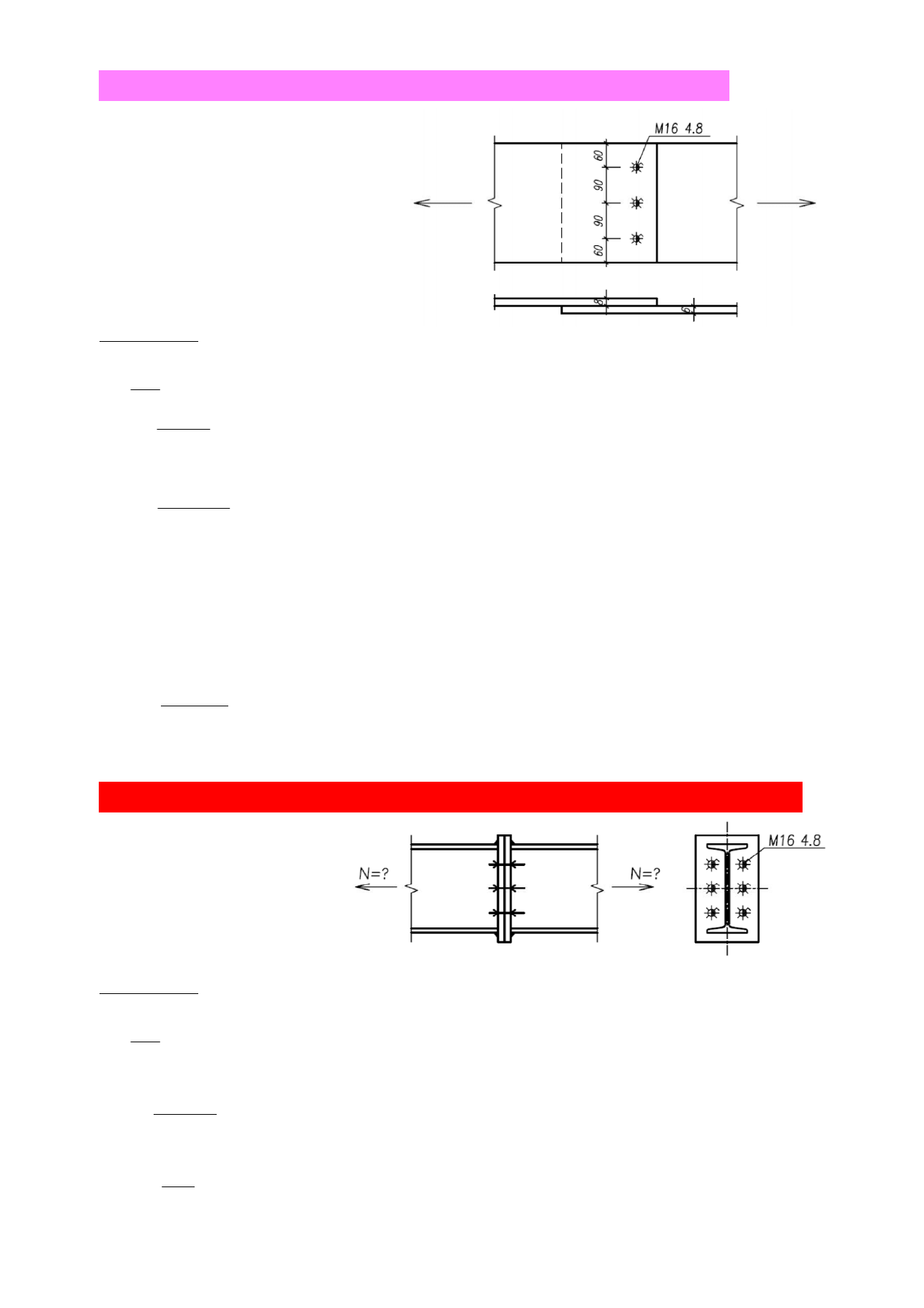
8 . Jaką maksymalną siłę może przenieść połączenie płaskowników? Śruby M16 kl.4.8; fy = 235 MPa,
fu = 360 MPa, fub = 400 MPa, fyb = 320 MPa, αv = 0,5, k1 = 2,5, αb = 1,0

fy 235 MPa





t1

8mm



fu 360 MPa





t2

6mm



fub 400 MPa





t

min t1 t2







6 mm







fyb 320 MPa





e1

60mm



αv

0.5



k1 2.5



p1

90mm



αb

1



γM2

1.25



d0

18mm



ROZWIĄZANIE:
Nośność na ścianie

A

π d

2


4

201.062 mm

2







Fv.Rd

αv fub



A



γM2

32.17 kN







Nośność śrub na docisk

Fb.Rd

k1 αb



fu



d

 t

γM2

69.12 kN







FRd min Fv.Rd Fb.Rd







32.17 kN







liczba śrub

n

3



FRd FRd n



96.51 kN







Nośność blachy na rozerwanie

Anet t 2 e1



2 p1





3 d0











1476 mm

2







NV.Rd

0.9 Anet



fu



γM2

382.579 kN







Nośnośćpołączenia FRd 96.51 kN







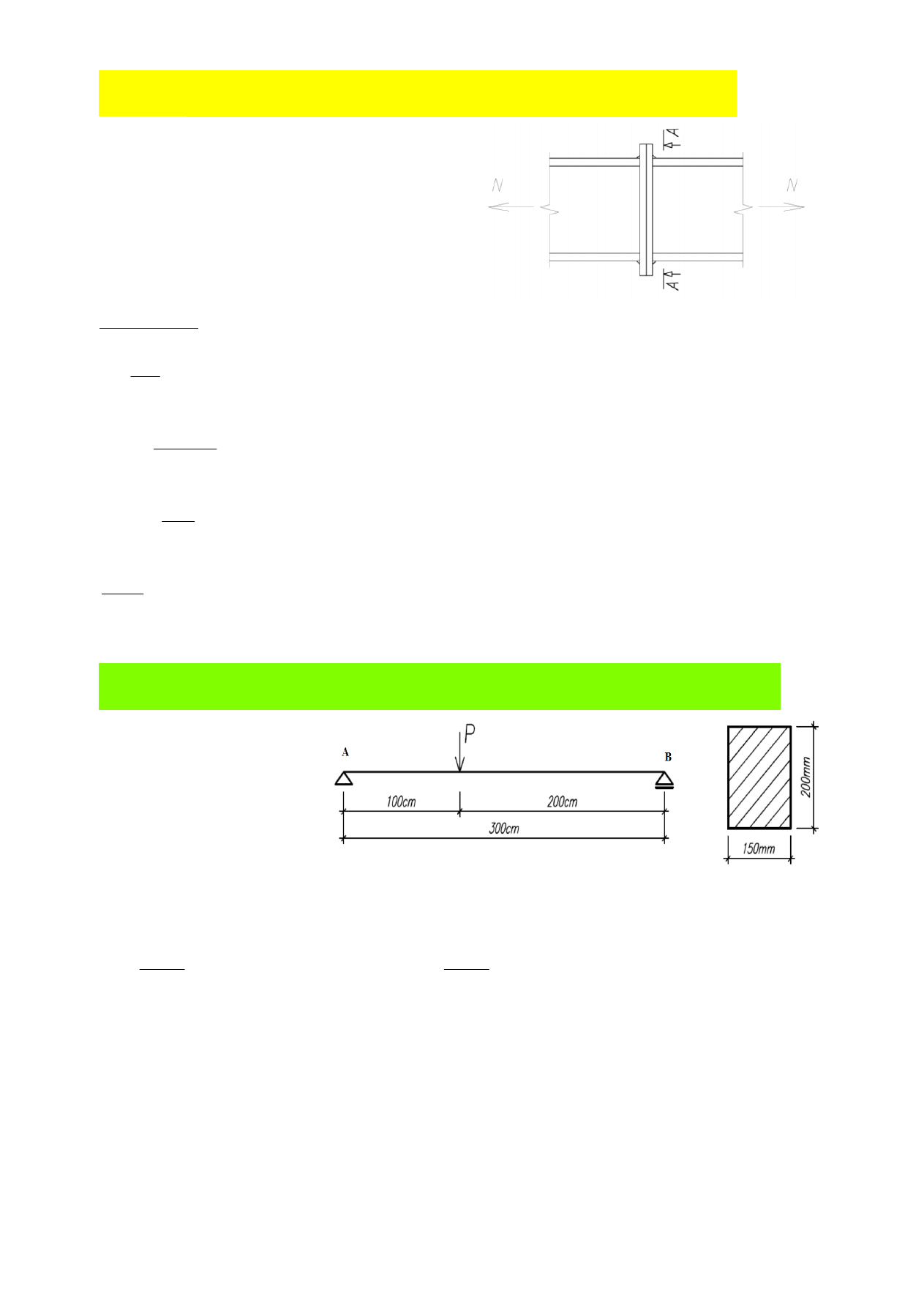
9. Jaką siłę przeniesie połączenie doczołowe Ι200 ze względu na nośność śrub? Śruby M16 kl.4.8 ; A1=33,5cm2;
fy = 235 MPa, fu = 360 MPa, fub = 400 MPa, fyb = 320 MPa,k2 = 0,9, As= 0,8A.

A1

33.5cm

2



As

0.8 A





fy 235 MPa





d

16mm



fu 360 MPa





d0

18mm



fub 400 MPa





γM2

1.25



fyb 320 MPa





k2

0.9



ROZWIĄZANIE:
Nośność łączników na rozciąganie

A

π d

2


4

201.062 mm

2







As

0.8 A



160.85 mm

2







Ft.Rd

0.9 fub



As



γM2

46.325 kN







Nośność grupy łącznków

n

6



Nośność profili

Npl.Rd

A1 fy



γM0

787.25 kN







FRd n Ft.Rd



277.948 kN







Nośnośćpołączenia FRd 277.948 kN







10. Określić liczbę śrub potrzebnych do czołowego połączenia Ι240.Schemat rozmieszczenia śrub
pokazać na przekroju A-A. Rozmieścić je w połączeniu. Śruby M16 kl.4.8; A1 = 46,1 cm2; fy = 235MPa,
fu=360 MPa, fub = 400MPa, fyb = 320 MPa, k2 = 0,9, As=0,8A.

A1

46.1cm

2



γM2

1.25



fy 235 MPa





fu 360 MPa





fub 400 MPa





fyb 320 MPa





k2 0.9



As

0.9A



ROZWIĄZANIE:
Nośność łączników na rozciąganie

A

π d

2


4

201.062 mm

2







As

0.8 A



160.85 mm

2







Ft.Rd

0.9 fub



As



γM2

46.325 kN







Nośność profili

Npl.Rd

A1 fy



γM0

1083.35 kN







Ilość śrub potrzebnych do połączenia

Npl.Rd

Ft.Rd

23.4



Narysować przykładowe rozmieszczenie śrub w połączeniu. Śrub potrzebnych 24szt

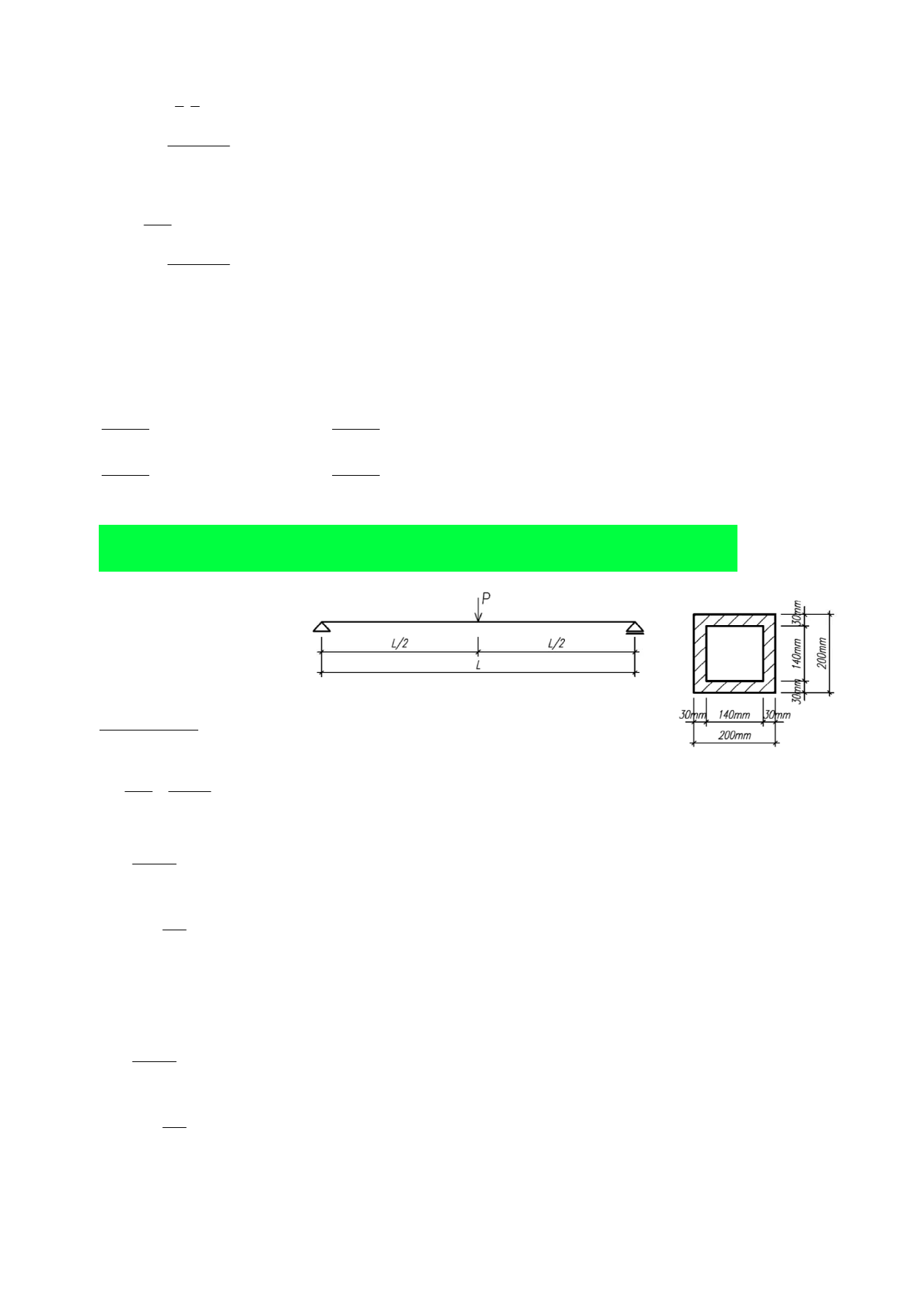
11. Dla belki stalowej o schemacie i przekroju poprzecznym jak na rysunku sprawdzić warunek stanu
granicznego nośności przy zginaniu. Sprawdzić w dwóch wariantach dla P1 = 100 kN i P2 = 300kN; χLt =0,9,
fy = 235 MPa.

P1

100kN



a1

100cm



P2

300kN



a2

200cm



χLt

0.9



b

150mm



fy 235 MPa





h

200mm



γM1

1.0



ROZWIĄZANIE:
Reakcje dla siłe P

1

Reakcje dla siłe P

2

ΣMb

0

=

ΣMb

0

=

VA a1 a2









P1 a2





0

=

VAA a1 a2









P2 a2





0

=

VA

P1 a2



a1 a2



66.667 kN







VAA

P2 a2



a1 a2



200 kN







ΣY

0

=

ΣY

0

=

VA VB



P1



0

=

VAA VBB



P2



0

=

VB

VA



P1



33.333 kN







VBB

VAA



P2



100 kN







Moment maksymalny dla P

1

Moment maksymalny dla P

2

x

a1 100 cm







x

a1 100 cm







M1

VA x



66.667 kN m









M2

VAA x



200 kN m









Klasy przekroju 1,2

Wpl 2 b

h
2



h
4













1500000 mm

3







Mb.Rd1

Wpl fy

 χLt



γM1

317.25 kN m









Klasa 3

Wel

b h

2



6

1000000 mm

3







Mb.Rd2

Wel fy

 χLt



γM1

211.5 kN m









Warunek SGN dla sił P

1

i P

2

MEd.1

M1 66.667 kN m









MEd.2

M2 200 kN m









klasy 1,2

klasa 3

MEd.1

Mb.Rd1

1.0



1



MEd.1

Mb.Rd2

1.0



1



Warunki spełnione

MEd.2

Mb.Rd1

1.0



1



MEd.2

Mb.Rd2

1.0



1



12. Dla belki stalowej o schemacie i przekroju poprzecznym jak na rysunku sprawdzić warunek stanu
granicznego użytkowania (SGU) dla dopuszczalnej strzałki ugięcia równej L/200 w dwóch wariantach:
P1 = 150 kN i L1 = 600 cm; P2 = 200 kN i L2 = 800 cm; fy = 235MPa.

P1

150kN



b

200mm



h

200mm



P2

200kN



b1

140mm



L1

600cm



h1

140mm



L2

800cm



fy 235 MPa





E

210GPa



ROZWIĄZANIE:

moment bezwładności przekroju

I

b h

3



12

b1 h1

3



12



101320000 mm

4







Ugięcie w belce dla siły P

1

f1

P1 L1

3



48 E

 I

31.724 mm







ugięcia maksymalne

Ymax1

L1

200

30 mm







Warunek SGU

f1 Ymax1



0



Warunek niespełniony

Ugięcie w belce dla siły P

2

f2

P2 L2

3



48 E

 I

100.264 mm







ugięcia maksymalne

Ymax2

L2

200

40 mm







Warunek SGU

f2 Ymax2



0



Warunek niespełniony