Analiza matematyczna 2, cze

,

´s´

c jedenasta

Tekst poprawiony 4 wrze´snia 2011, godz. 00:02

Zwyk la pro´sba: prosze

,

o informacje

,

o zauwa˙zonych b le

,

dach, poprawie

,

.

Opr´ocz miar na przestrzeni IR

k

istnieja

,

inne wa˙zne zbiory, np. dane r´ownaniem lub uk ladem

r´owna´

n. Zajmiemy sie

,

najprostszymi, z punktu widzenia tego wyk ladu, zbiorami tego typu. Be

,

da

,

tzw.

rozmaito´sci.* Poje

,

cie to w jawnej postaci wprowadzi l Hassler Whitney w 1936 roku, ale wyste

,

powa lo

ono w matematyce wcze´sniej i to od wielu lat .

Definicja rozmaito´sci zanurzonej w IR

k

Zbi´or M ⊂ IR

k

nazywany jest m –wymiarowa

,

rozmaito´scia

,

klasy C

r

wtedy i tylko wtedy, gdy dla

ka˙zdego punktu p ∈ M istnieje jego otoczenie U i homeomorfizm ϕ: U ∩ M

na

−−→ V , gdzie V jest

otwartym podzbiorem przestrzeni IR

m

, przekszta lcenie ϕ

−1

: V −→ IR

k

jest klasy C

r

i dla ka˙zdego

punktu y ∈ V r´o˙zniczka Dϕ

−1

(y) jest w lo˙zeniem (monomorfizmem). Przekszta lcenie ϕ nazywane

jest mapa

,

, przekszta lcenie ϕ

−1

— lokalna

,

parametryzacja

,

. Zbi´or map, kt´orych dziedziny pokrywaja

,

M nazywany jest atlasem.

Jak wida´c terminologia zwia

,

zana jest z geografia

,

. Nie ma w tym nic specjalnie dziwnego. S lowo

mapa oznacza w je

,

zyku potocznym jaki´s rysunek opisuja

,

cy fragment powierzchni Ziemi, np. mapa

Chin albo mapa Monaco. Kartograf musi przyja

,

´c jaka

,

´s metode

,

rysowania, czyli zdecydowa´c sie

,

na jakie´s przekszta lcenie wybranego obszaru na kartke

,

papieru, czyli podzbi´or p laszczyzny IR

2

.

Wymy´sla jakie´s siatki po to, by rzeczywistemu punktowi przypisa´c punkt p laszczyzny, czyli pare

,

liczb za pomoca

,

, kt´orych ten punkt jest opisany. Na og´o l ˙za

,

da sie

,

, by to przekszta lcenie by lo w

miare

,

porza

,

dne. W szko lach ca lego ´swiata wmawia sie

,

ludziom, ˙ze istnieje jaka´s skala mapy, tzn. ˙ze

to przekszta lcenie jest podobie´

nstwem. W przypadku ma lych obszar´ow tak w przybli˙zeniu jest, w

przypadku du˙zych — nie, bo po prostu podobie´

nstwa nie istnieja

,

(odpowiednie twierdzenie poznaja

,

Pa´

nstwo w przysz lo´sci, zapewne na zaje

,

ciach z geometrii r´o˙zniczkowej, ale i tak wszyscy wiedza

,

,

˙ze np. p´o lsfery zrobionej z papieru nie da sie

,

„rozp laszczy´c” bez jej rozrywania, jedno rozcie

,

cie nie

wystarczy). My nie zak ladamy, ˙ze ϕ ma spe lnia´c warunki niemo˙zliwe do spe lnienia.

Przyk lad 1. (sfera)

Niech M = S

k

= {x ∈ IR

k+1

:

kxk = 1} . Wyka˙zemy, ˙ze M jest rozmaito´scia

,

wymiaru k (ta

rozmaito´s´c nazywana jest sfera

,

k –wymiarowa

,

). Wska˙zemy najpierw atlas z lo˙zony z 2(k + 1) map.

Zwia

,

zanych z punktami ±e

j

= (0, . . . , 0, ±1, 0, . . . , 0) ( ±1 wyste

,

puje na j –tej wsp´o lrze

,

dnej). Niech

U

+

i

= {x ∈ IR

k+1

:

x

i

> 0} , ϕ

+

i

(x) = (x

1

, . . . , x

i−1

, x

i+1

, . . . , x

k+1

) , U

−

i

= {x ∈ IR

k+1

:

x

i

< 0} ,

ϕ

−

i

(x) = (x

1

, . . . , x

i−1

, x

i+1

, . . . , x

k+1

) . Przekszta lcenie ϕ

+

i

rozpatrujemy tylko na zbiorze S

k

∩U

+

i

.

Na tym zbiorze jest ono r´o˙znowarto´sciowe, bo wsp´o lrze

,

dne x

1

, . . . , x

i−1

, x

i+1

, . . . , x

k+1

wyzna-

czaja

,

x

i

=

q

1 − (x

2

1

+ · · · + x

2

i−1

+ x

2

i+1

+ · · · + x

2

k+1

) — wiemy bowiem, ˙ze x

i

> 0 . Przy okazji

*

termin angielski: manifold

139

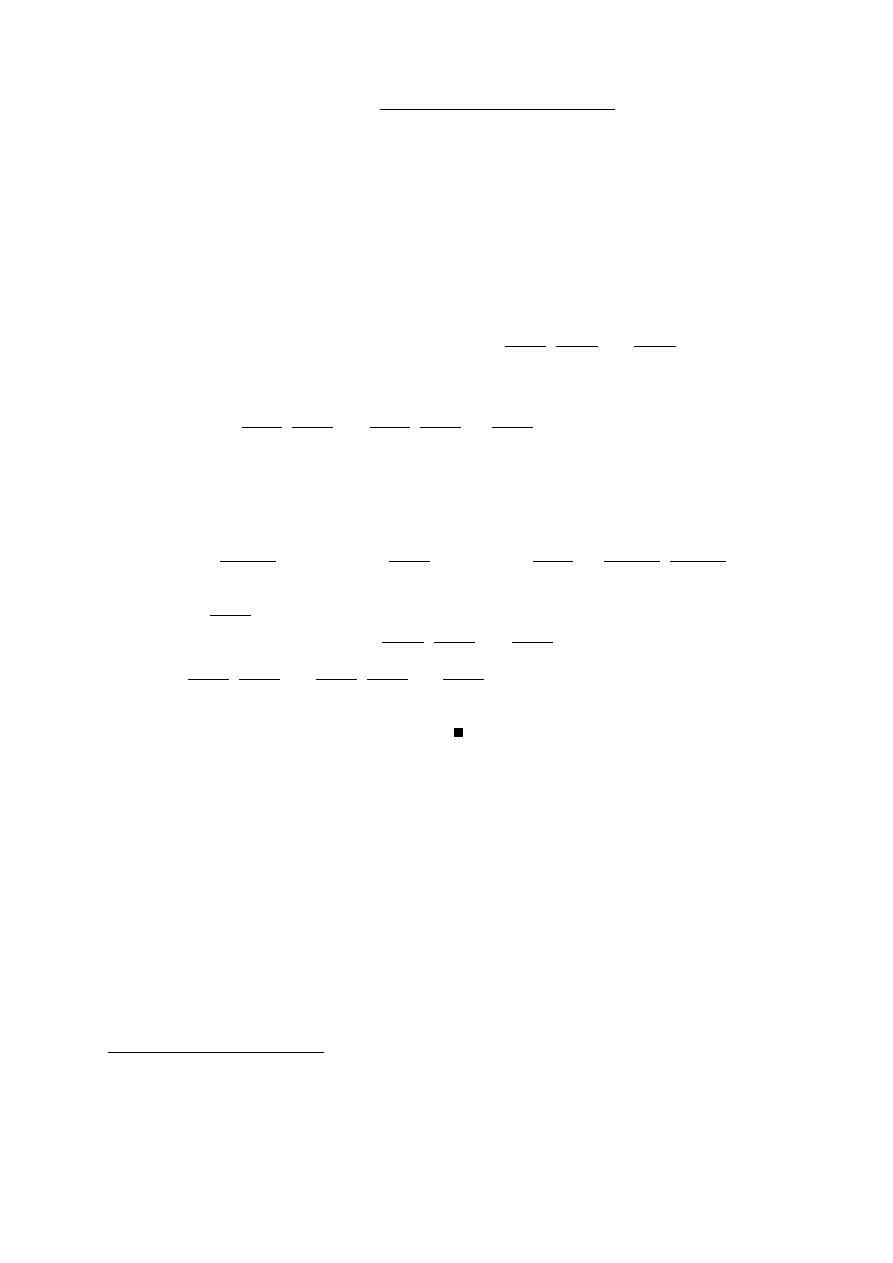
(ϕ

+

i

)

−1

(y

1

, y

2

, . . . , y

k

) = (y

1

, . . . , y

i−1

,

q

1 − (y

2

1

+ · · · + y

2

i−1

+ y

2

i

+ · · · + y

2

k

) , y

i

, . . . , y

k

) . Definiu-

jemy V

+

i

= ϕ

+

i

(U

+

i

∩S

k

) = {y ∈ IR

k

:

kyk < 1} . Z tego wzoru natychmiast wynika, ˙ze odwzorowa-

nie (ϕ

+

i

)

−1

jest klasy C

∞

, a jego r´o˙zniczka w dowolnym punkcie y ∈ V

+

i

jest w lo˙zeniem. Oznacza

to, ˙ze ϕ

+

i

jest mapa

,

. Podobnie okre´slamy mape

,

ϕ

−

i

. Jasne jest, ˙ze zbiory U

±

i

, i = 1, 2, . . . , k + 1

pokrywaja

,

ca la

,

sfere

,

S

k

. Okre´slili´smy wie

,

c atlas zgodnie z obietnica

,

, a to oznacza, ˙ze sfera S

k

jest

k –wymiarowa

,

rozmaito´scia

,

.

Poka˙zemy jeszcze jeden atlas, tym razem z lo˙zony z dwu map. Zaczynamy od okre´slenia dzie-

dzin: U

+

= {x ∈ IR

k+1

:

x

k+1

< 1} , U

−

= {x ∈ IR

k+1

:

x

k+1

> −1} . U

+

∩ S

k

to sfera

z wyja

,

tkiem punktu (0, . . . , 0, 1) . Definiujemy ϕ

+

(x) =

x

1

1−x

k+1

,

x

2

1−x

k+1

, . . . ,

x

k

1−x

k+1

. Zachodzi

r´owno´s´c x

k+1

(0, . . . , 0, 1) + (1 − x

k+1

)ϕ

+

(x) = x . Z niej wynika, ˙ze punkty x , ϕ

+

(x) i (0, . . . , 0, 1)

le˙za

,

na jednej prostej.

♣

ϕ

+

U

+

∩S

k

= IR

k

. Przekszta lcenie ϕ

−1

+

: IR

k

−→ U

+

∩S

k

⊆ IR

k+1

dane jest

wzorem ϕ

−1

+

(y) =

2y

1

kyk

2

+1

,

2y

2

kyk

2

+1

, . . . ,

2y

k

kyk

2

+1

,

kyk

2

−1

kyk

2

+1

=

1

kyk

2

+1

(2y, kyk

2

− 1) . Trzeba sprawdzi´c,

czy Dϕ

−1

+

(y) jest w lo˙zeniem (monomorfizmem). Mo˙zna oczywi´scie znale´z´c macierz przekszta lcenia

Dϕ

−1

+

(y) znajduja

,

c pochodne cza

,

stkowe, ale mo˙zna znale´z´c to przekszta lcenie nieco inaczej. Znamy

przecie˙z wzory na r´o˙zniczke

,

z lo˙zenia, r´o˙zniczke

,

iloczynu (wszystko jedno jakiego, np. skalarnego,

itp.). Mamy D(kyk

2

)(y)h = 2y · h . Sta

,

d i ze wspomnianych twierdze´

n wynika, ˙ze zachodzi r´owno´s´c

Dϕ

−1

+

(y)h =

−2y·h

(kyk

2

+1)

2

(2y, kyk

2

− 1) +

1

kyk

2

+1

(2h, 2y · h) =

2h

kyk

2

+1

+ y

−4y·h

(kyk

2

+1)

2

,

4y·h

(kyk

2

+1)

2

.

Je˙zeli Dϕ

−1

+

(y)h = 0 , to y · h = 0 (bo ostatnia wsp´o lrze

,

dna jest zerowa). Poprzednie te˙z sa

,

r´owne 0 , wie

,

c

2h

kyk

2

+1

= 0 , czyli h = 0 . Oznacza to , ˙ze ja

,

dro Dϕ

−1

+

(y) jest zerowe.

Analogicznie definiujemy ϕ

−

(x) =

x

1

1+x

k+1

,

x

2

1+x

k+1

, . . . ,

x

k

1+x

k+1

. Otrzymujemy wie

,

c r´owno´s´c

ϕ

−1

−

(y) =

2y

1

1+kyk

2

,

2y

2

1+kyk

2

, . . . ,

2y

k

1+kyk

2

,

1−kyk

2

1+kyk

2

=

1

1+kyk

2

(2y, 1 − kyk

2

) i powtarzaja

,

c poprzednie

rozumowanie wykazujemy, ˙ze Dϕ

−1

−

(y) jest r´o˙znowarto´sciowym przekszta lceniem liniowym z IR

k

do IR

k+1

. Wskazali´smy wie

,

c dwuelementowy atlas.

Zadanko trywialne

Czy istnieje atlas jednoelementowy na S

k

?

Zadanko prawie rozwia

,

zane 16 marca oko lo 13:02

Wykaza´c, ˙ze przekszta lcenia Dϕ

−1

+

(y) i Dϕ

−1

−

(y) sa

,

podobie´

nstwami. Dla jakich y ∈ IR

k

prze-

kszta lcenia D(ϕ

+

i

)

−1

(y) oraz D(ϕ

−

i

)

−1

(y) sa

,

podobie´

nstwami?

Twierdzenie charakteryzuja

,

ce mapy

Niech M ⊆ IR

k

. Naste

,

puja

,

ce warunki sa

,

r´ownowa˙zne

a. Punkt p ∈ M ma otoczenie otwarte U ⊆ IR

k

takie, ˙ze istnieje homeomorfizm

ϕ: U ∩ M

na

−−→ V ⊆ IR

m

taki, ˙ze V jest otwartym podzbiorem IR

m

taki, ˙ze ϕ

−1

: V

na

−−→ U ∩ M

jest klasy C

r

, r ≥ 1 i dla ka˙zdego y ∈ V r´o˙zniczka Dϕ

−1

(y): IR

m

−→ IR

k

jest w lo˙zeniem;

b. punkt p ma otoczenie otwarte U ⊆ IR

k

takie, ˙ze zbi´or U ∩ M jest wykresem funkcji m

♣

to przekszta lcenie nazywane jest rzutem stereograficznym z punktu e

k+1

.

140

zmiennych, tzn. istnieja

,

numery i

1

, i

2

, . . . , i

m

∈ {1, 2, . . . , k} oraz funkcje f

j

1

: e

U −→ IR ,

f

j

2

: e

U −→ IR , . . . , f

j

k−m

: e

U −→ IR , j

1

, j

1

, . . . , j

k−m

to numery r´o˙zne od i

1

, i

2

, . . . , i

m

wypi-

sane wg. wzrostu, e

U jest pewnym otwartym otoczeniem punktu (p

i

1

, p

i

2

, . . . , p

i

m

) ∈ IR

m

takie,

˙ze x ∈ U ∩ M wtedy i tylko wtedy, gdy x

j

s

= f

j

s

(x

i

1

, x

i

2

, . . . , x

i

m

) , dla s = 1, 2, . . . , k − m ;

c. Istnieje otoczenie otwarte U punktu p i funkcja F : U −→ IR

k−m

taka, ˙ze 0 jest jej warto´scia

,

regularna

,

i U ∩ M = F

−1

(0) .

Dow´

od. Zaczniemy od wykazania, ˙ze z warunku a wynika warunek b. Niech ϕ oznacza mape

,

okre´slona

,

w otoczeniu punktu p i niech ψ = (ϕ

|U ∩M

)

−1

: V −→ IR

k

oznacza lokalna

,

parametryzacje

,

otoczenia punktu p . Przekszta lcenie liniowe Dψ(y) jest w lo˙zeniem (monomorfizmem) dla ka˙zdego

y ∈ V . W szczeg´olno´sci dla y = ϕ(p) := q . Macierz tego przekszta lcenia ma k wierszy i m

kolumn. Poniewa˙z jest ono w lo˙zeniem, wie

,

c pewien minor wymiaru m × m jest r´o˙zny od 0 . Niech

i

1

, i

2

, . . . , i

m

be

,

da

,

numerami wierszy macierzy Dψ(q) wybranymi tak, ˙ze det

∂ψ

ir

∂y

s

1≤r,s≤m

6= 0 .

Zdefiniujmy odwzorowanie e

ψ = (ψ

i

1

, ψ

i

2

, . . . , ψ

i

m

) . Przekszta lcenie liniowe D e

ψ(q) jest izomorfiz-

mem. Z twierdzenia o odwracaniu funkcji wynika, ˙ze po przekszta lcenie e

ψ obcie

,

te do dostatecznie

ma lego otoczenia e

V ⊆ V punktu q jest dyfeomorfizmem. Rozwa˙zmy przekszta lcenie ψ ◦ e

ψ

−1

.

Z definicji wynika od razu, ˙ze dla ka˙zdego r ∈ {1, 2, . . . , m} zachodzi r´owno´s´c ψ

i

r

e

ψ

−1

(y)

= y

r

.

Definiujemy numery j

1

, j

2

, . . . , j

k−m

tak jak w sformu lowaniu twierdzenia, tzn. sa

,

to elementy zbioru

{1, 2, . . . , k}\{i

1

, i

2

, . . . , i

m

} wypisane w rosna

,

cym porza

,

dku i przyjmujemy f

j

s

= ψ

j

s

◦ e

ψ

−1

. Funkcje

te sa

,

okre´slone na zbiorze e

ψ( e

V ) , kt´ory jest otwarty jako dyfeomorficzny obraz zbioru otwartego.

Zbi´or ψ( e

V ) jest otwartym podzbiorem przestrzeni metrycznej M , bo ψ jest homeomorfizmem a

e

V otwartym podzbiorem dziedziny ψ , jest wie

,

c postaci e

U ∩ M dla pewnego zbioru e

U otwartego

w IR

k

. Wykazali´smy wie

,

c, ˙ze z warunku a wynika warunek b.

Z warunku b warunek a wynika natychmiast: przyjmujemy, ˙ze wsp´o lrze

,

dnymi parametryza-

cji ϕ o numerach i

1

, i

2

, . . . , i

m

sa

,

x

i

1

, x

i

2

, . . . , x

i

m

, a pozosta lymi liczby f

j

1

(x

i

1

, x

i

2

, . . . , x

i

m

) ,

f

j

2

(x

i

1

, x

i

2

, . . . , x

i

m

) ,. . . , f

j

k−m

(x

i

1

, x

i

2

, . . . , x

i

m

) .

Z warunku b warunek c wynika bez problemu: przyjmujemy F

s

(x) = x

j

s

−f

j

s

(x

i

1

, x

i

2

, . . . , x

i

m

) .

Jasne jest, ˙ze tak zdefiniowane odwzorowanie F spe lnia na lo˙zone warunki, np. rza

,

d jego r´o˙zniczka

przekszta lca IR

k

na IR

m

. Wynikanie w druga

,

strone

,

to bezpo´srednia konsekwencja twierdzenia o

funkcji uwik lanej.

Wniosek

Je´sli M ⊆ IR

k

jest m –wymiarowa

,

rozmaito´scia

,

i p ∈ M , to T

p

M jest m –wymiarowa

,

podprze-

strzenia

,

liniowa

,

przestrzeni IR

k

. Je´sli ϕ jest mapa

,

okre´slona

,

w otoczeniu punktu p i q = ϕ(p) ,

to T

p

M = D(ϕ

−1

)(q)(IR

m

) . Je´sli U jest otoczeniem punktu p , F : U −→ IR

k−m

odwzorowaniem

klasy C

r

, r ≥ 1 , 0 jest warto´scia

,

regularna

,

F i U ∩ M = F

−1

(0) , to T

p

M = KerDF (p) .

Ten wniosek wynika natychmiast z twierdze´

n o wektorach stycznych, kt´ore wykazali´smy w listo-

141

padzie. (zob. str. ≈ 64 tego tekstu)

Przyk lad 2. (torus dwuwymiarowy)

Niech ψ

α
β

=





cos β

− sin β

0

sin β

cos β

0

0

0

1









2+cos α

0

sin α



 =





(2+cos α) cos β

(2+cos α) sin β

sin α



. Wida´c wie

,

c, ˙ze zbi´or punkt´ow

postaci ψ

α

0

jest okre

,

giem o ´srodku

2

0
0

i promieniu 1 le˙za

,

cym w p laszczy´znie y = 0 ( x, y, z

to wsp´o lrze

,

dne w IR

3

). Ten okra

,

g obracamy o ka

,

t β wok´o l osi z . Wyka˙zemy, ˙ze otrzymany zbi´or

(zwany torusem) jest dwuwymiarowa

,

rozmaito´scia

,

w IR

3

. Poka˙zemy to pokazuja

,

c, ˙ze przez ogra-

niczenie ψ do zbioru otwartego zawartego w pewnym kwadracie otwartym o boku 2π otrzymu-

jemy lokalna

,

parametryzacje

,

. Jest jasne, ˙ze zmieniaja

,

c kwadraty otrzymamy lokalne parametry-

zacje, kt´orych obrazy pokrywaja

,

torus. Niech Q oznacza kwadrat otwarty o boku 2π . ψ

|Q

jest

r´o˙znowarto´sciowe i cia

,

g le. Je´sli U ⊆ Q jest zbiorem otwartym, to jego obraz ψ(U ) r´owny jest

ψ(IR

2

) \ ψ(Q \ U ) , jest wie

,

c r´o˙znica

,

ψ(IR

2

) i zbioru zwartego, a sta

,

d wynika, ˙ze jest otwartym pod-

zbiorem przestrzeni metrycznej ψ(IR

2

) . Wykazali´smy wie

,

c, ˙ze ψ

|Q

przekszta lca zbiory otwarte na

otwarte podzbiory ψ(IR

2

) , jest wie

,

c homeomorfizmem przekszta lcaja

,

cym zbi´or Q na zbi´or ψ(U ) .

Trzeba jeszcze zbada´c r´o˙zniczke

,

przekszta lcenia Dψ(y) dla y ∈ IR

2

. Mamy

Dψ

α
β

=





− sin α cos β

−(2+cos α) sin β

− sin α sin β

(2+cos α) cos β

cos α

0





Bez najmniejszego k lopotu stwierdzamy, ˙ze kolumny tej macierzy sa

,

wektorami prostopad lymi —

nie jest to dziwne, bo pierwsza z nich jest wektorem stycznym do „po ludnika”, a druga — do

„r´ownole˙znika”. D lugo´s´c pierwszej kolumny r´owna jest 1 , a drugiej — 2 + cos α . Dwa prostopad le,

niezerowe wektory sa

,

liniowo niezale˙zne, wie

,

c rza

,

d przekszta lcenia Dψ

α
β

: IR

2

−→ IR

3

jest r´owny 2 ,

jest wie

,

c ono r´o˙znowarto´sciowe. W ten spos´ob pokazali´smy, ˙ze w otoczeniu dowolnego punktu torusa

mo˙zna okre´sli´c mape

,

( (ψ

|Q

)

−1

), wie

,

c wykazali´smy, ˙ze jest on dwuwymiarowa

,

rozmaito´scia

,

zanurzona

,

w IR

3

.

W dw´och naste

,

pnych przyk ladach przydatne be

,

dzie przekszta lcenie, kt´orym sie

,

teraz przez

chwile

,

zajmiemy. Niech F (x, y, z) = (xy, yz, zx, x

2

− y

2

) dla dowolnych liczb x, y, z ∈ IR .

Je´sli F (x, y, z) = F (u, v, w) , to x

2

− y

2

= u

2

− v

2

oraz (x

2

+ y

2

)

2

= (x

2

− y

2

)

2

+ 4(xy)

2

=

= (u

2

− v

2

)

2

+ 4(uv)

2

= (u

2

+ v

2

)

2

, zatem x

2

+ y

2

= u

2

+ v

2

i wobec tego x

2

= u

2

i y

2

= v

2

.

Je´sli x = y = 0 , to musi te˙z by´c u = v = 0 . Mamy F (0, 0, z) = (0, 0, 0, 0) . Za l´o˙zmy teraz, ˙ze

przynajmniej jedna z liczb x, y jest r´o˙zna od 0 , np. x 6= 0 . Poniewa˙z x

2

= u

2

, wie

,

c r´ownie˙z u 6= 0 ,

dok ladniej u = x albo u = −x . W pierwszym przypadku z r´owno´sci xy = uv i xz = uw wynikaja

,

r´owno´sci y = v i z = w . W drugim analogiczne rozumowanie prowadzi do wniosku, ˙ze y = −v i

z = −w . Wykazali´smy wie

,

c, ˙ze je´sli (x, y) 6= (0, 0) , to

F (x, y, z) = F (u, v, w) ⇔ (x, y, z) = (u, v, w) lub (x, y, z) = −(u, v, w) .

142

Zajmiemy sie

,

teraz r´o˙zniczka

,

przekszta lcenia F . Mamy DF (x, y, z) =







y

x

0

0

z

y

z

0

x

2x

−2y

0





. Wida´c od

razu, ˙ze rza

,

d DF (0, 0, 0) = 0 . Je´sli x = y = 0 6= z , to rza

,

d DF (0, 0, z) jest r´owny 2 , ja

,

drem

przekszta lcenia DF (0, 0, z) jest w tym przypadku o´s z . Je´sli (x, y) 6= (0, 0) , to rza

,

d przekszta lcenia

DF (x, y, z) jest r´owny 3 .

Przyk lad 3. p laszczyzna rzutowa

Niech M = F (S

2

) , przypominamy S

2

⊆ IR

3

to sfera o ´srodku w punkcie 0 i promieniu 1 .

Wyka˙zemy, ˙ze M jest rozmaito´scia

,

dwuwymiarowa

,

.

J Zanim to zrobimy, opiszemy ten zbi´or nieco dok ladniej. Przekszta lcenie F nie jest r´o˙znowar-

to´sciowym przekszta lceniem sfery: odwzorowuje w jeden punkt dowolne dwa punkty antypodyczne.

Pare

,

punkt´ow antypodycznych mo˙zemy uto˙zsami´c z prosta

,

przechodza

,

ca

,

przez punkt 0 . Mo˙zna

wie

,

c uwa˙za´c, ˙ze F przekszta lca proste przechodza

,

ce przez pocza

,

tek uk ladu wsp´o lrze

,

dnych w punkty

przestrzeni czterowymiarowej, przy czym na zbiorze tych prostych F jest r´o˙znowarto´sciowe (je´sli

p, q ∈ S

2

i F (p) = F (q) , to p = ±q ). Jest ono te˙z cia

,

g le w naste

,

puja

,

cym znaczeniu: proste

tworza

,

ce ka

,

t bliski 0 przechodza

,

na punkty le˙za

,

ce w niedu˙zej odleg lo´sci. Mo˙zna wie

,

c uzna´c, ˙ze

dzie

,

ki przekszta lceniu F nadajemy zbiorowi prostych przechodza

,

cych przez punkt 0 strukture

,

roz-

maito´sci dwuwymiarowej. Zbi´or prostych przechodza

,

cych przez punkt 0 stanowi model p laszczyzny

rzutowej: chodzi o to, by doda´c do p laszczyzny „punkty w niesko´

nczono´sci” tak, by w nich prze-

cina ly sie

,

proste r´ownoleg le. Mo˙zna to uczyni´c np. w spos´ob, kt´ory opiszemy za chwile

,

. Za l´o˙zmy,

˙ze „naszym ´swiatem” jest p laszczyzna z = 1 . Przez ka˙zdy punkt tej p laszczyzny prowadzimy pro-

sta

,

przechodza

,

ca

,

r´ownie˙z przez 0 . Punktami „nowej” p laszczyzny, tzw. p laszczyzny rzutowej, be

,

da

,

w la´snie te proste. Je´sli jakie´s punkty le˙za

,

na jednej proste zawartej w p laszczy´znie z = 1 , to od-

powiadaja

,

ce im proste le˙za

,

w jednej p laszczy´znie zawieraja

,

cej punkt 0 . Jasne jest, ˙ze pomine

,

li´smy

z niewiadomych przyczyn proste r´ownoleg le do p laszczyzny z = 1 przechodza

,

ce przez punkt 0 .

No to je dodajemy. P laszczyzny przechodza

,

ce przez punkt 0 odpowiadaja

,

prostym na p laszczy´znie

z = 1 , p laszczyzna r´ownoleg la do p laszczyzny z = 1 to tzw. „prosta niew la´sciwa” lub „prosta w nie-

sko´

nczono´sci”. Teraz ka˙zde dwie „proste” przecinaja

,

sie

,

w dok ladnie jednym „punkcie”, tzn. ka˙zde

dwie p laszczyzny przechodza

,

ce przez punkt 0 maja

,

wsp´olna

,

prosta

,

przechodza

,

ca

,

przez 0 . Je´sli te

dwie p laszczyzny odpowiadaja

,

prostym r´ownoleg lym na p laszczy´znie z = 1 (czyli zawieraja

,

je), to

prosta wzd lu˙z, kt´orej sie

,

przecinaja

,

jest r´ownoleg la do p laszczyzny z = 1 , czyli jest „punktem w

niesko´

nczono´sci”. Tak okre´slona p laszczyzna rzutowa jest interesuja

,

cym obiektem geometrycznym,

rozpatrywane sa

,

r´ownie˙z przestrzenie rzutowe wy˙zszych wymiar´ow. Zacze

,

to ich u˙zywa´c w zwia

,

zku z

badaniem r´o˙znych rzut´ow, nie tylko prostopad lych, nie tylko r´ownoleg lych, r´ownie˙z ´srodkowych. Ten

obiekt okaza l sie

,

przydatny w matematyce, nie tylko w geometrii rzutowej, ale to za d luga opowie´s´c

na analize

,

druga

,

. I

143

Wr´o´cmy do dowodu tego, ˙ze M jest rozmaito´scia

,

. Niech ψ: V −→ S

2

be

,

dzie parametryzacja

,

zbioru U otwartego w przestrzeni metrycznej S

2

. Za l´o˙zmy jeszcze, ˙ze zbi´or U = ψ(V ) jest zawarty

w pewnej p´o lsferze otwartej Σ . Wtedy przekszta lcenie F jest r´o˙znowarto´sciowe na Σ ⊃ U . Wo-

bec tego przekszta lcenie F ◦ ψ jest kandydatem na parametryzacje

,

pewnego podzbioru przestrzeni

M . Oczywi´scie M = F (Σ) . Jest te˙z jasne, ˙ze zbiory F (U ) i F (Σ \ U ) sa

,

roz la

,

czne. Ten drugi

jest zwarty jako obraz cia

,

g ly zbioru zwartego, wie

,

c ten pierwszy F (U ) jest otwartym podzbiorem

przestrzeni metrycznej F Σ

= M . Wykazali´smy w la´snie, ˙ze F przekszta lca otwarte podzbiory

Σ na otwarte podzbiory M . Sta

,

d wynika, ˙ze F ◦ ψ przekszta lca otwarte podzbiory zbioru V na

otwarte podzbiory przestrzeni metrycznej M , a poniewa˙z jest przekszta lceniem r´o˙znowarto´sciowym

i cia

,

g lym, wie

,

c jest homeomorfizmem. Dψ(q) jest r´o˙znowarto´sciowe dla ka˙zdego q ∈ V , bo ψ jest

parametryzacja

,

. Zbi´or Dψ(q)(IR

2

) jest przestrzenia

,

styczna

,

do sfery S

2

w punkcie p = ψ(q) . Na

T

p

S

2

przekszta lcenie DF (p) jest r´o˙znowarto´sciowe: jest to oczywiste je´sli p 6= (0, 0, ±1) ; w tych

dw´och punktach te˙z tak jest, bo w nich przestrze´

n styczna jest pozioma, wie

,

c jedynym punktem

ja

,

dra DF (p) w niej le˙za

,

cym jest punkt 0 . Poniewa˙z otwartymi p´o lsferami mo˙zna pokry´c ca la

,

sfere

,

(wystarczy ich 6 ), wie

,

c wskazali´smy mape

,

w otoczeniu dowolnego punktu x ∈ M i zako´

nczyli´smy

dow´od.

Na zako´

nczenie rozwa˙zmy jeszcze obraz F (A) zbioru A =

(x, y, z) ∈ S

2

:

y ≥ 0, |z| ≤

1
2

.

Jasne jest, ˙ze jedyne pary punkt´ow antypodycznych w zbiorze A le˙za

,

w p laszczy´znie y = 0 .

Sa

,

to pary punkt´ow postaci (

√

1 − z

2

, 0, z) i (−

√

1 − z

2

, 0, z) . Mo˙zna wyobrazi´c sobie, ˙ze A to

po lowa pasa mie

,

dzy zwrotnikami. Przekszta lcenie F „skleja” cze

,

´sci „po ludnik´ow” ograniczaja

,

ce

ten p´o lpas ze zmiana

,

orientacji, np. punkt

√

3

2

, 0,

1
2

jest sklejany z punktem

−

√

3

2

, 0, −

1
2

, a

punkt

√

3

2

, 0, −

1
2

— z punktem

−

√

3

2

, 0,

1
2

. Zbi´or powsta ly przez takie sklejenie nazywany

jest wste

,

ga

,

M¨obiusa. Wykazali´smy, ˙ze p laszczyzna rzutowa zawiera wste

,

ge

,

M¨obiusa. Aby uzy-

ska´c reszte

,

p laszczyzny rzutowej nale˙zy do otrzymanej wste

,

gi M¨obiusa do la

,

czy´c zbi´or F (B) , gdzie

B = {(x, y, z) ∈ S

2

:

z >

1
2

} . Mo˙zna wie

,

c uzna´c, ˙ze p laszczyzne

,

rzutowa

,

otrzymujemy sklejaja

,

c

brzegami wste

,

ge

,

M¨obiusa ( F (A) ) z „ko lem” ( F (B) ). Topologowie m´owia

,

czasem, ˙ze p laszczyzna

rzutowa, to sfera z dziura

,

( F (B) ), kt´ora

,

to dziure

,

zaklejono wste

,

ga

,

M¨obiusa ( F (A) ).

Przyk lad 4. (butelka Kleina)

Niech T

2

oznacza dwuwymiarowy torus opisany wcze´sniej. Niech K = F (T

2

) . Wyka˙zemy, ˙ze zbi´or

K jest rozmaito´scia

,

. Jest ona nazywana butelka

,

Kleina.

Niech ψ oznacza przekszta lcenie rozwa˙zane w przyk ladzie 2, w kt´orym opisali´smy torus. Niech

Φ = F ◦ ψ . R niech oznacza kwadrat otwarty o boku π . Zbi´or ψ(R) nie zawiera ani jednej

pary punkt´ow antypodycznych, zatem przekszta lcenie F jest na nim r´o˙znowarto´sciowe, zatem Φ

jest r´o˙znowarto´sciowe na R . R´o˙zniczka DF (p) jest r´o˙znowarto´sciowa w ka˙zdym punkcie torusa

T

2

, bo nie zawiera on ani jednego punktu osi z . Sta

,

d wynika, ˙ze przekszta lcenie Φ = F ◦ ψ jest

r´o˙znowarto´sciowe, jest klasy C

∞

. Wyka˙zemy, ˙ze jest ono homeomorfizmem. Je´sli Q ⊇ R jest jakim-

144

kolwiek kwadratem o boku 2π a U ⊆ R dowolnym zbiorem otwartym, to zbiory Φ(U ) i Φ Q \ U

sa

,

roz la

,

czne, ich suma

,

jest K , drugi z nich jest zwarty jako cia

,

g ly obraz zbioru zwartego. Wynika

sta

,

d, ˙ze zbi´or Φ(U ) jest otwarty w K . Wynika sta

,

d, ˙ze przekszta lcenie Φ jest homeomorfizmem

zbioru R na zbi´or Φ(R) . Jasne jest, ˙ze dobieraja

,

c R do punktu p ∈ K mo˙zemy sparametryzowa´c

otoczenie danego punktu p . Wykazali´smy wie

,

c, ˙ze K jest dwuwymiarowa

,

rozmaito´scia

,

zanurzona

,

w IR

4

.

Podobnie jak w przypadku p laszczyzny rzutowej spr´obujemy co´s powiedzie´c o sposobie patrzenia

na butelke

,

Kleina.

Niech A =

(α, β):

π

2

≤ α ≤

3π

2

, 0 ≤ β ≤ π

,

B =

(α, β):

−

π

2

≤ α ≤

π

2

, 0 ≤ β ≤ π

.

Latwo mo˙zna zauwa˙zy´c, ˙ze Φ(A)

∪ Φ(B) = K , ˙ze zbi´or ψ(A) ∩ ψ(B) jest suma

,

dw´och roz la

,

cznych

p´o lokre

,

g´ow o ko´

ncach ψ

π

2

, 0

= (2, 0, 1) , ψ

π

2

, π

= (−2, 0, 1) i ψ

3π

2

, 0

= (2, 0, −1) , ψ

3π

2

, π

=

(−2, 0, −1) . Widoczne jest te˙z, ˙ze zbi´or Φ(A) = F (ψ(A)) jest wste

,

ga

,

M¨obiusa. To samo dotyczy

zbioru Φ(B) . Te dwie wste

,

gi M¨obiusa sa

,

„sklejone” brzegami.

Mo˙zna te˙z spojrze´c na to troche

,

inaczej. „Sklejamy” brzegi p´o ltorusa (dwa okre

,

gi) ze zmiana

,

orientacji i w wyniku tego otrzymujemy butelke

,

Kleina.

Mo˙zna jeszcze inaczej. Zdefiniujemy nowy zbi´or:

C = {(α, β):

|α −

π

2

| <

π

6

, 0 ≤ β ≤ π} ∪ {(α, β):

|α −

3π

2

| <

π

6

, 0 ≤ β ≤ π} .

Niech C

B

= {(α, β):

0 ≤ α ≤

π

3

, 0 ≤ β ≤ π} ∪ {(α, β):

5π

3

≤ α ≤ 2π, 0 ≤ β ≤ π} oraz

C

A

= {(α, β):

|α − π| <

π

3

, 0 ≤ β ≤ π} . Bez specjalnych trudno´sci mo˙zna stwierdzi´c, ˙ze Φ(C

A

)

jest wste

,

ga

,

M¨obiusa, troche

,

„we

,

˙zsza

,

” ni˙z Φ(A) . To samo jest prawda

,

w przypadku Φ(C

B

) . Zaj-

miemy sie

,

teraz zbiorem Φ(C) . Zdefiniujemy przekszta lcenie h : Φ(C) −→ IR

2

w naste

,

puja

,

cy

spos´ob:*

h Φ(α, β)

= h

(2 + cos α)

(2 + cos α) sin β cos β, sin α sin β, sin α cos β, (2 + cos α) cos 2β

=

=

(2 + cos α) cos β, (2 + cos α) sin β

,

gdy |α −

π

2

| <

π

6

, 0 ≤ β ≤ π;

(2 + cos(2π − α)) cos(β + π), (2 + cos(2π − α)) sin(β + π)

, gdy |α −

3π

2

| <

π

6

, 0 ≤ β ≤ π.

Pozostawiamy czytelnikom sprawdzenie, ˙ze h jest cia

,

g le i r´o˙znowarto´sciowe. Poniewa˙z interesuja

,

cy

nas zbi´or Φ(C) jest zwarty, wie

,

c h jest homeomorfizmem (na obraz). Wynika sta

,

d, ˙ze zbi´or Φ(C)

jest homeomorficzny ze pier´scieniem ko lowym, czyli ze sfera

,

z dwiema dziurami (ko lowymi). Wystar-

czy ka˙zda

,

z tych dwu dziur zaklei´c wste

,

ga

,

M¨obiusa, by otrzyma´c butelke

,

Kleina, kt´ora z pewnych

przyczyn nie nadaje sie

,

do noszenia piwa ani nawet mleka. Z jakich?

Te przyk lady dadza

,

jakie´s poje

,

cie o rozmaito´sciach.

*

Φ(α,β)= (2+cos α)

2

sin β cos β,(2+cos α) sin α sin β,(2+cos α) sin α cos β,(2+cos α)

2

cos 2β

=(2+cos α)(...)

145