WOJSKOWA AKADEMIA TECHNICZNA

LABORATORIUM

CYFROWEGO PRZETWARZANIA SYGNAŁÓW

SPRAWOZDANIE Z PRACY LABORATORYJNEJ NR 3

TEMAT:

Analiza widmowa sygnałów okresowych dyskretnych.
Dyskretna transformata Fouriera sygnału dźwiękowego.

PROWADZĄCY:

dr inż. Leszek Grad

WYKONUJĄCY:

Joanna Rutkowska

GRUPA:

I9G2S1

Ćwiczenie obejmuje: wykonanie zadanej operacji typu filtracyjnego na widmie sygnału dźwiękowego (LP, HP); zmianę
częstotliwości próbkowania sygnału dźwiękowego z wykorzystaniem DFT. Podzielone zostało na poszczególne zadania.
Wszystkie zadania do realizacji w formie skryptów w Matlabie.

Początkowy kod programu przedstawia się następująco:

[signal,fs] = wavread(

'dzwiek.wav'

);

sound(signal,fs);

% odtworzenie sygnału dźwiękowego

L = length(signal);

% długość sygnału

t = L / fs;
skala_t = 1/fs:1/fs:L/fs;

% miara czasowa sygnału

skala_f = fs/L:fs/L:fs;

% miara częstotliwościowa sygnału

fftowa = fft(signal);

% transformata fft na sygnale

%% WYKRESY SYGNAŁU I WIDMA

figure(1);
subplot(2,1,1);
plot(skala_t, signal);
title(

'Przebieg sygnału'

);

xlabel(

'Czas [s]'

);

ylabel(

'Amplituda'

);

axis

tight

;

subplot(2,1,2);

plot(skala_f,abs(fftowa)

,

'red'

);

% transformata przedstawiona kolorem czerwonym

title(

'Transformata fft sygnału'

);

xlabel(

'Częstotliwość [Hz]'

);

ylabel(

'Amplituda'

);

axis

tight

;

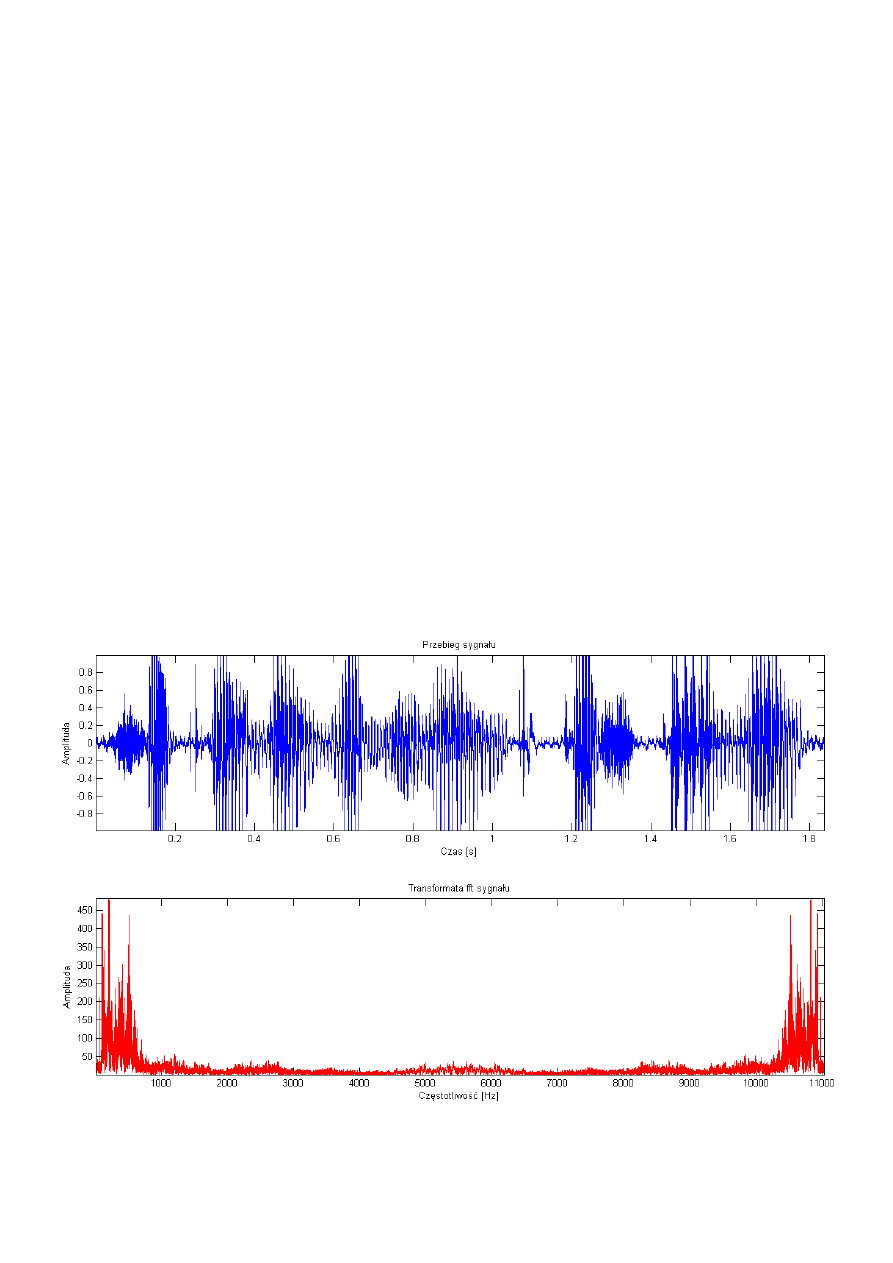
Podstawowy sygnał został przedstawiony na następujących wykresach:

Figura 1

Zadanie 1:

Wykonać operację na widmie sygnału dźwiękowego polegającą na usunięciu (wyzerowaniu) z niego
harmonicznych odpowiadających przedziałowi częstotliwości <fc,fs-fc> (filtr dolnoprzepustowy). Następnie
wykonać transformatę odwrotną, odsłuchać dźwięk, porównać z oryginałem również wyświetlając przebieg
czasowy oryginału i sygnału przetworzonego.

Kod programu realizujący zadanie 1 przedstawia się następująco:

%% FILTRACJA FILTREM DOLNOPRZEPUSTOWYM

fc = 1200/fs;

%przypisanie wartości fc(dla potrzeb zadania przyjmujemy ją sami)

LP_fft = fftowa;

%przypisanie fft na potrzeby filtru

LP_fft( floor( fc * L ) + 2 : ceil( L * ( 1 - fc ) ) ) = 0;

% wyzerowanie

harmonicznych sygnału z przedziału <fc,fs-fc>

LP_normal = ifft(LP_fft);

%transformata ifft w celu odzyskania sygnału czasowego

sound(LP_normal,fs);

%odtworzenie sygnału po filtracji filtrem dolnoprzepustowym

figure(2);
subplot(2,1,1);
plot(skala_t,LP_normal);
title({

'Przebieg czasowy sygnału'

;

'po wykonaniu filtracji dolnoprzepustowej'

});

xlabel(

'Czas [s]'

);

ylabel(

'Amplituda'

);

axis

tight

;

subplot(2,1,2);
plot(skala_f,abs(LP_fft),

'red'

);

%transformata przedstawiona kolorem czerwonym

title({

'Transformata sygnału'

;

'po wykonaniu filtracji dolnoprzepustowej'

});

xlabel(

'Częstotliwość [Hz]'

);

ylabel(

'Amplituda'

);

axis

tight

;

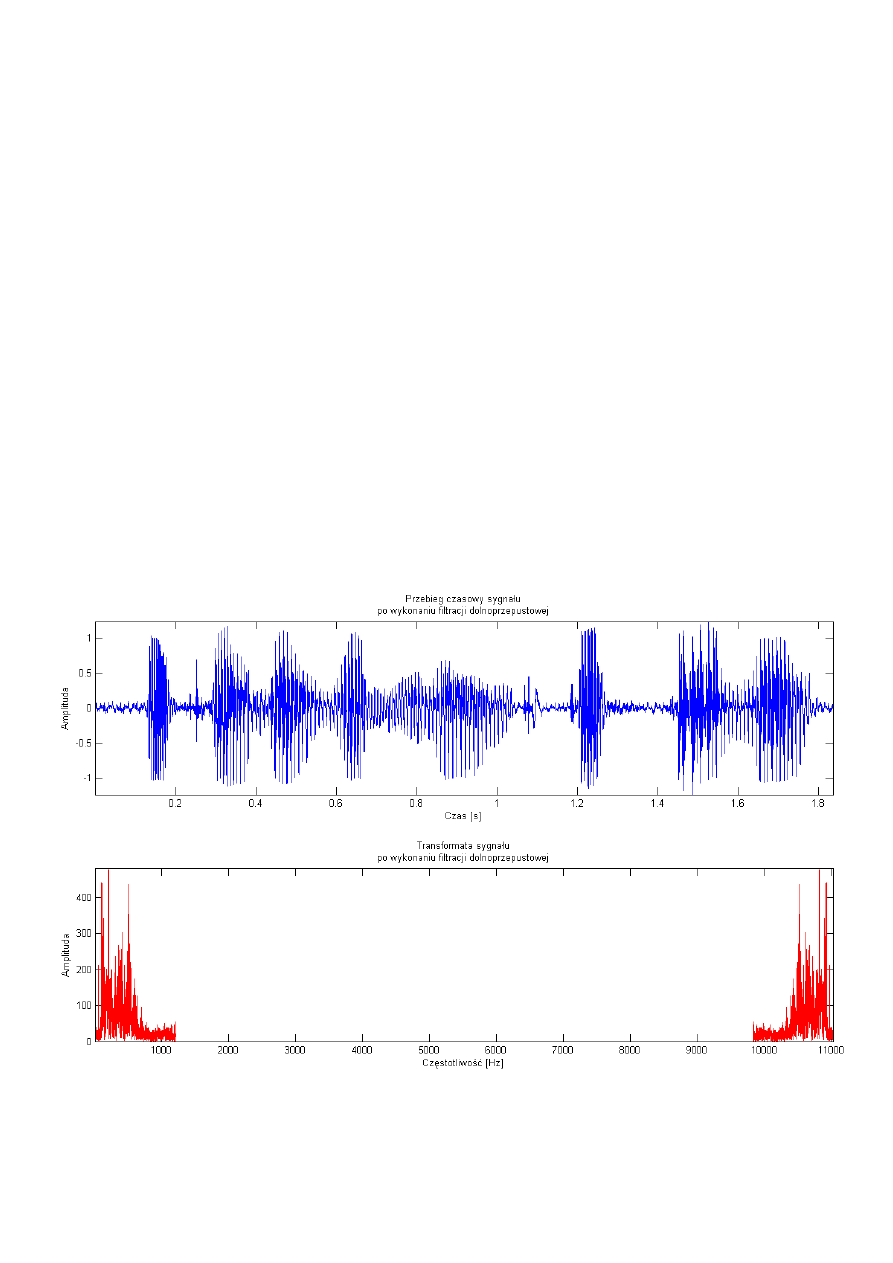
W ramach zadania otrzymano następujące wykresy:

Figura 2

Zadanie 2:

Powyższe czynności wykonać usuwając z widma elementy <0,fc> v <fs-fc,fs> (filtr górnoprzepustowy).
Porównać wyniki obydwu operacji.

Kod programu realizujący zadanie 2 przedstawia się następująco:

%% FILTRACJA FILTREM GÓRNOPRZEPUSTOWYM

fc2 = 1000/fs;

%przypisanie wartości fc2(dla potrzeb zadania przyjmujemy ją sami)

HP_fft = fftowa;

%przypisanie fft na potrzeby filtru

HP_fft( 2 : floor( fc2 * L ) + 2 ) = 0;

% wyzerowanie harmonicznych sygnału z przedziału <2,fc2>

HP_fft( ceil( L * ( 1 - fc2 ) ) : L ) = 0;

% wyzerowanie harmonicznych sygnału z przedziału

<fs-fc,fs>

HP_normal = ifft(HP_fft);

%transformata ifft w celu uzyskania sygnału czasowego

sound(HP_normal,fs);

%odtworzenie sygnału po filtracji filtrem górnoprzepustowym

figure(3);

subplot(2,1,1);

plot(skala_t,HP_normal);

title({

'Przebieg czasowy sygnału'

;

'po wykonaniu filtracji górnoprzepustowej'

});

xlabel(

'Czas [s]'

);

ylabel(

'Amplituda'

);

axis

tight

;

subplot(2,1,2);

plot(skala_f,abs(HP_fft),

'red'

);

%transformata przedstawiona kolorem czerwonym

title({

'Transformata sygnału'

;

'po wykonaniu filtracji górnoprzepustowej'

});

xlabel(

'Częstotliwość [Hz]'

);

ylabel(

'Amplituda'

);

axis

tight

;

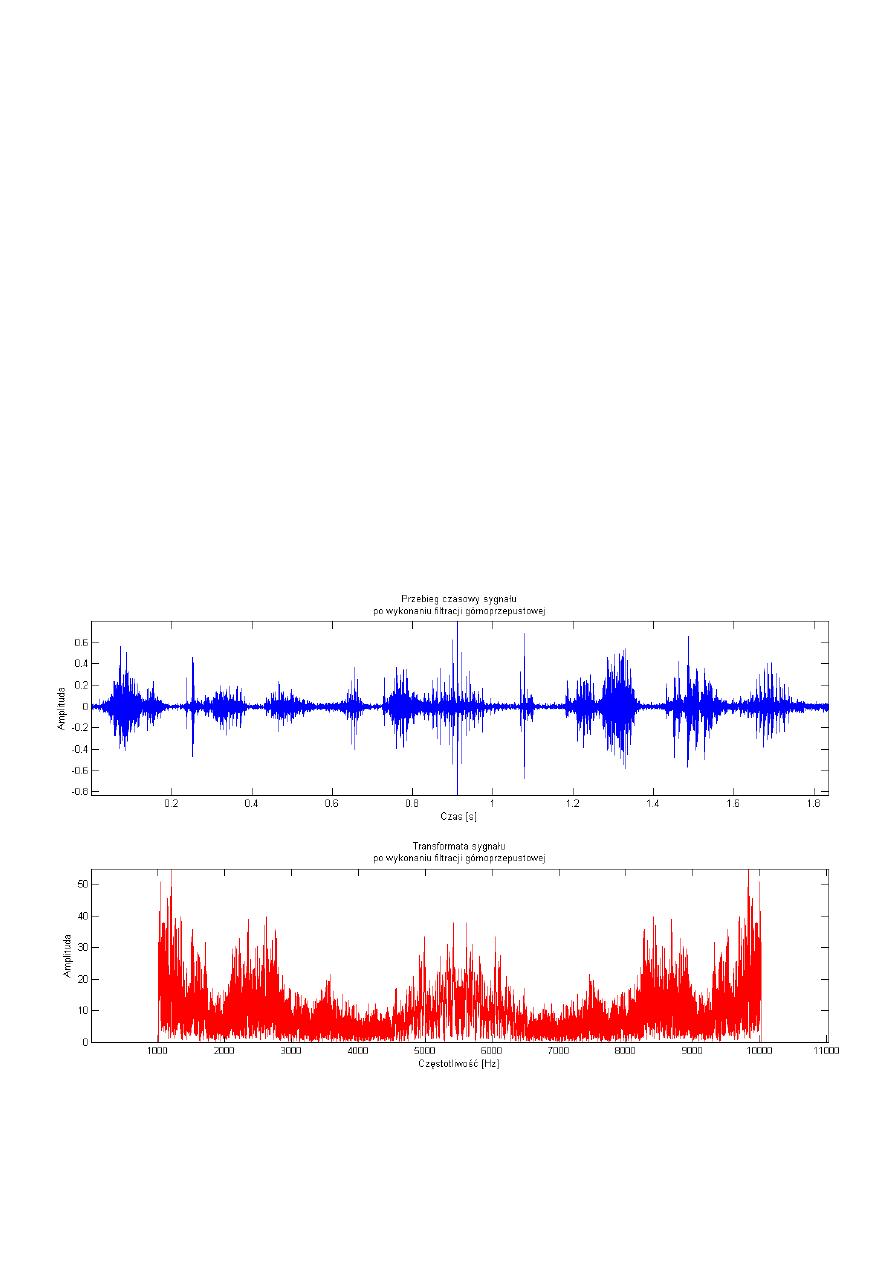
W ramach zadania otrzymano następujące wykresy:

Figura 3

Wnioski z wykonania zadania 1 i zadnia 2:

Zadanie polegało na wyzerowaniu próbek odpowiadających odpowiednim częstotliwościom podanym
z zadaniach. Dla zadania 1 zerowane były próbki odpowiadające wysokim częstotliwościom dźwięku, przez co
otrzymano ton dźwięku stał się niższy. Dla zadania 2 usunięte zostały tony niskie, zatem nowy dźwięk miał
ton wyższy w porównaniu z oryginalnym.
Pomimo modyfikacji, nowe dźwięki nadal były zrozumiałe i podobne brzmieniowe do oryginału.

Zadanie 3:

Korzystając z DFT zwiększyć częstotliwość próbkowania sygnału. W tym celu dokonać odsunięcia drugiej
połowy widma tak, aby ostatni prążek znalazł się na pozycji nowej częstotliwości próbkowania. Powstałą lukę
wypełnić zerami. Wykonać transformatę odwrotną. Zweryfikować otrzymane wyniki (np. poprzez
wyświetlenie sygnałów sprzed i po operacji różnymi kolorami symboli na jednym wykresie).

Kod programu realizujący zadanie 3 przedstawia się następująco:

%% ZWIĘKSZENIE CZĘSTOTLIWOŚCI PRÓBKOWANIA

more = floor(fs * 1.5);

% zwiększamy częstotliwość próbkowania sygnału(przyjęłam nową

częstotliwość równą 1.5fs)

x = floor( ( ( more / fs ) - 1 ) * L );

% określamy liczbę próbek zerowych

L2 = ( L + x );

%nowa liczność próbek

MORE_fft = zeros (1,L2);

% deklaracja nowej tablicy fft sygnału

MORE_fft( 1 : floor(L/2+ 1)) = fftowa( 1 : floor( L / 2 + 1) );

% przypisanie wartości dla

początkowych próbek w tablicy

MORE_fft( x + floor( L / 2 + 2 ) : x + L ) = fftowa( floor( L / 2 + 2 ) : L );

% przypisanie

wartości dla końcowych próbek w tablicy

MORE_normal = ifft(MORE_fft);

%transformata odwrotna

skala_t2 = 1/more : 1/more : L2/more;

% określenie nowej skali czasowej

skala_f2 = more/L2 : more/L2 : more;

% określenie nowej skali częstotliwościowej

sound(real(MORE_normal),more);

% odtworzenie nowego sygnału dźwiękowego

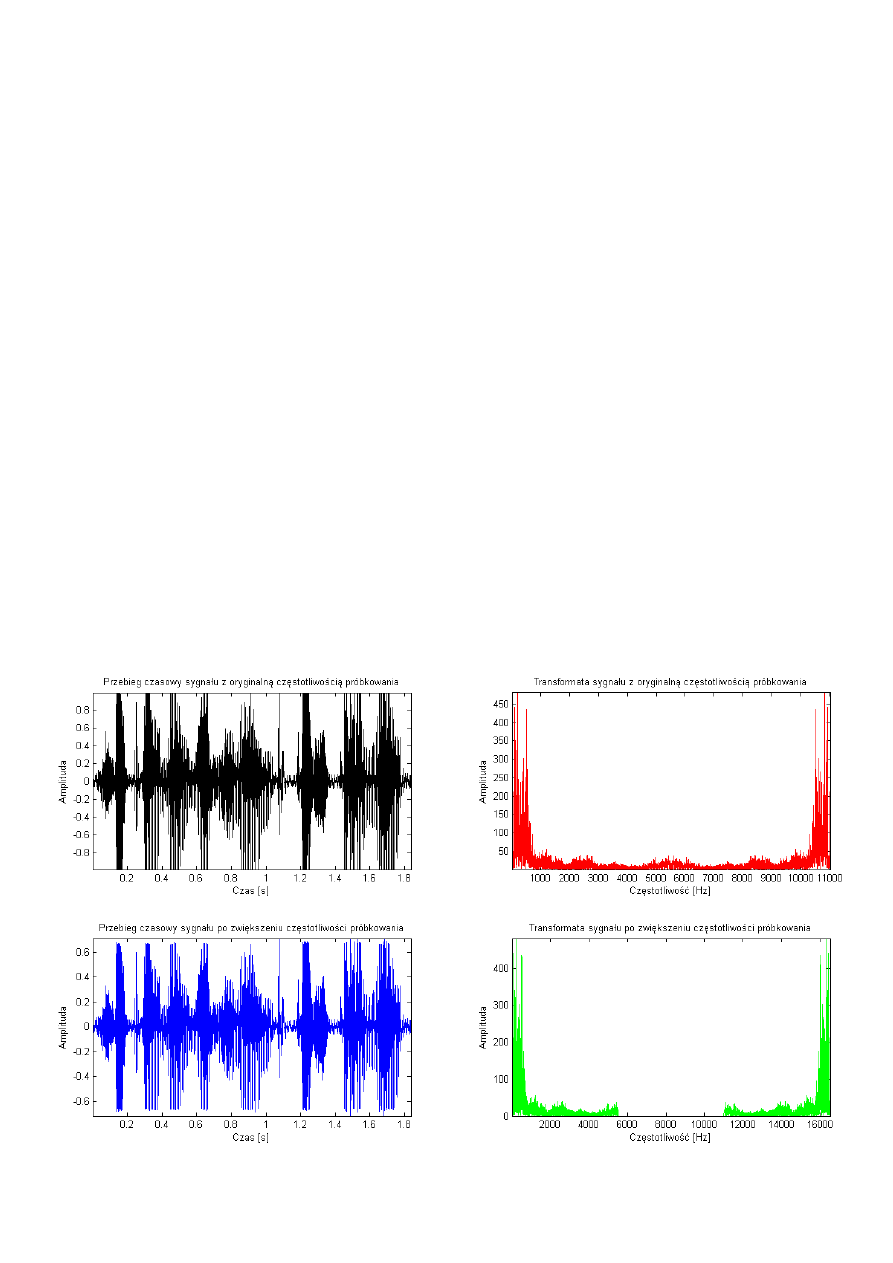
W ramach zadania otrzymano następujące wykresy:

Figura 4

Wnioski z wykonania zadania 3:

Zadanie polegało na zwiększeniu częstotliwości próbkowania sygnały dźwiękowego. Zadanie zostało
zrealizowane poprzez odsunięcie połowy próbek w widmie fft sygnały, a następnie wypełnienie luki zerami.
Zwiększona ilość próbek to większa częstotliwość próbkowania, a co za tym idzie jakość sygnału wzrosła,
przez co stał się ona bardziej zrozumiały dla odbiorcy w porównaniu z oryginalnym nagraniem.

Zadanie 4:

Korzystając z DFT zmniejszyć częstotliwość próbkowania sygnału postępując analogicznie jak wyżej.

Kod programu realizujący zadanie 4 przedstawia się następująco:

%% ZMNIEJSZENIE CZĘSTOTLIWOŚCI PRÓBKOWANIA

less = floor( fs * 0.5 );

% ustalamy nową częstotliwość próbkowania (przyjęłam 0.5fs)

a = floor( L * less / ( 2 * fs ) );

L3 = 2 * a + 1;

% ustalamy nową liczność próbek dla sygnału

LESS_fft = zeros( 1, L3 );

%deklaracja nowej tablicy dla transformaty fft sygnału

LESS_fft( 1 : floor( L3 / 2 + 1 ) ) = fftowa( 1 : floor( L3 / 2 + 1 ) );

%przepisanie

początkowych próbek do tablicy

LESS_fft( floor( L3 / 2 + 2 ) : L3 ) = fftowa( floor( L3 / 2 + 2 ) - L3 + L : L );

% przepisanie

końcowych próbek do tablicy

LESS_normal = ifft(LESS_fft);

% transformata odwrotna

skala_t3 = 1/less:1/less:L3/less;

% określenie nowej skali czasowej

skala_f3 = less/L3:less/L3:less;

% określenie nowej skali częstotliwościowej

sound(LESS_normal,less);

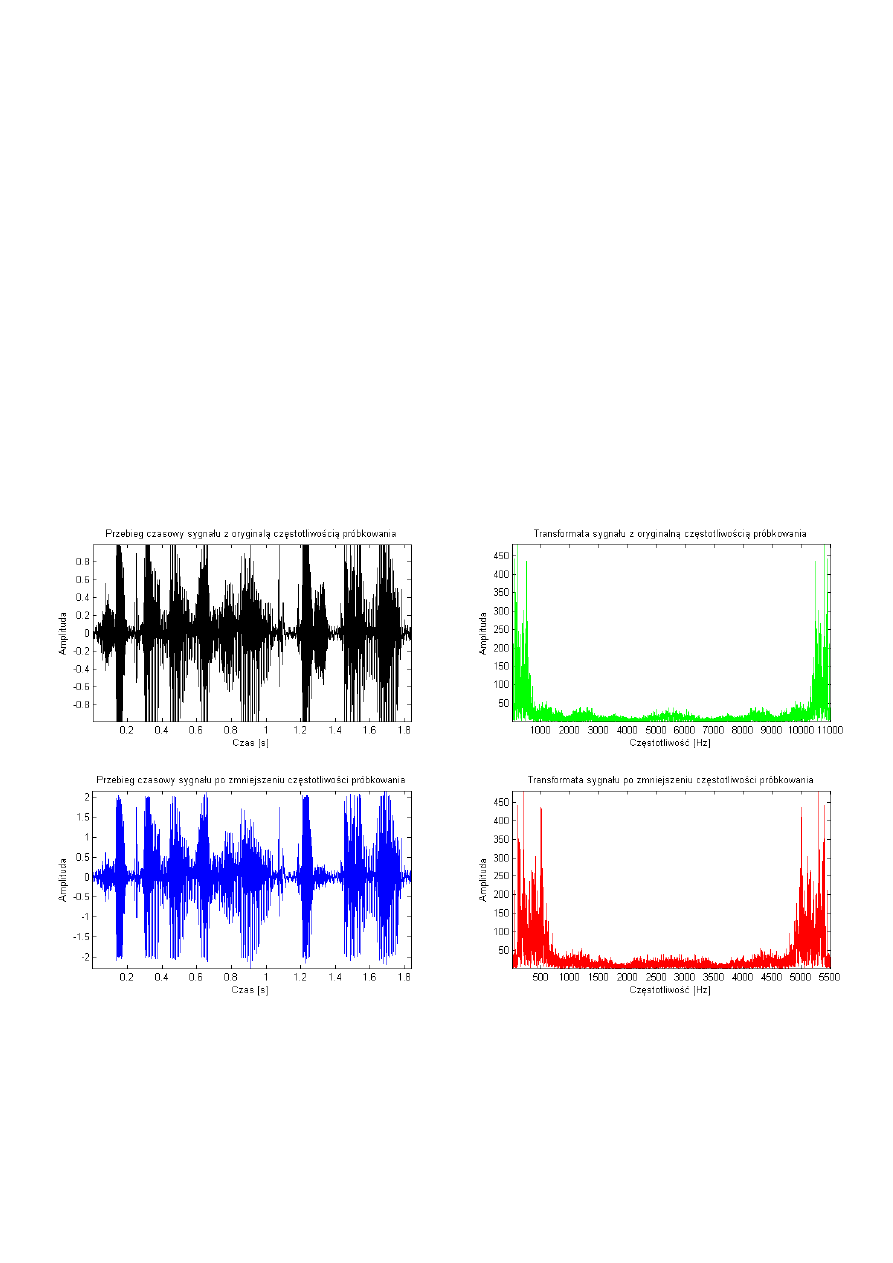
W ramach zadania otrzymano następujące wykresy:

Figura 5

Wnioski z wykonania zadania 4:

Zadanie polegało na zmniejszeniu częstotliwości próbkowania. Zostało ono zrealizowane poprzez przepisanie
do nowej tablicy(o połowę mniejszej niż tablica fft oryginalnego dźwięku) tylko 0,25 początkowych próbek
oraz 0,25 końcowych próbek. Otrzymany w ten sposób sygnał jest stłumiony, jakby oddalony, gorszy
jakościowo i mniej zrozumiały dla odbiorcy.

Wnioski w wykonania ćwiczenia:

Poprzez operacje na transformacie Fouriera sygnału dźwiękowego możemy wpływać na eksponowanie
pożądanych tonów w dźwięku jak także na tłumienie tych niechcianych. Umożliwiają one także modelowanie
jakości dźwięku.