Krzysztof KULA

Akademia Morska w Gdyni

AUTOMATYCZNE STROJENIE REGULATORA PID W UKŁADZIE

ON-LINE NA PODSTAWIE IDENTYFIKACJI METODĄ

PRZEKAŹNIKOWĄ

W artykule przedstawiono koncepcję adaptacji nastaw regulatora PID. Regulator nadrzędny
nadzoruje proces identyfikacji dynamiki układu otwartego i w razie potrzeby przestraja nastawy
regulatora PID. Identyfikacja dynamiki obiektu dokonywana jest za pomocą metody przekaźnikowej
bez przerywania procesu sterowń oraz szumów pomiarowych.

1.

WPROWADZENIE

Do zapewnienia zadawalającego sterowania większości procesów przemysło-

wych wystarcza regulator PI lub PID. Regulatory te niezmiennie od wielu lat
cieszą się uzasadnionym uznaniem użytkowników między innymi dzięki swej
prostocie. Chociaż regulatory cyfrowe mogłyby realizować dużo bardziej skompli-
kowane algorytmy sterowania i to bez konieczności rozbudowy swej struktury,
również większość z nich działa na podstawie algorytmu PID.

Jeżeli proces regulacji jest niestacjonarny bądź nieliniowy, to regulator PID

o stałych nastawach w dłuższym czasie przy zmianie punktu pracy nie będzie
w stanie zachować dobrej jakości sterowania. Mogą uczynić to regulatory adapta-
cyjne bądź regulatory strukturalnie odporne na zmianę parametrów. Regulatory
PID, aby mogły sprostać temu zadaniu, wymagają dostrajania swych nastaw,
a czasem i zmiany ich struktury. Mimo że takie dopasowanie do nowych warun-
ków może odbywać się jedynie okazjonalnie, to również w klasie regulatorów
adaptacyjnych regulatory PID jako regulatory bezpośredniego działania cieszą się
największą popularnością. Wynika to prawdopodobnie z tego, że są one najlepiej
znane kadrze nadzorującej pracę układów sterowania, a także w razie nieprawidło-
wych reakcji mechanizmu adaptacji i dostrajania umożliwiają odłączenie tzw.
regulatora nadrzędnego bez konieczności odłączania sterowania automatycznego.
Asumptem do przeprowadzenia adaptacji regulatora PID może być obserwowalne
pogorszenie jakości regulacji bądź planowana zmiana punktu pracy. Zmiana
nastaw bądź struktury powinna być w takim wypadku poprzedzona identyfikacją
dynamiki obiektu regulacji przynajmniej na poziomie stworzenia prostego modelu
oddającego w przybliżeniu właściwości badanego procesu. Podobnie ma to miejsce

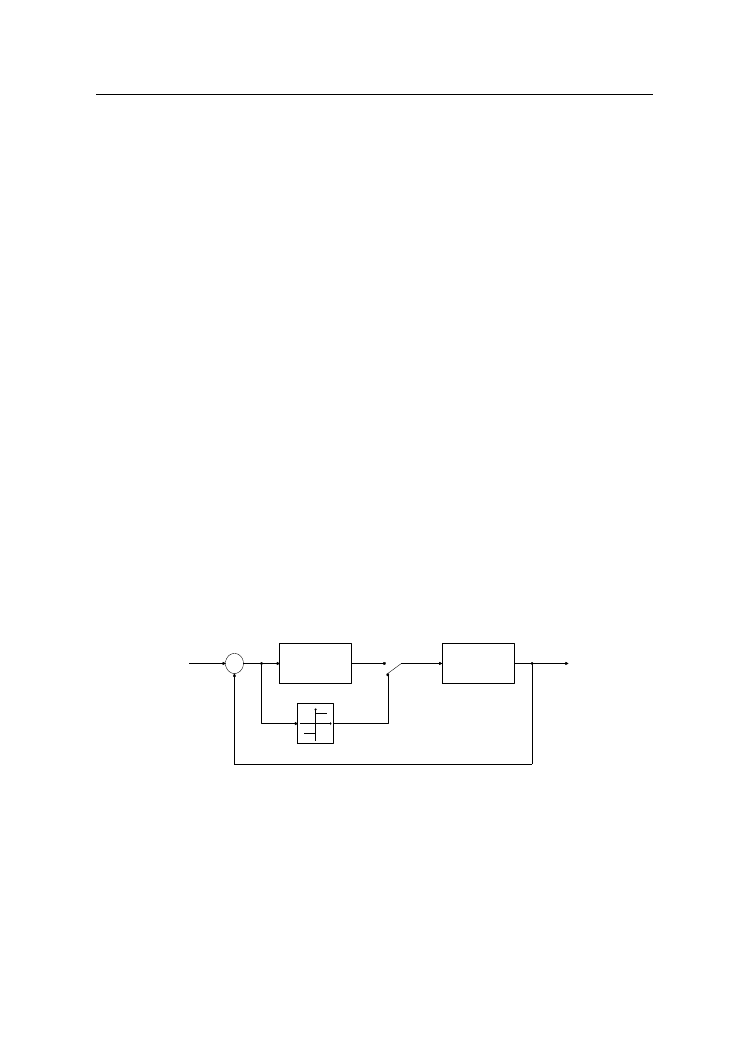
38

ZESZYTY NAUKOWE AKADEMII MORSKIEJ W GDYNI, nr 62, grudzień 2009

w układach regulacji adaptacyjnej, w których proces identyfikacji przebiega jednak
nieprzerwanie.

Do przeprowadzenia identyfikacji właściwości dynamicznych obiektu na po-

trzeby adaptacji regulatora PID w proponowanym rozwiązaniu sięgnięto po metodę
wzbudzenia w układzie drgań harmonicznych o niewielkiej amplitudzie. Koncep-
cję wykorzystania do tego celu przekaźnika sterowanego przedstawili Åstrom
i Hågglund. Opisana przez nich metoda badania parametrów cyklu granicznego [2]
pozwala na wyznaczenie jednego punktu charakterystyki częstotliwościowej, lecz
stwarza również możliwości na pomiar dalszych punktów tej charakterystyki i to
podczas trwania krótkiego eksperymentu identyfikacyjnego.

2. EKSPERYMENT IDENTYFIKACYJNY Z WYKORZYSTANIEM PRZEKAŹNIKA

Wykorzystanie znajomości wzmocnienia krytycznego i okresu oscylacji

układu na granicy stabilności, a tym samym pulsacji odcięcia, do wyznaczenia
nastaw regulatorów liniowych zaproponowali już w 1942 roku Ziegler, Nichols
oraz Rochester [12]. Do dziś wynik ich pracy znany jako reguła Zieglera-Nicholsa
pozostaje punktem odniesienia dla innych metod doboru nastaw regulatorów.
Jednak praktyczne stosowanie tej metody jest niewygodne, gdyż wymaga dopro-
wadzenia układu regulacji do granicy stabilności. Wolna od tej wady jest
wspomniana metoda przekaźnikowa. Schemat ideowy układu pozwalającego na
wyznaczenie parametrów cyklu granicznego przedstawiono na rysunku 1.

REGULATOR

P I D

OBIEKT

+

_

e

u

y

y

zad

Rys. 1.

Schemat ideowy wykorzystania regulatora dwupołożeniowego do pomiaru

Regulator liniowy przed uruchomieniem układu zostaje zastąpiony przekaźni-

kiem sterowanym. Aby wywołać drgania w takim układzie ze sprzężeniem
zwrotnym, wystarczy wyprowadzić układ ze stanu równowagi. Zgodnie z twier-
dzeniem Nyquista warunkiem powstania drgań harmonicznych w układzie
zamkniętym jest przejście charakterystyki amplitudowo-fazowej układu otwartego
przez punkt krytyczny płaszczyzny zmiennej zespolonej (-1, j0). Do analizy pracy
tego układu nieliniowego należy posłużyć się funkcją opisującą

)

,

(



A

J

zależną

K. Kula, Automatyczne strojenie regulatora PID w układzie on-line....

39

w ogólnym przypadku od pulsacji i amplitudy sygnału wejściowego. Warunkiem
powstania drgań będzie równość:

j

A

J

j

G

0

1

)

,

(

)

(













,

(1)

która przekłada się na dwa warunki:

)

(

1

)

(

A

J

j

G

o





oraz











))

(

arg(

arg

A

J

)

j

(

G

o

. (2)

Aby linearyzacja harmonicznej przebiegła poprawnie, część liniowa układu

regulacji wraz z urządzeniami wykonawczymi i torem pomiarowym musi mieć
właściwości filtru dolnoprzepustowego. Przy jego spełnieniu wzmocnienie
krytyczne po uwzględnieniu funkcji opisującej przekaźnika dwustanowego można
wyznaczyć z zależności:

A

B

K

kr









4

,

(3)

przy czym: B – amplituda sygnału sterującego u(t),
A – amplituda wielkości regulowanej y(t).

Okres drgań krytycznych tego układu powinien w przybliżeniu równać się

okresowi oscylacji, jakie wystąpią po wytrąceniu badanego układu ze stanu
równowagi.

osc

kr

T

T



(4)

Pulsacja odcięcia będzie zatem równa:

osc

o

T





2



.

(5)

3. REGULATOR ADAPTACYJNY

Koncepcję identyfikacji parametrów cyklu granicznego za pomocą przekaźnika

można wykorzystać do syntezy regulatora, którego nastawy adoptowane są na
bieżąco do nowych warunków pracy. Temat wykorzystania przekaźnika do
regulatorów adaptacyjnych był podejmowany przez różnych autorów. W projekcie
Litza i Majhi [6] przekaźnik dołączony był równolegle do regulatora PID,
natomiast Tan, Huang i Ferdons [10] w swym regulatorze samonastrajalnym przed
regulatorem PID dodali przekaźnik równolegle połączony z regulatorem typu P.
Sung i inni do wykorzystania sygnału testowego z przekaźnika sięgnęli po metodę
najmniejszych kwadratów [9]. Problematyką tą zajmowali się również Park [8],

40

ZESZYTY NAUKOWE AKADEMII MORSKIEJ W GDYNI, nr 62, grudzień 2009

Tan, Lee i Jiang [11] oraz Hang, Astrom [3], jednakże z ograniczeniem do
procesów o ustabilizowanym przebiegu wielkości wyjściowej oraz przy niewiel-
kich zakłóceniach. Proponowana w tym artykule struktura regulatora obejmuje
regulator bezpośredniego działania, będący regulatorem PI lub PID, oraz tzw.
regulator nadrzędny pełniący funkcję układu nadzorującego pracę układu
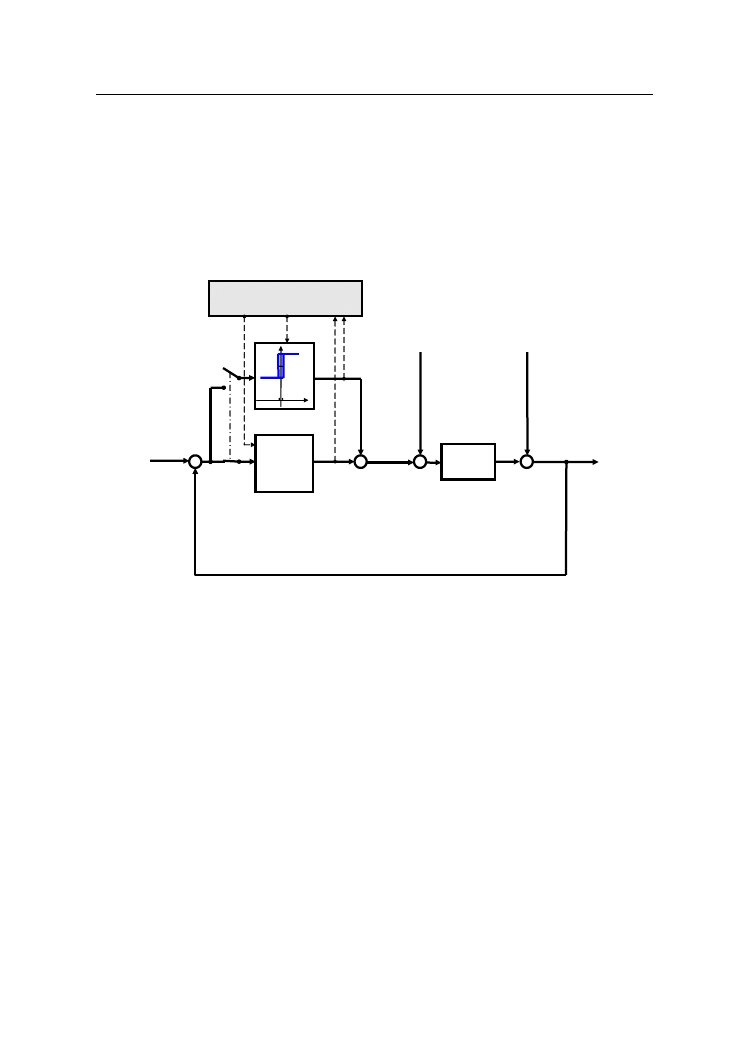
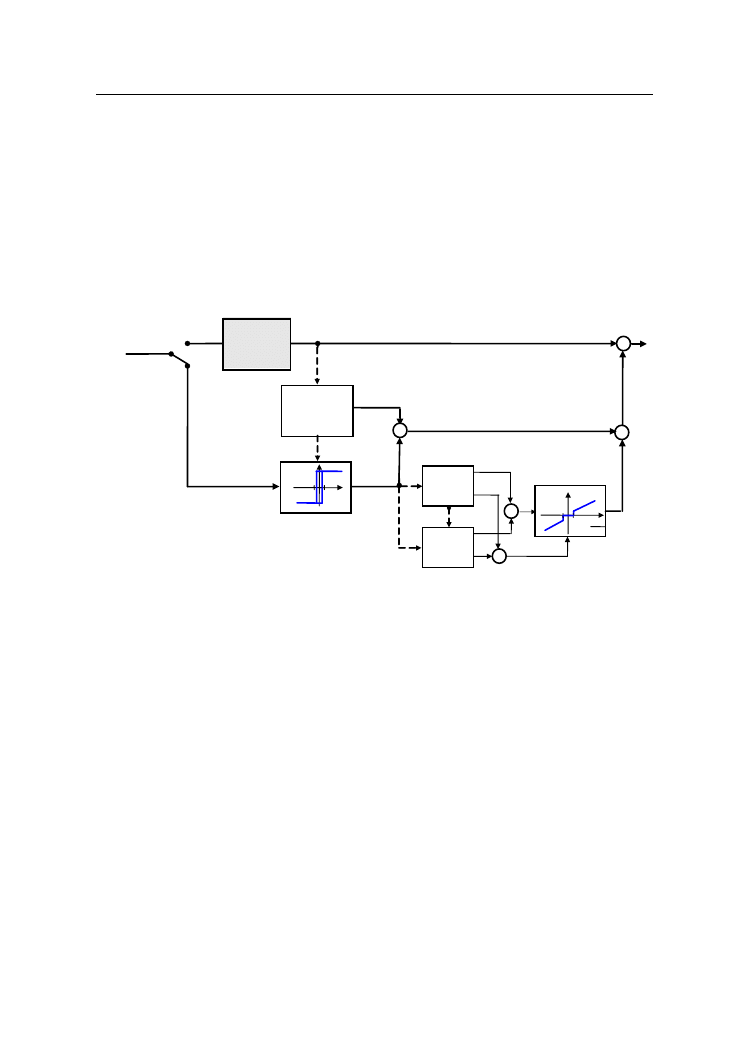
sterowania procesem. Schemat blokowy tego układu przedstawiono na rysunku 2.

Rys. 2. Schemat blokowy

proponowanego układu regulacji

Aby można było przeprowadzić automatyczne dostrajanie nastaw regulatora

PID on-line, niezbędne jest – w celu zapewnienia poprawnego pomiaru parame-
trów cyklu granicznego – właściwe ustawienie charakterystyki statycznej członu
nieliniowego zapewniającego powstanie w układzie stabilnych, niegasnących
drgań harmonicznych.

Punkt przełączania

Punkt przełączania przekaźnika ustawiany jest na wartość zerową. Wystarczy

wyprowadzić układ ze stanu równowagi, aby jego wielkość wyjściowa oscylowała
wokół poziomu odniesienia (w rozważaniach teoretycznych wokół zera). Jeśli
jednak dostrojenie regulatora ma się odbyć w trakcie normalnej pracy układu, to
przy przeprowadzaniu identyfikacji tą metodą mogą pojawić się problemy ze
sterowaniem obiektem, jak również z wygenerowaniem niegasnących drgań
harmonicznych, szczególnie w obecności zakłóceń. Kompensowanie stałego
zakłócenia implikuje utrzymywanie niezerowej wartości sterowania. W układzie
powinna być mierzona wielkość sterująca, tak aby można było w wybranym
okresie wyznaczyć jej wartość średnią (u

śr

). Po zainicjowaniu procesu identyfikacji

PROCES

REGULATOR

n a d r z ę d n y

REGULATOR

PID

_

+

+

+

y

zad

Zakłócenia

y

Szum
pomiarowy

+

+

a

B+a

e

-B+a

+

+



K. Kula, Automatyczne strojenie regulatora PID w układzie on-line....

41

sterowanie układem przejmuje regulator dwupołożeniowy. Jeżeli w układzie uchyb
regulacji będzie zmieniał znak, to powinny pojawić się oscylacje wywołane
sygnałem sterującym równym:

B

e

sign

u

t

u

śr







)

(

)

(

.

(6)

Jeżeli wartość średnia uchybu regulacji będzie równa 0, to powstałe drgania

będą symetryczne, a pomiar parametrów cyklu granicznego będzie dokładny na
tyle, na ile jest to możliwe. W przeciwnym razie sygnał wyjściowy z przekaźnika
musi być na tyle wysoki, aby zdołał doprowadzić do zmiany znaku uchybu.
Jednakże zwiększanie wartości B ma tę wadę, że gdy uda się wygenerować
drgania w układzie, to proporcjonalnie do niej wzrośnie również amplituda uchybu
regulacji. Ponadto na dokładność identyfikacji dynamiki procesu mają wpływ
zakłócenia zewnętrzne oraz szumy pomiarowe.

Wpływ zakłóceń stałych

Pojawienie się stałego zakłócenia deformuje pomiar parametrów, co skutkowa-

łoby niewłaściwym wyznaczeniem nastaw regulatora. Oscylacje wielkości regulo-
wanej stają się asymetryczne. Zmianie ulega ich okres. Zależności pomiędzy
poszczególnymi sygnałami opisane są w [4], natomiast sam efekt oddziaływania
obu sygnałów na wielkość regulowaną pokazano na rysunku 3.

W układzie z regulatorem PI, PID uchyb ustalony przy stałym zakłóceniu

sprowadzany jest do zera. Jeżeli zakłócenie oddziałuje na obiekt przed
przeprowadzeniem identyfikacji, to przy przełączeniu sterowania na regulację
dwupołożeniową oddziaływanie tego zakłócenia może na powrót doprowadzić do
powstania uchybu ustalonego.

0

10

20

30

40

45,97

60

66,45

80

-0,5

0,048

0

0,5

1

T

= 20,48

s

T

d

=

17,43

s

T

g

= 3,05 s

z

y

u+z

t

Rys. 3. Przebieg wiel

kości regulowanej w układzie z przekaźnikiem w obecności

stałego zakłócenia

Przed przełączeniem na tryb identyfikacji i dostrajania regulatora układ

zapamiętuje wartość średnią zadanej wielkości sterującej u

śr

, którą wypracował

42

ZESZYTY NAUKOWE AKADEMII MORSKIEJ W GDYNI, nr 62, grudzień 2009

regulator liniowy w ostatnim okresie obserwacji. Gdy zakłócenie pojawi się
w trakcie pomiarów, obniżając ich wiarygodność, identyfikacja powinna zostać
powtórzona od ponownego pomiaru u

śr

w zadanym okresie uśredniania. Ponieważ

zakłócenie rzadko kiedy jest stałe, po przejściu na tryb identyfikacji wartość
średnia uchybu regulacji może być różna od zera, a powstałe drgania mogą być
niesymetryczne. Aby pomiar parametrów cyklu był bliski wartości rzeczywistych,
konieczne jest dodatkowe skorygowanie sygnału sterującego do poziomu kompen-
sującego wpływ zakłócenia o wartość u

3

(rys. 4).

Rys. 4.

Schemat ideowy sterowania regulatorem dwupołożeniowym

Schemat ideowy układu sterowania za pomocą regulatora dwupołożeniowego

w obecności zakłóceń przedstawiono na rysunku 5. Zainicjowanie eksperymentu
identyfikacyjnego powoduje przejęcie kompensacji stałego zakłócenia przez
składową sygnału sterującego u

2

. Powinna ona zapobiec szybkiemu wzrostowi

uchybu regulacji, co uniemożliwiłoby przełączanie przekaźnika. Jeżeli uda się
doprowadzić do powstania drgań, to dodatnie zbocze sygnału wyjściowego
z przekaźnika u

1

inicjuje pomiar czasu T

g

, a zbocze ujemne rozpoczyna pomiar T

d

(rys. 3). Składowa u

3

generowana na wyjściu członu ze strefą nieczułości ma za

zadanie sprowadzić sterowanie u do poziomu, który po reakcji układu wykonaw-
czego sterowania zapewni zerową wartość średnią uchybu regulacji. Jeżeli czas
trwania poziomu górnego T

g

będzie równy czasowi T

d

, to sygnał wyjściowy członu

ze strefą nieczułości u

3

będzie równy 0, a oscylacje uchybu regulacji symetryczne.

Uzyskany w ten sposób pomiar okresu oscylacji:

kr

osc

T

T

T

T







2

1

(7)

odpowiada okresowi drgań krytycznych.

Pomiar

T

g

+

+

+

+

+

_

Pomiar

Td









e

+

+

u

1

u

2

P I D

Wartość

średnia

u

3

_

B

1

-1

+



u

+

0

+

+

K. Kula, Automatyczne strojenie regulatora PID w układzie on-line....

43

Rys. 5.

Przebieg wielkości wyjściowej regulatora dwupołożeniowego u przy występowaniu

szumu pomiarowego

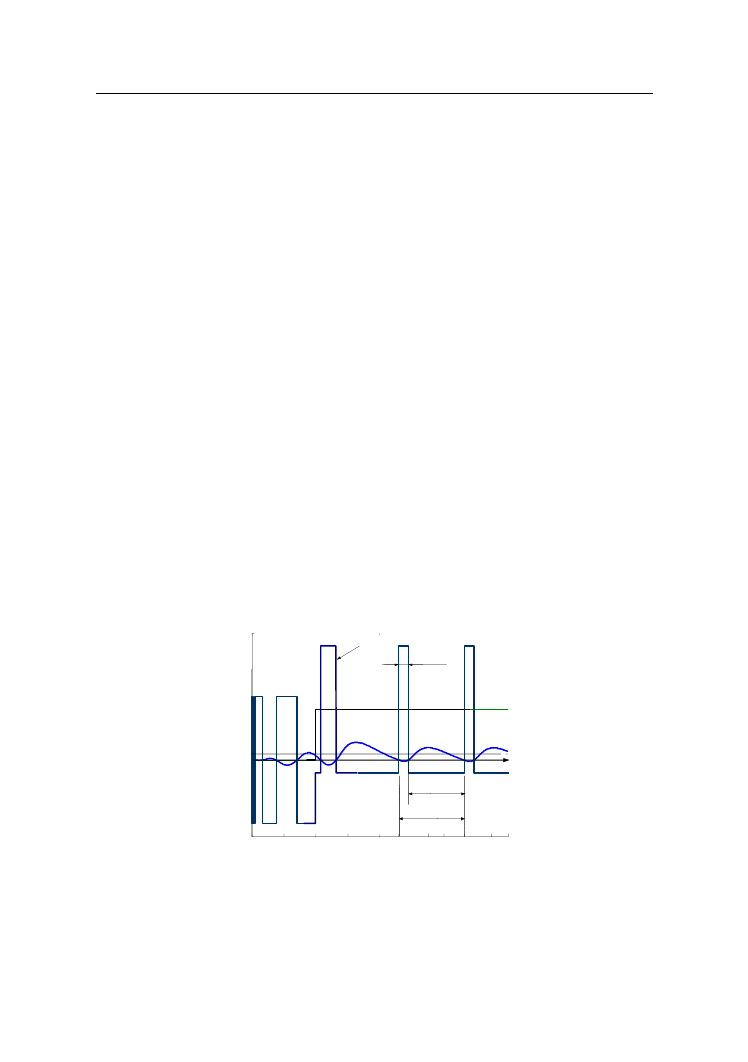
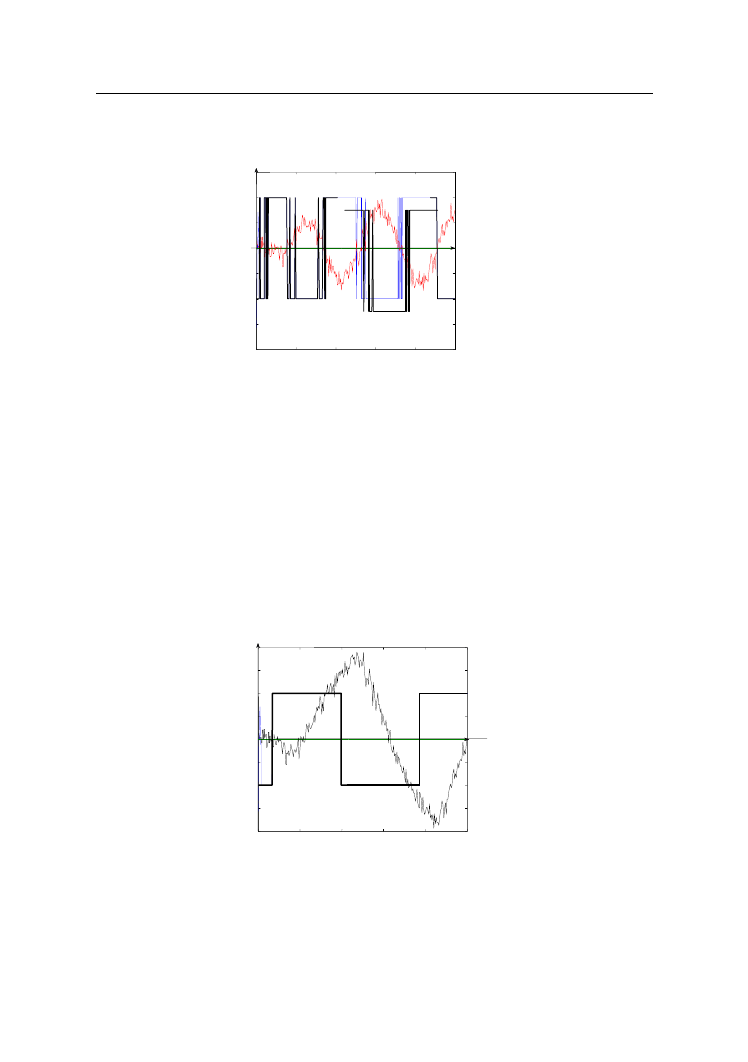
Oddziaływanie szumu pomiarowego

Gdy na mierzoną wielkość regulowaną nałoży się szum pomiarowy, to

w pobliżu punktu przełączania przekaźnika może dojść do niepożądanych zmian
jego stanu. Ilustruje to rysunek 6, na którym zasymulowano przebiegi wielkości
regulowanej wraz z nałożonym na nią szumem pomiarowym oraz wielkości
sterującej na wyjściu regulatora dwupołożeniowego. Pomiar okresu oscylacji, aby
mógł być wiarygodny, musi pozostawać stały w obserwowanym przedziale czasu.
Aby zapobiec występowaniu niepożądanych przełączeń, należy do przekaźnika
wprowadzić strefę histerezy.

Rys. 6.

Przebieg wielkości regulowanej y oraz sygnału wyjściowego przekaźnika

z histerezą

Strefa histerezy, jeśli jest odpowiednio szeroka, pozwala na uniknięcie

gwałtownego cofnięcia się przekaźnika do poprzedniego stanu, ale wydłuża okres

0

5

10

15

20

25

-0.3

-0.2

-

-

0.1

0

0.1

0.2

0.3

t

u

y

y.u

B=

0

5

10

15

20

25

-0.3

-

0.2

-0.1

0

0.1

0.2

0.3

y.u

y

u

t

44

ZESZYTY NAUKOWE AKADEMII MORSKIEJ W GDYNI, nr 62, grudzień 2009

przełączania tak, że nie pokrywa się on z okresem drgań krytycznych. Zmniejsza
ona również wartość obliczonego wzmocnienia K

kr

.

Aby błąd względny był mały, wskazane jest, by amplituda oscylacji wielkości

regulowanej A była co najmniej 3-krotnie większa od poziomu szumów. Stosownie
do tego musi być dopasowany poziom sygnału sterującego z przekaźnika B.
Szerokość histerezy wystarczy przyjąć dwukrotnie większą od amplitudy szumów.

Szum pomiarowy może również zakłócić pracę układu pomiaru czasu

opóźnienia przy wyznaczaniu modelu procesu [5], jednakże w tym wypadku
lepszym rozwiązaniem (w celu jego eliminacji) jest filtracja.

4. DOBÓR NASTAW REGULATORA

Nastawy regulatorów PID mogą być dobrane na podstawie znajomości

parametrów cyklu granicznego, jednakże szersze możliwości wyboru stwarzają
metody opierające się na znajomości parametrów modelu. Wprawdzie w wyniku
identyfikacji metodą przekaźnikową nie wyznacza się bezpośrednio wartości
parametrów modelu, to jednak można obliczyć je na podstawie pomierzonych
parametrów cyklu granicznego [5]. Ten sposób doboru nastaw narzuca się sam
w układach wykorzystujących model procesu, chociażby takich jak układ z predyk-
torem Smitha czy z modelem wewnętrznym. Do dalszych rozważań przyjęto model
w postaci członu inercyjnego pierwszego rzędu wraz z opóźnieniem o trans-
mitancji:

s

T

m

o

e

s

T

K

s

G









1

)

(

.

(8)

Wzmocnienie statyczne K może być wyznaczone on-line podczas trwania

eksperymentu identyfikacyjnego [4]. W obecności zakłóceń wartość ustalona
wielkości regulowanej jest równa:

z

K

u

K

y

z

ust

ust









1

1

,

(9)

a po zmianie wartości sterowania:

z

K

u

K

y

z

ust

ust









2

2

.

(10)

Po odjęciu drugiej zależności od pierwszej oraz uwzględnieniu, że sygnał

sterujący na wyjściu z przekaźnika ma wartość stałą, otrzymamy zależność na
wzmocnienie obiektu:

u

y

K

ust







.

(11)

K. Kula, Automatyczne strojenie regulatora PID w układzie on-line....

45

Opierając się na pomiarach wzmocnienia obiektu oraz wyznaczonych

parametrach cyklu granicznego, można określić parametry modelu na podstawie
wzorów Majhi i Athertona [7] lub Hanga i Ho [3]:

1

2

2

2









K

K

T

T

kr

osc

m



,

(12)

)

2

(

2

osc

osc

o

T

T

arctg

T

T















.

(13)

Wybór metody wyznaczania nastaw regulatora zależy w dużej mierze od tego,

jaki czynnik najczęściej powoduje odchyłki wielkości regulowanej od wartości
zadanej i czy tym samym układ powinien wykazać się wyższą sprawnością przy
zmianie wartości zadanej, czy przy kompensacji wpływu zakłóceń.

5. BADANIA SYMULACYJNE

Przyjęto, że obiekt regulacji jest przedziałami liniowy, natomiast zmiana

punktu pracy przy istniejących nieliniowościach może skutkować zmianą dynamiki
procesu regulacji. W punkcie pracy 1 obiekt ma transmitancję:

s

ob

e

s

s

,

,

s

G











2

1

7

8

4

1

4

2

)

(

.

Parametry modelu są równe K = 1,5, T = 6,44, T

o

= 1,68. Przy zmianie wartości

zadanej z y

zad1

na y

zad2

dynamikę układu opisuje transmitancja:

s

.

ob

e

s

,

s

,

,

s

G

5

1

2

2

56

7

7

5

1

4

2

)

(











.

Poszukiwane parametry cyklu granicznego, jak również samego modelu obiektu,
można wyznaczyć w tym wypadku za pomocą obliczeń.

Parametry cyklu granicznego są równe: K

kr

= 1,886 T

osc

= 9,37s,

natomiast parametry modelu (8) wynoszą: K = 2,4 T = 7,67 s T

o

= 2,41 s.

Wymagania stawiane przed układem sterowania zostały sformułowane

w postaci wskaźników jakości sterowania: uchyb ustalony ma dążyć do zera
e

ust

→0, przeregulowanie w granicach 15% przy minimalnym czasie regulacji. Na

podstawie pełnych informacji o tym obiekcie sterowanym w pierwszym zakresie
zmienności wielkości regulowanej wyznaczono nastawy regulatora PID według
metody Abbasa [1]:

f

c

o

e

d

R

b

a

K













, (14)

46

ZESZYTY NAUKOWE AKADEMII MORSKIEJ W GDYNI, nr 62, grudzień 2009

przy czym: χ – oczekiwane przeregulowanie w układzie zamkniętym,

R – opóźnienie względne zdefiniowane jako

T

T

R

o



.

Wartości współczynników a, b, c, d, e, f podane są w tabeli 1.

Tabela 1

Tabela współczynników Abbasa

Regulator

a

b

c

d

e

f

PID

0,177

0,348

-1,002

0,531

-0,359

0,713

Aby przeregulowanie było mniejsze od żądanego χ, nastawy regulatora PID

powinny być równe:

k

K

K

o

p



,

2

/

o

i

T

T

T





,

o

o

d

T

T

T

T

T







2

. (15)

Po podstawieniu do wzorów (15) parametrów modelu otrzymano nastawy regulato-
ra PID mającego zapewnić przy zmianie wartości zadanej przeregulowanie
mniejsze niż 15%:

K

p

= 2,21, T

i

= 8,33, T

d

= 0,95.

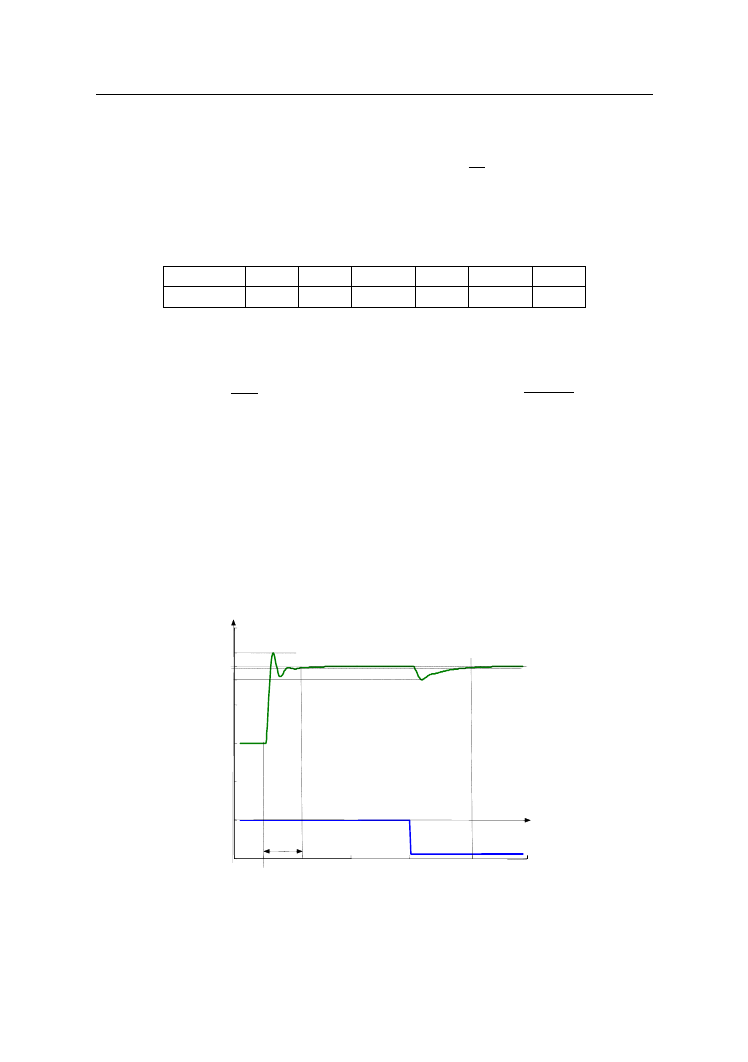
Przebieg wielkości regulowanej przy skokowej zmianie zakłócenia oraz

wartości zadanej w pierwszym zakresie zmienności wielkości wyjściowej przedsta-
wiono na rysunku 7. Dla tego obszaru pracy układu wyznaczono wskaźniki jakości
sterowania przy zmianie wartości zadanej.

Rys. 7.

Przebieg wielkości regulowanej przy skokowej zmianie zakłócenia z = 0,44

oraz wartości zadanej ∆y

zad1

= 1 z y

zad1

= 1 na 2 w pierwszym zakresie

zmienności wielkości wyjściowej

40

50

63.5

80

100

121.4

140

-0.5

0

0.5

1

1.5

2

2.5

2.1
7

1.82

z

y

y,z

y

=

zad

t

tr=13.5

K. Kula, Automatyczne strojenie regulatora PID w układzie on-line....

47

Dla sterowania przy zmianie wartości zadanej uzyskano następujące wskaźniki

jakości:

uchyb ustalony e

ust

= 0,

czas regulacji przy 2-procentowym przedziale tolerancji t

r

= 13,5 s,

maksymalne przeregulowanie χ = 17,4%.
Przy reakcji na stałe zakłócenie z = 0,44 wskaźniki te miały wartości odpo-

wiednio równe:

e

ust

= 0, t

r

= 21,4 s, χ = 40,9%.

W innym obszarze pracy, gdy dynamika obiektu uległa zmianie G

2ob

(s),

dotychczasowe nastawy regulatora nie mogły sprostać stawianym wymaganiom.
Dla sterowania przy zmianie wartości zadanej nastąpiło znaczne pogorszenie
wskaźników jakości: czas regulacji przy 2-procentowym przedziale tolerancji
liczonym względem przyrostu wartości zadanej, czyli równym w tym wypadku
±0,02, wyniósł t

r

= 432,1 s, a maksymalne przeregulowanie χ = 89,7%. Przy reak-

cji na stałe zakłócenie z = 0,44 wskaźniki te miały wartości odpowiednio równe:

e

ust

= 0, t

r

= 69,1 s, χ = 64,8%.

Sterowanie w innym obszarze wartości zdanych w związku ze znaczną zmianą

dynamiki obiektu wymaga jednak dopasowania nastaw regulatora, do czego zasto-
sowano metodę opisaną w punkcie 3 i 4.

Przeprowadzono eksperyment identyfikacyjny w układzie zamkniętym

w obecności zakłóceń z wykorzystaniem przekaźnika z histerezą o szerokości
strefy



= 0,003 i sygnale wyjściowym u(t) = B ±0,2.

Przed przełączeniem na tryb dostrajania w obecności zakłócenia z = 0,44

wartość średnia sygnału sterującego dla T

u

= 3 min wyniosła:







u

p

p

T

t

t

u

sr

dt

t

u

T

u

)

(

1

= 0,861.

(16)

Taką wartość nadano składowej u

2

. Po przełączeniu na automatyczne dostrajanie

przy wybranym arbitralnie poziomie sygnału wyjściowego przekaźnika B = 0,2
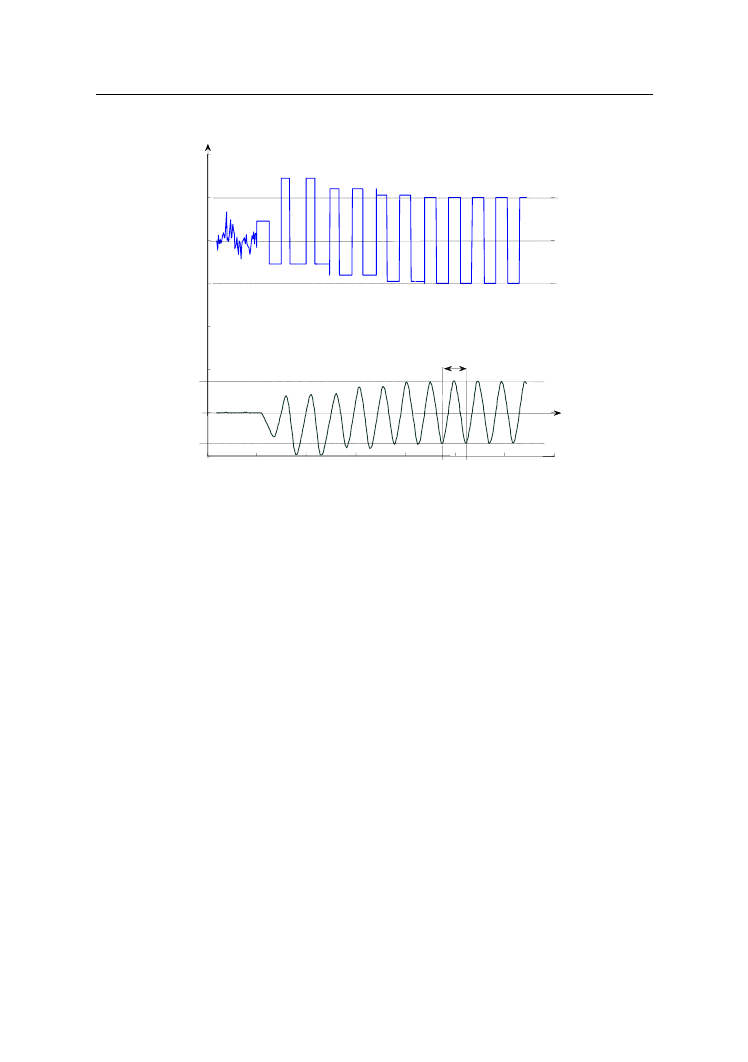
w układzie wzbudziły się drgania wymuszone działaniem regulatora dwupołoże-
niowego. Były to drgania asymetryczne – ich przebieg pokazano na rysunku 8.
Ponieważ różnica czasów ∆T = T

g

– T

d

jest ujemna i większa od szerokości strefy

nieczułości, sygnał u

3

będzie miał ten sam znak i pomniejszy sygnał sterujący u(t).

Po zrównaniu się obu czasów przy dopuszczalnym marginesie błędu powstałe
drgania mogą stanowić dane do dalszych obliczeń.

Pomierzono amplitudę drgań harmonicznych A = 0,143 oraz T

osc

= 9,58 s. Przy

uwzględnieniu wartości funkcji opisującej histerezy ze strefą nieczułości



= 0,003

wyznaczono wartość wzmocnienia krytycznego K

kr

= 1,78.

48

ZESZYTY NAUKOWE AKADEMII MORSKIEJ W GDYNI, nr 62, grudzień 2009

Rys. 8.

Przebieg procesu identyfikacji w obecności stałego zakłócenia

i szumu pomiarowego

Obliczenie wzmocnienia na podstawie eksperymentu identyfikacyjnego

wymagało pomiaru wielkości regulowanej przy sterowaniu w układzie ze stero-
waniem dwustanowym, gdy sygnał wyjściowy z przekaźnika został zmieniony
z u

1

= 0,76 na u

2

= 0,8. Odpowiednie wartości średnie z jednej minuty wyniosły

odpowiednio: y

1śr

= 2,86 oraz y

2śr

= 2,957. Wzmocnienie obiektu obliczone z (11)

jest równe K

ob

= 2,425.

Na podstawie obliczonego wzmocnienia statycznego oraz pomierzonych

parametrów cyklu granicznego wyznaczono z zależności (12, 13) pozostałe para-
metry modelu: T = 6,4 s, T

o

= 2,75 s. Po zakończeniu identyfikacji parametrów

obiektu sterowanego w drugim obszarze pracy mogą być wyznaczone nowe
nastawy regulatora PID: K

p

= 0,994, T

i

= 7,66, T

d

= 1,09.

Przy tak przestrojonym regulatorze kolejna zmiana wartości zadanej w obrębie

nowego obszaru pracy, jak również reakcja na zakłócenie, nie wywołuje takich
perturbacji w układzie jak przed adaptacją nastaw. Przebieg sterowania po adap-
tacji nastaw pokazano na rysunku 9.

380

400

420

440

460

480

500

520

0

0.2

0.4

0.6

0.8

1

1.2

u,e

u

e

t

Tosc=9.58

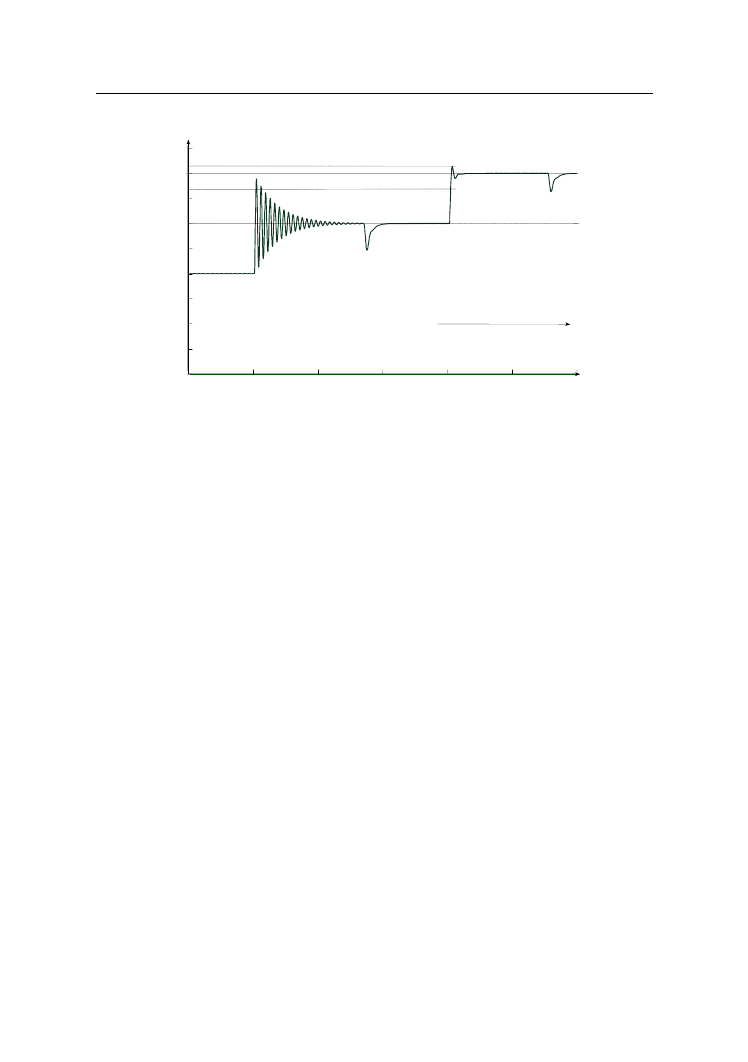
K. Kula, Automatyczne strojenie regulatora PID w układzie on-line....

49

Rys. 9.

Przebieg wielkości regulowanej w drugim obszarze pracy po przeprowadzeniu

adaptacji nastaw regulatora

6. PODSUMOWANIE

Zachowanie układu adaptacyjnego pracującego w nieprzewidywalnym środo-

wisku przemysłowym często odbiega znacznie od tego sprawdzanego w warun-
kach laboratoryjnych. Z tego powodu jego niezawodność jest często niewystarcza-
jąca. Proponowana w tym artykule koncepcja wykorzystania do identyfikacji
on-line metody przekaźnikowej pozwala na dostrojenie nastaw regulatora PID
stosownie do potrzeb w czasie normalnej pracy podczas oddziaływania zakłóceń
zewnętrznych oraz w obecności szumów. Przedstawiona metoda pozwala na
osiągnięcie 97-procentowej dokładności przy pomiarze parametrów cyklu granicz-
nego liczonej względem pomiaru dokonanego bez oddziaływania zakłóceń.

LITERATURA

1. Abbas A., A new set of controller tuning relations, ISA Transactions, 1997, vol. 36, no 3, s. 183–

187.

2. Åstrom K.J., Hågglund T., Automatic tuning of simple regulators with specifications on phase

and amplitude margins, Automatica, 1984, 20, s. 645–651.

3. Hang C.C, Åstrom K.J., Ho W.K., Relay auto-tuning in the presence of static load disturbance,

Automatica, 1993, 29 (2), s. 563–564.

200

300

400

500

600

700

800

0

0.5

1

1.5

2

3

3.5

4

4.14

Po dostrojeniu

y

t

50

ZESZYTY NAUKOWE AKADEMII MORSKIEJ W GDYNI, nr 62, grudzień 2009

4. Kula K., Automatyczne strojenie regulatorów przy występowaniu zakłóceń i szumów pomiaro-

wych, materiały konferencyjne „Modelowanie i Symulacja”, Kościelisko 2006, s. 293–300.

5. Kula K., Dostrajanie nastaw regulatora sterującego układem o dużych stałych czasowych opóź-

nienia, Elektronika, 2009, nr 2, s. 23–27.

6. Litz Majhi S., Relay based closed loop tuning of PID-controlers, Automatisierungstechnik, 2004,

vol. 52, nr 5, s. 202–208.

7. Majhi S., Atherton D.P., Obtaining controller parameters for a new Smith predictor, Automatica,

2000, 36, s. 1651–1658.

8. Park J.H., Sung S.W., Lee I.B., Improved relay auto-tuning with static load disturbance,

Automatica, 1997, vol. 33, no. 4, s. 711–715.

9. Sung S.W., Lee I-B., Lee B-K., On-line process identification and automatic tuning method for

PID controllers, Chemical Engineering Science, 1998, vol. 53, no 10, s. 1847–1859.

10. Tan K.K, Huang S., Ferdons R., Robust self-tuning PID controller for nonlinear systems, Journal

of Process Control, 2002, 12, s. 753–761.

11. Tan K.K., Lee T.H., Jiang X., Robust on-line relay automatic tuning of PID control systems ISA

Transactions, 2000, 39, s. 219–232.

12. Ziegler J.G., Nichols N.B., Rochester Optimum settings for automatic controllers, TRANS.

Asme 1942, 64, s. 759–766.

ON-LINE AUTOTUNING OF PID CONTROLLER USING

RELAY FEEDBACK METHOD

Summary

In this paper a method of adaptation of PID controller is proposed. The relay identification of
plant dynamic is realised by supervisor and if it will be nessesery can be used to tuning of controller
settings to improve the performance of control system. The simulation results in the presence of
disturbances and measuring noise are added.