POLITECHNIKA ŚWIĘTOKRZYSKA
Katedra Urządzeń Elektrycznych i Techniki Świetlnej
Materiałoznawstwo Elektryczne
ĆWICZENIE 13
BADANIE MATERIAŁÓW
I ELEMENTÓW PÓŁPRZEWODNIKOWYCH
I. WIADOMOŚCI TEORETYCZNE
1. Własności materiałów półprzewodnikowych
Półprzewodniki są to pierwiastki lub związki chemiczne o strukturze krystalicznej, których rezystywność w
temperaturze 20
°
C zawarta jest w przedziale 10
–4
÷
10
8
Ω
cm.
Rys. 13.1. Zakresy rezystywności skrośnej ważniejszych grup materiałów w temperaturze 20
°
C
Zasadniczą cechą materiałów półprzewodnikowych jest ich wrażliwość strukturalna, to znaczy silna
zależność własności elektrycznych, np. rezystywności, od:
−
temperatury,
−
zawartości domieszek chemicznych,
−
niedokładności budowy sieci krystalicznej,
−
oświetlenia,
−
stanu powierzchni,
−
innych czynników.
Do półprzewodników zalicza się bardzo dużą liczbę krystalicznych ciał stałych występujących
w przyrodzie. W praktyce jednak znaczenie mają jedynie nieliczne pierwiastki i związki chemiczne.
Pierwiastki: krzem (Si), german (Ge), selen (Se).
Związki chemiczne: antymonek indu (InSb), tellurek bizmutu (Bi
2
Te
3
), tellurek rtęci (HgTe), tlenek
miedziawy (Cu
2
O), węglik krzemu (SiC) - karborund, selenek rtęci (HgSe), ar-
senek indu (InAs), arsenek galu (InGa).
Do charakterystycznych właściwości półprzewodników należą:
a)
jednoczesne istnienie dwóch rodzajów nośników: elektronów i dziur,
b)
ujemny współczynnik temperaturowy rezystywności.
Występowanie powyższych właściwości daje się wyjaśnić na gruncie pasmowego modelu energe-
tycznego ciała stałego (rys. 13.2).
10
–4
10
8
10
18
Ω
cm
materiały
przewodzące
półprzewodnki
materiały izolacyjne
powietrze
Ć
wiczenie 13
2
a)
a)
pasmo
przewodnictwa
b)
pasmo
walen cyjne
pasmo
wzbronione
dziura
elektron
elektrony
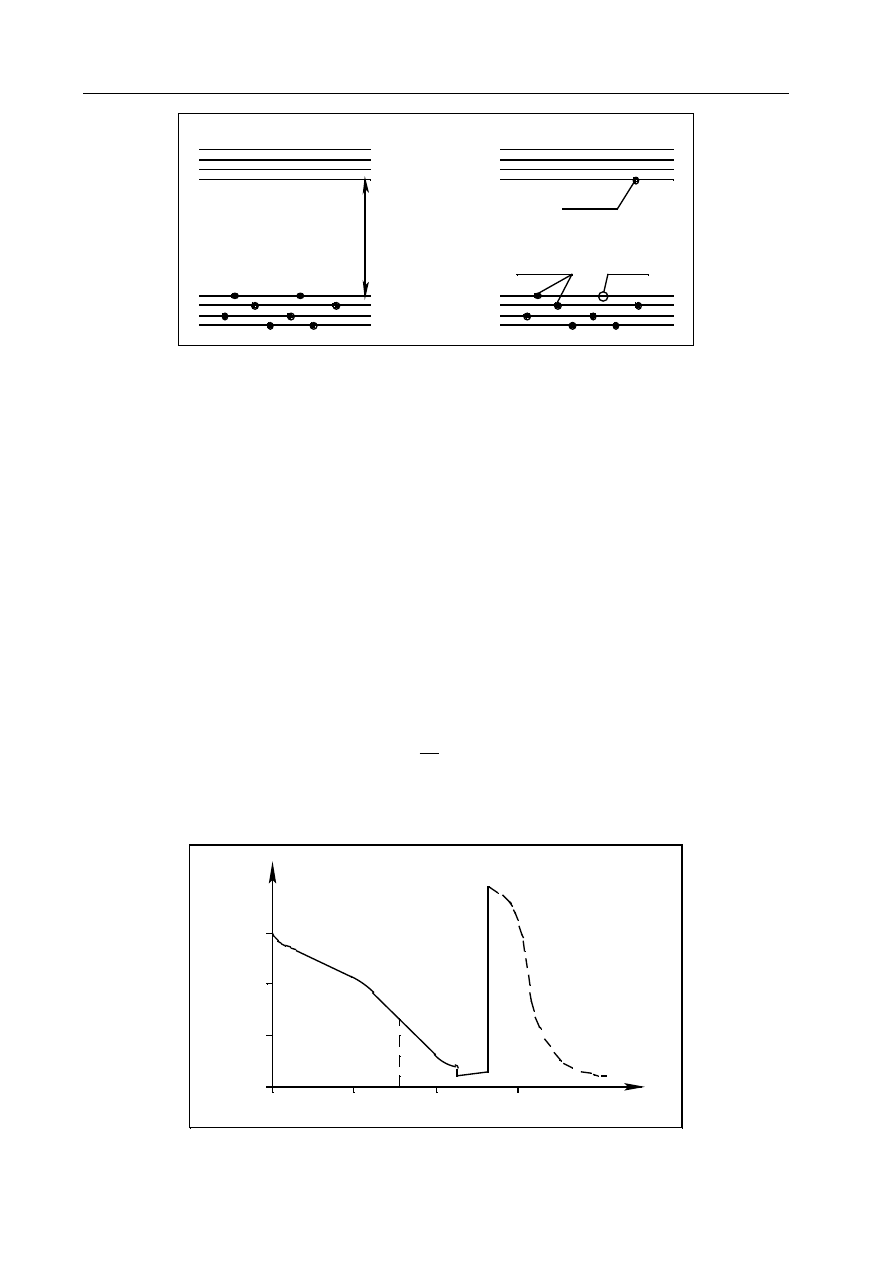
Rys. 13.2. Model pasmowy półprzewodnika samoistnego, np. germanu (a) oraz ilustracja pobu-
dzenia cieplnego elektronu (b) – jego przejście do pasma przewodnictwa
Dla półprzewodników szerokość pasma wzbronionego jest mniejsza od 2 eV. Jeżeli do kryształu zo-
stanie doprowadzona energia, np. cieplna, to elektrony z pasma walencyjnego mogą przejść do pasma
przewodnictwa - mogą zatem brać udział w przewodzeniu prądu. Przeniesienie elektronu do pasma prze-
wodnictwa to ubytek elektronu w paśmie walencyjnym. Puste miejsce po elektronie nazywa się dziurą.
Dziura jest równoważna ładunkowi dodatniemu. Miejsce dziury może zająć sąsiedni elektron, zacho-
dzi wtedy ruch dziury w krysztale odpowiadający przepływowi prądu elektrycznego. Istnieją więc jedno-
cześnie dwa rodzaje nośników: elektrony i dziury.
Przejście elektronów z pasma walencyjnego (podstawowego) do pasma przewodnictwa może nastąpić
pod działaniem:
−
promieni świetlnych,
−
promieni rentgenowskich,
−
pola elektrycznego,
−
temperatury.
W przypadku wzrostu temperatury liczba nośników elektryczności szybko rośnie, co pociąga za
sobą spadek rezystywności skrośnej. Zależność rezystywności od temperatury dla półprzewodników sa-
moistnych można przedstawić wzorem
ρ = ⋅
A e
E
kT
2
,
(13.1)
gdzie: E - szerokość pasma wzbronionego, T - temperatura bezwzględna, k - stała Boltzmanna, A -
współczynnik proporcjonalności.
10
10
para
25°C
−6
10
1000
100
K
T
5000
ρ
Ω
cm
5
10
plazma
1
ciecz
Rys. 13.3. Charakterystyka temperaturowa rezystywności skrośnej germanu
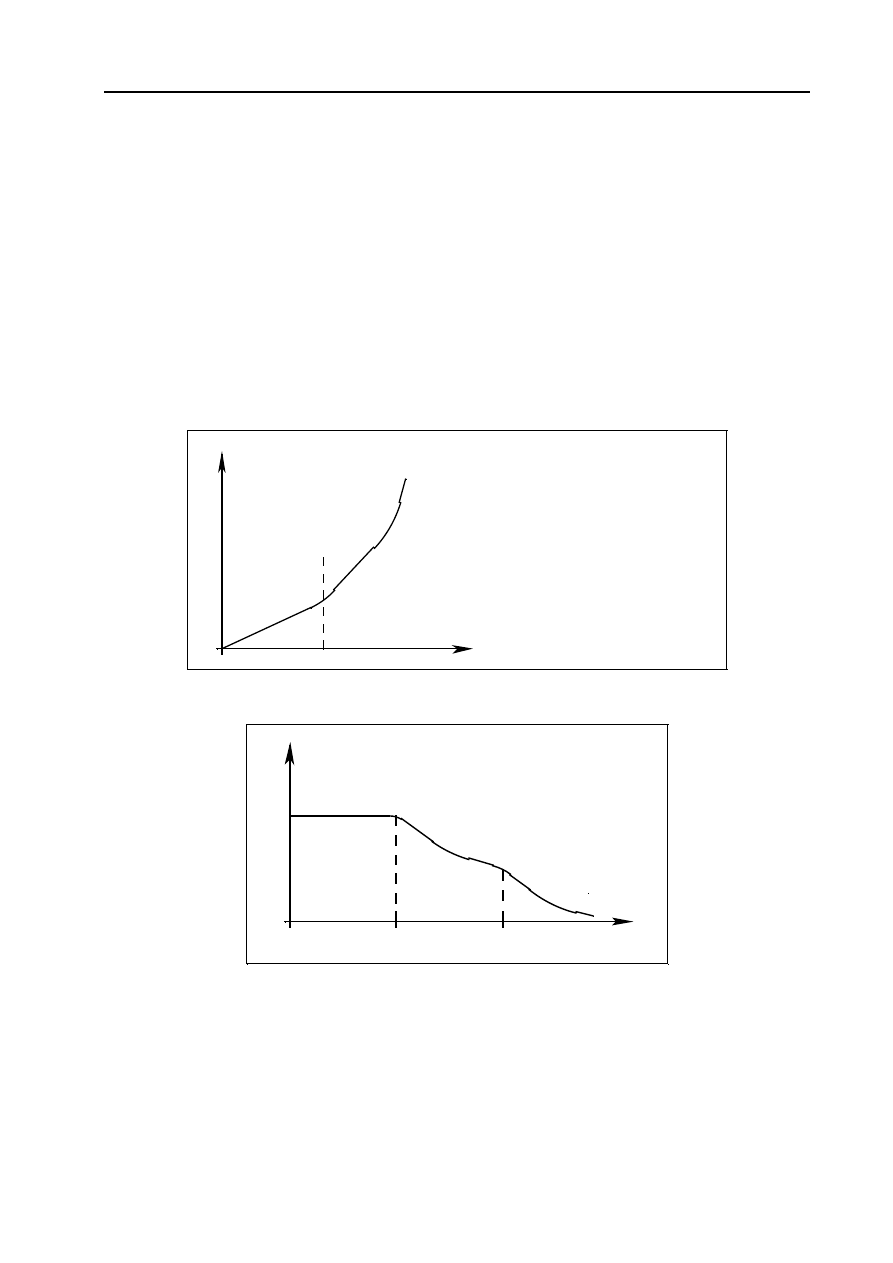
Badanie materiałów i elementów półprzewodnikowych
3
Przykład:
−
dla germanu E = 0,72 eV i przy 25
°
C
ρ
≈
60
Ω
cm,
−
dla krzemu E = 1,12 eV i przy 25
°
C
ρ
> 2
⋅
10
5
Ω
cm.
Rezystywność półprzewodników jest stała przy zmianach natężenia pola elektrycznego do około 1000
V/cm – półprzewodnik spełnia prawo Ohma.
Przy natężeniach rzędu 10.000 V/cm wzrasta liczba nośników elektryczności i wzrasta ich ruchliwość.
Dla natężeń pola rzędu 100
000 V/cm występuje poważne zmniejszenie rezystywności. Obserwuje się
wyraźne odstępstwo od prawa Ohma. Zależność rezystywności od natężenia pola opisywana jest wówczas
wzorem Poole’a
)
E
E
(
a
0
0
e
−
⋅
ρ
=
ρ
,
(13.2)
gdzie:
ρ
0
, a - stałe, E - natężenie pola E > E
0
= 1000 V/cm.
Dalszy wzrost natężenia pola elektrycznego powoduje nagrzewanie się półprzewodnika narastające w
sposób lawinowy. Skutkiem tego procesu jest przebicie i stopienie lub wyparowanie półprzewodnika w
obszarze gdzie występuje największa kumulacja ciepła.
Prawo Poole'a
E
J
Rys. 13.4. Typowa zależność gęstości prądu od natężenia pola w półprzewodniku
V/cm
100000
ρ
1000
E
Rys. 13.5. Zmiana rezystywności półprzewodników w funkcji natężenia pola
elektrycznego
2. Półprzewodniki samoistne i niesamoistne
Półprzewodniki, w których elektrony występują tylko w paśmie walencyjnym lub w paśmie przewod-
nictwa, nazywają się półprzewodnikami samoistnymi. Mają one równą liczbę ładunków: elektronów i
dziur. Liczbę elektronów lub dziur w 1 cm
3
nazywamy koncentracją i oznaczamy przez n (negative) dla
elektronów i p (positive) dla dziur. Przykładem półprzewodników samoistnych może być german – ciało
Różniczkowe prawo Ohma
J =
γ
⋅
E ,
stąd E =
ρ
⋅
J
Ć
wiczenie 13
4
stałe, o doskonałej sieci krystalicznej z naturalnymi własnościami półprzewodzącymi. Dla półprzewod-
nika samoistnego n = p.
Zasadnicze jednak znaczenie w technice półprzewodników mają atomy obcych ciał, nazywane do-
mieszkami, a znajdujące się w sieci krystalicznej półprzewodnika (germanu lub krzemu).
Atomy pierwiastków stanowiących domieszki mające pięć elektronów walencyjnych nazywają się
donorami. Należą do nich np.: fosfor (P) – dielektryk i arsen (As) - półprzewodnik.
Atomy stanowiące domieszki i mające trzy elektrony walencyjne nazywają się
akceptorami. Są to
np.: glin (Al), ind (In), gal (Ga).
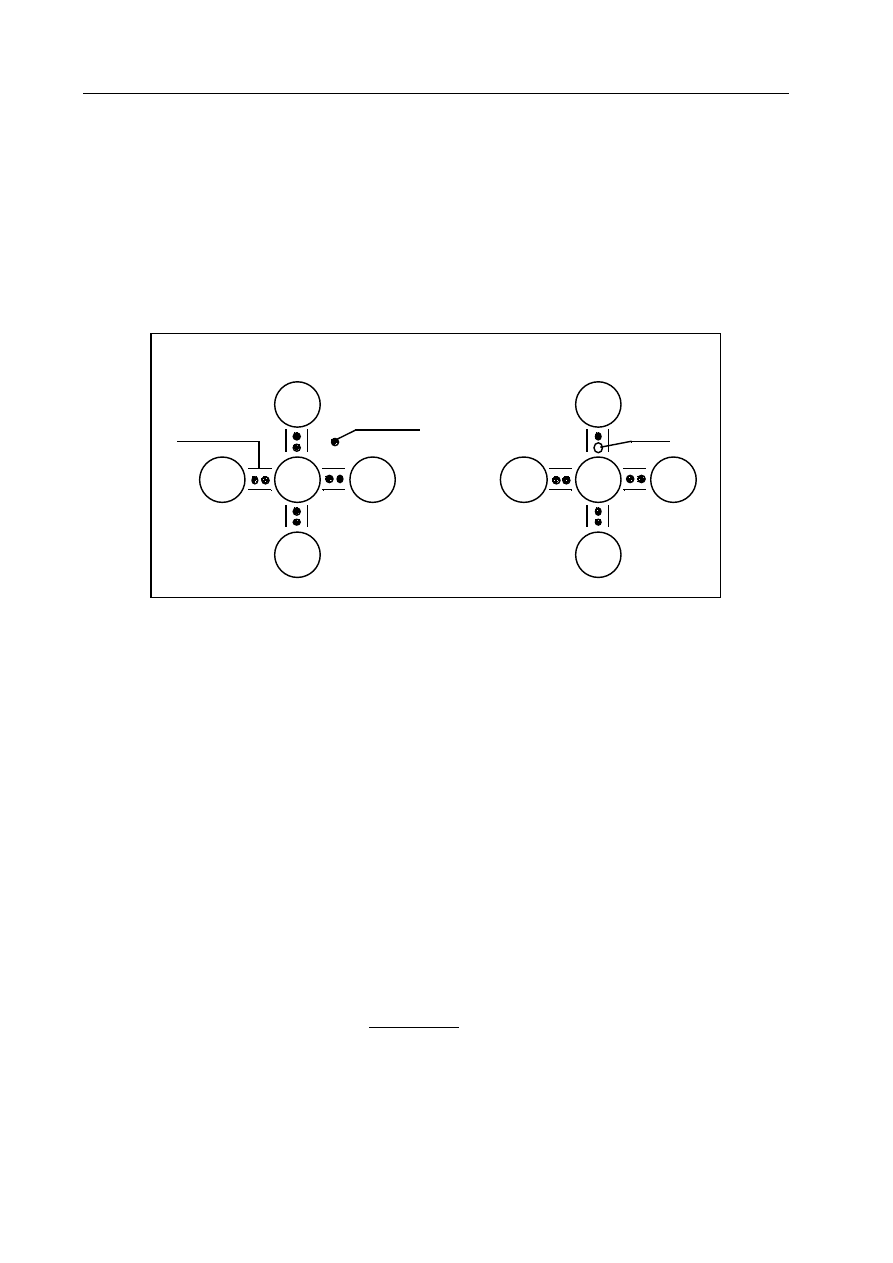
W przypadku wprowadzenia fosforu do sieci krystalicznej germanu, cztery z pięciu elektronów fosfo-
ru utworzą wiązania kowalentne z sąsiednimi atomami germanu, podczas gdy piąty elektron jest luźno
związany ze swym macierzystym atomem (rys. 13.6a).
dziura
b)
Ge
Ge
Ge
In
Ge
elektron
swobodny
a)
Ge
P
Ge
Ge
Ge
wiązanie
kowalentne
Rys. 13.6. Domieszki w germanie: fosfor (a) i ind (b)
Wystarcza niewielka energia aby piąty elektron został przeniesiony do pasma przewodnictwa i wziął
udział w przewodzeniu prądu. Takie atomy domieszek dają większą koncentrację elektronów niż dziur, a
więc warunkują przewodnictwo elektronowe. Półprzewodnik zawierający domieszki donorowe nazywa-
my półprzewodnikiem typu n.
Na pasmowym modelu energetycznym wprowadzenie atomu fosforu wytwarza nowy poziom energe-
tyczny (donorowy) leżący w górnej części pasma zabronionego i dla przeniesienia elektronów z pasma
donorowego do pasma przewodnictwa potrzebna jest stosunkowo niewielka energia z zewnątrz.
W przypadku wprowadzenia domieszek atomów z 3 elektronami walencyjnymi np. indu do sieci kry-
stalicznej germanu, w wiązaniach kowalentnych atomu indu z sąsiednimi atomami germanu będzie bra-
kowało jednego elektronu – jest to równoznaczne z istnieniem w tych wiązaniach dziur (rys. 13.6b).
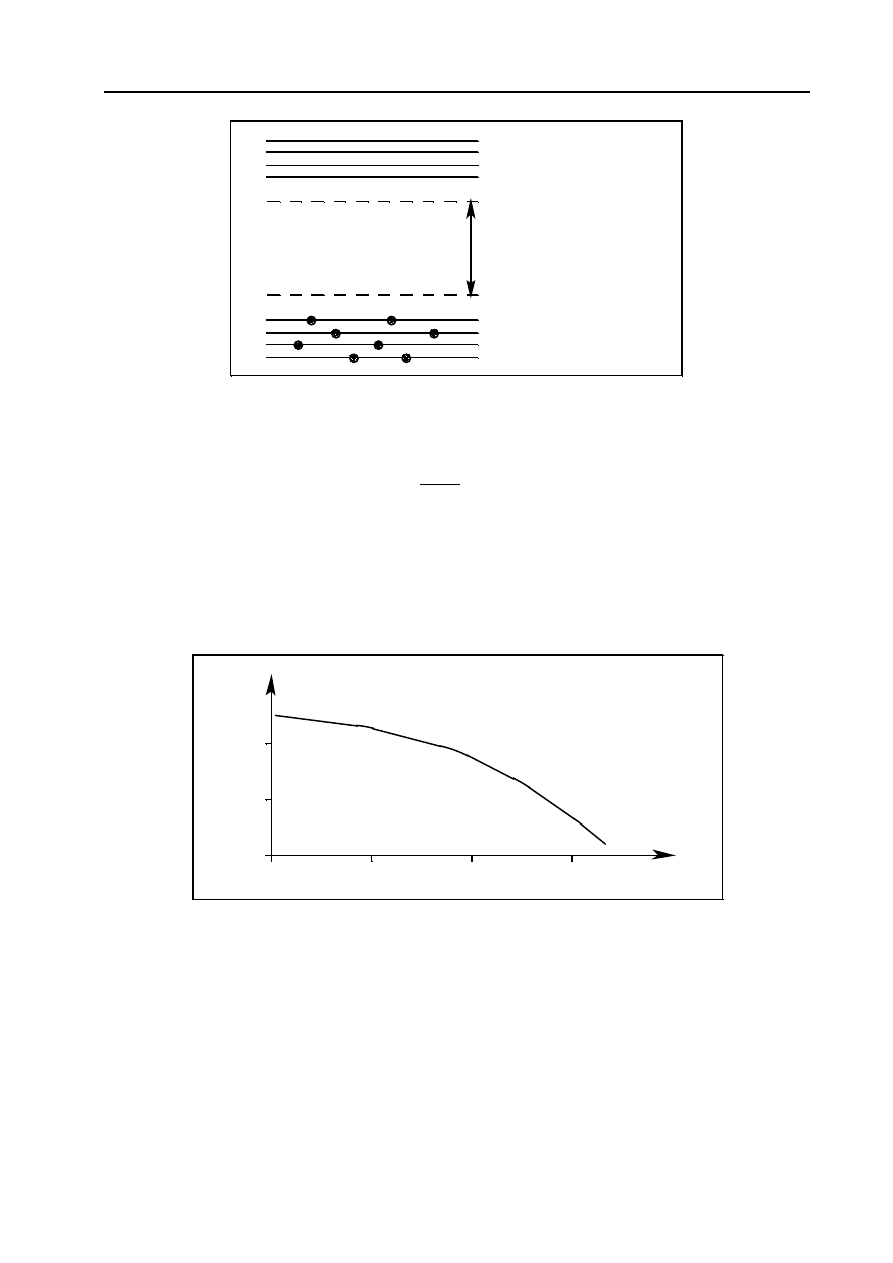
Na modelu pasmowym (rys. 13.7) pojawia się nowy poziom energetyczny, leżący w paśmie wzbro-
nionym w pobliżu pasma podstawowego, w którym powstają dziury. Domieszki akceptorowe wychwy-
tują elektrony z pasma walencyjnego, w którym powstaje przewodnictwo dziurowe. Półprzewodnik za-
wierający domieszki akceptorowe nazywamy półprzewodnikiem typu p.
W półprzewodnikach niesamoistnych (domieszkowanych) istnieją więc na ogół dwa nośniki ładun-
ków: elektrony i dziury. W półprzewodniku typu n podstawowymi (większościowymi) nośnikami są
elektrony, a w półprzewodniku typu p –dziury.
Rezystywność półprzewodnika domieszkowanego można wyrazić wzorem
)
pu
nu
(
q
1
p
n
+
=
ρ
,
(13.3)
gdzie: q - ładunek elektronu, n - koncentracja elektronów, u
n
- ruchliwość elektronów, p - koncentra-
cja dziur, u
p
- ruchliwość dziur.
Badanie materiałów i elementów półprzewodnikowych
5
poziom akceptorowy
pasmo
walen cyjne
poziom donorowy
pasmo
przewodnictwa
pasmo
wzbronione
Rys. 13.7. Pasmowy model energetyczny półprzewodnika domieszkowanego
Dla półprzewodnika typu n zachodzi nierówność n >> p zatem
n
n
u
n
q
1
=
ρ
.
(13.4)
Jak widać z wykresu na rysunku 13.8 przez odpowiednie dawkowanie domieszek tworzących pozio-
my donorowe (a także akceptorowe) można zmieniać ilość swobodnych nośników ładunku w danej tem-
peraturze, a przez to zmieniać w dużym zakresie rezystywność półprzewodnika.
Przez połączenie dwóch obszarów o różnym typie przewodnictwa powstaje złącze dziurowo-
elektronowe czyli złącze p-n. Istotną własnością złącza p-n jest asymetria rezystancji dla różnej polaryza-
cji przyłożonego napięcia. Stanowi ona podstawę działania: prostowników, tranzystorów, tyrystorów itp.
10
14
15
10
10
16
T
ρ
10
13
3
atomy/cm
Ω
cm
1
10
Rys. 13.8. Zależność rezystywności półprzewodnika germanowego typu n od zawartości domieszek
3. Otrzymywanie krzemu monokrystalicznego
Krzem jest obecnie podstawowym surowcem do wytwarzania elementów półprzewodnikowych. Jako
jeden z najobficiej występujących w skorupie ziemskiej pierwiastków – w postaci krzemówki (S
i
O
2
) oraz
krzemianów i glinokrzemianów - jest powszechnie dostępny. Droga do uzyskania krzemu o odpowiednio
wysokiej czystości i strukturze umożliwiającej zastosowanie go do produkcji elementów półprzewodni-
kowych, jest jednak długa i skomplikowana. Warto jednak zwrócić uwagę na fakt, że aby w procesie re-
dukcji (kolejny etap produkcji krzemu) nie nastąpiło zanieczyszczenie krzemu, pręty krzemowe polikrysta-
liczne są mocowane przy użyciu folii polietylenowej, gdyż dotknięcie dłonią spowodowało ich zanieczysz-
czenie.
Ć
wiczenie 13
6
O zanieczyszczeniach mówimy wówczas, gdy w krzemie półprzewodnikowym znajdują się pierwiast-
ki pochodzące z surowca, którego nie dodano w trakcie procesu technologicznego. Ilość zanieczyszczeń
nie może przekraczać jednego atomu pierwiastka zanieczyszczającego na co najmniej milion atomów
krzemu. Zawartość zanieczyszczeń oznacza się za pomocą analizy spektralnej. Domieszki to pierwiastki
celowo wprowadzane, aby uzyskać określony typ przewodnictwa.
Fakt, że krzem polikrystaliczny posiada wysoką czystość (1atom zanieczyszczeń przypada na 10
7
÷
10
10
atomów krzemu), nie zapewnia jeszcze całkowitej kontroli nad własnościami elektrycznymi pół-
przewodnika. Przewodnictwo krzemu zależy także od budowy sieci krystalicznej.
Materiał polikrystaliczny składa się z wielu zrośniętych kryształów, przy czym wpływ na sposób ich
rozmieszczenia i na wewnętrzną strukturę jest niewielki. Taki materiał o dużych niejednorodnościach (z
defektami sieci krystalicznej) nie jest jeszcze dobrym surowcem na elementy półprzewodnikowe i dlate-
go prowadzi się monokrystalizację, która pozwala otrzymać półprzewodnik o możliwie idealnej krystali-
zacji. Podczas tego procesu wprowadza się także domieszki donorowe i akceptorowe, których ilość musi
być bardzo ściśle kontrolowana.
Monokrystalizację prowadzi się dwiema metodami: tyglową (Czochralskiego) oraz beztyglową.
Metoda Czochralskiego polega na ciągnięciu monokryształu przez zanurzenie zarodka monokrysta-
licznego (tj. Małego monokryształu o właściwej strukturze) w tyglu kwarcowym zawierającym stopiony
polikryształ krzemu o temperaturze 1400
°
C (1673K) i powolne, ciągłe podnoszenie go przy jednocze-
snym obracaniu. Wskutek tego monokryształ – mający kształt walca – narasta od strony powierzchni
cieczy, a tuż nad jej lustrem następuje krzepnięcie. Powstają w ten sposób nowe płaszczyzny sieciowe
kryształu.
Część wyprodukowanych monokryształów tnie się za pomocą specjalnej piły na płytki, które są jesz-
cze szlifowane proszkiem korundowym (Al
2
O
3
). Z 9 kg krzemu hutniczego otrzymuje się 1 kg krzemu
polikrystalicznego. Natomiast z około 3,5 kg krzemu polikrystalicznego można uzyskać 1 kg krzemu
monokrystalicznego. Jednakże 1 kg krzemu monokrystalicznego to tysiące tranzystorów.
4. Elementy półprzewodnikowe i ich zastosowanie
Zastosowanie półprzewodników wynika ze specyficznych właściwości tej grupy materiałów np. ich
wrażliwości strukturalnej a także z szerokiego wykorzystania właściwości złącza p-n. Charakterystyka
elementów półprzewodnikowych została przedstawiona poniżej.
a. Opornik fotoelektryczny (fotorezystor). Wykorzystano zmianę rezystywności materiału pod
wpływem promieni świetlnych.
Materiały: krzem, german, selen, siarczki ołowiu i kadmu.
Zastosowanie: układy sygnalizacyjne i sterujące, pirometry radiacyjne, w technice filmowej i
telewizyjnej.
b. Termistor. Opornik półprzewodnikowy o dużym współczynniku temperaturowym rezystancji
(czuły na zmiany temperatury).
Materiały: tlenki cynku, manganu, tytanu, siarczek srebra.
Zastosowanie: dokładne i szybkie metody pomiaru temperatury, kompensacja zmian temperatu-
rowych w obwodach RLC, stabilizacja temperatury, automatyczna regulacja wzmocnienia.
c. Warystor. Rezystor półprzewodnikowy którego rezystancja jest zależna od wartości przyłożone-
go napięcia (albo też od wartości przepływającego prądu). Produkowane są jako rezystory pół-
przewodnikowe nieliniowe oraz tzw. płytki zmiennooporowe do wysokonapięciowych zaworo-
wych ograniczników przepięć.
Materiały: węglik krzemu (karborund SiC), tlenek cynku (ZnO).
Zastosowanie: stabilizacja napięć i prądów, ochrona przeciwprzepięciowa (odgromniki).
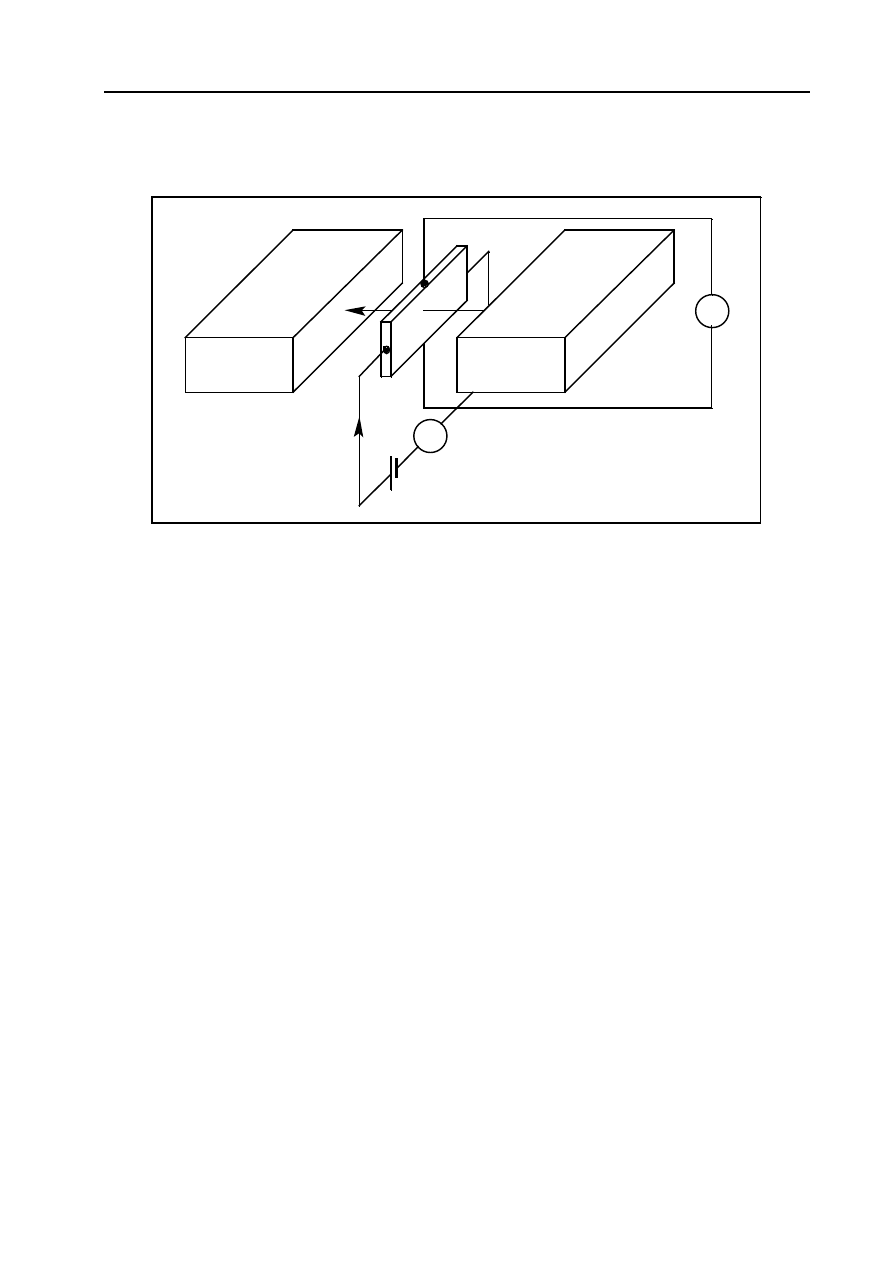
d. Hallotrony i gaussotrony. Hallotron to element półprzewodnikowy oparty na wykorzystaniu
zjawiska Halla. W płytce półprzewodnikowej włączonej w obwód prądu i umieszczonej w polu
magnetycznym, prostopadłym do jej powierzchni i kierunku prądu, powstaje tzw. napięcie Hal-
la, Element półprzewodnikowy w którym wykorzystano zależność rezystywności półprzewodni-
ka od pola magnetycznego nazywa się gaussotronem.
Badanie materiałów i elementów półprzewodnikowych
7
Materiały: german (Ge), arsenek indu (InAs), antymonek indu (InSb), tellurek rtęci (HgTe).
Zastosowanie: pomiar indukcji magnetycznej i natężenia pola magnetycznego, pośrednie pomia-
ry różnych wielkości fizycznych (np. prądu, energii elektrycznej, przesunięcia fazowego, drgań
mechanicznych, prędkości obrotowej i innych).
V
B
Α
N
I
S
H
U
Rys. 13.9. Zasada działania hallotronu: B - wektor indukcji magnetycznej, I - prąd sterujący, U
H
- napięcie Halla
e. Ogniwo fotoelektryczne. Pod wpływem naświetlenia powstaje różnica potencjałów pomiędzy
elektrodami przylegającymi do złącza p-n. Ogniwo fotoelektryczne jest zatem przetwornikiem
energii promieniowania w energię elektryczną.
Materiały: selen (Se), krzem (Si).
Zastosowanie: pomiary natężenia oświetlenia (luksomierze, światłomierze), ogniwa słoneczne.
f. Dioda. Diody półprzewodnikowe posiadają właściwość jednokierunkowego przewodzenia prądu
przez złącze p-n. Ze względu na technologię wykonania rozróżnia się: diody ostrzowe, war-
stwowe, tunelowe, fotodiody, diody elektroluminescencyjne (LED) i inne.
Materiały: krzem, german, selen.
Zastosowanie: w elektronice i energoelektronice (np. w układach prostowniczych, powielaczach
napięcia, układach przekształtnikowych, układach detekcyjnych).
g. Tranzystor. Tranzystor to trioda półprzewodnikowa (p-n-p lub n-p-n). Ze względu na budowę
rozróżnia się tranzystory: ostrzowe, ostrzowo-warstwowe, warstwowe, fototranzystory i inne.
Materiały: krzem (głównie), german, arsenek galu.
Zastosowanie: wzmacniacze, układy generacyjne, przetwornice itp.
h. Tyrystor. Tyrystor jest półprzewodnikowym zaworem sterowanym składającym się z czterech
warstw p-n-p-n.
Materiał: krzem.
Zastosowanie: przetworniki napięcia (falowniki), układy prostownicze o regulowanym napięciu,
przekaźniki półprzewodnikowe i inne.
i. Układ scalony. Układ elektroniczny mający postać jednolitej miniaturowej płytki półprzewodni-
kowej zamkniętej w obudowie. Przy zastosowaniu odpowiednich technologii półprzewodniko-
wych na wspólnym podłożu krzemowym wytwarza się wiele elementów układu (tyrystorów,
diod, kondensatorów, rezystorów). Osiągnięcia technologii wytwarzania układów scalonych
wpłynęły na rozwój układów o zwiększonej skali integracji. Postęp ten pozwolił na podjęcie
produkcji złożonych układów elektronicznych takich jak: pamięci półprzewodnikowe (RAM
i ROM), kalkulatory i mikroprocesory.
Ć
wiczenie 13
8
5. Technologia produkcji płytek zmiennooporowych
Oporniki półprzewodnikowe, zwane warystorami, znalazły największe zastosowanie w zaworowych
ogranicznikach przepięć w postaci płytek zmiennooporowych tworzących słup zmiennooporowy.
Podstawowym surowcem do produkcji płytek jest węglik krzemu (SiC) tzw. karborund, który otrzy-
muje się z koksu i piasku kwarcowego przez spiekanie w piecach łukowych w temperaturze około
2000
°
C.
Drugim podstawowym surowcem jest lepiszcze. Może to być szkło wodne, glinki ceramiczne bądź
syntetyczne żywice specjalne.
Mieszanina SiC + lepiszcze jest prasowana i formowana w płytki pod ciśnieniem 150 MPa, suszona i
wypiekana w temperaturze zależnej od rodzaju lepiszcza Powierzchnie boczne są lakierowane a czołowe
metalizowane. Metalizacja zapewnia równomierny rozkład prądu na powierzchni.
Zjawisko nieliniowości warystorów nie jest w pełni dotychczas rozeznane, niemniej jednak w każdej
teorii podstawę znaczenie przypisuje się istnieniu warstwy SiO
2
otaczającej ziarna węglika krzemu. War-
stwa wpływa zarówno na półprzewodnikowe własności materiału, jak i decyduje o jego nieliniowej cha-
rakterystyce.
6. Pytania kontrolne
1. Omówić własności materiałów półprzewodnikowych
2. Pasmowy model energetyczny ciała stałego
3. Domieszkowanie półprzewodników
4. Technologia produkcji krzemu monokrystalicznego
5. Zastosowanie półprzewodników
6. Produkcja płytek zmiennooporowych
Literatura
1.
Glazer W., Antoniewicz J.:
Wstęp do materiałoznawstwa elektrycznego. PWN, Warszawa 1971
2.
Kolbiński K., Słowikowski J.:
Materiałoznawstwo elektrotechniczne. WNT, Warszawa 1978
3.
Tietze U., Schenk Ch.:
Układy półprzewodnikowe. WNT, Warszawa 1996
II. BADANIA
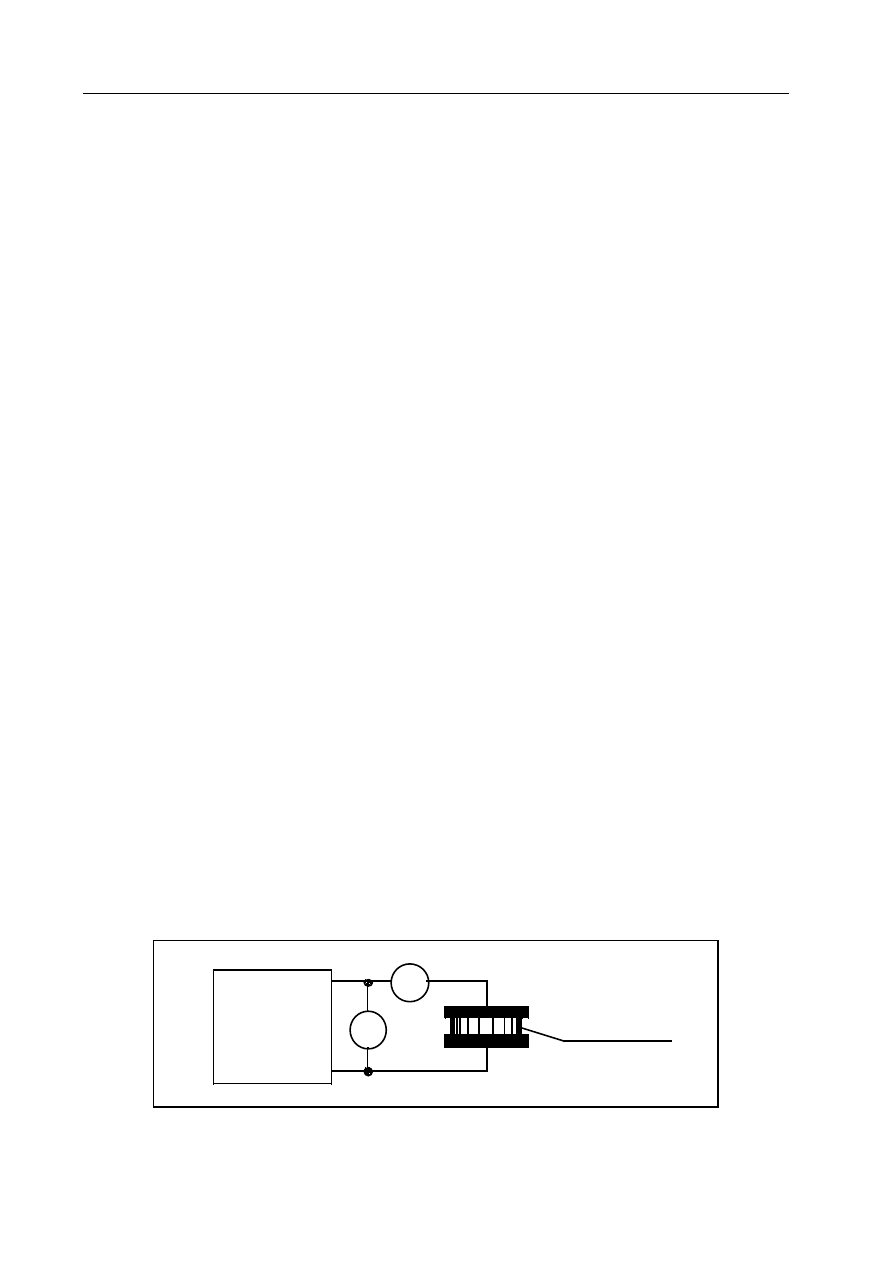
1. Pomiar charakterystyk napięciowo-prądowych
płytek zmiennooporowych
Schemat układu przedstawia rysunek 13.10. W ćwiczeniu należy:
−
zdjąć charakterystyki U = f
(I) dwóch płytek zmiennooporowych korzystając ze źródła napięcia
stałego w zakresie 0
÷
300V (rys. 13.10),
−
obliczyć rezystancję płytek (R = U/I); wyniki pomiarów i obliczeń przedstawić w tabeli 13.1,
Zasilacz
napięcia
stałego
Płytka
zmien nooporowa
V
mA
Rys. 13.10. Układ do zdejmowania charakterystyki napięciowo-prądowej
Badanie materiałów i elementów półprzewodnikowych
9
Tab. 13.1. Wyniki pomiarów i obliczeń
temperatura otoczenia
ϑ
= ..........
°
C
Próbka 1
Próbka 2
Lp.
U
I
R
U
I
R
V
mA
Ω
V
mA
Ω
1
2
−
wykreślić zależności U = f
(I) oraz R = f
(I),
−
zakładając zależność U = f
(I) w postaci
U
A I
= ⋅
α
(13.5)
obliczyć współczynniki A i
α
,
gdzie: A - stała zależna od kształtu i wielkości ziaren SiC oraz zastosowanej technologii,
α
-
współczynnik nieliniowości.
Przykład obliczenia
Logarytmując wyrażenia po obu stronach równania (13.5) otrzymamy
ln
ln
ln
U
A
I
=
+ ⋅
α
.
(13.6)
Podstawiając y = lnU, x = lnI oraz c = lnA otrzymujemy zależność (13.6) w postaci równania linii
prostej
y
c
x
= + ⋅
α
(13.7)
Równanie tej linii można wyznaczyć różnymi metodami, np. metodą najmniejszych kwadratów, me-
todą wybranych punktów, metodą średnich i innymi. Metoda najmniejszych kwadratów uważana za naj-
lepszą wynika z założenia, że wartości eksperymentalne są najlepiej przedstawione przez równanie, jeżeli
suma kwadratów różnic wartości zmierzonych i wyliczonych osiąga wartość minimalną. Największa
wada tej metody – pracochłonność – traci na znaczeniu po upowszechnieniu się metod komputerowych.
Przedstawiony przykład to znacznie prostsza metoda punktowa.
Dzielimy wszystkie punkty pomiarowe na dwie grupy (patrz tabela 13.2) o liczebnościach n
1
i n
2
(najlepiej n
1
= n
2
= n/2 przy parzystej liczbie pomiarów n) i obliczamy wartości średnie w obydwu gru-
pach.
Tab. 13.2. Wyznaczanie równania linii prostej
Lp.
U
I
y = lnU
x = lnI
–
V
A
–
–
1
U
1
I
1
y
1
= lnU
1
x
1
= lnI
1
2
U
2
I
2
y
2
x
2
.
...
...
...
...
.
...
...
...
...
n
1
U
n
1
I
n
1
y
n
1
x
n
1
y
y
n
i
n
i
1
1
1
1
=
=
Σ
x
x
n
i
n
i
1
1
1
1
=
=
Σ
Ć
wiczenie 13
10
n
1
+
1
U
n
1
1
+
I
n
1
1
+
y
n
1
1
+
x
n
1
1
+
n
1
+
2
U
n
1
2
+
I
n
1
2
+
y
n
1
2
+
x
n
1
2
+
.
...
...
...
...
.
...
...
...
...
n
U
n
I
n
y
n
x
n
y
y
n
i n
n
i
1
1
2
1
=
= +
Σ
x
x
n
i n
n
i
1
1
2
1
=
= +
Σ
Równanie linii prostej przechodzącej przez dwa punkty ( x
y
1
1
,
) i ( x
y
2
2
,
) ma postać
y
y
y
y
x
x
x
x
−
=
−
−
−
1
2
1
2
1
1
(
) ,
(13.8)
po przekształceniu
y
y
y
y
x
x
x
y
y
x
x
x
=
−
−
−
⋅
+
−
−
⋅
1
2
1
2
1
1
2
1
2
1
.
(13.9)
Z porównania wzorów (13.7) i (13.9) wynikają wzory na współczynniki A i
α
c
A
y
y
y
x
x
x
=
=
−
−
−
ln
1
2
1
2
2
1
,
(13.10)
a więc
A
e
y
y
y
x
x
x
=
−
−
−
1
2
1
2
1
1
,
α =
−
−
y
y
x
x
2
1
2
1
.
(13.11)
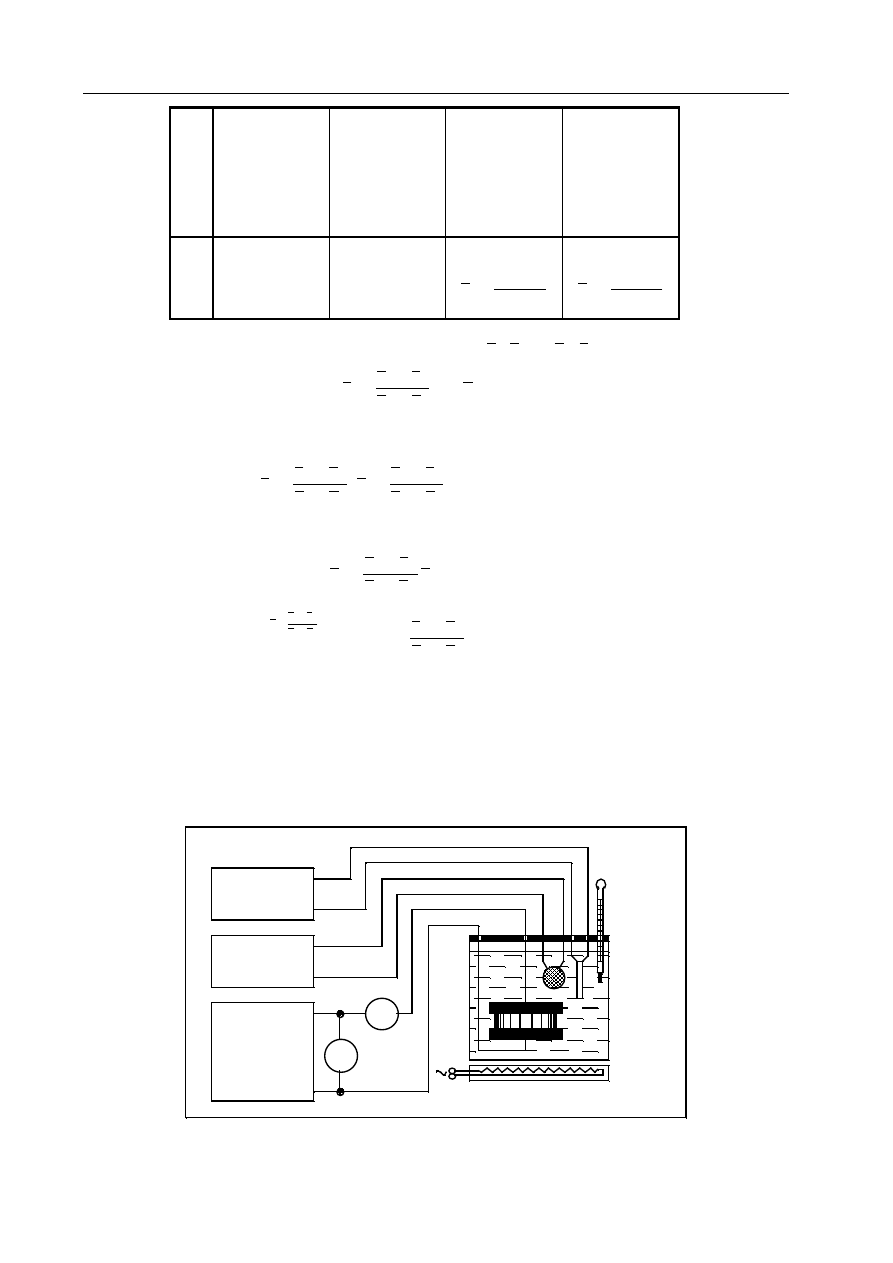
2. Pomiar charakterystyk R = f
(
ϑϑϑϑ
) termistora, czujnika platynowego
i płytki zmiennooporowej
Schemat układu przedstawia rysunek 13.11. W podgrzewanym naczyniu z olejem umieszczona została
płytka zmiennooporowa (warystor) wraz z elektrodami, dwa czujniki temperatury (platynowy i termisto-
rowy) oraz termometr.
V
Zasilacz
napięcia
stałego
grzejnik
termometr
mA
Ω
Ω
Rys. 13.11. Schemat układu do wyznaczania zależności rezystancji od temperatury
Badanie materiałów i elementów półprzewodnikowych
11
W ćwiczeniu należy:
−
wyznaczyć charakterystyki R = f
(
ϑ
) termistora, płytki zmiennooporowej i czujnika platynowego
w zakresie temperatur 20
÷
100
°
C. Zależność R = f
(
ϑ
) dla płytki zmiennooporowej należy
określić z charakterystyki I = f
(
ϑ
) przy U = const,
−
wyniki pomiarów i obliczeń przedstawić w tabeli 13.3,
−
wykreślić charakterystyki R = f
(
ϑ
),
−
wyznaczyć współczynniki temperaturowe rezystancji termistora i czujnika platynowego wiedząc
ż
e
R
R
ϑ
β
=
+ ⋅
20
1
(
)
∆ϑ
,
(13.12)
gdzie: R
ϑ
- rezystancja w temperaturze
ϑ
, R
20
- rezystancja w temperaturze 20
°
C,
β
- współczynnik
temperaturowy rezystancji.
Tab. 13.3. Wyniki pomiarów i obliczeń rezystancji elementów półprzewodnikowych
Warystor (U = ....... V)
Termistor
Czujnik platynowy
Lp.
ϑ
I
R
R
R
–
°
C
A
Ω
Ω
Ω
1
2
3. Wnioski
Wnioski powinny zawierać uwagi dotyczące przebiegu ćwiczenia oraz własne spostrzeżenia związane
z otrzymanymi wynikami badań. Należy również dokonać porównania wyników pomiarów i obliczeń dla
różnych warystorów oraz charakterystyk R = f
(
ϑ
) obydwu czujników. W przypadku wystąpienia roz-
bieżności między otrzymanymi wynikami i danymi literaturowymi należy wskazać źródło tych rozbieżno-
ś
ci.