METODA MONTE-CARLO

METODA MONTE-CARLO

MAREK NAWALANY

MAREK NAWALANY

PW

PW

METODA MONTE-CARLO

METODA MONTE-CARLO

• Prosty przykład

• Prosty przykład

• Historia

• Definicja

• Generatory liczb pseudo-losowych

• Generatory liczb pseudo-losowych

• Liczenie całek

• Liczenie całek

• Rozwiązywanie równań eliptycznych

• Rozwiązywanie równań eliptycznych
i parabolicznych

i parabolicznych

METODA MONTE-CARLO

METODA MONTE-CARLO

• Modelowanie struktury cieczy

• Modelowanie struktury cieczy

• Projektowanie zbiornika retencyjnego

• Projektowanie układów o wysokiej

niezawodności

niezawodności

• Symulacja ruchu drogowego

• Symulacja ruchu drogowego

• Symulacja eksperymentów

• Symulacja eksperymentów

• Określenie strefy oddziaływania

• Określenie strefy oddziaływania

M M-C [Prosty przykład]

M M-C [Prosty przykład]

2

π

π

=

=

Ο

r

S

4

π

π

=

=

=

Ο

kw

S

r

S

4

/

π

=

≅

Ο

Ο

S

N

4

/

π

=

≅

Ο

Ο

kw

kw

S

S

N

N

⇒

⇒

⇒

⇒

N

Ο

=

4

π

⇒

⇒

⇒

⇒

kw

N

N

Ο

=

4

π

M M-C [Historia]

M M-C [Historia]

Bacon XVIIw – igła Bacona =>

π

Bacon XVIIw – igła Bacona =>

π

E. Fermi 1930 – „Fermiac”(mechaniczne
urządzenie) => symulacja dyfuzji neutronów

urządzenie) => symulacja dyfuzji neutronów

W.von Neumann i St. Ulam 1940 => gen.

W.von Neumann i St. Ulam 1940 => gen.
liczb losowych + metoda odwrotnej
dystrybuanty+zastosowanie komputera +

dystrybuanty+zastosowanie komputera +
MC => masa krytyczna reaktora

MC => masa krytyczna reaktora

Rao 1940 – „proces urodzin” jako gen.
liczb losowych

M M-C [Definicja]

M M-C [Definicja]

Metody Monte Carlo stanowią

klasę algorytmów

wykorzystujących

wykorzystujących

losowe próbkowanie w celu

losowe próbkowanie w celu

policzenia rezultatu.

policzenia rezultatu.

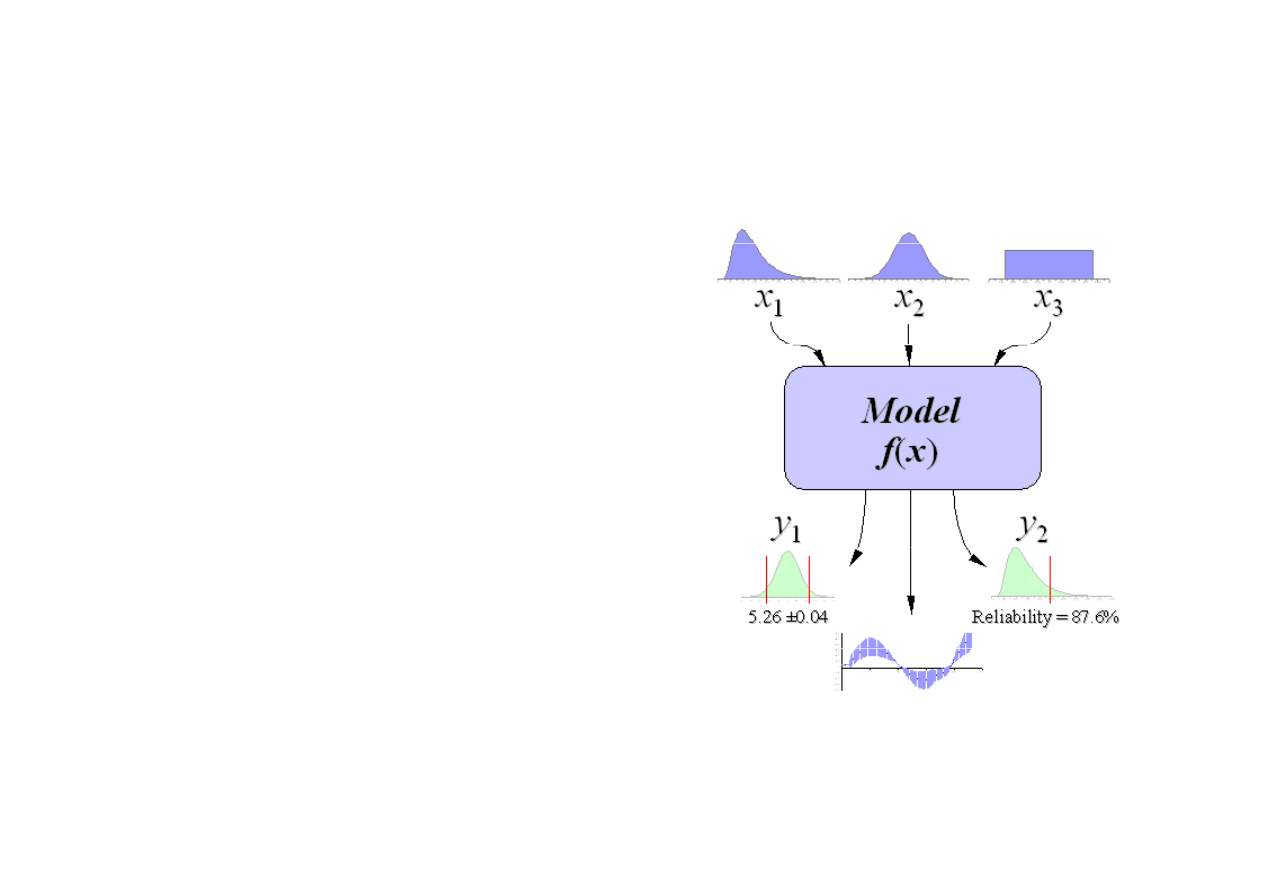
M M-C [Definicja]

M M-C [Definicja]

Są szczególnie przydatne

Są szczególnie przydatne
do symulowania układów
lub procesów o dużej

lub procesów o dużej
złożoności (np. cieczy,

złożoności (np. cieczy,
gazów, ośrodków
porowatych) gdy metody

porowatych) gdy metody
deterministyczne okazują

deterministyczne okazują
się niemożliwe do
zastosowania.

zastosowania.

M M-C [Gener. liczb pseudo-losowych(2a)]

M M-C [Gener. liczb pseudo-losowych(2a)]

Ciąg liczb pseudo-losowych o rozkładzie

Ciąg liczb pseudo-losowych o rozkładzie
równomiernym w przedziale (0,1) powstaje w
wyniku stosowania

wyniku stosowania
g e n e r a t o r a kongruencyjnego:

r

i+1

= (ar

i

+ c) mod m ,(i=0,1,...)

r

i+1

= (ar

i

+ c) mod m ,(i=0,1,...)

r

0

- seed

gdzie a = 69069, c = 0, m = 2

32

;

o k r e s T

∼∼∼∼

2

32

o k r e s T

∼∼∼∼

2

32

M M-C [Gener. liczb pseudo-losowych(2b)]

M M-C [Gener. liczb pseudo-losowych(2b)]

Ciąg liczb pseudo-losowych o

Ciąg liczb pseudo-losowych o
rozkładzie równomiernym w przedziale
(0,1) powstaje w wyniku stosowania

(0,1) powstaje w wyniku stosowania
g e n e r a t o r a Fibbonaciego:

g e n e r a t o r a Fibbonaciego:

r

= (r

+ r

) mod m ,(i=55,56,...)

r

i+1

= (r

i-24

+ r

i-55

) mod m ,(i=55,56,...)

r

0

,r

1

,...,r

55

- seed

r

0

,r

1

,...,r

55

- seed

gdzie m = 2

32

; o k r e s T

∼∼∼∼

2

32

(2

55

-1)

gdzie m = 2

32

; o k r e s T

∼∼∼∼

2

32

(2

55

-1)

M M-C [Gener. liczb pseudo-losowych(3)]

M M-C [Gener. liczb pseudo-losowych(3)]

γ

1

= µ

3

/σ

3

γ

1

= µ /σ

γ

2

= µ

4

/σ

4

- 3

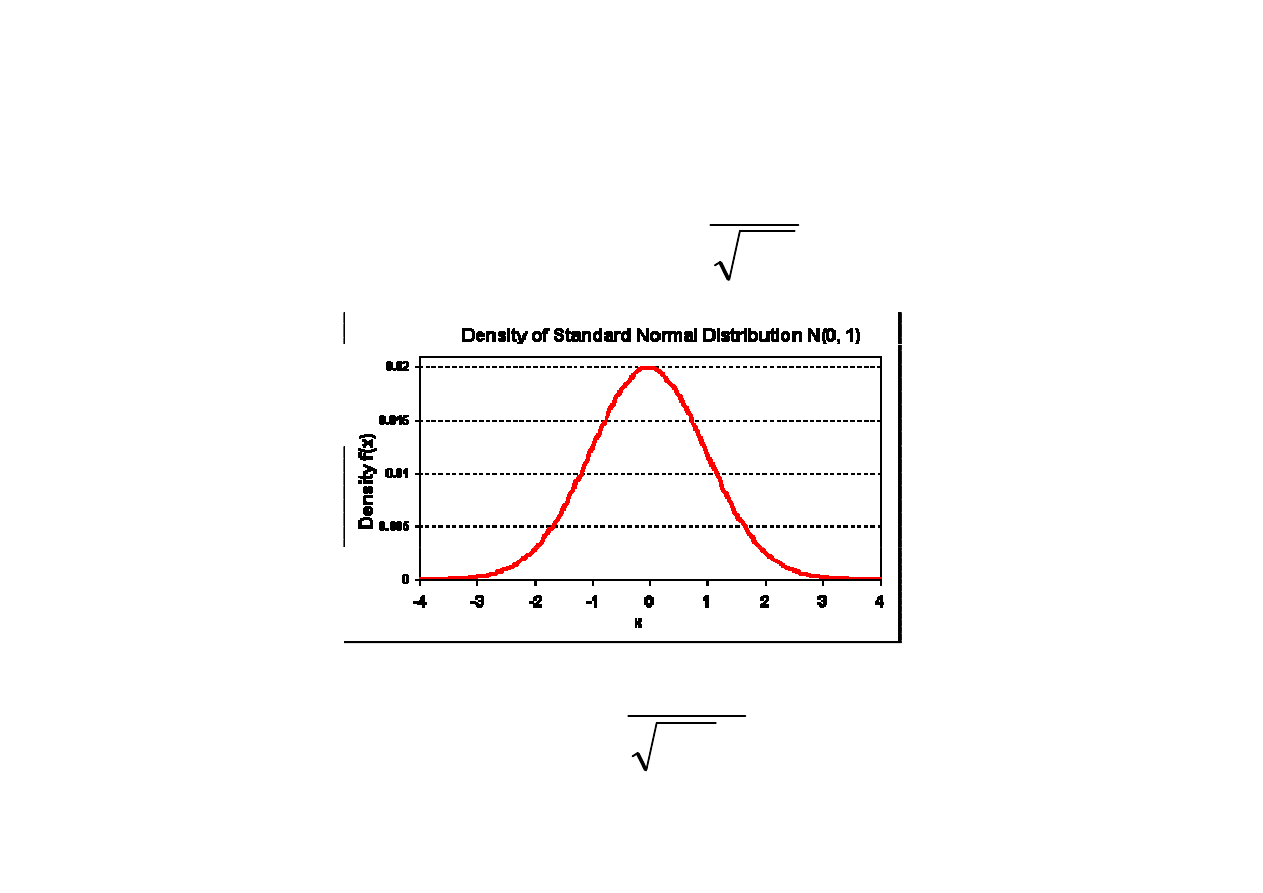
M M-C [Gener. liczb pseudo-losowych(4a)]

M M-C [Gener. liczb pseudo-losowych(4a)]

)

2

/

exp(

2

1

)

1

,

0

;

(

6

2

12

x

x

N

r

X

i

−−−−

====

≈≈≈≈

−−−−

====

∑

∑

∑

∑

ππππ

)

2

/

exp(

2

)

1

,

0

;

(

6

1

x

x

N

r

X

i

i

−−−−

====

≈≈≈≈

−−−−

====

∑

∑

∑

∑

====

ππππ

)

2

/

]

[

exp(

2

1

)

,

;

(

~

2

2

σ

µ

σ

σ

µ

µ

σ

−

−

Π

=

≈

+

=

x

x

N

X

X

2

σ

Π

M M-C [Gener. liczb pseudo-losowych(4b)]

M M-C [Gener. liczb pseudo-losowych(4b)]

Dygresja - UWAGA

Dygresja - UWAGA

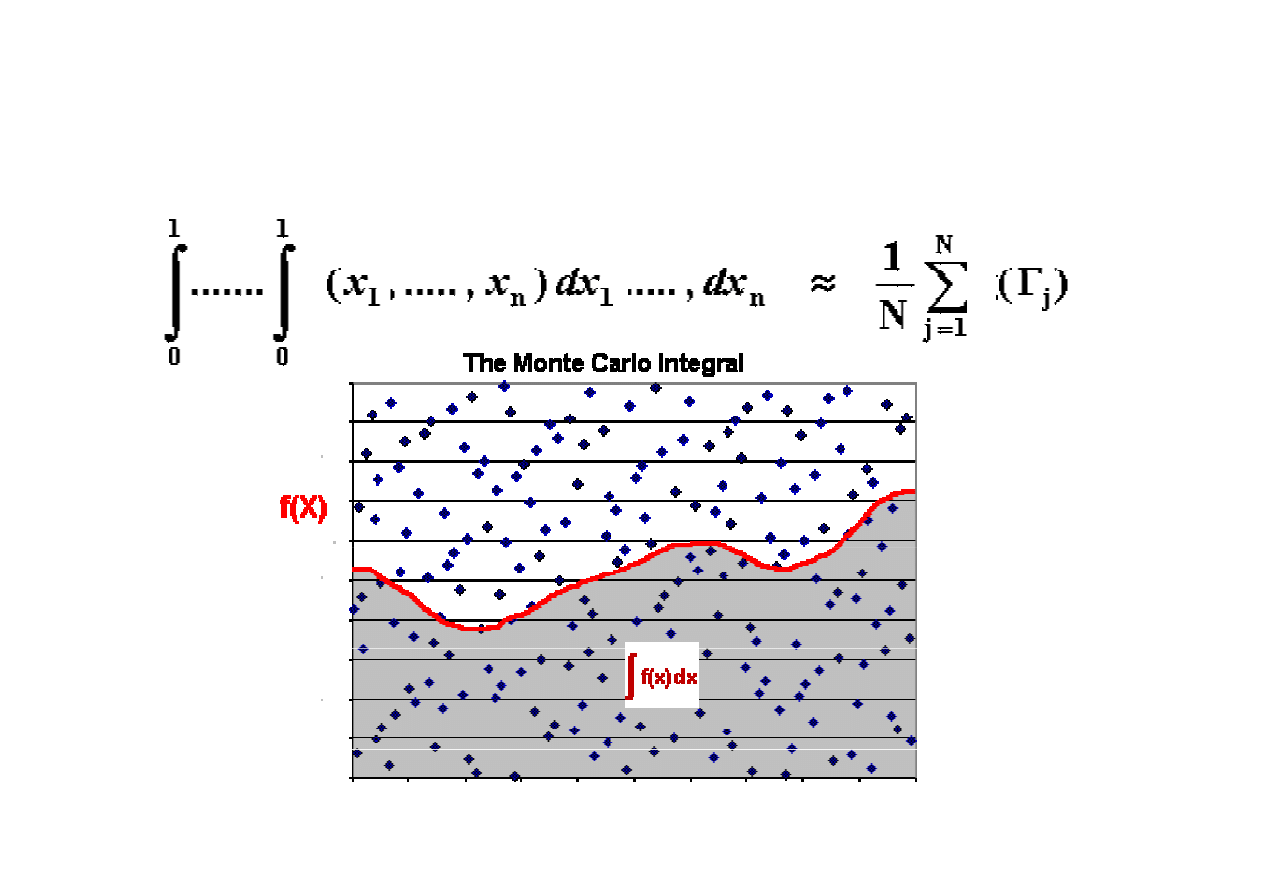
M M-C [Liczenie całek ]

M M-C [Liczenie całek ]

f

f

M M-C [Rozwiązywanie r. eliptycznych i

parabolicznych (1)]

Równanie transportu masy (1D)

)

t

,

x

(

C

)

t

,

x

(

C

)

t

,

x

(

C

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

S

x

)

t

,

x

(

C

v

)

x

)

t

,

x

(

C

D

(

x

t

)

t

,

x

(

C

±±±±

∂∂∂∂

∂∂∂∂

−−−−

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

====

∂∂∂∂

∂∂∂∂

Rozwiązanie (dla S = 0) ma postać (*)

x

x

x

t

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

Rozwiązanie (dla S = 0) ma postać (*)









αααα

−−−−

−−−−

πα

πα

πα

πα

====

vt

4

)

vt

x

(

exp

vt

4

An

M

)

t

,

x

(

C

2











αααα

−−−−

πα

πα

πα

πα

====

vt

4

exp

vt

4

An

)

t

,

x

(

C

L

L

ef

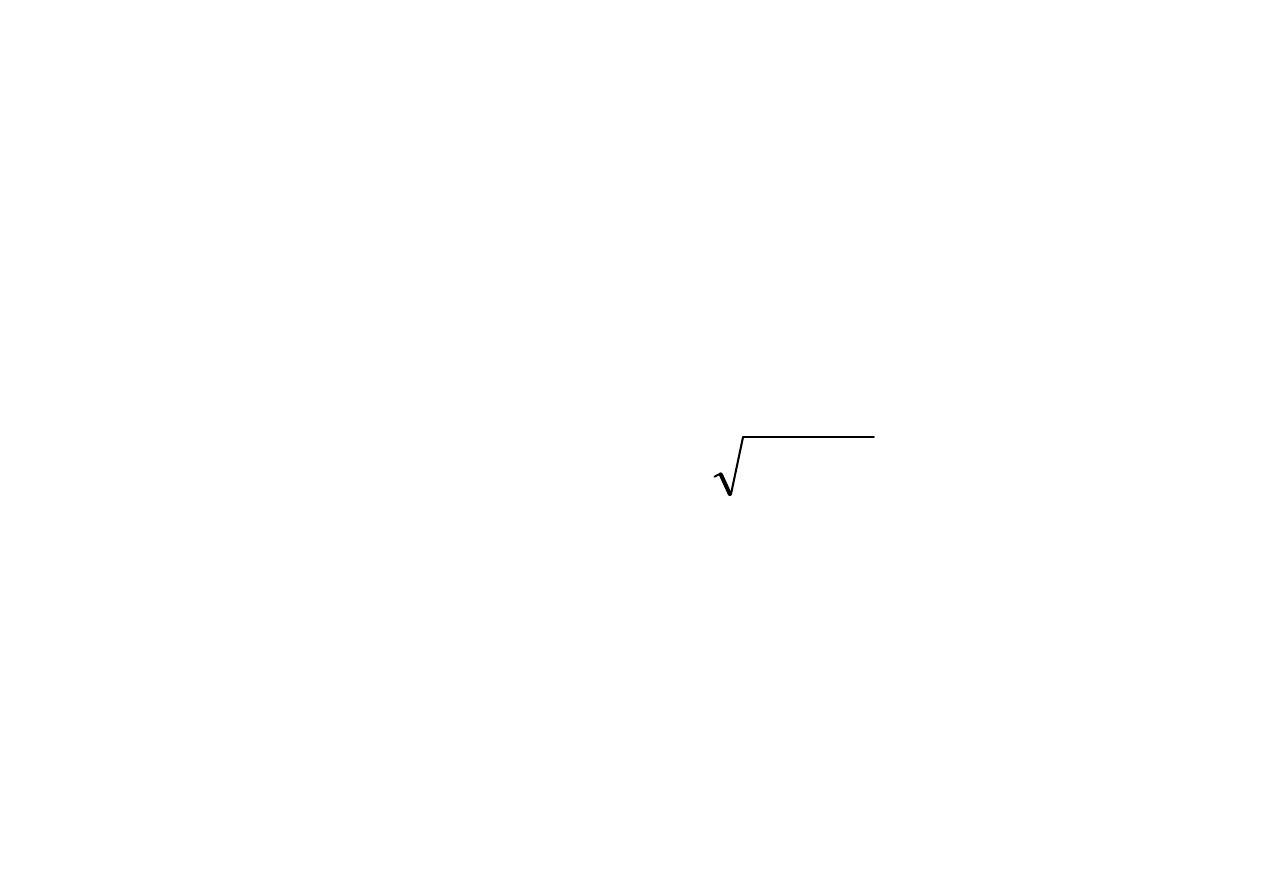
M M-C [Rozwiązywanie r. eliptycznych i

parabolicznych (2)]

Interpretacja probabilistyczna

rozwiązania (*)

(dla ustalonej chwili czasu t): stężenie ma

(dla ustalonej chwili czasu t): stężenie ma
rozkład Normalny o parametrach

vt

2

oraz

vt

αααα

====

σσσσ

====

µµµµ

Rozkład taki można uzyskać wprowadzając N

vt

2

oraz

vt

L

αααα

====

σσσσ

====

µµµµ

Rozkład taki można uzyskać wprowadzając N
cząstek o masie M/N w chwili t = 0 do ośrodka
porowatego w punkcie startowym x = 0 a

porowatego w punkcie startowym x

0

= 0 a

następnie rozważając losowe przemieszanie się

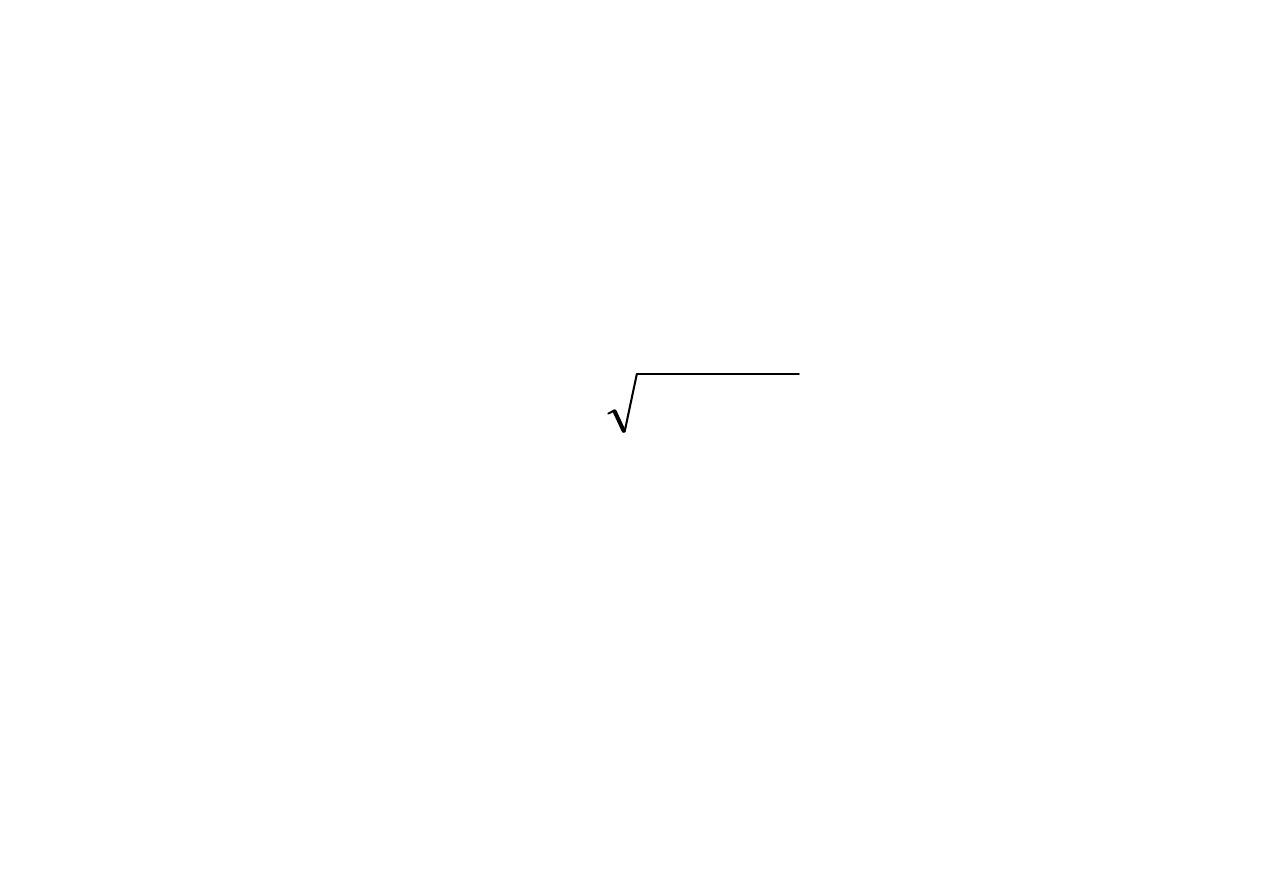
M M-C [Rozwiązywanie r. eliptycznych i

parabolicznych (3)]

każdej z tych cząsteczek w kolejnych
przedziałach czasu o

t

∆∆∆∆

przedziałach czasu o

oraz rejestrując dla wybranych chwil czasu

t

∆∆∆∆

t

v

2

X

t

v

x

L

∆∆∆∆

αααα

++++

∆∆∆∆

====

∆∆∆∆

oraz rejestrując dla wybranych chwil czasu
(technicznie, dla chwil t

i

= i*

∆

t, i=1,...) ich

(technicznie, dla chwil t

i

= i*

∆

t, i=1,...) ich

położenie w ustalonych przedziałach przestrzeni
(x

k

, x

k

+h), gdzie h- krok siatki przestrzennej.

(x

k

, x

k

+h), gdzie h- krok siatki przestrzennej.

Dla dostatecznie dużego N rozkład cząstek w
siatce zbiega do rozwiązania (*)

siatce zbiega do rozwiązania (*)

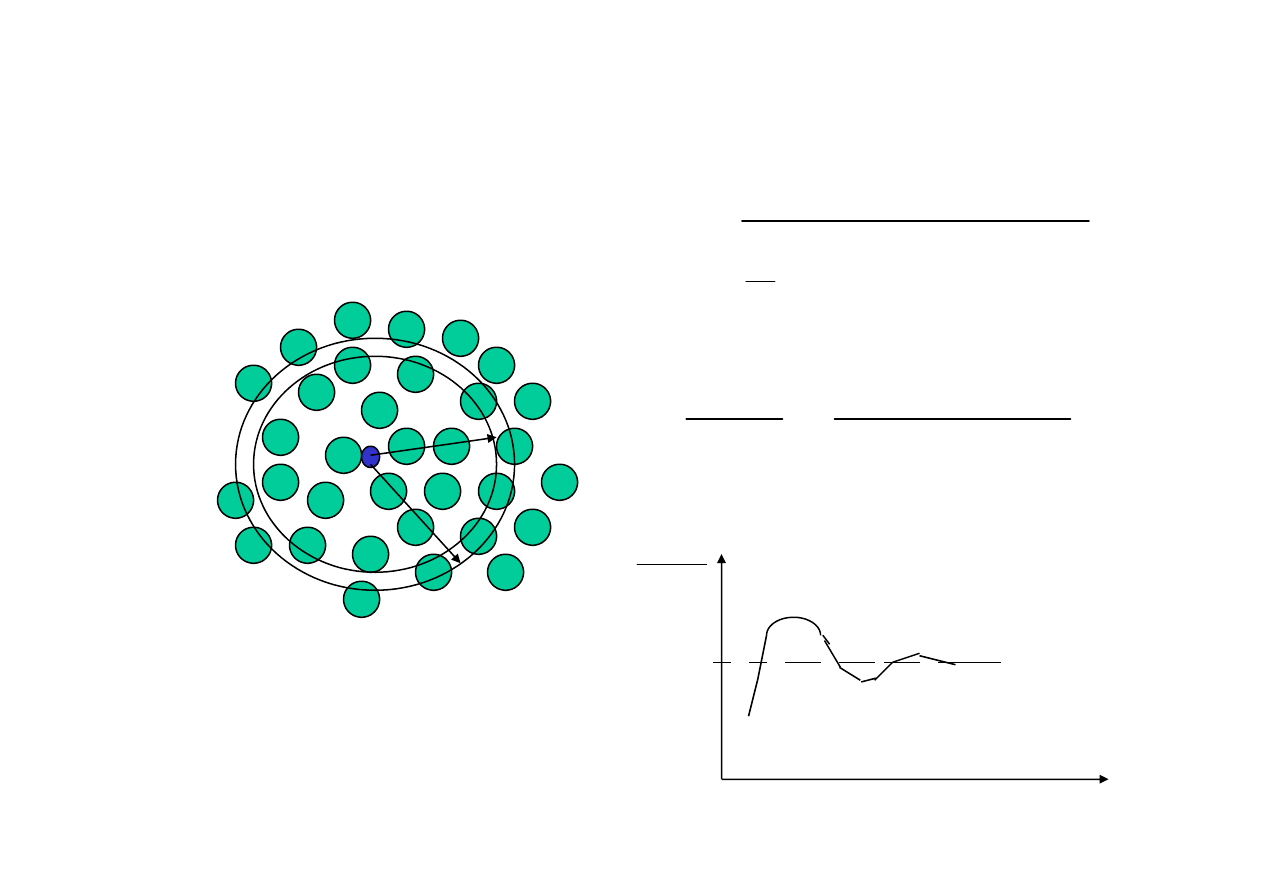
M M-C [Modelowanie struktury cieczy]

M M-C [Modelowanie struktury cieczy]

((((

))))

4

)

dr

r

,

r

(

m

)

r

(

3

++++

====

ρρρρ

((((

))))

]

r

dr

r

[

3

4

3

3

−−−−

++++

ππππ

r

N

dr

r

r

N

r

)

,

(

)

(

++++

≈≈≈≈

ρρρρ

ρρρρ

r

dr

r

++++

o

o

N

ρρρρ

r

ρ

)

(

o

r

ρ

ρ

)

(

1

r

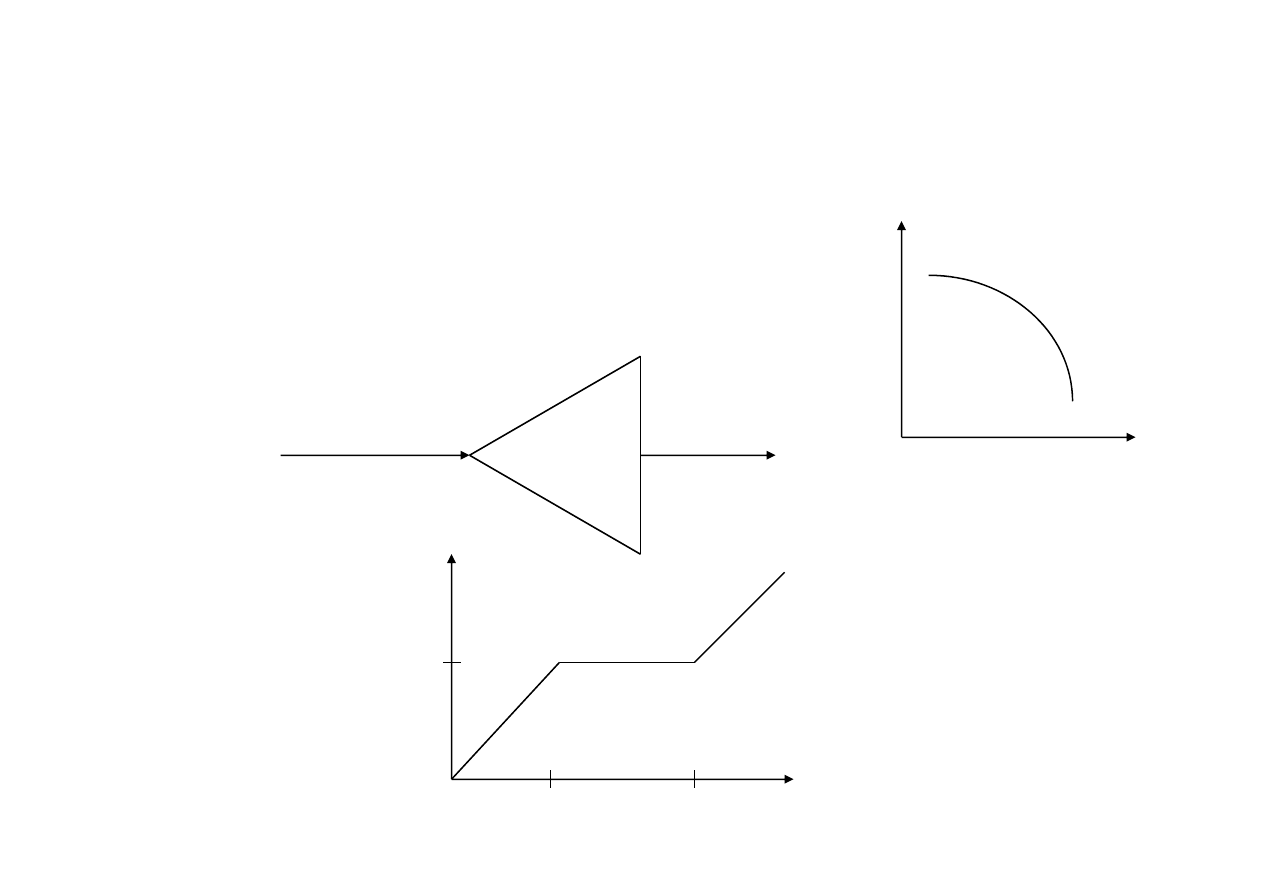
M M-C [Projektowanie zbiornika retencyjnego]

M M-C [Projektowanie zbiornika retencyjnego]

µ

(V)

µ

(V)

Y

X

V

Y

X

Y

V

V

Y

Y

X

Y

o

X

x

1

x

2

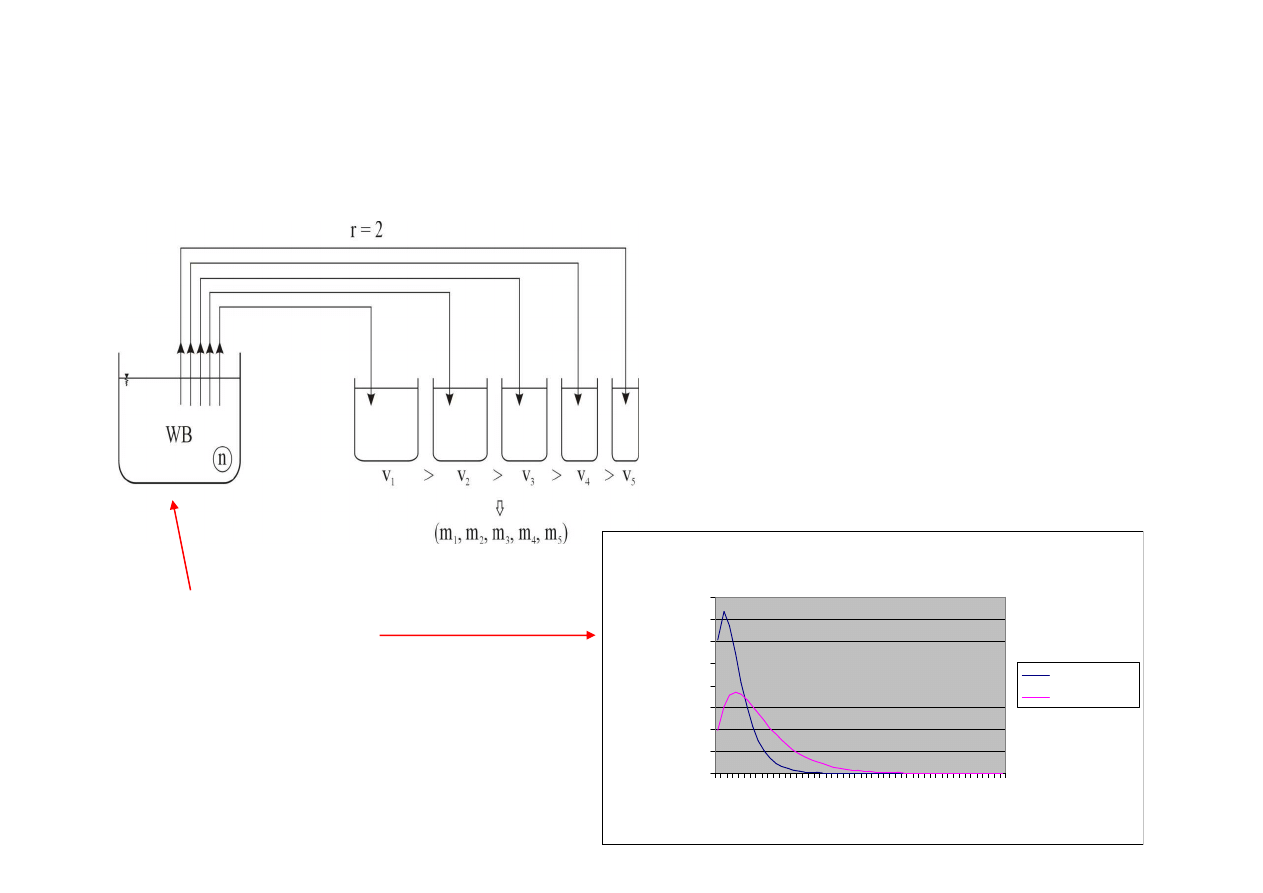
M M-C [

Symulacja eksperymentów FTT-1

]

M M-C [

Symulacja eksperymentów FTT-1

]

r 



[

]

j

j

m

r

j

m

j

j

j

p

p

m

r

n

m

P

−

+

−

+













=

)

(

1

)

(

)

|

(

]

exp[

1

)

(

n

V

p

j

j

⋅

−

−

=

+

Figure 6.1 P.d.f gamma

λ

λ

λ

n

ne

n

g

−

=

2

)

,

(

Figure 6.1 P.d.f gamma

3,00E-01

3,50E-01

4,00E-01

5,00E-02

1,00E-01

1,50E-01

2,00E-01

2,50E-01

3,00E-01

p

d

f

lambda = 1.0

lambda = 0.5

0,00E+00

5,00E-02

1

6

1

1

1

6

2

1

2

6

3

1

3

6

4

1

4

6

x

M M-C [

Symulacja eksperymentów FTT-2

]

M M-C [

Symulacja eksperymentów FTT-2

]

Uniform p.d.f.

Gamma p.d.f.

j

m

j

M-C

Theory

δδδδ

%

M-C

Theory

δδδδ

%

0

0,01002

0,01000

0,20000

0,00060

0,00060

0,00000

1

0

0,01002

0,01000

0,20000

0,00060

0,00060

0,00000

1

0,02005

0,02000

0,25000

0,00330

0,00330

0,00000

2

0,97100

0,97000

0,10309

0,99610

0,99600

0,01004

2

0

0,09990

0,10000

0,09595

0,03980

0,04000

0,50000

1

0,19734

0,19731

0,01520

0,14260

0,14220

0,28129

2

0,70214

0,70269

0,07827

0,81760

0,81770

0,01223

2

0,70214

0,70269

0,07827

0,81760

0,81770

0,01223

M M-C [Różne]

M M-C [Różne]

1. Projektowanie układów o
wysokiej niezawodności

wysokiej niezawodności

2. Symulacja ruchu drogowego

3. Określenie strefy oddziaływania

3. Określenie strefy oddziaływania

METODA MONTE-CARLO

METODA MONTE-CARLO

Dziękuję za uwagę.

Dziękuję za uwagę.