OBLICZANIE CAŁEK
OZNACZONYCH METODĄ
MONTE CARLO

Mateusz Gałecki

Czym jest Metoda Monte Carlo?

Metoda Monte Carlo została opracowana
przez zespół Johna von Neumanna podczas II
wojny światowej. Nazwa Monte Carlo miała
wskazywać na przypadkowy (losowy, hazardowy)
charakter zjawisk. Służy do matematycznego
modelowania procesów zbyt złożonych (obliczenia
całek, łańcuchów procesów statystycznych), aby
można było przewidzieć ich wyniki za pomocą
podejścia analitycznego.

Algorytm obliczania całki oznaczonej

metodą „chybił-trafił”

1.

Obliczamy supremum zbioru wartości funkcji na
przedziale całkowania

2.

Losujemy (rozkład jednostajny) pary liczb (x

i

,y

i

)

gdzie x

i

liczby z przedziału [a,b], gdzie a-dolna

granica całkowania, b-górna granica całkowania
oraz y

i

liczby z przedziału [0,c] gdzie c-

supremum zbioru wartości funkcji

3.

Sprawdzamy ile liczb y

i

jest mniejszych od

wartości funkcji w punktach x

i

4.

Dzielimy liczbę z pkt.3 przez ilość par z pkt.2
a następnie mnożymy przez iloczyn (b-a)c
otrzymując przybliżoną wartość całki.

Algorytm obliczania całki oznaczonej

metodą podstawową

1.

Losujemy (rozkład jednostajny) liczby z
przedziału [a,b], gdzie a-dolna granica
całkowania, b-górna granica całkowania

2.

Obliczamy wartości funkcji w punktach z
pkt1.

3.

Sumujemy liczby z pkt.2

4.

Mnożymy liczbę z pkt.3 przez (b-a) a
następnie dzielimy przez ilość liczb w
pkt.1 otrzymując przybliżoną wartość
całki

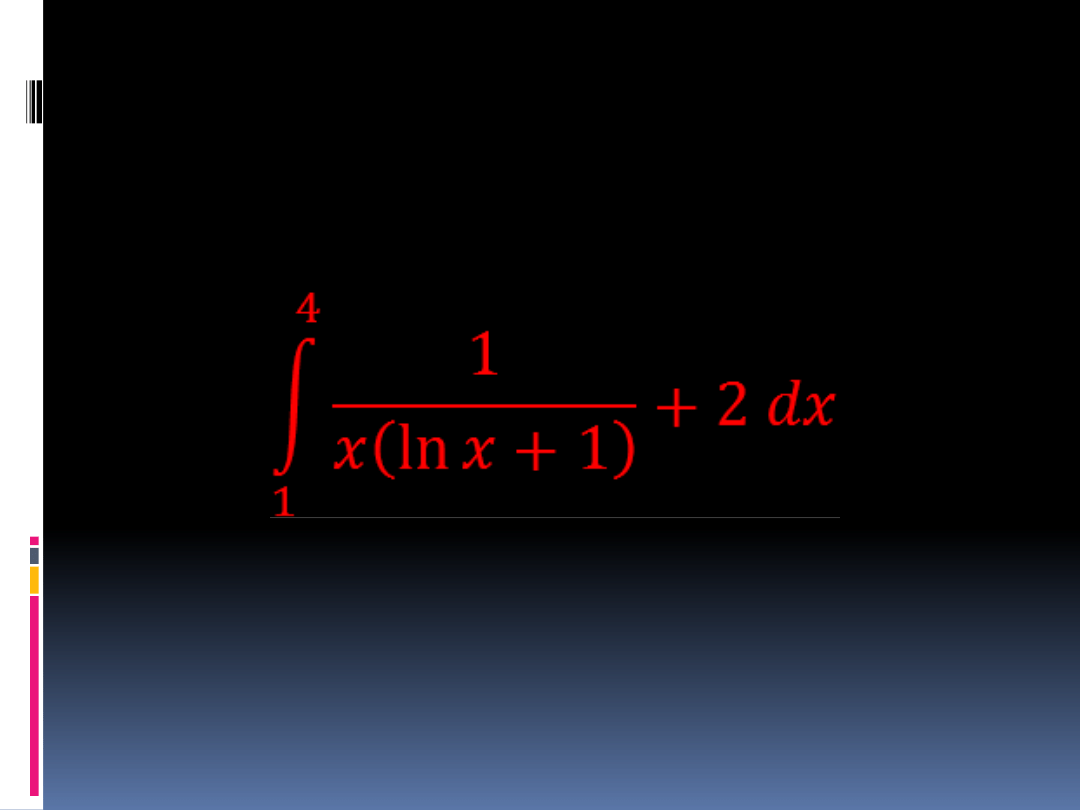
Przykład

Oblicz metodą „chybił-trafił” i metodą
podstawową całkę

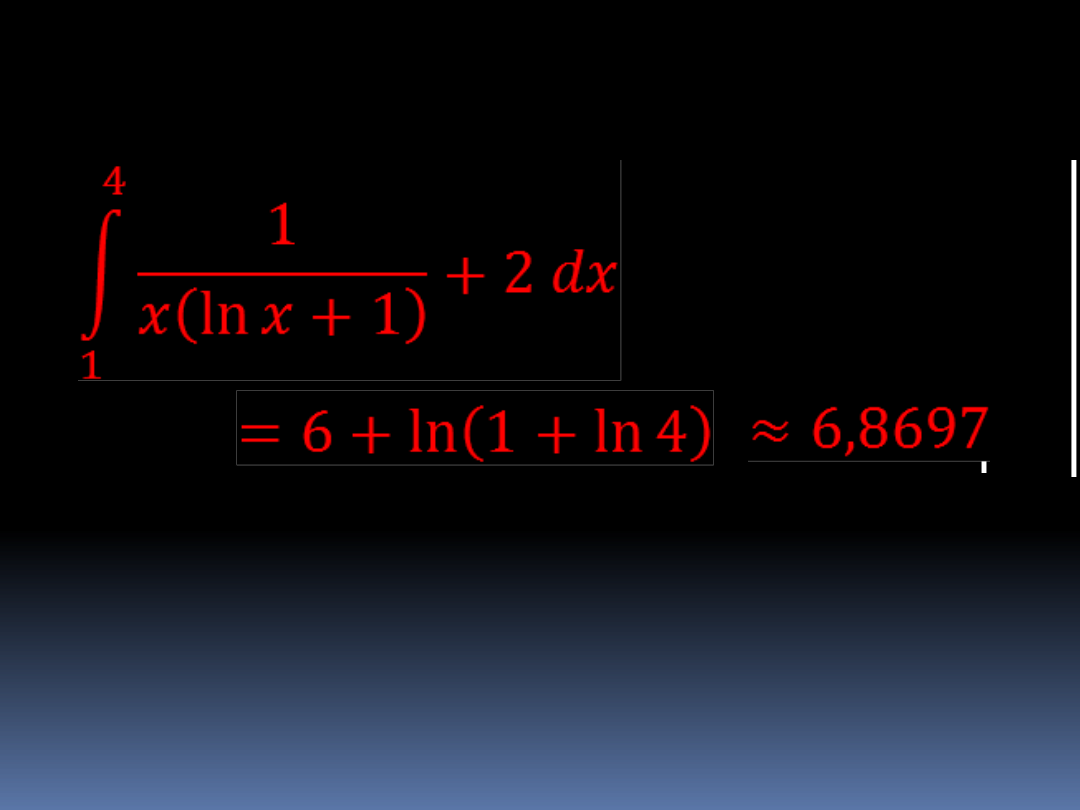
Wartość całki

Metoda „chybił-trafił”

Parametr

Liczba losowanych

punktów

100

1000

10000

Wartość minimalna

5.490000 6.489000 6.768000

Wartość maksymalna 8.010000 7.128000 6.964200

Wartość średnia

6.940800 6.849810 6.872193

Rozpiętość

2.520000 0.639000 0.196200

Odchylenie

standardowe

0.402346 0.113497 0.040468

Metoda podstawowa

Parametr

Liczba losowanych

punktów

100

1000

10000

Wartość minimalna

6.727558 6.829345 6.85629

Wartość maksymalna 7.045436 6.911557 6.882376

Wartość średnia

6.876307 6.871451 6.870031

Rozpiętość

0.317878 0.082212 0.026086

Odchylenie

standardowe

0.065598 0.017193 0.005349

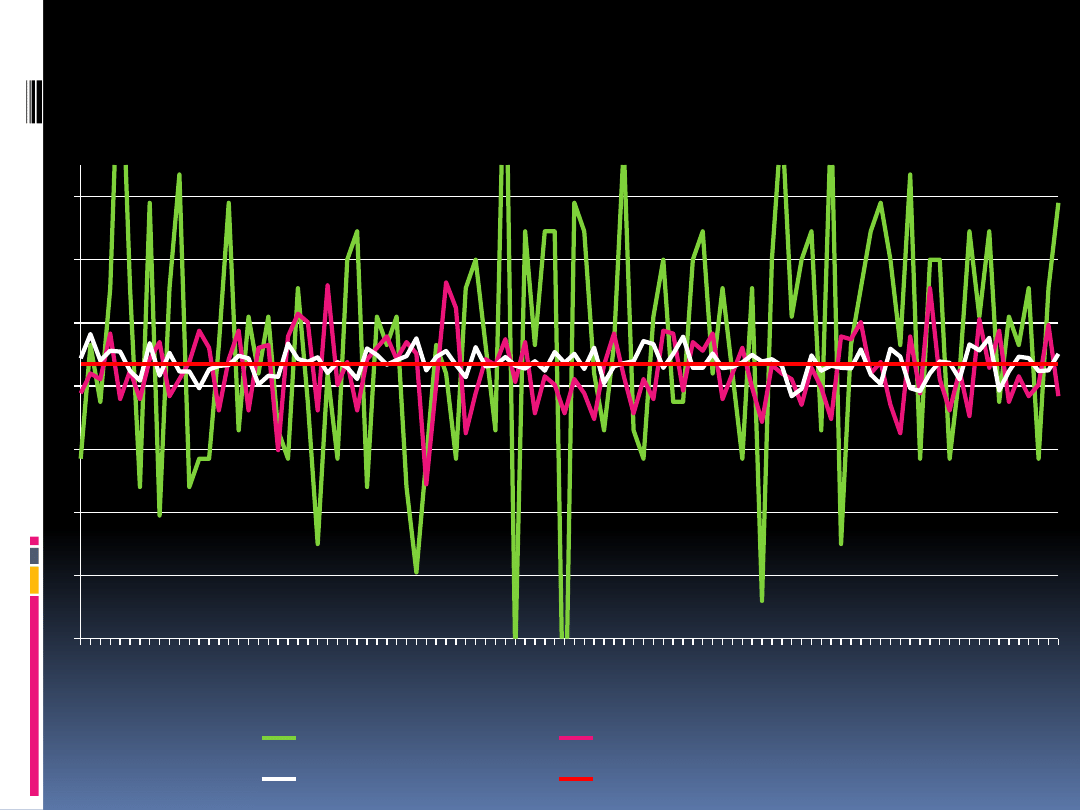
Wykres metoda „chybił-trafił”

1

7 13 19 25 31 37 43 49 55 61 67 73 79 85 91 97

6,0

6,2

6,4

6,6

6,8

7,0

7,2

7,4

100 punktów

1000 punktów

10000 punktów

Wartość całki

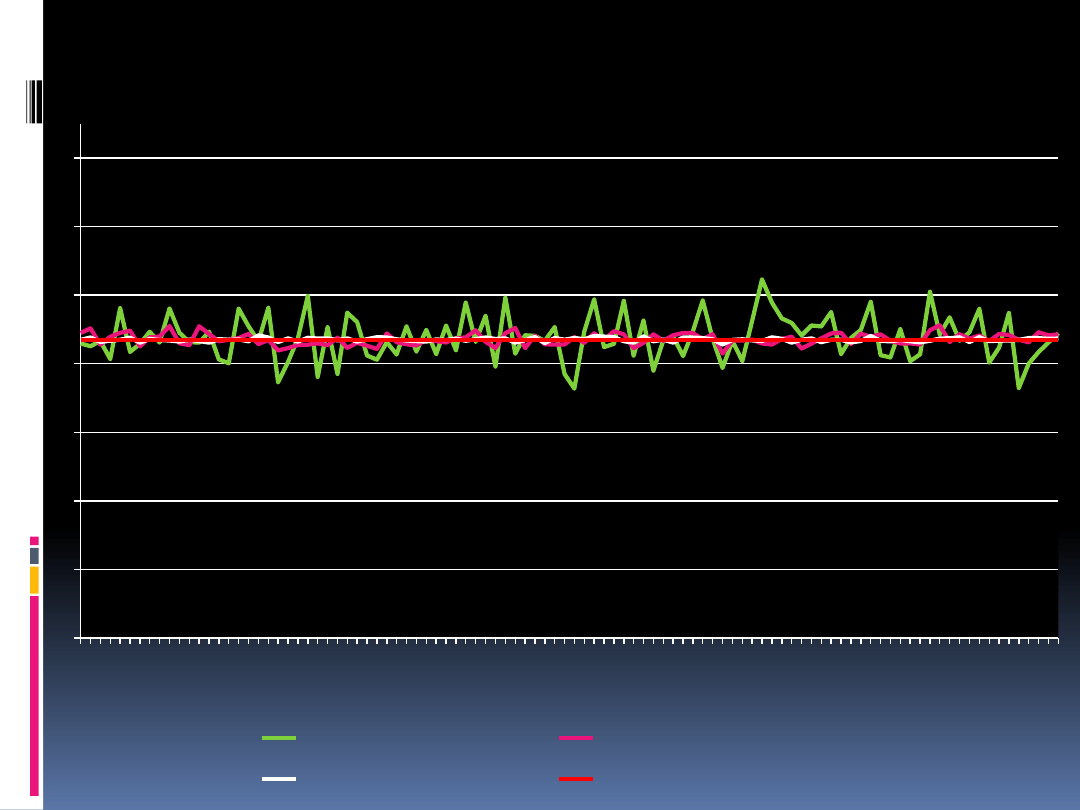
Wykres metoda podstawowa

1

7 13 19 25 31 37 43 49 55 61 67 73 79 85 91 97

6,0

6,2

6,4

6,6

6,8

7,0

7,2

7,4

100 punktów

1000 punktów

10000 punktów

Wartość całki

Wnioski



Jak możemy zobaczyć na wykresie rozpiętość wyników
w metodzie „chybił-trafił” jest duża dla prób złożonych
z niewielu punktów



Wartość całki obliczona metodą „chybił-trafił” dość
mocno odbiega od dokładnej wartości całki nawet przy
próbach wielopunktowych



Wyniki otrzymane metodą podstawową różnią się od
siebie niewiele



Metoda podstawowa przy próbach wieloelementowych
w dużym stopniu przybliża prawdziwą wartość całki



Metoda podstawowa daje o wiele lepsze wyniki niż
metoda „chybił-trafił”

Dziękuję za

uwagę

Mateusz

Gałecki