Skrypt W Rusin Analiza matematyczna 2

Wykłady z

Analizy Matematycznej II

Walter Rusin

28 lutego 2004

Spis treści

Wstęp

1 Twierdzenia o punktach stałych

1.1

Przestrzenie topologiczne

. . . . . . . . . . . . . . . . . . .

1.2

Twierdzenie Brouwera . . . . . . . . . . . . . . . . . . . . .

1.3

Przestrzenie metryczne i twierdzenie Banacha . . . . . . . .

1.4

Twierdzenie Kakutaniego

. . . . . . . . . . . . . . . . . . .

1.5

Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2 Równania różniczkowe zwyczajne

2.1

Deﬁnicja równania różniczkowego . . . . . . . . . . . . . . .

2.2

Podejście geometryczne

. . . . . . . . . . . . . . . . . . . .

2.3

Równania autonomiczne . . . . . . . . . . . . . . . . . . . .

2.4

Przykłady zagadnień . . . . . . . . . . . . . . . . . . . . . .

2.5

Badanie równań ruchu

†

. . . . . . . . . . . . . . . . . . . . .

2.5.1

Układy potencjalne o jednym stopniu swobody . . .

2.5.2

Układy potencjalne o dwóch stopniach swobody . . .

2.6

Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Istnienie i jednoznaczność rozwiązań

3.1

Twierdzenie Peano . . . . . . . . . . . . . . . . . . . . . . .

3.2

Twierdzenie Picarda-Lindelöfa . . . . . . . . . . . . . . . . .

3.3

Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

SPIS TREŚCI

4 Podstawowe klasy równań

4.1

Równania o zmiennych rozdzielonych . . . . . . . . . . . . .

4.2

Równania jednorodne

. . . . . . . . . . . . . . . . . . . . .

4.3

Równania w postaci różniczek zupełnych . . . . . . . . . . .

4.4

Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5 Zależność od danych

5.1

Ciągła zależność od warunku początkowego . . . . . . . . .

5.2

Zależność od prawej strony

. . . . . . . . . . . . . . . . . .

5.3

Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6 Równania liniowe skalarne

6.1

Czynnik całkujący . . . . . . . . . . . . . . . . . . . . . . .

6.2

Równania liniowe skalarne pierwszego rzędu . . . . . . . . .

6.3

Równanie Bernoulliego . . . . . . . . . . . . . . . . . . . . .

6.4

Równanie Riccatiego . . . . . . . . . . . . . . . . . . . . . .

6.5

Równanie Clairauta

†

. . . . . . . . . . . . . . . . . . . . . .

6.6

Równanie Lagrange’a-d’Alamberta

†

. . . . . . . . . . . . . .

6.7

Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7 Liniowe równania rzędu drugiego

7.1

Zagadnienie . . . . . . . . . . . . . . . . . . . . . . . . . . .

7.2

Równania o stałych współczynnikach . . . . . . . . . . . . .

7.3

Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8 Układy równań liniowych

8.1

Zagadnienie . . . . . . . . . . . . . . . . . . . . . . . . . . .

8.2

Układy o stałych współczynnikach . . . . . . . . . . . . . .

8.3

Równania skalarne wyższego rzędu . . . . . . . . . . . . . .

8.4

Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

9 Stabilność rozwiązań

10 Klasyﬁkacja punktów krytycznych układów

Wstęp

Zagadnienia przedstawione w niniejszym skrypcie odpowiadają wykładom
Analizy Matematycznej II prowadzonym przeze mnie wiosną 2004 roku.

Z uwagi na charakter studiów, materiał zawarty w poszczególnych wy-

kładach może wydawać się czasem bardzo okrojony i niekompletny dla osób
mających styczność z matematyką na innym poziomie. Dotyczy to szczegól-
nie rozdziału pierwszego zawierającego minimum niezbędnych pojęć topo-
logicznych. Czytając go należy mieć na względzie, że jest to namiastka se-
mestralnego wykładu topologii ogólnej, mająca na celu wprowadzenie pojęć
koniecznych do zrozumienia wybranych twierdzeń o punkcie stałym. Rów-
nania różniczkowe zwyczajne są bowiem bardzo szeroką dziedziną matema-
tyki, korzystającą z wielu metod innych jej obszarów. Starałem się jednak
w każdym rozdziale wprowadzić niezbędne pojęcia i obiekty potrzebne do
zrozumienia treści wykładów. Tych z Was, którzy są bardziej dociekliwi i
zainteresowani matematyką odsyłam zatem do licznych książek poświęco-
nych tematyce wykładu. W razie jakichkolwiek wątpliwości zachęcam Was
do uczęszczania na konsultacje. Matematyka ma raczej to do siebie, że na-
leży uczyć się jej systematycznie, choć nie ma na to reguły.

Na końcu każdego rozdziału zamieściłem zadania. Ponieważ przedmiot

odbywa się w wymiarze dwóch godzin tygodniowo, polecam ich rozwiązywa-
nie. Niektóre z nich oznaczone symbolem

† są nieco trudniejsze i wymagają

lepszego zrozumienia treści.

Należy pamiętać, że treść skryptu nie musi w 100% odpowiadać treści

wykładu, zachęcam więc do regularnego uczęszczania na zajęcia...

O czytelniku zakładam, że dysponuje znajomością podstawowych pojęć

SPIS TREŚCI

teorii mnogości wprowadzonej podczas kursu mateamtyki na I roku lub kur-
su logiki. W skrypcie stosuję notację standardową, spotykaną w większości
literatury, proszę pytać jeśli coś jest niejasne.

Rozdział 1

Twierdzenia o punktach
stałych

Teoria punktów stałych odwzorowań odgrywa ważną rolę w wielu działach
matematyki. Metody te wykorzystywane są w teorii równań różniczkowych
cząstkowych oraz zwyczajnych, metodach numerycznych. Pojawiają się czę-
sto w bardzo zaskakujących sytuacjach. W rozdziale niniejszym zajmiemy
się trzema twierdzeniami należącymi do tej klasy.

1.1

Przestrzenie topologiczne

Często sam zbiór nie jest interesującym pojęciem. Dopiero wyposażenie tego
zbioru w pewną strukturę daje możliwość rozwinięcia nowych pojęć. Dla nas
kluczowe będzie pojęcie przestrzeni topologicznej.

Deﬁnicja 1.1.1 Przestrzenią topologiczną nazywamy parę (X, O) złożoną
ze zbioru X i rodziny

O jego podzbiorów spełniającej warunki

(O1)

∅, X ∈ O

(O2) jeśli U

, U

∈ O to U

∩ U

∈ O

(O3) Jeśli U

∈ O to

∈ O gdzie α ∈ A - pewien zbiór indeksów.

ROZDZIAŁ 1. TWIERDZENIA O PUNKTACH STAŁYCH

Zbiór X będziemy nazywali przestrzenią, jego elementy punktami prze-

strzeni, a elementy rodziny

O będziemy nazywać zbiorami otwartymi w prze-

strzeni X. Rodzinę

O nazywać będziemy topologią na X. Jeśli dla pewnego

∈ X i zbioru otwartego U ∈ O mamy x ∈ U, to mówimy, że U jest otocze-

niem punktu x. Dopełnienia zbiorów otwartych w przestrzeni X nazywamy
zbiorami domkniętymi.

Deﬁnicja 1.1.2 Zbiór F nazwiemy domkniętym w przestrzeni X jeśli X

jest zbiorem otwartym w przestrzeni X.

Z praw De Morgana wynikają własności dualne do (O1)-(O3).

(D1)

∅, X są zbiorami domkniętymi

(D2) jeśli F

, F

są domknięte to F

∪ F

jest domknięty

(D3) Jeśli F

są domknięte to

jest domknięty, gdzie α

∈ A - pewien

zbiór indeksów.

Zbiory, które są jednocześnie otwarte i domknięte w przestrzeni X na-

zywamy zbiorami otwarto-domkniętymi.

Dla dowolnego zbioru A rozważmy rodzinę

wszystkich zbiorów do-

mkniętych zawierających A. Na mocy własności (D3) ich przecięcie również
jest zbiorem domkniętym. Jest to najmniejszy w sensie inkluzji taki zbiór.
Nazwiemy go domknięciem zbioru A i oznaczymy przez cl(A). Dualnie to
pojęcia domknięcia zbioru można zdeﬁniować pojęcie wnętrza zbioru jako
sumę mnogościową wszystkich zbiorów otwartych zawartych w A. Jest to
wówczas maksymalny w sensie inkluzji zbiór otwarty zawarty w zbiorze A.
Wnętrze zbioru A oznaczamy int(A).

Zauważmy, że najuboższą topologią, jaką można wprowadzić na każdym

zbiorze jest topologia

O = {∅, X}, w której jedynymi otwartymi zbiorami

są X-cała przestrzeń i

∅ - zbiór pusty. Najbogatszą topologią jest topologia,

w której

O = 2

, czyli w której każdy podzbiór zbioru X jest zbiorem

otwartym. Taką topologię nazwiemy topologią dyskretną. Dwie topologie

nazwiemy równoważnymi jeśli zbiór otwarty w przestrzeni (X, O

) jest

otwarty w przestrzeni (X, O

) oraz odwrtonie.

1.1. PRZESTRZENIE TOPOLOGICZNE

W dalszej części mówiąc przestrzeń będziemy mieli na myśli przestrzeń

topologiczną. Będziemy także opuszczać w notacji topologię pisząc X za-
miast (X, O) gdy nie będzie to prowadziło do nieporozumień (tzn. gdy X
jest wyposażone w jedną topologię). Będziemy także mówili, że zbiór U jest
otwarty zamiast zbiór U jest otwarty w X, gdy nie prowadzi to do nieporo-
zumień.

Deﬁnicja 1.1.3 Rodzinę zbiorów otwartych U

nazwiemy pokryciem otwar-

tym przestrzeni X jeśli zachodzi warunek

⊇ X.

Deﬁnicja 1.1.4 Przestrzenią zwartą nazwiemy przestrzeń, dla której z każ-
dego pokrycia otwartego można wybrać podpokrycie skończone.

Ważnym pojęciem jest pojęcie podprzestrzeni topologicznej.

Deﬁnicja 1.1.5 Podzbiór P

⊂ X przestrzeni topologicznej z topologią daną

jako

O ∩ P = {U ∩ P : U ∈ O} nazwiemy podprzestrzenią topologiczną z

topologią dziedziczoną z X.

Wiele własności dotyczących zbiorów deﬁniuje się przy użyciu pojęcia pod-
przestrzeni np. zbiorem zwartym w X nazwiemy zbiór, który jest zwarty
jako popdrzestrzeń topologiczna w X. Inaczej, zbiorami zwartymi są zbio-
ry, dla których z każdego ich pokrycia otwartego można wybrać podpokrycie
skończone.

Rozważmy teraz dwie przestrzenie topologiczne X i Y . Niech f : X → Y

będzie odwzorowaniem między nimi.

Deﬁnicja 1.1.6 Przekształcenie f : X → Y nazwiemy ciągłym jeśli dla
każdego zbioru otwartego U

⊆ Y zbiór f

−1

(U ) ⊆ X jest otwarty.

Zauważmy, że wprowadzona przed chwilą deﬁnicja przekształcenia ciągłe-
go odwołuje się wyłącznie do pojęcia zbioru otwartego. Analogicznie moż-
na zdeﬁniować przekształcenie ciągłe w terminach zbiorów domkniętych
mówiąc, że przekształcenie między dwiema przestrzeniami jest ciągłe gdy
przeciwobrazy zbiorów domkniętych są domknięte. Od tej pory mówiąc o

ROZDZIAŁ 1. TWIERDZENIA O PUNKTACH STAŁYCH

przekształceniach przestrzeni topologicznych mamy na myśli przekształce-
nia ciągłe.

Wśród przekształceń ciągłych przestrzeni istnieje pewna wyróżniona i

ważna klasa.

Deﬁnicja 1.1.7 Przekształcenie ciągłe f : X → Y nazwiemy homeomorﬁ-
zmem, jeśli jest ono "1-1" oraz "na" i dodatkowo odwzorowanie f

−1

: Y →

X jest ciągłe.

Jeśli między przestrzeniami X i Y istnieje homeomorﬁzm, to przestrzenie
te nazwiemy homeomorﬁcznymi. Bycie homeomorﬁcznymi jest silną zależ-
nością pomiędzy przestrzeniami. Relacja homeomorﬁczności, będąca relacją
równoważności dwóch przestrzeni, powoduje że przestrzenie homeomorﬁcz-
ne topologicznie są nierozróżnialne. To właśnie w tym sensie prawdziwe jest
powiedzenie, że "kubek i obrączka są tym samym". Dwie przestrzenie ho-
meomorﬁczne X i Y będziemy oznaczać X ∼

= Y .

Potrzebny nam będzie w dalszej części jeszcze jeden szczególny rodzaj

odwzorowań.

Deﬁnicja 1.1.8 Niech dane będzie odwzorowanie f : X → X. Przekształce-
nie f nazwiemy retrakcją przestrzeni X jeśli f

◦f = f. Obraz przekształcenia

f nazwiemy retraktem przestrzeni X.

Retrakcja jest zatem czymś na kształt rzutowania w przestrzeni topologicz-
nej.

Rozważmy teraz dwa odwzorowania ciągłe f, g : X → Y .

Deﬁnicja 1.1.9 Odwzorowanie ciągłe H : X × I → Y nazwiemy homoto-
pią pomiędzy przekształceniem f : X → Y i g : X → Y jeśli spełnia ono
H(x, 0) = f (x), H(x, 1) = g(x). O f i g powiemy wówczas, że są homoto-
pijne w homotopii H.

Relacja homotopijności przekształceń jest relacją równoważności. Będziemy

używać także oznaczenia f

∼ g lub krócej f ∼ g gdy dwa odwzorowania są

homotopijne. O homotopii należy myśleć jako o ciągłym przejściu od jed-
nego przekształcenia do drugiego. Jeśli spojrzeć na wykresy przekształceń

1.1. PRZESTRZENIE TOPOLOGICZNE

(zdeﬁniowane jako Graph(f ) = {(x, y) ∈ X × Y : y = f (x)}) to homotopia
oznacza "przekształcenie" wykresu odwzorowania f do wykresu odwzorowa-
nia g w sposób ciągły. Dla każdego punktu t

∈ I mamy odwzorowanie ciągłe

H(·, t) : X → Y . Parametr t nazywany jest również czasem homotopii.

Rozważmy dwa odwzorowania f, g : X → Y , gdzie przestrzeń Y jest wy-

pukła. Dowolne dwa odwzorowania w przestrzeń wypukłą są homotopijne.
Homotopię pomiędzy tymi odwzorowaniami można podać wprost wzorem
H(x, t) = (1 − t) · f (x) + t · g(x).

Mając zdeﬁniowane pojęcie homotopii dwóch przekształceń, możemy te-

raz wprowadzić pojęcie homotopijnej równoważności dwóch przestrzeni.

Deﬁnicja 1.1.10 Dwie przestrzenie X i Y nazwiemy homotopijnie równo-
ważnymi, jeśli istnieją odwzorowania f : X → Y i g : Y → X takie, że
g

◦ f ∼ id

i f

◦ g ∼ id

Relację homotopijnej równoważności dwóch przestrzeni oznaczać będziemy
X

Y . Ponieważ homotopijność przekształceń jest relacją równoważności,

to homotopijna równoważność dwóch przestrzeni także jest realcją równo-
ważności.

Przestrzeń X, która jest homotopijnie równoważna przestrzeni złożo-

nej z jednego punktu, zanurzonej w przestrzeni X, nazywamy ściągalną.
Ściągalność przestrzeni do punktu x

∈ X oznacza, że homotopijne są od-

wzorowania id

: X → X i ∗ : X → {x

}. Homotopię H : X × I → X

między odwzorowaniami id

∗ nazywamy ściągnięciem.

Zanim sformułujemy pierwsze twierdzenie o punkcie stałym zdeﬁniujmy

jeszcze pewną własność, która przysługuje niekedy przestrzeniom.

Deﬁnicja 1.1.11 Przestrzeń X ma własność punktu stałego, jeśli dla każ-
dego przekształcenia ciągłego f : X → X istnieje punkt x

∈ X taki, że

zachodzi f (x

) = x

Mając dane dwie przestrzenie X i Y oraz odwzorowanie f : X → Y

możemy skonstruować pewne specjalne klasy przestrzeni topologicznych,
mianowicie produkt przestrzeni, przestrzeń ilorazową, sklejenie przestrzeni,
cylinder przekształcenia, stożek przekształcenia oraz zawieszenie przestrzeni.

ROZDZIAŁ 1. TWIERDZENIA O PUNKTACH STAŁYCH

Deﬁnicja 1.1.12 Produktem przestrzeni topologicznych nazywać będziemy
przestrzeń topologiczną X

×Y z topologią wprowadzoną przez dowolne sumy

mnogościowe i skończone iloczyny mnogościowe zbiorów postaci U

× U

gdzie U

⊆ X i U

⊆ Y są otwarte.

Deﬁnicja 1.1.13 Niech

∼ będzie relacją równoważności w przestrzeni to-

pologicznej X. Przez przestrzeń ilorazową rozumieć będziemy przestrzeń klas
abstrakcji relacji

∼ czyli X/

∼

Mamy dane kanoniczne rzutowanie π : X → X/

∼

. W przestrzeni X/

∼

wprowadzamy najbogatszą topologię, w której przekształcenie π jest ciągłe
tzn. otwarte w X/

∼

są te zbiory U , których przeciwobrazy π

−1

(U ) są otwarte

w X. Rozważmy teraz odwzorowanie f : X → Y .

Deﬁnicja 1.1.14 Sklejeniem przestrzeni X i Y odwzorowaniem f : X → Y
nazwiemy przestrzeń X

∪

Y = (X

∪ Y )/

(x∼f(x))

Sklejenie odwzorowaniem f polega zatem na utożsamieniu punktu w X i
jego obrazu w Y .

Deﬁnicja 1.1.15 Cylindrem przekształcenia f : X → Y nazwiemy prze-
strzeń Z(f ) = (X × I

∪ Y )/

(x,1)∼f(x)

Deﬁnicja 1.1.16 Stożkiem przekształcenia f : X → Y nazwiemy prze-
strzeń C(f ) = Z(f )/

,1)∼(x

,1)

Deﬁnicja 1.1.17 Zawieszeniem przestrzeni X nazwiemy przestrzeń ΣX =
(X × I)/

,0)∼(x

,0),(x

,1)∼(x

,1)

Fakt 1.1.18 C(id

) ∼

= cl(B

n+1

Potrzebny nam będzie jeszcze jeden fakt, który z uwagi na zaawansowane
techniki topologii algebraicznej wykorzystywane w jego dowodzie, pozosta-
wimy nieudowodniony.

Fakt 1.1.19 Przestrzeń S

nie jest przestrzenią ściągalną.

1.2. TWIERDZENIE BROUWERA

1.2

Twierdzenie Brouwera

Mamy teraz prawie wszystkie narzędzia niezbędne do sformułowania i udo-
wodnienia twierdzenia Brouwera o punkcie stałym.

Twierdzenie 1.2.1 Następujące warunki są równoważne:

a) S

nie jest ściągalne

b) S

nie jest retraktem cl(B

n+1

)

c) cl(B

n+1

) ma własność punktu stałego.

Mianem twierdzenia Brouwera o punkcie stałym nazywamy właśnie c) w
twierdzeniu 1.2.1.
Dowód. Pokażmy nie wprost.

a) ⇒ b) Niech S

będzie retraktem cl(B

n+1

). Istnieje zatem retrakcja

r : cl(B

n+1

) → S

. Rozważmy teraz odwzorowania id

: S

→ cl(B

n+1

) -

włożenie sfery w domkniętą kulę, oraz

∗ : S

→ cl(B

n+1

) - przekształcenie

stałe w dowolny punkt w cl(B

n+1

). Ponieważ cl(B

n+1

) jest wypukła, to

odwzorowania id

oraz

∗ są homotopijne. Istnieje zatem homotopia H :

× I → cl(B

n+1

) od id

∗. Odwzorowanie r ◦ H : S

× I → S

jest

zatem homotopią od przekształcenia identycznościowego na sferze S

odzworowania stałego w punkt na sferze S

. To oznacza ściągalność sfery i

przeczy punktowi a).

b) ⇒ a) Przypuśćmy, że S

jest ściągalna. Istnieje zatem homotopia

H : S

× I → S

taka, że H(·, 0) = id

, H(·, 1) = ∗. Zauważmy, że

Graph(H) ∼

= C(id

) ∼

= cl(B

n+1

). Homotopia H jest zatem ciągłym prze-

kształceniem S

× I → cl(B

n+1

). Odwracając czas w homotopii H tzn.

rozważając homotpię H

(x, t) = H(x, 1 − t) otrzymamy ciągłe przekształce-

nie cl(B

n+1

) → S

× I. Mamy także kanoniczne odwzorowanie rzutowania

: S

× I → S

. Składając mamy pr

◦ H

: cl(B

n+1

) → S

- od-

wzorowanie ciągłe, będące retrakcją kuli cl(B

n+1

) na sferę S

. To przeczy

punktowi b).

b) ⇒ c) Przypuśćmy, że cl(B

n+1

) nie ma własności punktu stałego.

Istnieje zatem odwzorowanie ciągłe f : cl(B

n+1

) → cl(B

n+1

) takie, że

ROZDZIAŁ 1. TWIERDZENIA O PUNKTACH STAŁYCH

∀

x∈cl(B

n+1

)

f (x) = x. Wybierając więc dowolny punkt x ∈ cl(B

n+1

) prze-

prowadzamy odcinek przez punkt f (x) ∈ cl(B

n+1

) i określamy r(x) jako

przecięcie z S

przedłużenia tego odcinka od punktu f (x). Tak określone

przekształcenie r : cl(B

n+1

) → S

jest retrakcją kuli cl(B

n+1

) na sferę S

To przeczy punktowi b).

c) ⇒ b) Przypuśćmy, że istnieje retrakcja r : cl(B

n+1

) → S

. Rozważmy

przekształcenia a : S

→ S

zwane przekształceniem antypodycznym tzn.

przyporządkowujące x

→ −x oraz włożenie i : S

→ cl(B

n+1

). Przekształ-

cenie i

◦ a ◦ r : cl(B

n+1

) → cl(B

n+1

) jest ciągłym odwzorowaniem kuli w

siebie i nie ma punktu stałego, co przeczy punktowi c).

Twierdzenie Brouwera jest bardzo silnym twierdzeniem. Zauważmy, że

obowiązuje ono nie tylko dla kul, ale dla wszystkich przestrzeni homeomor-
ﬁcznych z kulą. Rozważmy bowiem przestrzeń X ∼

= cl(B

n+1

) i niech od-

wzorowanie h : X → cl(B

n+1

) będzie homeomorﬁzmem tych przestrzeni.

Niech f : X → X będzie ciągłym odwzorowaniem przestrzeni X w siebie.
Odwzorowanie h

◦ f ◦ h

−1

jest ciągłym odwzorowaniem kuli w siebie i na

mocy twierdzenia Brouwera ma punkt stały. Istnieje więc x

∗

∈ cl(B

n+1

)

taki, że (h ◦ f ◦ h

−1

)(x

∗

) = x

∗

. Mamy zatem (h ◦ f )(h

−1

∗

)) = x

∗

, czyli

f (h

−1

∗

)) = h

−1

∗

). Określając y

∗

= h

−1

∗

) mamy punkt stały prze-

kształcenia f : X → X.

1.3

Przestrzenie metryczne i twierdzenie Banacha

Wśród przestrzeni topologicznych na szczególną uwagę zasługują przestrze-
nie metryczne.

Deﬁnicja 1.3.1 Przestrzenią metryczną nazywamy parę (X, ) złożoną ze
zbioru X i funkcji : X × X → R spełniającej następujące warunki

(M1)

∀

∈X

, x

) 0 i (x

, x

) = 0 ⇔ x

= x

(M2)

∀

∈X

, x

) = (x

, x

)

(M3)

∀

∈X

, x

) (x

, x

) + (x

, x

)

1.3. PRZESTRZENIE METRYCZNE I TWIERDZENIE BANACHA 15

Podobnie jak w przypadku przestrzeni topologicznej będziemy w zapisie
opuszczać strukturę metryczną i pisać X zamiast (X, ). W przestrzeni me-
trycznej możemy w naturalny sposób zdeﬁniować kulę.

Deﬁnicja 1.3.2 Kulą otwartą o środku w punkcie x

∈ X i promieniu r > 0

nazwiemy zbiór B(x

, r) = {x ∈ X : (x

, x) < r}.

Każda przestrzeń metryczna jest przestrzenią topologiczną gdzie topolo-
gia wprowadzona jest przez rodzinę kul tzn. każdy zbiór otwarty jest sumą
mnogościową dowolnej liczby kul. Podczas podstawowego kursu analizy na I
roku poznaliście deﬁnicję ciągłości przekształcenia pomiędzy dwiema prze-
strzeniami metrycznymi (w szczególności dwiema przestrzeniami

R).

Deﬁnicja 1.3.3 Niech X, Y będą dwiema przestrzeniami metrycznymi, a
f : X → Y odwzorowaniem między nimi. Przekształcenie f nazwiemy cią-
głym w punkcie x

jeśli

∀

∃

δ>0

, x) < δ ⇒

(f (x

), f (x)) < .

Przekształcenie f nazwywamy ciągłym, jeśli jest ciągłe w każdym punkcie
x

∈ X.

W przestrzeni metrycznej zdeﬁniujmy ciągi zwane ciągami Cauchy’ego.

Deﬁnicja 1.3.4 Ciąg punktów (x

) w przestrzeni metrycznej X nazywamy

ciągiem Cauchy’ego jeśli

∀

∃

∈N

∀

m,n>n

, x

) < .

Ciągiem cauchy’ego nazywamy więc ciąg, którego dowolnie dalekie wyrazy
są dowolnie blisko siebie w sensie metryki na przestrzeni X. Każdy ciąg
zbieżny w przestrzeni X jest ciągiem Cauchy’ego, ale nie każdy ciąg Cau-
chy’ego jest zbieżny. Obserwacja ta prowadzi do następującej deﬁnicji.

Deﬁnicja 1.3.5 Przestrzeń metryczną, w której każdy ciąg Cauchyego jest
zbieżny do granicy w tej przestrzeni nazywamy przestrzenią zupełną.

Rozważmy teraz przekształcenie ciągłe zupełnej przestrzeni metrycznej X
w siebie.

Deﬁnicja 1.3.6 Przekształcenie f : X → X nazwiemy kontrakcją, jeśli
spełnia ono warunek

∀

∈X

(f (x

), f (x

)) c(x

, x

), gdzie c < 1.

ROZDZIAŁ 1. TWIERDZENIA O PUNKTACH STAŁYCH

Na mocy deﬁnicji, konktrakcja jest przekształceniem ciągłym. Możemy teraz
sformułować twierdzenie Banacha o punkcie stałym.

Twierdzenie 1.3.7 (Banach) Jeśli f : X → X jest kontrakcją na zupeł-
nej przestrzeni metrycznej X to f posiada dokładnie jeden punkt stały, tzn.
istnieje takie x

∗

∈ X, że f(x

∗

) = x

∗

Dowód. Niech x ∈ X i przyjmijmy x

= x. Deﬁniujemy rekurencyjnie ciąg

punktów x

= f (x

), x

= f (x

n−1

) dla n 2. Zauważmy, że ciąg (x

) jest

ciągiem Cauchy’ego. Istotnie, dla dowolnego n zachodzi

n+1

), f

)) c(f

), f

n−1

)) . . . c

(f (x

), x

)

Dla dowolnych indeksów m, n > k (bez straty ogólności możemy założyć
m

n) mamy zatem

), f

)) c

, f

n−m

)) c

((x

, f (x

))+

+(f (x

), f

)) + . . . + (f

n−m−1

), f

n−m

)))

(1 + c + c

+ . . . + c

n−m−1

)(x

, f (x

))

1 − c

, f (x

)).

Ponieważ (x

, f (x

)) jest stałe, a c

może zostać uczynione dowolnie małe

to prawa strona może zostać uczyniona dowolnie mała. Ponieważ X jest
z założenia przestrzenią zupełną, to ciąg (x

) ma granicę. Oznaczmy tę

granicę przez x

∗

. Z ciągłości f wynika, że x

∗

jest punktem stałym odwzoro-

wania f . Rzeczywiście, f (x

∗

) = f (lim

n→∞

)) = lim

n→∞

f (f

)) =

lim

n→∞

n+1

) = x

∗

. Pozostaje jeszcze wykazać jednoznaczność punk-

tu stałego. Jeśli x

∗

i x

∗

są dwoma różnymi punktami stałymi, to mamy

∗

, x

∗

) c(x

∗

, x

∗

), zatem (x

∗

, x

∗

) = 0 czyli x

∗

= x

∗

Twierdzenie Banacha odgrywa ważną rolę w dowodach istnienia i jedno-

znaczności rozwiązań równań różniczkowych cząstkowych. Z uwagi na jego
ogólność można je napotkać w wielu rozumowaniach w różnych obszarach
matematyki.

1.4. TWIERDZENIE KAKUTANIEGO

1.4

Twierdzenie Kakutaniego

Niech X i Y będą dwiema przestrzeniami topologicznymi.

Deﬁnicja 1.4.1 Odwzorowaniem wielowartościowym określamy odwzoro-
wanie F : X → 2

Dla punktu y

∈ Y możemy zdeﬁniować zbiór F

−1

(y) = {x ∈ X : y ∈

F (x)}. Dla B ⊆ Y mamy F

−1

(B) = {x ∈ X : F (x) ∩ B = ∅}. Wykresem

odwzorowania F jest zbiór Graph(F ) = {(x, y) ∈ X × Y : y ∈ F (x)}.

Deﬁnicja 1.4.2 Powiemy, że odwzorowanie wielowartościowe F : X → 2

jest górnie-półciągłe w x

∈ X jeśli dla każdego otoczenia V zbioru F (x) ist-

nieje otoczenie U punktu x takie, że F (U ) ⊆ V . Powiemy, że odwzorowanie
F jest górnie-półciągłe, jeśli jest górnie-półciągłe w każdym punkcie x

∈ X.

W dalszych rozważaniach będą nas interesować przekształcenia wielowar-
tościowe F : X → 2

o wartościach w rodzinie niepustych, zwartych i

wypukłych zbiorów przestrzeni Y .

W takim przypadku istenieje inna charakteryzacja odwzorowań górnie-

półciągłych, bardziej użyteczna z naszego punktu widzenia.

Deﬁnicja 1.4.3 Odwzorowanie F : X → 2

jest górnie-półciągłe, jeśli z

faktów x

→ x, y

→ y i y

∈ F (x

) wynika, że y ∈ F (x).

Z uwagi na zmianę charakteru przestrzeni, gdzie znajduje się obraz od-

wzorowania F zmieni się także pojęcie punktu stałego. Przez punkt stały
odwzorowania wielowartościowego rozumieć będziemy punkt x

∗

, dla którego

zachodzi x

∗

∈ F (x

∗

). Jeśli każde odwzorowanie wielowartościowe F : X →

ma punkt stały, to powiemy, że X ma własność punktu stałego w sensie

Kakutaniego.

Wynik uzyskany przez Kakutaniego wymaga wprowadzenia wielu pojęć i

narzędzi tzw. PL-topologii, znacznie wykraczających poza program wykładu
z Analizy Matematycznej II, dlatego zostanie przedstawiony bez dowodu.

Twierdzenie 1.4.4 (Kakutani) Niech X będzie zwartym, wypukłym pod-
zbiorem

. Wówczas X ma własność punktu stałego w sensie Kakutaniego.

ROZDZIAŁ 1. TWIERDZENIA O PUNKTACH STAŁYCH

Warto jednak wspomnieć, że twierdzenie Kakutaniego jest pewnym prze-
niesieniem twierdzenia Brouwera na przypadek odwzorowań wielowartościo-
wych. Po raz pierwszy twierdzenie Kakutaniego w ekonomii zostało zasto-
sowane przez Nash’a w jego teorii gier niekooperacyjnych, stąd waga pracy
Nash’a i Nagroda Nobla a nie Medal Fields’a

1.5

Zadania

1. Podzielić litery alfabetu łacińskiego na klasy homeomorﬁczności.

2. Z czym homeomorﬁczne są ΣS

, ΣS

3. Czy brzeg kwadratu na

może być jego retraktem ?

4. Udowodnij, że wykres dowolnego przekształcenia ciągłego f : I → I

przecina prostą y = x.

5. Sprawdź, że topologia dyskretna zdeﬁniowana w rozdziale 1.1 pokrywa

się z topologią wprowadzoną przez metrykę dyskretną tzn. metrykę
mającą własność

∀

, x

) = 1.

6. Załóżmy, że przestrzeń X jest metryzowalna (tzn. topologia w prze-

strzeni X pochodzi od jakiejś metryki). Niech Y będzie przestrzenią
topologiczną homeomorﬁczną z X. Udowodnij, że Y również jest me-
tryzowalna.

†

Z samolotu lecącego nad Warszawą wyrzucamy plan miasta. Udo-

wodnij, że Istnieje dokładnie jeden taki punkt na planie nakrywający
punkt w mieście, który przedstawia.

Rozdział 2

Równania różniczkowe
zwyczajne

Zajmiemy się teraz pojęciem równania różniczkowego zwyczajnego. Obiekt
ten pojawia się w sposób naturalny w wielu zagadnieniach. Wykład ten
prezentuje pewne podstawowe pojęcia teorii równań rózniczkowych zwyczaj-
nych, stanowiących pewnwgo rodzaju słownik, którego będziemy używać w
trakcie kolejnych wykładów.

2.1

Deﬁnicja równania różniczkowego

Zaczniemy od ogólnej deﬁnicji równania różniczkowego zwyczajnego.

Deﬁnicja 2.1.1 Równaniem różniczkowym zwyczajnym rzędu n nazywamy
równanie

F (t, x, ˙x, ¨

x, . . . , x

(n)

) = 0

(2.1)

wiążące zmienną niezależną t, zmienne zależne x i ich pochodne ˙x, ¨

x, . . .,

(n)

aż do rzędu n. Rozwiązaniem równania (2.1) nazywamy funkcję ϕ(t)

klasy C

, która podstawiona do równania w miejsce x zmienia to równanie

w tożsamość.

ROZDZIAŁ 2. RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE

Wszystkie funkcje występujące w równaniu (2.1) traktujemy jako funkcje
wektorowe o wartościach w przestrzeni rzeczywistej

Deﬁnicja 2.1.2 Wykres odwzorowania ϕ(t) w przestrzeni R

m+1

w zmien-

nych (t, x) nazywamy krzywą całkową równania (2.1).

Posługiwanie się równaniem różniczkowym w postaci (2.1) jest niewy-

godne i rzadko spotykane w praktyce. Jeśli najwyższa pochodna x

(n)

(t)

wchodzi do funkcji F w sposób nietrywialny, to najczęściej lokalnie speł-
nione są założenia twierdzenia o funkcji uwikłanej i równanie (2.1) można
rozwikłać względem najwyższej pochodnej

(n)

(t) = f (t, x, ˙x, . . . , x

(n−1)

)

(2.2)

Równanie rzędu n możemy w łatwy sposób sprowadzić do równania (układu
równań skalarnych) pierwszego rzędu. W tym celu oznaczmy

(t) = x(t), x

(t) = ˙x(t), . . . , x

n−1

(t) = x

(n−1)

(t).

Wprowadźmy nową zmienną ¯

x(t) = (x

(t), x

(t), . . . , x

n−1

(t)). Równanie

(2.2) możemy zatem zapisać jako równanie pierwszego rzędu

˙¯x = g(t, ¯x),

(2.3)

gdzie g(t, ¯

x) = (x

(t), x

(t), . . . , x

n−2

(t), f (t, x

, x

, . . . , x

n−1

)). W dalszej

części będziemy się zajmować równaniami (układami równań) pierwszego
rzędu, które można zapisać w postaci

˙x = f (t, x).

(2.4)

Niech G

⊂ R

m+1

będzie zbiorem spójnym, w którym prawa strona rów-

nania (2.4) jest dobrze określona. Zbiór G nazywać będziemy rozszerzoną
przestrzenią fazową równania (2.4), a jego rzut D na przestrzeń

zmien-

nych x nazwiemy przestrzenią fazową tego równania. W zbiorze G istnieje
zwykle bardzo wiele krzywych całkowych równania (2.4). Krzywe te tworzą
wieloparametrowe rodziny rozwiązań. Jeśli ϕ(t, c

, c

, . . . , c

) : R → R

2.2. PODEJŚCIE GEOMETRYCZNE

jest rodziną funkcji, sparametryzowaną m parametrami c

, c

, . . . , c

taką,

że dla każdego (c

, c

, . . . , c

) ∈ A ⊂ R

funkcja ϕ(t, c

, . . . , c

) jest krzy-

wą całkową równania (2.4) i dla każdego (t

, x

) ∈ G istnieją parametry

, . . . , c

) ∈ A, takie że ϕ(t, c

, . . . , c

) jest krzywą całkową przechodzą-

cą przez punkt (t

, x

), to rodzinę ϕ(t, c

, . . . , c

) nazwiemy rozwiązaniem

ogólnym równania (2.4). Oprócz pojęcia rozwiązania ogólnego będziemy się
posługiwać także pojęciem całka ogólna w przypadku, gdy będziemy dys-
ponować jedynie uwikłanym przedstawieniem rozwiązania ogólnego tzn.

Φ(t, x, c

, . . . , c

) = 0.

2.2

Podejście geometryczne

W celu zrozumienia geometrycznego sensu rozwiązań równania (2.4) roz-
patrzmy najpierw to równanie w przypadku skalarnym (m = 1). Niech
funkcja x(t) będzie rozwiązaniem tego równania. Rozważmy jej wykres jako
podzbiór (podrozmaitość klasy C

) płaszczyzny (t, x). Jak wiadomo wektor

styczny do wykresu funkcji x(t) ma postać (1, ˙x(t)) = (1, f (t, x)). Zatem
równanie (2.4) można odczytać następująco. Na

dane jest pole wekto-

rowe (1, f (t, x)). Szukamy krzywej, będącej wykresem funkcji x(t) i takiej,
że w każdym punkcie (t, x) leżącym na tej krzywej, wektor styczny do niej
jest równy (1, f (t, x)). Nie ma tu znaczenia, czy znajdujemy się na płasz-
czyźnie

czy w wyżej wymiarowej przestrzeni

m+1

. W ogólności w po-

wyższy sposób możemy deﬁniować równania różniczkowe na rozmaitościach
odpowiedniej klasy gładkości. Mając dane dostatecznie gładkie pole wekto-
rowe X

∈ V (M) na rozmaitości M odpowiedniej klasy gładkości i punkt

∈ M możemy znaleźć przynajmniej lokalnie krzywą c : [0, t) → M taką że

˙c(t) = X(c(t)) i c(0) = p. Rozwiązanie takiego równania nazwiemy potokiem

pola wektorowego X. W dalszej cześci ograniczymy się jednak do zagadnień
w przestrzeni euklidesowej.

Niech dane będzie pole wektorowe w

m+1

. Wybierzmy punkt (t

, x

a następnie poruszymy się w kierunku wektora stycznego (1, ˙x

, . . . , ˙x

Oznaczmy ten punkt przez (t

, x

), a z niego przejdźmy w kierunku wekto-

ra stycznego (1, ˙x

, . . . , ˙x

) itd. W ten sposób otrzymaliśmy jedną krzywą

ROZDZIAŁ 2. RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE

całkową. Aby otrzymać inną krzywą, wystartowalibyśmy z innego punktu
(t

, x

Z tego postępowania można wyciągnąć wniosek, że wybór punktu po-

czątkowego (t

, x

) pozwolił nam ograniczyć się tylko do jednej krzywej

całkowej. Prowadzi to do pojęcia warunku początkowego dla równania róż-
niczkowego (2.4).

Deﬁnicja 2.2.1 Warunek postaci x(t

) = x

ograniczający zbiór rozwiązań

równania pierwszego rzędu (2.4) nazywa się warunkiem początkowym lub wa-
runkiem Cauchy’ego. Równanie (2.4) uzupełnione warunkiem początkowym
nazywamy zagadnieniem Cauchy’ego lub zagadnieniem początkowym.

Deﬁnicja 2.2.2 Rozwiązaniem zagadnienia Cauchy’ego nazywamy funkcję
ϕ(t) klasy C

na przedziale [t

, t

+ α], spełniającą równanie (2.4) oraz wa-

runek początkowy.

Wróćmy na moment do równań wyższych rzędów. Warto sobie uświadomić,
że dla równania postaci (2.2) zadanie warunku początkowego wymaga za-
dania wartości nie tylko samej funkcji dla czasu t

, ale także wartości jej

− 1 pochodnych. Wynika to wprost z postaci równania pierwszego rzędu,

do której sprowadziliśmy równanie (2.2). Warunek Cauchy’ego dla tego rów-
nania ma postać ¯

x(t

) = X, gdzie X ∈ R

i mamy x(t

) = X

, ˙x(t

) = X

. . ., x

(n−1)

) = X

n−1

. Prowadzi to do następującej deﬁnicji zagadnienia

początkowego dla równania rzędu n, będącego całkowitą analogią do przy-
padku równania skalarnego.

Deﬁnicja 2.2.3 Jeśli dane jest równanie różniczkowe rzędu n, postaci (2.2)
w przestrzeni

, to zagadnienie Cauchy’ego dla tego równania przyjmuje

formę

(n)

= f (t, x, ˙x, . . . , x

(n−1)

x(t

) = x

, ˙x(t

) = x

, . . . , x

(n−1)

) = x

n−1

gdzie x

, x

, . . . , x

n−1

∈ R

2.3. RÓWNANIA AUTONOMICZNE

2.3

Równania autonomiczne

Wśród równań różniczkowych na uwagę zasługuje pewna szczególna ich kla-
sa.

Deﬁnicja 2.3.1 Równanie postaci (2.2), w którym prawa strona nie zale-
ży jawnie od zmiennej niezależnej, nazywamy równaniem autonomicznym.
Równanie to ma postać

˙x = f (x)

(2.5)

Zauważmy, że każde równanie nieautonomiczne w postaci (2.2) możemy
sprowadzić do równania autonomicznego przez podstawienie t = s, gdzie
s jest nową zmienną niezależną, a t jest traktowane jako kolejna składowa
wektora x. Wtedy równanie (2.2) można zapisać w postaci autonomicznej

x = ¯

f (¯

x),

gdzie ¯

x = (t, x) i ¯

f = (1, f ). Różniczkowanie oznacza różniczkowanie po

nowym parametrze s.

Ewolucję równania autonomicznego najwygodniej jest rozpatrywać w

przestrzeni fazowej takiego równania, czyli w zbiorze wszystkich możliwych
wartości zmiennej zależnej. Jeśli x

∈ R

to przestrzenią fazową tego rów-

nania jest podzbiór przestrzeni

Rozpatrując rozszerzoną przestrzeń fazową

m+1

mamy krzywe całko-

we będące wykresami konkretnych rozwiązań równania (2.2). Rzutując te
krzywe na

mamy krzywe fazowe będące obrazem rozwiązania.

2.4

Przykłady zagadnień

Równania różniczkowe zwyczajne spotkac możemy w wielu dziedzinach.
Najcześciej jednak natkniemy się na nie w ﬁzyce, a szczególnie w mechanice
klasycznej. Metody równań różniczkowych zwyczajnych używane są także
w bilogii, chemii.

Przykład 1. (Przykład zagadnienia prowadzącego do równania różniczko-
wego) Rozważmy proces rozmnażania się bakterii. Zakładamy, że bakterie

ROZDZIAŁ 2. RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE

znajdują się w środowisku o stałych parametrach, w związku z czym szyb-
kość i sposób ich rozmnażania się jest stały. Wiadomo, że w tych warunkach
bakterie rozmnażają się przez podział, w którego wyniku z jednej bakterii
powstaje k nowych. Podział ten następuje co τ minut. Znajdziemy wzór
opisujący wzrost populacji bakterii.

Przyjmiemy, że wszystkie bakterie dzielą się w tych samych chwilach:

, t

= t

+ τ, t

= t

+ 2τ, . . .

Jeśli N

oznacza liczbę bakterii w chwili t

, to zmianę tej liczby w czasie

opisuje równanie

i+1

= (1 + k)N

(2.6)

Znając N

czyli liczbę bakterii w chwili t

, możemy łatwo obliczyć

= (1 + k)

Jednak założenie, że bakterie dzielą się dokładnie w tych samych chwi-
lach, jest mało realistyczne (liczba τ jest średnim czasem między kolejnymi
podziałami, otrzymanym z eksperymentalnych badań biologów). Bardziej
realne jest założenie, że bakterie dzielą się w różnych chwilach, które są
równomiernie rozłożone w czasie, tzn. liczba podziałów w przedziale cza-
su (t, t + ∆t) zależy od ∆t, a nie zależy od t (oczywiście zależy także od
liczby bakterii). Aby znaleźć prawo opisujące wzrost populacji bakterii przy
założeniu równomiernego w czasie rozkładu chwil podziału, musimy zre-
zygnować z traktowania N (t) jako liczby bakterii w chwili t (a więc jako
liczby naturalnej). Przyjmijmy natomiast, że N (t) jest pewną miarą gęsto-
ści bakterii w środowisku i będziemy ją traktować jako liczbę rzeczywistą
(po to, żeby w dalszych rozważaniach uznać N (t) za gładkąfunkcję zmien-
nej t). Niech teraz N (t) będzie wielkością populacji w chwili t, a N (t + ∆t)
w chwili t + ∆t. Różnica N (t + ∆t) − N (t) jest przyrostem populacji w
przedziale czasu ∆t. Aby wyznaczyć ten przyrost, zauwazmy że co τ minut
następuje podział określonej bakterii, natomist co τ /N (t) minut następuje
podział jakiejś bakterii z populacji N (t) bakterii. Oznacza to, że w czasie
∆t nastąpi

∆t

τ /N (t)

1
τ

N (t)∆t

(2.7)

2.4. PRZYKŁADY ZAGADNIEŃ

podziałów. Ponieważ w każdym podziale z jednej bakterii tworzy się k bak-
terii, więc

N (t + ∆t) − N (t) =

k
τ

N (t).

(2.8)

Jeśli założymy, że N (t) jest funkcją różniczkowalną, to będziemy mogli do-
konać przejścia granicznego ∆t → 0. Otrzymamy wtedy równanie

N (t) =

k
τ

N (t),

(2.9)

które opisuje prawo wzrostu populacji bakterii. Mamy zatem przykład jak
z zagadnienia różnicowego (dyskretnego) przejść na przypadek różniczkowy
(ciągły).
Przykład 2.(Wahadło matematyczne) Wahadłem matematycznym nazy-
wamy punkt materialny o masie m zawieszony na długiej, cienkiej i nie-
rozciągliwej nici. Wykonuje on wahania wokół najniżej położonego punktu
O, zwanego środkiem wahań. Załóżmy, że wahadło wykonuje tylko małe
wahania i oznaczmy przez z odchylenie od środka wahań. Aby znaleźć przy-
spieszenie a wahadła w punkcie wyhylenia P zauważmy, że siła działająca
na punkt materialny o masie m jest dana przez składową ciążenia, stycz-
ną do toru wahań (składowa prostopadła do niej jest równoważona przez
sprężystość nici, na której wisi wahadło). Wtedy

ma = −mg sin(x),

gdzie x jest kątem wychylenia nici od pionu, g - przyspieszeniem w po-
lu grawitacyjnym ziemi. Znak

− po prwej stronie równania występuje w

skutek przeciwnych zwrotów wychylenia i działającej na punkt siły. Jeśli
przyspieszenie wahadła wyrazimy przez drugą pochodną odchylenia z, to
otrzymamy

m¨

z = −mg sin(x).

Zauważmy, że jeśli z mierzymy wzdłuż łuku, po którym porusza się punkt
materialny, to

z = xl,

ROZDZIAŁ 2. RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE

gdzie l jest długością wahadła. Ostatecznie otrzymujemy równanie wahadła

x = −

sin(x).

Skorzystamy teraz z założenia, że wahadło wykonuje tylko małe drgania i
możemy zastosować przybliżenie sin(x) ≈ x. Małe drgania wahadła daje się
zatem opisać równaniem

x = −kx,

gdzie k = g/l. Zagadnienie początkowe dla tego równania ma postać

⎧

⎪

⎨
⎪

⎩

x = −kx

x(t

) = x

˙x(t

) = x

Otrzymaliśmy zagadnienie Cauchy’ego drugiego rzędu.

Przykład z równaniem wahadła podsuwa na myśl inny sposób zada-

nia warunków określających rozwiązanie równania różniczkowego. Możemy
starać się opisać jego ruch podając nie połozenie początkowe i prędkość
początkową, ale wychylenie w chwili t

i wychylenie w chwili t

. Wtedy

odpowiednie zaganienie miałoby postać

⎧

⎪

⎨
⎪

⎩

x = −kx

x(t

) = x

x(t

) = x

(2.10)

Zagadnienie w postaci (2.10) nazywać będziemy zagadnieniem brzegowym.
Nazwa ta bierze się stąd, że starając się znaleźć rozwiązanie, podajemy jego
wartość na dwóch końcach przedziału, na którym poszukujemy rozwiązania.
Oczywiście postawienie zagadnienia brzegowego nie ogranicza się do równań
drugiego rzędu (choć dla tych równań jest to bardzo naturalny rodzaj wa-
runku). Można ten typ warunku formułować dla równań dowolnego rzędu
zadając dostatecznie wiele wartości.

Deﬁnicja 2.4.1 Niech dane będzie równanie w postaci (2.4) z funkcją f :
I

× R

→ R

, gdzie I = [a, b] ⊂ R. Zagadnienie brzegowe dla równania

2.5. BADANIE RÓWNAŃ RUCHU

†

(2.4) na przedziale [a, b] ma postać

q(x(a), x(b)) = 0,

(2.11)

gdzie q jest daną funkcją o wartościach w

Jeśli q jest funkcją liniową, która nie zależy od x(b) to warunek (2.11) spro-
wadza się do warunku Cauchy’ego. Można więc warunek (2.11) uważać za
ogólną postać warunku granicznego dla równania (układu) (2.4). Zauważ-
my, że rozwiązywanie zagadnienia początkowego jest na ogół łatwiejsze niż
zagadnienia brzegowego. W drugim przypadku musimy bowiem wcześniej
wiedzieć, że rozwiązanie określonej jest na całym odcinku [a, b], co nie za-
wsze jest prawdą.

2.5

Badanie równań ruchu

†

Równania różniczkowe zwyczajne, tak jak główne idee rachunku różniczko-
wego wywodzą się z zagadnień mechaniki Newtonowskiej. Przyjżyjmy się
dokładniej pewnym wybranym problemom.

Zanim to jednak nastąpi wprowdźmy pojęcie potencjału.

Deﬁnicja 2.5.1 Niech dany będzie Newtonowski układ mechaniczny

B ze

stanami opisanymi funkcją x : R → R

. Jeśli istnieje funkcja V : R

→ R

taka, że ¨

x = −∇V , to układ B nazwiemy układem potencjalnym. Funkcję V

nazwiemy funkcją potencjału lub potencjałem.

Układy potencjalne są zatem układami, w których pole sił jest polem gra-
dientowym pewnej funkcji skalarnej. Przykładem takiego pola jest w ujęciu
klasycznym pole grawitacyjne ziemi.

2.5.1

Układy potencjalne o jednym stopniu swobody

Deﬁnicja 2.5.2 Układem o jednym stopniu swobody nazwiemy układ opi-
sany przez jedno równanie różniczkowe

x = f (x), x ∈ R

(2.12)

ROZDZIAŁ 2. RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE

Energią kinetyczną nazywamy formę kwadratową

T =

1
2

˙x

Energią potencjalną nazywamy

U (x) = −

f (ζ) dζ

Znak

− został tak dobrany, by np. w przypadku rzutu kamieniem jego

energia potencjalna była tym większa, im wyżej znajduje się kamień. Energią
całkowitą układu nazwiemy E = T + U .

Twierdzenie 2.5.3 (Prawo zachowania energii) Energia całkowita dla
układu poruszającego się zgodnie z równaniem (2.12) nie ulega zmianie.

Dowód. Wykonajmy rachunek

(T + U ) = ˙x¨

x +

˙x = ˙x(¨

− f(x)) = 0.

Dowodzi to zatem, że E = const.

2.5.2

Układy potencjalne o dwóch stopniach swobody

Deﬁnicja 2.5.4 Przez układ o dwóch stopniach swobody rozumiemy układ
opisany równaniem różniczkowym

x = f (x), x ∈ R

(2.13)

Zauważmy, że i w tym przypadku zachodzi prawo zachowania energii cał-
kowitej 2.5.3. Musimy jednak inaczej rozumieć kwadrat prędkości w formie
energii kinetycznej. Teraz mamy na myśli iloczyn skalarny

˙x, ˙x.

Dowód. Bezpośredni rachunek daje

= ˙x, ¨

+ ∇U, ˙x = ¨x + ∇U, ˙x = 0

na mocy równań ruchu.

Wniosek 2.5.5 Jeśli w chwili początkowej energia całkowita wynosi E, to
cała trajektoria ruchu leży w obszarze, dla którego U (x) E. Inaczej, punkt
znajduje się cały czas wewnątrz studni potncjału U (x) E.

2.6. ZADANIA

2.6

Zadania

1. Sprawdzić, czy podana rodzina funkcji jest rozwiązaniem wskazanego

równania różniczkowego

(a) x(t) = c

cos 6t + c

sin 6t

x + 36x = 0

(b) x(t) = c

+ c

−6t

−

− 36x = 18t + 1

√

1 − t

(1 − t

) ˙x + tx = 2t

2. Znaleźć równanie różniczkowe (możliwie niskiego rzędu), którego roz-

wiązaniem jest zadana rodzina krzywych:

(a) x(t) = e

(b) x(t) = sin(t + c)

)

+ c

= 1

(d) t = c

+ c

x + c

3. Naszkicować przybliżony przebieg krzywych całkowych dla poniższych

równań, odgadując je z postaci pola wektorowego generowanego przez
te równania

(a) ˙x = x − t

(b) x ˙x + t = 0

x−3t

t+3x

(d) ˙x =

t+x

t−x

4. Opisać zbiór wszystkich ekstremów krzywych całkowych równania ˙x =

f (t, x).

5. Dane jest równanie różniczkowe ˙x = f (x, t), w którym prawa strona

spełnia warunek f (x, t) = f (−x, −t). Udowodnić, że jeśli funkcja ϕ(t)
jest rozwiązaniem tego równania, to także funkcja

−ϕ(−t) jest jego

rozwiązaniem. Znaleźć analogiczną własność rozwiązania, jeśli prawa
strona spełnia warunki f (x, t) = −f (x, −t) lub f (x, t) = −f (−x, t).

Dla jakich czasów jest określone to rozwiązanie?

ROZDZIAŁ 2. RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE

†

Załóżmy, że łódź płynie przez rzekę reprezentowaną jako pas [−a, a]×

R w poprzek od −a do a z jednostają prędkością v

. Prędkość nurtu

rzeki opisana jest funkcją v

(x) = 3

1 −

. Znaleźć zagadnienie

opisujące tor, po którym będzie poruszać się łódź.

Rozdział 3

Istnienie i jednoznaczność
rozwiązań

W rozdziale tym zajmiemy się zagadnieniem istenienia i jednoznaczności
rozwiązań równań różniczkowych zwyczajnych. Odpowiedź na te pytania
jest istotna w chwili, gdy nie potraﬁmy podać analitycznej formuły opi-
sującej rozwiązanie (o ile istnieje). Często w problemach zadajemy sobie
pytanie, czy działanie układu jest jedyne możliwe. Twierdzenia zawarte w
tym rozdziale dadzą nam odpowiedź.

3.1

Twierdzenie Peano

Równania różniczkowe zwyczajne są bardzo rozwiniętą dziedziną matema-
tyki. Mimo to potraﬁmy rozwiązywać efektywnie w postaci analitycznej
tylko nieliczne ich klasy, które poznamy później. Rezygnując więc z pytania
o możliwość efektywnego rozwiązania danego równania, spróbujmy zadać
pytanie ogólniejsze, ale łatwiejsze: jakie warunki musi spełniać równanie,
abyśmy mogli być pewni, że ma ono rozwiązanie (nawet jeśli nie potraﬁmy
go określić) i kiedy rozwiązanie jest jednoznaczne?

Pytanie to będziemy rozważać w możliwie ogólnej sytuacji, tzn. założy-

ROZDZIAŁ 3. ISTNIENIE I JEDNOZNACZNOŚĆ ROZWIĄZAŃ

my, że mamy dane równanie w postaci

˙x = f (t, x)

w przestrzeni liniowej. Przypomnijmy, ze x = x(t) ∈ R

, a f jest funkcją

f : R

m+1

→ R

Twierdzenie 3.1.1 (Peano) Niech K = [t

, t

+ a] × {x − x

b} ⊂

m+1

. Niech F : K → R

będzie funkcją ciągłą, sup

(t,x)∈K

F (t, x) = M.

Wtedy zagadnienie Cauchy’ego znalezienia takiej funkcji x(t), że

˙x = F (t, x)

(3.1)

i spełniony jest warunek x(t

) = x

, ma rozwiązanie na odcinku [t

, t

+ α],

α = min(a, b/M ).

Zanim przejdziemy do dowodu twierdzenia 3.1.1, potrzebny będzie nam

lemat.

Lemat 3.1.2 Zagadnienie Cauchy’ego (3.1) ma rozwiązanie x(t) różnicz-
kowalne na odcinku [t

, t

) lub [t

, t

] wtedy i tylko wtedy, gdy równanie

całkowe

x(t) = x

F (s, x(s))ds

(3.2)

ma rozwiązanie ciągłe.

Dowód. (lematu 3.1.2) Przypuśćmy, że funkcja x

(t) spełnia warunek (3.2).

Całkując obie strony równania ˙x = F (t, x) od t

do t i korzystając z warunku

x(t

) = x

otrzymujemy:

x(t) − x(t

) =

F (s, x(s))ds,

czyli

x(t) = x

F (s, x(s))ds.

3.1. TWIERDZENIE PEANO

Implikacja w drugą stronę wynika automatycznie z różniczkowania (3.2)
względem t. Zauważmy, że z ciągłości F wynika, że x(t) jest klasy C

Dowód. (twierdzenia 3.1.1) Dla dowolnej liczby naturalnej n deﬁniujemy na
przedziale [t

, t

+a] funkcję x

(t), kolejno na odcinkach [t

α, t

k+1

α],

k = 0, 1, . . . , n − 1 według wzoru

) = x

(t) = x

k
n

+ F

k
n

α, x

k
n

−

k
n

dla t

∈ (t

α, t

k+1

α]. Jak się później okaże, deﬁnicja ta ma sens

jeśli

α) − x

b. Tak zdeﬁniowany ciąg funkcji jest aproksy-

macją ewentualnego rozwiązania (o którym jeszcze nie wiemy, że istnieje)
funkcjami kawałkami liniowymi.

Przypuśćmy, że istnieje liczba t

: t

< t

+ α taka, że x

) −

= b i dla t

t t

mamy

) − x

b; w szczególności deﬁnicja

ciągu x

(t) mam sens dla t t

Funkcje x

(t) są Lipschitz-ciągłe ze stałą M tzn. zachodzi

∀

t,t

∈[t

+α]

(t) − x

) M |t − t

gdyż na odcinkach [t

α, t

k+1

α] są liniowe (aﬁniczne) z pochod-

ną F

α, x

, a

F M. Istnienie t

prowadzi więc do

sprzeczności, gdyż

b = x

(t) − x

) M |t

− t

| < M

= b.

Powyższą metodą możemy więc określić x

dla t

+ a i t t

Krzywa (t, x

(t)) będzie wówczas zawarta w K.

Jako Lipschitz-ciągłe z tą samą stałą M funkcje x

(t) są jednakowo

ciągłe, tzn.

∀

∃

δ>0

∀

t,t

∈[t

+α]

|t − t

| < δ ⇒ x

(t) − x

) < .

ROZDZIAŁ 3. ISTNIENIE I JEDNOZNACZNOŚĆ ROZWIĄZAŃ

Na mocy twierdzenia Arzeli-Ascoliego z ciągu x

możemy wybrać podciąg

jednostajnie zbieżny. Dla uproszczenia oznaczeń możemy przyjąć, że sam
ciąg x

zbiega jednostajnie do pewnej funkcji x(t). Pokażemy, że ta funkcja

jest rozwiązaniem problemu Cauchy’ego. W tym celu na podstawie lematu
3.1.2, wystarczy wykazać, że jest rozwiązaniem równania całkowego (3.2).
Niech φ

(t) = F (t

α, x

α)), dla t ∈ [t

α, t

k+1

α). Wówczas

(t) = x

(s)ds.

Zachodzi także Φ

(s) −→ F (s, x(s)), ponieważ x

α) −→ x(t

α),

a funkcja F jest jednostajnie ciągła. Zatem

x(t) = lim

n→∞

(t) = x

+ lim

n→∞

(s)ds = x

lim

n→∞

(s)ds =

= x

F (x(s))ds.

Powyższa równość kończy dowód.

Metoda przybliżania rozwiązań równania różniczkowego zwyczajnego

zastosowana w dowodzie twierdzenia 3.1.1 nazywa się otwartym schematem
Eulera i jest wykorzystywana przy numerycznym rozwiązywaniu równań.
Jest to najłatwiejsza metoda dająca w pewnych wypadakch zadowalające
wyniki.

Teraz, gdy jesteśmy wyposażeni w narzędzia pozwalające stwierdzić ist-

nienie rozwiązania, możemy przejść do kolejnego problemu, jakim jest jed-
noznaczność.

3.2

Twierdzenie Picarda-Lindelöfa

Załóżmy jak poprzednio, że dane jest zagadnienie Cauchy’ego (3.1). Za-
czniemy od przykładu interesującej nas sytuacji.

3.2. TWIERDZENIE PICARDA-LINDELÖFA

Przykład 1. Rozważmy następujące równanie:

˙x = x

, 0 < β < 1, x 0.

Stosując metodę rozdzielania zmiennych otrzymujemy

dx
x

= C +

o ile x

= 0, więc

1 − β

1−β

= C + t,

x(t) = (1 − β)

1−β

(t − C)

1−β

dla t > C (zaminiliśmy w oznaczeniach C na

−C). Dla t = C to rozwią-

zanie przedłuża się do x(C) = 0. Mamy wówczas prawostronną pochodną

˙x(C) = 0. Istnieje także inne rozwiązanie: x(t) ≡ 0. Zatem dla żadnego

∈ R nie ma jednoznaczności rozwiązań zagadnienia Cauchy’ego z warun-

kiem początkowym x(t

) = 0.

Startując zatem w punkcie (t

, 0) w przestrzeni fazowej będziemy mogli

poruszać się stycznie do pola wektorowego zadającego równanie (inaczej,
dla którego krzywe całkowe są potokiem tego pola wektorowego) na dwa
sposoby.

Twierdzenie 3.2.1 (Picard-Lindelöf ) Niech K, F będą takie jak w za-
łożeniach twierdzenia 3.1.1. Załóżmy dodatkowo, że F jest Lipschitz-ciągła
ze stałą L w kierunku x tzn. spełniony jest warunek

∀

(t,x),(t,y)∈K

F (t, x) − F (t, y) Lx − y,

to istnieje dokładnie jedno rozwiązanie problemu Cauchy’ego na [t

, t

+ α

gdzie α

= min(a,

) dla dowolnej ustalonej liczby 0 < τ < 1.

Dowód. Zauważmy, że operator liniowy L, zdeﬁniowany wzorem

L(u)(t) = x

F (u(s))ds

ROZDZIAŁ 3. ISTNIENIE I JEDNOZNACZNOŚĆ ROZWIĄZAŃ

przeprowadza przestrzeń C

z [t

, t

+α], o wartościach w zbiorze {x−x

} ⊂ R

, takich że u(t

) = x

w siebie, gdyż

L(u)(t) − x

F (s, u(s))ds M

= b.

Ponadto

L jest kontrakcją. Załóżmy bowiem, że mamy dwie funkcje u(t) i

v(t) klasy C

. Wtedy dla każdego t

t t

+ α

L(u)(t) − L(v)(t) =

(F (u(s)) − F (v(s)))ds

u(s) − v(s)ds τ

sup

+α

u(s) − v(s).

Przestrzeń C

jest przestrzenią Banacha. Zatem z tw. Banacha o punkcie

stałym (twierdzenie 1.3.7) istnieje dokładnie jeden punkt stały odwzorowa-
nia

L tzn. takie u(t), że L(u)(t) = u(t). Funkcja u(t) jest na mocy lematu

3.1.2 rozwiązaniem zagadnienia Cauchy’ego.

Żądanie Lipschitz-ciągłości prawej strony równania (3.1) powoduje za-

tem, że rozwiązanie zagadnienia jest jednoznaczne. Dowód twierdzenia 3.2.1
obrazuje także jak silnym narzędziem jest twierdzenie 1.3.7.

3.3

Zadania

1. Czy wykresy dwóch różnych rozwiązań danego równania mogą sie

przecinać w pewnym punkcie (t

, x

) jeśli równaniem tym jest:

(a) ˙x = x

+ t

(b) ¨

x = x

+ t

2. Czy poniższe równania, uzupełnione dowolnym warunkiem początko-

wym x(t

) = x

mają rozwiązania? Jeśli tak, to czy są one jedno-

znaczne?

(a) ˙x = t

− x

3.3. ZADANIA

(b) ˙x = tx + e

−x

†

Niech funkcja f : R → R będzie ciągła, a funkcja g : R → R niech

spełnia warunek Lipschitza. Udowodnić, że układ równań

˙x

= f (x

˙x

= g(x

)

uzupełniony dowolnym warunkiem początkowym, ma co najwyżej jed-
no rozwiązanie w dowolnym przedziale.

ROZDZIAŁ 3. ISTNIENIE I JEDNOZNACZNOŚĆ ROZWIĄZAŃ

Rozdział 4

Podstawowe klasy równań

Znamy już twierdzenia, dające nam możliwość orzeczenia, czy dane równa-
nie posiada rozwiązanie i czy jest ono jednoznaczne. Należy pamiętać, że
twierdzenia te są kryteriami dostatecznymi a nie koniecznymi. Zajmiemy
się teraz pewnymi klasami równań, których rozwiązania jesteśmy w sta-
nie bez trudu wyznaczyć analitycznie. Ograniczymy się tylko do przypadku
skalarnego.

4.1

Równania o zmiennych rozdzielonych

Równanie o zmiennych rozdzielonych jest najprostszą sytuacją równania
różniczkowego zwyczajnego. Poniższa deﬁnicja tłumaczy pochodzenie na-
zwy tej klasy równań.

Deﬁnicja 4.1.1 Równanie różniczkowe rzędu pierwszego

˙x = f (t, x)

nazywamy równaniem o zmiennych rozdzielonych, jeśli funkcja f (t, x) daje
się przedstawić w postaci iloczynu dwóch funkcji jednej zmiennej, tj.

f (t, x) = g

(t)g

(x).

ROZDZIAŁ 4. PODSTAWOWE KLASY RÓWNAŃ

Równanie o zmiennych rozdzielonych można rozwiązać w bardzo łatwy spo-
sób.

Twierdzenie 4.1.2 Dane jest równanie różniczkowe o zmiennych rozdzie-
lonych

˙x = g

(t)g

(x).

(4.1)

Niech funkcje g

(t) i g

(x) będą ciągłe dla t ∈ (a, b) i x ∈ (c, d) oraz niech

(x) nie ma zer na odcinku (c, d). Wtedy przez każdy punkt (t

, x

) prosto-

kąta Q = {(t, x) : t ∈ (a, b), x ∈ (c, d)} przechodzi dokładnie jedna krzywa
całkowa równania (4.1). Krzywa przechodząca przez punkt (t

, x

) jest dana

wzorem

x(t) = G

−1

(t) − G

) + G

)),

(4.2)

gdzie G

(t) jest funkcją pierwotną funkcji g

(t), a G

(x) - funkcją pierwotną

funkcji 1/g

(x).

Dowód. Podzielmy równanie (4.1) stronami przez g

(x). Otrzymamy

(x)

= g

(t).

Równość tę możemy zapisać inaczej w postaci

(x(t)) = g

(t),

(4.3)

gdzie G

(x) jest funkcją pierwotną dla 1/g

(x). Całkujemy równanie w prze-

dziale (t

, t) i otrzymujemy

(x(t)) − G

(x(t

)) = G

(t) − G

(4.4)

gdzie G

(t) jest funkcją pierwotną dla g

(t). Zauważmy, że G

jest funkcją

monotoniczną, bo G

= 1/g

= 0, czyli pochodna G

ma stały znak. Istnieje

więc funkcja G

−1

, odwrotna do G

. Wobec tego z (4.4) mamy

x(t) = G

−1

(t) − G

) + G

)),

wykorzystując fakt, że x(t

) = x

4.1. RÓWNANIA O ZMIENNYCH ROZDZIELONYCH

Równania o zmiennych rozdzielonych są w pewnym sensie podstawową

klasą równań, którą można rozwiązać analitycznie. Często w wielu zagad-
nieniach dotyczących różnych dziedzin skomplikowane równania, nie tylko
zwyczajne, rozwiązuje się postulując istnienie rozwiązania w postaci zmien-
nych rozdzielonych. Pochodzenie nazwy tej klasy równaniń jest naturalne.

Rozpatrzmy następujący przykład równania zwyczajnego.

Przykład 1. Rozwiążemy zagadnienie Cauchy’ego

˙x sin t − x cos t = 0, x

= 1.

(4.5)

Przekształćmy równanie (4.5) by otrzymać

˙x

cos t

sin t

(4.6)

Przekształcenie jest poprawne ze względu na warunek Cauchy’ego jaki roz-
patrujemy. Całkując równanie (4.6) dostajemy

ln |x| = ln | sin t| + C

co można zapisać jako

ln |x| = ln(|C

sin t|).

Z różnowartościowości funkcji ln otrzymujemy

x(t) = C

sin t.

Na mocy warunku x

= 1 otrzymujemy C

= 1. W ten sposób rozwiąza-

liśmy zagadnienie. Rozwiązaniem jest x(t) = sin t

W trakcie rozwiązywania zagadnienia pojawiła się stała całkowania C

później przekształcona do stałej C

= ln |C

|, która została ustalona później

na podstawie warunku Cauchy’ego. W celu uniknięcia uciążliwego wprowa-
dzania indeksów będziemy stosować konwencję stałej generycznej tzn. za-
miast pisać C

i przekształcać C

= ln |C

| będziemy pisać C zarówno przed

jak i po przekształceniu, mając jednak na uwadze ewentualne konsekwencje
wynikające z danej zamiany.

ROZDZIAŁ 4. PODSTAWOWE KLASY RÓWNAŃ

4.2

Równania jednorodne

Często przez odpowiednią zamianę zmiennych jesteśmy w stanie sprowadzić
jeden typ równania do już nam znanego. Tak będzie w przypadku omawia-
nych tu równań jednorodnych.

Deﬁnicja 4.2.1 Funkcja dwóch zmiennych f (x, y) nazywa się funkcją jed-
norodną stopnia n, jeśli f (tx, ty) = t

f (x, y).

Zanim zaczniemy rozpatrywać równania z funkcjami jednorodnymi, sformu-
łujemy nieco ogólniej zapis równania. Zauważmy bowiem, że w przypadku
pojedynczego równania decyzja, która zmienna jest zmienną zależną, a któ-
ra zmienną niezależną, jest dość arbitralna. Aby podkreślić tę dowolność
wyboru zmiennej zależnej, równanie

˙x = f (t, x)

będziemy zapisywać w postaci równości dwóch różniczek

dx = f (t, x)dt

lub też w postaci zachowującej pełną symetrię zmiennych

M (x, y)dx + N (x, y)dy = 0.

(4.7)

W celu zachowania pełnej symetrii zostały zmienione nawet nazwy zmien-
nych. Równanie to można zapisać oczywiście także w postaci

dy
dx

= −

M (x, y)

N (x, y)

Wprowadzenie takiego zapisu może się wydawać zbędne, jednakże w wielu
sytuacjach okazuje się, że postać ta prowadzi do łatwych całek.

Deﬁnicja 4.2.2 Równanie różniczkowe w postaci (4.7) nazywa się równa-
niem jednorodnym stopnia n, jesli funkcje M (x, y) i N (x, y) są funkcjami
jednorodnymi stopnia n.

4.2. RÓWNANIA JEDNORODNE

Często można znaleźć łatwiejszą metodę całkowania równań jednorodnych.
Poniższe twierdzenie prezentuje najogólniejszą metodę ich rozwiązywania.

Twierdzenie 4.2.3 Dane jest równanie jednorodne stopnia n w postaci
różniczek

M (x, y)dx + N (x, y)dy = 0.

(4.8)

O funkcjach M (x, y) i N (x, y) zakładamy, że są funkcjami ciągłymi w zbio-
rze Q = {(x, y) : a <

y
x

< b

} oraz

xM (x, y) + yN (x, y) = 0.

Wtedy przez każdy punkt (x

, y

) ∈ Q przechodzi dokładnie jedna krzywa

całkowa równania (4.8).

Dowód. Równanie (4.8) można sprowadzić do równania o zmiennych roz-
dzielonych przez każde z dwóch podstawień y = ux i x = vy. Wybierzmy
podstawienie y = ux. Pokażemy, jak wtedy przebiega całkowanie równania
(4.8).

M (x, y)dx + N (x, y)dy = M (x, ux)dx + N (x, ux)(xdu + udx) =

= x

M (1, u)dx + x

N (1, u)(xdu + udx) =

= x

(M (1, u) + uN (1, u))dx + x

n+1

N (1, u)du = 0.

Po przekształceniu otrzymujemy równanie o zmiennych rozdzielonych

= −

N (1, u)

M (1, u) + uN (1, u)

du.

(4.9)

Ponieważ M (1, u) + uN (1, u) = 0 więc występująca po prawej stronie rów-
nania funkcja jest ciągła i ma funkcję pierwotną G(u). Całkujemy równanie
(4.9) i otrzymujemy

ln |x| = G(u) + G

+ ln |x

ROZDZIAŁ 4. PODSTAWOWE KLASY RÓWNAŃ

skąd po przejściu do zmiennych (x, y) mamy

ln |x| = G

y
x

+ G

+ ln |x

Zauwazmy przy tym, że zgodnie z twierdzeniem 4.1.2 całkowanie równania
(4.9) jest możliwe tylko w takim obszarze Q, który nie zawiera punktów
(x, y) o współrzędnej x = 0. Jeśli obszar Q zawiera takie punkty, a nie
zawiera punktów o współrzędnej y = 0, to równanie (4.8) można rozwiązać,
stosując podstawienie x = vy.

Przykład 1. Znajdziemy rodzinę krzywych całkowych, opisanych równa-
niem

(x + y − 2)dx + (x − y + 4)dy = 0.

Równanie to nie jest równaniem jednorodnym, ale można je do postaci jed-
norodnej sprowadzić. Zróbmy podstawienie x = ξ + x

, y = µ + y

. Mamy

x + y − 2 = ξ + x

+ µ + y

− 2

− y + 4 = ξ + x

− µ − y

+ 4

Parę (x

, y

) wybieramy tak, by spełniony był układ

+ y

− y

= −4

W ten sposób otrzymujemy równanie jednorodne

(ξ + µ)dξ + (ξ − µ)dµ = 0.

Dalsze postępowanie jest już proste. Podstawiamy µ = uξ i mamy równanie

(ξ + uξ)dξ + (ξ − uξ)(ξdu + udξ) = 0.

Po uporządkowaniu wyrazów otrzymujemy równanie o zmiennych rozdzie-
lonych

(1 + 2u − u

)dξ + ξ(1 − u)du = 0.

4.3. RÓWNANIA W POSTACI RÓŻNICZEK ZUPEŁNYCH

Po scałkowaniu otrzymamy

ln |ξ| +

1
2

ln |1 + 2u − u

| = ln C,

czyli

(1 + 2u − u

) = C

Wracamy do zmiennych (x, y) i otrzymujemy równanie

(x + 1)

1 + 2

− 3

x + 1

−

(y − 3)

(x + 1)

= C

czyli

+ 2xy − y

− 4x + 8y = C.

Uwaga na stałe generyczne!

4.3

Równania w postaci różniczek zupełnych

Równanie w postaci różniczek (w postaci (4.7)) przypomina zapis różniczki
zupełnej funkcji dwóch zmiennych. Oczywiście, nie każde takie wyrażenie
jest w rzeczywistości różniczką zupełną jakiejś funkcji. Analiza dostarcza
nam jednak prostych sposobów sprawdzenia tego faktu.

Twierdzenie 4.3.1 Niech będzie dane wyrażenie

M (x, y)dx + N (x, y)dy

(4.10)

i niech funkcje M (x, y), N (x, y), M

(x, y) i N

(x, y) będą ciągłe w zbiorze

Q = {(x, y) : x ∈ (a, b), y ∈ (c, d)}. Jeśli w zbiorze Q jest spełniona równość

(x, y) = N

(x, y),

(4.11)

to wyrażenie (4.10) jest różniczką zupełną, czyli różniczką pewnej funkcji
F (x, y). Wtedy również całka krzywoliniowa

M (x, y)dx + N (x, y)dy,

(4.12)

liczona po drodze L zawartej w Q nie zależy od drogi całkowania.

ROZDZIAŁ 4. PODSTAWOWE KLASY RÓWNAŃ

Funkcje M (x, y) i N (x, y) możemy potraktować jako składowe pola wek-

torowego V (x, y) = (M (x, y), N (x, y)). Mówimym że pole takie jest poten-
cjalne, jeśli istnieje funkcja F (x, y) taka że

V (x, y) = ∇F (x, y).

Funkcję F nazywamy potencjałem pola. Korzystając z twierdzenia 4.3.1
można łatwo udowodnić istnienie rozwiązań dla równań w postaci różniczek
zupełnych.

Twierdzenie 4.3.2 Załóżmy, że w zbiorze Q = {(x, y) : x ∈ (a, b), y ∈
(c, d)} funkcje M (x, y), N (x, y), M

(x, y) i N

(x, y) są ciągłe i spełniają

równość

(x, y) = N

(x, y)

oraz jedna z funkcji M (x, y) lub N (x, y) jest różna od zera w kazdym punkcie
zbioru Q. Wtedy przez każdy punkt (x

, y

) ∈ Q przechodzi dokładnie jedna

krzywa całkowa równania

M (x, y)dx + N (x, y)dy = 0

(4.13)

Dowód. Załóżmy, że N (x, y) = 0. Wtedy równanie (4.13) można przepisać
w postaci

M (x, y) + N (x, y)

dy
dx

= 0.

(4.14)

Ponieważ rozważamy różniczkę zupełną, więc istnieje funkcja F (x, y), że

M (x, y) =

∂F

∂x

, N (x, y) =

∂F

∂y

Wobec tego równanie (4.14) można zapisać jako

dF (x, y(x))

= 0.

Rozwiązaniem tego równania jest F (x, y(x)) = C. Aby był spełniony wa-
runek początkowy należy przyjąć C = F (x

, y

) co jednocześnie gwaran-

tuje jednoznaczność rozwiązania (dlaczego?). Zauważmy także, że warunek

4.4. ZADANIA

N (x, y) = 0 gwarantuje spełnienie założeń twierdzenia o funkcji uwikłanej.
Oznacza to, że równanie F (x, y(x)) = C można rozwikłać zadając funkcję
y(x) w postaci jawnej.

Przykład 1. Znajdziemy krzywą całkową równania

(x + y)dx + (x − y)dy = 0,

przechodzącą przez punkt (1, 1). Całkując to równanie skorzystamy z faktu,
ze całka krzywoliniowa nie zależy od drogi całkowania. Całkę łączącą punkt
(1, 1) z punktem (x, y) obliczymy po łamanej przechodzącej przez punkt
(x, 1). Mamy

(x,y)

(1,1)

(t + s)dt + (t − s)ds =

(t + 1)dt +

(x − s)ds =

1
2

+ x −

3
2

+ xy −

1
2

− x +

1
2

+ xy −

1
2

− 1.

Oznacza to, że F (x, y) =

+xy −

−1. W celu znalezienia rozwiązania

naszego równania należy rozwikłać równanie F (x, y) = 0. Zauwazmy jen-
dak, że niemożliwe jest znalezienie rozwiązania w postaci funkcji y(x), bo
F

(1, 1) = 0. Ponieważ F

(1, 1) = 2 więc łatwo można znaleźć rozwiązanie

w postaci

x(y) = −y ±

2(y

+ 1).

W rozdziale następnym będziemy nadal zajmować się równaniami w postaci
różniczek zupełnych oraz równaniami, które a priori do tej klasy nie należą,
ale mogą być na nią zrzutowane.

4.4

Zadania

1. Znaleźć rozwiązania zagadnień Cauchy’ego

(a) y ln ydx + xdy = 0, y(1) = 1.

(b) xdy

− ydx = 0, y(1) = 0.

ROZDZIAŁ 4. PODSTAWOWE KLASY RÓWNAŃ

1 − y

dx + y

√

1 − x

dy = 0, y(0) = 1.

2. Scałkować równania

(a) t ˙x = x cos ln

(b) (2x − 4y + 6)dx + (x + y − 3)dy = 0

−

3. Scałkować równania

(a) 2xydx + (x

− y

)dy = 0

(b) (2 − 9xy

)xdx + (4y

− 6x

)ydy = 0

(c)

y
x

+ (y

+ ln x)dy = 0

†

Scałkować równania

(a)

+ 1

dx +

− 1

dy = 0

(b) (x

+ y)dx + (x

− x)dy = 0

Rozdział 5

Zależność od danych

Często dysponując jednym rozwiązaniem chcielibyśmy móc orzec co zmieni
się gdy zmienimy warunki początkowe lub prawą stronę równania. Rozdział
ten poświęcony jest twierdzeniom opisującym charakter tych właśnie zależ-
ności.

5.1

Ciągła zależność od warunku początkowego

W wielu zagadnieniach praktycznych mamy do czynienia z warunkiem Cau-
chy’ego. Rozwiązania są wyznaczone przez warunek początkowy. Można za-
dać pytanie czy zmiana punktu początkowego, z którego nasze rozwiązanie
startuje, wpływa w sposób ciągły na przebieg rozwiązania?

Twierdzenie 5.1.1 Niech dane będzie zagadnienie Cauchy’ego

˙x = f (t, x)

x(t

) = x

Jeśli funkcja f jest określona na G

⊆ R × R

i lipschitzowska ze względu na

∈ R

, natomiast φ(x

, t) = u(t) jest rozwiązaniem problemu Cauchy’ego

dla u(t

) = x

, na [t

, t

], a φ(y

, t) = v

(t) są rozwiązaniami problemu

cauchy’ego dla y

→ x

określonymi na [t

, t

], to v

(t) → u(t) dla t ∈

, t

ROZDZIAŁ 5. ZALEŻNOŚĆ OD DANYCH

W sformułowaniu twierdzenia można pominąć warunek określoności roz-

wiązań v

(t) na przedziale [t

, t

]. Ich istnienie na całym tym przedziale

wynika z twierdzeń o przedłużaniu rozwiązań, którymi nie będziemy się
zajmować.

Zanim przejdziemy do dowodu twierdzenia 5.1.1, potrzebujemy jeszcze

jednego pomocniczego narzędzia, które w teorii równań różniczkowych zwy-
czajnych oraz cząstkowych odgrywa bardzo ważną rolę.

Lemat 5.1.2 (Nierówność Gronwall’a) Niech K > 0, C 0, t

< t

Jeśli funkcja ciągła rzeczywista, nieujemna v : [t

, t

] → R spełnia nierów-

ność:

v(t) C +

Kv(s)ds

(5.1)

dla wszystkich t

∈ [t

, t

], to takze dla wszystkich t ∈ [t

, t

] spełnia nierów-

ność:

v(t) Ce

K(t−t

)

(5.2)

Dowód. Załóżmy najpierw, że C > 0. Oznaczmy U (t) = C +

Kv(s)ds.

Ponieważ K, v

0, mamy U(t) > 0. Zachodzi także U

(t) = Kv(t). Zało-

żenie (5.1) mówi, że v(t) U (t). Zatem (ln U (t))

(t)

U (t)

K, co oznacza,

że

ln U (t) − ln U (t

) =

(ln U (s))

K(t − t

Stąd v(t) U (t) U (t

K(t−t

)

. Jeśli C = 0 to możemy je zastąpić

dowolnym innym C

> 0. Wtedy

v(t) C

Kv(s)ds

zatem na mocy udowodnionej już części lematu v(t) C

K(t−t

)

. Z dowol-

ności C

otrzymujemy v(t) Ce

K(t−t

)

= 0.

Dowód. (twierdzenia 5.1.1) Załóżmy, że v

jest określona na [t

, t

]. mamy

wówczas

(t) − u(t) v

) − u(t

) +

(s) − u(s)ds,

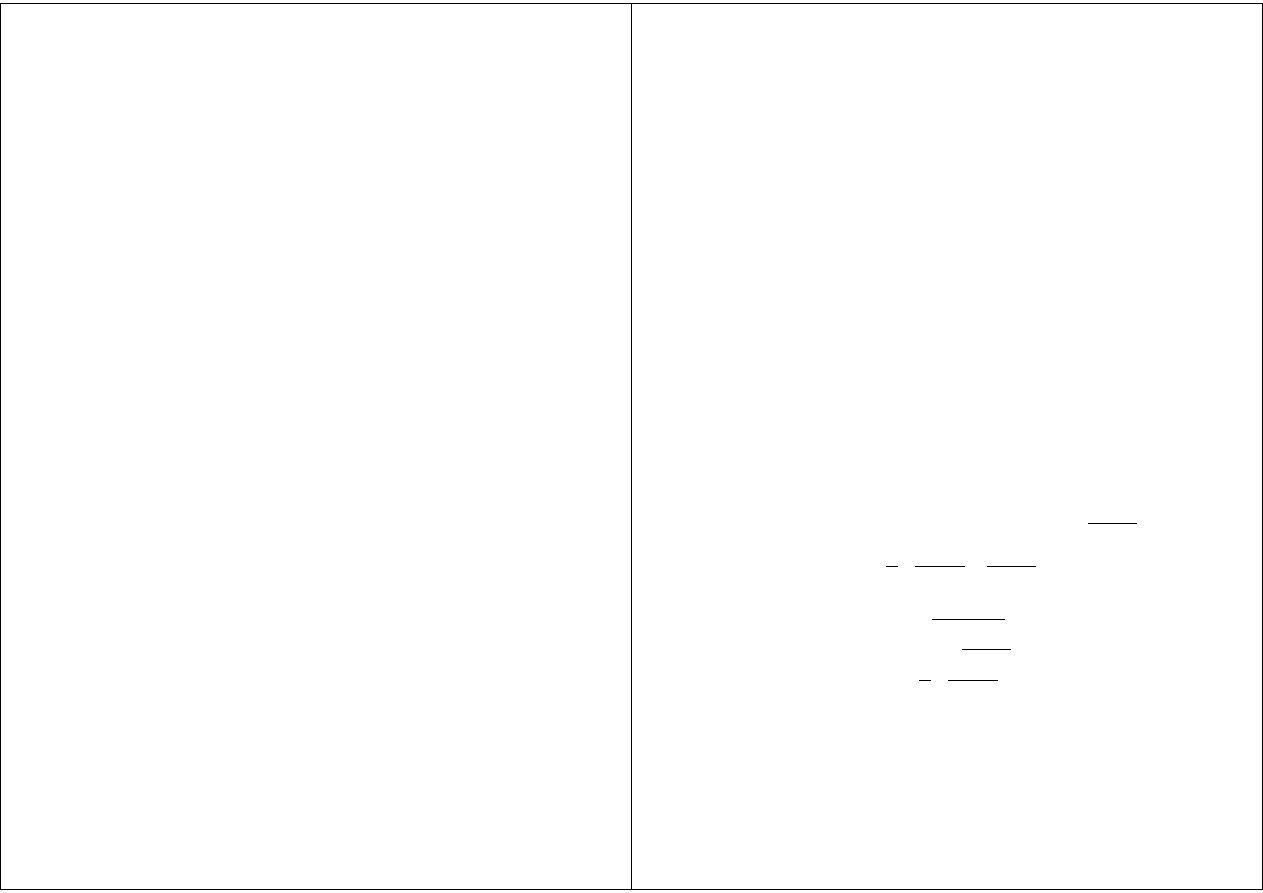
5.2. ZALEŻNOŚĆ OD PRAWEJ STRONY

gdzie L jest stałą Lipschitza funkcji f w kierunku x. Funkcja v(t) = v

(t)−

u(t) spełnia założenia lematu Gronwall’a (5.1.2) zatem

(t) − u(t) e

L(t−t

)

) − u(t

)

więc

) − u(t

) → 0 implikuje ∀

(t) − u(t) → 0.

5.2

Zależność od prawej strony

Zależność od funkcji występującej po prawej stronie równania rozumie się
najczęściej w ten sposób, że zakłada się, iż jest ona zalezna od trzech zmien-
nych f = f (t, x, λ), gdzie t jest zmienną niezależną, x zmienną zależną, a
λ jest traktowane jako dodatkowy parametr. Oznacza to rozważanie zagad-
nienia początkowego w postaci

˙x = f (t, x, λ)

x(t

) = x

(5.3)

Jeśli x(t) jest rozwiązaniem zagadnienia (5.3) to chcąc badać zależność tego
rozwiązania od warunków początkowych (t

, x

) i parametru λ, będziemy

traktowali to rozwiązanie jako funkcję wszystkich tych zmiennych, tj. x(t) =
ϕ(t, t

, x

, λ). Okazuje się, że sytuację tą można znacznie uprościć dokonując

zamiany zmiennych

→ t − t

, x

→ x − x

Zagadnienie (5.3) zmieni się wówczas na równoważne

˙x = f (t − t

, x

− x

, λ)

x(0) = 0

(5.4)

W tym zapisie zmienne x

, t

są dodatkowymi parametrami funkcji f . Ozna-

cza to, że zależność od warunków początkowych można sprowadzić do za-
leżności prawej strony równania od parametru. Możliwa jest także operacja
odwrtona. Możemy potraktować λ jako zmienną zależną, uzupełniając za-
gadnienie (5.3) równaniem

˙λ = 0,

ROZDZIAŁ 5. ZALEŻNOŚĆ OD DANYCH

z warunkiem początkowym

λ(t

) = λ

gdzie λ

jest ustaloną wartością parametru λ (wybraną dowolnie). Przyj-

mując

x = (x, λ) i ¯

f = (f, 0),

otrzymamy zagadnienie Cauchy’ego

˙¯x = ¯

f (t, ¯

x(t

) = ¯

(5.5)

Stąd widać, że zależność od parametru można sprowadzić do zależności
od warunku początkowego. Na podstawie twierdzenia 5.1.1 możemy zatem
wnioskować o ciągłej zależności rozwiązań od parametru, zamieniając za-
gadnienie zależności prawej strony na zagadnienie zależności od warunku
początkowego.

W większości wypadków regularność prawej strony równania jest wyższa

niż tylko lipschitzowskość. Obecnie zajmiemy się tym przypadkiem.

Twierdzenie 5.2.1 Niech f (t, x, λ) będzie funkcją klasy C

swoich argu-

mentów dla (t, x) ∈ Q ⊂ R

i λ

∈ G ⊂ R

, gdzie zbiory Q i G są otwarte.

Wtedy rozwiązanie x = x(t, t

, x

, λ) zagadnienia początkowego (5.3) jest

klasy C

względem zmiennych t, t

, x

, λ w otwartym zbiorze, na którym

jest określone. Jeśli przez y(t) oznaczymy macierz Jacobiego [

∂x(t,t

,λ)

∂λ

to spełnia ona równanie macierzowe

∂f (t, x, λ)

∂x

y +

∂f (t, x, λ)

∂λ

(5.6)

z warunkiem początkowym

y(t

) =

∂x(t

, t

, x

, λ)

∂λ

= 0.

Natomiast macierz Jacobiego z(t) = [

∂x(t,t

,λ)

∂x

] spełnia równanie

∂f (t, x, λ)

∂x

(5.7)

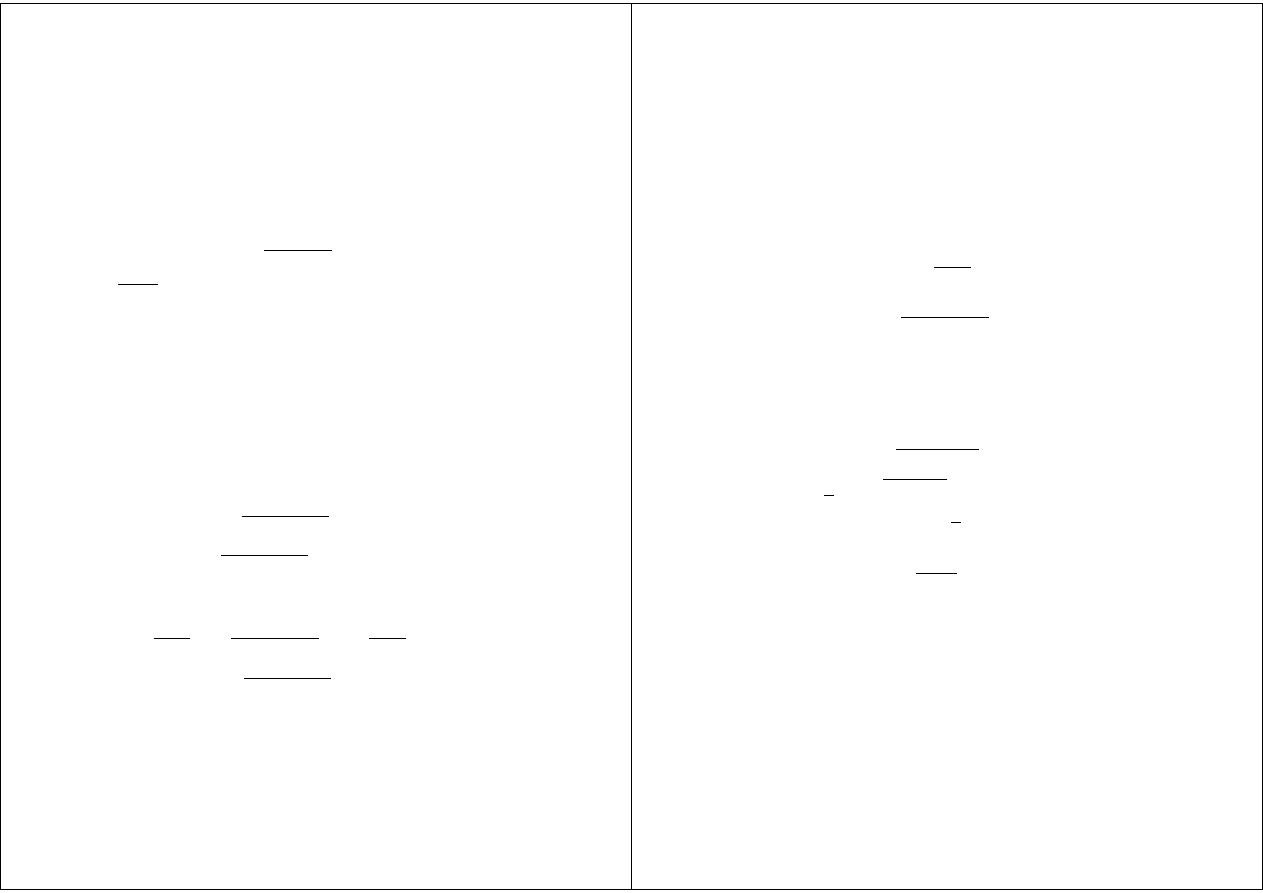
5.2. ZALEŻNOŚĆ OD PRAWEJ STRONY

z warunkiem początkowym

z(t

) =

∂x(t

, t

, x

, λ

∂x

= I

m×m

Dowód. Różniczkowalność w sposób ciągły względem t wynika z twierdze-
nia Picarda-Linedlöfa (twierdzenie 3.2.1). Na podstawie uwag uczynionych
wczesniej możemy zająć się zależnością rozwiązania od parametru λ. Poniżej
udowodnimy, że rozwiązanie (5.3) jest klasy C

jako funkcja tego parametru.

Dla uproszczenia zapisu ograniczymy się do rozważania przypadku jedno-
wymiarowego (skalarne λ). W przypadku λ będącego wektorem poniższe
rozumowanie należy przeprowadzić dla każdej ze składowych oddzielnie.

Niech ϕ(t, λ

) i ϕ(t, λ

) będą dwoma rozwiązaniami równania (5.3) z

tym samym warunkiem początkowym i różnymi wartościami parametru λ.
Niech U będzie zwartym podzbiorem Q i niech (t, ϕ(t, λ

)), (t, ϕ(t, λ

)) ∈ U

dla t

∈ J

= {t : |t − t

| α}. Rozważmy różnicę

∆ϕ = ϕ(t, λ

) − ϕ(t, λ

Korzystamy z całkowej postaci równania (5.3) i rozwijamy funkcję f (t, x, λ

)

w szereg Taylora wokół punktu λ

, skąd

∆ϕ(t) =

∂f (τ, ϕ(τ, λ

), λ

)

∂x

(τ )

∆ϕ(τ )dτ +

∂f (τ, ϕ(τ, λ

), λ

)

∂λ

(τ )

(λ

− λ

)dτ,

gdzie

(τ ) = o(λ

− λ

) i

(τ ) = o(λ

− λ

). Po podzieleniu obu stron tego

równania przez (λ

− λ

) otrzymujemy różnicową wersję równania (5.6)

∆ϕ(t)

− λ

∂f (τ, ϕ(τ, λ

), λ

)

∂x

(τ )

∆ϕ(τ )

− λ

dτ +

(5.8)

∂f (τ, ϕ(τ, λ

), λ

)

∂λ

(τ )

dτ.

ROZDZIAŁ 5. ZALEŻNOŚĆ OD DANYCH

Ponieważ równanie (5.6) spełnia warunki twierdzenia o istnieniu i jedno-
znaczności rozwiązań, więc niech y(t, λ) będzie jego rozwiązaniem. Oznacz-
my

u(t) =

∆ϕ(t)

− λ

− y(t, λ

Odejmijmy od równania (5.8) całkowąwersję równania (5.6) i otrzymujemy

u(t) =

∂f (τ, ϕ(τ, λ

), λ

)

∂x

(τ )

u(τ )dτ +

(

(τ )y(τ, λ

) +

(τ ))dτ.

Jeśli τ

∈ J

, to funkcja y(τ, λ

) jest ograniczona i

ζ = sup

τ ∈J

(τ )y(τ, λ

) +

(τ )| = o(λ

− λ

Zachodzi wtedy oszacowanie

|u(t)|

∂f (τ, ϕ(τ, λ

), λ

∂x

(τ )

|u(τ)| + ζ

dτ.

Niech K = sup

τ ∈J

∂f (τ,ϕ(τ,λ

),λ

)

∂x

|. Stała K jest skonczona, co wynika z

ciągłości

∂f
∂x

i zwartości U . Z lematu Gronwall’a otrzymujemy

|u(t)|

Kα

− 1).

Wynika stąd, że u(t) = o(λ

− λ

), czyli

∂ϕ(x, λ)

∂λ

= y(t, λ).

Wobec tego rozwiązanie równania (5.3) jest klasy C

względem λ, bo ma-

cierz Jacobiego jego pochodnej względem λ spełnia równanie (5.6) i jest
ciągła, co wynika z twierdzenia 5.1.1.

Wynik ten można uogólnić na wyższe klasy regularności prawej strony.

Wniosek 5.2.2 Jeśli w założeniach twierdzenia 5.2.1 funkcja f (t, x, λ) jest
klasy C

, gdzie r

1, to rozwiązanie x(t, t

, x

, λ) jest też kalsy C

5.3. ZADANIA

5.3

Zadania

1. Znaleźć wskazaną pochodną względem parametru lub warunku po-

czątkowego:

(a) ˙x = x + µ(t + x

), x(0) = 1. Znaleźć

∂x

∂µ

µ=0

(b) ˙x = 2t + µx

, x(0) = µ − 1. Znaleźć

∂x

∂µ

µ=0

+ tx

, x(2) = x

. Znaleźć

∂x

ROZDZIAŁ 5. ZALEŻNOŚĆ OD DANYCH

Rozdział 6

Równania liniowe skalarne

6.1

Czynnik całkujący

Równania w postaci różniczek zupełnych nie występują zbyt często. Bywa
jednak tak, że chociaż wyjściowe równanie nie jest w postaci różniczki zu-
pełnej, to po pomnożeniu przez pewną funkcję daje się sprowadzić do takiej
postaci. Funkcja taka nazywa się czynnikiem całkującym. Jeśli wyrażenie

M dx + N dy

pomnożymy przez czynnik całkujący µ(x, y)

µM dx + µN dy

i zażądamy żeby nowe wyrażenie było różniczką zupełną

∂µM

∂y

∂µN

∂x

to otrzymamy równanie cząstkowe

∂µ

∂y

− N

∂µ
∂x

= µ

∂N

∂x

−

∂M

∂y

(6.1)

ROZDZIAŁ 6. RÓWNANIA LINIOWE SKALARNE

Oczywiście rozwiązanie (6.1) nie jest wcale łatwiejsze od rozwiązania wyj-
ściowego równania zwyczajnego. Często jednak bywa, że wyrażenie M dx +
N dy jest bliskie różniczce zupełnej. Wtedy czynnik N

− M

, występujący

po prawej stronie równania (6.1), może być stały albo może być funkcją tyl-
ko jednej zmiennej. Sugeruje to często poszukiwanie czynnika całkującego
w postaci µ(x), µ(y) lub µ = µ(f ) gdzie f jest znaną funkcją x i y.
Przykład 1. Czynnikiem całkującym dla równania

(1 − x

y)dx + x

(y − x)dy = 0

jest µ(x) = x

−2

Przykład 2. Czynnikiem całkującym dla równania

dx + (x

− x)dy = 0

jest µ = (xy)

−1

6.2

Równania liniowe skalarne pierwszego rzędu

Obecnie zajmiemy się przypadkiem jednego równania liniowego pierwszego
rzędu.

Deﬁnicja 6.2.1 Równanie postaci

˙x + p(t)x = q(t)

(6.2)

gdzie p(t) i q(t) są funkcjami zmiennej t ∈ (a, b), nazywamy równaniem
liniowym. Jeśli q(t) ≡ 0 to równanie to nazywamy równaniem liniowym
jednorodnym.

Dla równania (6.2) bardzo łatwo otrzymać twierdzenie o istnieniu i jen-

doznaczności.

Twierdzenie 6.2.2 Jeśli funkcje p(t) i q(t) są ciągłe dla t ∈ (a, b), to
przez każdy punkt zbioru Q = (a, b) × R przechodzi dokładnie jedna krzywa
całkowa równania (6.2). maksymalnym przedziałem istnienia rozwiązania
jest przedział (a, b).

6.2. RÓWNANIA LINIOWE SKALARNE PIERWSZEGO RZĘDU

Dowód. Istnienie i jednoznaczność lokalnego rozwiązania wynika z twier-
dzenia Picarda-Lindelöfa, bo wyrażenie q(t)−p(t)x spełnia lokalnie warunek
Lipschitza. Należy jedynie udowodnić że rozwiązanie lokalne przedłuża się
na cały odcinek (a, b). Wystarczy w tym celu udowodnić, że rozwiązanie w
każdym punkcie jest ograniczone. Rozważmy zatem rozwiązanie x(t) prze-
chodzące przez punkt (t

, x

). Pokażemy, że jeśli t

∈ (a, b) to x(t

) jest

ograniczone. Rozwiązanie x(t) spełnia równanie całkowe

x(t) = x

−

p(s)x(s)ds +

q(s)ds,

więc mamy oszacowanie

|x(t

)| |x

q(s)ds| + K

|x(s)|ds,

gdzie K = sup

t∈[t

]

|p(t)|. Ponieważ odcinek [t

, t

] jest zwarty, więc funk-

cja q(t) jest ograniczona dla t ∈ [t

, t

] i

q(s)ds

= c < +∞.

Stąd

|x(t

)| c + K

|x(s)|ds.

Na mocy nierówności Gronwalla mamy

|x(t

)| ce

K(t

−t

)

Oznacza to, że rozwiązanie x(t) jest ograniczone na całym przedziale (a, b),
zatem rozwiązania lokalne możemy na cały ten przedział przedłużyć.

Dowód istnienia można także przeprowadzić konstruktywnie podając

metodę rozwiązywania równań liniowych skalarnych.

Dowód. (metoda uzmienniania stałej) Zauważmy że równanie postaci

˙x + p(t)x = 0,

ROZDZIAŁ 6. RÓWNANIA LINIOWE SKALARNE

czyli równanie jednorodne powstałe przez opuszczenie prawej strony w (6.2)
jest równaniem o zminnych rozdzielonych. Jego rozwiązanie ma postać

x(t) = C exp

−

p(s)ds

(6.3)

Aby znaleźć rozwiązanie równania niejednorodnego zastosujemy metodę
zwaną metodą uzmienniania stałej. W tym celu w miejsce stałej C wsta-
wimy nieznaną funkcję czasu z(t) i poszukujemy rozwiązania w postaci

x(t) = z(t) exp

−

p(s)ds

Po podstawieniu do równania (6.2) otrzymujemy

˙z(t) exp

−

p(s)ds

− z(t)p(t) exp

−

p(s)ds

+p(t)z(t) exp

−

p(s)ds

= q(t).

Po uporządkowaniu wyrazów otrzymujemy równanie dla z(t) w postaci

˙z(t) = q(t) exp

−

p(s)ds

którego rozwiązanie ma postać

z(t) = z(t

) +

q(τ ) exp

−

p(s)ds

dτ.

Po podstawieniu do równania (6.3) mamy

x(t) =

z(t

) +

q(τ ) exp

−

p(s)ds

dτ

exp

−

p(s)ds

Mamy zatem ogólną postać rozwiązania.

Uwaga: łatwiej jest powtórzyć zaprezentowaną procedurę niż korzystać z ostatecznej

postaci rozwiązania.

6.2. RÓWNANIA LINIOWE SKALARNE PIERWSZEGO RZĘDU

Na przedstawiony powyżej wynik można spojrzeć w inny sposób. Zdeﬁ-

niujmy operator

L określony na funkcjach różniczkowalnych jako

L(x) = ˙x + p(t)x.

Operator ten jest oczywiście liniowy

. Używając operatora

L równanie jed-

norodne możemy zapisać w postaci

L(x) = 0,

(6.4)

a niejednorodne jako

L(x) = q(t).

(6.5)

Jeśli popatrzymy na

L jako na przekształcenie liniowe to równanie (6.4)

opisuje jego jądro. Jak wiadomo z algebry liniowej jądro jest podprzestrzenią
liniową. Widać to choćby z równania (6.3). Rozwiązania równania (6.2.1)
możemy teraz opisać w terminach operatora

Twierdzenie 6.2.3 Niech będzie dany operator liniowy

L(x) = ˙x + p(t)x.

Wówczas

1. Jądro operatora

L jest przestrzenią jednowymiarową, jej bazą jest wek-

tor u(t) = exp

−

p(s)ds

2. Funkcja u

(t) =

q(τ ) exp

−

p(s)ds

dτ jest szczególnym rozwią-

zaniem równania niejednorodnego

L(x) = q(t).

3. Każde rozwiązanie równania niejednorodnego

L(x) = q(t) przedstawia

się w postaci sumy rozwiązania szczególnego u

(t) i pewnego rozwią-

zania z jądra operatora

Dla osób zaznajomionych z analizą funkcjonalną: jest również ciągły jako operator

→ C

ROZDZIAŁ 6. RÓWNANIA LINIOWE SKALARNE

6.3

Równanie Bernoulliego

Obok równań liniowych istnieją pewne rodzaje równań, które można spro-
wadzić przez odpowiednie podstawienie do równań tejże klasy. Rozważmy
równanie postaci

˙x + p(t)x + q(t)x

= 0.

(6.6)

Równanie to nosi nazwę równania Bernoulliego. Liczbę n nazywamy wy-
kładnikiem Bernoulliego. Dla n = 0 mamy do czynienia ze zwykłym rów-
naniem liniowym. Dla innych wartości wykładnika Bernoulliego równanie
(6.6) sprowadza się do równania liniowego przez podstawienie

z = x

1−n

Po podzieleniu równania (6.6) stronami przez x

otrzymamy

˙xx

−n

+ p(t)x

1−n

+ q(t) = 0.

(6.7)

Ponieważ ˙z = (1−n)x

−n

˙x to równanie (6.7) względem zmiennej z ma postać

1 − n

˙z + p(t)z + q(t) = 0,

czyli jest równaniem liniowym.

6.4

Równanie Riccatiego

Innym typem równania, które w pewnych przypadkach daje się sprowadzić
do równania liniowego, jest równanie postaci

˙x + p(t)x + q(t)x

+ r(t) = 0.

(6.8)

Równanie w tej postaci nazywa się równaniem Riccatiego i nie istnieje ogólny
sposób jego analitycznego całkowania. Jeśli jednak zanamy jedno rowiązanie
szczególne x

(t), to przez podstawienie u = x − x

można to równanie

6.5. RÓWNANIE CLAIRAUTA

†

sprowadzić do prostej postaci. Ponieważ ˙u = ˙x − ˙

, więc podstawiając tę

równość do lewej strony równania (6.8) otrzymujemy

+ ˙u + p(t)(x

+ u) + q(t)(x

+ u)

+ r(t) =

= ˙

+ p(t)x

+ q(t)x

+ r(t) + ˙u + p(t)u + 2q(t)x

u + q(t)u

= ˙u + p(t)u + 2q(t)x

u + q(t)u

Stąd wynika, że u(t) spełnia równanie

˙u + p(t)u + 2q(t)x

(t)u + q(t)u

= 0.

Jest to równanie Bernoulliego z wykładnikiem 2 i jako takie można je rozwią-
zać analitycznie. Oczywiście powstaje pytanie, w jakim stopniu metoda ta
jest skuteczna, tzn. jak można znaleźć szczególne rozwiązanie x

(t). Prawda

jest taka, że rozwiązanie x

(t) należy zgadnąć. Kedy jednak uda nam się

odgadnąć jedno rozwiązanie, wtedy przedstawiona metoda postępowania
pozwala znaleźć rozwiązanie ogólne tego równania.

6.5

Równanie Clairauta

†

Równanie postaci

x = t ˙x + f ( ˙x),

(6.9)

gdzie o ˙x i f zakładamy różniczkowalność w pewnych przedziałach nazywa-
my równaniem Clairauta. Różniczkując obie strony równania (6.9) mamy

˙x = ˙x + t¨

x + f

( ˙x)¨

skąd

x(t + f

( ˙x)) = 0.

Należy zatem rozpatrzyć dwa przypadki ¨

x = 0 lub t + f

( ˙x) = 0. Jeżeli

x = 0 to ˙x = C i po podstawieniu do równania (6.9) mamy

x = Ct + f (C).

ROZDZIAŁ 6. RÓWNANIA LINIOWE SKALARNE

Jeśli natomiast t + f

( ˙x) = 0 to rozwiązanie otrzymujemy jako rodzinę

krzywych parametrycznych w postaci (t, x) danych układem

t = −f

( ˙x)

x = t ˙x + f ( ˙x)

traktując ˙x jako parametr.

6.6

Równanie Lagrange’a-d’Alamberta

†

Równaniem Lagrange’a-d’Alamberta nazywamy równanie w postaci

x = tf ( ˙x) + g( ˙x),

(6.10)

w którym o funkcjach f i g zakładamy, że są danymi funkcjami klasy C

pewnym przedziale oraz f ( ˙x) ≡ ˙x. Poszukujemy rozwiązań równania (6.10)
klasy C

. Po zróżniczkowaniu stronami mamy

˙x = f ( ˙x) + tf

( ˙x)¨

x + g

( ˙x)¨

Podstawiając ˙x = p i ¨

x = ˙p mamy przy założeniu tf

(p) + g

(p) = 0

˙p =

− f(p)

(p) + g

(p)

(6.11)

Jeśli licznik p

− f(p) jest równy 0 przy wartościach p

, p

, . . . , p

to prze-

dział zmienności p rozbijamy na rozłączne przedziały nie zawierające owych
punktów. W każdym z nich pochodna ˙p zachowuje stały znak, co oznacza że
funkcja p jest ściśle monotoniczna. Istnieje zatem funkcja odwrotna t = t(p)
różniczkowalna w odpowiednim przedziale. Ponieważ

= 1/

przy zało-

żeniu

= 0, które mamy spełnione, to traktując równanie (6.11) jako

równanie funkcji t w zależności od zmiennej p mamy równanie

−

(p)

− f(p)

t =

(p)

− f(p)

bedące równaniem liniowym.

6.7. ZADANIA

6.7

Zadania

1. Rozwiązać równania

(a) t ˙x − 2x = 4t

(b) (2t + 1) ˙x = 4t + 2x

− t ˙x = 0

(d) (2x + y)dy = ydx + 4 ln ydy

2. Rozwiązać podane równania, sprowadzając je do postaci liniowej

(a) xdx = (x

− 2y + 1)dy

(b) t(e

− ˙x) = 2

− 1) ˙x sin x + 2t cos x = 2t − 2t

3. Rozwiązać równania

(a) t

˙x + tx + t

= 4

(b) 3 ˙x + x

= 0

= 5 − t

ROZDZIAŁ 6. RÓWNANIA LINIOWE SKALARNE

Rozdział 7

Liniowe równania rzędu
drugiego

7.1

Zagadnienie

W wielu zagadnieniach, nie tylko ﬁzycznych, mamy do czynienia z równania-
mi rzędów wyższych niż jeden. Przypomnijmy, że druga pochodna pewnej
wielkości określa szybkość zmiany tej wielkości. W zastosowaniach traktowa-
na jest ona jako informacja o przyspieszeniu. Interesować będą nas równania
liniowe.

Deﬁnicja 7.1.1 Równaniem liniowym rzędu drugiego nazywamy równanie
postaci:

x + p(t) ˙x + q(t)x = r(t).

(7.1)

Gdy r(t) ≡ 0, wówczas równanie (7.1) nazywamy równaniem jednorodnym,
w przeciwnym wypadku równanie to nazywamy równaniem niejednorodnym.

Dowody istnienia i jednoznaczności rozwiązań równań liniowych drugiego
rzędu na razie pominiemy. Zostaną one zaprezentowane, gdy będziemy w
posiadaniu narzędzi z obszaru układów równań liniowych pierwszego rzędu.
Jak pamiętamy z rozdziału 2, każde równanie rzędu wyższego niż pierwszy
można rozłożyć na układ równań rzędu pierwszego.

ROZDZIAŁ 7. LINIOWE RÓWNANIA RZĘDU DRUGIEGO

Podobnie jak w przypadku równań liniowych rzędu pierwszego, również

w tym przypadku możemy spojrzeć na zagadnienie w sposób geometryczny.
W rozdziale szóstym doszliśmy do wniosku, że rozwiązanie niejednorodnego
równania liniowego wyraża się jako warstwa aﬁniczna rozwiązania zagad-
nienia jednorodnego. Również w tym przypadku dowolne ϕ - rozwiązanie
równania (7.1) może zostać przedstawione jako suma ϕ

- jednego ustalonego

rozwiązania zagadnienia (7.1) oraz ˜

ϕ - dowolnego rozwiązania zagadnienia

jednorodnego, stowarzyszonego z (7.1)

x + p(t) ˙x + q(t)x = 0.

(7.2)

Zapisując powyższe wnioski przy użyciu języka algebry liniowej możemy
stwierdzić że zagadnienie (7.1) jest w istocie poszukiwaniem przeciwobrazu
elementu r(t) ∈ C

przy przekształceniu liniowym

L(x) = ¨x+p(t) ˙x+q(t)x.

Ponieważ porzuciliśmy świat skończenie wymiarowy przenosząc się w

przestrzenie funkcyjne, które ze swej natury są przestrzeniami o nieskoń-
czonej liczbie wymiarów, potrzebne jest nam zdeﬁniowanie pojęcia liniowej
niezależności układu wektorów będace wygodniejszym w użyciu niż stosowa-
ne dotychczas. Pojęcie to zostanie wprowadzone w nieco nietypowy sposób.

Niech x

(t) i x

(t) będą dwoma różnymi rozwiązaniami zagadnienia jed-

norodnego (7.2). Z liniowości wynikać powinno że dla dowolnych skalarów
c

i c

funkcja postaci c

(t) + c

(t) także jest rozwiązaniem równania

(7.2). W ogólności stwierdzenie to jest jednak nieprawdziwe.

Stwierdzenie 7.1.2 Niech x

(t) i x

(t) będą dwoma różnymi rozwiązania-

mi zagadnienia jednorodnego (7.2) określonymi na przedziale [a, b]. Funkcja
postaci c

(t)+c

(t) jest rozwiązaniem równania (7.2) wtedy i tylko wte-

dy, gdy

∀

t∈[a,b]

det

(t) x

(t)

˙x

(t)

˙x

(t)

= 0.

(7.3)

Dowód. (na razie pomijamy)

Warunek 7.3 pozwala nam sformułować

następującą deﬁnicję

Deﬁnicja 7.1.3 Układ funkcji (x

(t), x

(t)) nazwiemy liniowo niezależnym

gdy spełniony jest warunek 7.3.

7.2. RÓWNANIA O STAŁYCH WSPÓŁCZYNNIKACH

Macierz występującą w sformułowaniu warunku 7.3 nazywamy macierzą

Wrońskiego, jej wyznacznik zaś wrońskianem.

Rozważając operator

L możemy stwierdzić, że zagadnienia (7.1) i (7.2)

można sformułować jako rozwiązywanie zagadnień

L(x) = r(t) i L(x) = 0.

Podobnie do twierdzenia 6.2.3 możemy sformułować następujące twierdze-
nie.

Twierdzenie 7.1.4 Niech dany będzie operator liniowy

L : C

→ C

zada-

ny wzorem

L(x) = ¨x + p(t) ˙x + q(t)x. Wówczas

1. Jądro operatora

L jest dwuwymiarowe, jego bazę stanowią liniowo nie-

zależne funkcje x

(t) i x

(t).

2. Jeśli x

(t) jest rozwiązaniem równania L(x) = r(t), to jego ogólne

rozwiązanie wyraża się wzorem c

(t) + c

(t) + x

(t) gdzie c

, c

∈

Dowód. (na razie pomijamy)

7.2

Równania o stałych współczynnikach

Niestety nie potraﬁmy rozwiązywać równań liniowych rzędu drugiego w
ogólności jaką prezentuje postać 7.1. Jesteśmy jednak w stanie podać je-
go rozwiązania w przypadku, gdy funkcje p(t) i q(t) są funkcjami stałymi.
Do takich równań ograniczymy się w daleszej cześci rozważań.

Rozpatrzmy równanie w postaci

x + a ˙x + bx = r(t),

(7.4)

gdzie a, b

∈ R. Gdy rozpatrywaliśmy jednorodne równanie liniowe rzędu

pierwszego, ogólna postać jego rozwiązania miała formę e

λt

. Sprawdźmy,

czy podobne rozumowanie będzie miało rację bytu także w obecnej sytuacji.
Podstawmy x(t) = e

λt

do równania (7.4). Mamy wówczas

(λ

+ aλ + b)e

λt

= 0

ROZDZIAŁ 7. LINIOWE RÓWNANIA RZĘDU DRUGIEGO

skąd jako wniosek możemy wyciągnąć

+ aλ + b = 0.

(7.5)

Wielomian stanowiący lewą stronę równania nazywamy wielomianem cha-
rakterystycznym równania (7.4). Pochodzenie nazwy stanie się jasne w teorii
układów równań rzedu pierwszego. Rozpatrzmy dwa przypadki.

1. ∆ = 0. Istnieją wówczas λ

, λ

- dwa różne pierwiastki równania (7.5).

Bezpośrednim rachunkiem można w łatwy sposób sprawdzić, że odpowia-
dające im funkcje e

i e

stanowią układ liniowo niezależny. Rozwiązanie

ogólne zagadnienia niejednorodnego ma zatem postać

x(t) = x

(t) + c

+ c

Można sobie teraz zadać pytanie, co stanie się w wypadku, gdy pierwiastki
λ

i λ

są dwoma sprzeżonymi pierwiastkami zespolonymi

. Nie stanowi to

jednak wielkiego problemu, gdyż można posłużyć się następującym trickiem.
Jak wiemy każdą liczbę zespolona można zapisać w postaci z = e

α+iϕ

gdzie

jest moduem a ϕ argumentem. Inaczej z = e

(cos ϕ + i sin ϕ). Stąd,dla

= α + iβ oraz sprzeżonego do λ

pierwiastka λ

, mamy poniżesz wyra-

żenia.

= e

αt

(cosβt + i sin βt)

= e

αt

(cosβt − i sin βt)

Przekształcając otrzymamy

αt

cos βt =

1
2

+ e

)

αt

sin βt =

1
2

− e

)

Teraz jesteśmy w stanie rozwiązanie zapisać jako kombinację funkcji rzeczy-
wistych

x(t) = x

(t) + c

αt

sin βt + c

αt

cos βt.

Geometrycznie odpowiada to zamianie bazy przestrzeni

C traktowanej jako

przestrzń liniowa nad

R z kanonicznej {1, i} na skośną do niej.

Podkreślmy że rozpatrujemy warunek

∆ = 0, w szczególności ∆ < 0.

7.2. RÓWNANIA O STAŁYCH WSPÓŁCZYNNIKACH

1. ∆ = 0. W tym przypadku mamy jeden pierwiastek podwójny λ. Pierw-
szym wektorem rozpinającym jądro operatora tworzącego równanie będzie
zatem e

λt

. Poszukujemy drugiego wektora rozpinającego jądro, liniowo nie-

zależnego z pierwszym. Posłużymy się metodologią podobną do znajdowania
rozwiązań równań liniowych niejednorodnych. Załóżmy, ze drugi wektor ma
postać u(t)e

λt

. Podstawmy tę postać do równania jednorodnego

x + a ˙x + bx = 0

Otrzymamy wówczas

λt

+ 2 ˙uλe

λt

+ uλ

λt

+ aλe

λt

u + a ˙ue

λt

+ bue

λt

= 0

Po uporządkowaniu i podzieleniu przez e

λt

mamy

u + (2λ + a)

˙u + (λ

+ aλ + b)

u = 0

Zerowanie sie obu pokreślonych czynników wynika z założeń narzuconych
na λ. Drugi czynnik zeruje się, gdyż λ jest pierwiastkiem wielomianu cha-
rakterystycznego, zerowanie się pierwszego czynnika wynika z faktu, że λ
jest pierwiastkiem podwójnym. Ostatecznie zatem mamy

u = 0

skąd

u(t) = c

t + c

Drugim szukanym wektorem z bazy jądra operatora

L jest (c

t + c

λt

, co

po redukcji o c

λt

i skalowaniu przez 1/c

daje nam te

λt

Bezpośredni rachunek pokazuje liniową niezależność układu (e

λt

, te

λt

Dowolne rozwiązanie zagadnienia niejednorodnego ma zatem postać

x(t) = x

(t) + c

λt

+ c

λt

Dalsze związki prezentowanych tutaj metod z geometrią skończenie wy-

miarową staną się widoczne w momencie, gdy zaczniemy zajmować się ukła-
dami równań pierwszego rzędu.

ROZDZIAŁ 7. LINIOWE RÓWNANIA RZĘDU DRUGIEGO

7.3

Zadania

1. Rozwiąż poniższe równania

(a) ¨

x + ˙x − 2x = 0

(b) ¨

− 4 ˙x + 5x = 0

− 2 ˙x + x = 0

2. Rozwiąż poniższe równania

(a) ¨

− x = 2e

− t

(b) ¨

x + ˙x − 2x = 3te

x + x = 4 sin t

Rozdział 8

Układy równań liniowych

8.1

Zagadnienie

Jak stwierdziliśmy w rozdziale drugim, równania różniczkowe rzędów wyż-
szych niż jeden można przeformułować na wielowymiarowe zagadnienie niż-
szego rzędu. Odbywa się to kosztem wektoryzacji równania, co oznacza że
zamiast rozwiązywać równanie skalarne, rozwiązujemy układ takich równań.
Możemy postępowanie to interpretować jako rozwiązywanie pojedyńczego
równania, którego rozwiązaniem jest funkcja wektorowa.

W rozdziale tym zajmować się będziemy układami równań liniowych.

Dalej rozważać będziemy tylko układy pierwszego rzędu (por. rozdział dru-
gi). Układ taki ma postać

˙x = A(t)x + f (t).

(8.1)

Za warunek początkowy przyjmiemy

x(t

) = x

(8.2)

Równanie (8.1) wygląda w zasadzie tak samo jak równanie (6.2) z tą tylko
różnicą, że w równaniu (8.1) funkcja x(t) jest funkcją o wartościach wekto-
rowych w przestrzeni

x(t) = (x

(t), x

(t), . . . , x

(t)).

ROZDZIAŁ 8. UKŁADY RÓWNAŃ LINIOWYCH

Analogicznie funkcja f (t) jest funkjcą wektorową o wartościach w R

. Funk-

cja A(t) jest macierzą m × m

A(t) =

⎡
⎢

⎢

⎣

(t)

. . .

(t)

. . .

(t)

. ..

(t) a

(t) . . . a

(t)

⎤
⎥

⎥

⎦

Wiele własności udowodnionych dla zagadnień postaci (6.2) przenosi się na
zagadnienia rozpatrywane obecnie.

Twierdzenie 8.1.1 Jeśli funkcje A(t) i f (t) są ciągłe dla t ∈ (a, b), to
przez każdy punkt zbioru Q = (a, b) × R

przechodzi dokładnie jedna krzywa

całkowa równania (8.1). Maksymalnym przedziałem istnienia rozwiązania
jest przedział (a, b).

Dowód. Dowód twierdzenia przebiega analogicznie do dowodu twierdzenia
6.2.2. Różnica polega na zastąpieniu modułu

| · | normą · .

Podobnie jak w przypadku równań skalarnych pewną szczególną rolę od-

grywają przypadki gdy w zagadnieniu (8.1) funkcja f

≡ 0. Mamy wówczas

do czynienia z zagadnieniem jednorodnym. Z jednoznaczności rozwiązania
gwarantowanej przez twierdzenie 8.1.1 wynika następujący wniosek.

Wniosek 8.1.2 Jeśli x(t) jest rozwiązaniem zagadnienia jednorodnego

˙x = A(t)x

i x(t

) = 0 dla pewnego t

∈ (a, b), to x ≡ 0.

Prawdziwe jest także twierdzenie analogiczne to spotkanego wcześniej pod-
czas rozważania równań skalarnych, opisujące geometryczną naturę prze-
strzeni rozwiązań.

Twierdzenie 8.1.3 Prawdziwe są następujące stwierdzenia:

1. Rozwiązania równania jednorodnego tworzą m-wymiarową przestrzeń

liniową

8.1. ZAGADNIENIE

2. Jeśli x

(t) jest rozwiązaniem szczególnym równania niejednorodnego,

a wektory x

(t) i = 1, 2, . . . , m są bazą przestrzeni E, to rozwiązanie

ogólne równania niejednorodnego ma postać

x(t) = x

(t) + c

(t) + . . . + c

(t),

gdzie c

∈ R.

Dowód. Niech E będzie zbiorem wszystkich rozwiązań równania jednorod-
nego. Niech x

(t), x

(t) ∈ E. Wtedy łatwo sprawdzić, że

x(t) = c

(t) + c

(t) ∈ E.

Wobec tego

E jest przestrzenią liniową. Udowodnimy teraz, że dim E = m.

Niech t

∈ (a, b) i zdeﬁniujmy odwzorowanie L : x(t) → x(t

) = x

∈ R

Odwzorowanie L jest oczywiście liniowe. Ponieważ na mocy twierdzenia
8.1.1 istnieje rozwiązanie dla dowolnych danych początkowych, to odwzo-
rowanie to jest epimorﬁczne. Dalej, ze względu na wniosek 8.1.2 jądro tego
odwzorowania składa się tylko z wektora zerowego. Odwzorowanie L jest
zatem monomorﬁczne. Ustaliliśmy zatem izomorﬁzm między

E a R

. Udo-

wodniliśmy punkt 1) twierdzenia. Punktu 2) dowodzi się analogicznie jak
to ma miejsce w przypadku równań skalarnych.

Załóżmy teraz, że mamy jakąś bazę przestrzeni

E, złożonej z rozwiązań

równania jednorodnego. Baza ta składa się z funkcji x

(t), x

(t), . . . , x

(t).

Zbudujmy z tych funkcji macierz X(t), tak aby kolejne x

(t) stanowiły ko-

lumny macierzy X(t). Macierz X spełnia równanie macierzowe

X = A(t)X.

(8.3)

Wynika to z faktu, że kolumny macierzy spełniają to równanie. Co więcej,
można zauważyć że jeśli pewna macierz X spełnia to równanie, wówczas jej
kolumny także spełniają równanie analogiczne.

Dla dalszego toku rozumowania niezbędne jest poniższe twierdzenie.

ROZDZIAŁ 8. UKŁADY RÓWNAŃ LINIOWYCH

Twierdzenie 8.1.4 Niech X(t) będzie macierzą m × m spełniającą równa-
nie (8.3) w przedziale (a, b). Zdeﬁniujmy

∆(t) = det X(t).

Dla każdego t i każdego t

z przedziału (a, b) zachodzi

∆(t) = ∆(t

) exp

trA(s)ds.

Dowód. Niech A

(t) = [a

(t)] oraz X(t) = [x

j
i

(t)]. Z prawa różniczkowania

wyznacznika mamy

∆(t) =

˙x

. . .

˙x

. . . x

. .. ...

. . . x

+ . . . +

. . . x

. .. ...

˙x

. . .

˙x

Równanie (8.3 zapisane w postaci składowych macierzy X(t) ma postać

˙x

j
i

k=1

j
k

Korzystając z tych wyrażeń, otrzymujemy

∆(t) =

. . . a

. . .

. ..

. . .

+. . .+

. . .

. ..

. . . a

czyli

∆(t) = ∆(t)trA(t).

Całkujemy to równanie i otrzymujemy

∆(t) = ∆(t

) exp

trA(s)ds,

co należało pokazać.

Z powyższego twierdzenia nasuwa się od razu następujący wniosek.

8.1. ZAGADNIENIE

Wniosek 8.1.5 Jeśli ∆(t

) = 0 w pewnym punkcie t

∈ (a, b), to ∆(t) = 0

dla każdego t

∈ (a, b).

Deﬁnicja 8.1.6 macierz kwadratowa X(t) o wymiarze m × m spełniają-
ca równanie ˙

X = A(t)X nazywa się macierzą fundamentalną układu ˙x =

A(t)x. Wektory x

(t), x

(t), . . . , x

(t) będące jej kolumnami nazwiemy fun-

damentalnym układem rozwiązań. Wyznacznik ∆(t) nazywa się wtdy wy-
znacznikiem Wrońskiego

układu funkcji x

(t), x

(t), . . . , x

(t).

Zauważmy, że jeśli wyznacznik wrońskiego jest różny od zera w jakimś

punkcie przedziału, to jest on różny od zera w każdym punkcie tego przedzia-
łu. Powiemy wówczas, że funkcje tworzące układ fundamentalny są liniowo
niezależne. Stąd wynika łatwy sposób konstruowania układu fundamental-
nego.

Twierdzenie 8.1.7 Każde liniowe równanie jednorodne postaci ˙x = A(t)x
ma układ fundamentalny.

Dowód. Wybieramy m liniowo niezależnych wektorów w

: x

, x

, . . . , x

i rozwiązujemy równanie ˙x = A(t)x kolejno z warunkami x(t

) = x

. Otrzy-

mane rozwiązania x

(t) tworzą układ fundamentalny.

Zajmiemy się teraz równaniem niejednorodnym. Podobnie jak w przy-

padku równań skalarnych, także tutaj możliwa jest metoda uzmiennienia
stałej (wariacji parametru).

Twierdzenie 8.1.8 Niech dane będzie zagadnienie początkowe dla równa-
nia niejednorodnego

˙x = A(t)x + f (t)

x(t

) = x

Rozwiązanie tego zagadnienia ma postać

x(t) = X(t)X

−1

+ X(t)

−1

(s)f (s)ds,

gdzie X(t) jest macierzą fundamentalną układu jednorodnego.

Wyznacznik Wrońskiego określa się także mianem "wrońskian".

ROZDZIAŁ 8. UKŁADY RÓWNAŃ LINIOWYCH

Dowód. Niech x

(t), . . . , x

(t) będą układem fundamentalnym rozwiązań

równania jednorodnego. Wtedy każde rozwiązanie zagadnienia jednorodne-
go można zapisać jako kombinację

x(t) = c

(t) + . . . + c

(t).

Rozwiązania szukamy więc w postaci

x(t) = c

(t)x

(t) + . . . + c

(t)x

(t).

Niech X(t) będzie macierzą fundamentalną, której kolumnami są wektory
x

(t),

C(t) = (c

(t), c

(t), . . . , c

(t)).

Wtedy poszukiwane rozwiązanie można zapisać w prostszej formie jako
x(t) = X(t)C(t). Po podstawieniu tego wyrażenia do równania mamy

X(t)C(t) + X ˙

C(t) = A(t)X(t)C(t) + f (t).

Ponieważ X(t) spełnia równanie jednorodne to mamy

X(t) ˙

C(t) = f (t).

Macierz fundamentalna jest macierzą nieosobliwą zatem istnieje X

−1

(t) i

ostatnie równanie przyjmuje postać

C(t) = X

−1

(t)f (t).

Całkujemy to równanie, skąd otrzymujemy

C(t) = C(t

) +

−1

(s)f (s)ds.

Jeśli ma być spełniony warunek początkowy, to

X(t

)C(t

) = x

czyli

C(t

) = X

−1

Wtedy

C(t) = X

−1

(s)f (s)ds.

Mnożymy ostatnią równość przez X(t) i otrzymujemy tezę twierdzenia.

8.2. UKŁADY O STAŁYCH WSPÓŁCZYNNIKACH

8.2

Układy o stałych współczynnikach

Zajmując się równaniem liniowym skalarnym drugiego rzędu powiedzieli-
śmy, że nie potraﬁmy rozwiązywać owego zagadnienia w przypadku, gdy
współczynniki równania nie są stałe. W dalszym ciągu zajmować będziemy
się zatem układami równań pierwszego rzędu o stałych współczynnikach.
Dla układów takich istnieją skuteczne metody całkowania.

Rozważmy układ jednorodny

˙x = Rx,

(8.4)

gdzie R jest stałą macierzą o wymiarze m

× m, oraz warunek początkowy

x(t

) = x

(8.5)

Gdyby równanie (8.4) było równaniem skalarnym, to rozwiązanie zagad-
nienia Cauchy’ego miałoby postać x(t) = x

R(t−t

)

. Będziemy starali się

pokazać, że identyczny wzrów zachodzi także dla równania wektorowego.
Zanim jednak to nastąpi musimy zdeﬁniować obiekt e

gdzie A jest macie-

rzą.

Deﬁnicja 8.2.1 Jeśli A jest macierzą kwadratową m

×m, to e

deﬁniujemy

jako sumę szeregu

= I + A +

+ . . . +

+ . . . ,

(8.6)

gdzie A

traktujemy jako n-krotne złożenie operatora A ze sobą.

Jeśli norma operatora A jest ograniczona (w przestrzeniach skończenie wy-
miarowych, czyli takich w których się poruszamy, operatory liniowe jako
przekształcenia ciągłe mają normę ograniczoną) to z ograniczenia owego
wynika zbieżność powyższego szeregu.
Przykład 1. Obliczymy e

dla macierzy

A =

⎡
⎢

⎣

1 1 0
0 1 0
0 0 2

⎤
⎥

⎦

ROZDZIAŁ 8. UKŁADY RÓWNAŃ LINIOWYCH

Rozłóżmy macierz A na sumę A = A

+ B gdzie

⎡
⎢

⎣

1 0 0
0 1 0
0 0 2

⎤
⎥

⎦

B =

⎡
⎢

⎣

0 1 0
0 0 0
0 0 0

⎤
⎥

⎦

Ponieważ dla macierzy A

i B iloczyn A

B jest przemienny to z wzoru

(8.6) wynika, że

= e

Bezpośredni rachunek połączony z odrobiną spostrzegawczości daje

⎡
⎢

⎣

e 0

0 e

0 0 e

⎤
⎥

⎦

Aby obliczyć pozostałą część, czyli e

, posłużymy się obserwacją że macierz

B jest w istocie elementem nilpotentnym pierścienia macierzy. Nilpotentność
oznacza istnienie takiego n

∈ N że B

= 0. Rzeczywiście B

= 0. Bezpo-

średni rachunek daje

⎡
⎢

⎣

1 1 0
0 1 0
0 0 1

⎤
⎥

⎦

Ostatecznie mamy

= e

⎡
⎢

⎣

e e

0 e

0 0 e

⎤
⎥

⎦

Należy tu zwrócić szczególną uwagę na fakt, że na poprawność powyższego
rozumowania istotny wpływ ma przemienność macierzy A

oraz B.

Biorąc dwa operatory rzutowe na dwie różne podprzestrzenie liniowe (jest jasne że ope-
ratory takie nie komutują ze sobą, inaczej nie są ze sobą przemienne) otrzymamy różne
wyniki biorąc

oraz

Możemy teraz sformułować podstawowe twierdzenie.

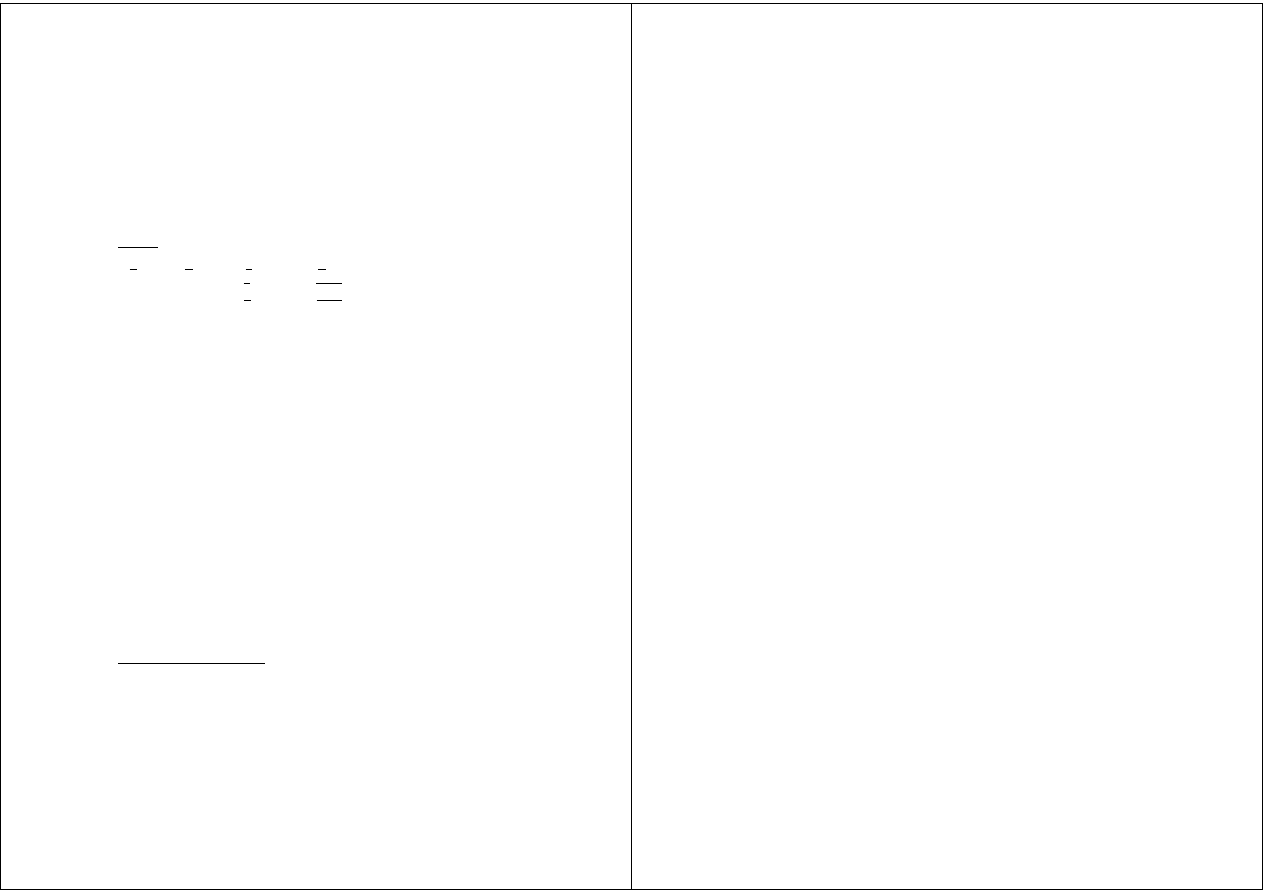
8.2. UKŁADY O STAŁYCH WSPÓŁCZYNNIKACH

Twierdzenie 8.2.2 Macierzą fundamentalną równania (8.5) jest exp(Rt).

Dowód. Korzystając ze wzoru (8.6) liczymy pochodną macierzy

exp(Rt)

(I + Rt +

+ . . . +

+ . . .) =

= R + R

+ . . . +

(n−1)!

(n−1)

= R(I + Rt +

+ . . . +

(n−1)!

(n−1)

+ . . .) = Re

Oznacza to, że X(t) = e

spełnia równanie

X = RX.

Wobec uwag w poprzedniej sekcji, macierz X jest więc macierzą fundamen-
talną układu (8.4).

Zajmiemy się teraz problemem znajdowania macierzy fundamentalnej

dla układu zadanego dowolną macierzą. Jeśli R jest macierzą diagonalną,
tzn. ma postać

R =

⎡
⎢

⎢

⎣

. . .

. .. ...

. . . λ

⎤
⎥

⎥

⎦

to z wzoru (8.6) wynika, że

⎡
⎢

⎢

⎣

. . .

. ..

. . . e

⎤
⎥

⎥

⎦

Jeśli macierz R nie jest w postaci diagonalnej, to posłużymy się znanym
z algebry liniowej rozkładem Jordanowskim przestrzeni na podprzestrze-
nie niezmiennicze. Wiadomo, że macierz R jest rzeczywista. Będziemy ją

Uwaga: korzystamy tu z twierdzenia o różniczkowaniu jednostajnie zbieżnego szeregu

funkcyjnego wyraz po wyrazie!

ROZDZIAŁ 8. UKŁADY RÓWNAŃ LINIOWYCH

traktować jako przekształcenie R : C

→ C

. Na mocy tw. Jordana istnie-

je nieosobliwe przekształcenie Q, takie że Q

−1

RQ = J, przy czym J jest

macierzą w kanonicznej postaci Jordana

J =

⎡
⎢

⎢

⎣

. . .

. .. ...

. . . J

⎤
⎥

⎥

⎦

gdzie każda z klatek J

jst klatką diagonalną albo klatką w postaci

⎡
⎢

⎢

⎣

0 . . .

1 . . .

. .. ...

0 . . .

0 . . . λ

⎤
⎥

⎥

⎦

(8.7)

Przestrzeń

rozpada się na sumę prostą przestrzeni H

o tej własności,

że każda H

jest niezmiennicza dla J i J ma w H

wektor własny o wartości

własnej λ

. Z blokowej postaci macierzy J wynika że

⎡
⎢

⎢

⎣

. . .

. ..

. . . e

⎤
⎥

⎥

⎦

Wystarczy zatem skonstruować e

. Jeśli macierz J

jest diagonalna, to

wiemy jak konstruować funkcję wykładniczą. Jeśli natomiast J

ma postać

(8.7) to postępujemy następująco. Rozkładamy J

na sumę

= λ

+ K

gdzie indeksem k oznaczono wymiar przestrzeni niezmienniczej H

. Oczy-

wiście macierze I

i K

są przemienne zatem

= e

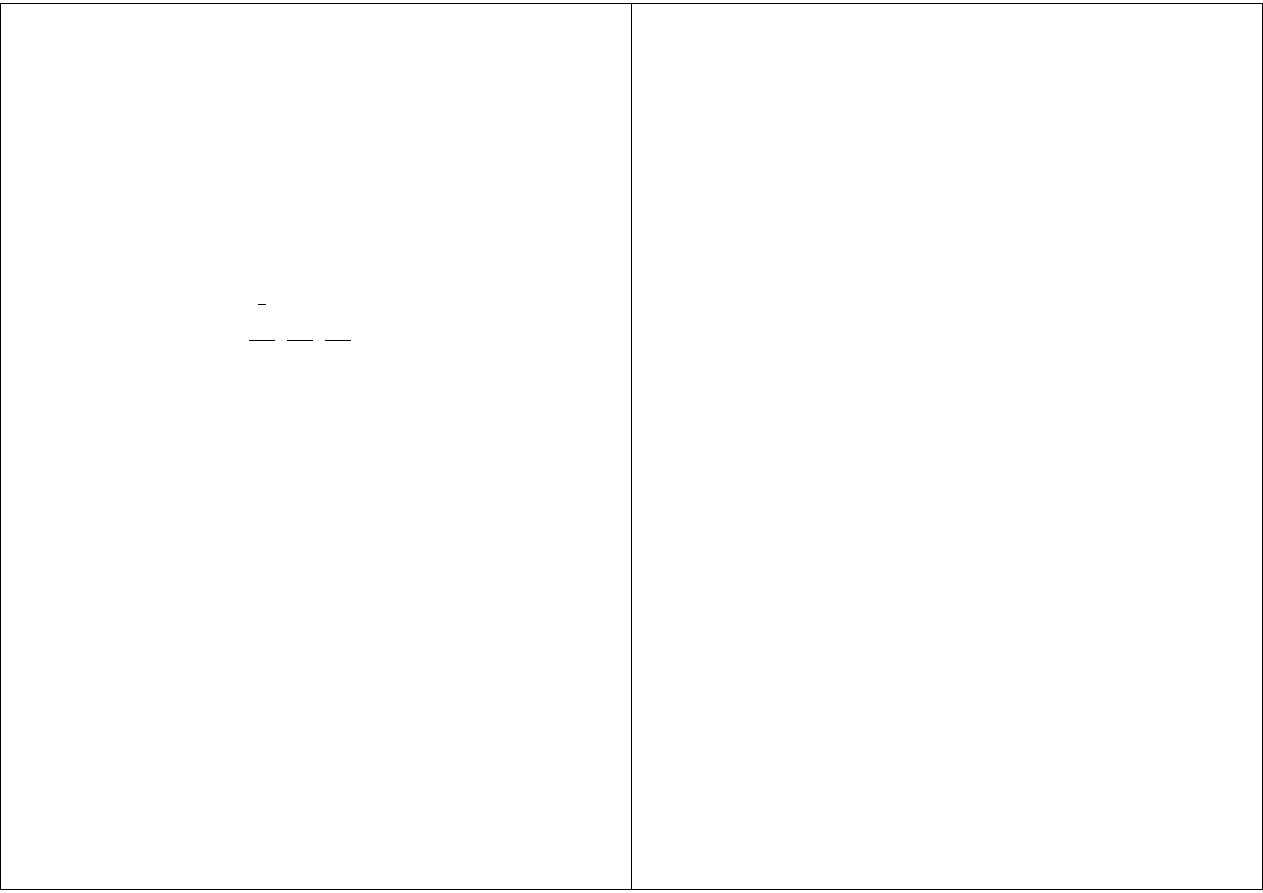
8.2. UKŁADY O STAŁYCH WSPÓŁCZYNNIKACH

Oznacza to, że wystarczy znaleźć e

. Obliczając kolejne potęgi macie-

rzy K

przekonujemy się, że jest ona macierzą nilpotentną. Bezpośrednim

rachunkiem możliwym do wykonania w warunkach domowego zacisza otrzy-
mujemy

⎡
⎢

⎢

⎣

. . . 0

. .. ...

k−1

(k−1)!

k−2

(k−2)!

k−3

(k−3)!

. . . 1

⎤
⎥

⎥

⎦

Stąd zaś otrzymujemy e

a następnie exp(Jt). Mając tę ostatnią funkcję i

przekształcenie Q, które sprowadza R do postaci Jordana, zauważamy że

= QJ

−1

co łatwo pokazać przy użyciu indukcji. Korzystając z tej równości, otrzy-
mujemy

exp(Rt) = Q exp(Jt)Q

−1

skąd można znaleźć macierz fundamentalną exp(Rt).

Widać, że uciążliwa procedura obliczania szeregów nieskończonych zo-

stała zastąpiona rachunkiem zamiany bazy z kanonicznej na bazę Jordana.
Powoduje to jednak kłopoty związane ze znaelzieniem macierzy transforma-
cji bazy. Jak więc postępować w praktyce chcąc wyznaczyć macierz funda-
mentalną układu (8.4)?

Mając macierz R, znajdujemy przede wszystkim jej wartości własne. Jak

wiadomo z kursu alegebry liniowej są to pierwiastki wielomianu charakte-
rystycznego

det(R − λI) = 0

Każdy pierwiastek tego wielomianu jest wartością własną operatora R i
odpowiada mu jakiś wektor własny. Nie ma tu jednak wzajemnie jedno-
znacznej odpowiedniości, gdyż pierwiastki mogą być wielokrotne, a odpo-
wiadające im wartości własne mogą mieć mniejszą krotność, czyli mniejszą
liczbę odpowiadających im wektorów własnych.

ROZDZIAŁ 8. UKŁADY RÓWNAŃ LINIOWYCH

Jeśli jakiś λ

jest pierwiastkiem wielomianu charakterystycznego, to jest

jednocześnie wartością własną macierzy R. Oznacza to, że po sprowadze-
niu macierzy R do postaci Jordana jest kolumna, w której λ

występuje w

miejscu przecięcia diagonali z tą właśnie kolumną, a pozostałe elementy ko-
lumny są zerowe. Jeśli macierz Jordana jest diagonalna, to jest to oczywiste.
Jeśli klatka Jordana ma postać (8.7) to kolumną tą jest pierwsza kolumna
macierzy J zawierająca element λ

. Oznacza to, że wektor x(t) = e

dla

pewnego stałego wektora v

jest rozwiązaniem (8.4). Po wstawieniu tego

rozwiązania x(t) do (8.4) otrzymujemy

= Re

skąd po uproszczeniu mamy

= λ

Oznacza to, że wektor v

jest wektorem własnym macierzy R, odpowiadają-

cym wartości własnej λ

. Powyższa obserwacja pozwala rozwiązać problem

wyznaczenia macierzy fundamentalnej w przypadku, gdy wszystkie warto-
ści własne są parami różne. Mamy wtedy m pierwiastków λ

, λ

, . . . , λ

m odpowiadających im wektorów własnych v

, v

, . . . , v

. Z kursu algebry

liniowej wiemy, że wektory v

są liniowo niezależne, więc funkcje

, e

, . . . , e

(8.8)

tworzą bazę przestrzeni rozwiązań równania (8.4) i wyznaczają macierz fun-
damentalną exp(Rt). Należy tylko zauważyć, że dla t = 0 macierz exp(Rt)
jest macierzą jednostkową. Jeśli więc wektory (8.8) wyznaczają macierz
X(t), to aby z tej macierzy znaleźć exp(Rt) - należy przyjąć

exp(Rt) = X(t)X

−1

(0).

Podobnie przebiega poszukiwanie macierzy fundamentalnej, gdy pierwiastki
wielomianu charakterystycznego są jednokrotne, ale wśród nich znajdują się
pierwiastki zespolone. Jeśli λ jest zespoloną wartością własną macierzy R,
natomiast v odpowiadającym jej wektorem własnym, to funkcja

x(t) = e

λt

8.2. UKŁADY O STAŁYCH WSPÓŁCZYNNIKACH

jest oczywiście rozwiązaniem równania (8.4), ale rozwiązaniem zespolonym.
Aby otrzymać rozwiązania rzeczywiste, uczyńmy następujące spostrzeżenie.
Ponieważ wielomian charakterystyczny ma współczynniki rzeczywiste, więc
pierwiastki zespolone występują parami jako sprzężone liczby zespolone.
Niech λ

= α + iβ, λ

= α − iβ będą taką parą wartości własnych macierzy

R. Niech v

= u + iw będzie wektorem własnym odpowiadającym wartości

własnej λ

= Rv

gdzie u, w są wektorami rzeczywistymi. Wtedy wektorem własnym odpo-
wiadającym wartości własnej λ

jest wektor v

= u − iv. Równości

= Rv

można zaspisać jako

(αu − βw) + i(αw + βu) = Ru + iRw

(αu − βw) − i(αw + βu) = Ru − iRw.

Jeśli więc

(t) = e

(t) =

1
2

(t) + x

(t)) = e

αt

(u cos βt − w sin βt)

(t) =

(t) − x

(t)) = e

αt

(w cos βt + u sin βt)

są dwoma liniowo niezależnymi rozwiązaniami rzeczywistymi równania (8.4).

Przypadek pierwiastków wielokrotnych jest nieco trudniejszy. Zauważ-

my, że wystarczy ograniczyć się tylko do pierwiastków rzeczywistych. W
przypadku wielokrotnych pierwiastków zespolonych należy przeprowadzić
modyﬁkacje rozwiązań opisane powyżej.

Niech więc λ

będzie wartością własną macierzy R o krotności n

. Oczy-

wiście λ

jest wartością własną macierzy R. Załóżmy jednak, że λ

ma ν

ROZDZIAŁ 8. UKŁADY RÓWNAŃ LINIOWYCH

wektorów własnych oraz ν

< n

. Z algebry liniowej wiadomo, że jeśli rów-

nanie

(R − λ

I)v = 0

ma ν

liniowo niezależnych rozwiązań, to równanie

(R − λ

)

v = 0

ma co najmniej ν

+ 1 liniowo niezależnych rozwiązań, a

(R − λ

−ν

v = 0

ma co najmnije n

liniowo niezależnych rozwiązań. W celu efektywnego

znalezienia tych wektorów zauważmy, że jeśli v jest dowolnym wektorem, to
exp(Rt)v jest rozwiązaniem równanai (8.4). Korzystając z deﬁnicji funkcji
wykładniczej dla macierzy R, otrzymujemy rozwinięcie

exp(Rt)v = e

λt

v + t(R − λI)v +

(R − λI)

v + . . .

(8.9)

Jeśli λ jest wartościąwłasną macierzy R, a v odpowiadajacym jej wektorem
własnym, to

(R − λI)v = 0

i z rozwinięcia (8.9) pozostaje tylko e

λt

v., która to funkcja, jak już wiemy,

jest rozwiązaniem równania (8.4). Jeśli λ jest wielokrotnym pierwiastkiem
wielomianu charakterystycznego, ale ma niewystarczającąliczbę wektorów
własnych, to możemy poszukiwać takich wektorów v, że

(R − λI)v = 0,

(R − λI)

v = 0.

Wtedy w rozwinięciu (8.9) pozostają tylko dwa pierwsze wyrazy i funkcja

x(t) = e

λt

(I + t(R − λI))v

8.3. RÓWNANIA SKALARNE WYŻSZEGO RZĘDU

jest rozwiązaniem równania (8.4). W algebrze liniowej dowodzi się, że wek-
tory spełniające

(R − λI)v = 0,

(R − λI)

v = 0.

sąliniowo niezależne od wktoró, które spełniają

(R − λI)v = 0.

Własność ta przenosi się na wyższe potęgi, co gwarantuje nam możliwość
znalezienia wystarczającej liczby liniowo niezależnych wektorów a zatem
wystarczającej liczby liniowo niezależnych rozwiązań równania (8.4).

8.3

Równania skalarne wyższego rzędu

Zajmiemy się teraz jednym równaniem liniowym rzędu m

(m)

+ p

m−1

(t)x

(m−1)

+ . . . + p

(t) ˙x + p

(t)x = q(t).

(8.10)

Zagadnienie Cauchy’wgo dla tego równania polega na zadaniu w chwili t

wartości funkcji x oraz jej pochodnych do rzędu m

− 1

x(t

) = x

, ˙x(t

) = x

, . . . , x

(m−1)

) = x

m−1

Jak już zostało wyjaśnione w rozdziale drugim, równanie (8.10) z warunkami
początkowymi można sprowadzić do zagadnienia początkowego dla układu
pierwszego rzędu. Wystarczy w tym celu zdeﬁniować

= x

(k)

Równanie (8.10) zmienia się wtedy w układ

⎧

⎪

⎨
⎪

⎪

⎩

˙x

= x

˙x

= x

˙x

m−2

= x

m−1

˙x

m−1

= −p

m−1

(t)x

m−1

− . . . − p

(t)x

+ q(t)

ROZDZIAŁ 8. UKŁADY RÓWNAŃ LINIOWYCH

a warunki początkowe stają się warunkami dla układu x

) = x

. Za-

mieniwszy skalarne zagadnienie wyższego rzędu na wektorowe zagadnienie
rzędu pierwszego możemy wykorzsytać zdobyte wcześniej umiejętności i
znajdując układ fundamentalny zagadnienia znaleźć jego rozwiązanie. W
przypadku stałych współczynników równania postępowanie to można nieco
uprościć. Niech będzie dane równanie jednorodne rzędu m o stałych współ-
czynnikach

(m)

+ a

m−1

(m−1)

+ . . . + a

˙x + a

x = 0.

(8.11)

Równanie to można sprowadzić do równania pierwszego rzędu

X = RX

gdzie

X =

⎛
⎜

⎜

⎝

˙x

(m−1)

⎞
⎟

⎟

⎠

R =

⎡
⎢

⎢

⎣

. . .

. ..

−a

. . .

−a

m−1

⎤
⎥

⎥

⎦

Znajdujemy wielomian charakterystyczny macierzy R

p(λ) = det(λI − R) = λ

m−1

i=0

(8.12)

Jeśli λ

jest pierwiastkiem wielomianu p(λ), to e

jest rozwiązaniem rów-

nania (8.11). Jeśli więc wielomian p(λ) ma m różnych pierwiastków, to ma-
my m liniowo niezależnych rozwiązań dla (8.11). Jak pamiętamy z poprzed-
niej części, komplikacje pojawiają się przy pierwiastkach wielokrotnych. W
przypadku równania (8.11) rozwiązanie jest jednak łatwiejsze do obliczenia
(nie trzeba znajdować wektorów własnych).

Twierdzenie 8.3.1 Jeśli λ

jest k-krotnym pierwiastkiem wielomianu cha-

rakterystycznego (8.12), 1 k m, to funkcje e

, te

, . . . , t

k−1

są

liniowo niezależnymi rozwiązaniami równania (8.11).

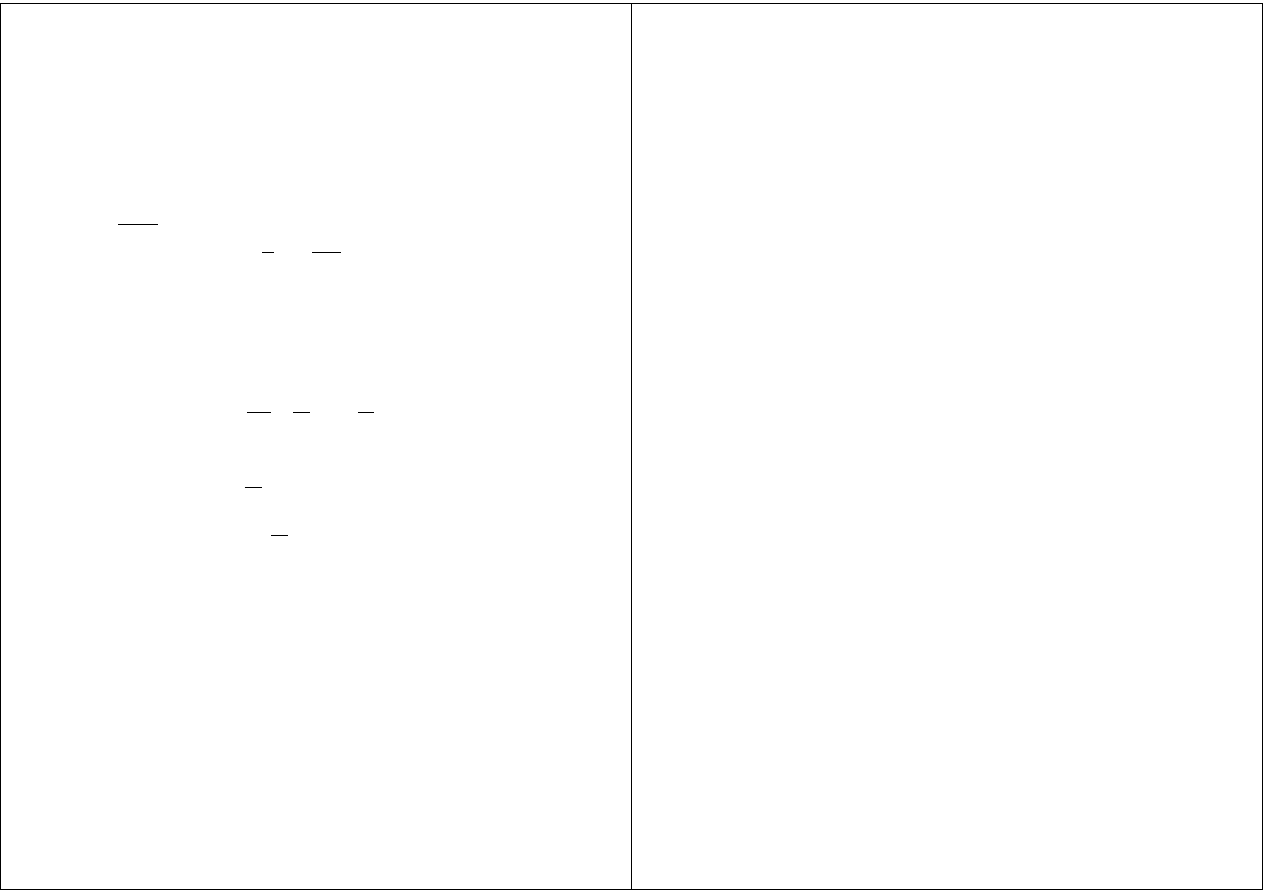
8.4. ZADANIA

Dowód. Jeśli λ

jest k-krotnym pierwiastkiem wielomianu p(λ), to

p(λ

) =

dλ

(λ

) =

k−1

dλ

k−1

(λ

) = 0

Niech

L(x) ≡ x

(m)

+ sum

m−1

i=0

(i)

tzn. L(x) jest operatorem po lewej stronie równania (8.11). Zauważmy na-
stępująca własność tego operatora

L(e

λt

) = p(λ)e

λt

Rozważmy funkcję t

λt

i poddajmy ją działaniu operatora L

L(t

λt

) = L(

∂

λt

∂λ

) =

∂

∂λ

L(e

λt

) =

∂

∂λ

(p(λ)e

λt

(8.13)

Dla i = 0, 1, . . . , k − 1 stosujemy wzór Leibniza do ostatniego wyrazenia w
(8.13), otrzymujemy wtedy sumę wyrazów postaci

−t

i−j

∂

∂λ

(λ)e

λt

, j = 0, 1, 2, . . . , i.

Ponieważ dla j

k − 1

∂

(λ

) = 0,

więc

L(t

) = 0.

Funkcje t

są zatem rozwiązaniami równania (8.11). Liniowa niezależność

tych funkcji wynika z liniowej niezależności wielomianów różnych stopni.

8.4

Zadania

1. Dla równania ˙x = Ax znaleźć macierz fundamentalną X(t), taką że

X(0) = I, jeśli macierz A jest dana wzorem:

ROZDZIAŁ 8. UKŁADY RÓWNAŃ LINIOWYCH

(a)

−1

−4

(b)

−1 8

(c)

⎡
⎢

⎣

1 −1

−1 0

⎤
⎥

⎦

2. Rozwiązać układ równań sprowadzając do układu rzędu pierwszego

(a)

− 2¨x

+ ˙x

+ x

− 3x

= 0

4¨

− 2¨x

− ˙x

− 2x

+ 5x

= 0

(b)

− 2x

+ 3x

= 0

− x

+ 2x

= 0

Wyszukiwarka

Podobne podstrony:
Analiza Matematyczna 1 stary skrypt id 60884 (2)
Analiza Matematyczna I Skrypt UMK
WYKLAD ANALIZA MATEMATYCZNA
Analiza matematyczna, lista analiza 2008 6 szeregi
Analiza Matematyczna 1 Gewert Skoczylas zadania
Analiza Matematyczna Twierdzenia
Analiza matematyczna 1
Praca domowa 2a Analiza Matematyczna
Zadania z Analizy Matematycznej, Matematyka
zestaw9, Matematyka stosowana, Analiza, Analiza matematyczna dla leniwych
Analiza matematycza opracowanie pytań
Kolos 3 Analiza matematyczna
analiza matematyczna 7
Analiza matematyczna 2 Przyklady i zadania
cw 13 Analiza Matematyczna (calki) id

więcej podobnych podstron