Fizyka statystyczna.

Parametry makroskopowe

Fizyka statystyczna

v

,

k

E

,

2

v

parametry makroskopowe

Rozważmy gaz jednoatomowy.
Dla każdej cząstki możemy określić: x , y , z , p

x

, p

y

, p

z

.

Jeżeli w pewnej chwili znamy dla każdej cząstki te współrzędne to mówimy, że znamy
stan mikroskopowy układu.

Określonemu makrostanowi układu odpowiada wiele mikrostanów.

Hipoteza Boltzmanna

Wszystkie mikrostany realizujące możliwe

makrostany są jednakowo prawdopodobne.

⇓

Liczbę mikrostanów odpowiadających danemu makrostanowi nazywamy

prawdopodobieństwem termodynamicznym danego makrostanu.

1

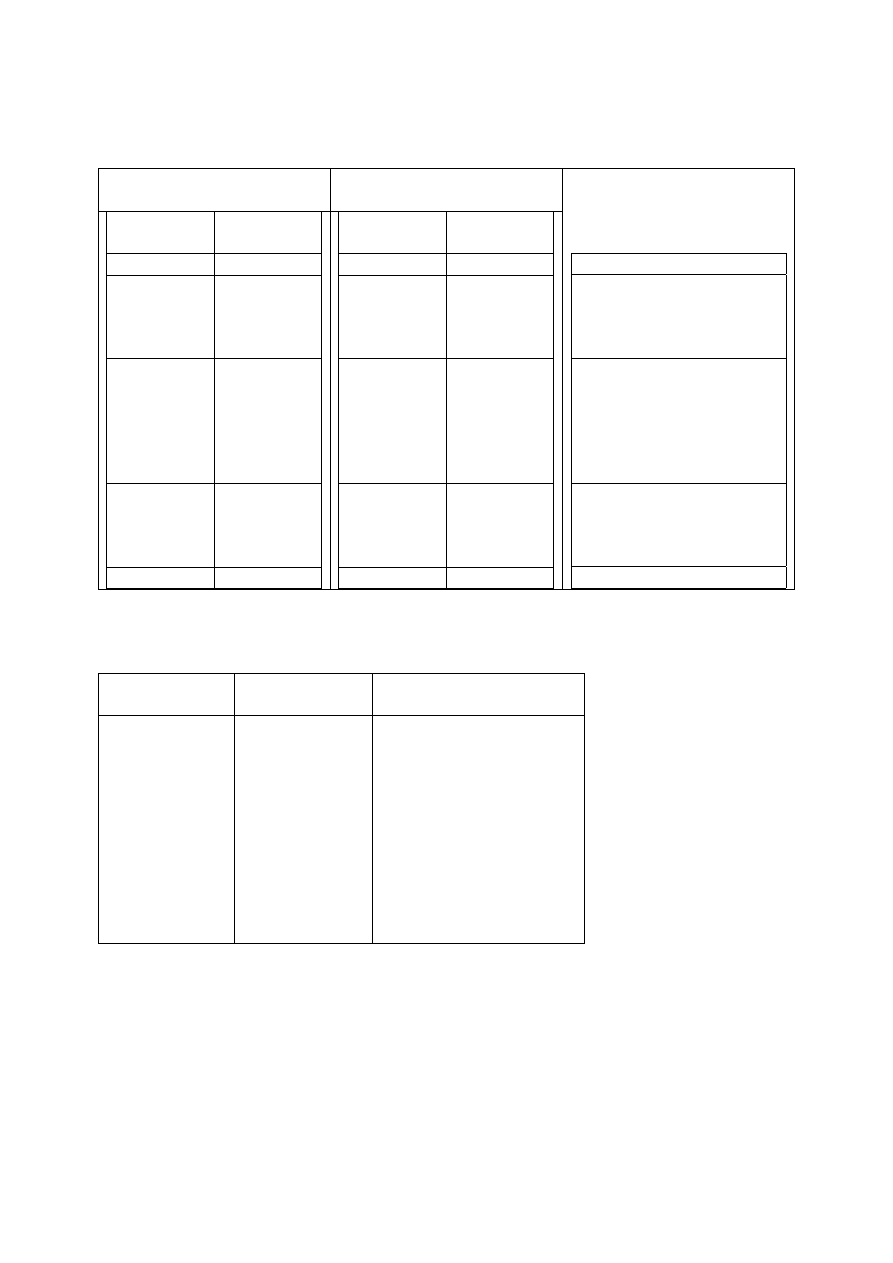
Rozważmy następującą sytuację:
N = 4 rozróżnialne cząstki w naczyniu podzielonym na dwie części, L i P.

Mikrostany Makrostany

Prawdopodobieństwo

termodynamiczne

Cząstki w L

Cząstki w P

---

1234

1
2
3
4

234
134
124
123

12
13
14
23
24
34

34
24
23
14
13
12

234
134
124
123

1
2
3
4

1234

---

Liczba

cząstek w L

Liczba

cząstek w P

0 4

1

3

2

2

3

1

4 0

1

4

6

4

1

Dla N = 1 0

Liczba

cząsteczek w L

Liczba

cząsteczek w p

Prawdopodobieństwo

termodynamiczne

0
1
2
3
4
5
6
7
8
9

10

10

9
8
7
6
5
4
3
2
1
0

1

10
45

120
210
252
210
120

45
10

1

Największe
prawdopodobieństwo
termodynamiczne mają
makrostany
odpowiadające
równomiernemu
rozkładowi cząstek

Stąd mamy 2

10

= 1024 możliwych mikrostanów.

Dla N = 40 mielibyśmy 2

40

≈ 10

12

możliwych mikrostanów i przy mikrostanach

zmieniających się co sekundę trzeba czekać ok. 35000 lat na fluktuację, w której jedna z
połówek naczynia byłaby pusta.

2

Rozważmy układ N rozróżnialnych cząstek, które dzielimy pomiędzy k komórek:

{

k

n

n ,...,

1

}

- makrostan.

Prawdopodobieństwo termodynamiczne jest określane następująco:

!

!...

!

!

2

1

k

n

n

n

N

P

=

Rozpatrzmy N cząstek gazu zamkniętych w naczyniu o objętości V.
V/k - układ dzielimy na k jednakowych komórek.
Szukamy takiego rozkładu, dla którego P = P

max

. Oczywiście wtedy dP = 0 . Wygodniej jest

rozważać ln P:

( )

∑

=

−

=

k

n

i

n

N

P

1

!

ln

!

ln

ln

N, n

i

bardzo duże, można przybliżyć silnię za pomocą wzoru Stirlinga:

x

x

x

x

−

= ln

)

!

ln(

(

)

∑

∑

−

−

−

=

i

i

i

n

n

n

N

N

N

P

ln

ln

ln

=

,

∑

−

i

i

n

n

N

N

ln

ln

∑

=

i

i

n

N

Mamy znaleźć d(lnP) = 0 , ale pod dodatkowym warunkiem stałości całkowitej liczby
cząstek:

(

) ∑

∑

=

=

=

0

i

i

dn

n

d

dN

(

) (

)

(

) (

)

[

]

(

)

(

)

∑

∑

∑

∑

−

=













+

−

=

=

+

−

=













−

=

i

i

i

i

i

i

i

i

i

i

i

i

i

i

dn

n

dn

n

n

dn

n

dn

n

n

d

n

n

n

d

N

N

d

P

d

ln

ln

ln

ln

ln

ln

ln

Mamy więc:

(

)

0

ln

=

−

∑

i

i

dn

n

i

0

=

∑

i

dn

Metoda mnożników Lagrange’a:

+

• α

Stąd otrzymujemy:

(

)

0

ln

=

−

∑

i

i

dn

n

α

Aby to równanie było spełnione dla dowolnych dn

i

, musi być spełniony warunek:

3

α

α

e

n

n

i

i

=

⇒

= ln

Normalizację można uzyskać z warunku:

α

ke

N

n

i

=

=

∑

Otrzymujemy:

k

N

n

i

=

Najbardziej prawdopodobny jest makrostan odpowiadający równomiernemu rozkładowi
cząstek gazu w całej objętości.

Ocena półszerokości maksimum rozkładu prawdopodobieństwa.

∑

∑

∆













∂

∂

+

∆













∂

∂

+

=

2

ln

ln

ln

ln

2

max

2

2

max

max

i

i

i

i

n

n

P

n

n

P

P

P

P – prawdopodobieństwo termodynamiczne makrostanu, w którym poszczególne liczby n

i

różnią się o

∆n

i

od swych wartości w stanie równowagi statystycznej ( dla P = P

max

).

Ze wzoru na ln P mamy:

i

i

n

n

P

1

ln

2

2

−

=

∂

∂

(*)

Z warunku na maksimum P dostajemy:

∑

=

∆













∂

∂

0

ln

max

i

i

n

n

P

(**)

Podstawiając (*) i (**) do wyrażenia na ln P oraz wprowadzając oznaczenie

i

i

i

n

n

∆

=

δ

,

dostajemy:

∑

−

=

2

max

2

1

ln

ln

i

i

n

P

P

δ .

Zatem:











−

=

∑

2

max

2

1

exp

i

i

n

P

P

δ

Jeśli założymy, że wszystkie

δ

i

są jednakowe tzn.

δ

i

=

δ, to wtedy:











−

=











−

=

∑

N

P

n

P

P

i

2

max

2

max

2

1

exp

2

1

exp

δ

δ

4

W 1 cm

3

gazu znajduje się około N=10

19

cząsteczek. Załóżmy, że rozkład cząstek różni się o

δ=10

-8

od rozkładu najbardziej prawdopodobnego. Wówczas:

500

max

16

19

max

10

10

2

1

exp

−

−

=













⋅

⋅

−

≈

e

P

P

P

!

Wynika stąd, że tylko mikrostany bardzo zbliżone do rozkładu najbardziej prawdopodobnego
mają prawdopodobieństwo wystąpienia znacząco różne od zera.

Entropia w fizyce statystycznej.

Boltzmann podał związek pomiędzy entropią a prawdopodobieństwem termodynamicznym:

P

S

ln

∝

. Planck wprowadził do tego wzoru współczynnik proporcjonalności k:

P

k

S

ln

=

,

K

J

k

23

10

38

,

1

−

⋅

=

.

Proporcjonalność S do lnP wynika z następującego rozumowania: rozważmy dwa układy
określone przez ich prawdopodobieństwa termodynamiczne oraz entropie: (P

a

, S

a

) i (P

b

, S

b

).

Załóżmy też, że entropia jest funkcją P: S=f(P). Ponieważ entropia jest parametrem
ekstensywnym:

,

b

a

b

a

S

S

S

+

=

+

oraz:

,

b

a

b

a

P

P

P

⋅

=

+

zatem po podstawieniu S=f(P) do pierwszej z tych równości mamy:

(

)

(

)

( ) (

.

b

a

b

a

b

a

P

f

P

f

P

P

f

P

f

+

=

⋅

=

+

)

Stąd wynika, że funkcją taką może być f(x)=ln(x).

5