Proces adiabatyczny q = 0

dU = w

el

Praca objętościowa w odwracalnym
procesie

V

dV

nRT

pdV

w

el









V

dV

nRT

dU





dU = n c

V

dT

V

dV

RT

dT

c

V













2

1

2

1

V

V

T

T

V

V

dV

R

T

dT

c

1

2

1

2

V

V

V

ln

T

T

ln

R

c





2

1

R

c

1

2

V

V

T

T

V















Układ nie wymienia ciepła z otoczeniem

I ZASADA TERMODYNAMIKI

dU = q

el

+ w

el

rozdzielamy zmienne
całkujemy
delogarytmujemy

2

1

R

c

1

2

V

V

ln

T

T

ln

v















Proces adiabatyczny q = 0

2

1

R

c

1

2

V

V

T

T

V















nR

pV

T



2

1

R

c

1

1

2

2

V

V

V

p

V

p

V















V

c

R

2

1

1

1

2

2

V

V

V

p

V

p















1

γ

c

c

c

c

R

V

V

p

V









V

p

c

c

γ



1

γ

2

1

1

1

2

2

V

V

V

p

V

p

















γ

1

1

γ

2

2

1

γ

1

1

1

1

γ

2

2

2

V

p

V

p

V

V

p

V

V

p









pV



= const

I ZASADA TERMODYNAMIKI

gdzie

Przemiana adiabatyczna q = 0

V

p

c

c

γ



const

pV

γ





= 1 pV = const

Proces izotermiczny

 

const

nR

T

p

p

p

nRT

p

γ

γ

γ

γ





















const

p

T

const

p

T

γ

γ

1

γ

1

γ













const

pV

γ



Adiabatyczne rozprężanie gazu

doskonałego q=0

W sposób odwracalny

:

dU = -pdV

gdy q

el

= 0

V

dV

nRT

dT

nc

V





1

2

1

2

V

V

V

ln

T

T

ln

R

c





2

1

R

c

1

2

V

V

T

T

V















C

C

γ

V

V

T

T

V

p

1

γ

2

1

1

2





















V

nRT

p



I ZASADA TERMODYNAMIKI

Temperatura koocowa gazu po rozprężaniu
adiabatycznym odwracalnym

Praca wykonana przez gaz podczas
odwracalnego rozprężania adiabatycznego

w =



U = n c

v

(T

2

- T

1

)

dU = n c

V

dT

Adiabatyczne rozprężanie gazu

doskonałego q=0

dU = -pdV

gdy q

el

= 0

W sposób nieodwracalny
przeciwko stałemu zewnętrznemu ciśnieniu:
p = p

z

= const.









































1

1

2

2

z

1

2

V

1

2

z

1

2

V

V

V

z

T

T

V

z

V

p

nRT

p

nRT

p

)

T

(T

nc

)

V

(V

p

)

T

(T

nc

dV

p

dT

nc

dV

p

dT

nc

2

1

2

1

p

z

= p

2

R

c

p

p

R

c

T

T

p

p

RT

T

c

RT

T

c

V

1

z

V

1

2

1

z

1

1

V

2

2

V



























Temperatura koocowa gazu po adiabatycznym
rozprężaniu przeciwko stałemu ciśnieniu zależy
od rodzaju gazu (c

v

).

I ZASADA TERMODYNAMIKI

Praca wykonana przez gaz podczas
nieodwracalnego rozprężania adiabatycznego

w =



U = n c

v

(T

2

- T

1

)

dU = n c

V

dT

I zasada termodynamiki

w przemianach gazu doskonałego

dU = q

el

+ w

el

c

p

– c

V

= R

dU = q

el

– pdV

H = U + pV

dU = dH – nRdT

dH = dU + d(pV)

dH = dU + d(nRT)

pV = nRT

dH = dU + nRdT

dU = nc

V

dT

dH = nc

p

dT

nc

V

dT = nc

p

dT - nRdT

c

V

= c

p

- R

I zasada termodynamiki
w przemianach gazu doskonałego

Proces izochoryczny, V = const.

dV = 0

dU = q

el

– pdV

dU = q

el

nc

V

dT = q

el

Jeżeli c

V

= const w zakresie temp. T

1

- T

2

to

∆ U = q

V

= nc

V

(T

2

– T

1

) ;

w = 0

const

T

p



I zasada termodynamiki
w przemianach gazu doskonałego

Proces izobaryczny, p = const, dp = 0

dU = q

el

– pdV

q

el

= dU + pdV = dH = nc

p

dT

Jeżeli c

P

= const w zakresie temp. T

1

- T

2

to

∆U = q

p

- p∆V,

q

p

= ∆H = n c

p

( T

2

– T

1

); w = - p ( V

2

– V

1

)

cons t

T

V



Proces izotermiczny

,

T = const

, dT = 0

pV = const

dU = q

el

– pdV

q

el

= pdV

I zasada termodynamiki
w przemianach gazu doskonałego

dU = nc

V

dT

dH = nc

p

dT

dH = 0

dU = 0

w = - n RT ln (V

2

/ V

1

) = n RT ln ( p

1

/ p

2

)

q = - w = n RT ln (V

2

/ V

1

) = n RT ln ( p

1

/ p

2

)

.

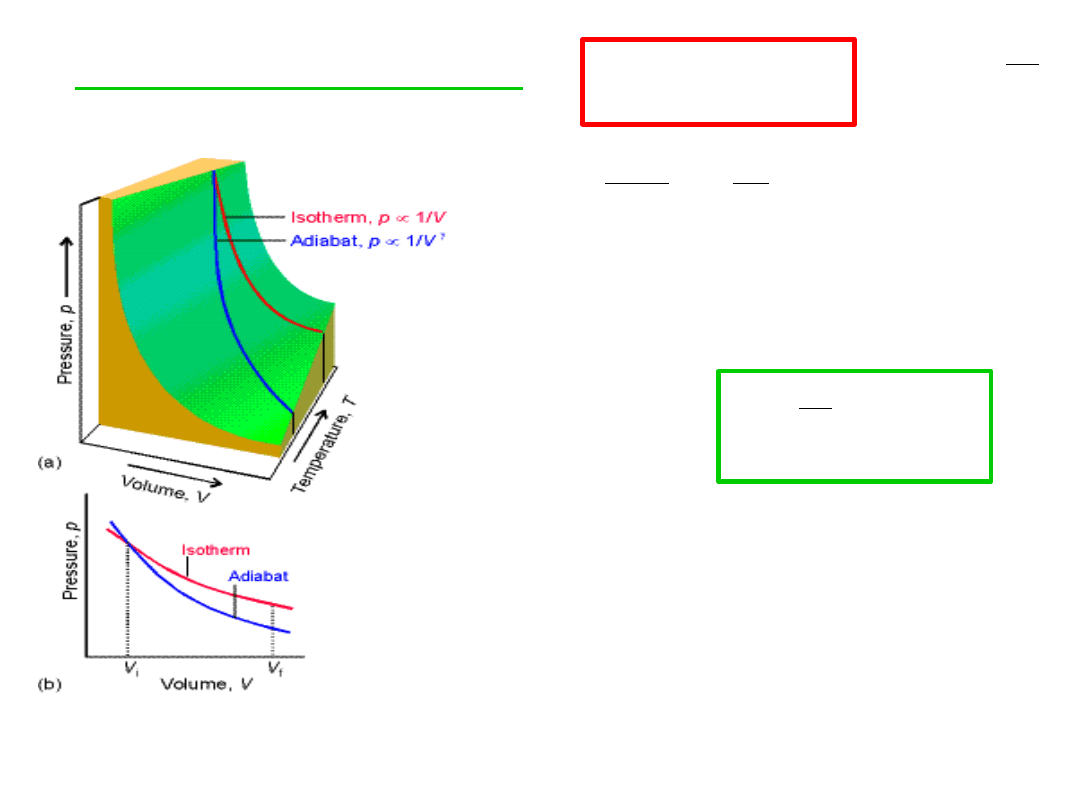
Proces adiabatyczny, q = 0

pV



= const,



= c

p

/c

V

dU = q

el

– pdV

dU = - pdV

n c

V

dT = - pdV

Jeżeli c

V

=const w zakresie temp. T

1

- T

2

to

∆ U = n c

V

(T

2

– T

1

)

w = n c

V

(T

2

– T

1

) = ( n c

V

/ nR )



( p

2

V

2

- p

1

V

1

)= 1 / (



- 1)



(p

2

V

2

– p

1

V

1

)

I zasada termodynamiki
w przemianach gazu doskonałego

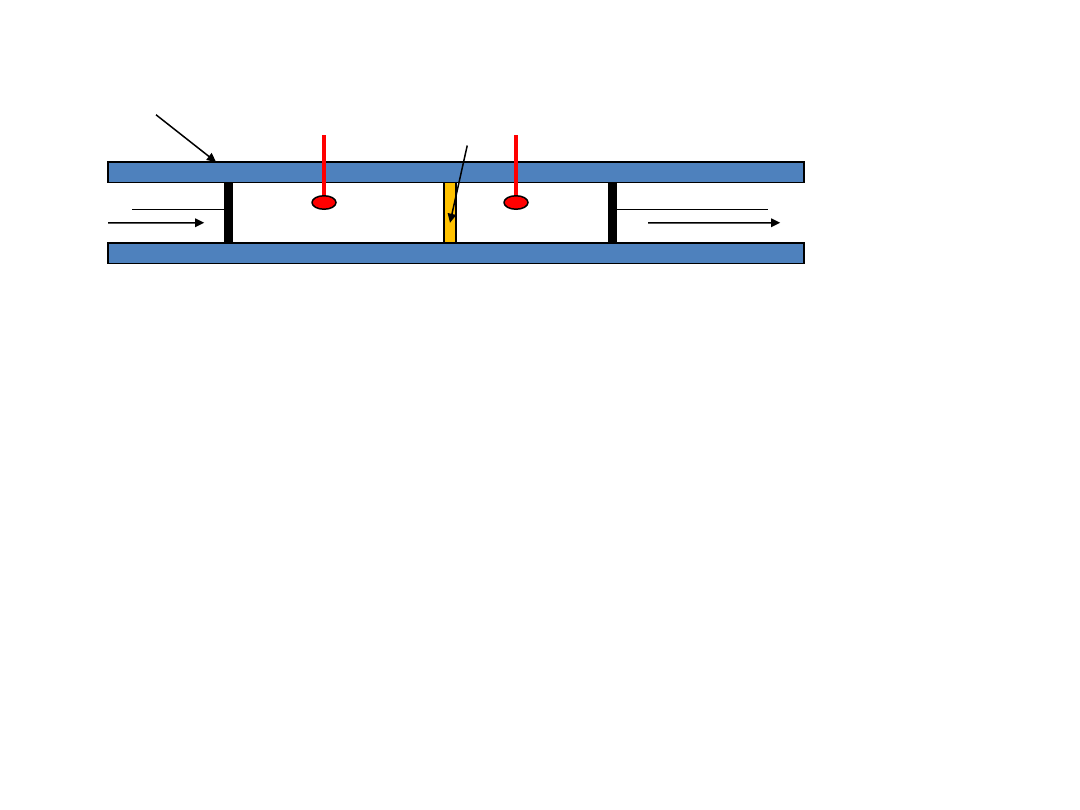
Doświadczenie Joule’a – Thompsona rozprężanie gazu przez zawór dławiący

T

1

T

2

p

1

p

2

Ścianki adiabatyczne
q = 0

porowata
przegroda

1

1

1

1

0

V

1

1

V

p

)

V

(0

p

dV

p

w

1















praca wykonana na gazie w lewej komorze

2

2

2

2

V

0

2

2

V

p

0)

(V

p

dV

p

w

2

















praca wykonana przez gaz w prawej komorze

Praca układu w = w

1

+ w

2

Zmiana energii wewnętrznej układu: ∆U = w, bo q=0

U

2

– U

1

= p

1

V

1

- p

2

V

2

U

2

+ p

2

V

2

= U

1

+ p

1

V

1

H

2

= H

1

∆H=0

Cel doświadczenia – określenie zależności pomiędzy temperaturą i ciśnieniem podczas rozprężania gazu
przez zawór dławiący w termicznie izolowanym zbiorniku.

Gaz z lewej komory przetłaczany jest pod stałym wyższym ciśnieniem p

1

do komory prawej, która

zamknięta jest tłokiem pod stałym niższym ciśnieniem p

2

.

Izolacja termiczna uniemożliwia wymianę

ciepła z otoczeniem.

Temperatura gazu w komorze o niższym ciśnieniu była niższa.

Rozprężanie gazu przez zawór dławiący jest
procesem izoentalpowym

P

1

> P

2

Współczynnik Joule’a-Thomsona:

W eksperymencie J-T stwierdzono, że procesowi rozprężania gazu przez zawór dławiący towarzyszy
ochładzanie lub ogrzanie gazu.

0

dT

T

H

dp

p

H

dH

p

T







































dp

p

H

dT

T

H

T

p





































p

T

H

T

H

p

H

dp

dT

















































Współczynnik Joule’a - Thompsona

p

T

JT

c

p

H

μ





















p

JT

T

c

μ

p

H





















H

JT

dp

dT

μ















Wpływ temperatury i ciśnienia na entalpię gazu rzeczywistego:

H = f(T,p)

Izotermiczny współczynnik
Joule’a-Thomsona:

JT

p

T

T

μ

c

p

H

μ























Zmiana entalpii gazu

rzeczywistego dH = c

p

dT -



JT

c

p

dp

doskonałego dH = c

p

dT

dp

p

H

dT

T

H

dH

T

p





































c

p

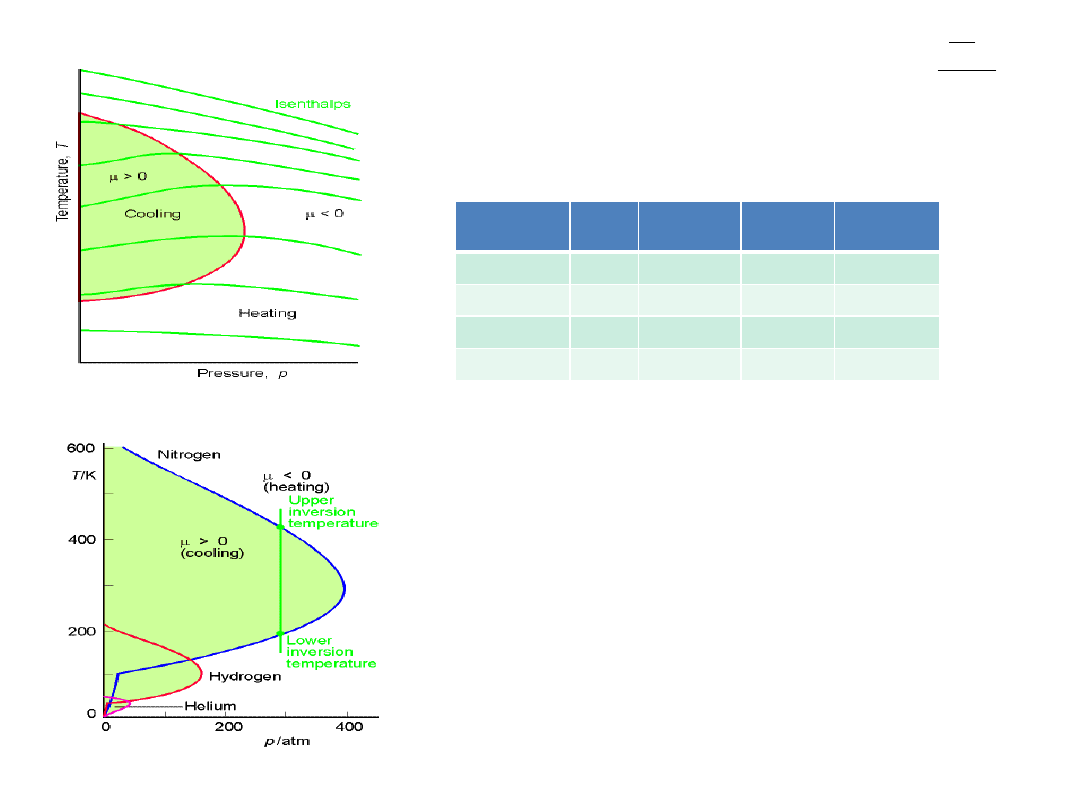
Współczynnik Joule’a-Thomsona zależy temperatury

rozprężanie ochładza gaz tylko wtedy, gdy temperatura
gazu leży pomiędzy dolną i górną temperaturą inwersji

Temperatury inwersji dla: azotu, wodoru i helu

gaz

T

inw

T

top

T

wrz

(



JT

)

298

Ar

723

83,8

87,3

CO

2

1500

197,7

1,11

He

40

4,2

-0,06

N

2

621

63,3

77,4

0,25

Efekt Joule’a – Thomsona -
ochładzanie się gazu podczas jego rozprężania jest
wykorzystywane w

procesie skraplania gazu

.

W skraplarce Lindego gaz rozpręża się kilkakrotnie w
zamkniętym obiegu, ochładzając w przeciwprądzie gaz
rozprężany. Kiedy jego temperatura spadnie poniżej
temperatury wrzenia następuje skroplenie

p

T

JT

c

p

H

μ





















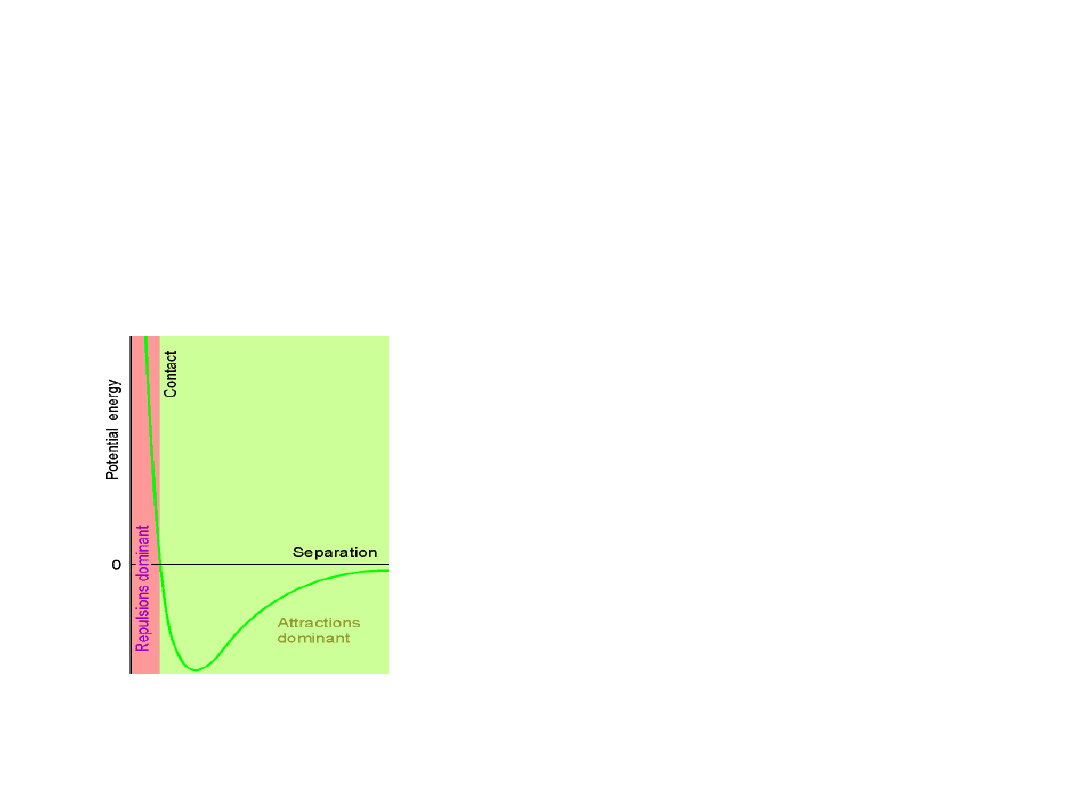
Gazy rzeczywiste

Różnice w zachowaniu się gazów rzeczywistych w porównaniu z gazem doskonałym
wynikają z:
 oddziaływao międzycząsteczkowych
 objętości własnej cząsteczek

Energia oddziaływao (energia potencjalna) dwóch cząsteczek gazu zależy od ich
wzajemnej odległości

Duża energia potencjalna występuje przy małych odległościach – dominują siły
odpychania

Ujemna energia potencjalna występuje przy odległościach pośrednich
– dominują siły przyciągania

Przy dużych odległościach energia potencjalna dąży do 0
-oddziaływania międzycząsteczkowe zanikają.

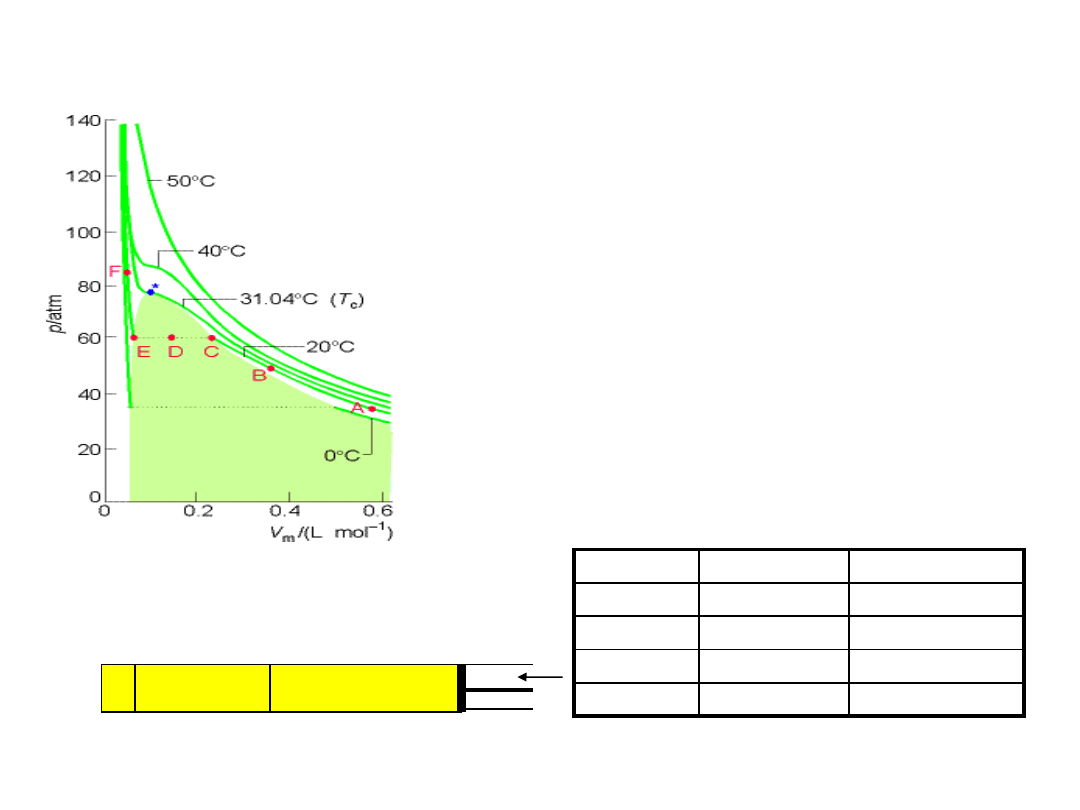
Doświadczalne izotermy CO

2

Odchylenia od równania stanu gazu doskonałego wzrastają gdy p↗ , T↘

1869 r Thomas Andrews

warunki krytyczne dla gazów (∗)

Doświadczalne izotermy CO

2

w zakresie temperatur 0-50

0

C

Temperatura krytyczna T

kr

Dla T >T

kr

gaz zachowuje się jak gaz doskonały, nie skrapla

się w czasie sprężania.
Tworzy się płynna

faza nadkrytyczna:

nie ciecz, bo nie

posiada powierzchni rozdziału od gazu; i nie gaz, bo jej
gęstośd jest porównywalna z gęstością cieczy.

Dla T<T

kr

skraplanie gazu

gaz

T

kr

[K]

p

kr

[Pa]

O

2

154,3

50,4 x 10

5

N

2

126,0

33,9 x 10

5

H

2

33,2

13,0 x 10

5

CO

2

304,19

74,0 x 10

5

Parametry krytyczne

F E D

C B A

gaz

skraplanie

ciec
z

Sprężanie CO

2

w temp. 20

0

C

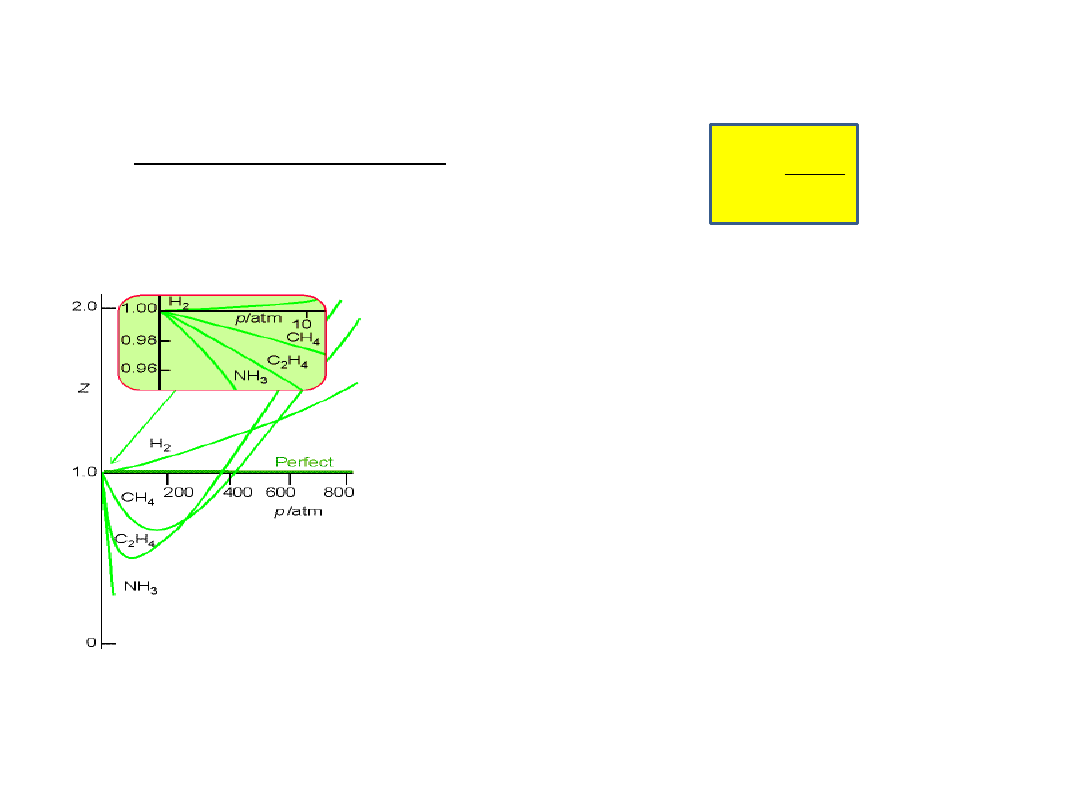
Gazy rzeczywiste

pV

m

= z RT

Współczynnik ściśliwości gazu charakteryzuje siły
oddziaływao międzycząsteczkowych i zależy od
rodzaju gazu, ciśnienia i temperatury.

RT

pV

z

m



dla gazów rzeczywistych z



1

z< 1 silne oddziaływania przyciągające,
V

rz

m

< V

m

gazu doskonałego.

z> 1 dominuje odpychanie cząsteczek,
V

rz

m

>V

m

gazu doskonałego.

dla gazu doskonałego z=1

1

lim

0





z

p

Zależnośd z = f(p) w temp.
273K

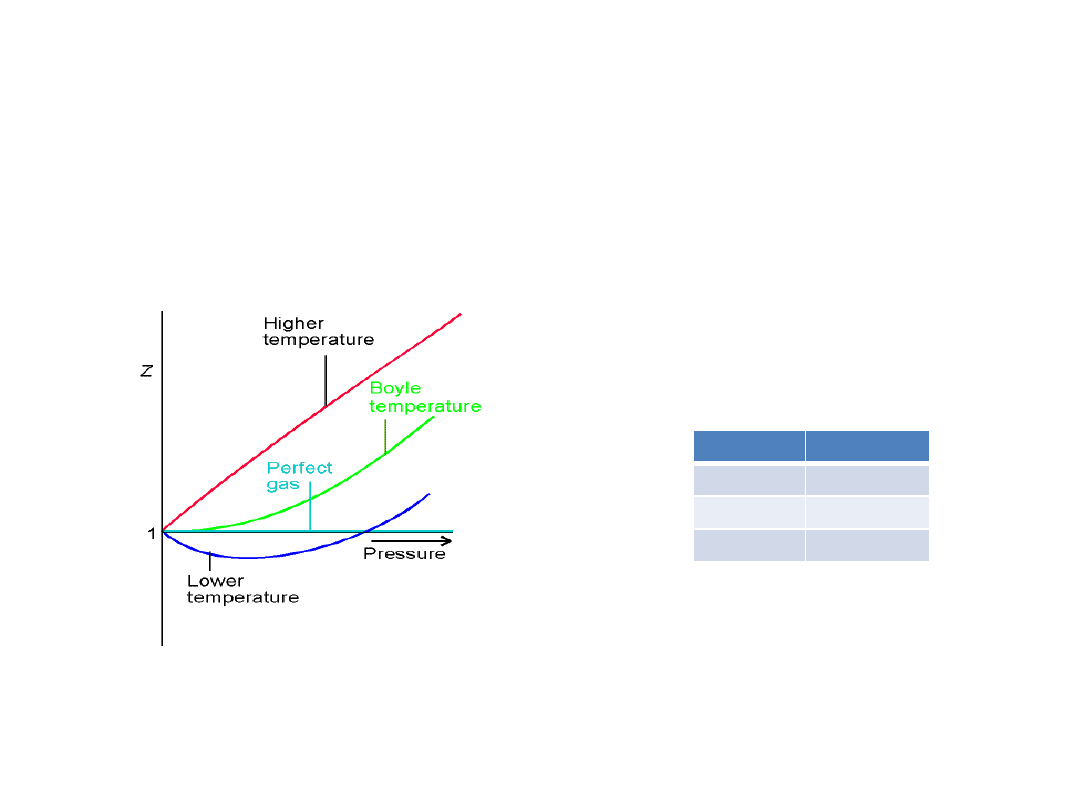
Gazy rzeczywiste

pV

m

= z RT

Dla gazów rzeczywistych
gdy p→ 0 to z →1 z różnym nachyleniem w zależności od temperatury.

W temperaturze Boyle’a T

B

właściwości gazów rzeczywistych zbliżają się do

właściwości gazu doskonałego w zakresie niskich ciśnieo.

Zależnośd z = f(p) w różnych temperaturach

gaz

T

B

[K]

Ar

411,5

CO

2

714,8

N

2

346,8

Równania stanu gazu rzeczywistego

Równanie wirialne (siłowe):

pV

m

= zRT

...)

p

C

p

B

RT(1

pV

2

'

'

m





























...

V

C

V

B

1

RT

pV

2

m

m

m

B, B’, C, C’ ….
eksperymentalnie wyznaczane
współczynniki wirialne

Równania stanu gazu rzeczywistego





RT

b

V

V

a

p

m

2

m





















Równanie van der Waalsa

Współczynniki van der Waalsa można obliczyd z parametrów krytycznych gazu :

V

m,kr

= 3b





zr

zr

2

zr

zr

8T

1

3V

V

3

p





















Równie van der Waalsa w postaci zredukowanej





nRT

nb

V

V

n

a

p

2





































cząsteczki gazu posiadają określoną objętośd i kształt –

parametr b = objętośd wyłączona 1 mola cząsteczek gazu

b = 4(4/3



r

3

) N

A

 między cząsteczkami występują siły oddziaływania proporcjonalne (parametr a) do kwadratu
stężenia molowego gazu

2

kr

27b

a

p



27bR

8a

T

kr



Jeżeli parametry stanu gazu podzielimy przez odpowiednie parametry krytyczne otrzymamy tzw.
parametry zredukowane:

T

zr

= T / T

kr

, p

zr

= p / p

kr

,

V

zr

= V

m

/ V

m

,

kr

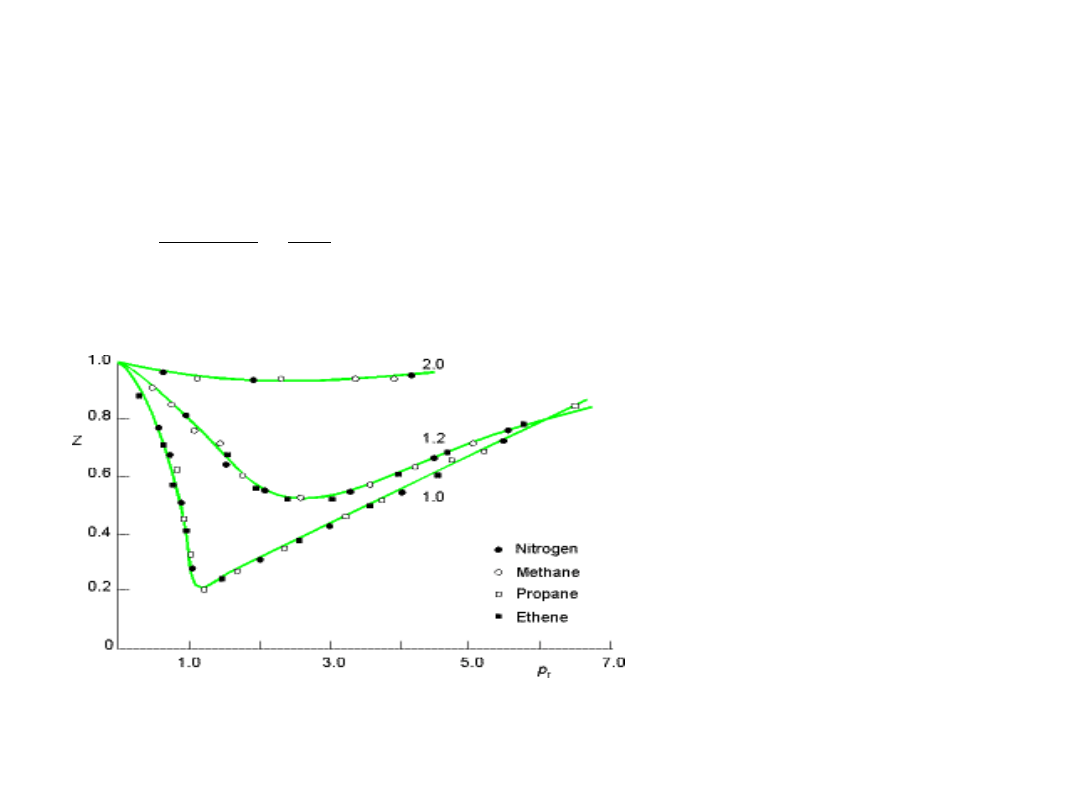
Zasada stanów odpowiadających sobie

Różne gazy wykazują zbliżone właściwości fizyczne, gdy znajdują się pod tym
samym zredukowanym ciśnieniem i w tej samej zredukowanej temperaturze .

2

zr

zr

zr

zr

V

3

1

3V

8T

p







Zredukowane równanie van der Waalsa
wyraża ciśnienie w funkcji objętości
niezależnie od rodzaju gazu.

Zależnośd współczynników ściśliwości z od zredukowanego ciśnienia p

zr

dla różnych temperatur zredukowanych

N

2

CH

4

CH

3

–CH

2

–CH

3

CH

2

=CH

2