II zasada termodynamiki

II zasada termodynamiki wprowadza

ENTROPIĘ (S)

termodynamiczną funkcję stanu, która wskazuje kierunek przemian samorzutnych

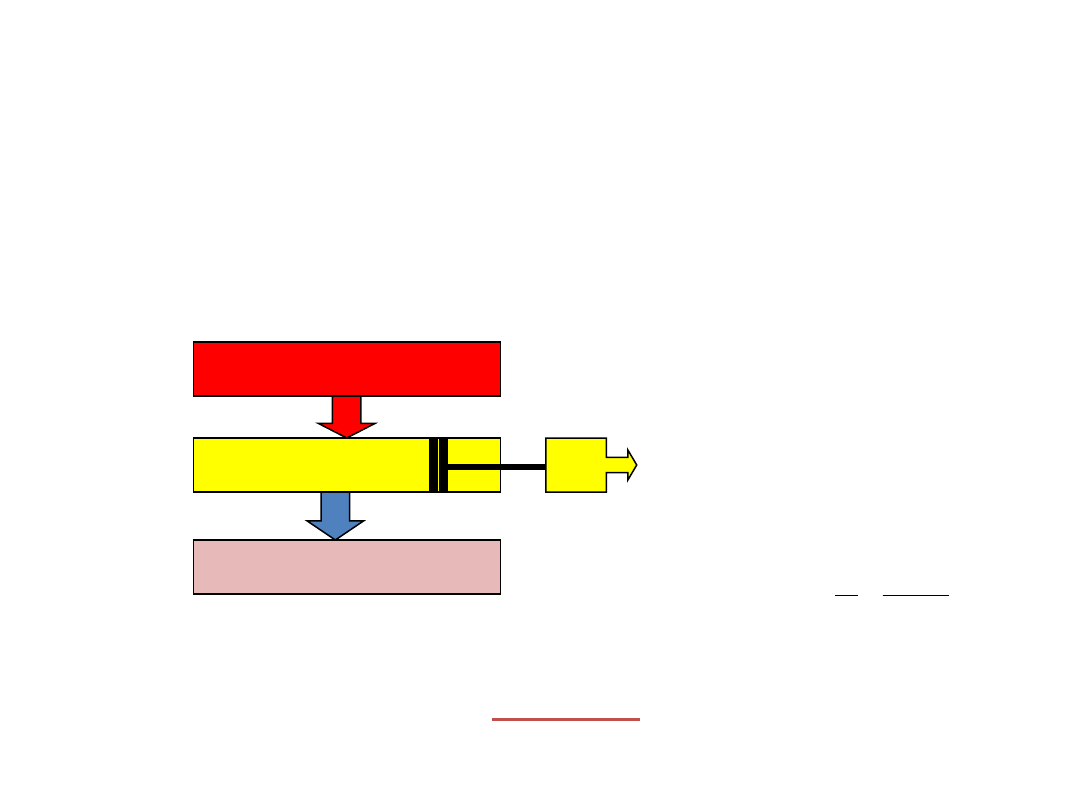
Zbiornik ciepła

Ciało robocze
(maszyna)

chłodnica

T

1

T

2

q

1

q

2

w

T

1

> T

2

Zamknięty cykl roboczy:
ciało robocze wraca do stanu początkowego

∆U = 0

∆U = q + w

- w = q = q

1

+ q

2

Wydajnośd maszyny cieplnej

1

2

1

1

q

q

q

q

w

η







(q

2

< 0)

zajmuje się


kierunkiem przepływu ciepła

,

 tym jaka częśd ciepła może byd zamieniona na pracę



oraz kiedy proces przebiega samorzutnie

Maszyna cieplna

Clausius 1850: „Ciepło nie może przechodzid samorzutnie
od ciała chłodniejszego do ciała cieplejszego”

Thomson 1851: „Ciepło najzimniejszego z ciał biorących

udział w procesie kołowym nie może byd źródłem pracy

Rudolf Julius Emanuel Clausius (1822-1888)

II zasada termodynamiki

William Thomson. Lord Kelvin (1892)

1824-1907

Nicolas Léonard Sadi Carnot

1796-1832

Fizyk, inżynier wojskowy i matematyk francuski
autor teorii silników cieplnych, w tym cyklu idealnego silnika
cieplnego – tzw. cyklu Carnota

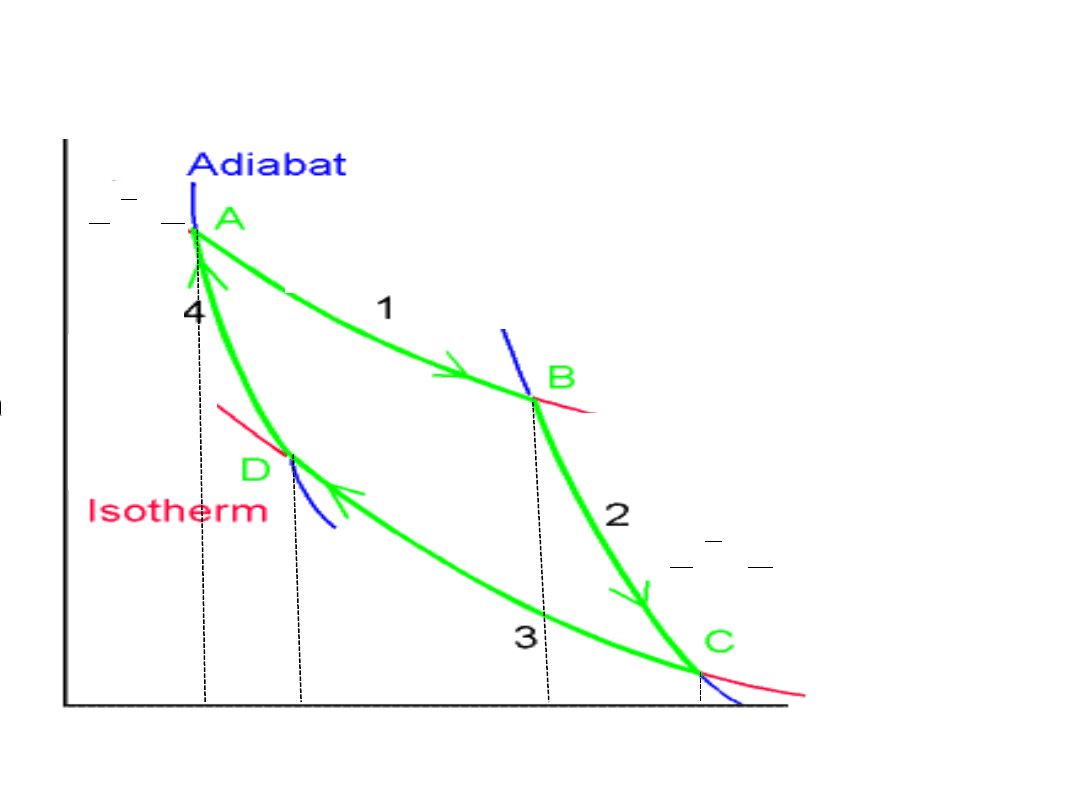
Cykl Carnota

:

zamknięty cykl

czterech odwracalnych

przemian gazu doskonałego

w

3

= -nRT

2

ln (V

4

/ V

3

)

w

2

= nc

V

(T

2

–T

1

)

w

4

=nc

V

(T

1

–T

2

)

4

1

R

c

1

2

V

V

T

T

V















T

1

=const

T

2

=const

w

1

= - nRT

1

ln (V

2

/ V

1

)

q

2

= 0

3

2

R

c

1

2

V

V

T

T

V















q

4

= 0

P

V

1

V

4

V

V

2

V

3

1 = A



B

Ciepło q

1

przepływa od źródła ciepła do maszyny

(gazu) Gaz rozpręża się V

1

→ V

2

w odwracalnym procesie

izotermicznym:

T

1

= const ∆ U

1

= 0,

q

1

= - w

1

2 = B



C

Gaz rozpręża się V

2

→ V

3

w

odwracalnym procesie adiabatycznym:

q

2

= 0

,

T

1

↘ T

2

,

∆U

2

= w

2

3 = C



D

Tłok spręża gaz V

3

→ V

4

w

odwracalnym procesie izoterm.: T

2

= const

ciepło q

3

przepływa z gazu do chłodnicy,

∆ U

3

= 0

q

3

= - w

3

4 = D



A

Tłok spręża

gaz V

4

→ V

1

w

odwracalnym procesie
adiabatycznym:

q

4

= 0

,

T

2

↗ T

1

,

∆U

4

= w

4

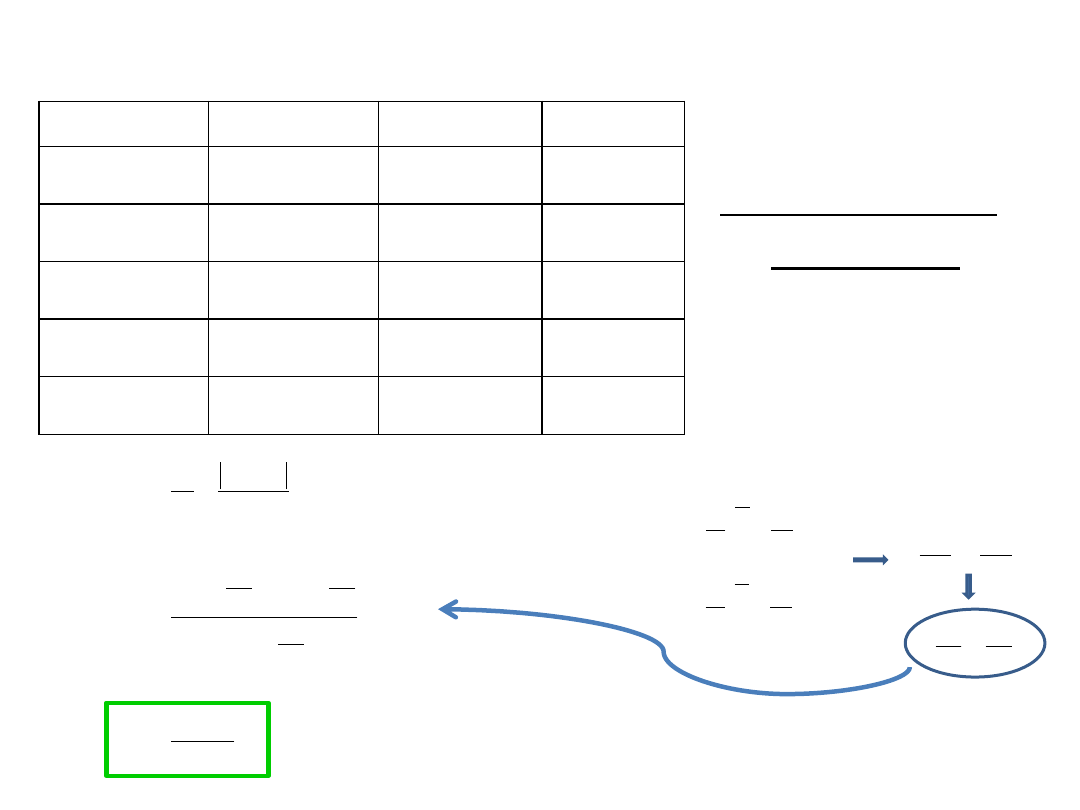
Bilans energetyczny w odwracalnym cyklu Carnota

przemiana

Ciepło, q

Praca, w



U

1. Izotermiczna

T

1

= const

nRT

1

ln(V

2

/V

1

)

-nRT

1

ln(V

2

/V

1

)

0

2. Adiabatyczna

q

2

= 0

0

nc

V

(T

2

-T

1

)

nc

V

(T

2

-T

1

)

3. Izotermiczna

T

2

= const.

nRT

2

ln(V

4

/V

3

)

-nRT

2

ln(V

4

/V

3

)

0

4.Adiabatyczna

q

4

= 0

0

nc

V

(T

1

-T

2

)

nc

V

(T

1

-T

2

)

Cały cykl
Carnota

nRT

1

ln(V

2

/V

1

)

+nRT

2

ln(V

4

/V

3

)

-nRT

1

ln(V

2

/V

1

)

-nRT

2

ln(V

4

/V

3

)

0

Sprawnośd silnika cieplnego



= wykonana praca

ciepło pochłonięte

1

2

1

1

2

1

4

3

2

1

2

1

1

3

1

1

T

T

T

η

V

V

ln

RT

V

V

ln

RT

V

V

ln

RT

η

q

q

q

q

w

η















3

2

R

c

1

2

V

V

T

T

V















4

1

R

c

1

2

V

V

T

T

V















4

3

1

2

V

V

V

V



Z równao adiabat (2) i (4)

4

1

3

2

V

V

V

V



(2)

(4)

 

max (100%) gdy T

2



0

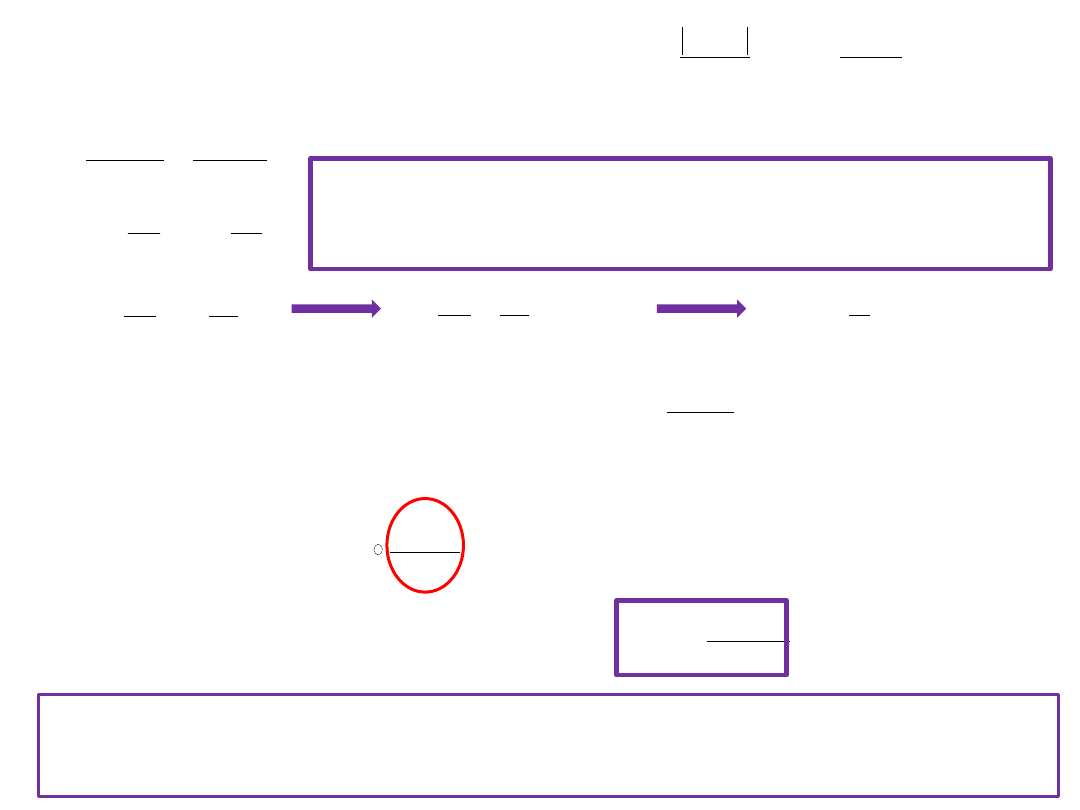
1

2

1

1

3

1

T

T

T

η

q

q

q

η









Analizując sprawnośd maszyny cieplnej Carnota

otrzymujemy:

1

2

1

1

3

1

T

T

T

q

q

q







q

3

< 0 oddane chłodnicy

W procesie cyklicznym nie można zamienid ciepła na pracę bez
równoczesnego przeniesienia części tego ciepła ze zbiornika ciepła
(T

1

) do chłodnicy (T

2

)

1

2

1

3

T

T

1

q

q

1







1

1

2

3

T

q

T

q





0

T

q

T

q

1

1

2

3





0

T

q





Dowolny

cykl odwracalny

dla gazu doskonałego można

uważad za sumę wielkiej liczby cykli Carnota





0

T

q

)

(

i

odw

i





q

i

– ciepło wymienione w temperaturze T

i

w i-tym odwracalnym procesie cyklu zamkniętego

0

T

dq

odw





Wyrażenie pod całką jest różniczką funkcji stanu

ENTROPII S

T

dq

dS

odw



Gdy układ zamknięty o temperaturze T wymienia z otoczeniem ciepło q w procesie
odwracalnym to ENTROPIA tego układu zmienia się o wartośd dS

PRZYPOMNIENIE

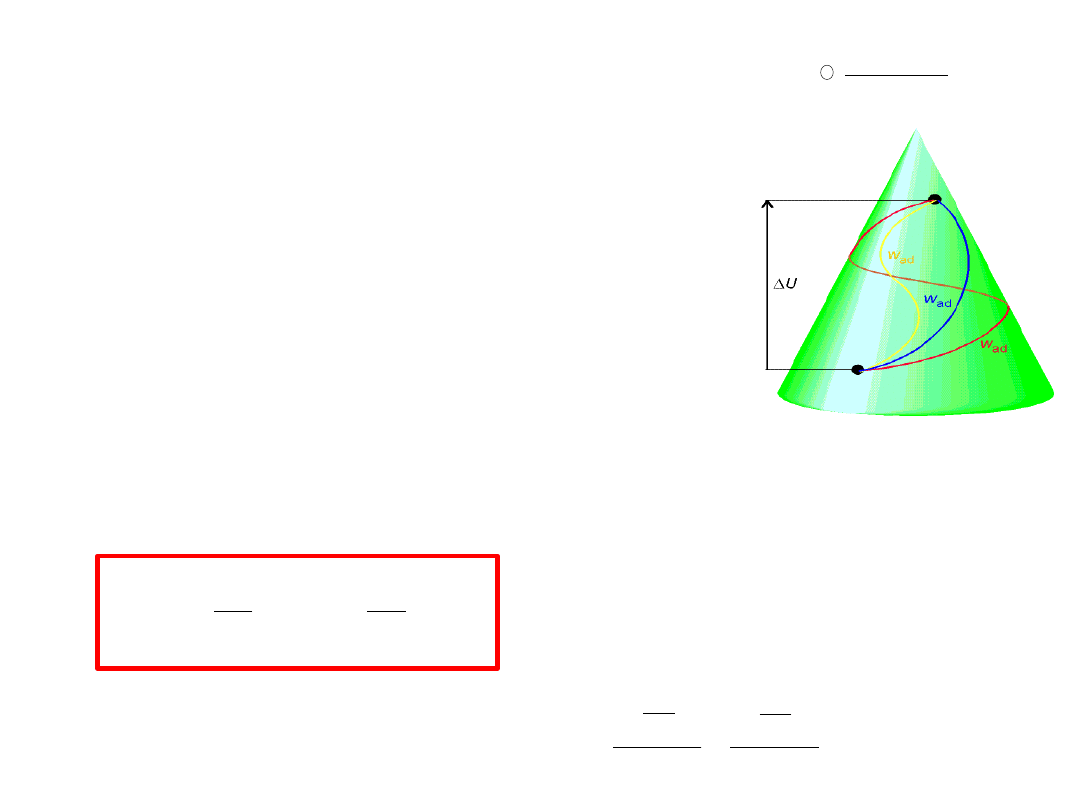
1. Funkcja stanu jest niezależna od drogi zależy jedynie od stanu

początkowego i koocowego układu.

2. Zmiana funkcji stanu w cyklu zamkniętym (takim, który wraca do

stanu początkowego) wynosi 0

Jeśli całka krzywoliniowa po drodze zamkniętej ∮ dF = 0,
to dF jest różniczką zupełną

dy

y

F

dx

x

F

dF

x

y





































x

y

F

y

x

F

x

y











































3. Drugie pochodne cząstkowe funkcji stanu

są sobie równe

WŁAŚCIWOŚCI

funkcji stanu

F= f (x,y)

PRZYPOMNIENIE

0

T

dq

odw





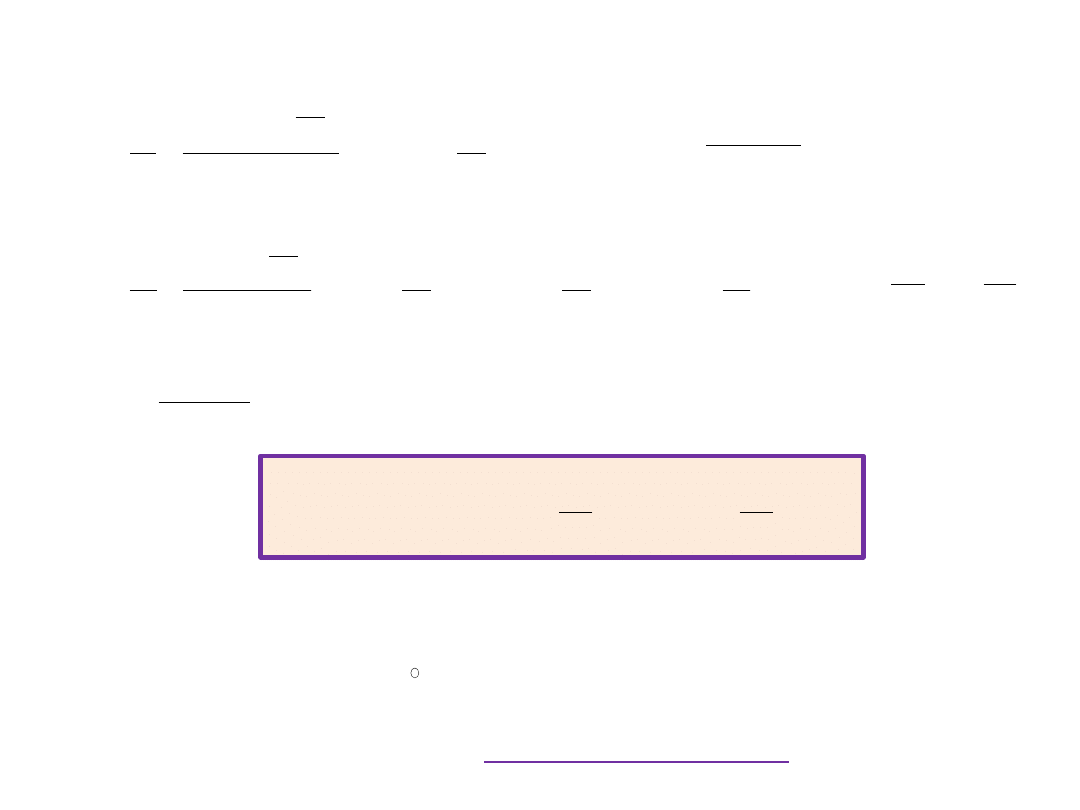
Zmiana entropii w cyklu Carnota:







































1

2

1

1

2

1

1

1

1

V

V

ln

R

n

T

V

V

ln

T

R

n

T

q

ΔS

0

T

0)

dq(

ΔS

2

1

T

T

2







































































1

2

4

3

3

4

2

3

4

2

2

3

3

V

V

nRTln

V

V

nRTln

V

V

nRln

T

V

V

ln

nRT

T

q

ΔS

0

T

0)

dq(

ΔS

1

2

T

T

4









0

V

V

ln

R

n

V

V

ln

R

n

ΔS

ΔS

1

2

1

2

i

i





































































1

2

4

3

V

V

V

V





0

dS

bo

.

Entropia w zamkniętym cyklu przemian odwracalnych nie uległa zmianie,



S = 0,

co można zapisad:

czyli entropia jest funkcją stanu.

ENTROPIA

Ciepło i praca zależą od sposobu przeprowadzenia procesu

Ciepło wymienione w izotermicznym procesie odwracalnym:

q

odw

= -w

odw

(max) = - nRT ln(V

2

/ V

1

)

jest większe od ciepła wymienionego w nieodwracalnym procesie izotermicznym

q

nod

=-w

nod

= -p

2

(V

2

– V

1

)

q

odw

> q

nod

T

dq

T

dq

dS

nieod

odw





jest funkcją stanu

Zmiana entropii układu wywołana przebiegiem jakiegoś procesu zależy od stanu początkowego i koocowego
układu ∆S = S

2

– S

1

, nie zależy od tego czy proces był odwracalny czy nieodwracalny.

T

dq

dS



ENTROPII nie potrafimy zmierzyd możemy ją tylko obliczyd.
Zmianę entropii możemy obliczyd gdy przemiany zachodzą
odwracalnie.
Aby obliczyd ∆S dla procesu nieodwracalnego trzeba go
zastąpid odwracalnymi etapami przejśd ze stanu 1 do 2.

S

1

(T

1

, p

1

,V

1

)

S

2

(T

2

, p

2

,V

2

)

ENTROPIA jest kryterium samorzutności i stanu równowagi procesu zachodzącego
w układzie izolowanym.

0

T

q

dS





0

T

q

dS





Jeżeli proces przebiega samorzutnie

Jeżeli układ znajduje się w stanie równowagi

T

q

dS



W procesach nieodwracalnych tj. samorzutnych
występuje nadmiar entropii.

∮dS = 0

ENTROPIA jako kryterium samorzutności procesu

Analiza cyklu Carnota pozwoliła na zdefiniowanie entropii w ujęciu makroskopowym i wyrażenie
jej za pomocą wielkości fizycznych (q,T)

T

dq

dS



W cyklu Carnota wymiana ciepła następuje między

układem

i

otoczeniem, które dostarcza (zb. ciepła)

lub odbiera (chłodnica) wymienione ciepło

.

Połączenie układu i otoczenia stanowi UKŁAD IZOLOWANY

.

ENTROPIA układu izolowanego

U = const. dU=0 (I zasada termodynamiki)

Niech T

A

> T

B

q ≅ 0

T

A

= const

T

B

= const

A

B

T

A

T

B

∆S = ∆S

A

+ ∆S

B

∆S

A

=q

A

/ T

A

∆S

B

=q

B

/ T

B

q

A

= - q q

B

= q

0

T

T

T

T

q

T

1

T

1

q

T

q

T

q

T

q

T

q

ΔS

B

A

B

A

A

B

B

A

B

B

A

A



































Jeżeli w układzie izolowanym zachodzą nieodwracalne przemiany to
zachodzą tak, że entropia układu rośnie: ∆S > 0
Dla procesu zachodzącego odwracalnie, tzn. pod wpływem nieskooczenie
małej siły napędowej T

A

≅ T

B

∆S = 0

Części A i B układu izolowanego
można potraktowad jak układ (A) i
otoczenie (B)

We wszystkich procesach nieodwracalnych tj SAMORZUTNYCH,
łączna entropia układu i otoczenia wzrasta.

q

đw

obj

= 0, V = const dV = 0

PROCESY SAMORZUTNE

zachodzą w przyrodzie i biegną do momentu osiągnięcia przez UKŁAD STANU RÓWNOWAGI np.
przechodzenie ciepła z ciała o wyższej temp. do ciała o niższej temp. czy dyfuzja substancji
rozpuszczonej z roztworu stężonego do rozcieoczonego

Podział procesów zachodzących w przyrodzie (wg kryt. możliwości wykonania pracy):

SAMORZUTNE

w < 0 (rozprężanie gazu, reakcje chem.)

układ wykonuje pracę

RÓWNOWAGOWE

w = 0 (reakcja w stanie równowgi A + B ⇄ C)

NIESAMORZUTNE

w > 0

pracę trzeba wykonad na układzie ( sprężanie gazu )

Siłą napędową procesów samorzutnych jest różnica wielkości intensywnych:

∆p – rozprężanie gazu, ∆T – przepływ energii cieplnej, ∆



,



c - przepływ masy (dyfuzja), ∆E - przepływ ładunków

elektr.( E potencjał elektryczny)
Gdy różnica wielkości intensywnych = 0 proces samorzutny ustaje a zachodzi proces równowagowy.

Naturalne procesy w przyrodzie są samorzutne i przebiegają w
sposób nieodwracalny, a więc ich entropia wzrasta.

Clausius:

„ENERGIA wszechświata jest stała

( I zasada termodynamiki),

a jego ENTROPIA dąży stale do max.
( II zasada termodynamiki)

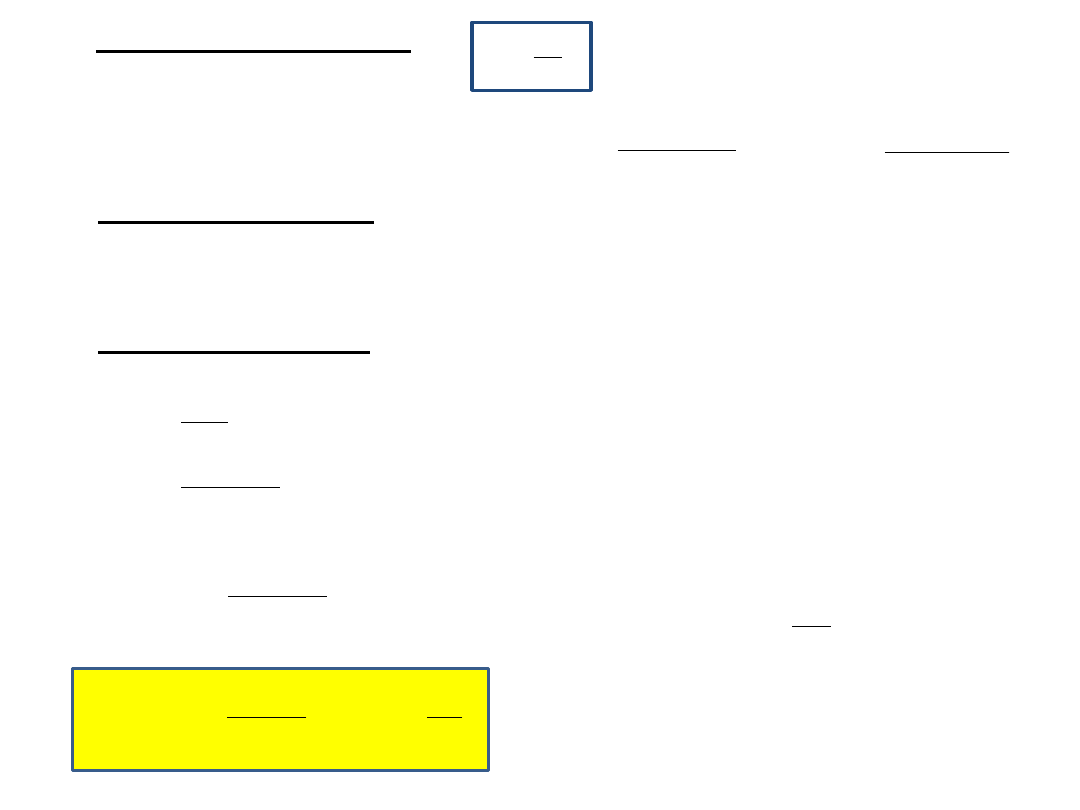
Obliczanie zmian entropii

1.

Przemiana adiabatyczna

q

el

= 0

dS = 0 ∆S = 0

2.

Przemiana izochoryczna

V = const q

el

= dU

T

dq

dS



q

el

= dU - w

el

jeśli w = w

obj

q

el

= dU + pdV

q

el

= dH - Vdp

T

pdV

dU

dS





1

2

V

T

T

V

S

S

T

T

V

V

T

T

ln

nc

T

dT

c

n

ΔS

T

dT

nc

dS

T

dT

nc

dS

T

dU

dS

2

1

2

1

2

1

















Jeśli c

V

= f (T)

dlnT

c

n

ΔS

dlnT

T

dT

2

1

lnT

lnT

V







Proces nie musi byd odwracalny

T

Vdp

dH

dS





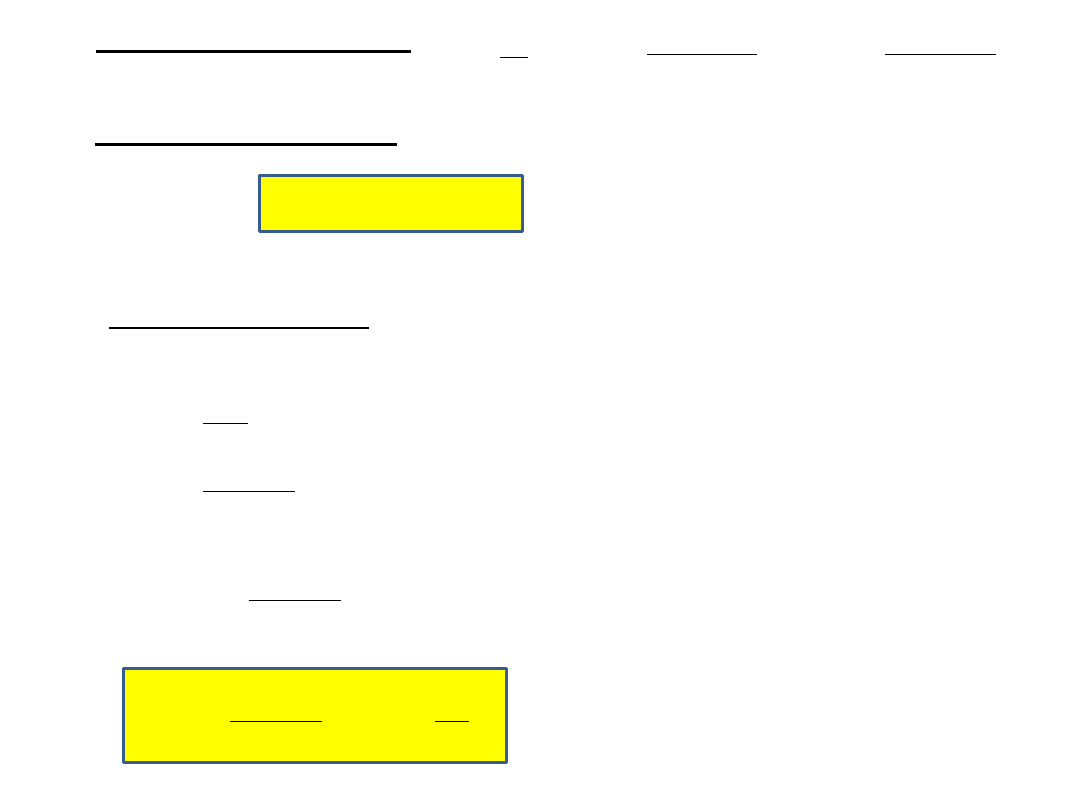
T

dq

dS



T

pdV

dU

dS





4. Przemiana izobaryczna

p= const

q

el

= dU +pdV

q

el

= dH – Vdp = dH

1

2

p

T

T

p

S

S

T

T

p

p

T

T

ln

nc

T

dT

nc

ΔS

T

dT

nc

dS

T

dT

nc

dS

T

dH

dS

2

1

2

1

2

1

















dlnT

c

n

ΔS

2

1

lnT

lnT

p





Jeśli c

p

= f (T)

Proces nie musi byd odwracalny

Obliczanie zmian entropii

3. Przemiana izotermiczna

T = const q

el

=- w

el

= nRT ln(V

2

/ V

1

)

∆S = n R ln(V

2

/ V

1

)

T

Vdp

dH

dS





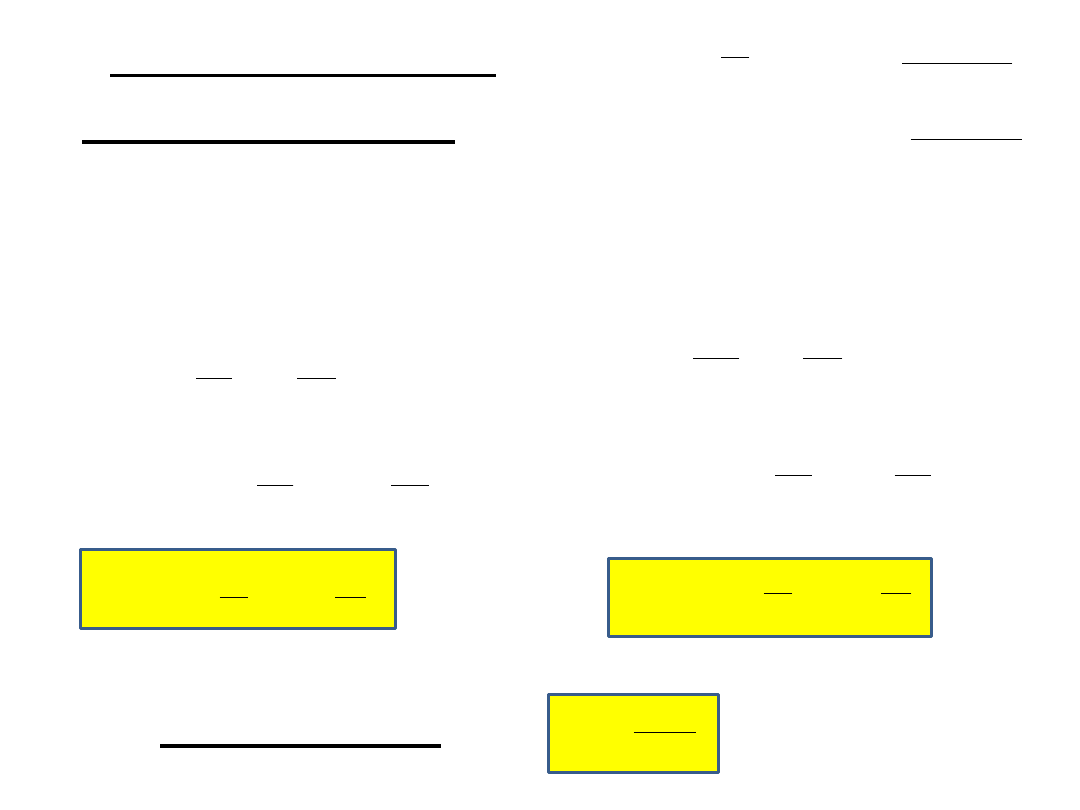
5. Obliczanie zmian entropii

w dowolnej przemianie

q

el

= dU + pdV

q

el

= dH - Vdp

q

el

= nc

V

dT + (nRT/V)dV

q

el

= nc

p

dT – (nRT/p)dp

1

2

1

2

V

V

V

T

T

V

S

S

V

V

V

nRln

T

T

ln

nc

ΔS

V

dV

nR

T

dT

nc

dS

V

dV

nR

T

dT

nc

dS

2

1

2

1

2

1



















6. Przemiana fazowa:

f

p,

f

p,

T

H

Δ

ΔS



1

2

1

2

p

p

p

T

T

p

S

S

p

p

p

nRln

T

T

ln

nc

ΔS

p

dp

nR

T

dT

nc

dS

dp

p

nR

dT

T

nc

dS

2

1

2

1

2

1



















T

dq

dS



T

pdV

dU

dS





T

Vdp

dH

dS





Statystyczna interpretacja ENTROPII

Do opisu entropii 1mola = 6,023 x 10

23

cząsteczek stosuje się

prawdopodobieostwo termodynamiczne W:

S = k

B

lnW

statystyczna definicja ENTROPII

podana przez Maxa Planck’a,

k

B

–stała Boltzmanna= 1,38 x 10

-23

J / K

W

( podstawowe pojęcie termodynamiki statystycznej)



-

określa liczbę położeo cząsteczki w dowolnym układzie zmiennych stanu (p,T,V, n

i

), czyli liczbę

sposobów podziału energii



- stanowi miarę uporządkowania układu w danym stanie ( dla 1 mola at. He w temp.298K W ~ 10

25

)



- jest tym mniejsze im wyższy jest stopieo uporządkowania



-

dla kryształu doskonałego w temp.0 K, w którym wszystkie cząsteczki mają ściśle określone

położenia w przestrzeni oraz pędy, W = 1 i jest to jego minimalna wartośd

.

W ujęciu molekularnym ENTROPIA jest miarą liczby sposobów podziału ENERGII WEWNĘTRZNEJ
między poszczególne cząsteczki i poszczególne rodzaje ich ruchów.

ENTROPIA jest miarą różnorodności stanów energetycznych cząsteczek układu - miarą
nieuporządkowania energetycznego cząsteczek.

Z równania

S = k

B

lnW

wynika, że

dla dowolnej substancji w postaci kryształu doskonałego standardowa entropia
w temperaturze 0 K równa jest 0

lim S = 0

teoremat cieplny Nernsta

T → 0

Gdy T→ 0, to S→ 0

III zasada termodynamiki S

0

0

= 0

wg Planck’a

„ W temperaturze zera bezwzględnego entropia ciała indywidualnego doskonale
krystalicznego jest równa 0”.

Statystyczna interpretacja ENTROPII

ENTROPIA jest jedyną funkcją termodynamiczną, dla której możemy policzyd jej
wartośd bezwzględną.

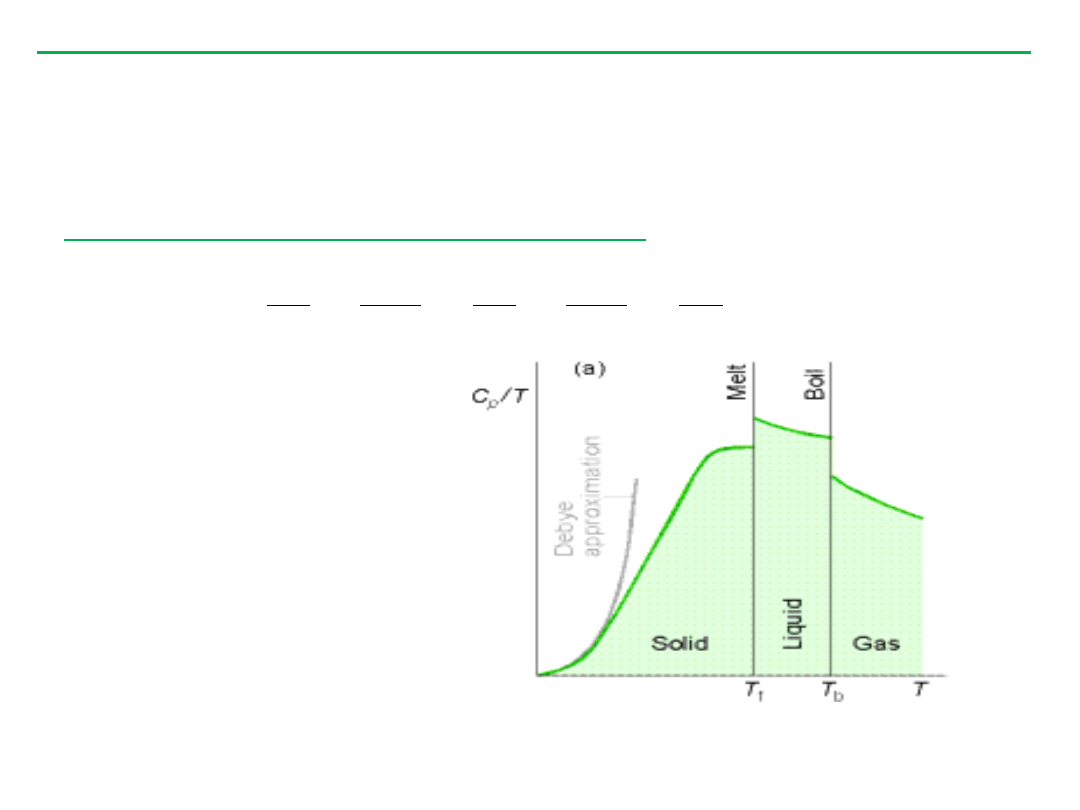
Standardowa entropia molowa S

0

pierwiastków i związków chemicznych

S

0

298

– standardowa entropia molowa w 298K

S

0

T

- standardowa entropia molowa w temp.T

Na podst. III zasady termodynamiki można obliczyd absolutne wartości entropii czystych pierwiastków
lub związków w dowolnym stanie skupienia i w dowolnej temperaturze.

ENTROPIA 1 mola związku (pierwiastka) w temperaturze T:

dT

T

c

T

ΔH

dT

T

c

T

ΔH

dT

T

c

S(0)

S

T

T

p(g)

wrz

par

T

T

p(c)

top

top

T

0

p(s)

T

wrz

wrz

top

top



















gdzie:
• c

p

– izobaryczne ciepło molowe,

(s) – faza stała
(c) – faza ciekła,
(g) – faza gazowa

• H

top

– entalpia topnienia

• H

wrz

– entalpia parowania

• T

top

– temp. topnienia

• T

wrz

– temp. wrzenia

c

p

w zakresie temp. 0-10 K wyznacza się

na podst ekstrapolacji Debye’a

c

p

= aT

3

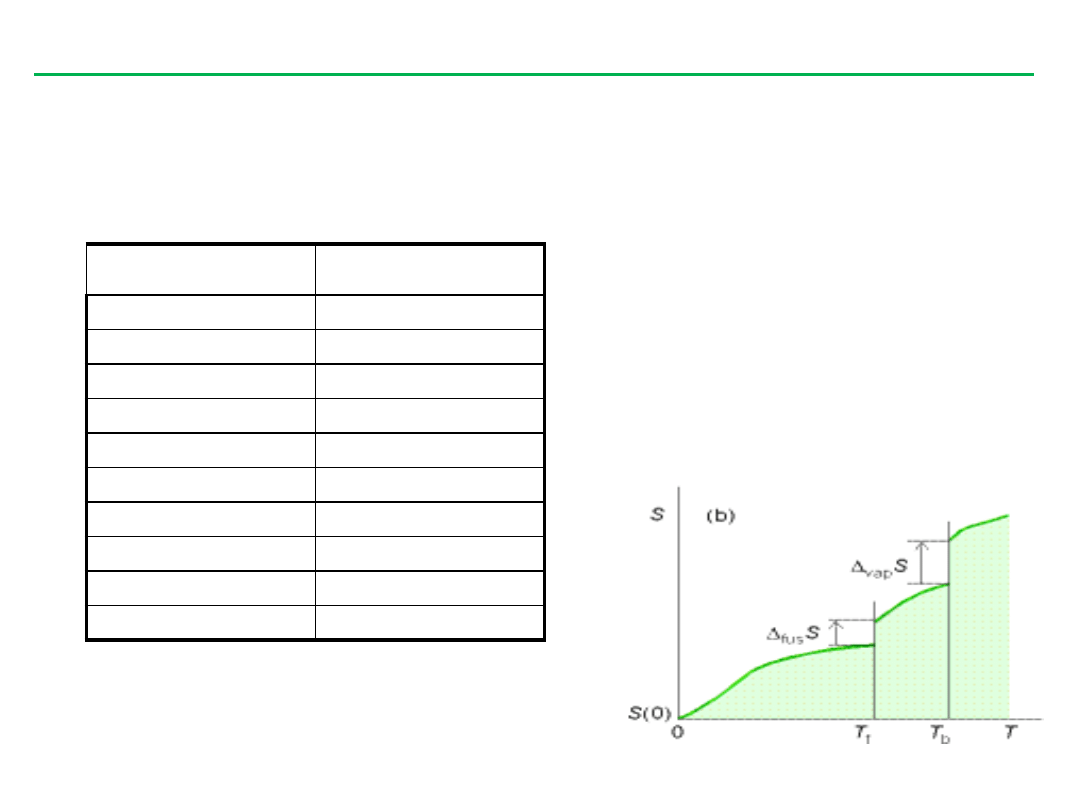
substancja

S

0

298

[J



mol

-1

K

-1

]

C (grafit)

5,73

C (diament)

2,50

NaCl

72,31

H

2

O (c)

69,93

Hg

75,95

H

2

130,45

O

2

204,86

H

2

O (g)

188,55

NH

3

192,32

CO

2

213,51

Standardowe entropie w 298K

Standardowa entropia molowa S

0

pierwiastków i związków chemicznych

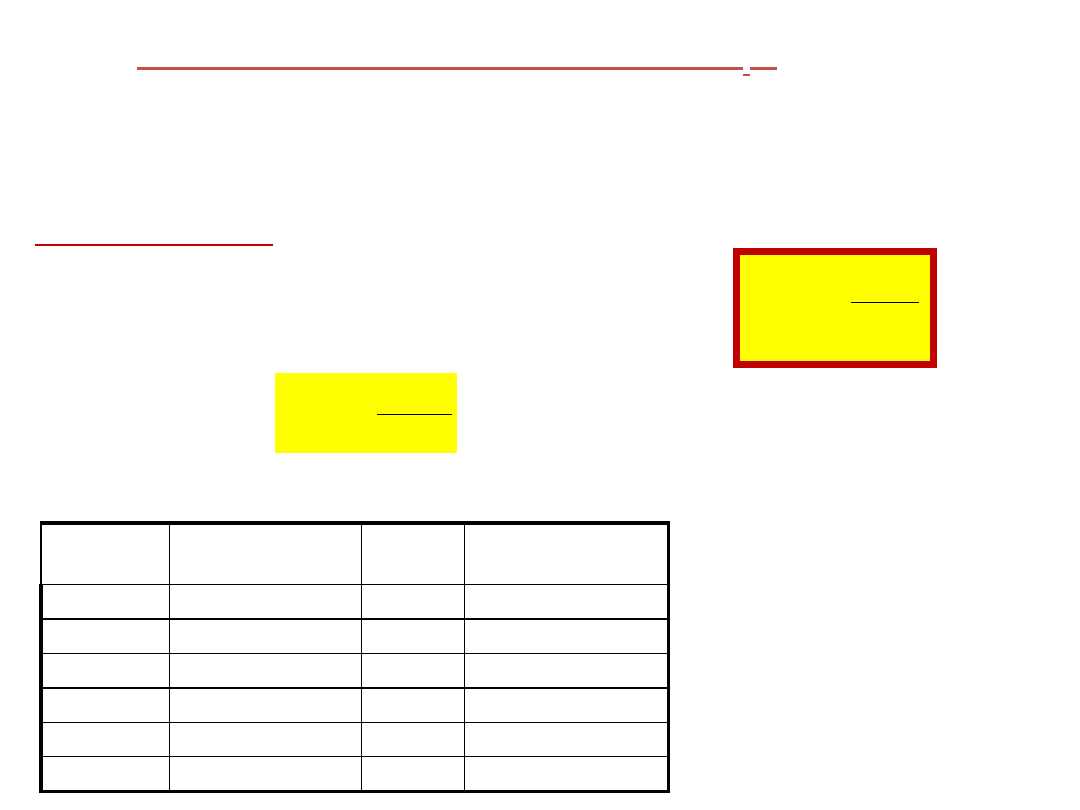
Standardowa entropia reakcji chemicznej ∆

r

S

0

0

im

substraty

i

0

j m

produkty

j

0

S

ν

S

ν

S











r

to różnica entropii pomiędzy czystymi
rozdzielonymi produktami a czystymi
rozdzielonymi substratami przy czym
wszystkie reagenty znajdują się w stanie
standardowym dla danej temperatury.

ENTROPIA przemiany to stosunek ilości ciepła
wymienionego w procesie do temperatury tej wymiany.

f

p,

f

p,

f

p,

T

H

Δ

S

Δ



substancja

∆

par

H

0

[kJ



mol

-1

]

T

wrz

[

0

C]

∆

par

S

0

[J



K

-1



mol

-1

]

C

6

H

6

+30,8

80,1

+87,2

CCl

4

+30,0

76,7

+85,8

c-heksan

+30,1

80,7

+85,1

H

2

S

+18,7

-60,4

+87,9

CH

4

+8,18

-161,5

+73,2

H

2

O

+40,7

100,0

109,1

Standardowa entropia molowa ∆S

0

przemiany

Dla wielu cieczy

∆

par

S

0

~ 85 J / K mol

reguła Troutona

f

p,

0

f

p,

0

f

p,

T

H

Δ

S

Δ



Standardowe molowe entropie parowania

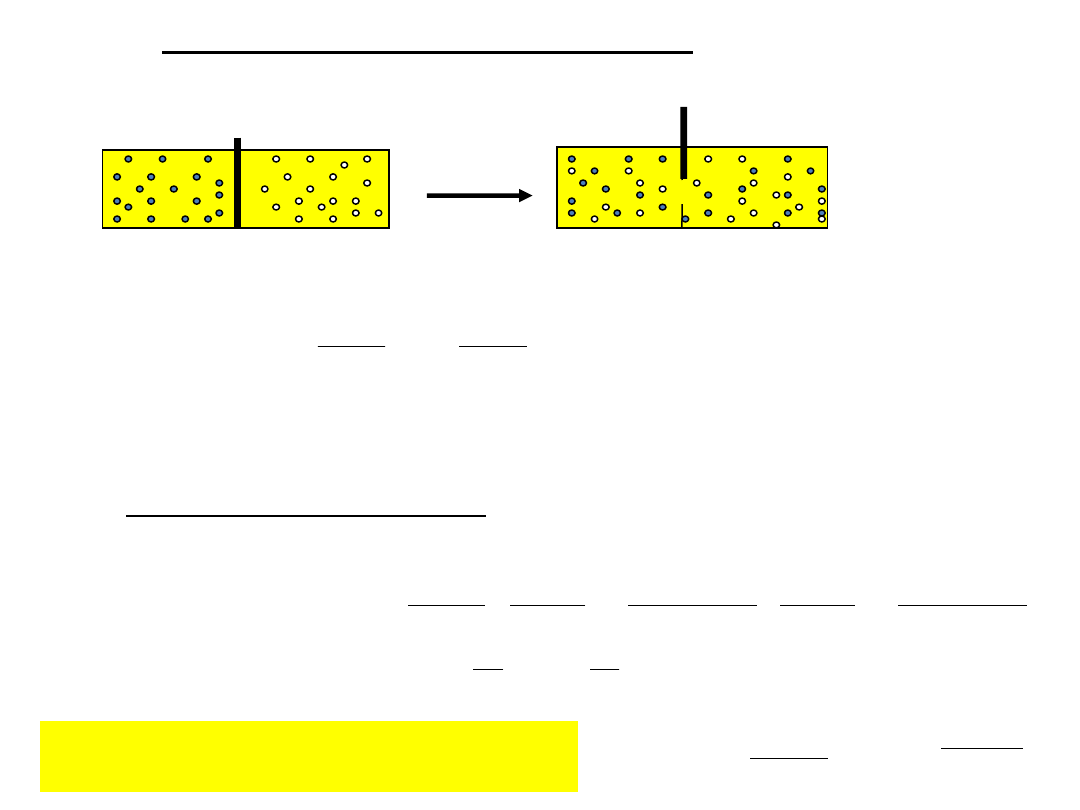
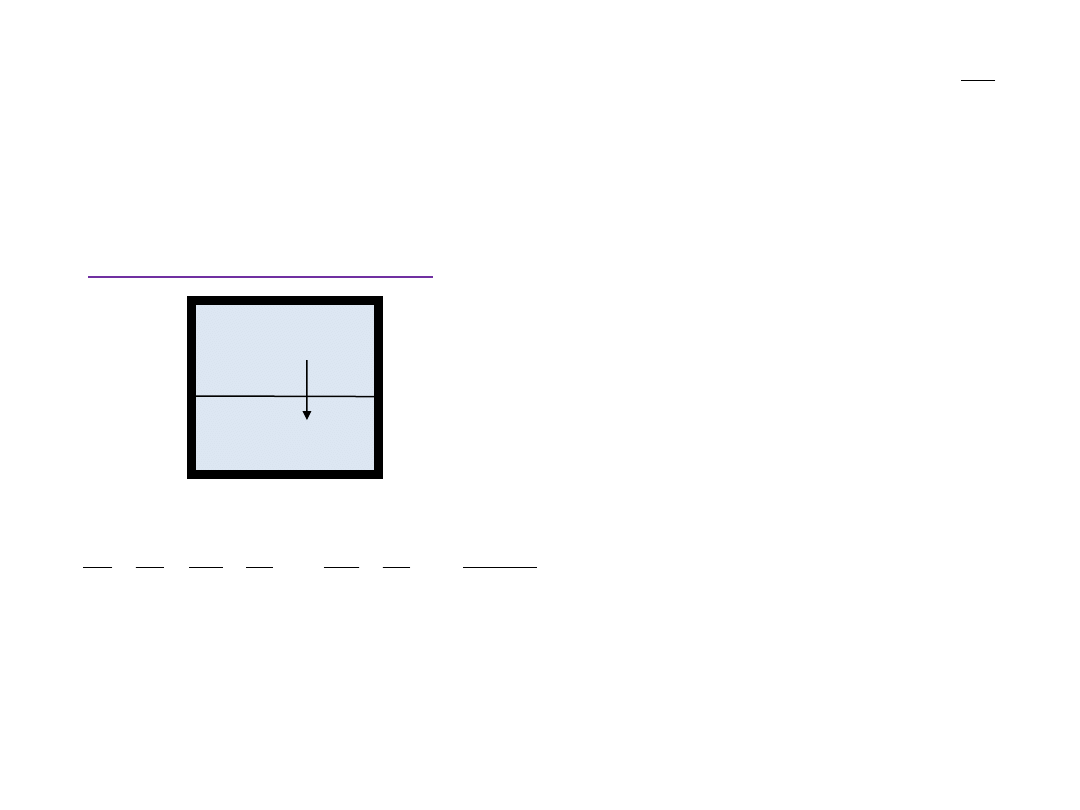
Entropia mieszania gazów doskonałych

Gaz A

n

A

Gaz B

n

B

∆S > 0

V

A

V

B

Stan przed mieszaniem (1)

Stan po zmieszaniu (2)

W warunkach T = const gazy A (n

A

) i B(n

b

) rozprężają się niezależnie od siebie do całego zbiornika.

∆S

miesz

= ∆S

A

+ ∆S

B

B

B

A

B

A

B

A

A

V

V

V

Rln

n

V

V

V

Rln

n









V

m

– objętośd 1 mola gazu doskonałego w danych warunkach p i T

V

A

= n

A

V

m

V

B

= n

B

V

m

W wyniku mieszania wzrasta objętośd przestrzeni dostępnej dla każdej cząsteczki, a więc także swoboda jej ruchu.
Wzrasta liczba sposobów podziału energii wewn. ( głównie translacyjnej) pomiędzy poszczególne cząsteczki, czyli
prawdopodobieostwo termodynamiczne W ↗, a S ↗ zgodnie z równaniem Boltzmanna: S = k

B

ln W

Średnia molowa entropia mieszania

B

B

A

A

miesz

m

B

m

B

m

A

B

A

B

m

A

m

B

m

A

B

A

A

B

A

miesz

miesz

x

1

Rln

x

x

1

Rln

x

ΔS

V

n

V

n

V

n

Rln

n

n

n

V

n

V

n

V

n

Rln

n

n

n

n

n

ΔS

ΔS

























B

A

A

A

n

n

n

x





B

A

B

B

n

n

n

x





Proces samorzutny ∆S

miesz

> 0

)

lnx

x

lnx

R(x

S

Δ

B

B

A

A

miesz









Termodynamiczna skala temperatury

Z wyrażenia na wydajnośd maszyny cieplnej

1

2

1

T

T

T

η





wynika, że silnik cieplny ma maksymalną wydajnośd gdy T

2

= 0

Na tym wyniku Kelvin oparł swoją termodynamiczną skalę temperatury.

Jako jednostkę podstawową skali przyjął stopieo Celsjusza

.

Najniższa temperatura jaką udało się uzyskad to
20 nK = 20 x 10

-9

K

T[K] = 0[

0

C] + 273,15

Jak można osiągnąd bardzo niskie temperatury?

Z doświadczenia Joule’a – Thomsona wynika, że ekspansja gazu prowadzona poniżej jego
temperatury inwersji prowadzi do jego ochłodzenia.
W urządzeniu przeciwprądowym (Siemens 1860r) następuje wymiana ciepła między gazem
rozprężonym i ochłodzonym a gazem sprężonym, prowadząca do stopniowego ochładzania się gazu
aż do jego skroplenia.

Destylacja ciekłego powietrza daje

ciekły O

2

T

wrz

= 90 K

i

ciekły N

2

T

wrz

= 77 K.

Ekspansja

H

2

ochłodzonego za pomocą ciekłego azotu (poniżej temp.193 K) powoduje jego

skroplenie w temperaturze

22 K

.

Ciekły H

2

pozwala na schłodzenie i skroplenie

He T

wrz

= 4 K.

Zmniejszenie ciśnienia nad helem

pozwala uzyskad temp.

1 K.

Temp. < 1 K

uzyskuje się metodą rozmagnesowywania adiabatycznego ( 1926 r P.Debye i W.F. Giauque)

Kryształ soli paramagnetycznej ochładza się do temperatury ciekłego helu w obecności pola

magnetycznego.

Po odizolowaniu termicznym kryształu wyłącza się pole magnetyczne. Kryształ ulega samorzutnemu

adiabatycznemu rozmagnesowaniu. Entropia wzrasta kosztem energii oscylacyjnej sieci krystalicznej soli i
temperatura kryształu obniża się. W ten sposób uzyskano

temp. 10

-7

K.

Stosując metodę jądrowego rozmagnesowania adiabatycznego dla Cu ustanowiono światowy rekord
niskiej

temp. 2 x 10

-8

K.