1. Zakres opracowania

1) Ukształtowanie obiektu – wyznaczenie podstawowych gabarytów

konstrukcji.

2) Obliczenie ci

ęż

arów i poło

ż

enia

ś

rodka ci

ęż

ko

ś

ci układu urz

ą

dzenia +

fundament.

3) Wyznaczenie momentów bezwładno

ś

ci mas układu wzgl

ę

dem płaszczyzn i

osi głównych.

4) Okre

ś

lenie sztywno

ś

ci podło

ż

a gruntowego.

5) Okre

ś

lenie cz

ę

stotliwo

ś

ci drga

ń

własnych układu.

6) Wyznaczenie amplitud drga

ń

obiektu.

2. Dane maszyny i podło

ż

a

Silnik :

– średnica silnika [mm] d

1

= 1200

– długość silnika [mm] l

1

= 1500

– masa silnika [Mg] m

1

= 6,5

Urządzenie :

– średnica urządzenia d

2

= 1000

– długość urządzenia l

2

= 1250

– masa urządzenia m

2

= 2,75

Pozostałe dane :

– odstęp między silnikem a urządzeniem [mm] lx = 400
– prędkość obrotowa urządzenia [obr./min] n

m

= 800

– przyjęto ciężar betonu [Mg/m

3

] γ

bet

= 2,5

3. Ukształtowanie obiektu – wyznaczenie podstawowych gabarytów
konstrukcji

Wyznaczenie niezb

ę

dnych gabarytów fundamentu:

1) Cokół pod urz

ą

dzenie.

a) długo

ść

cokołu : l

3

= 100 + l

2

+ 100 = 100 + 1250 + 100 = 1450 [mm]

b) szeroko

ść

cokołu : b

3

= 100 + d

2

+ 100 = 100 + 1000 + 100 = 1200 [mm]

c) wysoko

ść

cokołu : h

3

= 0,5d

1

- 0,5 d

2

= 0,5*1200 – 0,5*1000 = 100 [mm]

d) masa cokołu : m

3

=

γ

bet

* l

3

* b

3

*

h

3

= 2,5*1,45*1,2*0,10 = 0,543[Mg]

2)Blok fundamentowy

Wyznaczenie

ś

rodka ci

ęż

ko

ś

ci zespołu maszyn :

Z

0

=

m

2

∗0+m

3

∗0+m

1

∗(0,5∗l

1

+l

x

+0,5∗l

2

)

m

1

+m

2

+m

3

=

2,5

∗0+0,543∗0+6,5∗(

150

2

+40+

125

2

)

6,5

+2,75+0,543

=

= 1,17 [m]

Wyznaczenie wymiarów bloku fundamentowego :

Warunek 1:

(m

1

+m

2

)∗(4÷5)≈m

4

m

1

+ m

2

= 6,5 + 2,75 = 9,25 [Mg]

9,25* 4 = 37,0 [Mg] 9,25*5 = 46,25 [Mg]

zatem m

4

= (37,0;46,25) [Mg]

Warunek 2:

h

4

=(0,60 ;1,50)[m]

- wysoko

ść

bloku fundamentowego

przyj

ę

to : h

4

= 1,0 [m]

Warunek 3:

b

4

h

4

>2 → b

4

>2∗h

4

= 2*1,0 = 2,0 [m]

przyj

ę

to : b

4

= 3,0 [m]

m

4

=

γ

bet

∗l

4

∗b

4

∗h

4

=2,5∗l

4

∗3,0∗1,1=7,5∗l

4

[Mg ]

(37,0 ; 46,25)=7,5∗l

4

→ l

4

=(4,99 ;6,16)[m]

przyj

ę

to : l

4

= 5,5 [m]

Warunek 4 :

l

4

>l

1

+l

x

+l

2

+0,50

= 1,5 + 0,4 + 1,25 + 0,5 = 3,65 [m] < l

4

= 5,5 [m]

Gabaryty bloku fundamentowego wynosz

ą

:

a) długo

ść

bloku : l

4

= 5500 [mm]

b) szeroko

ść

bloku : b

4

= 3000 [mm]

c) wysoko

ść

bloku : h

4

= 1000 [mm]

d) masa bloku : m

4

=

γ

bet

* l

4

* b

4

*

h

4

= 2,5*5,5*3,0*1,0 = 41,25 [Mg]

4. Obliczenie ci

ęż

arów i poło

ż

enia

ś

rodka ci

ęż

ko

ś

ci układu

Wyznaczenie ci

ęż

arów elementu układu :

a) silnik :

q

1

=m

1

∗g=6,5[ Mg ]∗10,0[m/ s

2

]=65,0 [kN ]

b) urz

ą

dzenie :

q

2

=m

2

∗g =2,75[ Mg ]∗10,0[m/ s

2

]=27,5[kN ]

c) cokół :

q

3

=m

3

∗g=0,543 [Mg]∗10,0 [m/s

2

]=5,43 [kN ]

d) blok fundamentowy :

q

4

=m

4

∗g =41,25[Mg ]∗10,0 [m/s

2

]=412,5[ kN ]

Q

=q

1

+q

2

+q

3

+q

4

=65,0+27,5+5,43+412,5=510,4 [kN ]

Wyznaczenie

ś

rodka ci

ęż

ko

ś

ci całego układu :

O

ś

główna ''Z'' układu pokrywa si

ę

z osi

ą

'z0' (o

ś

główna zespołu maszyn) oraz z

osi

ą

'z4' (o

ś

główna bloku fundamentowego).

Poło

ż

enie płaszczyzny XY okre

ś

lam z nast

ę

puj

ą

cej zale

ż

no

ś

ci (wzgl

ę

dem

'x1y1'='x2y2'):

XY

=

m

1

∗0+m

2

∗0+m

3

∗(0,5∗h

3

+0,05+0,5∗d

2

)+m

4

∗(0,5∗h

4

+0,05+0,5∗d

1

)

m

1

+m

2

+m

3

+m

4

=

XY

=

0,543

∗(0,5∗0,1+0,05+0,5∗1,0)+41,25∗(0,5∗1,0+0,05+0,5∗1,2)

6,5

+2,75+0,543+41,25

= 0,935[m]

5. Charakterystyka warto

ś

ci sił wzbudzaj

ą

cych

Silnik :

P

d ,s

=0,2 G

w

=0,2∗6,5∗10=13,0[kN ]

Urz

ą

dzenie :

P

d , p

=0,2 G

w

=0,2∗2,75∗10=5,5[kN ]

6.Sprawdzenie nacisku na podło

ż

e gruntowe

Podło

ż

em pod fundament jest nast

ę

puj

ą

cy grunt :

•

grunt : Gp

•

stan wilgotno

ś

ci : wn

•

stopie

ń

plastyczno

ś

ci : I

L

= 0,3

Dla przyj

ę

tego podło

ż

a ustalono nast

ę

puj

ą

ce parametry geotechniczne :

•

w

n

= 17

• ρ

d

= 21,0 [kN/m

3

]

ρ

d

(r)

= 0,9 * 21,0 = 18,9 [kN/m

3

]

• ρ

b

= 21,5 [kN/m

3

]

ρ

b

(r)

= 0,9 * 21,5 = 19,35 [kN/m

3

]

• ф

= 18

0

•

Cu = 36

0

Cu

(r)

= 0,9 * 36 = 32,4

•

N

B

= 1,04

•

N

C

= 13,1

•

N

D

= 5,26

•

D

min

= 1,0 m

p

=

1,2

∗(65,0+27,5)+1,1∗(5,43+412,5)

5,5

∗3,0

=34,5[kPa ]

Q

f

=(1+0,3

B

L

)∗N

c

∗c

u

(r )

+(1+1,5∗

B

L

)∗N

d

∗

ρ

D

(r )

∗g∗D

min

+(1 0,25∗

B
L

)∗N

B

∗

ρ

B

(r )

∗g∗L

(1+0,3∗

3,0
5,5

)∗13,1∗32,4+(1+1,5∗

3,0
5,5

)∗5,26∗18,9∗10∗1,0+(1 0,25∗

3,0
5,5

)

*

1,04

∗19,35∗10∗3,0

= (493,89+ 1807,52+521,39) = 2822,8 [kPa]

p

<0,81 Q

f

=2258,24 [kPa]

34,5 [kPa]< 2258,24 [kPa] warunek spełniony

7. Wyznaczenie momentów bezwładno

ś

ci mas

układu wzgl

ę

dem

płaszczyzn i osi głównych

Momenty bezwładno

ś

ci mas wzgl

ę

dem płaszczyzn głównych wyznaczono ze

wzorów :

a) dla prostopadło

ś

cianu b) dla walca

θ

xy

(i)

=M ∗(

h

(i)

2

12

+z

(i)

2

)

θ

xy

(i)

=M ∗(

d

(i)

2

16

+z

(i)

2

)

θ

xz

(i)

=M ∗(

b

(i)

2

12

+ y

(i)

2

)

θ

xz

(i)

=M ∗(

d

(i)

2

16

+ y

(i)

2

)

θ

yz

(i)

=M ∗(

l

(i )

2

16

+x

(i)

2

)

θ

yz

(i)

=M ∗(

l

(i )

2

12

+x

(i )

2

)

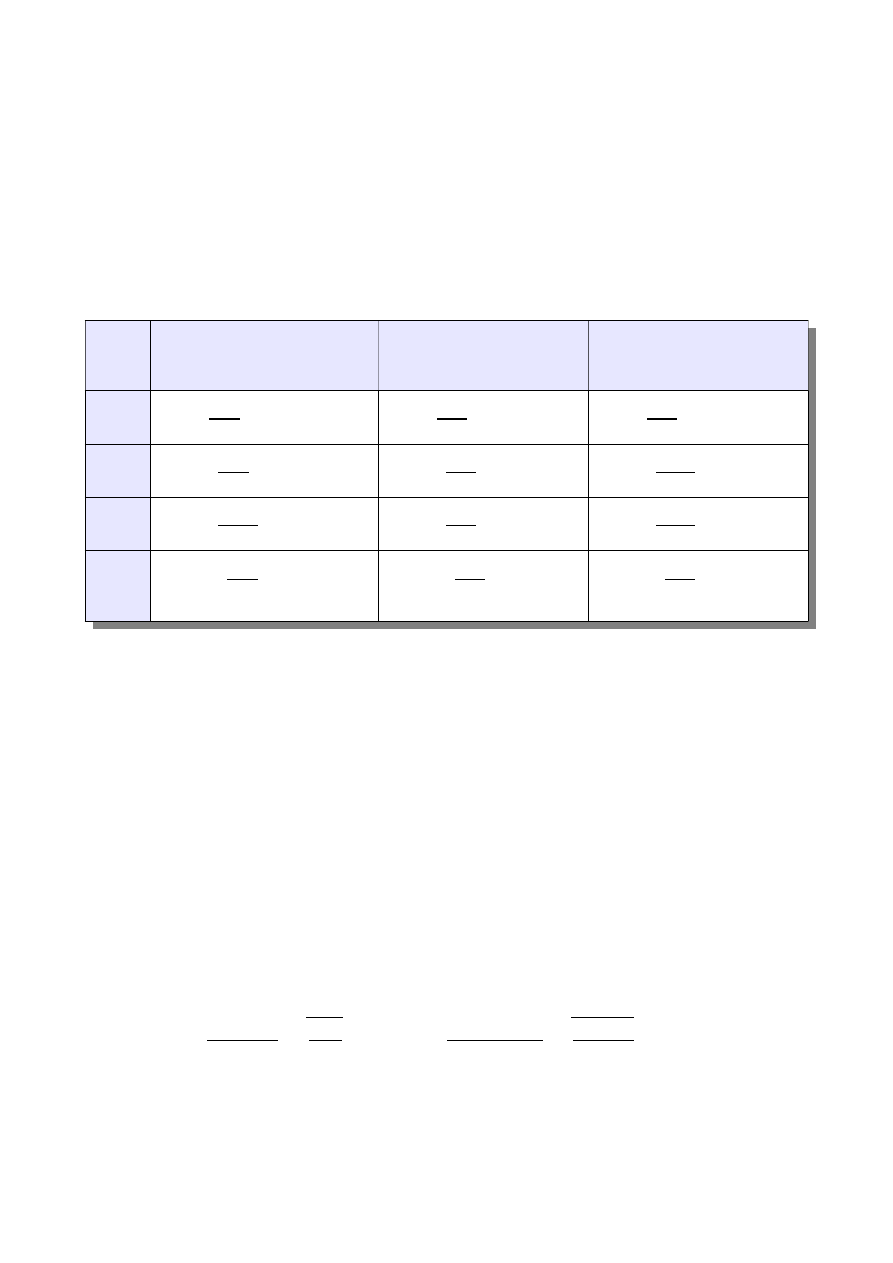
m

1

=(x

1,

y

1,

z

1

)=(0,605 ;0 ;0,935)

m

2

=(x

2,

y

2,

z

2

)=(1,17 ;0 ;0,935)

m

3

=(x

3,

y

3,

z

3

)=(1,17 ; 0 ;0,335)

m

4

=( x

4,

y

4,

z

4

)=(0 ;0 ;0,215)

Eleme

nt

θ

xy

[ Mg∗m

2

]

θ

xz

[Mg∗m

2

]

θ

yz

[ Mg∗m

2

]

Silnik

6,5

∗(

1,2

2

16

+0,935

2

)=6,26

6,5

∗(

1,2

2

16

+0

2

)=0,585

6,5

∗(

1,5

2

12

+0,585

2

)=3,59

Pompa

2,75

∗(

1,0

2

16

+0,935

2

)=2,57

2,75

∗(

1,0

2

16

+0

2

)=0,17

2,75

∗(

1,25

2

12

+1,17

2

)=4,12

Cokół

0,54

∗(

0,10

2

12

+0,335

2

)=0,06

0,54

∗(

1,2

2

12

+0

2

)=0,065

0,54

∗(

1,45

2

12

+1,17

2

)=0,84

Funda

m-ent

41,25

∗(

1,0

2

12

+0,215

2

)=5,34

41,25

∗(

3,0

2

12

+0

2

)=30,93

41,25

∗(

5,5

2

12

+0

2

)=103,98

Σ

θ

x

,

y

=14,23[Mg∗m

2

]

Σ

θ

x

,

z

=31,75[Mg∗m

2

]

Σ

θ

y

,

z

=112,55[ Mg∗m

2

]

θ

x

=θ

xy

+θ

xz

=14,23+31,75=45,98[ Mg∗m

2

]

θ

y

=θ

xy

+θ

yz

=14,23+112,55=126,78[ Mg∗m

2

]

θ

z

=θ

xz

+θ

yz

=31,75+112,55=144,3[ Mg∗m

2

]

8. Dynamiczne współczynniki podatno

ś

ci podło

ż

a gruntowego

8.1 Współczynnik spr

ęż

ystego równomiernego pionowego ugi

ę

cia

C

0

=18,4 [MPa /m]

C

z

=C

0

∗[1,0+

2

∗(a+b)

∆∗F

]∗

√

p

0,02

=18,4∗[1,0+

2

∗(5,5+3,0)

1,0

∗5,5∗3,0

]∗

√

0,03045

0,02

=49,0[MPa / m]

8.2 Współczynnik spr

ęż

ystego równomiernego poziomego przesuwu

C

x

=0,70∗C

z

=0,70∗49,0=34,34 [Mpa / m]

8.3Współczynnik spr

ęż

ystego nierównomiernego pionowego ugi

ę

cia

w płaszczy

ź

nie podłu

ż

nej

C

ϕ

xz

=C

0

∗[1,0+

2

∗(a+3b)

∆∗F

]∗

√

p

0,02

=18,4∗[1,0+

2

∗(5,5+3∗3,0)

1,0

∗5,5∗3,0

]∗

√

0,03093

0,02

=66,57[ MPa /m]

w płaszczy

ź

nie poprzecznej

C

ϕ

yx

=C

0

∗[1,0+

2

∗(3a+b)

∆∗F

]∗

√

p

0,02

=18,4∗[1,0+

2

∗(3∗5,5+3,0)

1,0

∗5,5∗3,0

]∗

√

0,03093

0,02

=81,21[MPa / m]

8.4Współczynnik spr

ęż

ystego nierównomiernego poziomego przesuwu

C

ψ

=1,1∗C

z

=1,1∗49,0=53,966[MPa / m]

9.Dynamiczna sztywno

ść

podło

ż

a gruntowego

9.1 Sztywno

ść

pionowa

K

z

=C

z

∗F=49,0∗5,5∗3,0=809,49[ MN /m]=809490 [kN / m]

9.2 Sztywno

ść

pozioma

K

y

=K

x

=C

x

∗F =34,34∗5,5∗3,0=566,61[MN /m]=566610[ kN /m]

9.3 Sztywno

ść

wahadłowa

K

ϕ

xz

=C

ϕ

xz

∗I

y

=66,64∗

3,0

∗5,5

3

12

=2771,807[MN /m]=2771807 [kNm]

K

ϕ

yz

=C

ϕ

yz

∗I

x

=81,21∗

5,5

∗3,0

3

12

=1012,522 [MN / m]=1012522[kNm]

9.4 Sztywno

ść

skr

ę

tna

K

ψ

=C

ψ

∗I

0

=53,966∗(

3,0

∗5,5

3

12

+

5,5

∗3,0

3

12

)=2912,477 [MNm]=2912477 [kNm]

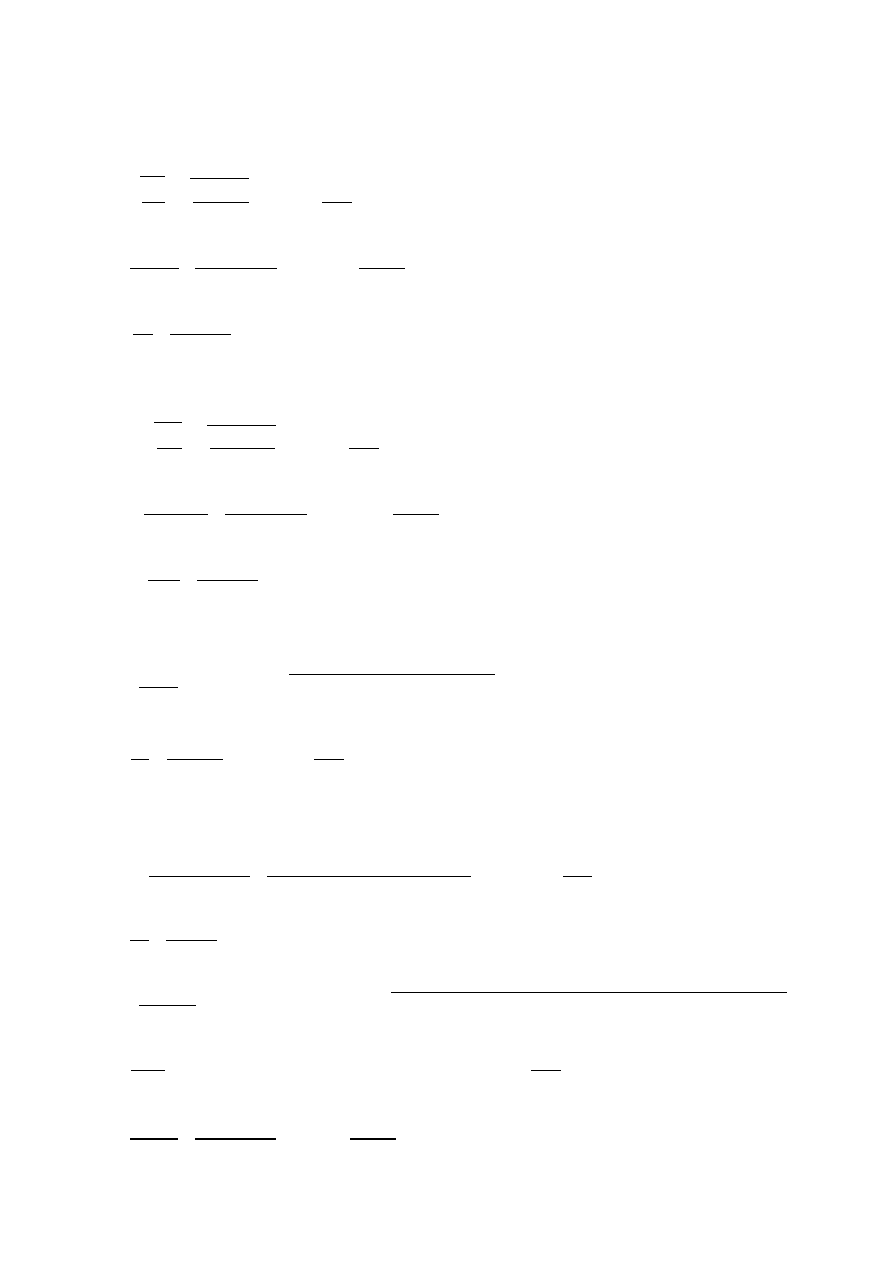
10. Okre

ś

lenie cz

ę

sto

ś

ci drga

ń

własnych układu

10.1 Pr

ę

dko

ść

k

ą

towa drga

ń

własnych pionowych

λ

z

=

√

K

z

m

=

√

809490

51,04

=126,08[

rad

s

]

n

z

=

30

∗λ

z

π

=

30

∗126,08

3,14

=1204,58[

drgań

min

]

f

z

=

n

z

60

=

1204,58

60

=20,07[ Hz ]

10.2 Drgania własne skr

ę

tne

λ

ψ

,

z

=

√

K

ψ

θ

z

=

√

2912477

144,3

=142,06 [

rad

s

]

n

ψ

,

z

=

30

∗λ

ψ

,

z

π

=

30

∗142,06

3,14

=1357,3 4 [

drgań

min

]

f

ψ

,

z

=

n

ψ

,

z

60

=

1357,34

60

=22,62[ Hz]

10.3 Drgania w płaszczy

ź

nie podłu

ż

nej

λ

1,2

2

=

1

2

∗δ

y

∗(λ

x

2

+λ

ϕ

2

,

xz

±

√

(λ

x

2

+λ

ϕ

2

,

xz

)

2

4

δ

y

∗λ

x

2

∗λ

ϕ

2

,

xz

)

λ

x

2

=

k

x

m

=

566610

51,04

=11127,45[

rad

s

]

2

θ

Y

=θ

y

+m∗h

2

=126,78+51,04∗0,715

2

=152,877[Mgm

2

]

λ

ϕ

2

,

xz

=

K

ϕ

xz

m

∗g∗h

θ

Y

=

2771807 51,04

∗10∗0,715

152,87

=18140,08[

rad

s

]

2

δ

y

=

θ

y

θ

Y

=

126,78
152,87

=0,83

λ

1,2

2

=

1

2

∗0,83

∗(11127,45+18140,08±

√

(11127,45+18140,08)

2

4

∗0,83∗11127,45∗18140,08)

λ

1

2

=

1

1,66

∗(29267,53+15843,92)=27175,57 ⇒λ

1

=164,85[

rad

s

]

n

1

=

30

∗λ

1

π

=

30

∗164,85

3,14

=1575,0 [

drgań

min

]

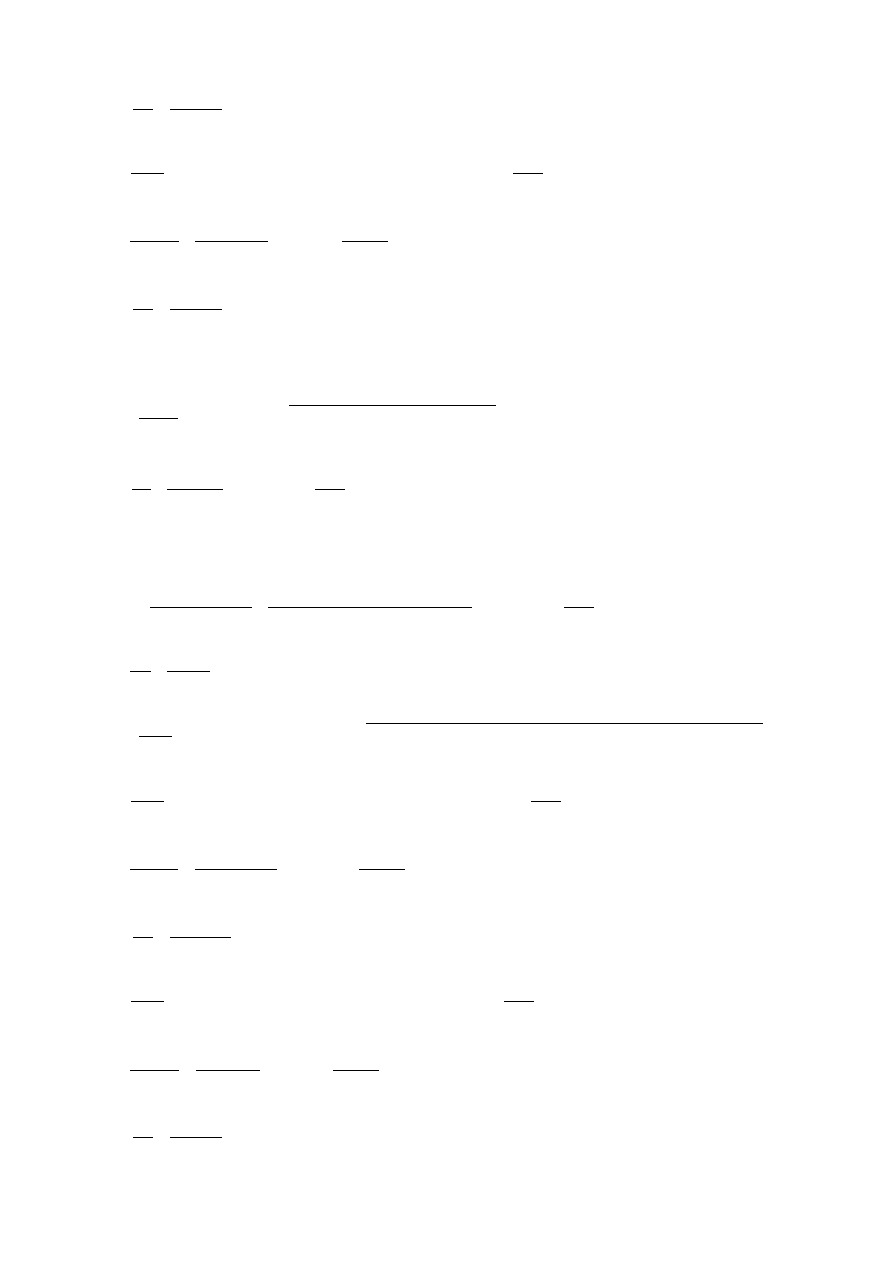
f

1

=

n

1

60

=

1575,0

60

=26,25[ Hz ]

λ

2

2

=

1

1,66

∗(29267,53 15843,92)=8086,51⇒ λ

2

=89,92[

rad

s

]

n

2

=

30

∗λ

2

π

=

30

∗89,92

3,14

=859,15[

drgań

min

]

f

2

=

n

2

60

=

864,85

60

=14,31[ Hz]

10.4 Drgania w płaszczy

ź

nie poprzecznej

λ

3,4

2

=

1

2

∗δ

x

∗(λ

y

2

+λ

ϕ

2

,

yz

±

√

(λ

y

2

+λ

ϕ

2

,

yz

)

2

4

δ

x

∗λ

y

2

∗λ

ϕ

2

,

yz

)

λ

y

2

=

k

y

m

=

566610

51,04

=11127,45[

rad

s

]

2

θ

X

=θ

x

+m∗h

2

=45,98+51,04∗0,715

2

=71,97[ Mgm

2

]

λ

ϕ

2

,

yz

=

K

ϕ

yz

m

∗g∗h

θ

X

=

1012522 51,04

∗10∗0,715

71,97

=14063,59[

rad

s

]

2

δ

x

=

θ

x

θ

X

=

45,98
71,97

=0,63

λ

3,4

2

=

1

1,26

∗(11127,45+14063,59±

√

(11127,45+14063,59)

2

4

∗0,63∗11127,45∗14063,59)

λ

3

2

=

1

1,26

∗(25191,04+15499,32)=32293,93⇒ λ

3

=179,70[

rad

s

]

n

3

=

30

∗λ

3

π

=

30

∗179,70

3,14

=1717,09[

drgań

min

]

f

3

=

n

3

60

=

1717,09

60

=28,61[ Hz ]

λ

4

2

=

1

1,26

∗(25195,61 15502,61)=7691,84⇒ λ

4

=87,7 [

rad

s

]

n

4

=

30

∗λ

4

π

=

30

∗87,7

3,14

=837,98 [

drgań

min

]

f

4

=

n

4

60

=

837,98

60

=13,96[ Hz ]

n

1

1575,0

[

drgań

min

]

f

1

26,25

[Hz ]

n

2

859,15

[

drgań

min

]

f

2

14,31

[ Hz ]

n

3

1717,09

[

drgań

min

]

f

3

28,61

[Hz ]

n

4

837,98

[

drgań

min

]

f

4

13,96

[ Hz ]

n

ψ

752,10

[

drgań

min

]

f

ψ

12,53

[ Hz ]

n

z

1204,58

[

drgań

min

]

f

z

20,07

[Hz ]

11. Obliczanie amplitudy drga

ń

Obroty maszyn w zakresie n = 200 ÷ 3000

w zwi

ą

zku z tym dla ka

ż

dej cz

ę

stotliwo

ś

ci istnieje mo

ż

liwo

ść

wyst

ą

pienia

rezonansu.
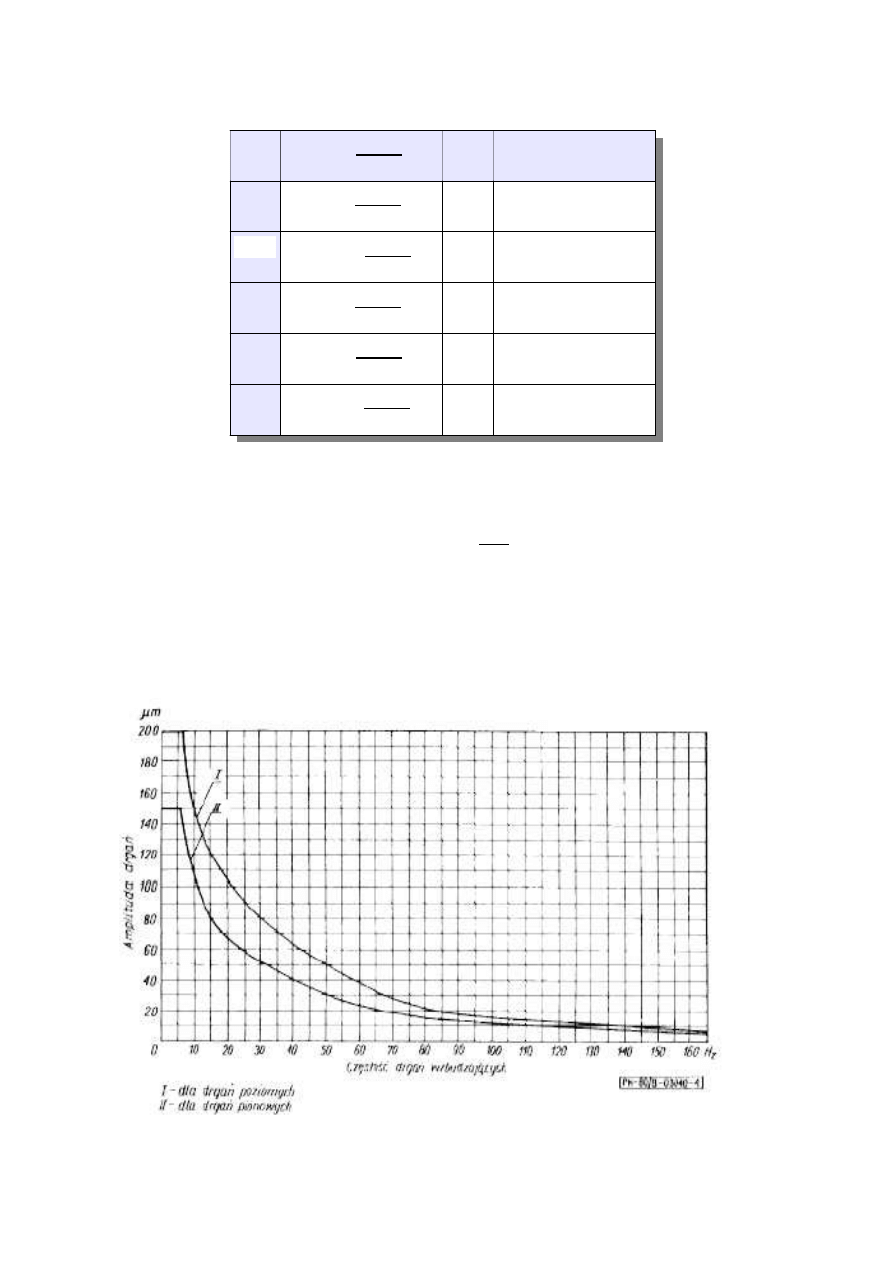
Dopuszczalne amplitudy drga

ń

wyznaczono na podstawie wykresu:

[

obr

min

]

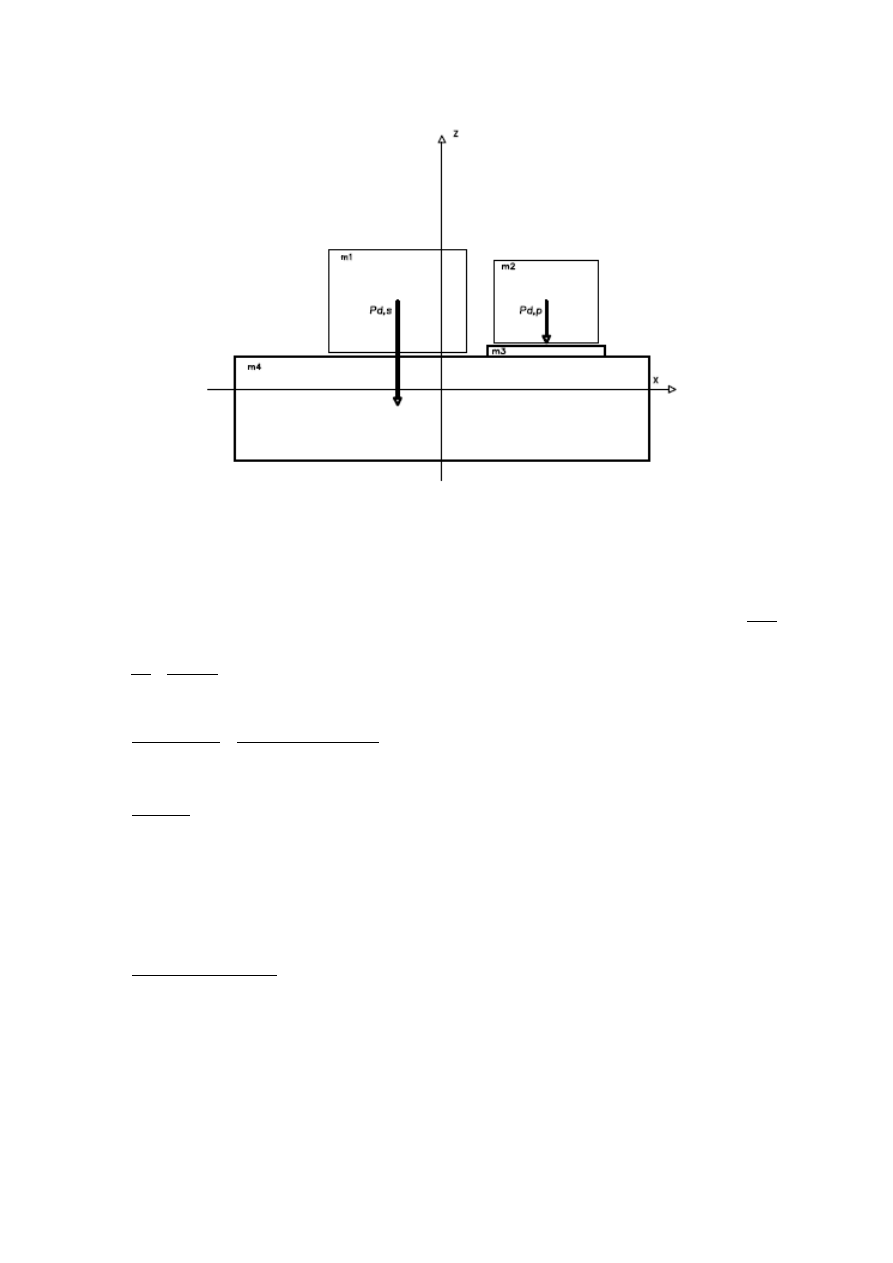
11.1 Przypadek 1: siły wzbudzaj

ą

ce działaj

ą

pionowo (zwroty zgodne)

P

z

=P

d , s

+P

d , p

=6,5+2,75=9,25[ kN ]

M

y

= P

d , s

∗e

s

+P

d , p

∗e

p

= 6,5∗0,605+2,75∗1,17= 0,715 [kNm]

Siły działaj

ą

ce z cz

ę

sto

ś

ci

ą

równ

ą

pr

ę

dko

ś

ci obrotowej maszyny n

m

= 800

η

z

=

ω

1

λ

z

=

83,77

126,08

=0,66

A

z

=

P

z

K

z

∗(1 η

z

2

)

=

9,25

809490

∗(1 0,66

2

)

=2,02∗10

5

[m]=20,2[µ m]

φ

y

=

M

y

∗B

x

∆

φ

y

B

x

=K

x

m

∗ω

2

=566610 51,04∗83,77

2

=208441,24[kNm]

∆

ϕ y

=m θ

y

∗(λ

1

2

ω

2

)∗(λ

2

2

ω

2

)=51,04∗126,78∗(27175,57 83,77

2

)∗(8086,51 83,77

2

)=1,4∗10

11

φ

y

=

0,715

∗208441,24

1,4

∗10

11

= 1,06∗10

6

[rad ]

A '

z

= A

z

+φ

y

∗x=20,2 1,06∗10

6

∗2,75=20,2 [µ m]<A

z

, dop

=83,0[µ m]

[

obr

min

]

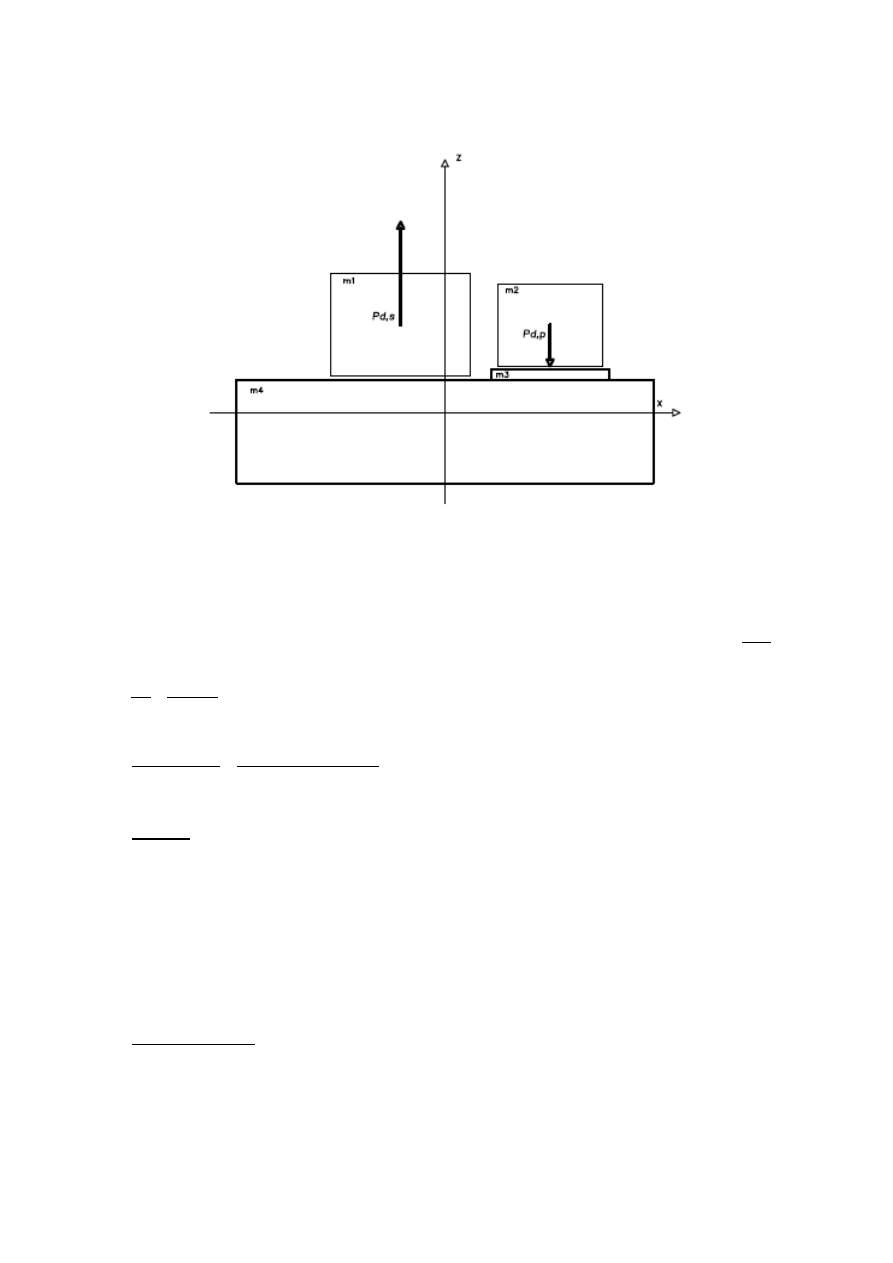
11.2 Przypadek 2: siły wzbudzaj

ą

ce działaj

ą

pionowo (zwroty przeciwne)

P

z

= P

d , s

+P

d , p

= 6,5+2,75= 3,25[ kN ]

M

y

= P

d , s

∗e

s

+P

d , p

∗e

p

=6,5∗0,605+2,75∗1,17=7,15[ kNm]

Siły działaj

ą

ce z cz

ę

sto

ś

ci

ą

równ

ą

pr

ę

dko

ś

ci obrotowej maszyny n

m

= 800

η

z

=

ω

1

λ

z

=

83,77

126,08

=0,66

A

z

=

P

z

K

z

∗(1 η

z

2

)

=

3,25

809490

∗(1 0,66

2

)

=7,11∗10

6

[m]=7,11[µ m]

φ

y

=

M

y

∗B

x

∆

φ

y

B

x

=K

x

m

∗ω

2

=566610 51,04∗83,77

2

=208441,24[kNm]

∆

ϕ y

=m θ

y

∗(λ

1

2

ω

2

)∗(λ

2

2

∗

Φ

∗ω)=51,04∗126,78

*

(27175,57 83,77

2

)∗(8086,51∗0,003∗83,77)=2,65∗10

11

φ

y

=

7,15

∗208441,24

2,65

∗10

11

=5,62∗10

6

[rad ]

A '

z

= A

z

+φ

y

∗x=7,11+5,62∗10

6

∗( 2,75)=7,11 [µ m]<A

z

, dop

=83,0 [µ m]

[

obr

min

]

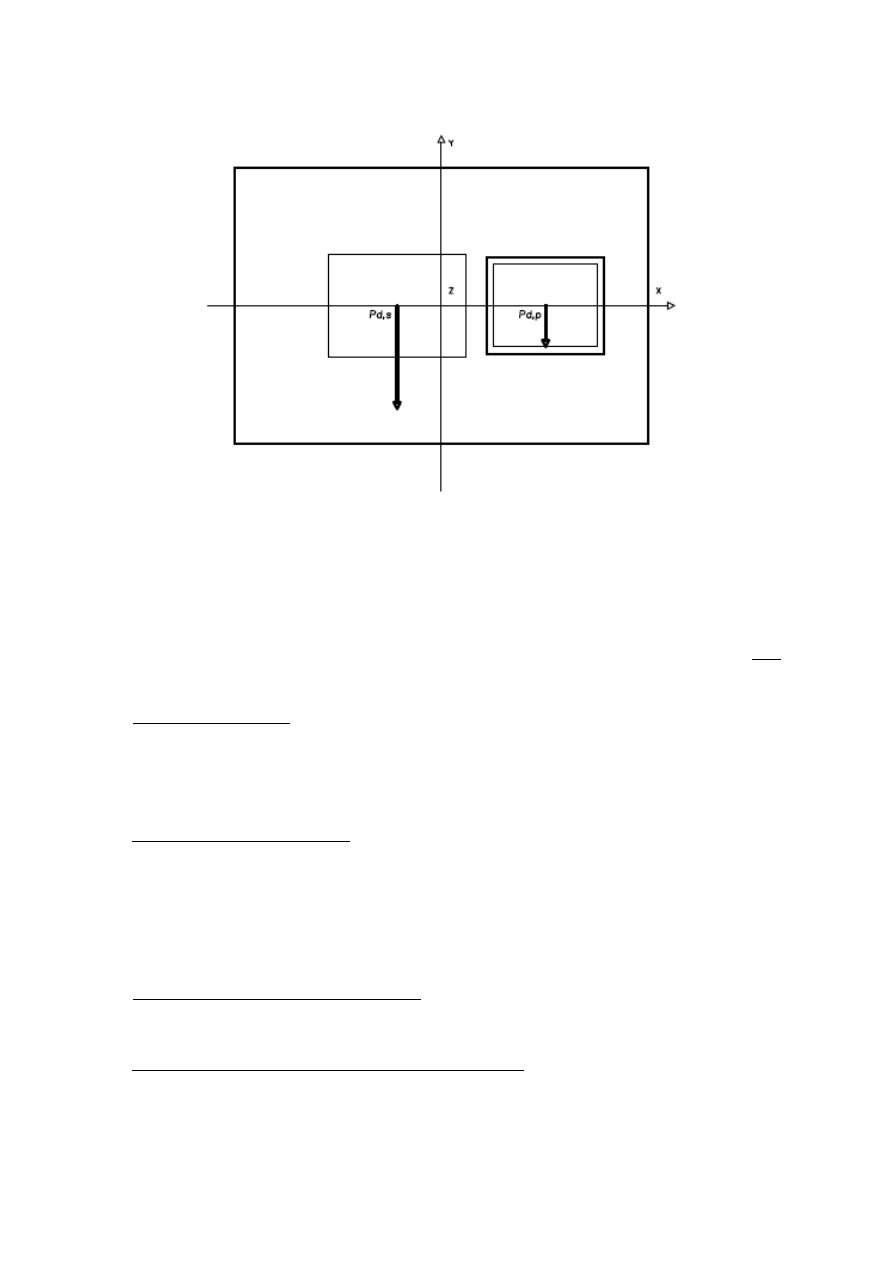
11.3 Przypadek 3: siły wzbudzaj

ą

ce działaj

ą

poziomo (zwroty zgodne)

P

z

=P

d , s

+P

d , p

=6,5+2,75=9,25[ kN ]

M

z

= P

d ,s

∗e

s

+P

d , p

∗e

p

= 6,5∗0,605+2,75∗1,17= 0,715[kNm]

M

x

=P

d , s

∗e

s

+ P

d , p

∗e

p

=6,5∗0,935+2,75∗0,935=8,64 [kNm]

Siły działaj

ą

ce z cz

ę

sto

ś

ci

ą

równ

ą

pr

ę

dko

ś

ci obrotowej maszyny n

m

= 800

A

y

=

P

y

∗B

φ x

+M

x

∗K

y

∗h

∆

φ x

B

φ x

=K

φ

yz

+K

y

∗h

2

θ

x

∗ω

2

=1012522+566610∗0,715

2

45,98

∗83,77

2

=979772,16[ kNm]

φ

x

=

M

x

∗(k

y

m

∗ω

2

)+P

y

∗K

y

∗h

∆

φ

x

∆

ϕ x

=mθ

x

∗(λ

3

2

ω

2

)∗(λ

4

2

∗

Φ

∗ω)=51,04∗45,98∗(32293,93 83,77

2

)

*

(7691,84∗0,003∗83,77)=1,14∗10

11

A

y

=

9,25

∗979772,16+8,64∗566610∗0,715

1,14

∗10

11

=1,10∗10

4

[ m]=110[µ m]

φ

x

=

8,64

∗(566610 51,04∗83,77

2

)+9,25∗566610∗0,715

1,14

∗10

11

=4,86∗10

5

[rad ]

A '

y

= A

y

+φ

x

∗z=110+(5,46∗10

5

∗0,5)=110[µ m]< A

y , dop

=125,0[µ m]

[

obr

min

]