
290
WYKŁAD Nr 23
FUNKCJE ZESPOLONE
1. FUNKCJE ZESPOLONE ZMIENNEJ RZECZYWISTEJ
Def.1.1. (funkcja zespolona zmiennej rzeczywistej)
Niech będzie dany przedział
R
⊆
T
. Funkcją zespoloną zmiennej rzeczywistej nazywamy
przyporządkowanie każdej liczbie rzeczywistej
T
t
∈ dokładnie jednej liczby zespolonej należącej do
otwartej płaszczyzny zespolonej Gaussa.
Przyjmujemy następujące oznaczenia:
T
t
t
z
z
∈
=
dla
)
(
lub też
)
(
)
(
t
jy
t
x
z
+
=
, przy czym
)
(
)
(
Im
),
(
)
(
Re
t
y
t
z
t
x
t
z
=
=
Określenie funkcji zespolonej zmiennej rzeczywistej jest równoważne z określeniem dwóch funkcji
rzeczywistych zmiennej rzeczywistej:
)
(
),
(
t
y
t
x
. Zatem badanie funkcji zespolonych zmiennej
rzeczywistej sprowadza się do badania dwóch funkcji rzeczywistych.
Uwaga
: Równość
)
(
)
(
t
jy
t
x
z
+
=
jest równoważna następującemu układowi równań:
T
t
t
y
y
t
x
x
∈
=
=
)
(
)
(
.
Jeśli jest to przedstawienie parametryczne pewnej linii na płaszczyźnie, to
)
(t
z
z
=
jest przedstawieniem
tej linii w postaci zespolonej.
Przykład: Jaką linię przedstawia równanie
π
∈
+
=
2
,
0
,
0
t
re
z
z
jt
.
Rozwiązanie:
Korzystając ze wzoru Eulera
t
j
t
e
jt
sin
cos
+
=
otrzymujemy:
(
)
t
j
t
r
jy
x
z
sin
cos
0
0
+
+
+
=
.
Zatem po grupowaniu mamy:
(
)
t
r
y
j
t
r
x
z
sin
cos
0
0
+
+
+
=
.
Równość ta odpowiada następującemu układowi:
π
∈
+
=
+
=
2
,
0
sin
cos
0
0
t
t
r
y
y
t
r
x
x
,
czyli
π
∈
=
−
=
−
2
,
0
sin
cos
0
0
t
t
r
y
y
t
r
x
x
.
Stąd podnosząc obustronnie do kwadratu i sumując otrzymane wyrażenia mamy:
(
)
(
)
t
r
t
r
y
y
x
x
2
2
2
2
2
0
2
0
sin
cos
+
=
−
+
−
, więc
(
)
(
)
2
2
0
2
0
r
y
y
x
x
=
−
+
−
.
Jest to równanie okręgu o środku w punkcie
(
)
0
0
0
, y
x
z
=
i promieniu r.
Niektóre przedstawienia parametryczne krzywych na płaszczyźnie zespolonej:
a)
Niech
Z
∈
2
1
, z
z
. Krzywa o opisie parametrycznym
(
)
t
z
z
z
t
z
1
2
1
)
(
−
+
=
dla
1
,
0
∈
t
przedstawia odcinek o początku w punkcie
1
z
i końcu w punkcie
2
z
.
b)
Niech
{ }
0
\
,
0
Z
Z
∈
∈
a
z
Linia o przedstawieniu parametrycznym
t
a
z
t
z
+
=
1
)
(
, gdzie
R
∈
t
przedstawia prostą o kierunku a i przechodzącą przez punkt
0
z
.

291
c)
Niech
0
,
,
0
>
∈
∈
r
r
z
R
Z
. Krzywa o opisie parametrycznym
jt
re
z
z
+
=
0
dla
π
∈
2
,
0
t
przedstawia dodatnio skierowany okrąg o środku w punkcie
(
)
0
0
0
, y
x
z
=
i promieniu r.
d)
Elipsa o środku
0
z
i półosiach a, b równoległych do osi Re z ma następujące przedstawienie
parametryczne:
t
jb
t
a
z
t
z
sin
cos
)
(
0
+
+
=
, gdzie
π
∈
2
,
0
t
.
Tw.1.1. (warunek konieczny i dostateczny istnienia granicy funkcji
)
(t
z
z
=
)
Na to, aby funkcja
)
(t
z
z
=
miała w punkcie
T
t
∈
0
granicę
jh
g
+
potrzeba i wystarcza, by część
rzeczywista i część urojona funkcji
)
(t
z
z
=
miały w tym punkcie odpowiednio granice g i h.
Def.1.2. (pochodna funkcji
)
(t
z
)
Pochodną funkcji zespolonej zmiennej rzeczywistej w punkcie
0
t
nazywamy granicę:
t
t
z
t
t
z
t
∆
−
∆
+
→
∆
)
(
)
(
lim
0
0
0
,
czyli
t
z
t
∆
∆
→
∆
0
lim
, a oznaczamy ją
)
(
0
t
z′
.
Tw.1.2. (o istnieniu pochodnej funkcji zespolonej zmiennej rzeczywistej)
Na to, aby funkcja
)
(t
z
z
=
miała w punkcie
T
t
∈
0
pochodną
)
(
0
t
z′
potrzeba i wystarcza, by istniały
pochodne części rzeczywistej i części urojonej tej funkcji w punkcie
0
t
. Wówczas prawdziwy jest
następujący wzór:
)
(
)
(
)
(
0
0
0
t
y
j
t
x
t
z
′
+
′
=
′
Uzasadnienie: Ponieważ
t
y
j
t
x
t
z
∆
∆
+
∆
∆
=
∆
∆
, więc istnienie pochodnej
)
(
0
t
z′
jest równoważne istnieniu
pochodnych
)
(
0
t
x′
i
)
(
0
t
y′
.
Przykład: Obliczyć
)
0
(
z′
, jeżeli
jt
e
t
z
jt
2
)
(
2
−
=
.
Rozwiązanie:
Korzystając ze wzoru Eulera:
ϕ
+
ϕ
=
ϕ
sin
cos
j
e
j
mamy:
(
)
t
t
j
t
jt
t
j
t
t
z
2
2
sin
2
cos
2
2
sin
2
cos
)
(
−
+
=
−
+
=
czyli
t
t
t
y
t
t
x
2
2
sin
)
(
,
2
cos
)
(
−
=
=
stąd
2
2
cos
2
)
(
,
2
sin
2
)
(
−
=
′
−
=
′
t
t
y
t
t
x
dla każdego t.
Zatem na podstawie Tw.1.2. otrzymujemy:
(
)
2
2
cos
2
2
sin
2
)
(
0
0
0
−
+
−
=
′
t
j
t
t
z
.
Ostatecznie dla
0
0
=
t
otrzymamy
0
)
0
(
=
′
z
Równanie stycznej do krzywej
)
(t
z
z
=
w punkcie
0
t
ma postać
t
t
z
t
z
z
⋅
′
+
=
)
(
)
(
0
0
, gdzie
R
∈
t
.
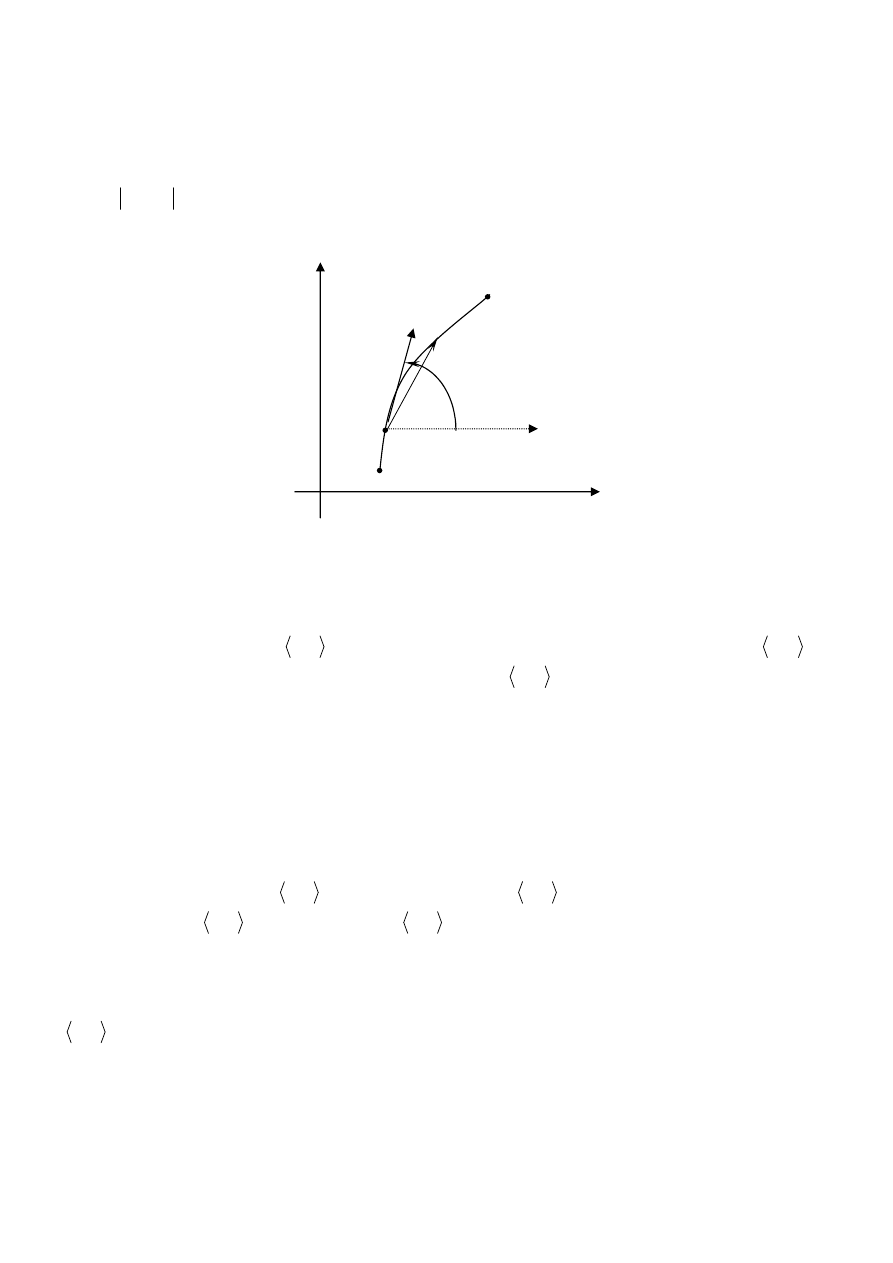
292
Interpretacja geometryczna pochodnej funkcji
)
(t
z
Jeżeli L jest gładkim łukiem, o przedstawieniu parametrycznym
T
t
t
z
z
∈
=
,
)
(
, skierowanym zgodnie ze
wzrostem parametru t, to przy założeniu
( )
0
0
≠
′ t
z
, wektor
[
]
)
(
),
(
0
0
t
y
t
x
′
′
=
s
r
jest styczny do linii L w
punkcie
)
(
0
t
z
i skierowany zgodnie z tym łukiem.
Moduł
)
(
0
t
z′
przedstawia wówczas długość wektora s
r
, a argument
)
(
Arg
0
t
z′
- zbiór wszystkich miar
łukowych kąta skierowanego, jaki wektor s
r
tworzy z osią rzeczywistą.
Rys.1. Interpretacja geometryczna pochodnej funkcji
)
(t
z
Def.1.3. (całka oznaczona funkcji zespolonej zmiennej rzeczywistej)
Niech
)
(
)
(
)
(
t
jy
t
x
t
z
+
=
,
β
α
∈
,
t
. Jeżeli funkcje
)
(
i
)
(
t
y
t
x
są całkowalne w przedziale
β
α,
to
całkę oznaczoną z funkcji zespolonej
)
(t
z
z
=
na przedziale
β
α,
definiujemy następująco:
∫
∫
∫
β
α
β
α
β
α
+
=
dt
t
y
j
dt
t
x
dt
t
z
)
(
)
(
)
(
Uwaga
: W przypadku całek oznaczonych z funkcji zespolonej zmiennej rzeczywistej wykorzystujemy
znane wzory i twierdzenia z analizy rzeczywistej.
Def.1.4. (funkcja pierwotna)
Niech
)
(
)
(
)
(
t
jy
t
x
t
z
+
=
,
β
α
∈
,
t
. Mówimy, że funkcja
Z
→
β
α,
:
W
jest funkcją pierwotną funkcji
)
(t
z
na przedziale
β
α,
, gdy dla każdego
β
α
∈
,
t
mamy
)
(
)
(
t
z
t
W
=
′
Tw.1.3. (wzór Newtona – Leibniza)
Niech
)
(
)
(
)
(
t
jY
t
X
t
W
+
=
będzie funkcją pierwotną funkcji
)
(
)
(
)
(
t
jy
t
x
t
z
+
=
ciągłej na przedziale
β
α,
. Wówczas zachodzi związek:
)
(
)
(
)
(
α
−
β
=
∫
β
α
W
W
dt
t
z
Uwaga:
Funkcje
)
(
),
(
t
Y
t
X
są funkcjami pierwotnymi odpowiednio części rzeczywistej i części urojonej
funkcji
)
(t
z
, tj. funkcji:
)
(
),
(
t
y
t
x
.
s
r
z
Im
L
)
(
0
t
z
z
Re
)
(
0
t
t
z
∆
+
z
∆
δ

293
Przykład: Obliczyć
(
)
∫
π
+
2
0
2
cos
dt
tj
t
.
Rozwiązanie:
Korzystając z Def.1.3. i Tw.1.3. mamy:
(
)
4
1
0
2
0
sin
2
sin
sin
2
cos
2
cos
2
2
2
0
2
2
0
2
0
2
0
2
0
π
+
=
−
π
+
−
π
=
+
=
+
=
+
π
π
π
π
π
∫
∫
∫
j
j
t
j
t
tdt
j
tdt
dt
tj
t
.
Ostatecznie
(
)
j
dt
tj
t
4
1
2
cos
2
2
0
π
+
=
+
∫
π
.
2. FUNKCJE ZESPOLONE ZMIENNEJ ZESPOLONEJ
Def.2.1. (funkcja zespolona zmiennej zespolonej)
Niech
Ω - pewien niepusty zbiór liczb zespolonych.
Jeżeli każdej liczbie zespolonej
Ω
∈
z
przyporządkujemy dokładnie jedną liczbę zespoloną w, to
mówimy, że w zbiorze
Ω została określona funkcja zespolona zmiennej zespolonej.
Oznaczamy
)
(z
f
w
=
dla
Ω
∈
z
lub
)
,
(
)
,
(
y
x
v
j
y
x
u
w
+
=
,
gdzie
)
(
Im
)
,
(
),
(
Re
)
,
(
,
Im
,
Re
z
f
y
x
v
z
f
y
x
u
z
y
z
x
=
=
=
=
.
Funkcję
)
,
(
y
x
u
nazywamy częścią rzeczywistą, natomiast funkcję
)
,
(
y
x
v
– częścią urojoną funkcji
)
(z
f
.
Przykład: Znaleźć część rzeczywistą i część urojoną funkcji
z
z
z
f
1
)
(
+
=
.
Rozwiązanie:
Niech
jy
x
z
+
=
, wówczas
2
2
2
2
2
2
1
1
)
(
y
x
y
j
y
x
x
y
x
jy
x
z
f
+
+
+
+
=
+
+
+
=
Stąd
+
=
+
+
=
2
2
2
2
)
,
(
1
)
,
(
y
x
y
y
x
v
y
x
x
y
x
u

294
Przykład: Dana jest para funkcji
−
=
+
=
y
x
v
y
x
u
2
. Utworzyć funkcję zespoloną
)
(z
f
o części rzeczywistej u
i części urojonej v.
Rozwiązanie:
Korzystając z Def.2.1. mamy:
(
)
y
x
j
y
x
z
f
2
)
(
−
+
+
=
.
Uwaga
:
j
z
z
y
z
z
x
2
,
2
−
=
+
=
Stąd na podstawie Uwagi:
2
2
2
2
2
2
2
2
2
2
)
(
z
z
z
z
j
z
z
j
z
z
j
z
z
z
z
j
j
z
z
z
z
z
f
−
−
+
+
−
−
+
=
−
−
+
+
−
+
+
=
Ostatecznie po przekształceniach:
z
j
z
z
f
+
+
−
=
2
3
2
1
)
(
.
Def.2.2. (granica funkcji zespolonej zmiennej zespolonej)
Niech
)
,
(
)
,
(
)
(
y
x
v
j
y
x
u
z
f
+
=
określona na zbiorze
Z
⊆
Ω
,
Ω
∈
0
z
.
Mówimy, że liczba zespolona g jest granicą właściwą funkcji
)
(z
f
w punkcie
0
0
0
jy
x
z
+
=
, gdy
=
=
⇔
=
→
→
→
g
y
x
v
g
y
x
u
g
z
f
y
x
y
x
y
x
y
x
z
z
Im
)
,
(
lim
Re
)
,
(
lim
)
(
lim
)
,
(
)
,
(
)
,
(
)
,
(
0
0
0
Def.2.3. (pochodna funkcji zespolonej zmiennej zespolonej)
Niech
)
,
(
)
,
(
)
(
y
x
v
j
y
x
u
z
f
+
=
– funkcja określona w pewnym otoczeniu Q punktu
0
z
.
Symbolem
z
∆ oznaczamy przyrost zmiennej z taki, że
Q
z
z
z
∈
∆
+
≠
∆
0
i
0
. Przyrostowi
z
∆
odpowiada przyrost
w
∆
wartości funkcji:
v
j
u
z
f
z
z
f
w
∆
+
∆
=
−
∆
+
=
∆
)
(
)
(
0
0
.
Granicę właściwą
z
z
f
z
z
f
z
∆
−
∆
+
→
∆
)
(
)
(
lim
0
0
0
nazywamy pochodną funkcji
)
(z
f
w punkcie
0
z
i oznaczamy
)
(
0
z
f ′
.
Przykład: Obliczyć na podstawie definicji pochodną funkcji
2
3
)
(
z
z
f
=
w punkcie
0
z
Rozwiązanie:
Korzystając z Def.2.3. mamy:
(
)
[
]
(
)
0
0
0
2
0
2
0
2
0
0
2
0
2
0
0
0
6
2
lim
3
2
lim
3
3
)
(
3
lim
)
(
z
z
z
z
z
z
z
z
z
z
z
z
z
z
f
z
z
z
=
∆
+
=
∆
−
∆
+
∆
+
=
∆
−
∆
+
=
′
→
∆
→
∆
→
∆
Jeśli istnieje
)
(
0
z
f ′
, to funkcja jest ciągła w punkcie
0
z
.

295
Tw.2.1. (warunek konieczny istnienia
)
(
0
z
f ′
)
Jeżeli funkcja
)
(z
f
ma w punkcie
0
0
0
jy
x
z
+
=
pochodną
)
(
0
z
f ′
, to pochodne cząstkowe
y
v
x
v
y
u
x
u
∂
∂
∂
∂
∂
∂
∂
∂
,
,
,
istnieją w punkcie
(
)
0
0
, y
x
i spełniają warunki:
(*)
x
v
y
u
y
v
x
u
∂
∂
−
=
∂
∂
∂
∂
=
∂
∂
i
Uwaga
: Równości określone wzorami (*) nazywamy WARUNKAMI CAUCHY’EGO – RIEMANNA.
Tw.2.2. (warunek wystarczający istnienia
)
(
0
z
f ′
)
Jeżeli funkcje
)
,
(
i
)
,
(
y
x
v
y
x
u
są różniczkowalne w punkcie
(
)
0
0
, y
x
oraz spełniają w tym punkcie
warunki Cauchy’ego – Riemanna, to funkcja
)
,
(
)
,
(
)
(
y
x
v
j
y
x
u
z
f
+
=
ma pochodną w punkcie
0
0
0
jy
x
z
+
=
.
Tw.2.3.
Jeżeli funkcje
)
,
(
i
)
,
(
y
x
v
y
x
u
są ciągłe w obszarze D oraz spełniają na tym obszarze warunki
Cauchy’ego – Riemanna, to funkcja
)
,
(
)
,
(
)
(
y
x
v
j
y
x
u
z
f
+
=
ma pochodną w obszarze D.
Jeżeli
)
(
0
z
f ′
istnieje dla każdego
Ω
∈
0
z
, to na zbiorze
Ω określona jest funkcja pochodna
)
(z
f ′
.
Zamiast
)
(z
f ′
piszemy często
dz
df
.
Twierdzenia o obliczaniu pochodnych
)
(z
f ′
Tw.2.4.
Jeżeli
)
(z
f
jest stała, to
0
)
(
=
′ z
f
Tw.2.5.
Jeżeli
N
∈
=
n
z
z
f
n
,
)
(
, to
1
)
(
−
⋅
=
′
n
z
n
z
f
Tw.2.6. (o działaniach arytmetycznych na pochodnych)
Jeżeli istnieją pochodne
)
(z
f ′
i
)
(z
h′
, to
1)
[
]
)
(
)
(
)
(
)
(
z
h
z
f
z
h
z
f
′
±
′
=
′
±
2)
[
]
)
(
)
(
)
(
)
(
)
(
)
(
z
h
z
f
z
h
z
f
z
h
z
f
′
⋅
+
⋅
′
=
′
⋅
3)
0
)
(
,
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
≠
′
⋅
−
⋅
′
=
′
z
h
z
h
z
h
z
f
z
h
z
f
z
h
z
f

296
Tw.2.7. (o pochodnej funkcji złożonej)
Jeżeli funkcja
)
(z
ϕ
=
ζ
ma pochodną
)
(z
ϕ′
oraz funkcja
)
(
ζ
= f
w
ma pochodną
)
(
ζ
′
f
, to funkcja
złożona
[
]
)
(
)
(
gdzie
),
(
z
f
z
F
z
F
w
ϕ
=
=
ma pochodną
)
(
)
(
)
(
z
f
z
F
ϕ′
⋅
ζ
′
=
′
.
Def.2.4. (pochodna rzędu n+1)
Pochodną rzędu n+1 funkcji
)
(z
f
definiujemy jako
(
)
( )
( )
z
z
f
z
z
f
z
f
n
n
z
n
∆
−
∆
+
=
→
∆
+
)
(
)
(
lim
)
(
0
1
.
Def.2.5. (funkcja holomorficzna w punkcie)
Funkcję zmiennej zespolonej
)
(z
f
nazywamy funkcją holomorficzną w punkcie
0
z
, jeżeli ma pochodną
)
(z
f ′
w pewnym otoczeniu Q punktu
0
z
.
Def.2.6. (funkcja holomorficzna w obszarze)
Jeżeli funkcja
)
(z
f
jest holomorficzna w każdym punkcie obszaru D, to mówimy, że jest holomorficzna
w tym obszarze.
Uwaga
: Holomorficzność w obszarze oznacza istnienie pochodnej w każdym punkcie tego obszaru.
Tw.2.8
Jeżeli funkcja
)
(z
f
jest holomorficzna w obszarze D, funkcje
)
,
(
i
)
,
(
y
x
v
y
x
u
posiadają ciągłe
pochodne cząstkowe rzędu drugiego w D, to funkcje te spełniają równania
(**)
0
i
0
2
2
2
2
2
2
2
2
=
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
y
v
x
v
y
u
x
u
Def.2.7. (funkcja harmoniczna)
Funkcję rzeczywistą dwóch zmiennych
)
,
(
y
x
g
nazywamy funkcją harmoniczną, jeżeli spełnia
równanie Laplace’a
:
0
2
2
2
2
=
∂
∂
+
∂
∂
y
g
x
g
.
Uwaga
: Z Tw.2.8. i Def.2.7. wynika, że część rzeczywista i część urojona funkcji holomorficznej na
pewnym obszarze są funkcjami harmonicznymi na tym obszarze.
Przykład:
Znaleźć funkcję holomorficzną
)
(z
f
, jeśli jej część rzeczywista
y
e
x
y
x
u
x
cos
2
)
,
(
−
=
.
Rozwiązanie:
Niech
)
(
Im
)
,
(
z
f
y
x
v
=
.
Jeśli funkcja
)
(z
f
jest holomorficzna w pewnym obszarze to posiada pochodną w każdym punkcie tego
obszaru, a zatem funkcje
)
,
(
i
)
,
(
y
x
v
y
x
u
spełniają w tym obszarze warunki Cauchy’ ego – Riemanna.
Stąd
y
u
x
v
x
u
y
v
∂
∂
−
=
∂
∂
∂
∂
=
∂
∂
i
.

297
Obliczamy, więc pochodne cząstkowe danej funkcji
)
,
(
y
x
u
:
(
)
y
e
y
e
x
x
u
x
x
x
cos
2
cos
2
'
−
=
−
=
∂
∂
(
)
y
e
y
e
x
y
u
x
y
x
sin
cos
2
'
−
=
−
=
∂
∂
Zatem
(1)
y
e
y
v
x
cos
2
−
=
∂
∂
i
(2)
y
e
x
v
x
sin
−
=
∂
∂
Całkujemy równanie (2) względem x i otrzymujemy:
(3)
)
(
sin
)
,
(
y
y
e
y
x
v
x
ϕ
+
−
=
,
gdzie
)
( y
ϕ
– funkcja różniczkowalna zmiennej y.
Różniczkujemy równanie (3) po y i mamy:
(4)
)
(
cos
y
y
e
y
v
x
ϕ′
+
−
=
∂
∂
Porównując (1) i (4) otrzymamy:
,
2
)
(
=
ϕ′ y
czyli
C
y
y
+
=
ϕ
2
)
(
.
Stąd
C
y
y
e
y
x
v
x
+
+
−
=
2
sin
)
,
(
Wobec tego funkcja
)
(z
f
ma postać
(
)
C
y
y
e
j
y
e
x
z
f
x
x
+
+
−
+
−
=
2
sin
cos
2
)
(
Należy teraz prawą stronę równości wyrazić przez zmienną z, gdzie
jy
x
z
+
=
.
Korzystając ze wzoru Eulera i grupowania wyrazów mamy:
(
)
(
)
Cj
e
z
Cj
e
jy
x
Cj
y
je
y
e
jy
x
z
f
z
jy
x
x
x
+
−
=
+
−
+
=
+
+
−
+
=
+
2
2
sin
cos
2
2
)
(
Ostatecznie
A
e
z
z
f
z
+
−
= 2
)
(
,
gdzie A – dowolna stała urojona, która stanowi wartość funkcji
)
(z
f
w początku układu,
)
0
(
f
A
=
.
3. FUNKCJE ELEMENTARNE ZMIENNEJ ZESPOLONEJ
Do funkcji elementarnych zaliczane są: wielomiany, funkcje wymierne, funkcja potęgowa, funkcja
wykładnicza, funkcje trygonometryczne, funkcje odwrotne do wymienionych oraz wszystkie funkcje
otrzymane w wyniku skończenie wielu superpozycji. Wielomiany i funkcje wymierne określa się dla
zmiennej zespolonej analogicznie jak dla zmiennej rzeczywistej. Pozostałe funkcje elementarne zmiennej
zespolonej wymagają zdefiniowania.

298
Funkcja wykładnicza
Dla dowolnej liczby zespolonej
jy
x
z
+
=
funkcję wykładniczą określamy następująco:
(
)
y
j
y
e
e
x
z
sin
cos
+
=
Funkcja wykładnicza zmiennej zespolonej
z
e
jest funkcją okresową o okresie
j
π
2
, bowiem zastępując
liczbę z liczbą
j
z
π
+ 2
otrzymujemy:
(
)
(
)
(
)
[
]
(
)
z
x
x
y
j
x
j
z
e
y
j
y
e
y
j
y
e
e
e
=
+
=
π
+
+
π
+
=
=
π
+
+
π
+
sin
cos
2
sin
2
cos
2
2
Funkcja logarytmiczna
Logarytmem (wieloznacznym) liczby zespolonej
0
≠
z
nazywamy każdą liczbę zespoloną
jv
u
w
+
=
spełniającą warunek
z
e
w
=
i oznaczamy symbolem Ln.
Równość
w
z
=
Ln
oznacza, że
z
e
w
=
.
Podstawiając w tej ostatniej równości
jv
u
w
+
=
oraz
(
)
ϕ
+
ϕ
=
sin
cos
j
r
z
, gdzie
z
z
r
arg
,
=
ϕ
=
,
otrzymujemy równość:
(
)
(
)
ϕ
+
ϕ
=
+
sin
cos
sin
cos
j
r
v
j
v
e
u
z której wynika, że
r
e
u
=
, czyli
z
r
u
ln
ln
=
=
(w tym przypadku ln oznacza logarytm naturalny w
dziedzinie rzeczywistej) oraz że
π
+
ϕ
=
k
v
2
, (k – dowolna liczba całkowita), czyli
z
v
Arg
=
.
Z powyższych związków otrzymujemy:
z
j
z
z
Arg
ln
Ln
+
=
Uwaga:
Logarytm zera nie istnieje, gdyż
0
≠
w
e
.
Uwaga:
Wieloznaczność Ln z wynika z wieloznaczności Arg z.
Jeśli Arg z zastąpimy argumentem głównym arg z, to otrzymamy jednoznaczną funkcję zmiennej
zespolonej z, określoną dla
0
≠
z
, którą nazywamy logarytmem głównym, a oznaczamy ln. Stąd
z
j
z
z
arg
ln
ln
+
=
Między logarytmem wieloznacznym a logarytmem głównym zachodzi związek
j
k
z
z
π
+
=
2
ln
Ln
Przykład: Obliczyć Ln z oraz ln z, jeśli
j
z
3
3
3
+
−
=
.
Rozwiązanie:
Moduł i argument główny liczby z wynoszą odpowiednio:
6
36
=
=
z
,
3
2
arg
π
=
z
.
Stąd
(
)
(
)
3
2
6
ln
3
3
3
ln
,
2
3
2
6
ln
3
3
3
Ln
π
+
=
+
−
π
+
π
+
=
+
−
j
j
k
j
j
.
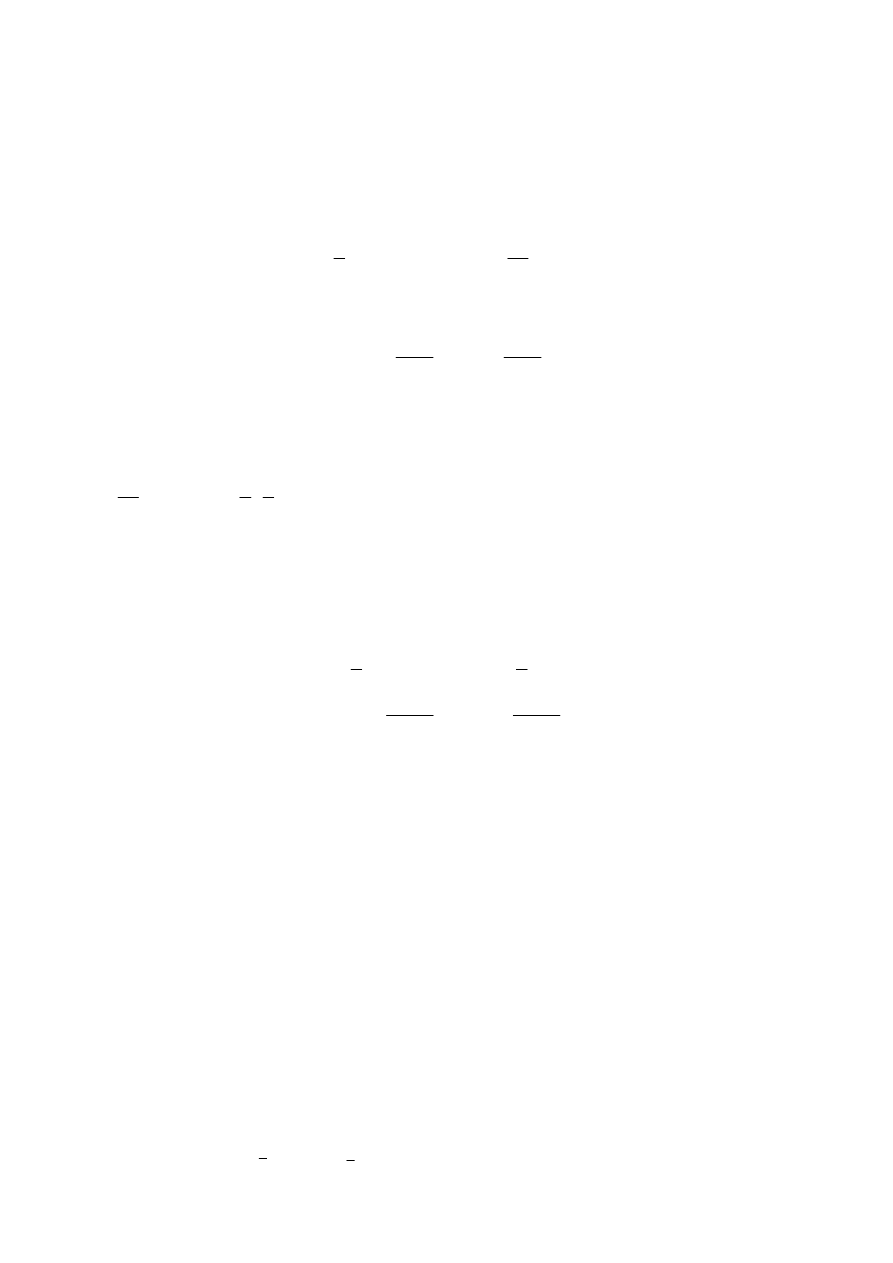
299
Związek między funkcją wykładniczą a funkcjami trygonometrycznymi
Ponieważ
z
j
z
e
jz
sin
cos
+
=
, więc zastępując z przez – z otrzymamy
z
j
z
e
jz
sin
cos
−
=
−
.
Rozwiązując układ tych dwóch równań (tj. układ
−
=
+
=
−
z
j
z
e
z
j
z
e
jz
jz
sin
cos
sin
cos
) względem
z
z
sin
,
cos
,
otrzymujemy równości:
(
)
(
)
jz
jz
jz
jz
e
e
j
z
e
e
z
−
−
−
=
+
=
2
1
sin
,
2
1
cos
Pozostałe funkcje definiujemy następująco:
z
z
z
z
z
z
sin
cos
ctg
,
cos
sin
tg
=
=
Przykład: Obliczyć
j
sin .
Rozwiązanie:
(
)
(
)
1
sinh
2
1
1
2
1
sin
1
1
1
1
⋅
=
−
⋅
−
=
−
=
−
−
j
e
e
j
e
e
j
j
.
Związek między funkcją wykładniczą a funkcjami hiperbolicznymi
Funkcje hiperboliczne definiujemy na płaszczyźnie zespolonej za pomocą funkcji wykładniczej
analogicznie jak dla zmiennej rzeczywistej.
(
)
(
)
z
z
z
z
e
e
z
e
e
z
−
−
+
=
−
=
2
1
cosh
,
2
1
sinh
z
z
z
z
z
z
sinh
cosh
ctgh
,
cosh
sinh
tgh
=
=
Funkcja potęgowa
Niech
s
z
,
będą dowolnymi liczbami zespolonymi,
0
≠
z
.
Potęgą o podstawie z i wykładniku s nazywamy każdą liczbę zespoloną określoną wzorem:
z
s
s
e
z
Ln
=
.
Potęga
s
z
ma na ogół nieskończenie wiele wartości:
(
)
j
k
s
z
s
j
k
z
s
s
e
e
e
z
π
π
+
=
=
2
ln
2
ln
, gdzie
...
,
2
,
1
,
0
±
±
=
k
Liczbę
z
s
e
ln
nazywamy wartością główną potęgi.
Uwaga:
Jeśli s – liczba całkowita to potęga ma dokładnie jedną wartość, bo wówczas
1
2
=
π
j
k
s
e
.
Przykład: Obliczyć:
( )
j
j
j
,
1
−
.
Rozwiązanie:
( )
( )
(
)
(
)
π
−
π
−
π
+
π
+
π
+
−
=
=
=
−
k
j
k
j
j
j
k
j
j
e
e
e
2
2
1
ln
2
1
ln
1
(
)
π
−
π
−
π
+
π
+
π
+
=
=
=
k
j
k
j
j
j
k
j
j
j
e
e
e
j
2
2
2
2
1
ln
2
ln

300
Ostatecznie:
( )
π
−
π
−
=
−
k
j
e
2
1
,
π
−
π
−
=
k
j
e
j
2
2
.
4.CAŁKA FUNKCJI ZMIENNEJ ZESPOLONEJ
Def.4.1. (funkcja pierwotna)
Jeśli w obszarze D jest dana holomorficzna funkcja f zmiennej zespolonej z, to każdą funkcję F zmiennej
z
, która w obszarze D ma pochodną równą funkcji f
D
z
z
f
z
F
∈
=
′
)
(
)
(
nazywamy funkcją pierwotną funkcji f w obszarze D.
Def.4.2. (całka nieoznaczona funkcji f w obszarze D)
Jeśli F jest funkcją pierwotną funkcji f w obszarze D, to wyrażenie
∫
∈
+
=
D
z
C
z
F
dz
z
f
)
(
)
(
gdzie C – dowolna stała zespolona, nazywamy całką nieoznaczoną funkcji f w obszarze D.
Uwaga
: Całki nieoznaczone funkcji elementarnych zmiennej zespolonej oblicza się według tych samych
reguł co całki tych samych funkcji zmiennej rzeczywistej.
Przykład: Obliczyć
(
)
∫
−
dz
z
z
A
n
0
, gdzie
0
,
oraz
1
z
A
n
−
≠
– stałe zespolone.
Rozwiązanie:
Jeśli n – liczba całkowita,
const
z
const
A
n
=
=
−
≠
0
,
oraz
1
, to
(
)
(
)
C
z
z
n
A
dz
z
z
A
n
n
+
−
+
=
−
+
∫
1
0
0
1
.
Obszarem istnienia tej całki jest cała płaszczyzna zespolona, gdy
...
,
2
,
1
,
0
=
n
, względnie płaszczyzna
bez punktu
0
z
, gdy
...
,
4
,
3
,
2
−
−
−
=
n
Def.4.3. (całka funkcji
)
(z
f
wzdłuż łuku AB )
Niech
)
(z
f
będzie funkcją holomorficzną zmiennej zespolonej określoną na zwykłym łuku skierowanym
AB
, o przedstawieniu parametrycznym
β
α
∈
=
,
),
(
t
t
z
z
, zgodnym z kierunkiem tego łuku.
Przedział
β
α,
dzielimy na n podprzedziałów za pomocą punktów
k
t
,
n
k
...,
,
1
,
0
=
, takich, że
β
=
<
<
<
<
=
α
−
n
n
t
t
t
t
1
1
0
...
.
Oznaczamy
)
(
k
k
t
z
z
=
,
n
k
...,
,
1
,
0
=
oraz
1
−
−
=
∆
k
k
k
z
z
z
,
n
k
...,
,
2
,
1
=
.
Na każdym łuku
AB
z
z
k
k
⊂
−
1
wybieramy punkt
k
ζ ,
n
k
...,
,
2
,
1
=
i tworzymy sumę całkową
∑
=
∆
ζ
=
n
k
k
k
n
z
f
S
1
)
(
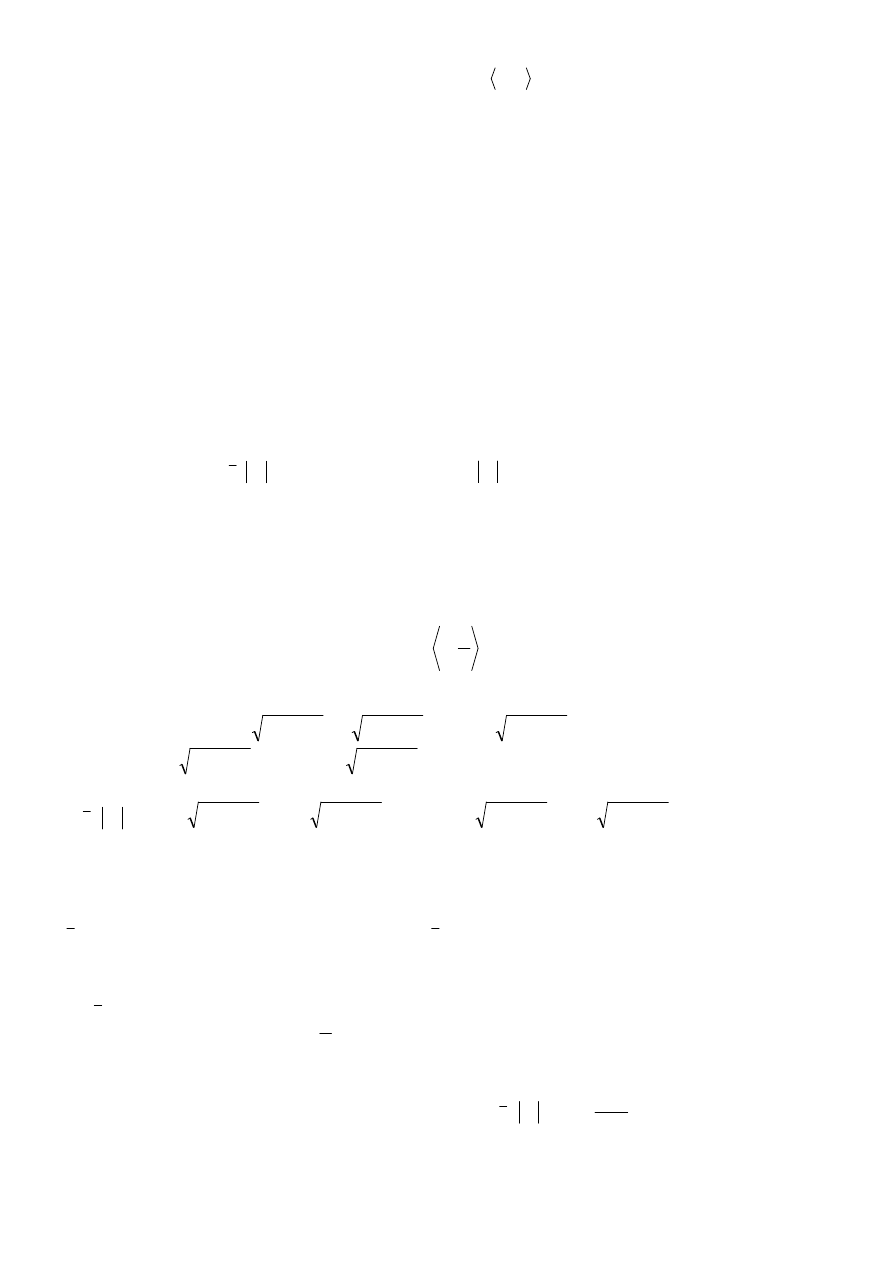
301
Jeśli dla każdego normalnego ciągu podziałów przedziału
β
α,
ciąg sum całkowych
n
S
jest zbieżny do
tej samej granicy skończonej, niezależnie od wyboru punktów
k
ζ , to tę granicę nazywamy całką funkcji
)
(z
f
wzdłuż łuku AB i oznaczamy symbolem
∫
AB
dz
z
f
)
(
Tw.4.1.
Jeżeli
)
(
Im
)
,
(
),
(
Re
)
,
(
z
f
y
x
v
z
f
y
x
u
=
=
to całka
∫
AB
dz
z
f
)
(
istnieje wtedy i tylko wtedy, gdy istnieją
całki krzywoliniowe skierowane
∫
∫
+
−
AB
AB
y
d
u
dx
v
y
d
v
dx
u
oraz
, przy czym
∫
∫
∫
+
+
−
=
AB
AB
AB
dy
u
dx
v
j
dy
v
dx
u
dz
z
f
)
(
Przykład: Obliczyć
∫
⋅
AB
dz
z
z
, gdzie AB – łuk okręgu
R
z
=
zawartym między punktami
R
z
=
oraz
j
R
z
=
.
Rozwiązanie:
Łuk AB jest łukiem okręgu o środku w początku układu współrzędnych i promieniu R leżącym w
pierwszej ćwiartce układu współrzędnych, skierowanym dodatnio.
Równanie tego okręgu
2
,
0
,
sin
cos
)
(
π
∈
+
=
t
t
jR
t
R
t
z
, czyli
t
R
t
y
t
R
t
x
sin
)
(
,
cos
)
(
=
=
.
Niech
jy
x
z
+
=
.
Wówczas
(
)
(
)
2
2
2
2
2
2
)
(
y
x
y
j
y
x
x
y
x
jy
x
z
f
+
−
+
+
=
+
−
=
.
Stąd
2
2
2
2
)
,
(
,
)
,
(
y
x
y
y
x
v
y
x
x
y
x
u
+
−
=
+
=
.
dy
y
x
x
dx
y
x
y
j
dy
y
x
y
dx
y
x
x
dz
z
z
AB
AB
AB
2
2
2
2
2
2
2
2
+
+
+
−
+
+
+
+
=
⋅
∫
∫
∫
Korzystając z twierdzenia o zamianie całki krzywoliniowej skierowanej na całkę oznaczoną mamy
(
)
[
]
(
)
[
]
=
⋅
⋅
+
−
⋅
⋅
−
+
⋅
⋅
+
−
⋅
⋅
∫
∫
π
π
2
0
2
0
cos
cos
sin
sin
cos
sin
sin
cos
dt
t
R
R
t
R
t
R
R
t
R
j
dt
t
R
R
t
R
t
R
R
t
R
(
)
2
cos
sin
3
2
0
2
2
3
π
⋅
=
+
=
∫
π
R
j
dt
t
t
R
j
Ostatecznie powyższa całka po wskazanym łuku wynosi:
2
3
R
j
dz
z
z
AB
π
=
⋅
∫
.

302
Uwaga
: Jeśli całka
∫
AB
dz
z
f
)
(
istnieje to mówimy, że
)
(z
f
jest całkowalna wzdłuż łuku AB.
Własności całki
∫
AB
dz
z
f
)
(
Jeśli funkcje
)
(
i
)
(
z
h
z
f
są całkowalne wzdłuż łuku AB, k – dowolna stała, to
1)
∫
∫
=
AB
AB
dz
z
f
k
dz
z
f
k
)
(
)
(
,
2)
[
]
∫
∫
∫
+
=
+
AB
AB
AB
dz
z
h
dz
z
f
dz
z
h
z
f
)
(
)
(
)
(
)
(
.
Tw.4.2. (o zamianie całki na całkę oznaczoną)
Jeżeli funkcja
)
(z
f
jest ciągła na zwykłym łuku gładkim
{
}
β
α
∈
=
=
,
),
(
:
t
t
z
z
z
AB
, skierowanym
zgodnie ze wzrostem parametru t, to
[
]
∫
∫
β
α
′
⋅
=
dt
t
z
t
z
f
dz
z
f
AB
)
(
)
(
)
(
Uwaga
: Jeśli łuk AB jest zamknięty (A = B), czyli krzywa jest krzywą Jordana, to oznaczamy go jedną
literą C i zamiast
∫
AB
dz
z
f
)
(
piszemy zwykle
∫
C
dz
z
f
)
(
.
Przykład: Obliczyć
(
)
∫
−
C
n
z
z
dz
0
, gdzie C – okrąg
R
z
z
=
−
0
skierowany dodatnio, n – liczba całkowita.
Rozwiązanie:
Równanie okręgu o środku w punkcie
0
z
i promieniu R zapisujemy następująco:
π
∈
+
=
2
,
0
,
0
t
e
R
z
z
jt
zatem
jt
e
jR
t
z
=
′ )
(
.
Stąd
(
)
(
)
∫
∫
∫
π
−
−
π
=
=
−
2
0
1
1
2
0
0
dt
e
R
j
dt
e
R
e
jR
z
z
dz
t
n
j
n
jnt
n
jt
C
n
Dla
1
≠
n
mamy:
(
)
(
)
0
1
1
)
1
(
1
)
1
(
1
2
0
)
1
(
1
2
0
1
1
=
−
−
=
−
=
−
π
=
=
−
−
π
−
−
∫
n
t
t
t
n
j
n
t
n
j
n
R
n
n
j
e
R
j
dt
e
R
j
Dla
1
=
n
mamy:
(
)
π
⋅
=
=
=
∫
∫
∫
π
π
π
−
−
2
2
0
2
0
0
0
2
0
1
1
j
dt
j
dt
e
R
j
dt
e
R
j
t
n
j
n
.
Ostatecznie
(
)
≠
=
π
=
−
∫
1
dla
0
1
dla
2
0
n
n
j
z
z
dz
C
n
.

303
Uwaga
: Całka funkcji ciągłej wzdłuż łuku kawałkami gładkiego istnieje i równa się sumie całek wzdłuż
gładkich części tego łuku.
Tw.4.3. (o module całki)
Jeżeli funkcja
)
(z
f
jest ciągła na kawałkami gładkim łuku zwykłym AB, to
ML
dz
z
f
AB
≤
∫
)
(
gdzie L – długość łuku AB, natomiast
)
(
sup
z
f
M
AB
=
Tw.4.4. (podstawowe tw. Cauchy’ego)
Jeżeli funkcja
)
(z
f
jest holomorficzna w obszarze jednospójnym D, a C jest kawałkami gładką krzywą
Jordana zawartą w tym obszarze, to
0
)
(
=
∫
C
dz
z
f
Wnioski z podstawowego twierdzenia Cauchy’ego
Wniosek 1: Jeżeli funkcja
)
(z
f
jest holomorficzna w obszarze jednospójnym D, to całka
∫
AB
dz
z
f
)
(
wzdłuż kawałkami gładkiego łuku
D
AB
⊂
nie zależy od kształtu tego łuku, a jedynie od
punktów A i B.
Zamiast
∫
AB
dz
z
f
)
(
możemy zapisać
B
z
A
z
dz
z
f
z
z
=
=
∫
2
1
,
gdzie
,
)
(
2
1
.
Wniosek 2: Jeżeli funkcja
)
(z
f
jest holomorficzna w obszarze jednospójnym D,
)
(z
F
jest funkcją
pierwotną funkcji
)
(z
f
na tym obszarze oraz
D
z
z
∈
2
1
,
, to
)
(
)
(
)
(
1
2
2
1
z
F
z
F
dz
z
f
z
z
−
=
∫
.
Wniosek 3: Jeżeli funkcja
)
(z
f
jest holomorficzna w obszarze jednospójnym D z wyjątkiem punktów
n
z
z
...,
,
1
należących do wnętrza kawałkami gładkiej krzywej Jordana
D
C
⊂
, to
∑ ∫
∫
=
=
n
k
K
C
k
dz
z
f
dz
z
f
1
)
(
)
(
,
gdzie
k
K
– okrąg o środku
n
k
z
k
...,
,
1
,
=
zawarty we wnętrzu krzywej C i o promieniu na
tyle małym, żeby
0
/
≠
∩
i
k
K
K
dla
n
i
k
i
k
...,
,
2
,
1
,
,
=
≠
.
Tw.4.5. (o wzorze całkowym Cauchy’ego)
Jeżeli funkcja
)
(z
f
jest holomorficzna w obszarze jednospójnym D,
D
C
⊂
jest kawałkami gładką
krzywą Jordana zawartą w tym obszarze oraz
0
z
należy do wnętrza krzywej C, to
(*)
dz
z
z
z
f
j
z
f
C
∫
−
π
=
0
0
)
(
2
1
)
(

304
Równość (*) nazywamy wzorem całkowym Cauchy’ego.
Tw.4.6.
Jeżeli funkcja
)
(z
f
jest holomorficzna w obszarze D, to ma w tym obszarze pochodną każdego rzędu,
przy czym
( )
(
)
dz
z
z
z
f
j
n
z
f
K
n
n
∫
+
−
π
=
1
0
0
)
(
2
!
)
(
dla każdego
N
∈
n
i każdego
D
z
∈
0
, gdzie K – dowolny okrąg o środku
0
z
zawarty wraz ze swym
wnętrzem w obszarze D.
Przykład: Obliczyć
(
)
∫
−
π
C
z
z
z
dz
e
j
3
1
2
1
, wiedząc, że:
a)
punkt
0
1
=
z
leży wewnątrz, a punkt
1
2
=
z
na zewnątrz krzywej C,
b)
punkt
0
1
=
z
leży na zewnątrz, a punkt
1
2
=
z
wewnątrz krzywej C,
c)
punkty
0
1
=
z
,
1
2
=
z
leżą wewnątrz krzywej C,
d)
punkty
0
1
=
z
,
1
2
=
z
leżą na zewnątrz krzywej C.
Rozwiązanie:
Funkcja podcałkowa jest holomorficzna na płaszczyźnie zespolonej z wyjątkiem punktów
0
1
=
z
,
1
2
=
z
.
Ad. a)
W tym przypadku
0
1
=
z
leży wewnątrz, a punkt
1
2
=
z
na zewnątrz krzywej C, więc
(
)
(
)
(
)
∫
∫
∫
−
−
π
=
−
π
=
−
π
1
1
0
1
2
1
1
2
1
1
2
1
3
3
3
K
z
K
z
C
z
dz
z
z
e
j
dz
z
z
e
j
z
z
dz
e
j
,
gdzie
1
K
– okrąg o środku
1
z
zawarty wraz ze swym wnętrzem we wnętrzu krzywej C.
Korzystając ze wzoru całkowego Cauchy’ego dla
(
)
3
0
1
)
(
,
0
z
e
z
f
z
z
−
=
=
mamy:
dz
z
z
f
j
f
K
∫
−
π
=
0
)
(
2
1
)
0
(
.
Zatem
(
)
(
)
(
)
1
1
0
1
2
1
1
2
1
0
3
3
3
1
=
−
=
−
−
π
=
−
π
=
∫
∫
z
z
K
z
C
z
z
e
dz
z
z
e
j
z
z
dz
e
j
Ad. b)
W tym przypadku
1
2
=
z
leży wewnątrz krzywej C, natomiast
0
1
=
z
na zewnątrz, więc
(
)
(
)
(
)
∫
∫
∫
−
π
=
−
π
=
−
π
2
2
3
3
3
1
2
1
1
2
1
1
2
1
K
z
K
z
C
z
dz
z
z
e
j
dz
z
z
e
j
z
z
dz
e
j
,

305
gdzie
2
K
– okrąg o środku
2
z
zawarty wraz ze swym wnętrzem we wnętrzu krzywej C.
Korzystając z Tw. 4.6. dla
z
e
z
f
z
z
=
=
)
(
,
1
0
,
2
=
n
otrzymamy
(
)
!
)
1
(
1
)
(
2
1
1
2
n
f
dz
z
z
f
j
K
′
′
=
−
π
∫
+
czyli
(
)
(
)
(
)
=
′
−
−
=
′
−
−
=
″
−
=
−
−
π
=
−
π
=
=
=
∫
∫
1
2
1
2
1
3
3
1
2
1
2
1
2
1
1
2
1
1
2
1
2
z
z
z
z
z
z
K
z
z
C
z
z
z
e
z
e
ze
z
e
z
dz
z
e
j
z
z
dz
e
j
(
)
(
)
2
1
2
1
2
1
1
2
1
1
1
4
2
2
e
e
z
z
z
e
z
e
z
z
e
z
z
z
z
−
=
−
=
−
−
+
−
−
=
=
Ad. c)
W tym przypadku zarówno punkt
0
1
=
z
, jak i punkt
1
2
=
z
leżą wewnątrz krzywej C, więc korzystając z
Wniosku 3 oraz poprzednich podpunktów zadania mamy
(
)
(
)
(
)
2
1
1
2
1
1
2
1
1
2
1
2
1
3
3
3
e
z
z
dz
e
j
z
z
dz
e
j
z
z
dz
e
j
K
z
K
z
C
z
−
=
−
π
+
−
π
=
−
π
∫
∫
∫
Ad. d)
Ponieważ punkty
0
1
=
z
,
1
2
=
z
leżą na zewnątrz krzywej C, więc funkcja jest holomorficzna w pewnym
obszarze jednospójnym D, a C jest kawałkami gładką krzywą Jordana zawartą w tym obszarze.
Korzystając z podstawowego twierdzenia Cauchy’ego mamy
(
)
0
1
2
1
3
=
−
π
∫
C
z
z
z
dz
e
j
.
Wyszukiwarka
Podobne podstrony:
Microsoft Word W24 Funkcje zespolone
Microsoft Word L23 funkcje zespolone
Microsoft Word W15 funkcje 2 zmiennych i ekstrema
Microsoft Word L15 funkcje 2 zmiennych i ekstrema
Microsoft Word W16 pochodne zlozone funkcji 2 zm
Zespoły neurologiczne Microsoft Word
3 funkcje zespolone Nieznany (2)
Microsoft Word W14 Szeregi Fouriera
New Microsoft Word Document (2)
Nowy Dokument programu Microsoft Word (5)
Nowy Dokument programu Microsoft Word
Nowy Dokument programu Microsoft Word
FUNKCJE ZESPOLONE 2
Microsoft Word zrodla infor I czesc pprawiona 2 do wydr
Microsoft Word PARAMETRY KOMPUTERÓW mój
PROBLEMY FUNKCJONOWANIA ZESPOŁÓW WIRTUALNYCH, Socjologia i Psychologia
więcej podobnych podstron