Wykład #5
Podstawy aksonometrii
Rzuty Monge`a, powszechnie stosowane w praktyce inżynierskiej, wymagają pewnej wprawy w odczytywaniu i
dlatego często dla uzyskania plastycznego, łatwego do odczytania obrazu używa się rzutów aksonometrycznych,
czyli aksonometrii.
Aksonometria jest odmianą rzutu równoległego ( ukośnego, bądź prostokątnego względem rzutni
aksonometrycznej ) . Polega on na odwzorowaniu za pomocą jednego rzutu równoległego, który ustala związki
miarowe zachodzące pomiędzy elementami odwzorowywanej bryły.
Ze względu na łatwość czytania aksonometrii jest ona często stosowana w praktyce np. w rysunkach
ilustrujących instrukcje obsługi, w rysunkach ofertowych, a także w szkicowaniu odręcznym.
Odwzorowanie w aksonometrii
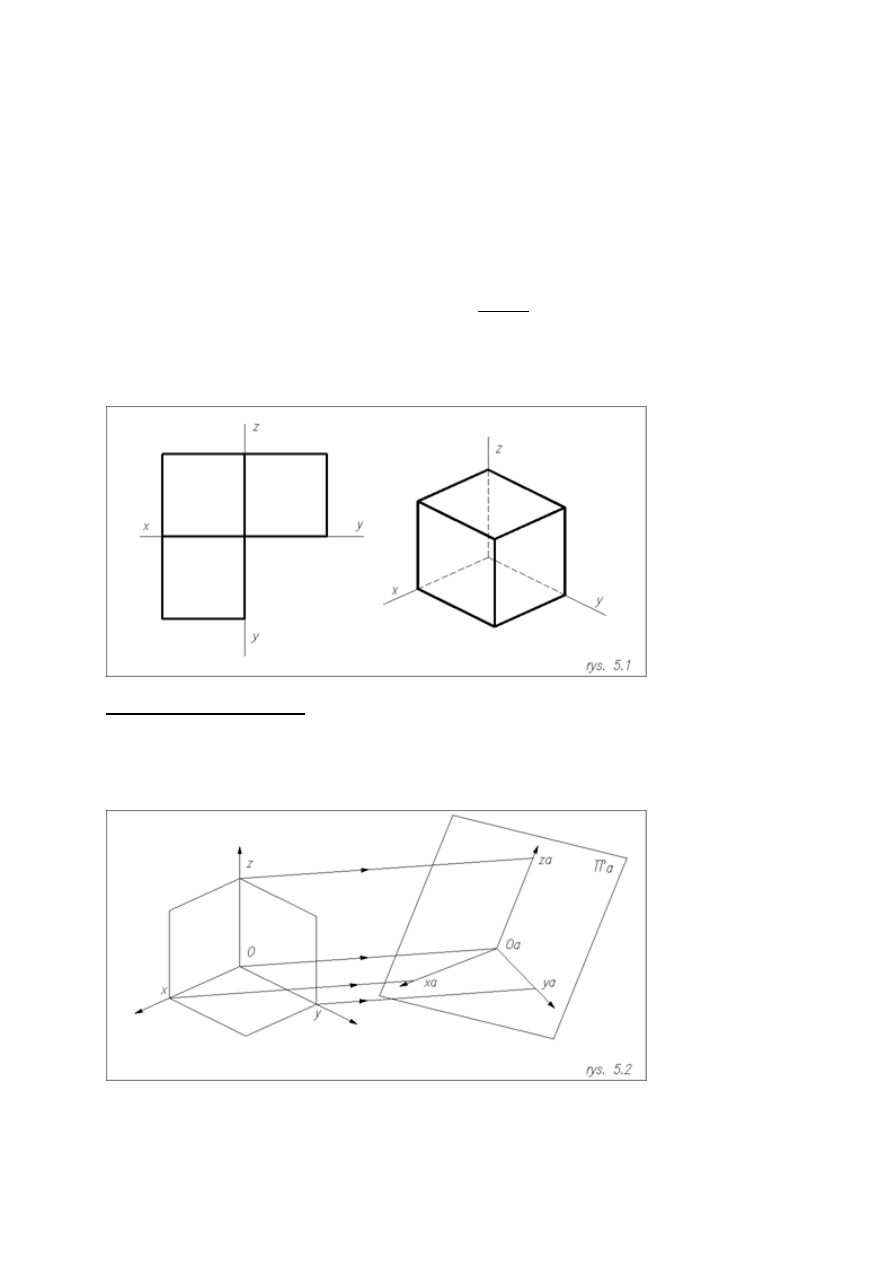
Wyobraźmy sobie znany już układ prostokątny trzech rzutni
π
1
,
π
2
,
π
3
. Dowolnie względem niego
wprowadzamy nową rzutnię, która jest nową płaszczyzną rysunkową ( naszą kartką papieru) i nazywana jest
rzutnią aksonometryczną
π
a
.
Aksonometria jest rzutowaniem równoległym przestrzeni rzutowej po kierunku rzutowania k na rzutnię
aksonometryczną, gdzie otrzymujemy obraz – rzut aksonometryczny.
Jeżeli promień rzutowania jest prostopadły do rzutni aksonometrycznej to otrzymamy aksonometrię prostokątną
jeżeli zaś jest w dowolnym ukośnym kierunku, otrzymamy aksonometrię ukośną
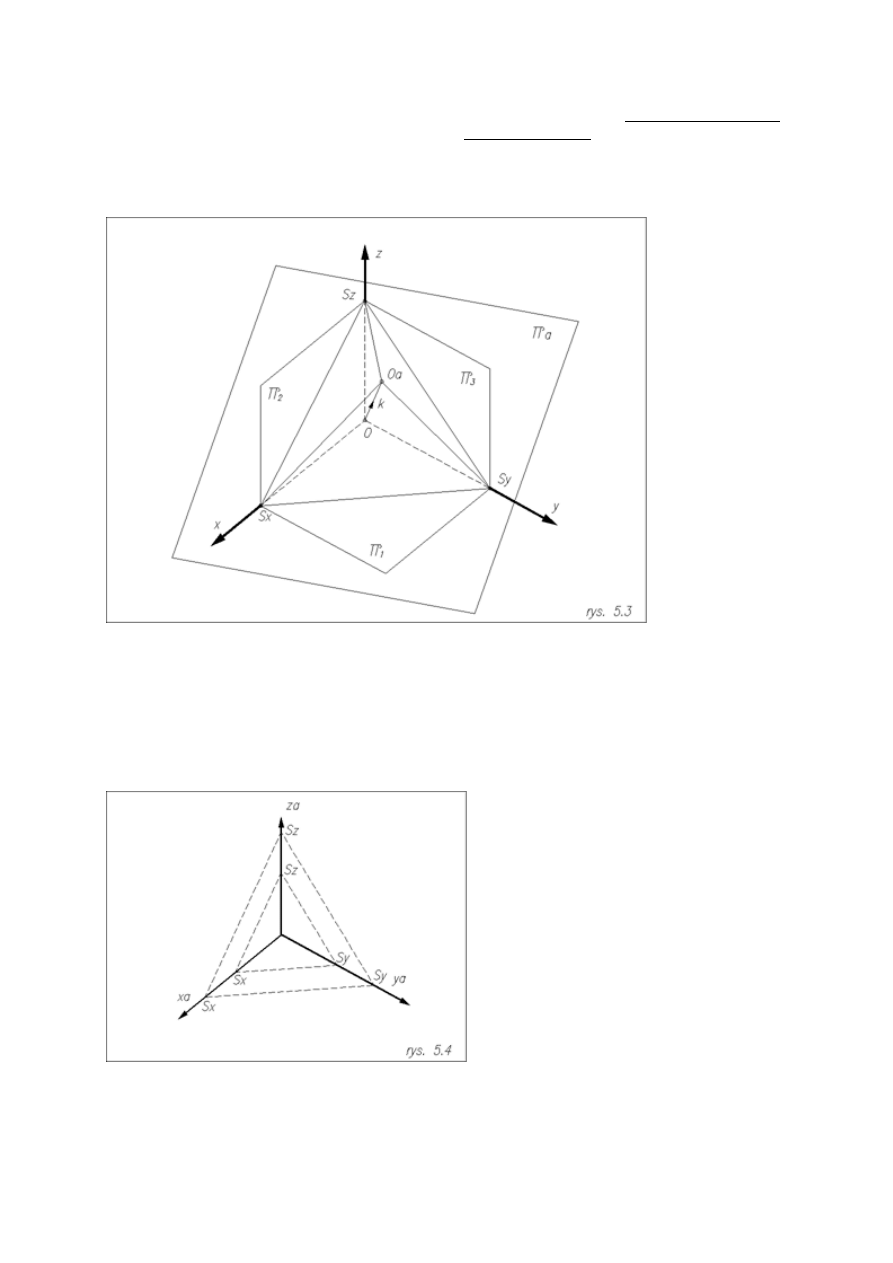
Usytuujmy teraz rzutnię aksonometryczną tak, aby znalazła się przed układem prostokątnym i nachylała się nad
początkiem układu (punktem 0)
Widzimy, że płaszczyzna
π
a
przenika się z płaszczyznami układu prostokątnego po trójkącie, którego
wierzchołkami są punkty przebicia osi x, y ,z z rzutnią
π
a
. Punkty te opisujemy kolejno jako S
x
..., tworzą one
trójkąt śladów aksonometrycznych o bokach s
1
..., będących krawędziami rzutni aksonometrycznej z rzutniami
układu prostokątnego.
Zauważmy, że obraz aksonometryczny pozostanie ten sam po równoległym przesunięciu rzutni
π
a
,zmieni się
tylko wielkość trójkąta śladów.
Rzut aksonometryczny punktu
Punkt jest jednoznacznie określony jeżeli jest dany jego rzut aksonometryczny i aksonometria chociaż jednego
jego rzutu prostokątnego np. A
a
I
Można wtedy wykreślić aksonometrie A
a
II
i A
a
III
jego rzutu pionowego i
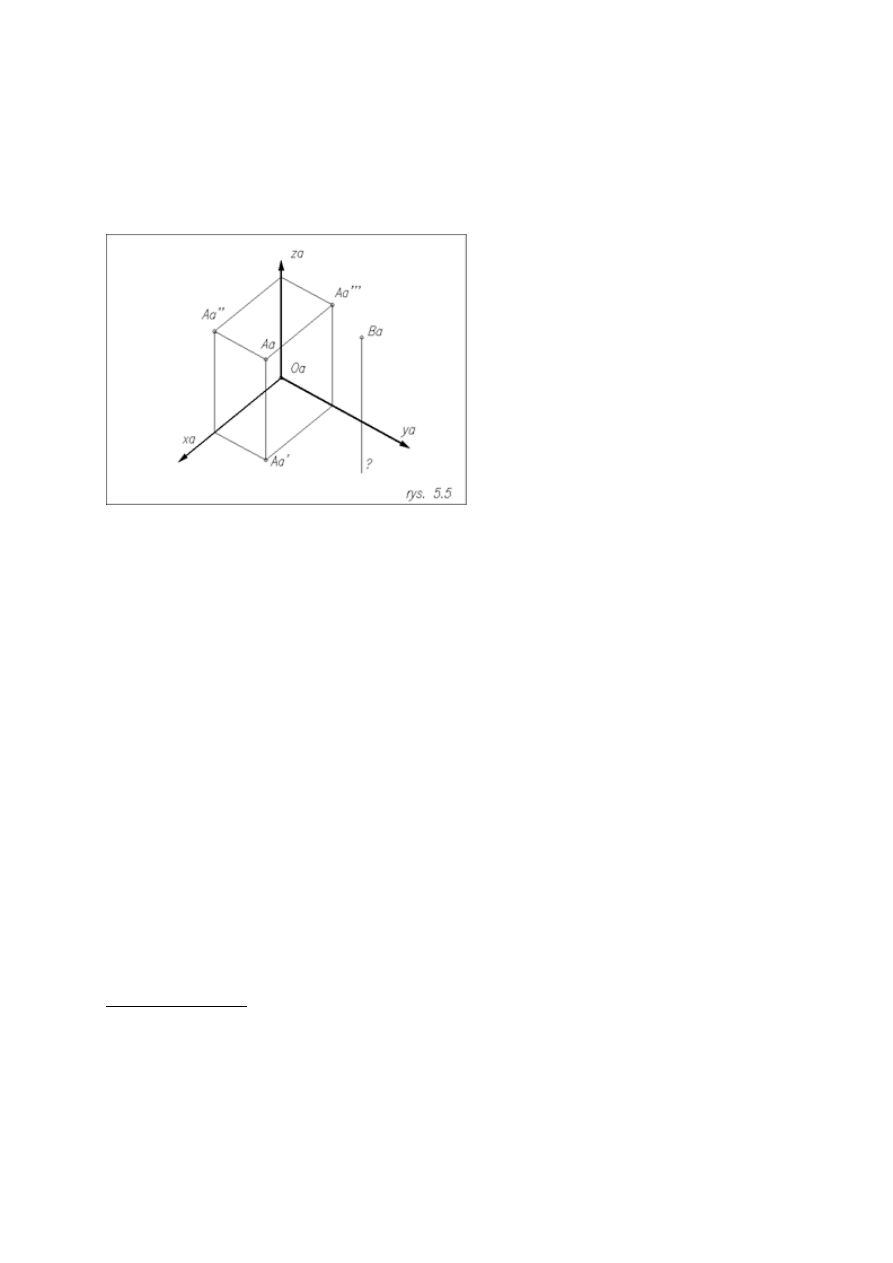
bocznego. Zlokalizowanie punktu w układzie prostokątnym służy ustaleniu położenia punktu względem rzutni
aksonometrycznej. Ze względów praktycznych rezygnujemy z każdorazowego zaznaczania indeksu a w
oznaczeniach aksonometrycznych rzutów prostokątnych punktu. Będziemy je opisywać A
I
, A
II
, A
III
pamiętając ,
ż
e są to rzuty aksonometryczne.
Zauważmy , że samo określenie punktu w rzucie aksonometrycznym np. punktu B nie wystarczy do
jednoznacznego określenia jego położenia. Nie wiemy na jakiej wysokości znajduje się punkt i nie potrafimy
odbudować jego rzutów prostokątnych.
Własności rzutu aksonometrycznego
Z własności rzutu równoległego wynika, że dla aksonometrii jest zachowane;
1.aksonometria punktu jest punktem, aksonometria prostej jest prostą (z wyjątkiem położenia równoległego do
k)
2.jeżeli punkt i prosta do siebie przynależą to w aksonometrii przynależność jest również zachowana
3.jeżeli dwie proste są do siebie równoległe to w aksonometrii równoległość też jest zachowana, w szczególności
aksonometrie prostych równoległych do osi układu współrzędnych są równoległe do osi aksonometrycznych,
stosunek długości odcinka równoległego do osi współrzędnych do długości jego rzutu aksonometrycznego jest
stała. Nie zależy od długości odcinka.
4.długości odcinków równoległych w aksonometrii mają się do siebie jak długości danych odcinków
5.aksonometria utworu leżącego w płaszczyźnie równoległej do rzutu jest przystająca, stąd aksonometria jest
niezależna od odległości rzutni aksonometrycznej od początku układu prostokątnego
6.aksonometria płaszczyzny równoległej do kierunku rzutowania jest linią prostą- jest to płaszczyzna rzutująca
Aksonometria ukośna
W aksonometrii ukośnej prosta k, czyli kierunek rzutowania z założenia nie jest prostopadła do rzutni
aksonometrycznej. W rozważaniach będziemy korzystali z twierdzenie Pohlke`go, którego dowód pomijamy.
Twierdzenie Pohlke`go
Trzy dowolne odcinki leżące na rzutni i wychodzące z jednego punktu O
a
, ale nie leżące na jednej prostej,
można uważać za rzut równoległy trzech odcinków równej długości wychodzących z punktu O i wzajemnie
prostopadłych.
Z powyższego twierdzenia można wywnioskować, iż zawsze uda się dobrać taki kierunek rzutowania i
ustawienie względem rzutni trzech odcinków jednostkowych wzajemnie prostopadłych, że z góry ustalone trzy
dowolne odcinki wychodzące z jednego punktu mogą być ich rzutem.
A zatem w aksonometrii ukośnej można przyjąć;
1.dowolne kąty pomiędzy osiami aksonometrycznymi, przy założeniu, że nie leżą one na jednej prostej oraz
2.dowolnie przyjęte odcinki na tych osiach można uważać za odcinki jednostkowe
W rysowaniu rzutów aksonometrii ukośnej istnieje więc duża dowolność w obieraniu osi i odcinków
jednostkowych. Nie oznacza to jednak , że każda aksonometria jest jednakowo dobrze czytelna i przejrzysta.
Najczęściej stosowane w praktyce są aksonometrie kawalerska i wojskowa, które uzyskuje się poprzez
równoległe usytuowanie jednej z rzutni do rzutni aksonometrycznej.
Aksonometria kawalerska
Płaszczyzna
π
2
( osie x, y ) jest równoległa do rzutni aksonometrycznej.
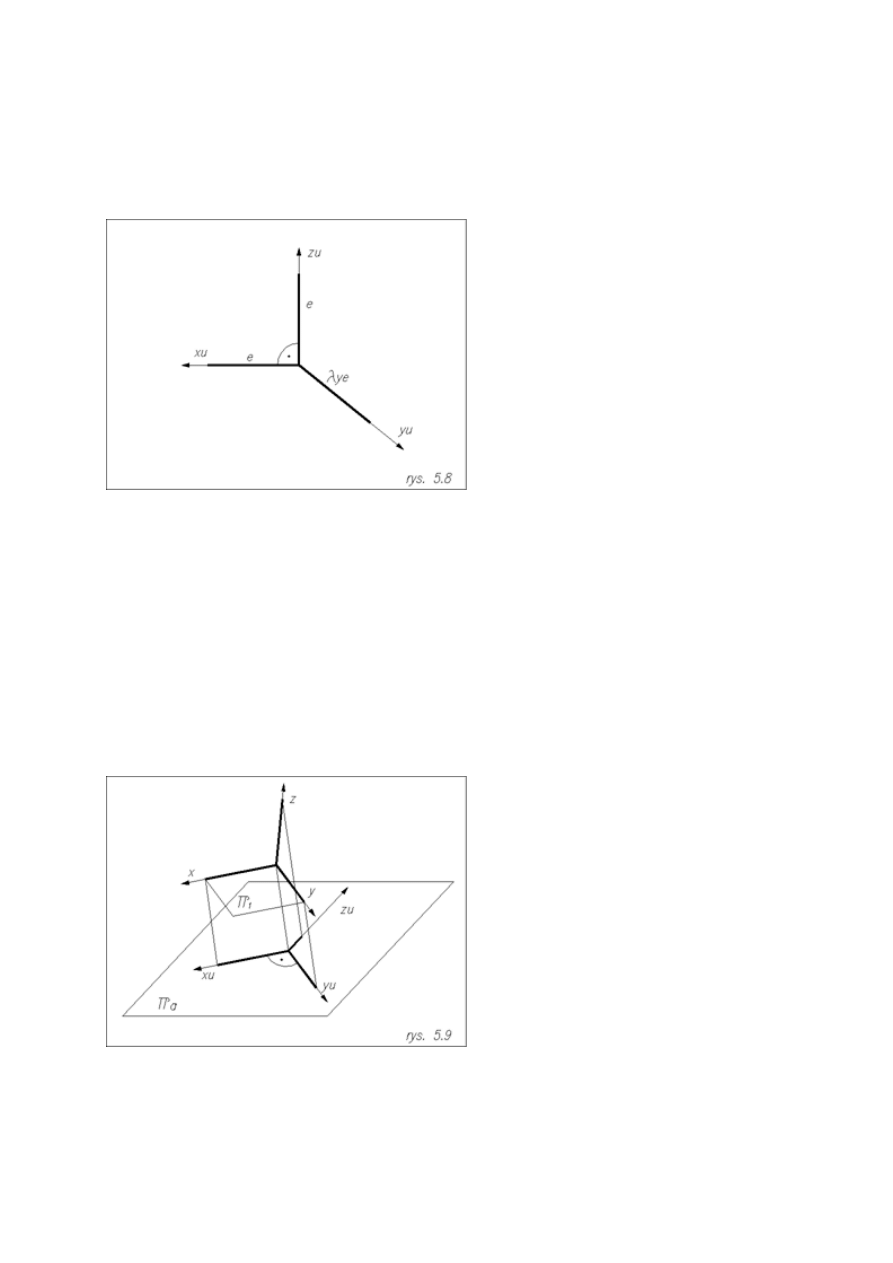
Na rzucie aksonometrycznym osie x
u
, y
u
tworzą kąt prosty , a oś y
u
zwykle nachylona jest pod jednym z kątów
30
°
,45
°
, 60
°
do poziomu.
Odwzorowania utworów płaskich leżących w płaszczyznach równoległych do rzutni pionowej
π
2
obywa się bez
zniekształceń.
Wymiary po osiach x, z pozostają bez zmian , natomiast wymiary wzdłuż osi y zmieniają się zgodnie ze
współczynnikiem proporcjonalności
λ
y
, który na ogół przyjmuje jedną z wartości : 1 ,3/4, ˝, 2/3 .
Aksonometrię kawalerską często stosuje się w rysunkach warsztatowych elementów konstrukcji.
Jest to jedna z najczęściej stosowanych aksonometrii , nie tylko ze względu na prostotę konstrukcji.
Dodatkowym atutem tej aksononetrii jest łatwość rysowania okręgów w płaszczyznach równoległych do rzutni
pionowej, są one okręgami.
Aksonometria wojskowa
Płaszczyzna
π
1
( osie x, y ) jest równoległa do rzutni aksonometrycznej.
Osie x
u
, y
u
tworzą kąt prosty , a oś z
u
ze względów rysunkowych przyjmuje położenie pionowe.
W tak przyjętej aksonometrii wszystkie utwory płaskie leżące w płaszczyznach równoległych do rzutni poziomej
π
1
odwzorowane
są bez zakłóceń. Jedynie rzędne wysokości równoległe do osi z zmieniają się.
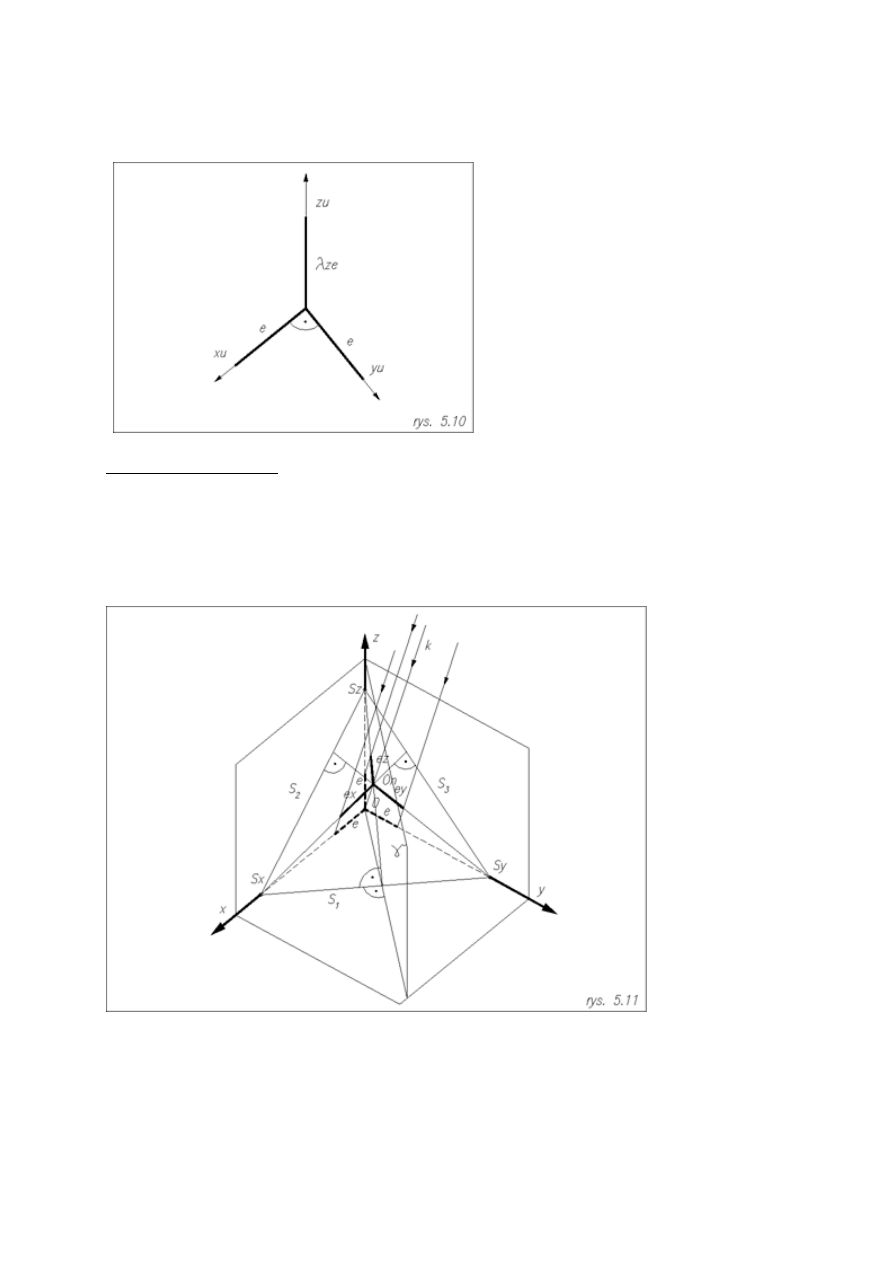
Zmiany te określa współczynnik proporcjonalności
λ
z
, który najczęściej przyjmuje postać ułamków prostych 3,
2/3, 1 . Aksonometria wojskowa najczęściej jest stosowana w rysowaniu planów miast lub budynków.
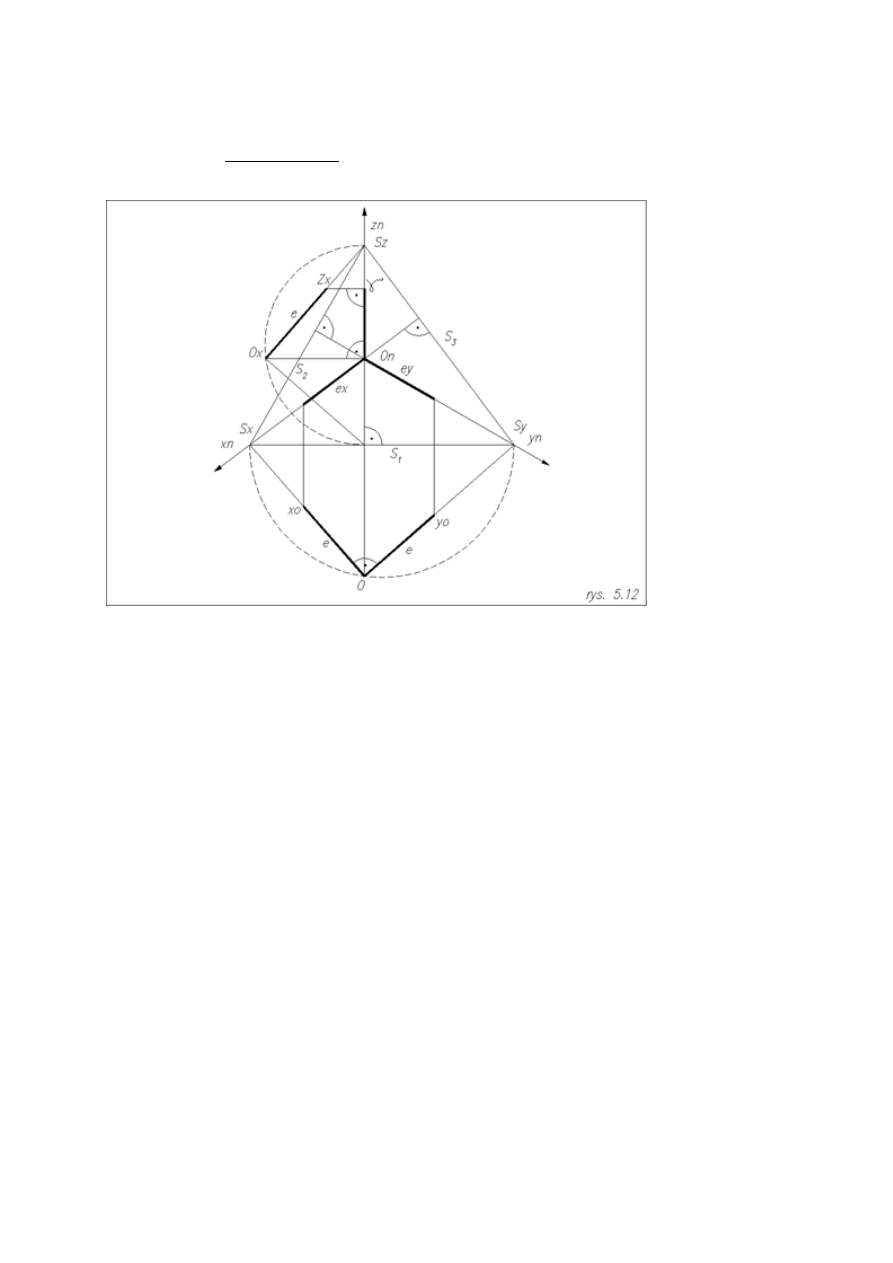
Aksonometria prostokątna
Szczególnym przypadkiem aksonometrii , zachowującym powiązania metryczne, jest aksonometria prostokątna,
w której kierunek rzutowania jest prostopadły do rzutni aksonometrycznej.
Trójkąt śladów w aksonomertii prostokątnej ma szczególne właściwości. Mianowicie osie aksonometryczne są
prostymi, na których leżą wysokości trójkąta śladów aksonometrycznych.
Ponieważ jest z
⊥
π
1
, a prosta s
1
jest jedną z prostych
π
1
, dlatego z
⊥
s
1
Jeżeli popatrzymy teraz na rzutnię aksonometryczną, zauważymy, że jedno z ramion kąta ( s
1
) leży na rzutni, a
zatem rzut tego kąta na rzutnię jest kątem prostym.
Mamy więc z
n
⊥
s
1
Analogicznie y
n
⊥
s
2
i x
n
⊥
s
3
Trójkąt śladów jest zawsze ostrokątny i jak to udowodniliśmy , osie aksonometrii prostokątnej pokrywają się z
kierunkami wysokości trójkąta śladów aksonometrycznych.
Przyjrzyjmy się teraz trójkątowi śladów na rzutni aksonometrycznej, którą jest nasza kartka papieru. Możemy z
niego odczytać stosunek skrótów proporcjonalnych, jakim ulegają odcinki leżące na osiach, lub do nich
równoległe.
Dokonajmy kładu osi x i y wraz z rzutnią
π
1
dokoła prostej s
1
na rzutnię aksonometryczną . Na rzutni otrzymany
tą płaszczyznę w rzeczywistych wymiarach, osie są prostopadłe , wymiary na osiach rzeczywiste.
Jeżeli kąt pomiędzy osiami x i y oprzemy na półokręgu, wtedy uzyskamy pewność, że jest on prosty. Punkt O
znajduje się na odnoszącej prostopadłej do s
1
obrazującej tor obrotu punktu O. Na osiach x
o
, y
o
odmierzamy
rzeczywiste długości odcinków jednostkowych ( przyjętych przez nas ) , a następnie prostopadle do s
1
wracamy
na osie aksonometryczne.
Konstuując skróty na osi z posługujemy się płaszczyzną
χ
zawierającą z, z
n
i prostopadłą do rzutni
aksonometrycznej. Dokonujemy kładu bocznego tej płaszczyzny na rzutnię aksonometryczną wokół osi z
n
W kładzie na osi z
o
odmierzamy rzeczywistą wartość odcinka jednostkowego, a następnie wracamy z nim na oś
z
n
prostopadle do osi kładu.
Skrócenia aksonometryczne
W przypadku bardziej skomplikowanych obiektów wygodnie jest skonstruować kąty skrótów proporcjonalnych
dla danych osi. Powołujemy się na własność rzutu aksonometrycznego o stałym stosunku odcinka równoległego
do osi do jego rzutu.( punkt3 własności rzutu aksonometrycznego)
Równorzędne sposoby określania aksonometrii
1.dane są osie aksonometryczne x, y z określone kątami pomiędzy nimi
Konstruujemy trójkąt śladów aksonometrycznych. Trójkąt ma dowolny wymiar. Kierunki osi muszą być zgodne
z kierunkami wysokości trójkąta śladów aksonometrycznych.
2.dany jest trójkąt śladów aksonometrycznych
Konstruujemy osie wychodząc kolejno z punktów S
x
,S
y
,S
z
zachowując warunek kąta prostego.
3.aksonometria jest określona stosunkiem skróceń na poszczególnych osiach. W naszym kursie nie będziemy
korzystać z tego sposobu określania aksonometrii.
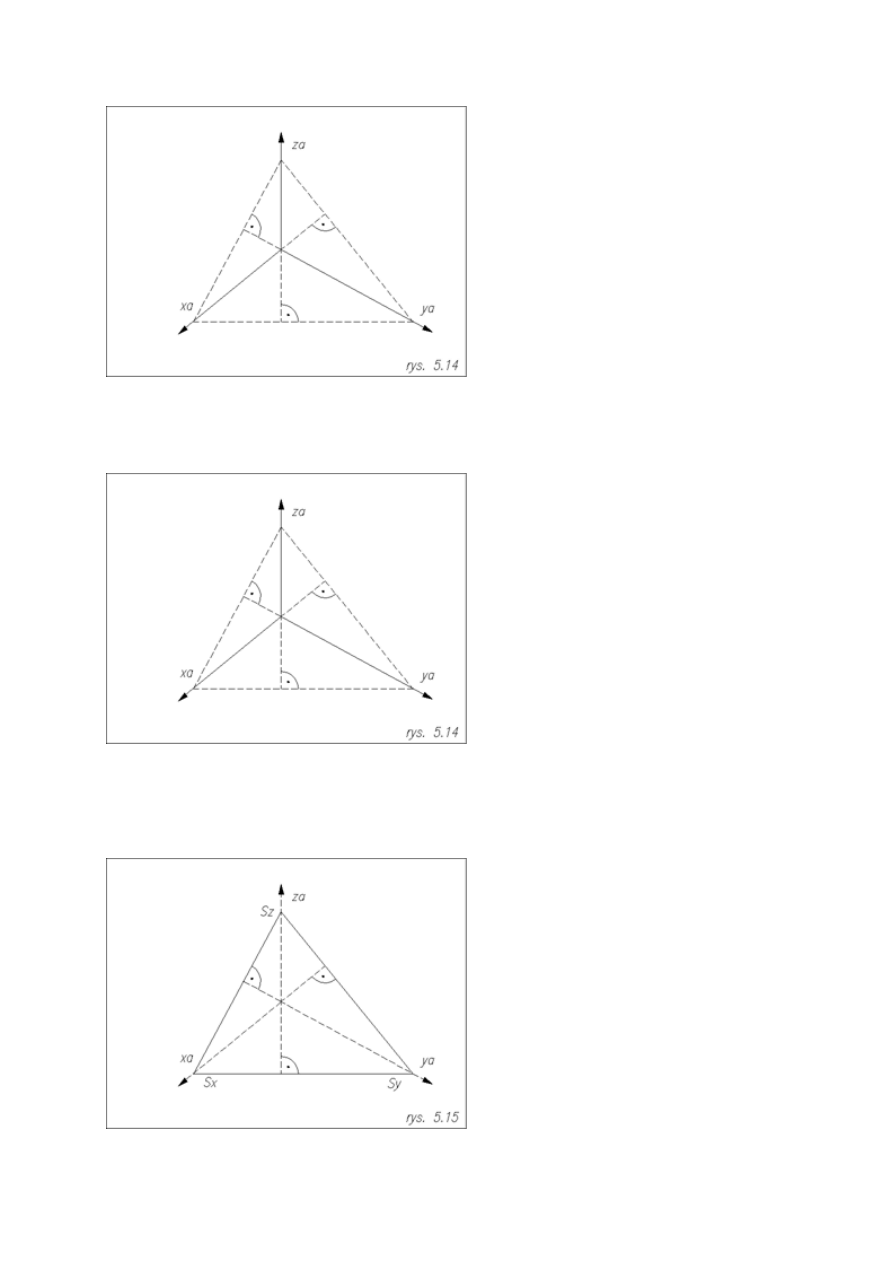
Rodzaje aksonometrii prostokątnej
Izometria
Trójkąt śladów aksonometrycznych jest trójkątem równobocznym , osie aksonometryczne tworzą między sobą
równe kąty 120
°
. Skrócenia na wszystkich osiach są jednakowe.
Dimetria
Trójkąt śladów aksonometrycznych jest trójkątem równoramiennym .Dwa kąty pomiędzy rzutami osi są równe
otrzymujemy tylko dwa rodzaje skrótów.
Anizometria
Trójkąt śladów nie jest trójkątem szczególnym, każda z osi ma inne skrócenia