1

3. Przemiany energii za pomocą pola magnetycznego w przetwornikach o

ruchu obrotowym

Bardzo ważną grupę układów elektromechanicznych stanowią maszyny, których głównym celem

jest wytwarzanie energii elektrycznej lub wykonywanie pracy mechanicznej. Maszyny takie są
nazywane elektromechanicznymi przetwornikami energii. Największe znaczenie mają obecnie
przetworniki, które przetwarzają energię elektryczną na energię mechaniczną ruchu obrotowego lub
odwrotnie, w których przemiana energii dokonuje się za pomocą pola magnetycznego. Ich aktualna
budowa i konstrukcje ukształtowały się w wyniku ponad 100 lat rozwoju. Nie jest celem tego
opracowania szczegółowy ich opis, lecz przedstawienie ogólnych praw oraz zależności rządzących
elektromechanicznymi przemianami energii dla tej klasy przetworników.

Elektromechaniczne przetworniki energii o ruchu obrotowym składają się z dwóch części, z

których jedna jest nieruchoma, a druga może wykonywać nieograniczony ruch obrotowy. Części te są
rozdzielone szczeliną powietrzną. Przynajmniej na jednej z części muszą znajdować się obwody
elektryczne w postaci cewek umożliwiające dostarczanie lub odbiór energii elektrycznej. Na częściach
ruchomej i nieruchomej umieszczony jest magnetowód, w którym wytwarzane jest pole magnetyczne,
stanowiące medium za pomocą, którego energia jest przetwarzana. Elementy stanowiące magnetowód,
czyli obwód magnetyczny przetwornika, mają kształt współosiowych walców, których powierzchnie
od strony szczeliny powietrznej są odpowiednio ukształtowane, nadając przetwornikowi odpowiednie
właściwości. Obwód magnetyczny przetwornika wykonywany jest z materiałów o bardzo dobrych
właściwościach magnetycznych, w taki sposób, aby ograniczyć przewodność elektryczną
magnetowodu. Cewki, stanowiące uzwojenia przetwornika, wykonywane są z materiałów dobrze
przewodzących prąd, aby ograniczyć straty mocy. Cewki te umieszczone są w specjalnie
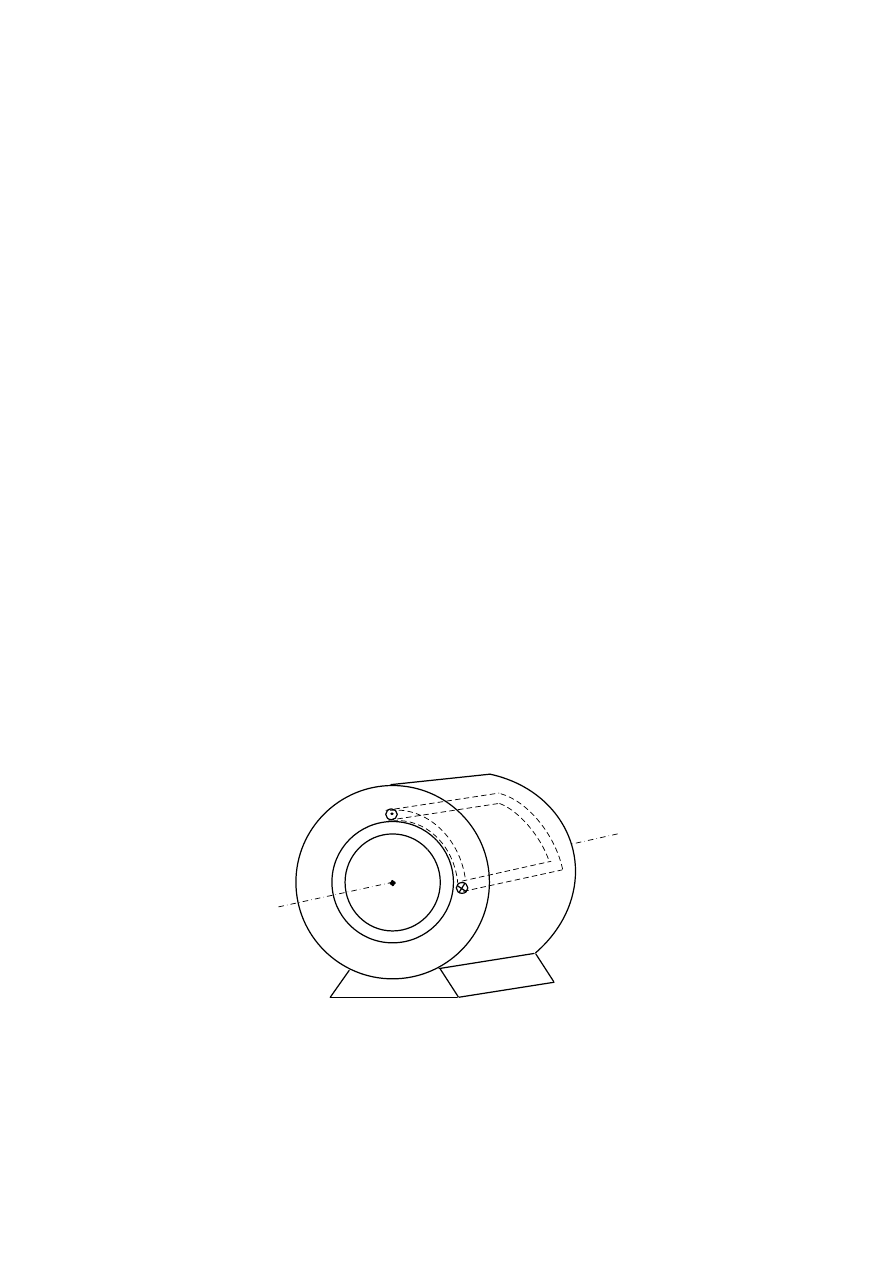
ukształtowanych żłobkach biegnących równolegle do osi obrotu przetwornika. Schematycznie
ilustruje to Rys. 3.1. Bardziej szczegółowy opis obwodu magnetycznego oraz sposobu wykonania
cewek takich przetworników można znaleźć w książkach poświeconych budowie i konstrukcji maszyn
elektrycznych różnych typów.

Przetworniki opisane powyżej mogą być rozpatrywane, jako układy elektromechaniczne utworzone

ze zbioru cewek umieszczonych we wspólnym obwodzie magnetycznym. Mechaniczną część
przetwornika, w najprostszym ujęciu, stanowi część obrotowa przetwornika o zadanym, stałym
momencie bezwładności, która może wykonywać nieograniczony ruch obrotowy.

cewka

Rys. 3.1. Ogólna budowa elektromechanicznego przetwornika energii o ruchu obrotowym

Zgodnie z tym, co już powiedziano, aby opisać przemiany energii w takich przetwornikach należy

zapisać funkcję Lagrange’a. Będzie się ona składać jedynie, z koenergii, gdyż w samym przetworniku
nie ma kondensatorów, a w układzie mechanicznym, przy jego najprostszej reprezentacji, nie ma
elementów sprężystych. Koenergię obrotowej części przetwornika określa funkcja

2

2

ko

J

2

1

ω

⋅

=

E

w której

ω

jest prędkością kątową a ‘J’ jest momentem bezwładności. Należy jeszcze określić

koenergię zbioru cewek, które są wzajemnie sprzężone magnetycznie, gdyż są umieszczone we
wspólnym obwodzie magnetycznym. Fakt sprzężenia magnetycznego cewek objawia się tym, że
strumień skojarzony danej cewki (dla przypomnienia – strumień skojarzony cewki jest to suma
strumieni magnetycznych sprzężonych z poszczególnymi zwojami cewki) jest zależny nie tylko od jej
prądu, lecz także od prądów wszystkich pozostałych cewek. Sposób obliczania koenergii układu
cewek przetwornika zostanie pokazany na przykładzie dwóch cewek, z których jedna umieszczona jest
na części nieruchomej a druga na części obrotowej. Obydwie części mają kształt cylindrycznych
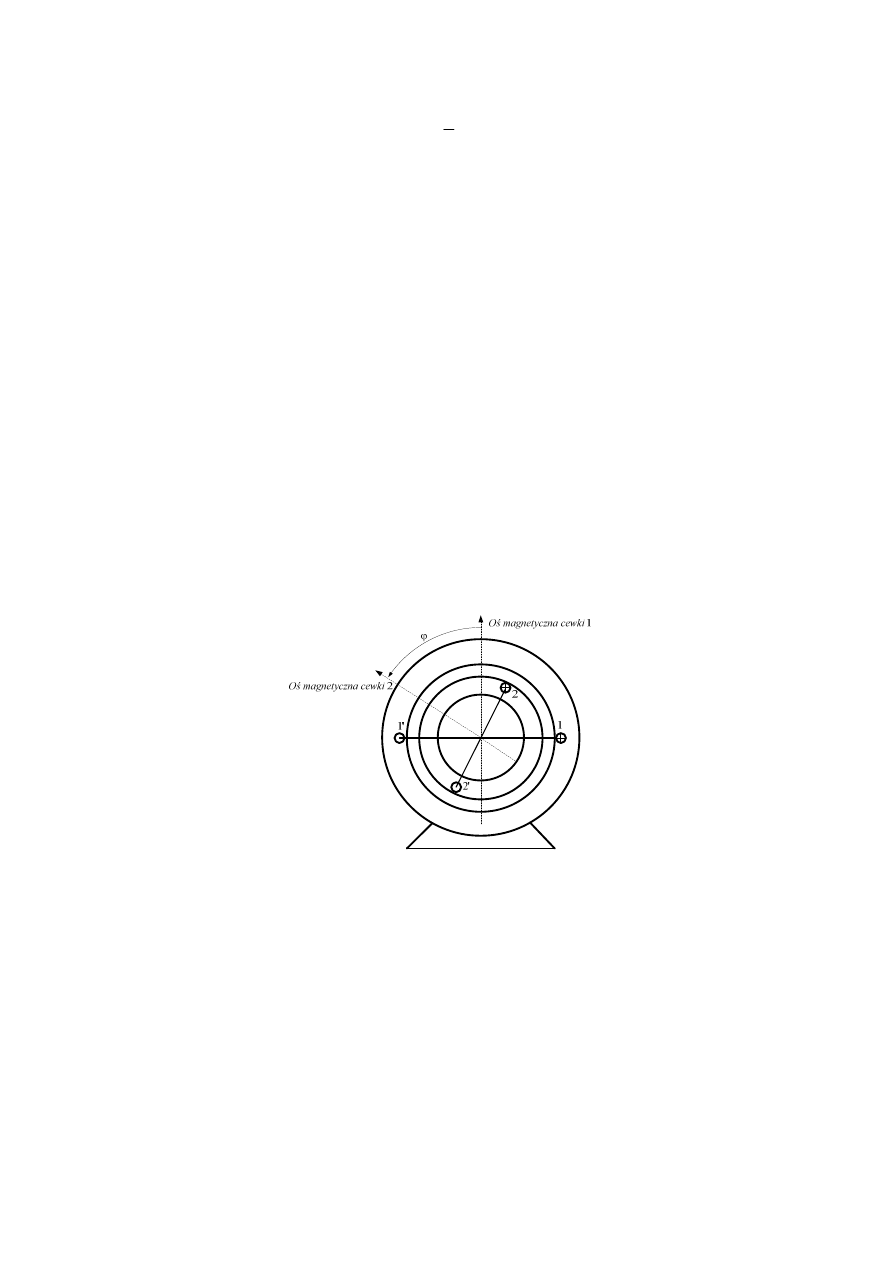
walców rozdzielonych równomierną szczeliną powietrzną. Rozmieszczenie cewek ilustruje
symbolicznie Rys. 3.2., który przedstawia przekrój poprzeczny tzw. czynnej części przetwornika.
Zaznaczono na nim miejsca umieszczenia cewki ‘1’, na części nieruchomej oraz cewki ‘2’ na części
obrotowej. Cewki te są sprzężone magnetycznie gdyż znajdują się we wspólnym obwodzie
magnetycznym, który – dla uproszenia – jest liniowy. Strumienie skojarzone cewek opisane są
wówczas zależnościami

2

,2

1

1

,1

1

1

L

L

i

i

⋅

+

⋅

=

ψ

2

,2

2

1

,1

2

2

L

L

i

i

⋅

+

⋅

=

ψ

(3.1)

w których występują indukcyjności własne cewek

L

,1

1

,

L

,2

2

oraz indukcyjności wzajemne

L

,2

1

,

,1

2

L

, uwzględniające fakt ich sprzężenia magnetycznego. Z tych zależności wynikają definicje

indukcyjności własnych i wzajemnych, które są współczynnikami proporcjonalności między
strumieniami skojarzonymi a prądami.

Rys. 3.2. Przekrój poprzeczny przetwornika o dwóch cewkach z symbolicznie zaznaczonymi miejscami ich usytuowania.

Koenergię tych dwóch cewek można obliczyć, jako sumę koenergii każdej z cewek. Zgodnie z

wzorem określającym koenergię cewki należy obliczyć dwie całki

(

)

1

2

,2

1

1

,1

1

ko,1

'

d

L

'

L

1

i

i

i

E

i

o

∫

⋅

+

⋅

=

(

)

2

2

,2

2

1

,1

2

ko,2

'

d

'

L

L

2

i

i

i

E

i

o

∫

⋅

+

⋅

=

(3.2)

Powstaje problem, jaką przyjąć wartość prądu cewki ‘2’, gdy obliczana jest koenergia cewki ‘1’ oraz
prądu cewki ‘1’ przy obliczaniu koenergii cewki ‘2’, gdyż koenergia zbioru tych dwóch cewek będzie
zależeć od obydwóch prądów. Problem ten można rozwiązać następująco. Ze względu na
jednoznaczność charakterystyk cewek ich łączna energia – a zatem i koenergia – nie może być zależna
od sposobu jej gromadzenia. Energia i koenergia zbioru tych cewek zależeć będzie jedynie od

3

końcowych wartości pary prądów

)

,

(

2

1

i

i

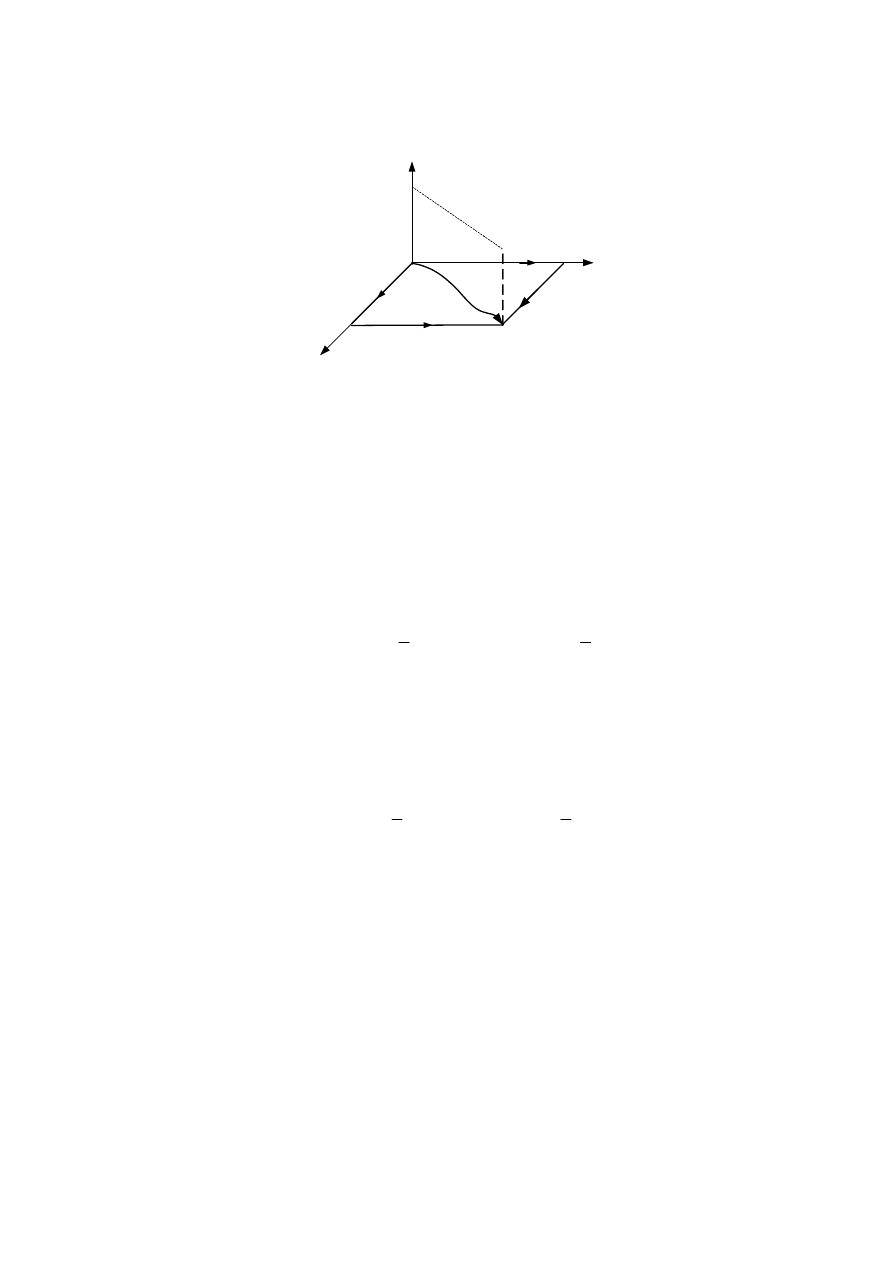
i nie będzie zależeć od sposobu dojścia do tych wartości, co

ilustruje Rys. 3.3.

E

ko

i

1

'

i

2

'

i

1

i

2

i

2

i

1

)

,

(

2

1

ko

i

i

E

)

,

(

2

1

i

i

Rys. 3.3. Ilustracja różnych sposobów gromadzenia energii w dwóch cewkach

Proces gromadzenia energii można dowolnie uporządkować. W celu obliczenia koenergii wygodnie
jest założyć, że gromadzenie energii następuje w dwóch etapach:

- w pierwszym etapie prąd cewki ‘1’ jest zmieniany od wartości 0 do wartości

1

i ,

- w drugim etapie prąd cewki ‘2’ jest zmieniany od wartości 0 do wartości

2

i , prąd cewki ‘1’

pozostaje bez zmian.

Takiemu sposobowi gromadzenia – wariant energii odpowiada wzór na koenergię

(

)

=

⋅

+

⋅

+

⋅

=

+

=

∫

∫

2

2

,2

2

1

,1

2

1

1

,1

1

ko,2

ko,1

ko

'

d

'

L

L

'

d

'

L

2

1

i

i

i

i

i

E

E

E

i

o

i

o

2

2

,2

2

2

1

,1

2

2

1

1,1

)

(

L

2

1

L

)

(

L

2

1

i

i

i

i

⋅

+

⋅

⋅

+

⋅

=

(3.3)

Gdy kolejność gromadzenia energii zostanie zmieniona, tj. rozpoczniemy proces gromadzenia od
cewki ‘2’, wzór na koenergię przyjmie postać

(

)

=

⋅

+

⋅

+

⋅

=

∫

∫

1

1

,1

1

2

,2

1

2

2

,2

2

ko

'

d

'

L

L

'

d

'

L

1

2

i

i

i

i

i

E

i

o

i

o

2

2

,2

2

2

1

,1

2

2

1

1,1

)

(

L

2

1

L

)

(

L

2

1

i

i

i

i

⋅

+

⋅

⋅

+

⋅

=

(3.3a)

Ponieważ koenergie w obydwóch przypadkach muszą być równe współczynniki indukcyjności
wzajemnej musza być sobie równe

M

L

L

1

2

2

1

=

=

,

,

. Ta bardzo ważna właściwość indukcyjności

wzajemnych dotyczy dowolnej pary cewek i wynika z zasady, że energia zgromadzona w układzie
cewek nie zależy od sposobu jej zgromadzenia.

Analizując koenergię cewek w przetworniku z Rys. 3.2. należy zauważyć, że sprzężenie

magnetyczne cewek jest zależne od położenia kątowego części obrotowej względem części
nieruchomej. Jakościowa analiza tych sprzężeń prowadzi do wniosków, że indukcyjności własne
cewek tego przetwornika nie zależą od wzajemnego położenia cewek, gdyż dla dowolnego ustawienia
części obrotowej przekształtnika kształt obwodu magnetycznego pozostaje niezmienny zarówno dla
cewki położonej na części nieruchomej jak i dla cewki na części obrotowej. Zatem strumień
wytworzony przez każdą z cewek z osobna nie zależy od kąta obrotu i w konsekwencji indukcyjności
własne każdej z cewek są stałe. Zmienia się natomiast stopień wzajemnego sprzężenia cewek w
zależności od kąta położenia części obrotowej. Nietrudno jakościowo stwierdzić, że dla kąta

0

=

ϕ

sprzężenie będzie maksymalne, a zatem i indukcyjność wzajemna przyjmie największą wartość. Dla

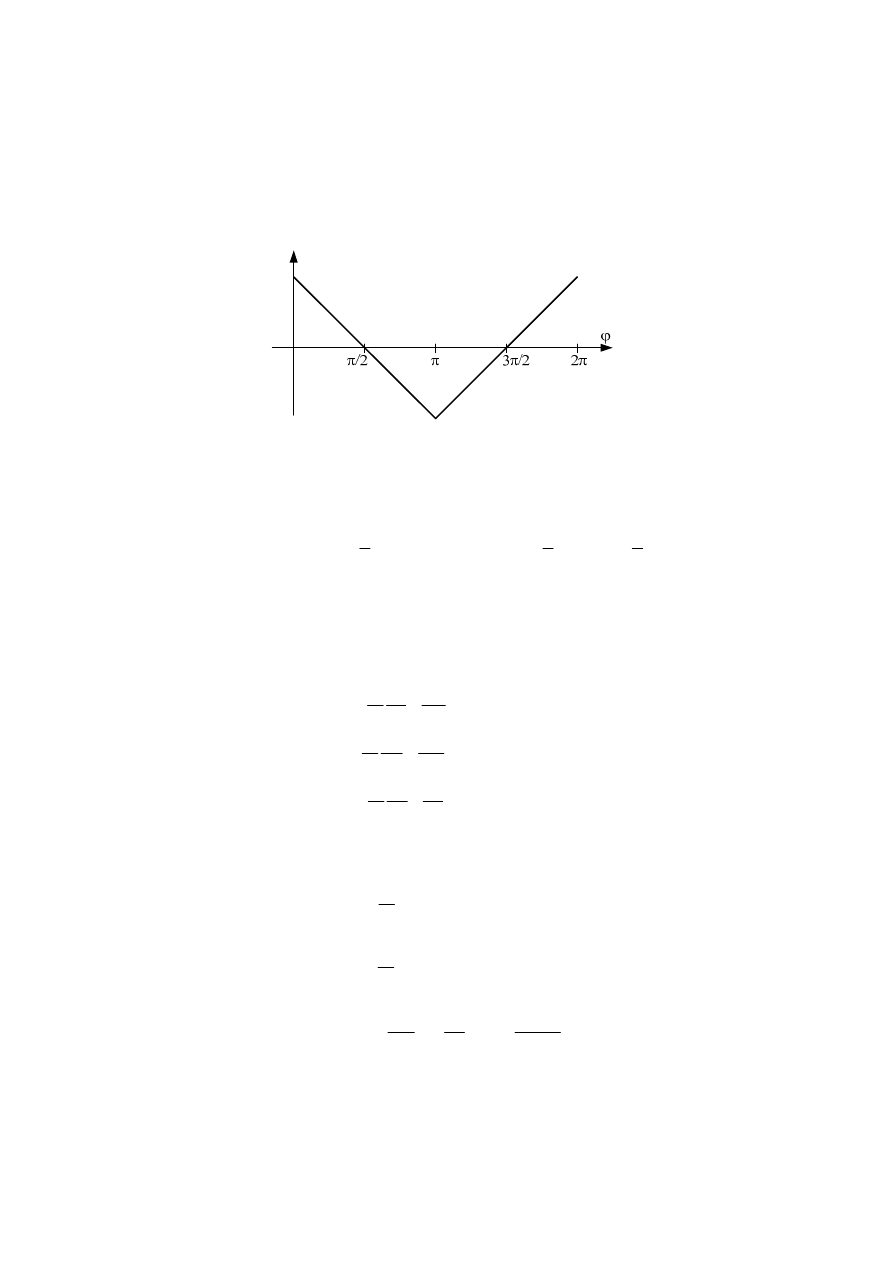
4

kątów

o

0

9

=

ϕ

oraz

o

0

27

=

ϕ

cewki nie będą magnetycznie sprzężone, więc indukcyjność wzajemna

będzie równała się zero, natomiast dla kąta

o

0

18

=

ϕ

sprzężenie będzie maksymalne, lecz przeciwne.

Te zmiany wartości indukcyjności wzajemnej przestawia Rys. 3.4. W przedziałach między tymi
punktami charakterystycznymi zmiany indukcyjności wzajemnej będą w przybliżeniu liniowe, lecz nie
jest to na tym poziomie rozważań istotne. Najważniejszym jest stwierdzenie, że indukcyjności
wzajemne będą funkcjami kąta obrotu

)

M(

ϕ

Rys. 3.4. Zmienność indukcyjności wzajemnych w funkcji kąta obrotu

ϕ

Ostatecznie funkcję Lagrange’a dla przetwornika z Rys. 3.2 można zapisać w postaci

2

2

1

,1

1

1

2

2

2

2,2

J

2

1

)

(

L

2

1

)

M(

)

(

L

2

1

ω

+

⋅

+

⋅

⋅

ϕ

+

⋅

=

i

i

i

i

L

(3.4)

Należy zauważyć, że nie występuje w niej energia potencjalna, gdyż nie ma w układzie
kondensatorów ani elementów sprężystych ograniczających ruch obrotowy. Równania tego
przetwornika można otrzymać zapisując równania Lagrange’a. W tym przypadku są to trzy równania
o postaciach

1

1

1

1

1

R

d

d

i

u

q

L

i

L

t

⋅

−

=

∂

∂

−

∂

∂

2

2

2

2

2

R

d

d

i

u

q

L

i

L

t

⋅

−

=

∂

∂

−

∂

∂

ω

⋅

−

=

ϕ

∂

∂

−

ω

∂

∂

D

d

d

z

m

L

L

t

Po wykonaniu operacji matematycznych otrzymuje się układ równań różniczkowych

(

)

1

1

1

2

1

,1

1

R

)

M(

L

d

d

u

i

i

i

t

=

⋅

+

⋅

ϕ

+

⋅

(3.5a)

(

)

2

2

2

2

,2

2

1

R

L

)

M(

d

d

u

i

i

i

t

=

⋅

+

⋅

+

⋅

ϕ

(3.5b)

1

2

z

2

2

)

M(

d

d

D

d

d

J

i

i

m

t

t

⋅

⋅

ϕ

∂

ϕ

∂

+

=

ϕ

+

ϕ

(3.5c)

Pierwsze dwa równania opisują obwody elektryczne przetwornika, trzecie opisuje ruch obrotowy i jest
nazywane równaniem mechanicznym. Wyrażenie

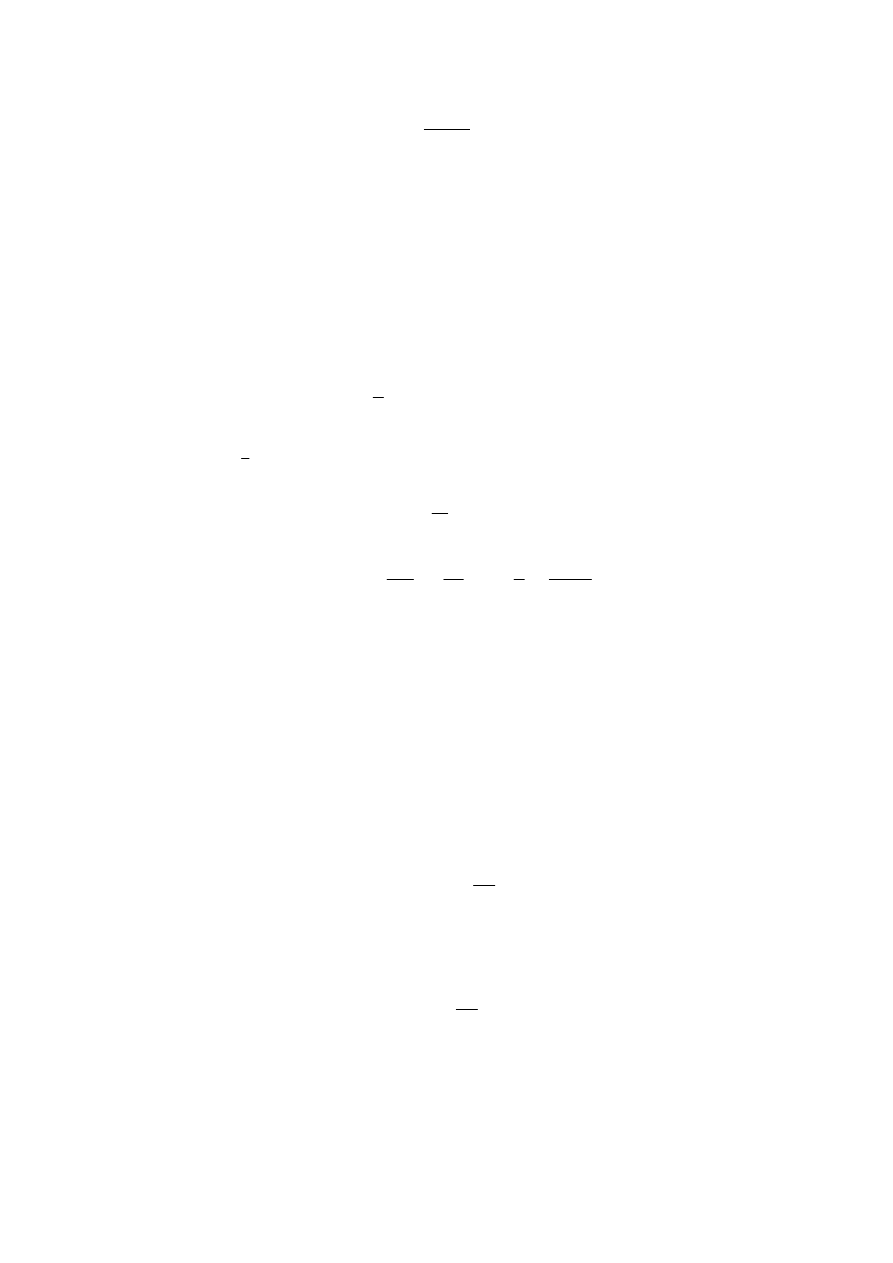
5

1

2

el

)

M(

i

i

m

⋅

⋅

ϕ

∂

ϕ

∂

=

określa moment elektromagnetyczny przetwornika. Równania te wygodnie jest zapisywać w formie
macierzowej. W tym celu należy zapisać zależności strumieni sprzężonych od prądów w postaci













⋅













ϕ

ϕ

=













ψ

ψ

2

1

,2

2

,1

1

2

1

L

)

M(

)

M(

L

i

i

(3.6)

lub w skrócie

i

L

⋅

ϕ

=

Ψ

)

(

, gdzie

Ψ

Ψ

Ψ

Ψ

oraz

i są wektorami, odpowiednio strumieni sprzężonych i

prądów, a

)

(

ϕ

L

jest macierzą indukcyjności. Funkcję koenergii

ko

E

można teraz zapisać jako

[

]













⋅













ϕ

ϕ

⋅

=

2

1

,2

2

,1

1

2

1

ko

L

)

M(

)

M(

L

2

1

i

i

i

i

E

(3.7)

lub w skrócie

i

L

i

⋅

ϕ

⋅

=

)

(

2

1

ko

T

E

. Równania przetwornika przyjmują w postaci macierzowej formę

(

)

u

i

R

i

L

=

⋅

+

⋅

ϕ

)

(

d

d

t

(3.8a)

i

L

i

⋅

ϕ

∂

ϕ

∂

⋅

+

=

ϕ

+

ϕ

)

(

2

1

d

d

D

d

d

J

z

2

2

T

m

t

t

(3.8b)

↓

**************************************************************************↓

Macierzowa postać równań nie ulegnie zmianie, gdy przetwornik o ruchu obrotowym posiadał

będzie N niezależnych cewek. Dla zbioru N cewek strumień skojarzony każdej z nich jest określony
związkiem

N

N

,

,

2

,2

1

,1

L

L

L

L

i

i

i

i

n

n

n

n

n

n

n

⋅

+

+

⋅

+

⋅

+

⋅

=

ψ

L

L

dla

)

N

,...,

2

,

1

(

=

n

(3.9)

który opisuje strumień skojarzony cewki o numerze ‘

n’ jako funkcję prądów wszystkich pozostałych

cewek od ‘1’ do ‘N’. Indukcyjności wzajemne

n,k

L

są definiowane jako stosunek strumienia

skojarzonego cewki ‘

n’, wytworzonego przez prąd cewki ‘k’, do wartości tego prądu, przy założeniu,

ż

e prądy we wszystkich pozostałych cewkach nie płyną

k

n

n,k

i

ψ

=

L

k

n

≠

(3.10)

Indukcyjności własne określa stosunek strumienia skojarzonego danej cewki wytworzonego przez jej
własny prąd do tego prądu

n

n

n,n

i

ψ

=

L

Związki między strumieniami skojarzonymi a prądami dla zbioru N cewek można zapisać w postaci

i

L

⋅

ϕ

=

Ψ

)

(

(3.11)

6

lecz teraz wektory strumieni skojarzonych oraz prądów są N wymiarowe i także macierz
indukcyjności ma wymiary

)

N

N

(

×

. W zapisie tym symbolicznie zaznaczono, że niektóre elementy

macierzy indukcyjności mogą zależeć od kąta obrotu

ϕ

. Na pewno będą to indukcyjności wzajemne

par cewek, z których jedna znajduje się na części nieruchomej, a druga na części obrotowej. Zgodnie z
definicją koenergię cewki ‘n’ określa całka

n

i

o

n

n

n

n

n

n

n

i

o

n

i

i

i

i

i

i

E

n

n

'

d

)

L

'

L

L

(L

d

N

N

,

,

2

,2

1

,1

ko

∫

∫

⋅

+

+

⋅

+

+

⋅

+

⋅

=

ψ

=

L

L

(3.12)

z której wynika, że koenergia danej cewki jest zależna od wartości prądów we wszystkich cewkach.
Koenergię zbioru cewek, gdy ich prądy mają wartości

)

,...,

,

,

(

N

3

2

1

i

i

i

i

, można obliczyć sumując

koenergie poszczególnych cewek zgodnie z wzorem

(

)

(

)

+

+

+

+

+

+

=

∫

∫

∫

3

3

,3

2

,2

1

,1

2

2

,2

1

,1

1

1

,1

ko

d

L

L

L

d

L

L

d

L

3

2

1

i

i

i

i

i

i

i

i

i

E

i

o

n

n

n

i

o

n

n

i

o

n

(

)

N

N

N

,

3

,3

2

,2

1

,1

d

L

L

L

L

N

i

i

i

i

i

i

o

n

n

n

n

∫

+

+

+

+

+

+

L

L

(3.13)

Wzór ten otrzymuje się, jako wynik następującego sposobu gromadzenia energii:

- prąd cewki ‘1’ zmienia się od wartości zero do wartości

1

i

,

- prąd cewki ‘2’ zmienia się od wartości zero do wartości

2

i

nie zmieniając wartości prądu

1

i

,

- prąd cewki ‘3’ zmienia się od wartości zero do wartości

3

i

nie zmieniając wartości prądów

1

i

oraz

2

i

,

- …... ,
- prąd cewki ‘N’ zmienia się od wartości zero do wartości

N

i

nie zmieniając wartości prądów

)

,...,

,

,

(

1

-

N

3

2

1

i

i

i

i

.

Wynik całkowania daje następującą ogólną postać funkcji koenergii

∑∑

=

=

⋅

⋅

ϕ

=

N

1

N

1

,

ko

)

(

L

2

1

n

k

k

n

k

n

i

i

E

(3.14)

W zapisie macierzowym funkcja koenergii ma postać

i

L

i

⋅

ϕ

⋅

=

)

(

2

1

ko

T

E

(3.14a)

lecz teraz wektor prądów

i

oraz macierz indukcyjności

)

(

ϕ

L

są N-wymiarowe. Równania

przetwornika o N cewkach w liniowym obwodzie magnetycznym przyjmują ogólną postać

n

n

n

i

u

i

E

t

⋅

−

=

∂

∂

n

ko

R

d

d

dla

)

N

,...,

2

,

1

(

=

n

ω

⋅

−

=

ϕ

∂

∂

−

ω

D

d

d

J

z

ko

m

E

t

Po wykonaniu operacji matematycznych przewidzianych w tych równaniach otrzymuje się układ
równań

7

(

)

u

i

R

i

L

=

⋅

+

⋅

ϕ

)

(

d

d

t

(3.15a)

i

L

i

⋅

ϕ

∂

ϕ

∂

⋅

+

=

ϕ

+

ϕ

)

(

2

1

d

d

D

d

d

J

z

2

2

T

m

t

t

(3.15b)

który ma postać analogiczną jak dla rozważanego wcześniej przetwornika o dwóch cewkach i jedynie
wymiary wektorów napięć i prądów oraz macierzy indukcyjności są inne. Ta postać równań jest
niezmienna dla całej klasy przetworników o ruch obrotowym przetwarzających energie za pomocą
pola magnetycznego. Nietrudno zauważyć, że najważniejszą rolę pełni w tych równaniach macierz
indukcyjności. W macierzy indukcyjności są reprezentowane wszystkie charakterystyczne cechy
obwodu magnetycznego oraz rozmieszczenia cewek przetwornika.

↑

***************************************************************************↑

Niezależnie od budowy przetwornika macierz indukcyjności ma następujące cechy matematyczne,

które są związane z właściwościami fizycznymi:

-

macierz indukcyjności jest nieosobliwa

0

)

(

det

≠

ϕ

L

(3.16)

Właściwość ta wynika z fizycznego faktu, że sprzężenia magnetyczne rzeczywistych cewek nie
mogą być całkowite, co matematycznie wyraża nierówność

( )

2

,

,

,

L

L

L

k

n

k

k

n

n

<

⋅

dla

)

N

,...,

2

,

1

(

,

=

k

n

Oznacza to, że zarówno strumienie skojarzone są jednoznacznie określone przez prądy cewek jak i
prądy cewek są jednoznacznie określone przez strumienie skojarzone.

-

macierz indukcyjności jest symetryczna

(

)

T

)

(

)

(

ϕ

=

ϕ

L

L

(3.17)

Właściwość ta wynika z fizycznego faktu, że energia i koenergia zgromadzona w układzie cewek nie
zależą od sposobu ich gromadzenia, co zostało już powyżej objaśnione. Matematycznie wyraża to
równość indukcyjności wzajemnych każdej pary cewek

n

k

k

n

,

,

L

L

=

dla

)

N

,...,

2

,

1

(

,

=

k

n

- macierz indukcyjności dla przetworników o ruchu obrotowy jest okresowa

)

π

2

(

)

(

+

ϕ

=

ϕ

L

L

(3.18)

Właściwość ta wynika z fizycznego faktu, że przetworniku o ruch obrotowym po obrocie o kąt pełny
wszystkie cewki powracają do poprzednich pozycji, a więc ich indukcyjności własne i wzajemne
przyjmują poprzednie wartości. Oznacza to, że każdy z elementów macierzy, który jest zależny od
kąta obrotu, jest okresową funkcją tego kąta

)

π

2

(

L

)

(

L

,

,

+

ϕ

=

ϕ

k

n

k

n

dla

)

N

,...,

2

,

1

(

,

=

k

n

8

↓

***************************************************************************↓

Rozważania przedstawione powyżej dotyczyły przypadku, gdy obwód magnetyczny, w którym

umieszczone są cewki, jest liniowy, tzn. indukcja magnetyczna w każdym jego punkcie obwodu
magnetycznego jest proporcjonalna do wartości natężenia pola magnetycznego. W ogólnym
przypadku, gdy charakterystyki cewek są nieliniowymi funkcjami prądów oraz kąta obrotu

ϕ

)

,

,...,

,

(

N

2

1

ϕ

ψ

i

i

i

n

dla

)

N

,...,

2

,

1

(

=

n

koenergię określa wzór

∑∫

=

ϕ

ψ

=

N

1

0

2

1

ko

'

)

,

0

,...,

0

,

'

,...,

,

(

n

i

n

n

n

n

di

i

i

i

E

który wynika z sumowania koenergii poszczególnych cewek o nieliniowych charakterystykach przy
sposobie gromadzenia energii opisanym powyżej dla cewek o charakterystykach liniowych. Równania
przetwornika z nieliniowym obwodem magnetycznym, po wykonaniu operacji na funkcji koenergii
przewidzianych w równaniach Lagrange’a, przyjmują postaci

n

n

u

i

t

=

⋅

+

ψ

n

n

R

d

d

dla

)

N

,...,

2

,

1

(

=

n

ϕ

∂

∂

+

=

ϕ

+

ϕ

ko

z

2

2

d

d

D

d

d

J

E

m

t

t

Dalsze analizy procesów przetwarzania energii będą prowadzone przy założeniu liniowości obwodu
magnetycznego przetworników, czyli wykorzystujące macierz indukcyjności. W rzeczywistych
przetwornikach obwody magnetyczne są wykonywane z materiałów ferromagnetycznych, które
ulegają nasycaniu magnetycznemu. Opis przetworników równaniami zakładającymi liniowość
magnetyczną mogą prowadzić do rozbieżności między wartościami obliczanymi z tych równań oraz
mierzonymi w rzeczywistym przetworniku.

↑

***************************************************************************↑

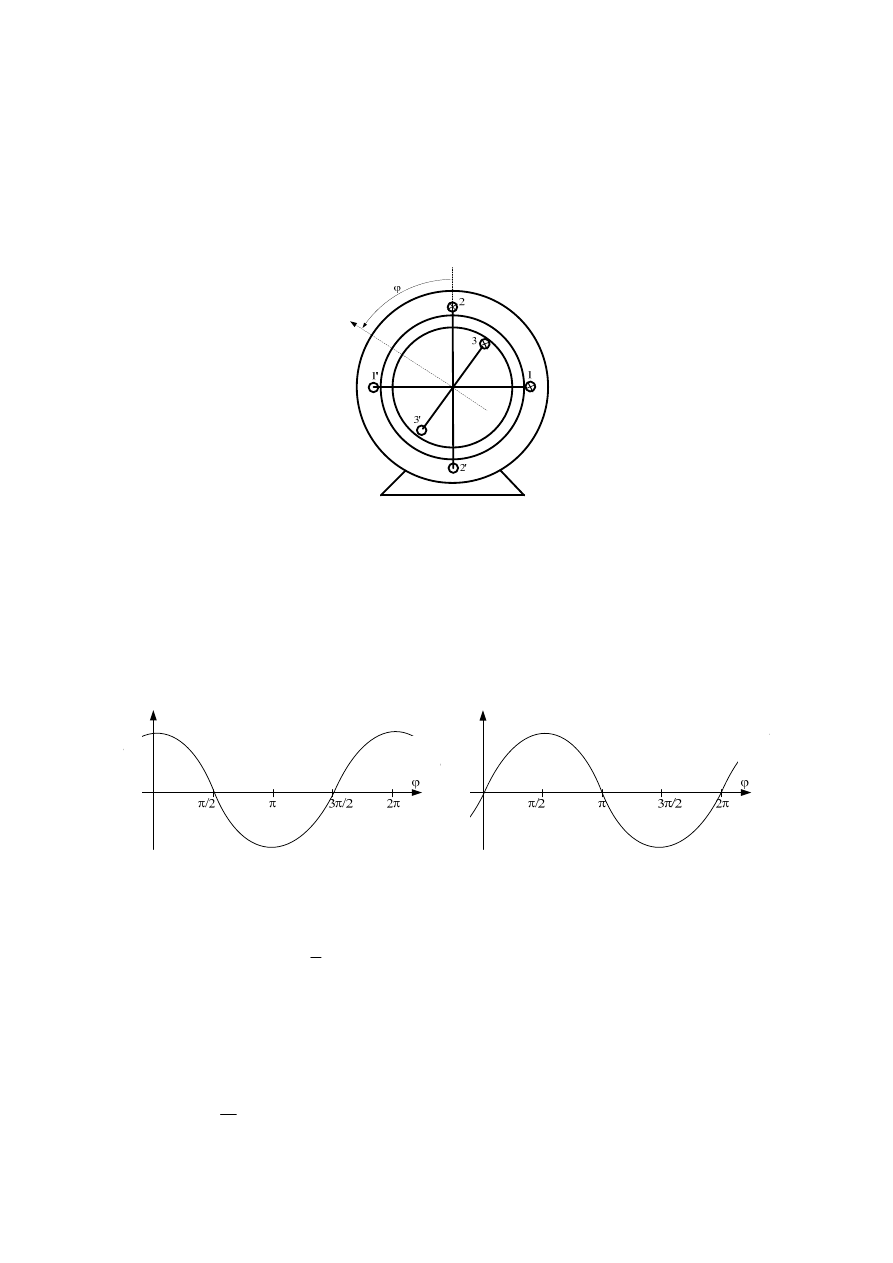
9

Przykłady

P. 3.1/. Dla przetwornika elektromechanicznego cylindrycznego o ruchu obrotowym określić

jakościowo aproksymowane zależności indukcyjności od kąta obrotu

ϕ

zakładając, że cewki

na części nieruchomej (stojanie) posiadają taką samą liczbę zwojów, a następnie zapisać
funkcję ko-energii dla tych cewek i na tej podstawie bezpośrednio utworzyć równania
Lagrange’a.

W przetworniku cylindrycznym jedynie indukcyjności wzajemne pomiędzy cewkami stojana i wirnika
(

1

,

3

3

,

1

L

L

=

oraz

2

,

3

3

,

2

L

L

=

) zależą od kąta obrotu

ϕ

, natomiast pozostałe indukcyjności zarówno

własne jak i wzajemne są stałe ze względu na gładkość szczeliny powietrznej. Sprzężenia
magnetyczne dla prostopadłego wzajemnego ustawienia osi cewek są równe zero natomiast, gdy osie
cewek są równoległe sprzężenia osiągają maksima i mogą być zgodne lub przeciwne w zależności od
strzałkowania. Indukcyjności pomiędzy przemieszczającymi się kątowo uzwojeniami stojana i wirnika
można w pierwszym przybliżeniu aproksymować funkcjami sinusoidalnymi, które dla rozważanego
przypadku przedstawiają się następująco

)

cos(

M

)

(

L

1,3

ϕ

⋅

=

ϕ

)

sin(

M

)

(

L

2,3

ϕ

⋅

=

ϕ

Forma kwadratowa ko-energii uzwojeń może, zatem być zapisana następująco

[

]





















⋅





















ϕ

ϕ

ϕ

ϕ

⋅

=

3

2

1

3

,

3

3,2

3,1

,3

2

2

,

2

,1

2

,3

1

,2

1

,1

1

3

2

1

ko

L

)

(

L

)

(

L

)

(

L

L

L

)

(

L

L

L

2

1

i

i

i

i

i

i

E

Równania napięciowe przetwornika zgodnie z przedstawionymi wcześniej wyprowadzeniami
przybierają formę





















⋅





















−





















=









































⋅





















ϕ

ϕ

ϕ

ϕ

3

2

1

3

2

1

3

2

1

3

2

1

3

,

3

3,2

3,1

,3

2

2

,

2

,1

2

,3

1

,2

1

,1

1

R

R

R

L

)

(

L

)

(

L

)

(

L

L

L

)

(

L

L

L

i

i

i

u

u

u

i

i

i

dt

d

10

natomiast równanie mechaniczne wygląda następująco

ω

−

+

=

ω

D

d

d

J

z

em

m

m

t

gdzie

[

]

3

2

3

1

3

2

,3

2

3

1

,3

1

3

2

1

3

,

3

3,2

3,1

,3

2

2

,

2

,1

2

,3

1

,2

1

,1

1

3

2

1

ko

em

)

cos(

M

)

sin(

M

)

(

L

)

(

L

)

L

)

(

L

)

(

L

)

(

L

L

L

)

(

L

L

L

(

2

1

i

i

i

i

i

i

i

i

i

i

i

i

i

i

E

m

ϕ

+

ϕ

−

=

ϕ

∂

ϕ

∂

+

ϕ

∂

ϕ

∂

=

=





















⋅





















ϕ

ϕ

ϕ

ϕ

ϕ

∂

∂

⋅

=

ϕ

∂

∂

=

W celu rozwiązania przedstawionego układu równań należy posłużyć się metodami numerycznymi,
które zazwyczaj wymagają sprowadzenia do postaci normalnej zgodnie z przykładem z rozdziału 2.

P. 3.2/. Zapisać zależność na ko-energię układu dwóch nieliniowych cewek, jeżeli funkcja opisująca

ich charakterystyki dana jest zależnością

2

2

1

2

2

1

2

2

2

1

2

1

1

1

)

(

A

4

L

M

)

(

A

4

M

L

i

i

i

i

i

i

i

i

+

+

=

ψ

+

+

=

ψ

Rozwiązanie bazować będzie na ogólnej zależności przedstawiającej funkcję ko-energii układu cewek

sprzężonych

∑∫

=

ϕ

ψ

=

N

1

0

2

1

ko

'

)

,

0

,...,

0

,

'

,...,

,

(

n

i

n

n

n

n

di

i

i

i

E

, więc dla naszego dwuwymiarowego przypadku,

gdy

2

N

=

wyrażenie to sprowadza się po postaci

∫

∫

ψ

+

ψ

=

2

1

0

2

2

1

2

0

1

1

1

ko

'

)

'

,

(

'

)

0

,

'

(

i

i

di

i

i

di

i

E

Po podstawieniu zależności opisujących charakterystyki cewek i wykonaniu całkowań otrzymamy

2

2

2

1

2

2

2

2

1

2

1

2

1

1

2

1

0

2

2

2

1

2

2

1

0

1

2

1

1

1

ko

)

(

)

(

A

2

)

(

L

M

)

(

L

'

)

'

)

(

A

4

'

L

(M

'

)

)

0

(

'

A

4

0

M

'

(L

2

1

i

i

i

i

i

i

di

i

i

i

i

di

i

i

E

i

i

+

+

+

=

=

+

+

+

+

⋅

+

=

∫

∫

Zadania

Zad. 3.1/. Dla układu z rysunku zapisać funkcję Lagrange’a oraz odpowiadające jej równania

u(t)

L

1

L

2

M

C

R

1

R

2

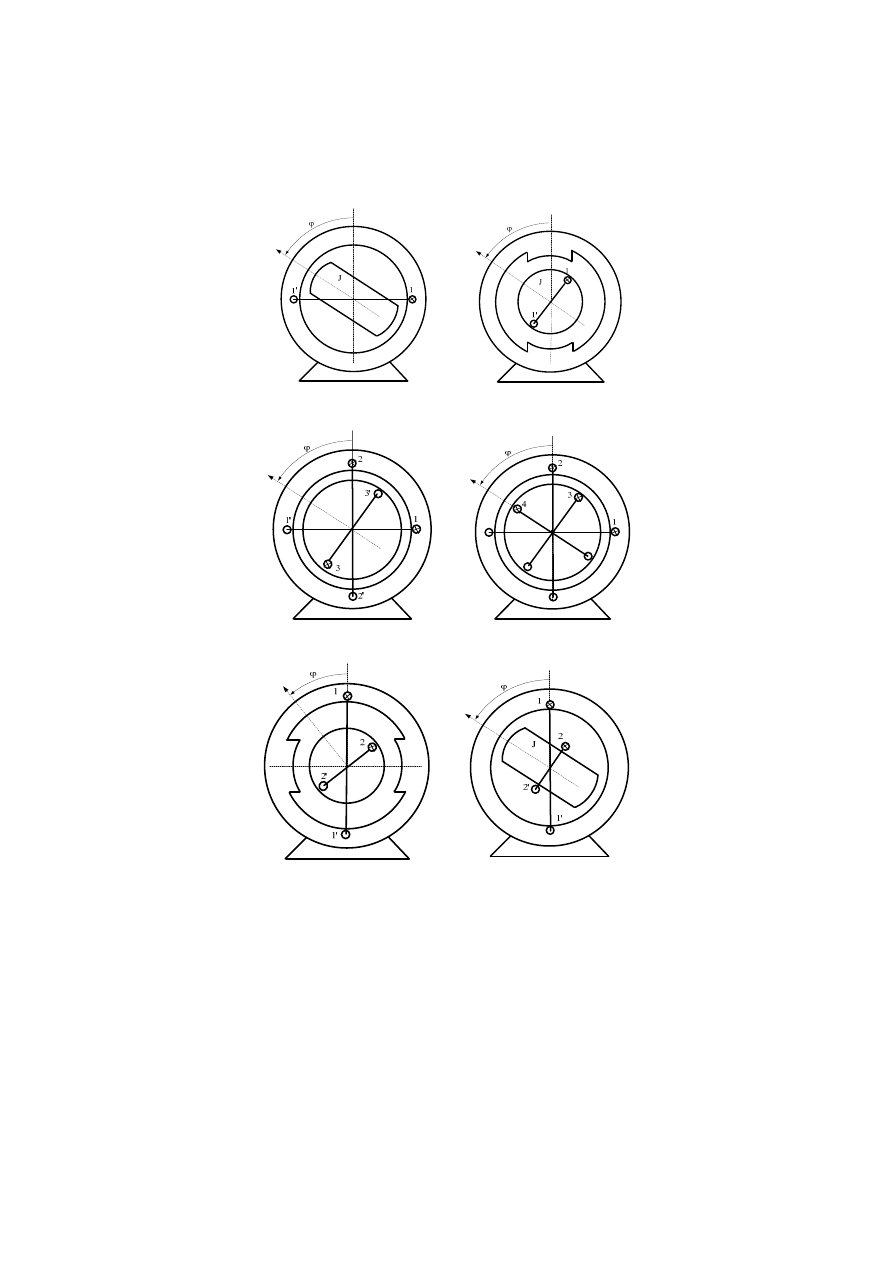
11

Zad. 3.2/. Dla przetworników elektromechanicznych o ruchu obrotowym z poniższych rysunków

określić jakościowo zależności indukcyjności od kąta położenia części ruchomej

ϕ

,

a następnie zapisać formę kwadratową ko-energii i na tej podstawie zapisać bezpośrednio
równania Lagrange’a.

a/. b/.

1'

2'

3'

4'

c/. d/.

e/. f/.