X L V I I I K O N F E R E N C J A N AU K O W A
KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN
I KOMITETU NAUKI PZITB
Opole – Krynica
2002
Piotr IWICKI
1
ANALIZA WPŁ YWU NAPRĘ Ż EŃ POWALCOWNICZYCH
I POSPAWALNICZYCH NA SIŁ Ę KRYTYCZNĄ WYBOCZENIA
SKRĘ TNEGO PRĘ TA DWUTEOWEGO
1. Wstę p
Po procesie walcowania belek dwuteowych oraz po spawaniu blachownic stalowych
pozostają naprężenia własne. Przyjmuje się ró żne rozkłady tych naprężeń w przekroju
poprzecznym pręta. W pracy rozpatrzono trzy modele rozkładu naprężeń w przekroju
poprzecznym pręta. Zbadano wpływ tych naprężeń na siłę krytyczną wyboczenia skrętnego
pręta o przekroju dwuteowym. Przyjęto klasyczne założenia teorii prętó w cienkoś ciennych
[1]. Za pomocą metod analizy wrażliwoś ci [2] wyznaczono wariację siły krytycznej na skutek
zmian wartoś ci naprężeń pospawalniczych i powalcowniczych. Uzyskano linie wpływu zmian
siły krytycznej przy wariacji naprężeń wzdłuż długoś ci pręta.
2. Wariacja siły krytycznej przy uwzglę dnieniu naprę ż eń pospawalniczych
i powalcowniczych
2.1. Wpływ naprę ż eń na siłę krytyczną wyboczenia skrę tnego
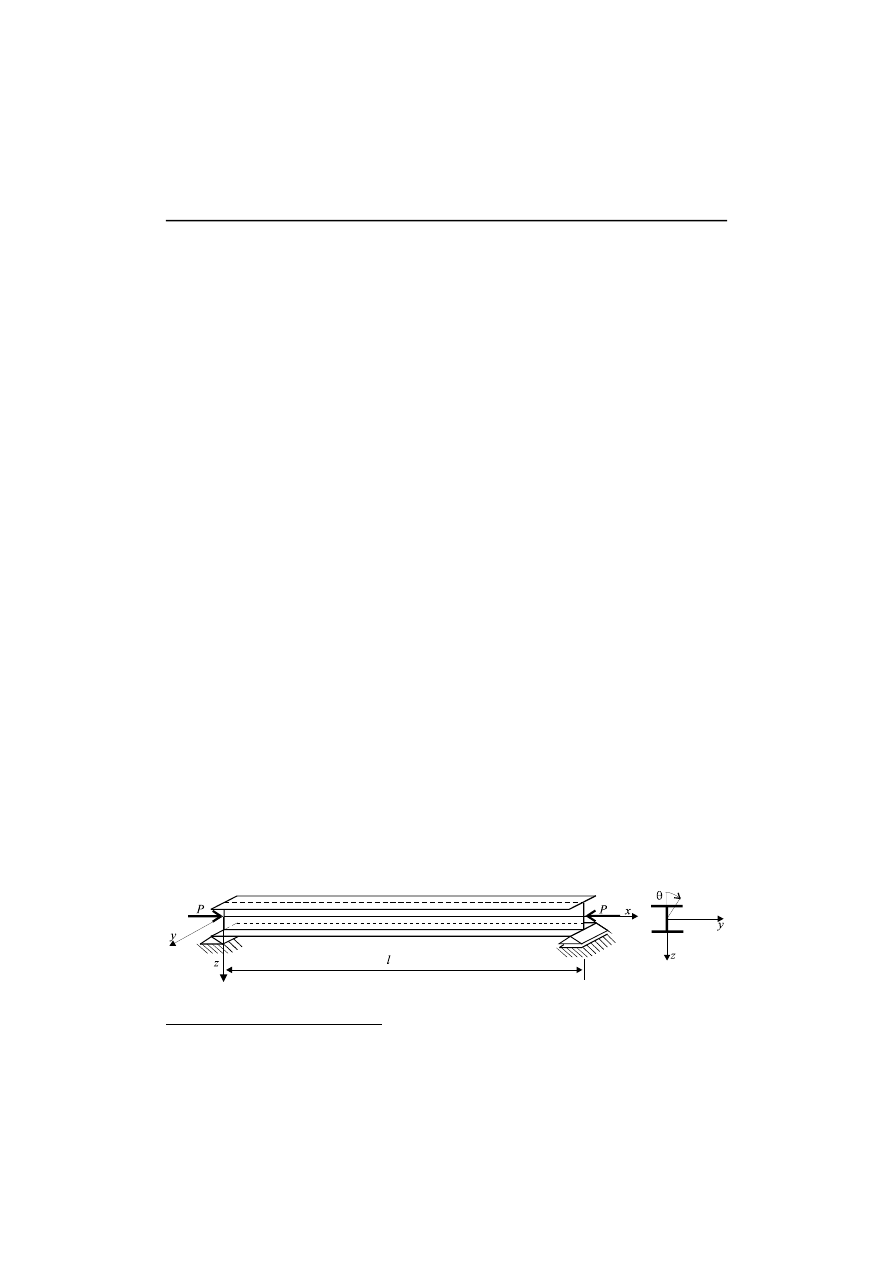
Rozpatrzmy pręt o przekroju dwuteowym osiowo ś ciskany siłą P (rys. 1). Po walcowaniu lub
spawaniu w przekroju poprzecznym pręta występuje samo ró wnoważący się stan naprężeń .
W literaturze dotyczą cej tego zagadnienia oraz w przepisach normowych można znaleźć
ró żne rozkłady tych naprężeń [3], [4] (rys. 2, 4, 5).
Rys. 1. Pręt cienkoś cienny
1
Dr inż., Wydział Inżynierii Lą dowej, Politechnika Gdań ska
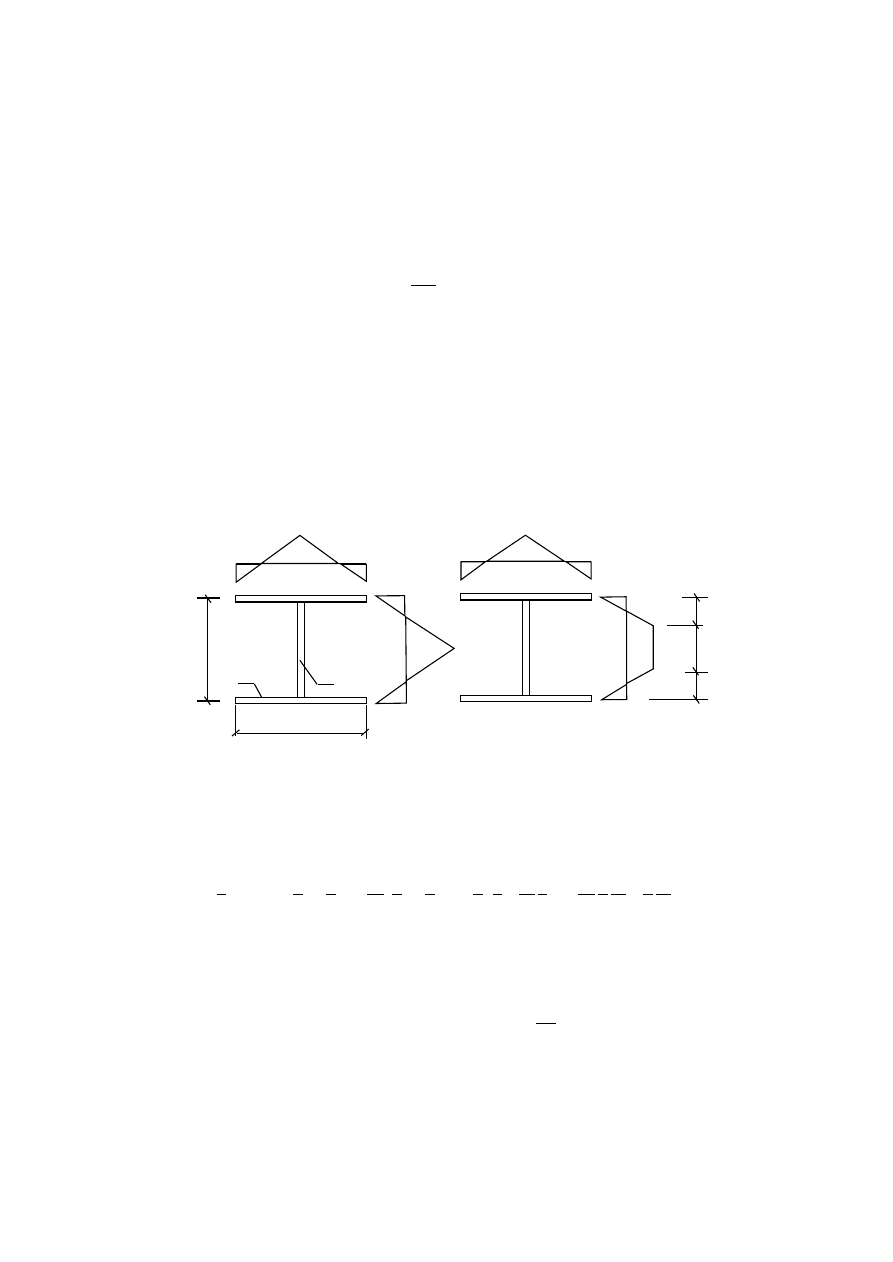
62
Wpływ naprężęń w ró żniczkowym ró wnaniu ró wnowagi pręta opisać można za pomocą stałej
R
w
[1]
:
(
)
,
0
0
=
¢
÷
÷
ø
ö
ç
ç
è
æ
Q¢
÷
÷
ø
ö
ç
ç
è
æ
-
-
+
²
Q ¢¢
w
s
kr
R
J
G
A
J
P
EJ
w
(1)
gdzie stała
w
R opisana jest zależnoś cią :
(
)
+
=
2
2
dA
y
z
R
xw
A
w
s
ò
,
(2)
natomiast
w
EJ jest sztywnoś cią bimomentową pręta, P
kr
oznacza siłę krytyczną ,
0
J jest
biegunowym momentem bezwładnoś ci,
S
GJ sztywnoś cią czystego skręcania,
xw
s
są
naprężeniami normalnymi a
Q
oznacza ką t skręcenia przekroju poprzecznego pręta.
Rys. 2. Rozkład naprężeń powalcowniczych lub pospawalniczych
w przekroju poprzecznym pręta
Rozważono trzy rozkłady naprężeń własnych w przekroju poprzecznym pręta. Dla
pierwszego z analizowanych rozkładó w naprężeń (rys. 2.a) wykorzystują c zależnoś ć (2)
możemy obliczyć stałą
w
R :
ïþ
ï
ý
ü
ú
û
ù
ê
ë
é
-
+
÷
ø
ö
ç
è
æ
+
ú
ú
û
ù
ê
ê
ë
é
÷
ø
ö
ç
è
æ
+
ïî
ï
í
ì
-
÷
ø
ö
ç
è
æ
+
´
w
f
w
f
f
w
f
w
t
t
h
b
t
t
h
b
σ
σ
t
t
b
h
b
h
σ
σ
b
h
b
t
R
2
1
3
2
2
1
2
3
2
1
3
2
4
1
2
1
6
1
4
1
=
s
(3)
Znak stałej
w
R zależy jednak od relacji wymiaró w przekroju poprzecznego i wartoś ci
przyjmowanych naprężeń . Na przykład dla
f
w
t
t
h
b
=
=
,
otrzymamy zależnoś ć:
÷÷
ø
ö
çç
è
æ
-
´
2
1
3
2
1439
.
1
1
0.29167
=
s
s
s
b
t
R
f
w
,
(4)
/
1
s
h/4
h/2
h/4
/
1
s
/
2
s
/
2
s
/
3
s
+
/
3
s
/
1
s
/
1
s
/
2
s
/
2
s
b
h
t
w
t
f
+
+
+
+
+
a)
b)
63
w któ rej dla:
0
875
.
0
,
0
875
.
0
2
1
2
1
>
®
<
<
®
>
w
w
R
R
s
s
s
s
.
(5)
Analogiczne rozumowanie można przedstawić dla rozkładu naprężeń przedstawionych na
rys. 2b. Stała
w
R opisana jest wzorem:
ïþ
ï
ý
ü
ú
ú
û
ù
ê
ê
ë
é
÷÷
ø
ö
çç
è
æ
-
-
÷
ø
ö
ç
è
æ
+
÷
÷
ø
ö
ç
ç
è
æ
÷
ø
ö
ç
è
æ
+
ïî
ï
í
ì
-
÷
ø
ö
ç
è
æ
+
´
2
1
3
2
2
1
2
2
3
1
3
5
1
8
1
2
1
6
1
4
1
=
σ
σ
h
b
t
t
b
h
t
t
b
h
σ
σ
b
h
b
t
R
w
f
f
w
f
w
s
(6)
Zakładają c, że
f
w
t
t
h
b
=
=
,
znak
w
R zależy ró wnież od proporcji naprężeń
2
1
s
s
:
÷÷
ø
ö
çç
è
æ
-
´
2
1
3
2
1923
.
1
1
0.27083
=
s
s
s
b
t
R
f
w
(7)
0
8387
.
0
,
0
8387
.
0
2
1
2
1
>
®
<
<
®
>
w
w
R
R
s
s
s
s
(8)
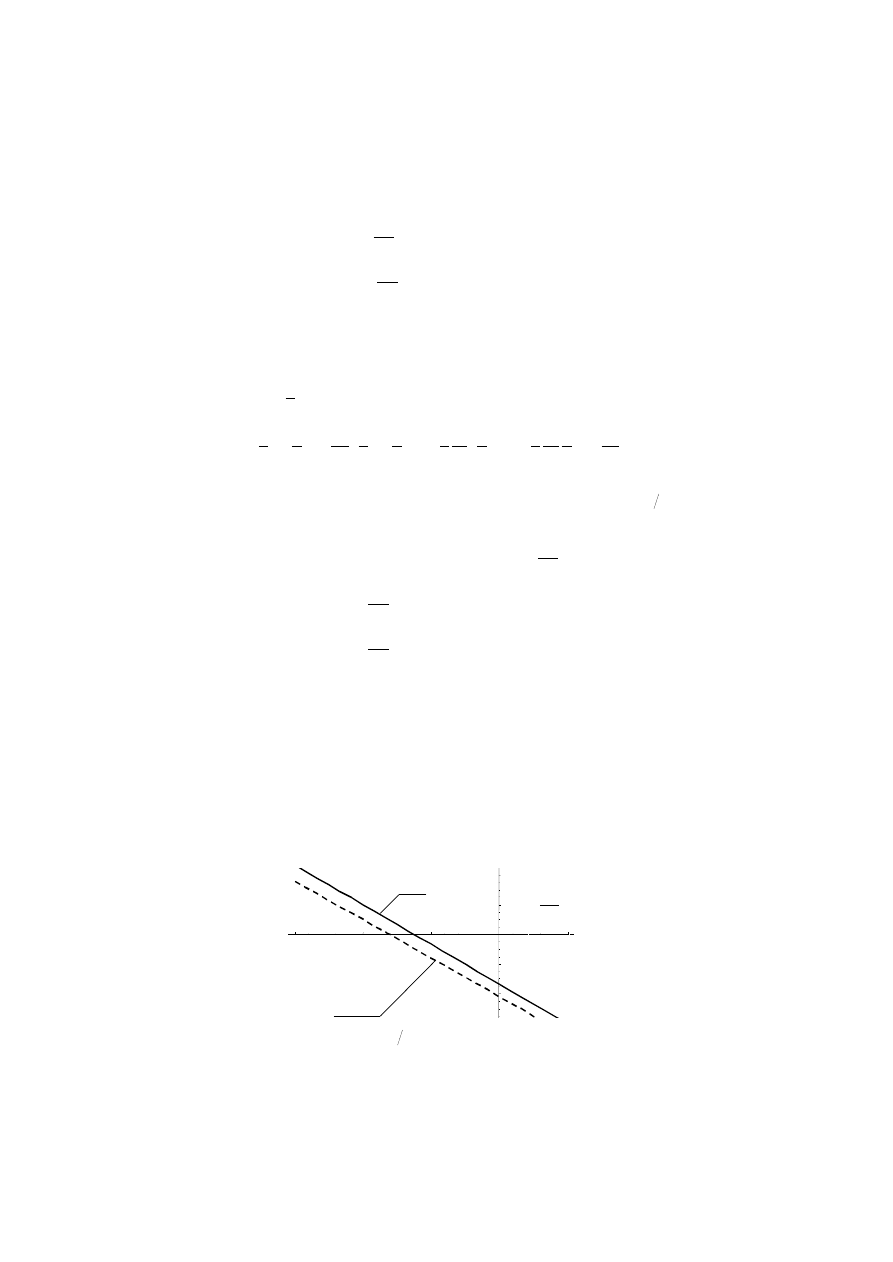
Zależnoś ć stałej
w
R od przyjętych proporcji naprężeń w przekroju poprzecznym pręta
przedstawiono graficznie na rys.3 przyjmują c, że:
f
w
t
t
h
b
=
=
,
. Rozkład naprężeń
pospawalniczych lub powalcowniczych powinien być ś ciś le okreś lony, tak aby nie budził
wą tpliwoś ci co do wpływu tych naprężeń na siłę krytyczną wyboczenia skrętnego pręta. Dla
dodatnich wartoś ci
w
R otrzymalibyś my bowiem wzrost siły krytycznej co ś wiadczyłoby o
korzystnym wpływie naprężeń na statecznoś ć konstrukcji. Polska norma [5] w ogó le nie
precyzuje zalecanych rozkładó w naprężeń pospawalniczych lub powalcowniczych co należy
uznać za pewien mankament tej normy.
2
1
s
s
2
1
s
s
0.7
0.8
0.9
1.1
-0.2
0.2
0.4
Rw1
Rw2
2
1
s
s
Rys. 3. Zależnś ć stałej
w
R od
2
1
s
s
dla powyższych wariantó w rozkładu naprężeń
64
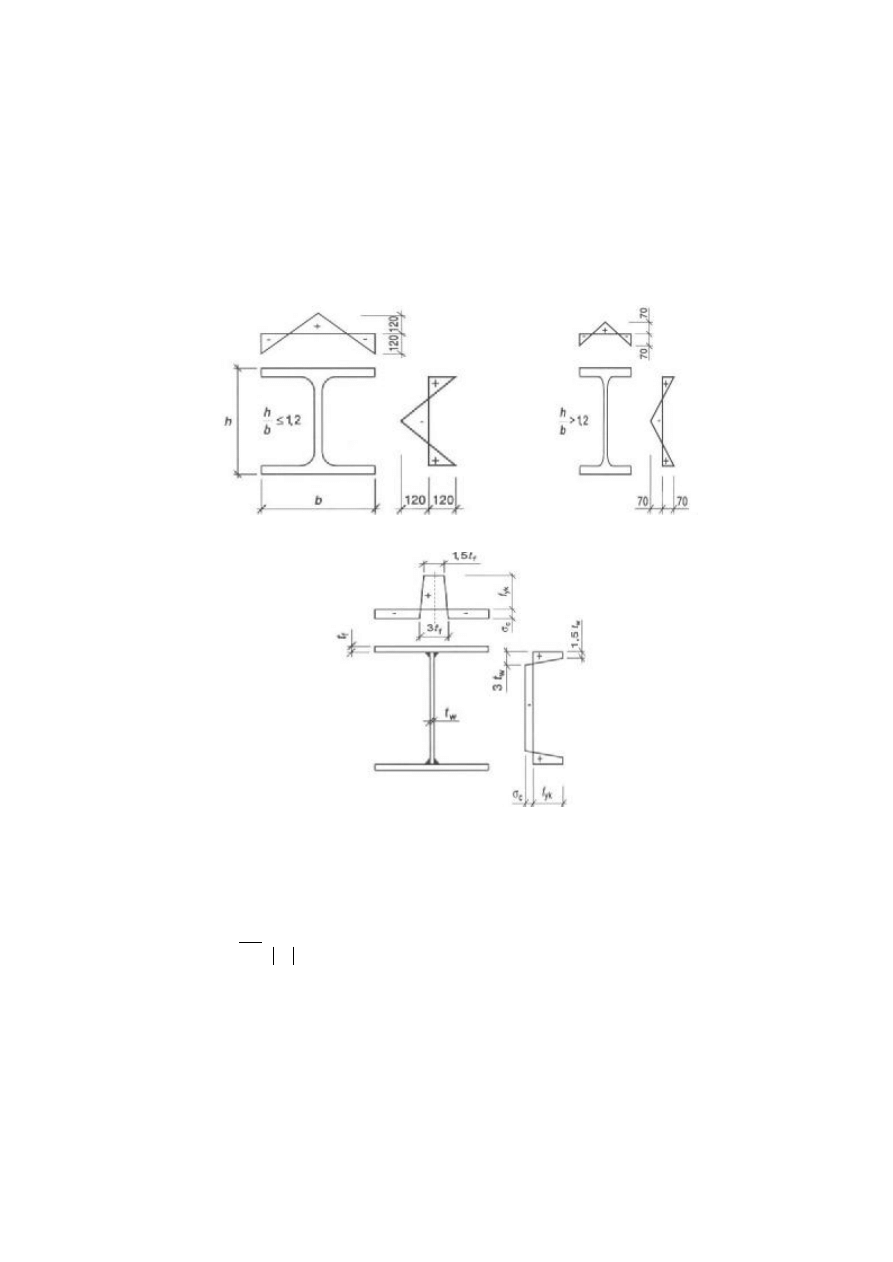
Natomiast w szwedzkiej normie dotyczą cej konstrukcji stalowych [4] nie tylko okreś la się
rozkłady naprężeń powalcowniczych (rys. 4) i pospawalniczych (rys. 5) ale ró wnież
precyzuje się wartoś ci tych naprężeń w ró żnych typach prętó w dwuteowych. Rozkład
naprężeń powalcowniczych odpowiada wcześ niej przedstawionemu na rys. 2a z tym, że
okreś lenie wartoś ci naprężeń nie powoduje wą tpliwoś ci co do znaku stałej
w
R .
Rys. 4. Rozkład naprężeń powalcowniczych według normy [4]
Rys. 5. Rozkład naprężeń pospawalniczych według normy [4]
Dla rozkładu naprężeń pospawalniczych z rys. 5 wykorzystują c zależnoś ć (2) można obliczyć
wspó łczynnik
w
R :
(
)
(
)
÷
÷
÷
÷
ø
ö
ç
ç
ç
ç
è
æ
÷
÷
ø
ö
ç
ç
è
æ
+
-
+
-
+
+
+
-
-
´
+
+
+
+
-
´
=
4
3
2
2
3
4
2
2
2
2
3
2
2
2
4
3
4
w
1620
1008
216
16
405
216
96
32
216
1620
1008
405
192
1
w
w
w
w
f
f
f
f
c
w
f
w
w
f
yk
t
ht
t
h
t
h
t
t
h
t
bh
t
b
t
t
h
t
ht
t
f
R
s
,
(9)
gdzie
c
s
oznacza naprężenia ś ciskają ce w przekroju poprzecznym pręta wynikają ce z warunku
ró wnowagi sił normalnych a
yk
f
oznacza wytrzymałoś ć charakterystyczną materiału pręta.
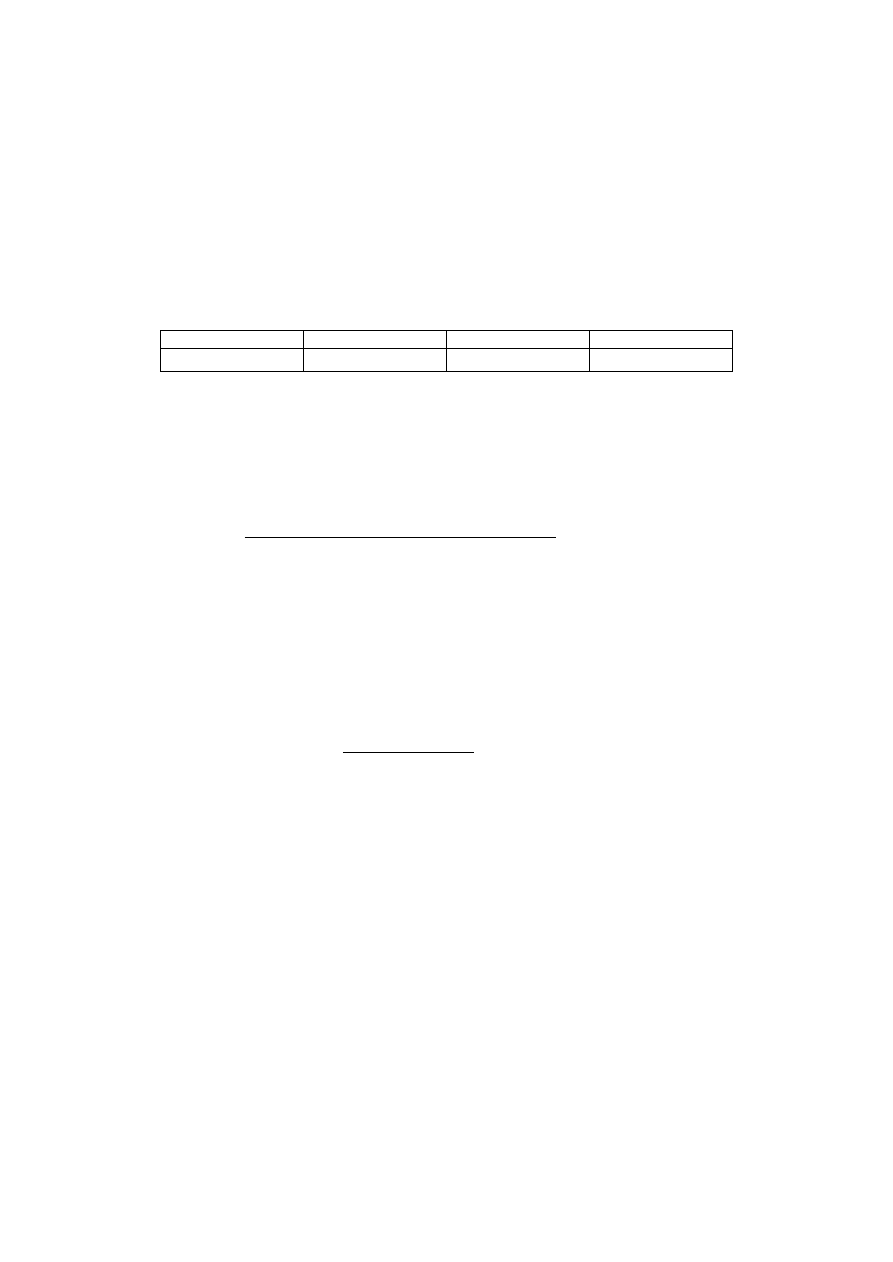
65
Przy założeniu
MPa
f
yk
210
2
1
=
=
=
s
s
oraz dla wymiaró w przekroju poprzecznego pręta
z przykładu numerycznego (rys. 6) poró wnano wartoś ci stałej
w
R dla trzech
przedstawionych rozkładó w naprężeń (tab. 1). Najbardziej niekorzystne zmniejszenie siły
krytycznej wyboczenia skrętnego pręta wystą piłoby w przypadku rozkładu nr 2.
Tablica 1. Poró wnanie stałej
w
R dla ró żnych schemató w naprężeń
Rozkład 1 (rys.2a)
Rozkład 2 (rys.2b)
Rozkład 3 (rys.5)
w
R [kNm
2
]
-0.7
-0.875
-0.233
2.2. Wariacja siły krytycznej prę ta
Pierwsza wariacja siły krytycznej wyboczenia skrętnego pręta w zależnoś ci od wariacji
zmiennych projektowych dana jest wzorem [6]:
(
)
(
)
( )
(
)
( )
udx
x
dx
r
dx
u
r
P
GJ
EJ
P
l
u
l
l
u
cr
u
d
u
d
d
d
w
ò
ò
ò
L
=
Q¢
Q¢
-
Q¢
+
Q ¢¢
=
0
0
2
2
0
0
2
2
0
2
2
kr
,
,
,
,
(10)
gdzie u oznacza zmienną projektową a (..), oznacza ró żniczkowanie względem zmiennej
projektowej. Uwzględniają c ró wnanie (1) można wyznaczyć pierwszą wariację siły
krytycznej wyboczenia skrętnego pręta w zależnoś ci od wariacji zmiennych opisują cych
naprężenia pospawalnicze lub powalcownicze w następują cej formie:
( )
(
)
( )
udx
x
dx
r
dx
u
R
P
l
u
P
l
l
u
w
kr
d
d
d
ò
ò
ò
L
=
Q¢
Q¢
=
0
0
2
2
0
0
2
kr
,
.
(11)
Funkcja
( )
x
u
P
kr
L
jest linią wpływu wariacji siły krytycznej przy jednostkowych zmianach
parametró w okreś lają cych wartoś ci naprężeń pospawalniczych lub powalcowniczych wzdłuż
długoś ci pręta co wyjaś niono na poniższym przykładzie.
3. Przykład numeryczny
Dla pręta cienkoś ciennego ś ciskanego siłami
2
1
, P
P
(rys. 6) wyznaczono pierwszą wariację
siły krytycznej wyboczenia skrętnego w zależnoś ci od wariacji naprężeń powalcowniczych
1
s
, przyjmują c rozkład naprężeń zgodny z modelem przedstawionym na rys. 2a. Przyjęto
ró wnież, że naprężenia powalcownicze
1
s
=100MPa. W analizie uwzględniono ró żne relacje
sił ś ciskają cych w poszczegó lnych częś ciach pręta, oznaczają c przez k stosunek sił
66
ś ciskają cych (
(
)
1
2
1
P
P
P
k
+
=
). Przy uwzględnieniu naprężeń powalcowniczych siła
krytyczna wyboczenia skrętnego pręta wynosi P
kr0
=1295.2 kN (dla k = 2), podczas gdy przy
pominięciu wpływu naprężeń powalcowniczych siła krytyczna jest większa tylko o około
1.59% i wynosi 1315.8 kN. Z przytoczonego przykładu wynika, że wpływ naprężeń
powalcowniczych na siłę krytyczną wyboczenia skrętnego pręta jest w tym przypadku
nieduży, ale nie jest on wcale jednakowy w poszczegó lnych częś ciach pręta.
L=8.0m
b=0.2m
h=0.2m
g=0.01m
t=0.01m
E=210GPa
G=80.77GPa
x
z
y
x =3.6m
P
P
P
02
2
1
1+2
Rys. 6. Pręt cienkoś cienny ś ciskany siłami P
1
i P
2
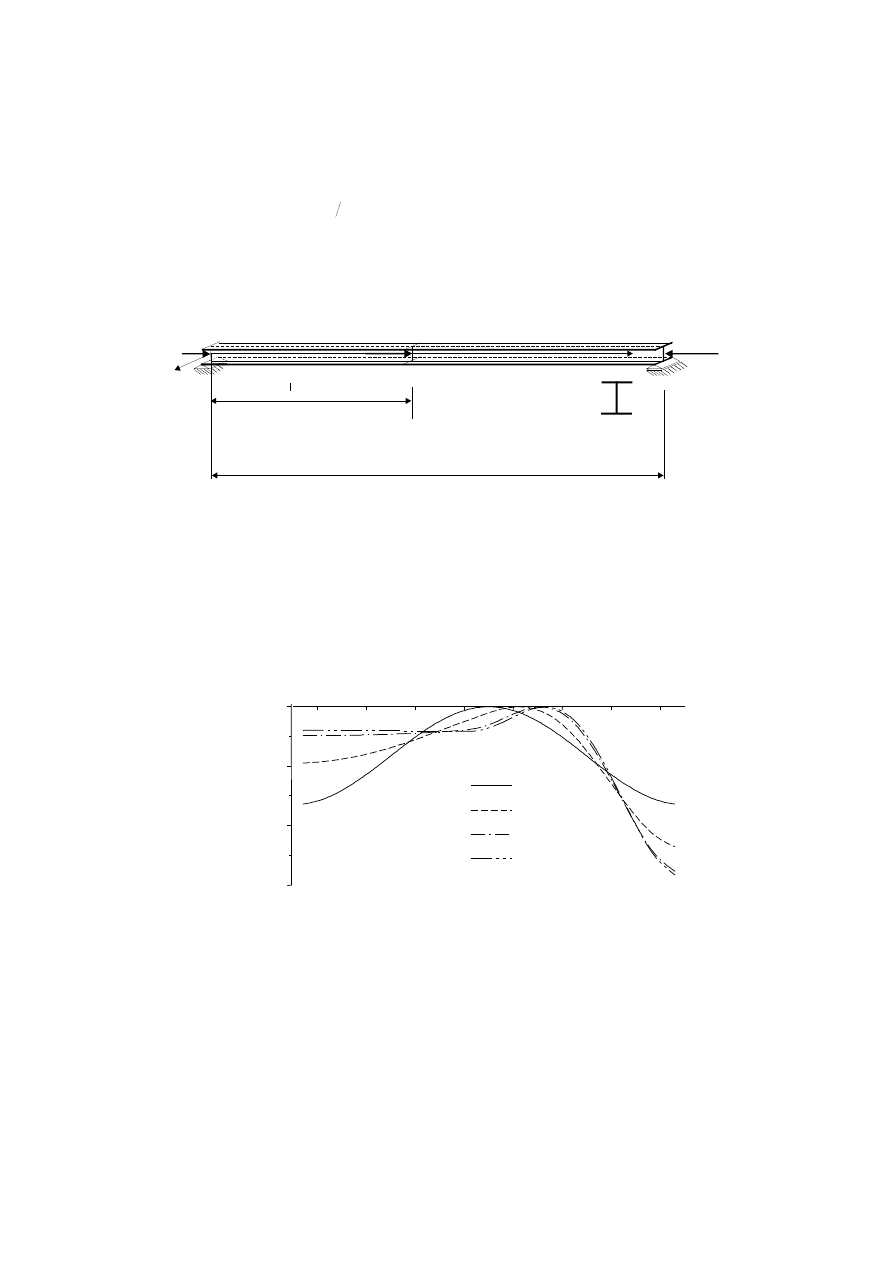
Zilustrowane to zostało na rys.7. Przedstawiono tutaj linie wpływu względnej wariacji siły
krytycznej przy jednostkowych zmianach naprężeń powalcowniczych wzdłuż długoś ci pręta.
Jak widać bezwzględne wartoś ci na wykresie wzrastają w pobliżu podpó r pręta dla
okreś lonej proporcji sił ś ciskają cych, natomiast wraz ze wzrostem wspó łczynnika k wpływ
naprężeń w bardziej obcią żonej częś ci pręta zaczyna dominować. Wszystkie wartoś ci
odniesiono do począ tkowej wartoś ci siły krytycznej (dla k=2 i
1
s
=100MPa).
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
x [m]
-6.0E-7
-4.0E-7
-2.0E-7
0.0E+0
L
P
kr
s
/
P
kr
[1/
m ]
k=1
k=2
k=5
k=8
1
Rys. 7. Linia wpływu względnej wariacji siły krytycznej wyboczenia skrętnego pręta
przy jednostkowych wariacjach naprężeń powalcowniczych wzdłuż długoś ci pręta
Wykres z rys. 7 ma jeszcze inne praktyczne znaczenie polegają ce na tym, że przy
założeniu pewnych wariacji naprężeń wzdłuż długoś ci pręta i scałkowaniu wykresu uzyskać
można liniową aproksymację ś cisłej zależnoś ci względnej siły krytycznej wyboczenia
skrętnego od względnych naprężeń powalcowniczych (rys. 8). Jak widać przebieg
rzeczywistej funkcji względnej siły krytycznej wyboczenia skrętnego od względnych
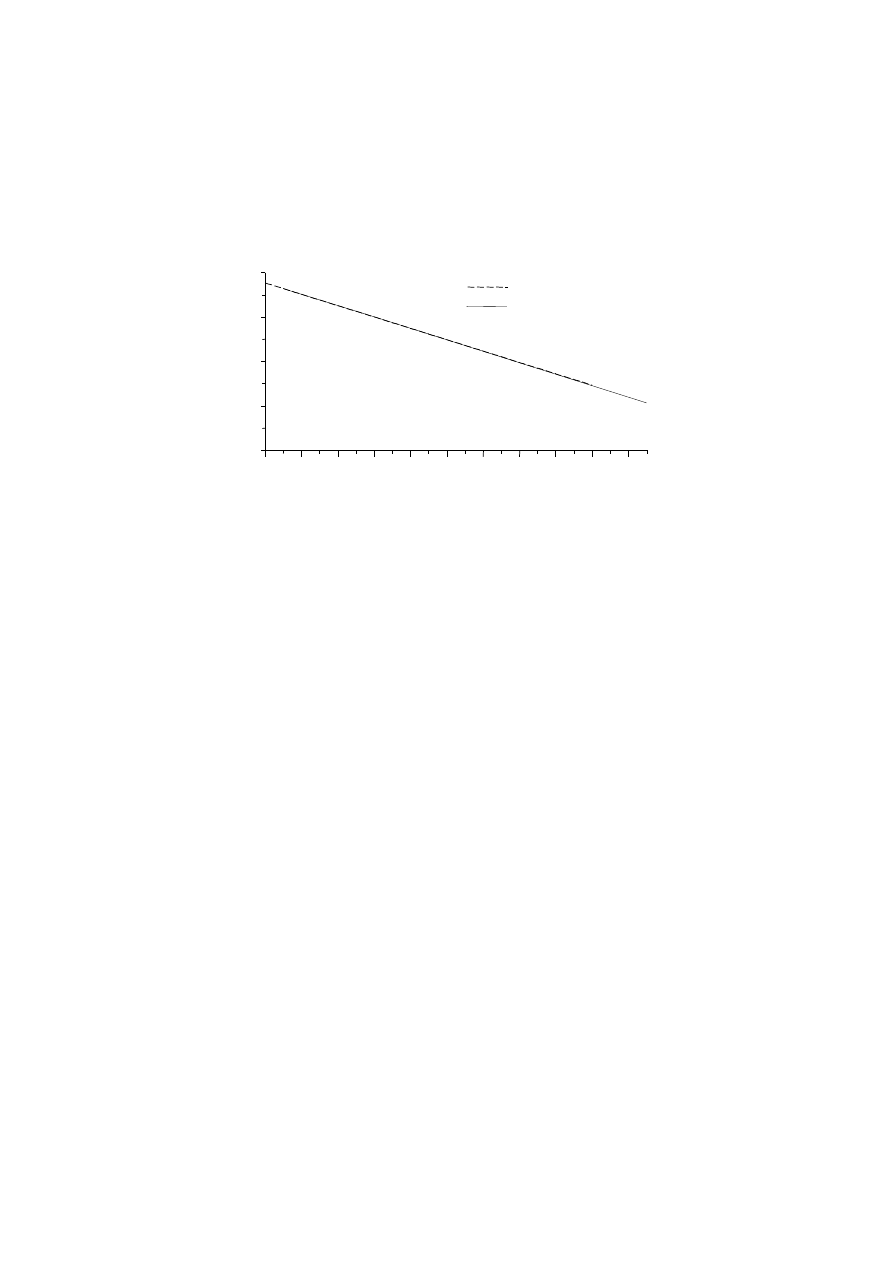
67
naprężeń powalcowniczych jest też prostoliniowy a więc analiza wrażliwoś ci pozwala łatwo
okreś lić funkcję rzeczywistą .
0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4
s
1
/
s
10
0.7
0.8
0.9
1.0
1.1
P
kr
/
P
kr0
analiza wrażliwości k=2
rozwią zanie ścisłe
Rys. 8. Aproksymacji liniowa ś cisłej zależnoś ci względniej siły krytycznej wyboczenia
skrętnego przy stałej wariacji naprężeń powalcowniczych wzdłuż długoś ci pręta ( k =2)
4. Wnioski końcowe
Z przeprowadzonej analizy wynika, że naprężenia pospawalnicze i powalcownicze mają
niekorzystny wpływ na pracę pręta, gdyż powodują one spadek siły krytycznej. Wpływ ten
jest największy w strefach przypodporowych oraz tam gdzie występują większe siły
ś ciskają ce.
Z poró wnania liniowego rozkładu naprężeń z rozkładem zmieniają cym się skokowo,
zakładają cym pewną lokalizację stref plastycznych w pobliżu spoin (3t
w
,3t
f
)
wynika, że przy
tych samych wartoś ciach naprężeń , większy wpływ na siłę krytyczną mają naprężenia o
rozkładzie liniowym.
Analiza wrażliwoś ci pozwala na przybliżone wyznaczenie wariacji siły krytycznej pręta
cienkoś ciennego przy wariacji naprężeń powalcowniczych lub pospawalniczych bez potrzeby
dokonywania ponownej analizy konstrukcji.
Literatura
[1] VLASOV, V. Z., Thin walled elastic beams. Israel Program for Scientific Translations.
Jerusalem, Israel, 1961.
[2] HAUG E. J., CHOI K. K., KOMKOV V., Design sensitivity analysis of structural
system. Academic Press, Orlando, (1986).
[3] RYKALUK K., Pozostają ce naprężenia spawalnicze w wybranych stanach
granicznych nośności. Wydawnictwo Politechniki Wrocławskiej, Wrocław, (1981).
[4] Boverkets handbok om stalkonstruktioner. Boverket, Byggavdelningen. Stockholm,
Sverige 1994.
[5] PN-90/B-03200 Konstrukcje stalowe. Obliczenia statyczne i projektowanie.
[6] SZYMCZAK Cz., Analiza wrażliwoś ci obcią żeń krytycznych prętó w cienkoś ciennych.
XLII Konferencja Naukowa KILiW PAN i KN PZITB, Krakó w-Krynica,t.2, (1996),
169-176.
68
INFLUENCE OF INITIAL WELDING AND ROLLING STRESSES
ON THE CRITICAL TORSIONAL LOAD OF THIN-WALLED
COLUMNS WITH BISYMMETRIC CROSS-SECTION
Summary
The influence of initial welding and rolling stresses on the critical torsional load of the thin-
walled column with bisymmetric open cross-section has been investigated. The
considerations are based on the classical assumptions of the theory of thin-walled beams
with nondeformable cross-section. The first variation of the critical torsional load of the
column due to a variation of welding and rolling stresses derived. Three stress distribution
models are taken into account. The graphs of influence lines of the critical torsional load
variation due to some variations of the design variables are presented.