www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
T
O ˙ZSAMO ´SCI TRYGONOMETRYCZNE
Bogactwo to ˙zsamo´sci trygonometrycznych jest niew ˛
atpliwie ´zródłem frustracji niejednego
ucznia – trzeba du ˙zo wprawy, ˙zeby sprawnie si˛e nimi posługiwa´c. Z drugiej strony, dzi˛eki
tym to ˙zsamo´sciom ´swiat trygonometrii jest niezwykle ciekawy.
Jedynka trygonometryczna
Najpopularniejsz ˛
a to ˙zsamo´sci ˛
a trygonometryczn ˛
a jest jedynka trygonometryczna
sin
2
α
+
cos
2
α
=
1
Jedynk˛e musi zna´c ka ˙zdy i nale ˙zy my´sle´c, ˙ze pozwala ona zamienia´c sin
2
α
na cos
2
α
i od-
wrotnie.
Zbadajmy zbiór warto´sci funkcji f
(
x
) =
3 sin
2
x
+
5 cos
2
x.
Z jedynki trygonometrycznej mamy
f
(
x
) =
3
(
1
−
cos
2
x
) +
5 cos
2
x
=
3
+
2 cos
2
x.
Korzystaj ˛
ac teraz z nierówno´sci 0
6
cos
2
x
6
1 łatwo uzasadni´c, ˙ze zbiór warto´sci
f
(
x
)
to przedział
h
3, 5
i
.
Wzory redukcyjne
Jest wiele wzorów redukcyjnych i dokładnie omówili´smy je w
o wzorach reduk-
cyjnych. Najwa ˙zniejsze z nich to
sin
π
2
−
x
=
cos x
cos
π
2
−
x
=
sin x
sin
π
2
+
x
=
cos x
cos
π
2
+
x
= −
sin x
sin
(
π
−
x
) =
sin x
cos
(
π
−
x
) = −
cos x
sin
(
π
+
x
) = −
sin x
cos
(
π
+
x
) = −
cos x.
oraz
tg
π
2
−
x
=
ctg x
ctg
π
2
−
x
=
tg x
tg
π
2
+
x
= −
ctg x
ctg
π
2
+
x
= −
tg x
tg
(
π
−
x
) = −
tg x
ctg
(
π
−
x
) = −
ctg x
tg
(
π
+
x
) =
tg x
ctg
(
π
+
x
) =
ctg x.
Wzory te pozwalaj ˛
a przesuwa´c argument funkcji trygonometrycznych o wielokrotno´s´c
π
2
.
Ponadto wzory z
π
2
pozwalaj ˛
a zamienia´c funkcj˛e sinus/tangens na cosinus/cotangens i od-
wrotnie.
Materiał pobrany z serwisu
1
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Obliczmy tg
−
411π
4
.
Liczymy
tg
−
411π
4
= −
tg
411π
4
= −
tg
102π
+
3π
4
=
= −
tg
3π
4
= −
tg
π
2
+
π
4
=
ctg
π
4
=
1.
Rozwi ˛
a ˙zmy nierówno´s´c cos
π
4
+
x
sin
π
4
−
x
>
1.
Przekształcamy lew ˛
a stron˛e.
cos
π
4
+
x
sin
π
2
−
π
4
+
x
=
=
cos
π
4
+
x
·
cos
π
4
+
x
=
cos
2
π
4
+
x
.
Mamy zatem
cos
2
π
4
+
x
>
1
⇐⇒
cos
2
π
4
+
x
=
1
⇐⇒
cos
π
4
+
x
= ±
1
⇐⇒
π
4
+
x
=
kπ
⇐⇒
x
= −
π
4
+
kπ.
Podwojenie k ˛
ata
Mamy dwa niezwykle u ˙zyteczne wzorki
sin 2x
=
2 sin x cos x
cos 2x
=
cos
2
x
−
sin
2
x.
Korzystaj ˛
ac z jedynki trygonometrycznej, drugi z tych wzorów mo ˙zemy zapisa´c w postaci
cos 2x
=
2 cos
2
x
−
1
=
1
−
2 sin
2
x.
Wzory te bardzo cz˛esto wyst˛epuj ˛
a w zadaniach szkolnych, wi˛ec warto wyrobi´c sobie nawyk,
˙ze jak widzimy praw ˛
a stron˛e którego´s z tych wzorów, to dzwoni nam dzwoneczek sin 2x/
cos 2x.
Wyznaczmy zbiór warto´sci funkcji f
(
x
) =
sin 3x cos 3x.
Ze wzoru na sin 2x mamy
f
(
x
) =
sin 3x cos 3x
=
1
2
sin 6x.
A wi˛ec zbiór warto´sci funkcji f to przedział
h−
1
2
,
1
2
i
(bo zbiór warto´sci sin 6x to
przedział
h−
1, 1
i
).
Materiał pobrany z serwisu
2

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Rozwi ˛
a ˙zmy równanie sin
2
x
=
cos
2
x.
Ze wzoru na cos 2x, mo ˙zemy równanie przekształci´c nast˛epuj ˛
aco
cos
2
x
−
sin
2
x
=
0
cos 2x
=
0
2x
=
π
2
+
kπ
⇐⇒
x
=
π
4
+
kπ
2
, k
∈
C
.
Sumy i ró˙znice k ˛
atów
Wzory troch˛e ogólniejsze od wzorów na sinus/cosinus podwojonego k ˛
ata:
sin
(
x
+
y
) =
sin x cos y
+
sin y cos x
sin
(
x
−
y
) =
sin x cos y
−
sin y cos x
cos
(
x
+
y
) =
cos x cos y
−
sin x sin y
cos
(
x
−
y
) =
cos x cos y
+
sin x sin y.
W zasadzie wystarczy pami˛eta´c tylko pierwszy i trzeci z tych wzorów, dwa pozostałe do-
stajemy wstawiaj ˛
ac do nich
−
y zamiast y.
Oczywiste zastosowanie tych wzorów to mo ˙zliwo´s´c obliczenia funkcji trygonometrycz-
nych k ˛
ata x
+
y je ˙zeli znamy funkcje k ˛
atów x i y.
Obliczmy sin 75
◦
.
Liczymy
sin 75
◦
=
sin
(
30
◦
+
45
◦
) =
sin 30
◦
cos 45
◦
+
sin 45
◦
cos 30
◦
=
=
1
2
·
√
2
2
+
√
2
2
·
√
3
2
=
√
2
+
√
6
4
.
Uzasadnij, ˙ze je ˙zeli cos x
=
0 to sin
(
x
+
y
) =
sin
(
x
−
y
)
.
Na mocy powy ˙zszych wzorów mamy
sin
(
x
+
y
) =
sin x cos y
+
sin y cos x
=
sin x cos y
sin
(
x
−
y
) =
sin x cos y
−
sin y cos x
=
sin x cos y
=
sin
(
x
+
y
)
.
Materiał pobrany z serwisu
3

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Sumy i ró˙znice funkcji
Ostatnia seria wzorków to wzory na sumy i ró ˙znice sinusów/cosinusów.
sin x
+
sin y
=
2 sin
x
+
y
2
cos
x
−
y
2
sin x
−
sin y
=
2 sin
x
−
y
2
cos
x
+
y
2
cos x
+
cos y
=
2 cos
x
+
y
2
cos
x
−
y
2
cos x
−
cos y
= −
2 sin
x
+
y
2
sin
x
−
y
2
.
Wzory te s ˛
a bardzo u ˙zyteczne w równaniach i nierówno´sciach, gdy ˙z pozwalaj ˛
a zamienia´c
równania typu suma równa 0, na równania typu iloczyn równy 0, a te drugie rozwi ˛
azuje si˛e o
wiele łatwiej.
Rozwi ˛
a ˙zmy równanie cos 4x
−
cos 2x
=
0.
Z wzoru na ró ˙znic˛e cosinusów mamy
−
2 sin 3x sin x
=
0.
Czyli 3x
=
kπ lub x
=
kπ. St ˛
ad x
=
kπ
3
, k
∈
C
.
Zadania
.info
Podoba Ci się ten poradnik?
Pokaż go koleżankom i kolegom ze szkoły!
T
IPS
& T
RICKS
1
Jedynka trygonometryczna pozwala pozbywa´c si˛e sinusów i cosinusów je ˙zeli spotykaj ˛
a si˛e
w kwadratach. Czasami te kwadraty warto zrobi´c samemu.
Rozwi ˛
a ˙zmy równanie
|
sin x
| + |
cos x
| =
√
2.
Obie strony s ˛
a nieujemne, wi˛ec podnosimy równanie stronami do kwadratu.
sin
2
x
+
2
|
sin x cos x
| +
cos
2
x
=
2
|
sin 2x
| =
1
sin 2x
= ±
1
⇐⇒
cos 2x
=
0
⇐⇒
2x
=
π
2
+
kπ
⇐⇒
x
=
π
4
+
kπ
2
.
Materiał pobrany z serwisu
4

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Oblicz sin
4
x
+
cos
4
x, je ˙zeli sin x cos x
=
1
4
.
Liczymy
sin
4
x
+
cos
4
x
= (
sin
2
x
+
cos
2
x
)
2
−
2 sin
2
x cos
2
x
=
1
−
2
·
1
16
=
7
8
.
2
Jedynka trygonometryczna pozwala prawie wyliczy´c wszystkie funkcje trygonometryczne
je ˙zeli znamy jedn ˛
a z nich. Prawie, bo zawsze jest problem z wyborem znaku. Aby ustali´c
znaki musimy wiedzie´c, w której ´cwiartce jest k ˛
at.
Wyznaczmy sin α je ˙zeli tg α
=
3
4
i α
∈ h
π
,
3π
2
i
.
Liczymy
sin α
cos α
=
3
4
4 sin α
=
3 cos α
/
()
2
16 sin
2
α
=
9 cos
2
α
=
9
(
1
−
sin
2
α
)
25 sin
2
α
=
9
⇒
sin α
= −
3
5
.
Znak wybrali´smy korzystaj ˛
ac z warunku α
∈ h
π
,
3π
2
i
. Po wi˛ecej informacji na temat ustala-
nia znaku funkcji trygonometrycznych odsyłam do
o wzorach redukcyjnych.
3
Wzory cos 2α
=
2 cos
2
α
−
1
=
1
−
2 sin
2
α
mo ˙zna zapisa´c w postaci
cos
2
α
=
cos 2α
+
1
2
sin
2
α
=
1
−
cos 2α
2
.
To, w niektórych sytuacjach, pozwala nam pozbywa´c si˛e kwadratów sinusów i cosinusów
(kosztem zamiany α na 2α).
Rozwi ˛
a ˙zmy równanie 2 sin
2
x
=
1. Z powy ˙zszego wzoru mamy
1
−
cos 2x
=
1
⇐⇒
cos 2x
=
0
⇐⇒
2x
=
π
2
+
kπ
⇐⇒
x
=
π
4
+
kπ
2
.
Oblicz warto´s´c wyra ˙zenia cos
2 π
12
−
sin
2 π
8
.
Przekształcamy (korzystaj ˛
ac z powy ˙zszych wzorów).
cos
π
6
+
1
2
−
1
−
cos
π
4
2
=
√
3
2
+
√
2
2
2
=
√
3
+
√
2
4
.
Materiał pobrany z serwisu
5

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
4
Wzory na sinus/cosinus sumy s ˛
a cz˛esto wykorzystywane od prawa do lewa, czyli pozwalaj ˛
a
zwin ˛
a´c sum˛e do jednego sinusa/cosinusa.
Rozwi ˛
a ˙zmy równanie sin x
+
cos x
=
1.
sin x
+
cos x
=
1
/
·
√
2
2
sin
π
4
sin x
+
cos
π
4
cos x
=
√
2
2
cos
x
−
π
4
=
√
2
2
x
−
π
4
=
π
4
+
2kπ
∨
x
−
π
4
= −
π
4
+
2kπ
x
=
π
2
+
2kπ
∨
x
=
2kπ.
5
Czasami, aby zastosowa´c wzór na sum˛e sinusów/cosinusów musimy jednego sinusa/cosinusa
zrobi´c sobie sami.
Uzasadnijmy to ˙zsamo´s´c
1
+
sin x
1
−
sin x
=
tg
(
π
4
+
x
2
)
ctg
(
π
4
−
x
2
)
.
Przekształcamy lew ˛
a stron˛e
1
+
sin x
1
−
sin x
=
sin
π
2
+
sin x
sin
π
2
−
sin x
=
2 sin
π
2
+
x
2
cos
π
2
−
x
2
2 sin
π
2
−
x
2
cos
π
2
+
x
2
=
=
sin
(
π
4
+
x
2
)
cos
(
π
4
+
x
2
)
·
cos
(
π
4
−
x
2
)
sin
(
π
4
−
x
2
)
=
tg
π
4
+
x
2
ctg
π
4
−
x
2
.
Zdarza si˛e te ˙z, ˙ze u ˙zywamy tych wzorów w drug ˛
a stron˛e.
Upro´s´cmy wyra ˙zenie
sin
(
x
−
y
)
cos
(
x
+
y
) +
1
2
sin 2y
sin 2x
.
Przekształcamy korzystaj ˛
ac ze wzoru na ró ˙znic˛e sinusów.
sin
(
x
−
y
)
cos
(
x
+
y
) +
1
2
sin 2y
sin 2x
=
=
1
2
(
sin 2x
−
sin 2y
) +
1
2
sin 2y
sin 2x
=
1
2
sin 2x
sin 2x
=
1
2
.
Materiał pobrany z serwisu
6

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
6
Na ogół pozbywamy si˛e tangensa i cotangensa zamieniaj ˛
ac je na sinus i cosinus, lub pozby-
wamy si˛e samego cotangensa zamieniaj ˛
ac go na
1
tg x
.
Upro´scimy wyra ˙zenie
(
1
−
sin α
)(
tg α
+
1
cos α
)
.
(
1
−
sin α
)
tg α
+
1
cos α
= (
1
−
sin α
)
sin α
cos α
+
1
cos α
=
= (
1
−
sin α
)
sin α
+
1
cos α
=
1
−
sin
2
α
cos α
=
cos
2
α
cos α
=
cos α.
Uzasadnij, ˙ze dla dowolnego x
6=
kπ
4
, gdzie k
∈
C
, spełniona jest nierówno´s´c
1
+
ctg x
1
+
tg x
·
ctg x
>
0.
Przekształcamy lew ˛
a stron˛e.
1
+
ctg x
1
+
tg x
·
ctg x
=
1
+
1
tg x
1
+
tg x
·
ctg x
=
tg x
+
1
tg x
1
+
tg x
·
ctg x
=
=
1
tg x
·
ctg x
=
ctg
2
x.
Otrzymane wyra ˙zenie jest oczywi´scie dodatnie (bo x
6=
kπ
2
).
7
Przed chwil ˛
a napisali´smy, ˙ze na ogół pozbywamy si˛e tangensa i cotangensa, ale zdarza si˛e,
˙ze wygodnie jest post ˛
api´c odwrotnie.
Rozwi ˛
a ˙zmy równanie sin x
=
√
3 cos x.
Jest jasne, ˙ze nie mo ˙ze by´c cos x
=
0, wi˛ec podzielmy równanie przez cos x.
sin x
cos x
=
√
3
⇐⇒
tg x
=
√
3
⇐⇒
x
=
π
3
+
kπ.
8
Nie mo ˙zna nie wspomnie´c o do´s´c przykrej, a niestety lubianej przez nauczycieli, kwestii
dziedziny to ˙zsamo´sci trygonometrycznych. Otó ˙z to ˙zsamo´sci trygonometryczne s ˛
a spełnio-
ne tylko w swojej dziedzinie, i czasami nauczyciele oczekuj ˛
a, ˙zeby odpowied´z na pytanie
czy równo´s´c jest to˙zsamo´sci ˛
a? zawierała w sobie ustalenie jaka jest dziedzina to ˙zsamo´sci.
Materiał pobrany z serwisu
7

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Sprawd´zmy czy równo´s´c sin 2x
=
2
tg x
+
ctg x
jest to ˙zsamo´sci ˛
a.
Przekształcamy praw ˛
a stron˛e
2
tg x
+
ctg x
=
2
sin x
cos x
+
cos x
sin x
=
2
sin
2
x
+
cos
2
x
sin cos x
=
2 sin x cos x
=
sin 2x.
Dla jakich x-ów powy ˙zsze rachunki maj ˛
a sens? Musz ˛
a by´c zdefiniowane funkcje
tg x i ctg x, czyli musi by´c sin x
6=
0 i cos x
6=
0. Daje to nam x
6=
kπ
2
.
Jeszcze trzeba si˛e zastanowi´c, czy mo ˙ze by´c tg x
+
ctg x
=
0? – to jest jednak nie-
mo ˙zliwe, bo funkcje te s ˛
a zawsze tego samego znaku i nigdy nie zeruj ˛
a si˛e jedno-
cze´snie. Mo ˙zna te ˙z to łatwo policzy´c:
tg x
+
ctg x
=
tg x
+
1
tg x
=
tg
2
x
+
1
tg x
6=
0.
9
Jako ciekawostk˛e warto poda´c wzory
sin x
=
2 tg
x
2
1
+
tg
2 x
2
cos x
=
1
−
tg
2 x
2
1
+
tg
2 x
2
tg x
=
2 tg
x
2
1
−
tg
2 x
2
ctg x
=
1
−
tg
2 x
2
2 tg
x
2
Wzory te oznaczaj ˛
a, ˙ze (przynajmniej teoretycznie) mo ˙zna ka ˙zde wyra ˙zenie z funkcjami try-
gonometrycznymi tego samego k ˛
ata, zamieni´c (przez podstawienie t
=
tg
x
2
) na wyra ˙zenie
bez funkcji trygonometrycznych (sztuczk˛e t˛e wykorzystuje si˛e np. przy liczeniu całek). Je-
dyny kłopot, to ˙ze otrzymane wyra ˙zenie mo ˙ze by´c do´s´c skomplikowane.
Rozwi ˛
a ˙zmy równanie
sin x
1
+
cos x
=
1.
Podstawiamy t
=
tg
x
2
i mamy
2t
1
+
t
2
1
+
1
−
t
2
1
+
t
2
=
1
2t
2
=
1
⇐⇒
t
=
1
tg
x
2
=
1
⇐⇒
x
2
=
π
4
+
kπ
⇐⇒
x
=
π
2
+
2kπ.
Tak naprawd˛e, to powinni´smy jeszcze sprawdzi´c, ˙ze podstawienie miało sens, tzn.,
˙ze cos
x
2
6=
0, to jest jednak do´s´c proste, bo w przeciwnym wypadku byłoby sin x
=
0.
Materiał pobrany z serwisu
8
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
10
Czasami u ˙zywa si˛e jeszcze jednego wzoru:
tg
(
x
−
y
) =
tg x
−
tg y
1
+
tg x tg y
.
Wzór ten jest bardzo wygodny je ˙zeli chcemy obliczy´c k ˛
at pod jakim przecinaj ˛
a si˛e proste,
gdy mamy ich równania (je ˙zeli umiemy liczy´c pochodne, to mo ˙zemy w ten sam sposób
liczy´c k ˛
aty przeci˛ecia si˛e dowolnych krzywych, niekoniecznie prostych).
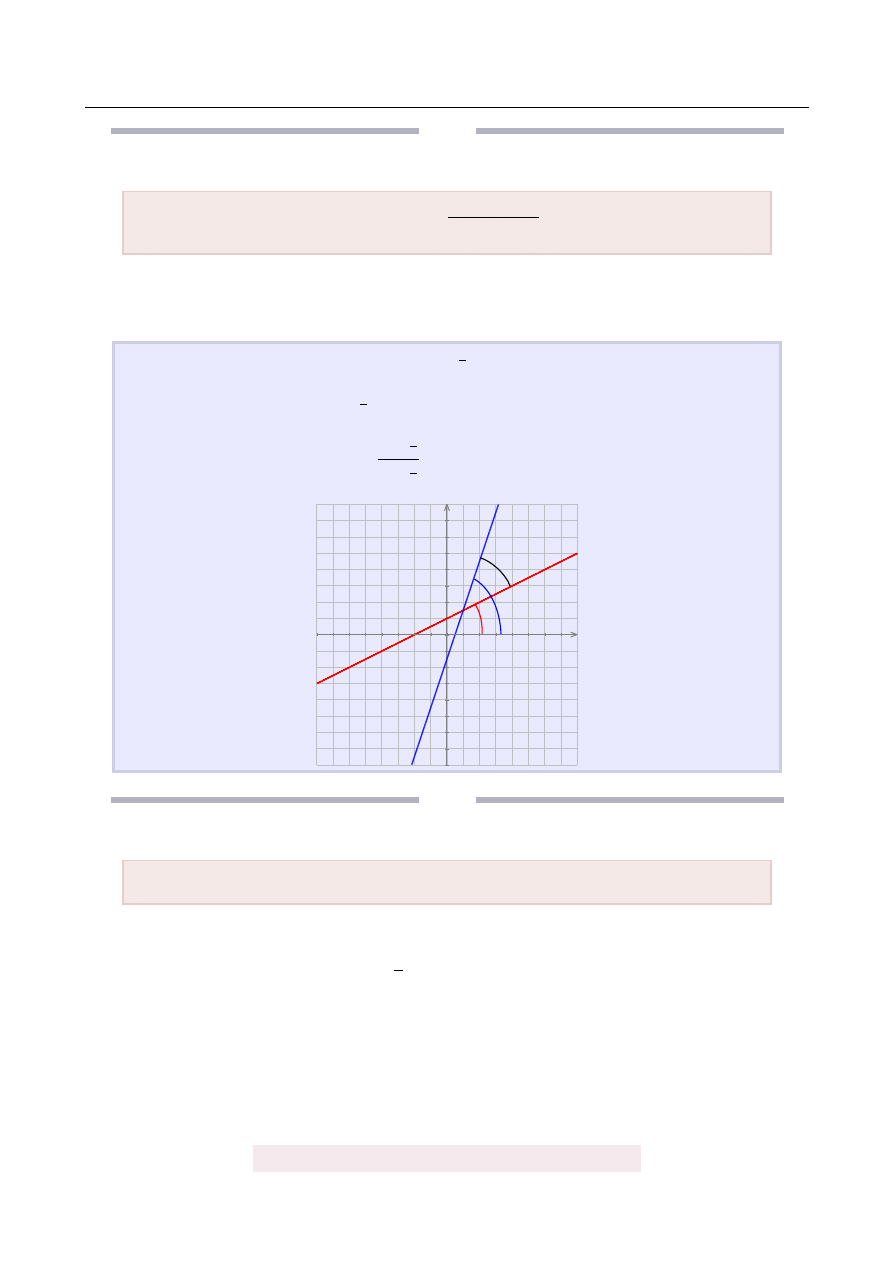
Pod jakim k ˛
atem przecinaj ˛
a si˛e proste y
=
1
2
x
+
2 i y
=
3x
−
3?
Je ˙zeli pierwsza tworzy z osi ˛
a Ox k ˛
at α, a druga β to mamy wyliczy´c β
−
α
. Mo ˙zemy
to zrobi´c, bo wiemy, ˙ze tg α
=
1
2
i tg β
=
3. Mamy zatem
tg
(
β
−
α
) =
3
−
1
2
1
+
3
2
=
1
⇒
β
−
α
=
45
◦
.
-10
-2
+2
+10
x
-10
-2
+2
+10
y
y=
0.5
x+
2
y=
3
x
-3
β
α
β-α
11
Ze wzoru na cosinus sumy łatwo wyprowadzi´c wzór
cos 3α
=
4 cos
3
α
−
3 cos α.
Je ˙zeli we´zmiemy teraz np. 3α
=
60
◦
, to widzimy, ˙ze cos 20
◦
jest pierwiastkiem równania
1
2
=
4x
3
−
3x.
Wida´c wi˛ec bliski zwi ˛
azek mi˛edzy obliczaniem funkcji trygonometrycznych, a rozwi ˛
azy-
waniem równa ´n wielomianowych. Co wi˛ecej, w tym przykładzie, otrzymany wielomian
nie ma pierwiastków wymiernych, wi˛ec znalezienie jego pierwiastków jest bardzo trudne
(w dodatku nie da si˛e ich przyzwoicie zapisa´c nie u ˙zywaj ˛
ac liczb zespolonych). To powinno
ilustrowa´c dlaczego obliczanie funkcji trygonometrycznych (z wyj ˛
atkiem kilku szkolnych
przykładów: 30
◦
, 60
◦
itp.) jest trudne, lub wr˛ecz niemo ˙zliwe.
Materiał pobrany z serwisu
9
Wyszukiwarka
Podobne podstrony:
tozsamosci trygonometryczne, Matematyka
Konspekt; tozsamosci trygonomet Nieznany
Wzory trygonometryczne, tożsamości trygonometryczne Medianauka pl
Tożsamości trygonometryczne
W10b Teoria Ja tozsamosc
trygonometria 2
Nie pozwól ukraść swojej tożsamości
rozdział 10 Tożsamość indywidualna i zbiorowa, Wstęp do filozofii współczesnej A.Nogal
T2, Kulturoznawstwo UAM, Tożsamości kulturowe (W)
Tożsamość i postawa wychowawcy - Kim jest i jaki powinien być wychowawca, MGR
Poczucie tożsamości seksualnej u osób niepełnosprawnych intelektualnie
ściąga matma funkcje trygonomertyczne
ZABAWA I TOŻSAMOŚĆ
Obliczenie przewyższeń niwelacja trygonometryczna
Kwiek Dylematy tożsamości 1 Kojeve
Funkcje trygonometryczne dowody
Mamzer H Wielokulturowość a kształtowanie tożsamości jednostki
więcej podobnych podstron