RÓWNANIA RÓWNOWAGI
1
RÓWNANIA RÓWNOWAGI (RÓWNANIA NAVIERA)
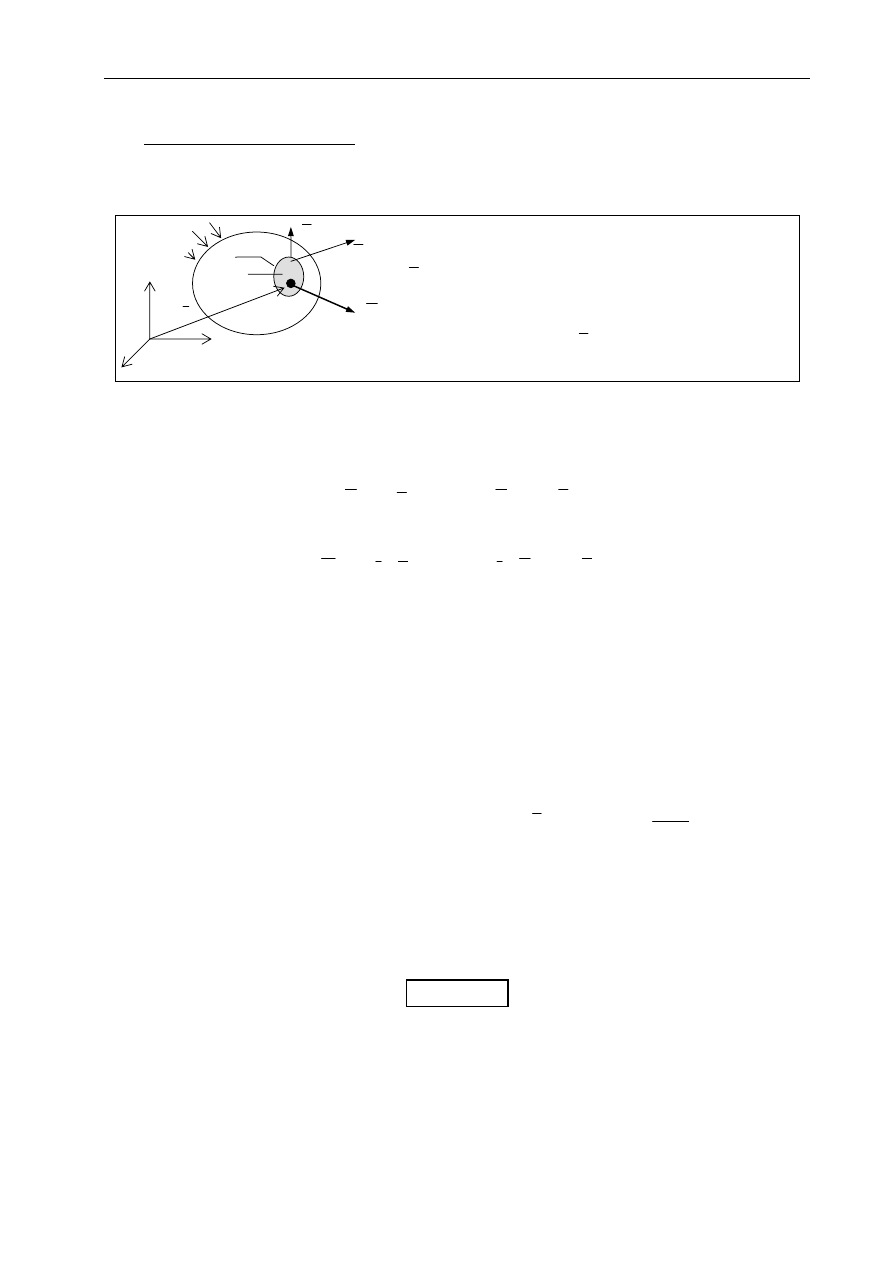
Sformułowanie zagadnienia: Dowolne ciało obciążone ukł. sił zewnętrznych (Z)
≡ 0
pozostaje w równowadze. Z wnętrza ciała wycinamy element o objętości V
o
i powierzchni
S
o
. Określić warunki równowagi wyciętego elementu.
tw. o równoważności układu sił zewnętrznych i wewnętrznych
ukł. sił działających na wycięty element jest układem zerowym
S
p dS
X dV
S
V
=
+
=
∫∫
∫∫∫
ν
0
0
0
0
0
M
r p dS
r X dV
S
V
=
×
+
×
=
∫∫
∫∫∫
ν
0
0
0
0
0
warunek równowagi sił
S
p dS
X dV
i
i
S
i
V
=
+
=
∫∫
∫∫∫
ν
0
0
0
0
0
S
dS
X dV
i
i j
S
j
i
V
=
+
=
∫∫
∫∫∫
σ α
ν
0
0
0
0
0
Twierdzenie Gaussa
(
)
σ α
σ
ν
∂ σ
∂
ν
i j
S
j
i j
S
j
i j
j
V
dS
x
dS
x
dV
0
0
0
0
0
0
∫∫
∫∫
∫∫∫
=
=
cos
,
(
)
S
dV
X dV
X
dV
i
i j j
V
i
V
i j j
i
V
=
+
=
+
=
∫∫∫
∫∫∫
∫∫∫
σ
σ
,
,
0
0
0
0
0
0
0
RÓWNANIA RÓWNOWAGI - RÓWNANIA NAVIERA
σ
i j j
i
X
,
+
= 0
σ
σ
σ
11 1
12 2
13 3
1
0
,
,
,
+
+
+
=
X
σ
σ
σ
21 1
22 2
23 3
2
0
,
,
,
+
+
+
=
X
σ
σ
σ
31 1
32 2
33 3
3
0
,
,
,
+
+
+
=
X
X = (X
1
, X
2
, X
3
) - wektor sił masowych w dowolnym
punkcie wewnątrz objętości V
0
(
)
p
p
p
p
ν
ν
ν
ν
=
1
2
3
;
;
- wektor naprężenia w dowol-
nym punkcie na powierzchni
S
0
o normalnej
(
)
ν
α
α
α
ν
ν
ν
=
1
2
3
;
;
x
1
x
2
x
3
ν
p
ν
r
S
0
V
0
X

RÓWNANIA RÓWNOWAGI
2
warunek równowagi momentów
M
e
x p
dS
e
x X dV
i
i jk
j
k
S
i jk
j
k
V
=
+
=
∫∫
∫∫∫
ν
0
0
0
0
0
M
e
x
dS
e
x X dV
i
i jk
j
k m
S
m
i jk
j
k
V
=
+
∫∫
∫∫∫
σ
α
ν
0
0
0
0
(
)
M
x
e
x
dV
e
x X dV
i
m
i jk
j
k m
V
i jk
j
k
V
=
+
∫∫∫
∫∫∫
∂
∂
σ
0
0
0
0
(
)
M
e
e
x
dV
e
x X dV
i
imk
k m
i jk
j
k m m
V
i jk
j
k
V
=
+
+
∫∫∫
∫∫∫
σ
σ
,
0
0
0
0
(
)
[
]
M
e
e
x
X
dV
i
imk
k m
i jk
j
k m m
k
V
=
+
+
=
∫∫∫
σ
σ
,
0
0
0
e
imk
k m
σ
= 0
np. i = 1
e
e
e
e
e
e
e
mk
k m
k
k
k
k
k
k
1
11
1
12
2
13
3
111
11
112
21
113
31
σ
σ
σ
σ
σ
σ
σ
=
+
+
=
+
+
+
+
+
+
+
+
+
=
e
e
e
e
e
e
121
12
122
22
123
3 2
131
13
13 2
23
13 3
3 3
σ
σ
σ
σ
σ
σ
=
+
=
−
=
e
e
123
3 2
13 2
23
3 2
23
0
σ
σ
σ
σ
σ
σ
3 2
23
=
SYMETRIA TENSORA NAPRĘŻENIA
σ
σ
i j
ji
=
WNIOSKI
1) Tensor naprężenia zawiera 6 nieznanych składowych, których nie można wyznaczyć
korzystając tylko z równań Naviera, których jest jedynie 3.
2) Równania Naviera są równaniami różniczkowymi, przy ich całkowaniu pojawią się zatem
stałe całkowania. Wyznacza się je na podstawie analizy elementu ciała zawierającego
część jego powierzchni zewnętrznej. Dzięki temu możliwe jest powiązanie naprężeń w
punktach na powierzchni z obciążeniem zewnętrznym. Relacje wiążące naprężenia z
obciążeniem zewnętrznym ciała noszą nazwę STATYCZNYCH WARUNKÓW
BRZEGOWYCH.
STATYCZNE WARUNKI BRZEGOWE
1
STATYCZNE WARUNKI BRZEGOWE
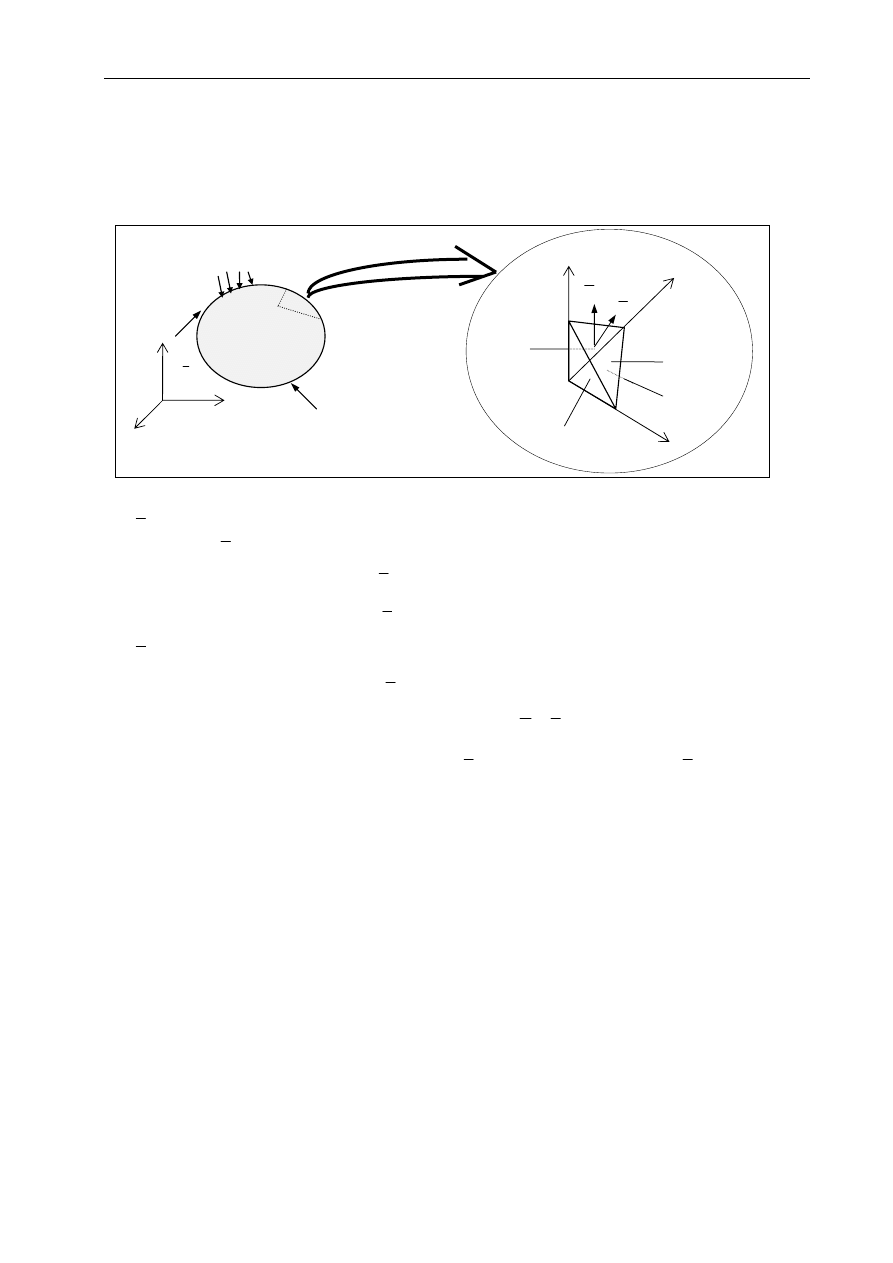
W celu powiązania naprężeń z obciążeniem zewnętrznym wycinamy z ciała element
objętościowy w kształcie czworościanu, którego 3 ścianki są równoległe do płaszczyzn układu
współrzędnych, a ścianka ukośna aproksymuje część powierzchni zewnętrznej ciała.
q
ν
- uśredniona gęstość obciążenia zewnętrznego na ściance
∆ F o zewnętrznym wersorze
normalnym
ν
(
)
q
q
q
q
ν
ν
ν
ν
=
1
2
3
,
,
(
)
ν
α
α
α
ν
ν
ν
=
1
2
3
,
,
p
i
- uśrednione wektory naprężenia na ściankach
∆ Fi
(
)
p
i
i
i
i
= σ
σ
σ
1
2
3
,
,
warunek równowagi sił działających na czworościan S
= 0
Zauważmy, że poszukiwanie związku wektora q
ν
z wektorami naprężenia p
i
jest formalnie
identyczne z zadaniem wyznaczania wektora naprężenia na ściance
∆ F jako funkcji wektorów
naprężenia na ściankach
∆ Fi (czyli składowymi tensora narężenia). Mamy zatem:
q
i
i j
j
ν
ν
σ α
=
q
ν
ν
ν
ν
σ
α
σ
α
σ
α
1
11
1
12
2
13
3
=
+
+
q
ν
ν
ν
ν
σ
α
σ
α
σ
α
2
21
1
22
2
23
3
=
+
+
q
ν
ν
ν
ν
σ
α
σ
α
σ
α
3
31
1
32
2
33
3
=
+
+
WARUNKI KONIECZNE tego, aby dowolny tensor symetryczny II rzędu był tensorem
naprężenia :
1)
składowe tensora muszą spełniać równania Naviera,
2)
składowe tensora muszą spełniać statyczne warunki brzegowe.
x
1
x
2
x
3
r
D
B
A
x
1
x
2
x
3
ν
q
ν
A
B
C
D
∆F
1
∆F
2
∆F
3
∆F
Wyszukiwarka
Podobne podstrony:
Równanie równowagi płyny, mechanika plynów
Obliczyć reakcje i siłę w cięgnie z równań równowagi
Równania równowagi, Podstawy techniki, Pobrane notatki
18 Równania równoważności, metoda charakterystyk
18 Równania równoważności, metoda charakterystyk
Równanie równowagi płyny, mechanika plynów
Obliczyć reakcje i siłę w cięgnie z równań równowagi
FIZYKA LAB-113, Ruch wahadła matematycznego o długości l wychylonego z położenia równowagi można opi
Rozwiązywanie układów równań
Równowaga kwasowo zasadowa fizjot3
APARATURA DO OCENY RÓWNOWAGI STATYCZNEJ
Równanie Laplace’a
Rownanie Maxwella
5a Równowaga kwasowo
więcej podobnych podstron