Równanie Poissona
dla = 0 przyjmuje postać
i nazywa się równaniem
Laplace’a.
Klasę funkcji spełniających równanie Laplace’a nazywa się
funkcjami harmonicznymi.
Twierdzenie: Jeśli (x,y,z) spełnia równanie Laplace’a to średnia
wartość funkcji na powierzchni dowolnej kuli równa się wartości
potencjału w środku tej kuli
Równanie Laplace’a
o
2
0
2
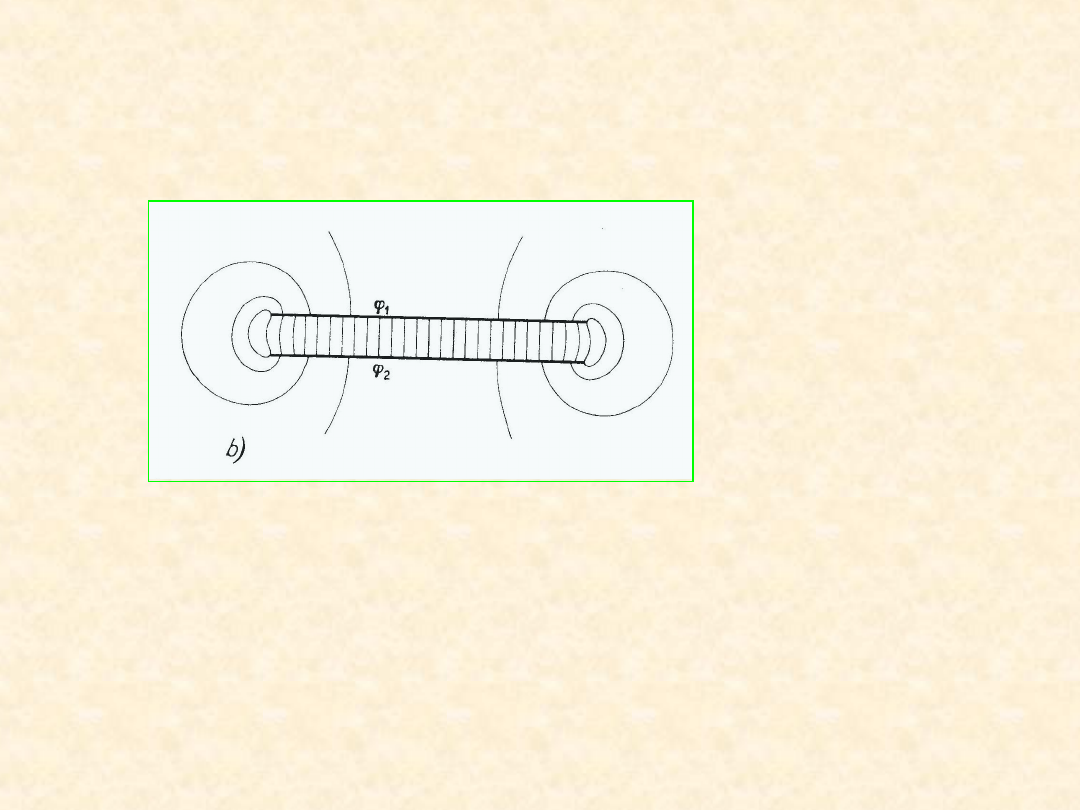
Sfera o promieniu r znajduje się w polu ładunku punktowego q.
Ładunek próbny q
o
rozmieszczamy równomiernie na powierzchni
kuli. Wykonana przy tym praca jest równa
q
śr
o
o
śr
o
r
q
q
q
W
4
średnia wartość
potencjału wytworzonego
przez ładunek q na
sferze
Praca wykonana przy przeniesieniu ładunku q z nieskończoności
w polu ładunku próbnego q
o
rozłożonego na powierzchni S jest
taka sama – i identyczna gdyby ładunek próbny umieszczony
był w środku kuli.
Potencjały od wielu źródeł dodają się do siebie, twierdzenie to
jest słuszne dla dowolnych źródeł leżących na zewnątrz
powierzchni S
Z tej własności potencjału wynika, że:
nie można skonstruować pola elektrostatycznego, które w próżni
utrzymywałoby ładunek w trwałej równowadze.
Załóżmy, że istnieje pole elektrostatyczne, w którym istnieje
punkt trwałej równowagi dodatnio naładowanej cząstki.
P
Wewnątrz kuli musi istnieć pole skierowane
do środka, aby punkt P wrócił do
pierwotnego położenia – jest to sprzeczne z
prawem Gaussa: wewnątrz obszaru nie ma
ujemnego źródła.
W pustym obszarze nie może istnieć pole skierowane tylko
do wewnątrz. Nie może również istnieć pole skierowane
tylko na zewnątrz.
Potencjał pola w położeniu trwałej równowagi naładowanej
cząstki musi być mniejszy lub większy niż potencjał w punktach
sąsiednich
+q
-q
0
ot
P
0
ot
P
Nie jest to możliwe dla funkcji, której średnia na powierzchni kuli
jest równa jej wartości w środku kuli.
q
q
P
ot
W
ot
P
)
(
+q
1
+q
2
q
o
0
0
F
E
równowaga nietrwała
Własności elektryczne ciał zależne są od ruchliwości nośników
ładunku – elektronów, jonów.
Jak wygląda pole wewnątrz przewodnika po ustaleniu się
stacjonarnego rozkładu ładunków?
Rozkład stacjonarny wszystkie siły się równoważą
jeśli na nośniki ładunku działają siły niekulombowskie, to
oznacza, że w przewodniku istnieje pewne skończone pole
elektryczne znoszące działanie innych sił.
Jednorodny izotropowy przewodnik - pole
musi znikać
wewnątrz takiego przewodnika.
Przewodniki prądu w polu
elektrostatycznym
Elektrycznie obojętne,
nieprzewodzące ciało zawiera
unieruchomione ładunki dodatnie i
ujemne.
Pole elektryczne jest jednakowe
wewnątrz ciała i poza nim.
Ładunki zostały uwolnione i
zaczynają się poruszać.
Ruch ładunków będzie trwał
do osiągnięcia stanu
równowagi – nie przesuwają
się poza powierzchnię
przewodnika. Wewnątrz
wytwarza się pole
kompensujące pole
początkowe
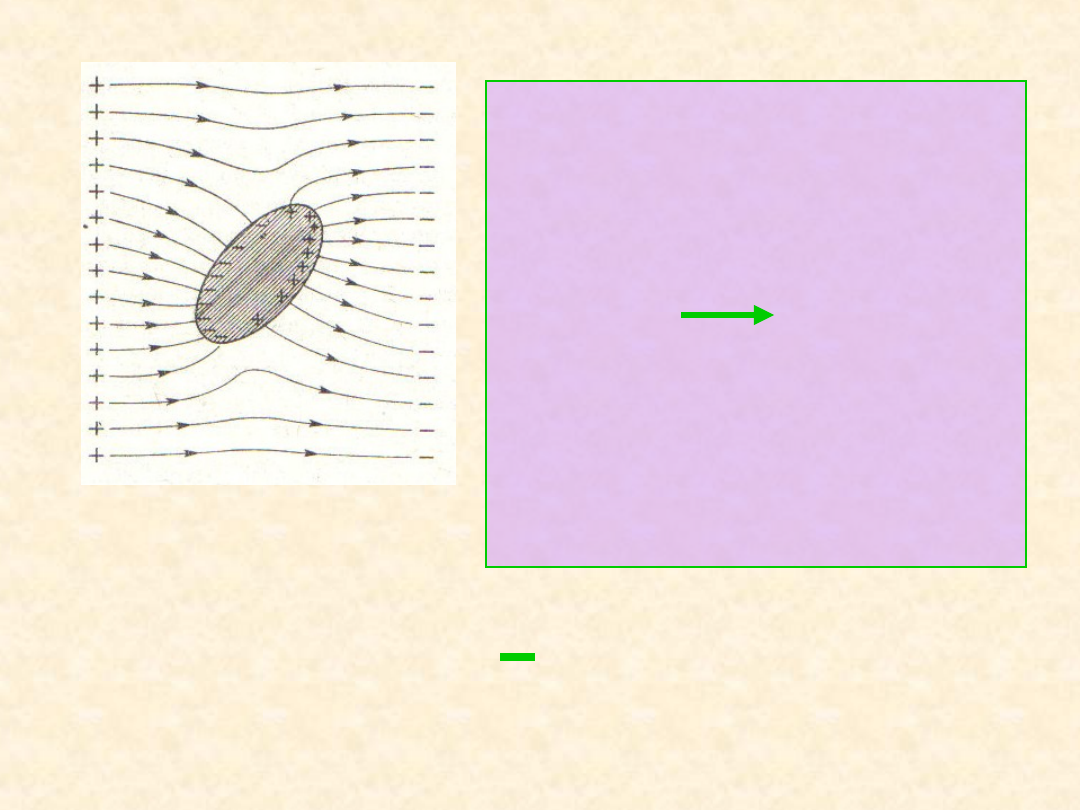
Stan równowagi – pole
wewnątrz przewodnika musi
znikać – gdyby tak nie było
ładunki poruszałyby się nadal (F
= qE).
Potencjał może zmienić się
gwałtownie na powierzchni
przewodnika – skok potencjału –
na zewnątrz E 0.
const
E
0
Powierzchnia przewodnika powierzchnia ekwipotencjalna
Wewnątrz przewodnika pole , na powierzchni następuje
gwałtowny skok pola elektrycznego na powierzchni
znajdują się ładunki o gęstości powierzchniowej
q
1
q
2
q
3
1
3
2
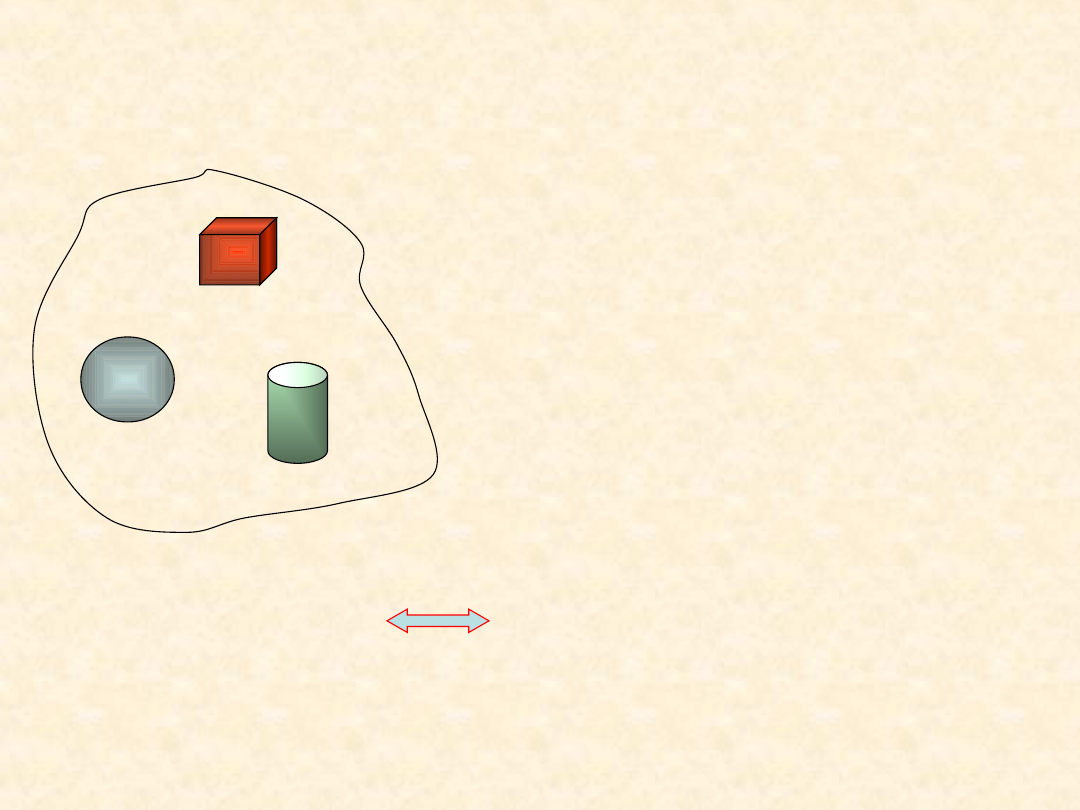
Układ przewodników umieszczonych w próżni
Z ekwipotencjalności powierzchni
dowolnego
przewodnika wynika, że
pole elektryczne
musi być prostopadłe do tej
powierzchni w dowolnym punkcie.
grad
E
0
E
E
0
E
0
0
Q
n
A
E
A
d
E
Całkowity ładunek jest równy ładunkowi
powierzchniowemu
A
A
n
A
A
d
E
dA
E
dA
Q
dA
dQ
0
0
E jest całkowitym polem układu, pochodzącym od
wszystkich
ładunków – bliskich i dalekich, których ładunek powierzchniowy
jest częścią. Rozkład ładunku powierzchniowego musi być taki,
aby spełniony był warunek
0
n
E
0
2
2
E
0
1
2
E
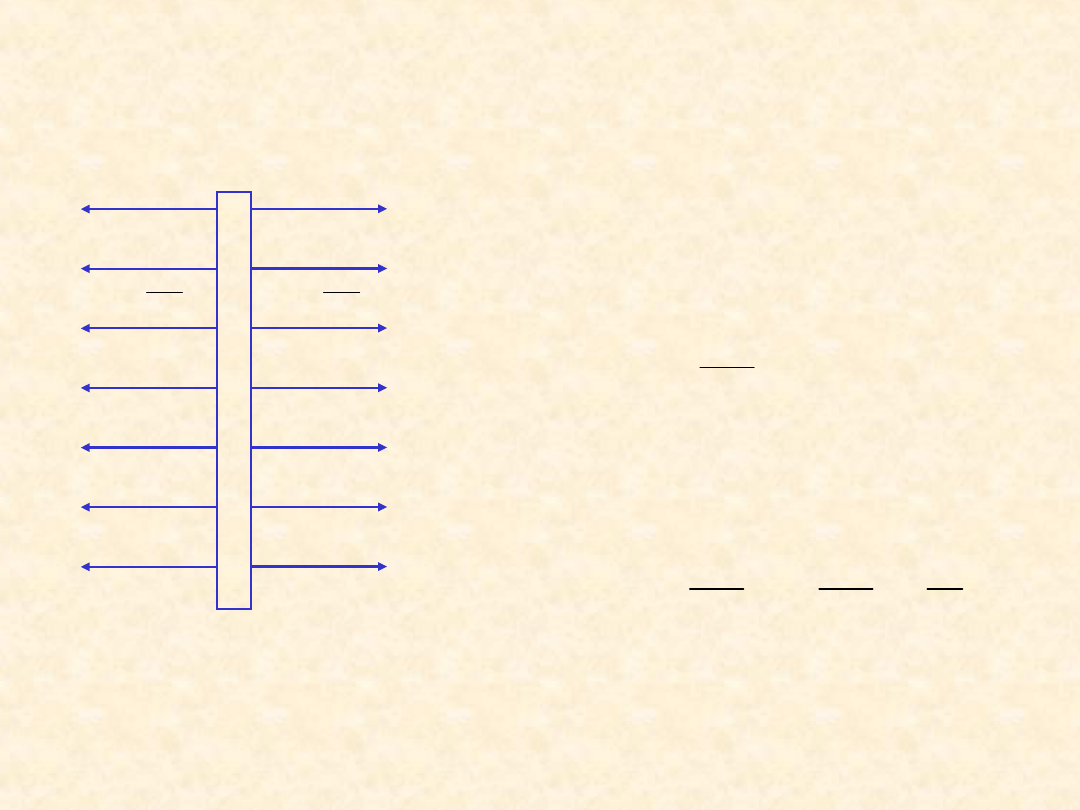
Odosobniona płaszczyzna naładowana ładunkiem o
gęstości powierzchniowej - brak innych źródeł
Natężenie pola – ze względu na
symetrię wynosi z każdej strony
płaszczyzny
Zmiana składowej E
x
wynosi
0
2
E
0
0
0
2
1
2
2
E
E
E
x
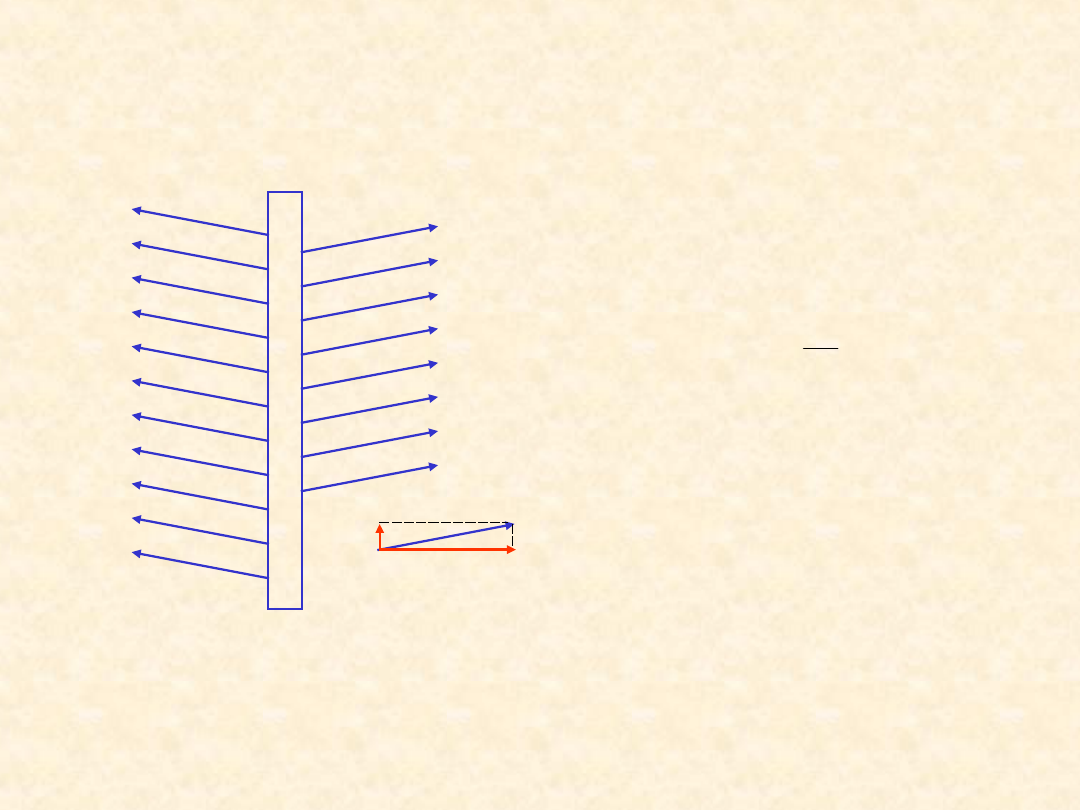
Jeśli występują dodatkowe
ładunki w układzie, to możemy
stwierdzić, że zmiana składowej
E
x
wynosi
natomiast zmiana składowej E
y
0
x
E
0
y
E
Odosobniona płaszczyzna naładowana ładunkiem o
gęstości powierzchniowej
E
x
E
y
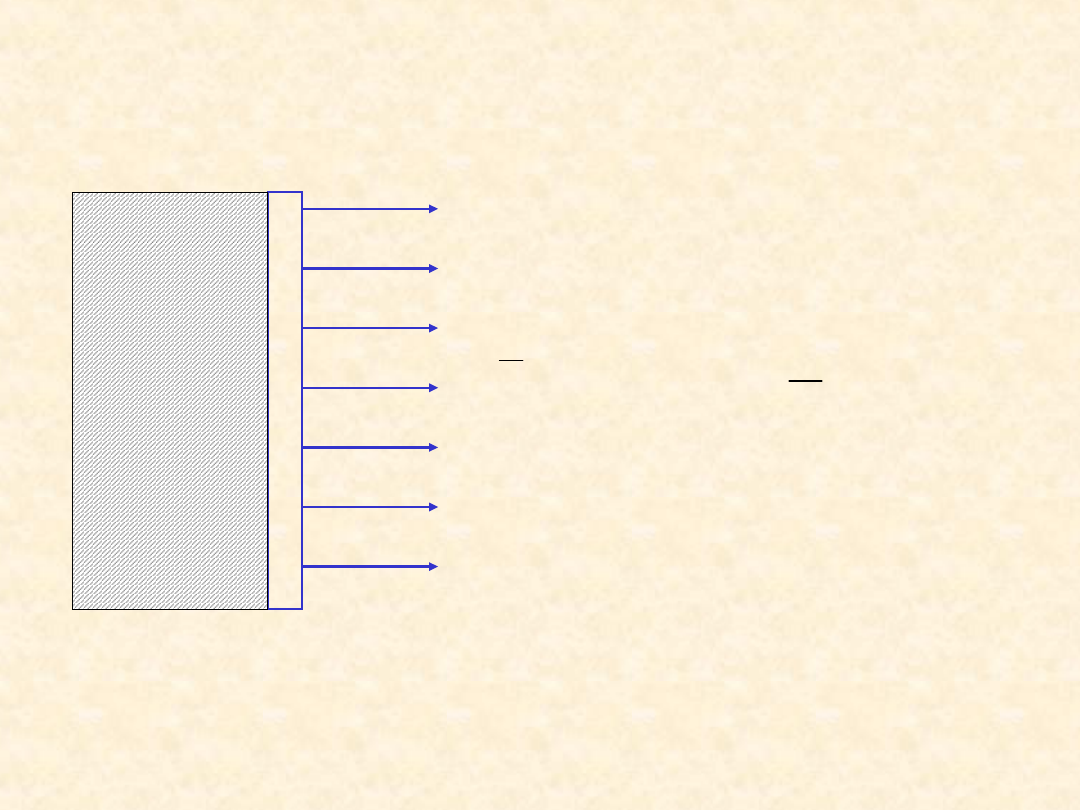
0
E
E=0
Jeśli ośrodek po jednej stronie
powierzchni jest przewodnikiem,
wówczas pole po drugiej stronie
jest prostopadłe do powierzchni i
wynosi
0
E
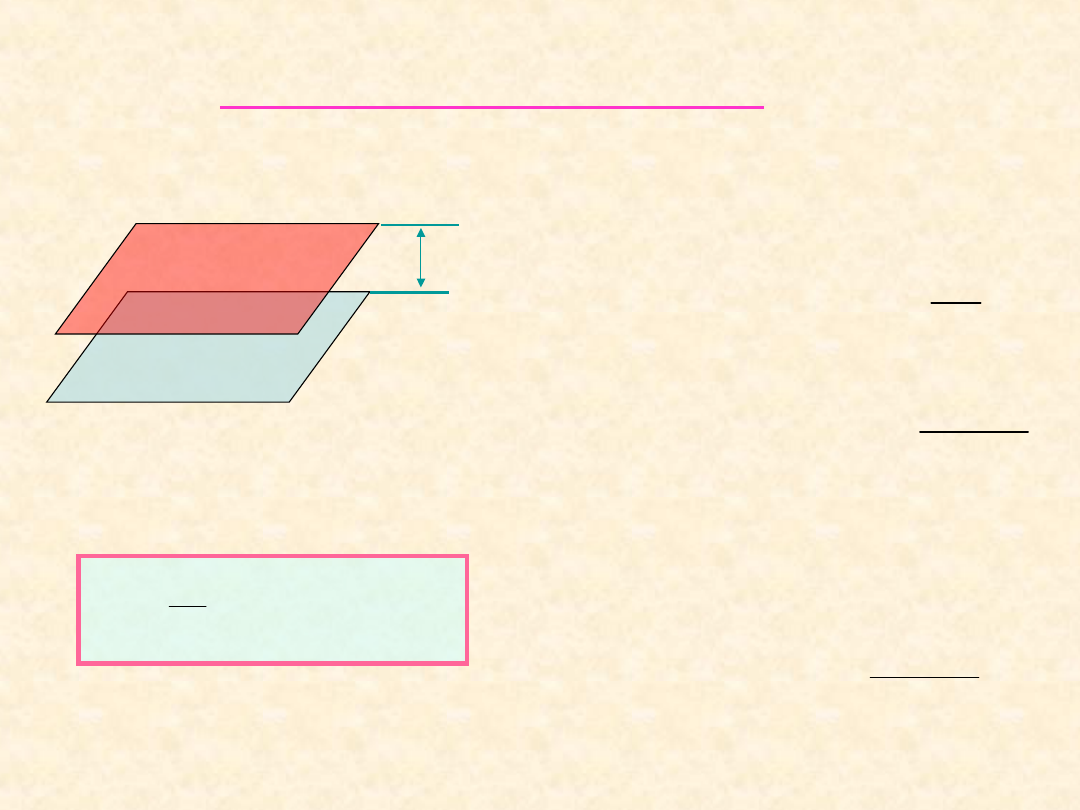
Pojemność elektryczna
+q
-q
1
2
d
S
Jeśli pole wewnątrz płyt jest
jednorodne to
dx
d
E
E
d
E
d
Edx
d
2
1
0
2
1
Gęstość powierzchniowa ładunku na wewnętrznej powierzchni płyty
n
n
E
E
0
0
Całkowity ładunek na okładce
d
S
ES
S
q
2
1
0
0
zaniedbano efekty brzegowe – przybliżona wartość ładunku
Pole kondensatora płaskiego
f
d
S
q
2
1
0
Dla płyt kołowych
0,2
0,1
0,05
0,02
0,01
f
1,286 1,167 1,094 1,042 1,023
d/R
Para płytek – kondensator. Dla ustalonej pary przewodników
2
1
2
1
0
2
1
0
C
d
S
d
S
q
const
C - pojemność kondensatora
2
1
q
C
V
C
F
1
1
1
Energia zmagazynowana w
kondensatorze
+q
-q
1
2
d
S
Ładunek +dq przenosimy z
ujemnej płytki na dodatnią –
zwiększamy jej ładunek do q+dq.
Wykonana przy tym praca
C
q
qdq
C
W
dq
C
q
dq
dW
k
q
k
2
1
2
0
2
1
2
2
1
2
2
1
2
C
C
q
E
k
p
d
S
C
0
d
E
2
1
W kondensatorze płaskim
2
0
2
0
2
2
1
2
2
1
2
1
E
Sd
Ed
d
S
C
E
p
V
E
E
p
2
2
0
gęstość energii
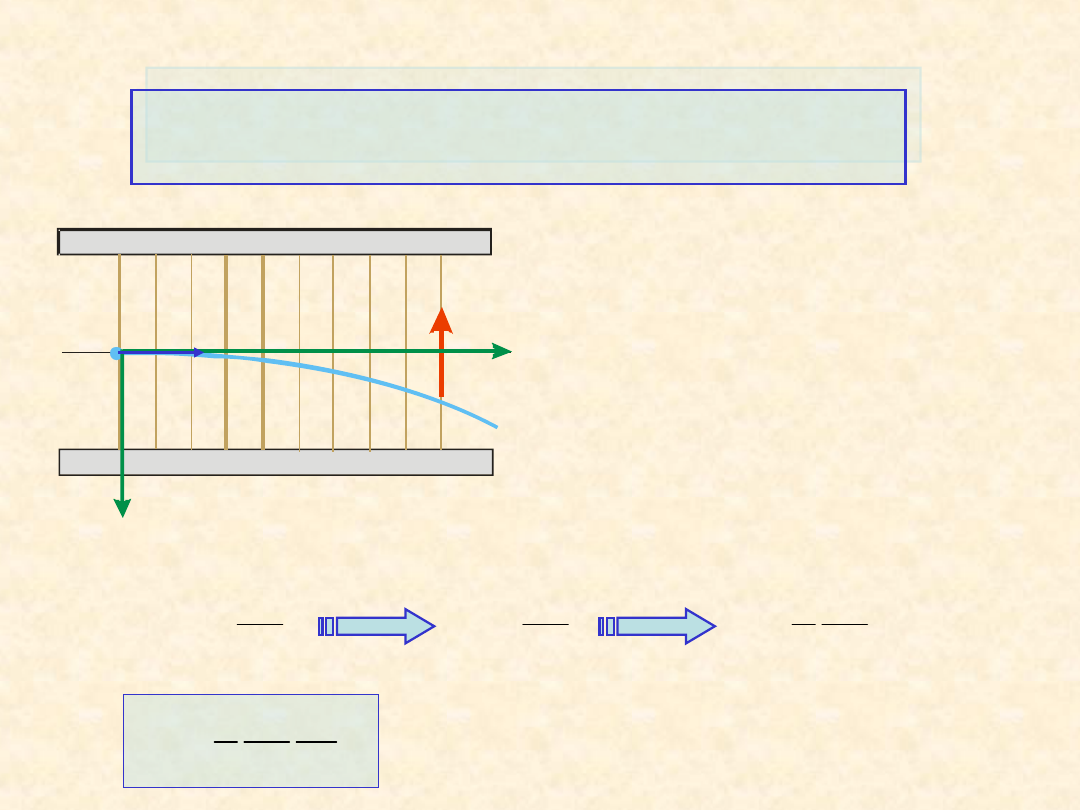
Ruch ładunku w polu elektrostatycznym
- - - - - -
+ + + + +
-
E
x
y
Elektron wpada do
jednorodnego pola
elektrycznego z prędkością
E
v
v
Równania ruchu elektronu
eE
ma
F
ma
F
y
y
x
x
0
2
2
1
0
t
m
eE
y
t
m
eE
v
m
eE
a
vt
x
v
v
a
y
y
x
x
2
2
2
1
v
x
m
eE
y
równanie toru
- - - - - -
+ + + + +
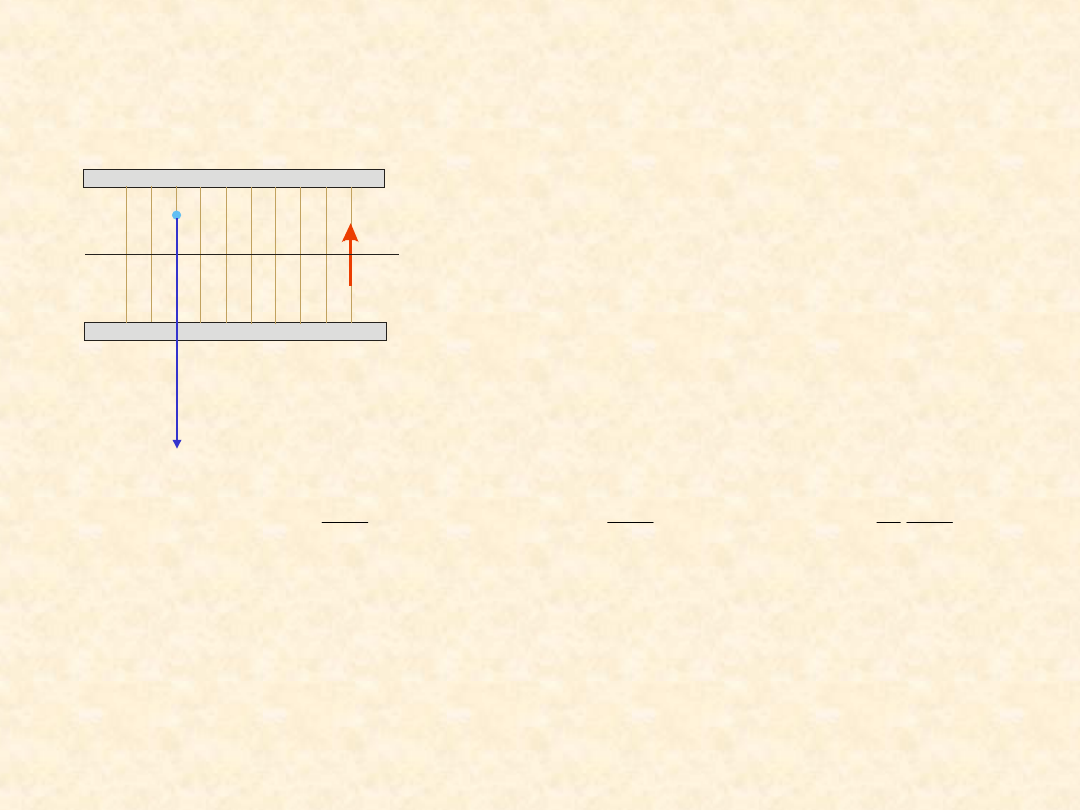
Elektron umieszczamy w jednorodnym
polu elektrycznym.
-
Uzyska on prędkość skierowaną
przeciwnie do linii sił pola.
y
2
2
1
0
0
0
t
m
eE
y
t
m
eE
v
m
eE
a
x
v
a
y
y
x
x
Pole elektryczne
przyspiesza
ładunek !!!
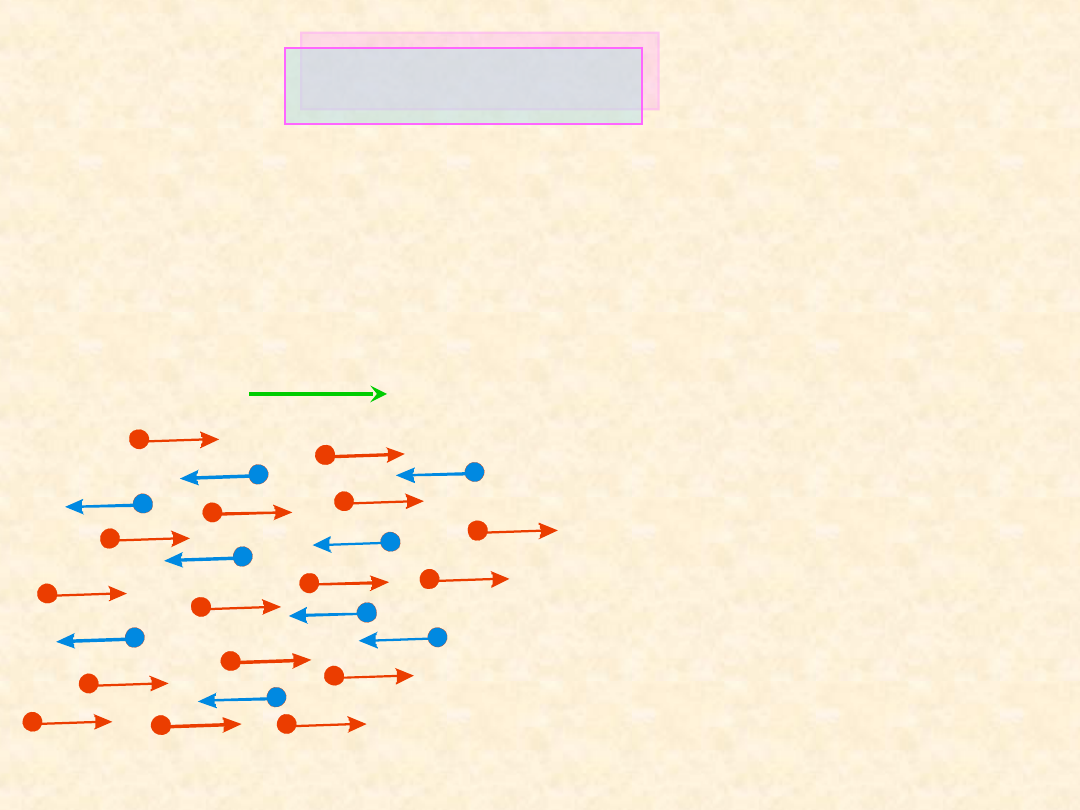
Prąd elektryczny
E
Wszystkie atomy i cząsteczki w naszym otoczeniu są w
nieustannym ruchu. Ten ruch, bez względu na to, czy atomy są
naładowane czy nie jeszcze nie tworzy prądu elektrycznego.
Prąd pojawia się dopiero
wtedy, gdy w tym ruchu
chaotycznym zostanie
wyróżniony jakiś kierunek,
preferujący poruszanie się w
jakąś stronę. Najczęściej
wyróżnienie kierunku w
ruchu ładunków odbywa się
poprzez przyłożenie pola
elektrycznego.
+
-
Umownym kierunkiem prądu jest kierunek wyznaczony przez
ruch ładunków dodatnich (czyli kierunek zgodny z
kierunkiem pola elektrycznego).
Rzeczywisty ruch ładunków elektrycznych:
metale
- nośnikami prądu są elektrony - kierunek ich ruchu jest
dokładnie przeciwny do umownego kierunku prądu
elektrolity
- nośnikami prądu mogą być jony (+ lub -). Jony te
poruszają się przeciwne strony, jednak prądy jakie są z nimi
związane dodają się, bo prąd jonów ujemnych jest traktowany
jako przeciwny do ich ruchu;
półprzewodniki
- nośnikami mogą być zarówno ujemne
elektrony, jak i dodatnie dziury – dziury tworzą prąd zgodny z
ich kierunkiem ruchu, prąd elektronowy jest przeciwny do
ruchu ładunków go tworzących;
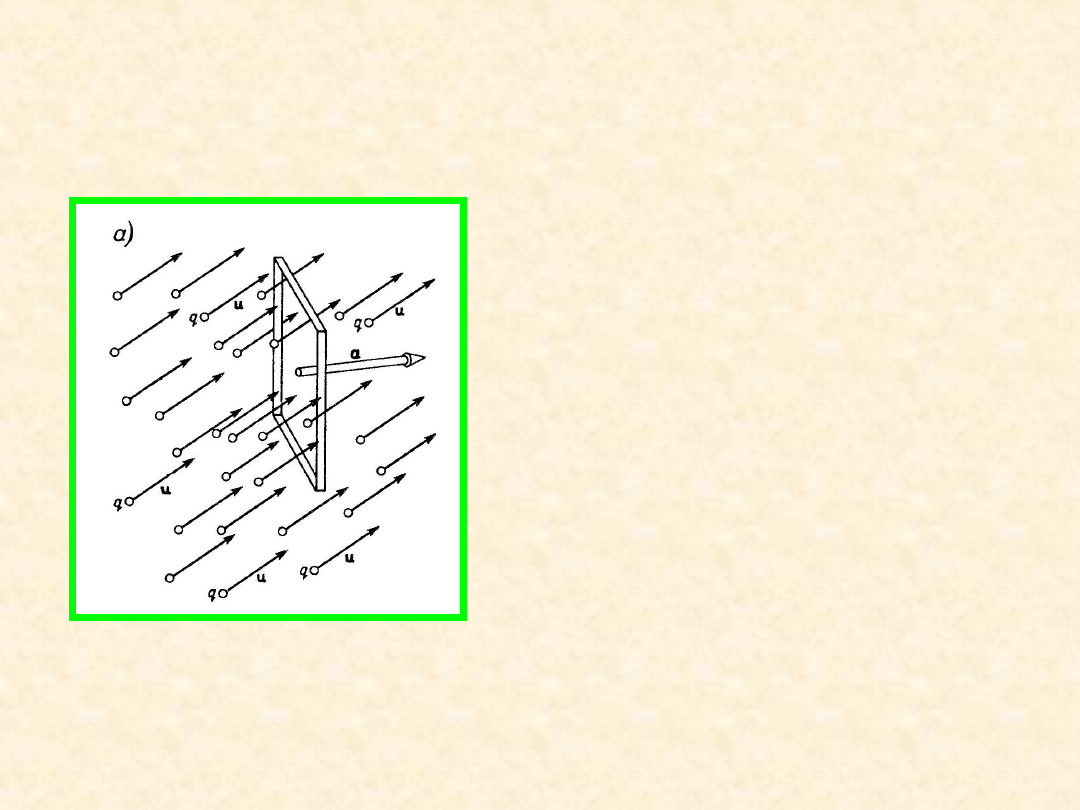
Niech wszystkie cząstki poruszają się z taką samą prędkością i
przenoszą taki sam ładunek. Ile cząstek przejdzie przez ramkę o
polu a w czasie t?
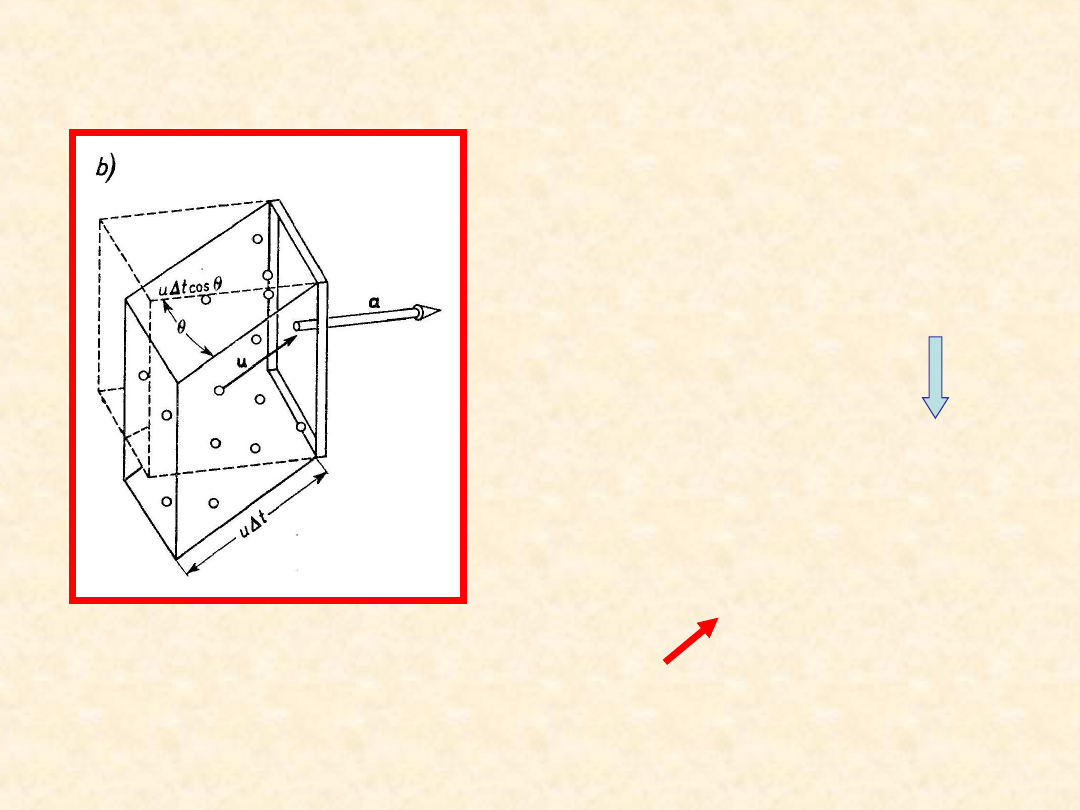
Cząstki, które mają przejść przez
ramkę po czasie t znajdują się w
graniastosłupie o wymiarach
- pole podstawy
a
-
długość krawędzi
ut
Objętość graniastosłupa =
autcos
t
u
a
Średnia liczba cząstek w tej objętości
t
u
a
n
koncentracja
Średnia prędkość przepływu ładunku przez ramkę – natężenie prądu
u
a
qn
t
t
u
a
n
q
I
)
(
W przypadku różnych nośników poruszających się z różnymi
prędkościami
i
i
i
i
u
n
q
a
u
a
n
q
u
a
n
q
I
2
2
2
1
1
1
i
i
i
i
u
n
q
j
gęstość prądu
a natężenie prądu płynącego przez przekrój a
a
j
I
Średnia prędkość nośników ładunku, np. elektronów
i
i
i
e
u
n
N
u
1
u
eN
u
n
q
j
e
i
i
i
i
Gęstość prądu zależy od średniej prędkości nośników prądu.
Jeśli nie ma wyróżnionego kierunku ruchu, wówczas
0
u
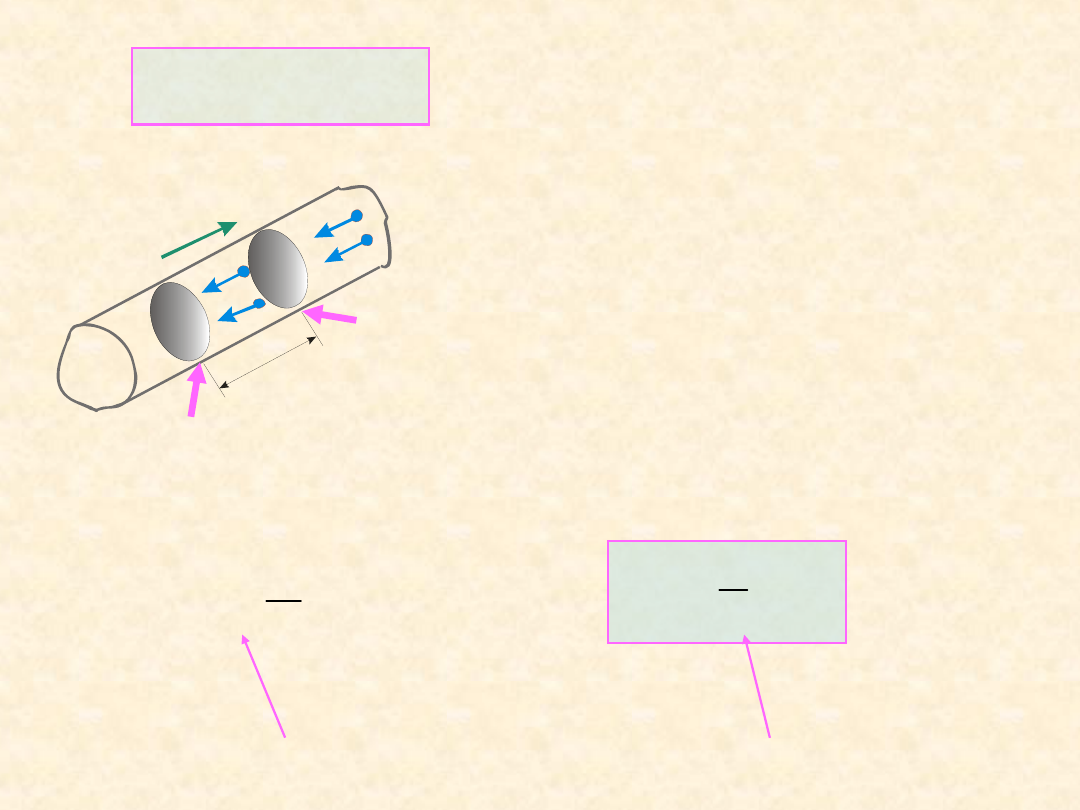
Prądy stacjonarne
S
a
d
j
I
Natężenie prądu płynącego przez długi przewodnik o przekroju S
Prądy stacjonarne, jeśli
dla dowolnego punktu w przestrzeni.
const
t
j
)
(
t
j
div
V
S
dV
dt
d
a
d
j
Niemożliwe jest odpływanie ładunków z jakiegoś miejsca bez
zmniejszania wartości ładunku znajdującego się w tym miejscu
prawo zachowania ładunku
Prawo Ohma
-
A
E
l
1
2
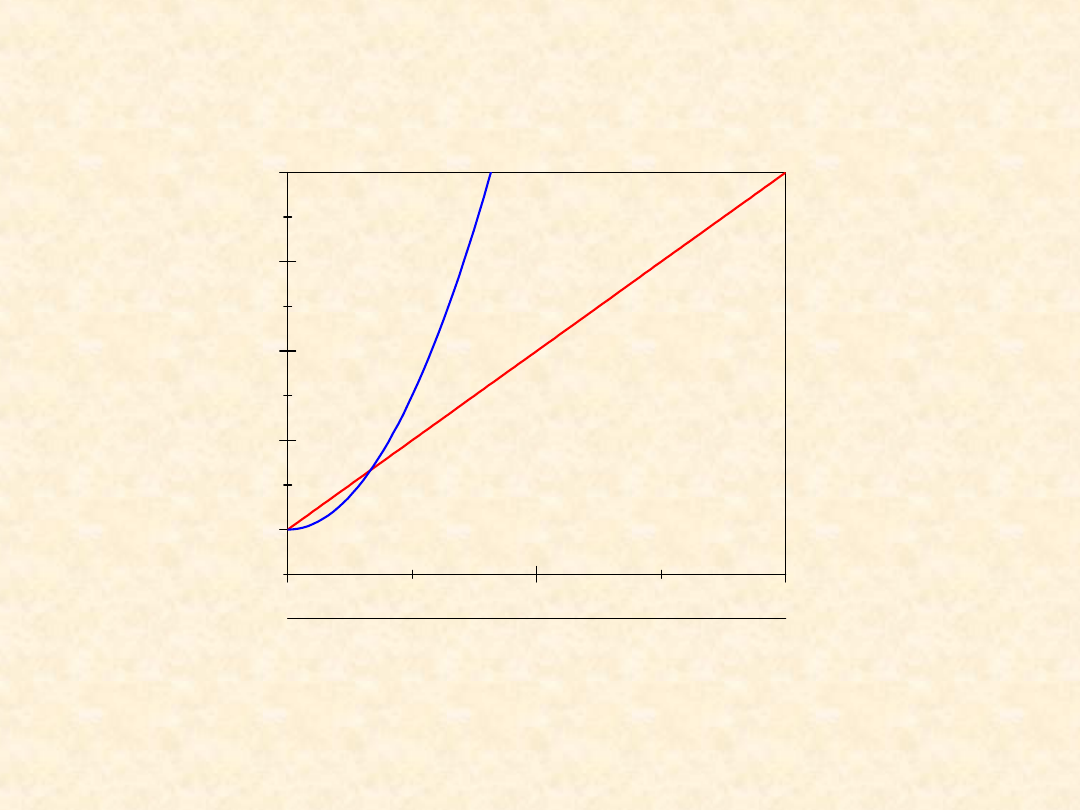
Prawo Ohma
Z doświadczenia wynika, że natężenie
prądu płynącego w przewodniku jest
proporcjonalne do przyłożonego
napięcia
jeśli temperatura przewodnika jest
stała.
U
I
U
R
I
1
oporność przewodnika
1
2
U
A
l
R
oporność właściwa
0
2
4
2
4
6
8
10
napięcie
n
a
tę
że
n
ie
p
rą
d
u
A
j
I
U
R
I
1
A
l
R
l
U
E
E
E
j
El
l
A
jA
1
prawo Ohma w
postaci polowej
(różniczkowej)
1
przewodność właściwa