(1)

(1)

(2)

(2)

restart;
with plots :
Tpocz

d 50 : Tl d 0 : Tp d 100 : Td d 0 : Tg d 100 :

n

d 50 : m d 50 : iter d 500 :

T

d Array 0 ..n, 0 ..m :

U

d Array 0 ..n, 0 ..m :

for i from 1 to n K1 do
for j from 1 to m K 1 do
T i, j

d Tpocz :

T i, 0

d Tl :

T i, m

d Tp :

T 0, j

d Td :

T n, j

d Tg :

T n, 0

d

T n K1, 0 C T n, 1

2

:

T n, m

d

T n K 1, m CT n, m K 1

2

:

T 0, m

d

T 0, m K 1 CT 1, m

2

:

T 0, 0

d

T 1, 0 C T 0, 1

2

:

end do:
end do:
print T ;

0..50 x 0..50 Array

Data Type: anything

Storage: rectangular

Order: Fortran_order

from 1 to iter do
for i from 1 to n K1 do
for j from 1 to m K 1 do
U i, j

d 0.25$ T i K1, j CT i C1, j CT i, j K1 CT i, j C1

end do:
end do:
for i from 1 to n K1 do
for j from 1 to m K 1 do
T i, j

d U i, j

end do:
end do:
end do:
print T

0..50 x 0..50 Array

Data Type: anything

Storage: rectangular

Order: Fortran_order

listcontplot

seq

seq T k, l , k = 0 .. n

, l = 0 .. m , contours = 10, 20, 30, 40, 50, 60, 70, 80, 90 ,

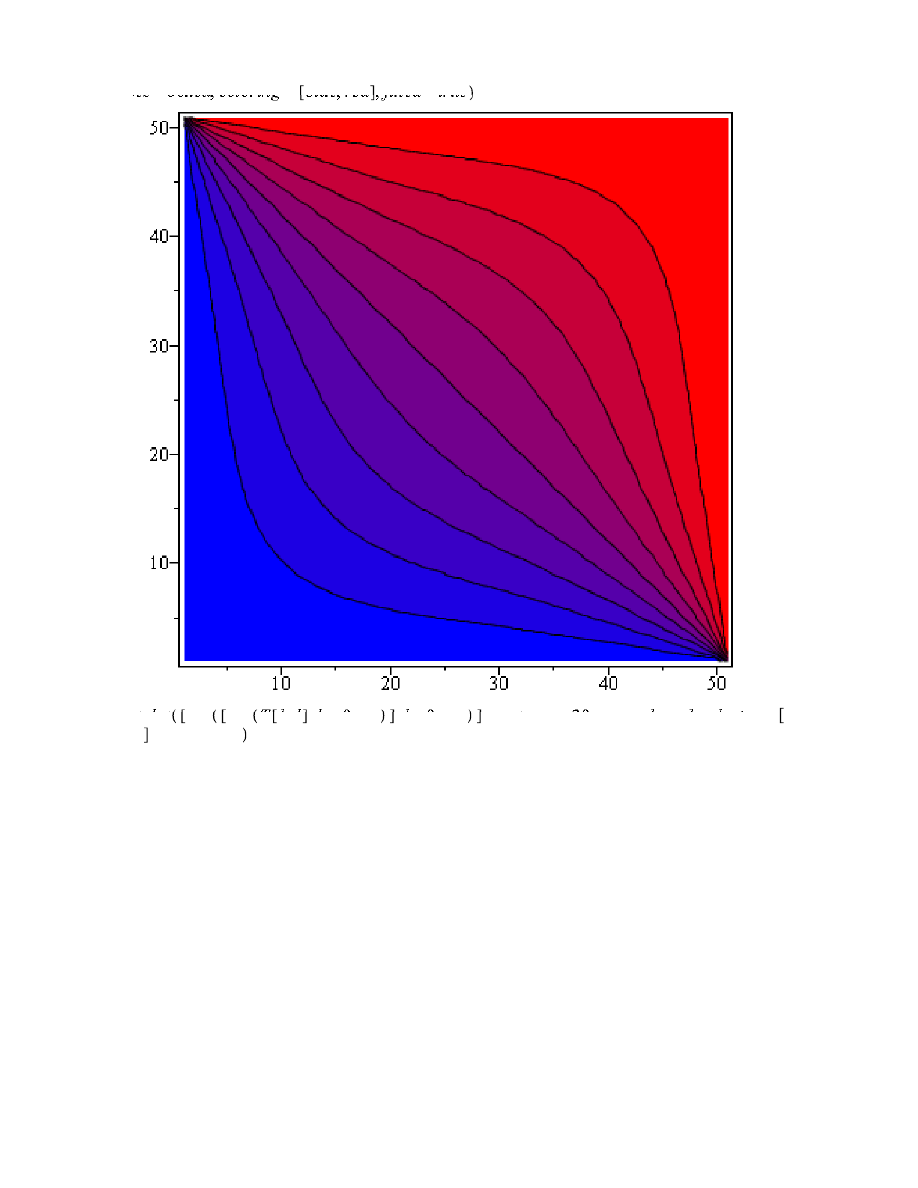
axes = boxed, coloring = blue, red , filled = true

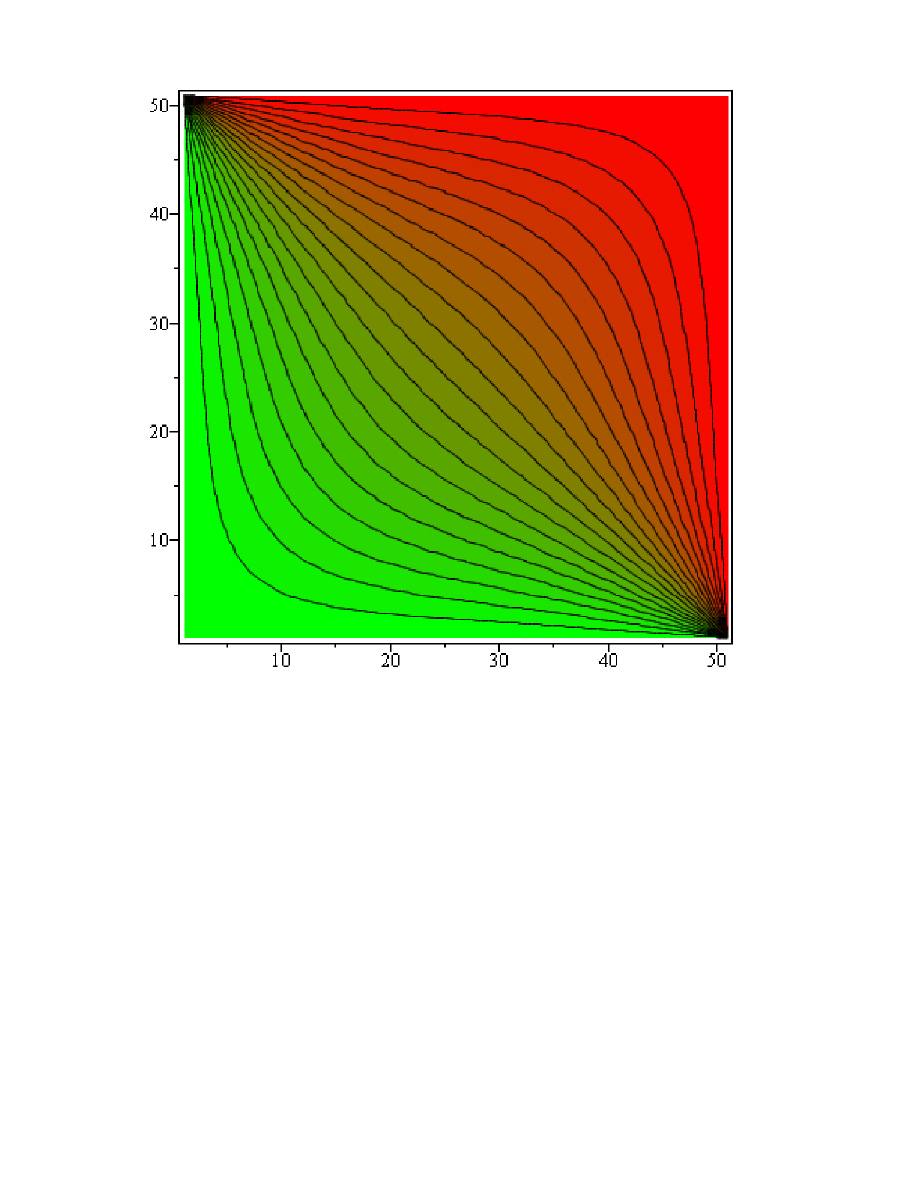
listcontplot

seq

seq T k, l , k = 0 .. n

, l = 0 .. m , contours = 20, axes = boxed, coloring = green,

red , filled = true