1
1.
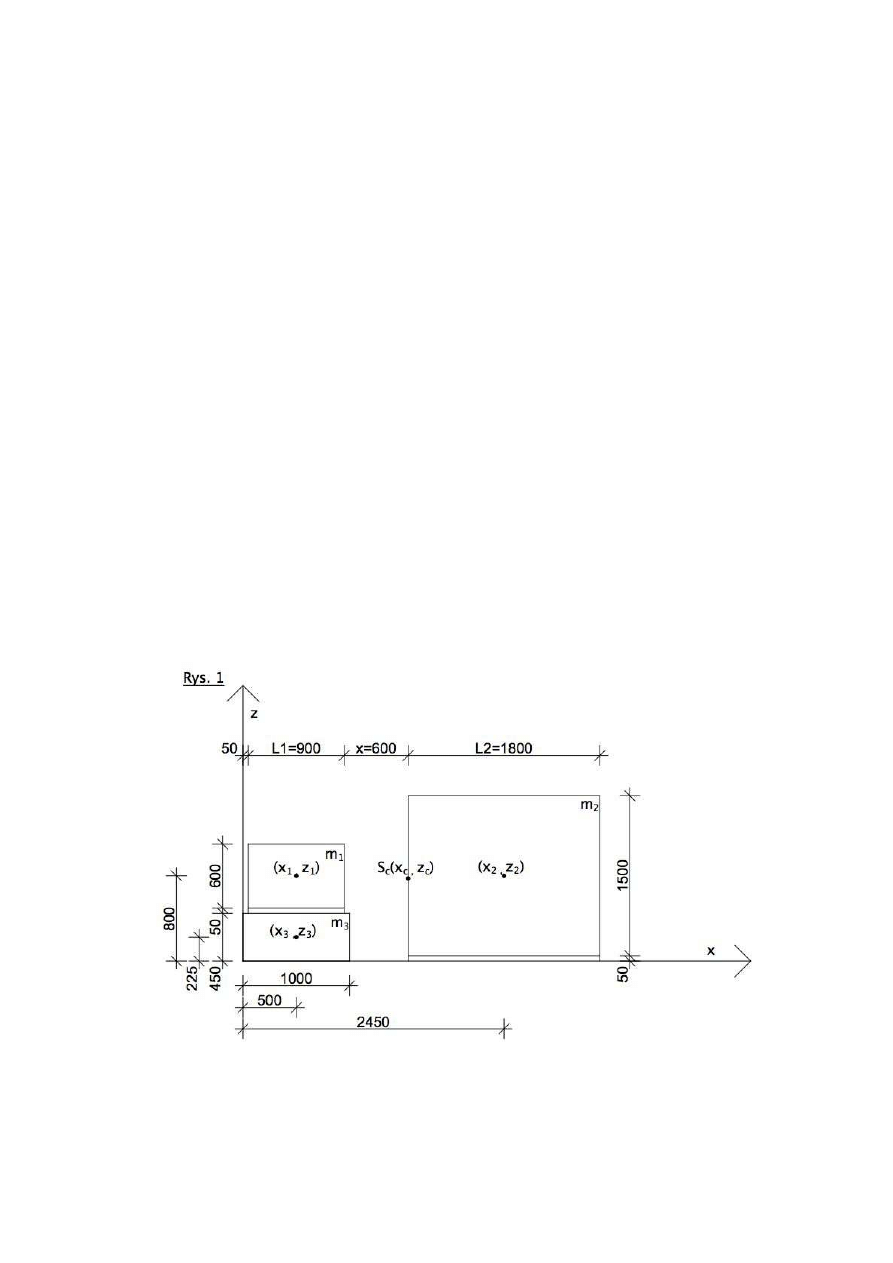
Geometria konstrukcji.
a)
Dane:
•
Silnik:
d
1
= 600mm
l
1
= 900mm
m
1
= 0,9Mg
•
Pompa:
d
2
= 1500mm
l
2
= 1800mm
m
2
= 8 Mg
•
Cokół żelbetowy pod silnikiem:
b
3
= 700mm
h
3
= (1500-600)/2=450mm
l
3
= 900 + 2*50=1000mm
m
3
= 0,7*0,45*0,1*2,4 = 0,76Mg (przyjęto ciężar betonu 2,4T/m
3
)
•
Warstwa wyrównawcza pod silnikiem i wentylatorem: 50mm
•
Odległość między silnikiem, a wentylatorem: x = 600mm

2
b)
Wyznaczenie środka ciężkości układu:
C
i
i
C
C
C
C
M
m
x
X
Z
X
S
∑
⋅
=
)
,
(
C
i
i
C
M
m
z
Z
∑
⋅
=
M
c
= m
1
+ m
2
+ m
3
= 0,9 + 8 + 0,76 = 9,66 Mg
Współrzędne środków ciężkości m
1
; m
2
; m
3
:
Silnik:
m
1
(x
1
, z
1
) = (500, 800)
Wentylator:
m
2
(x
2
, z
2
) = (2450, 800)
Cokół pod silnikiem:
m
3
(x
3
, z
4
) = (500, 225)
mm
Z
mm
Y
Z
X
S
C
C
C
C
C
8
,
754
66
,
9
76
,
0
225
8
800
9
,
0
800
90
,
2114
66
,
9
76
,
0
500
8
2450
9
,
0
500
)
,
(
=
⋅
+
⋅
+
⋅
=
=
⋅
+
⋅
+
⋅
=
2.
Wyznaczenie ciężarów i położenie głównego środka ciężkości całego układu.
a)
Obliczenie ciężarów:
•
Silnik: m
1
= 0,9 Mg
•
Wentylator: m
2
= 8 Mg
•
Cokół żelbetowy pod silnikiem: m
3
= 0,76 Mg
•
M
c
= m
1
+ m
2
+ m
3
= 0,9 + 8 + 0,76 = 9,66 Mg
b)
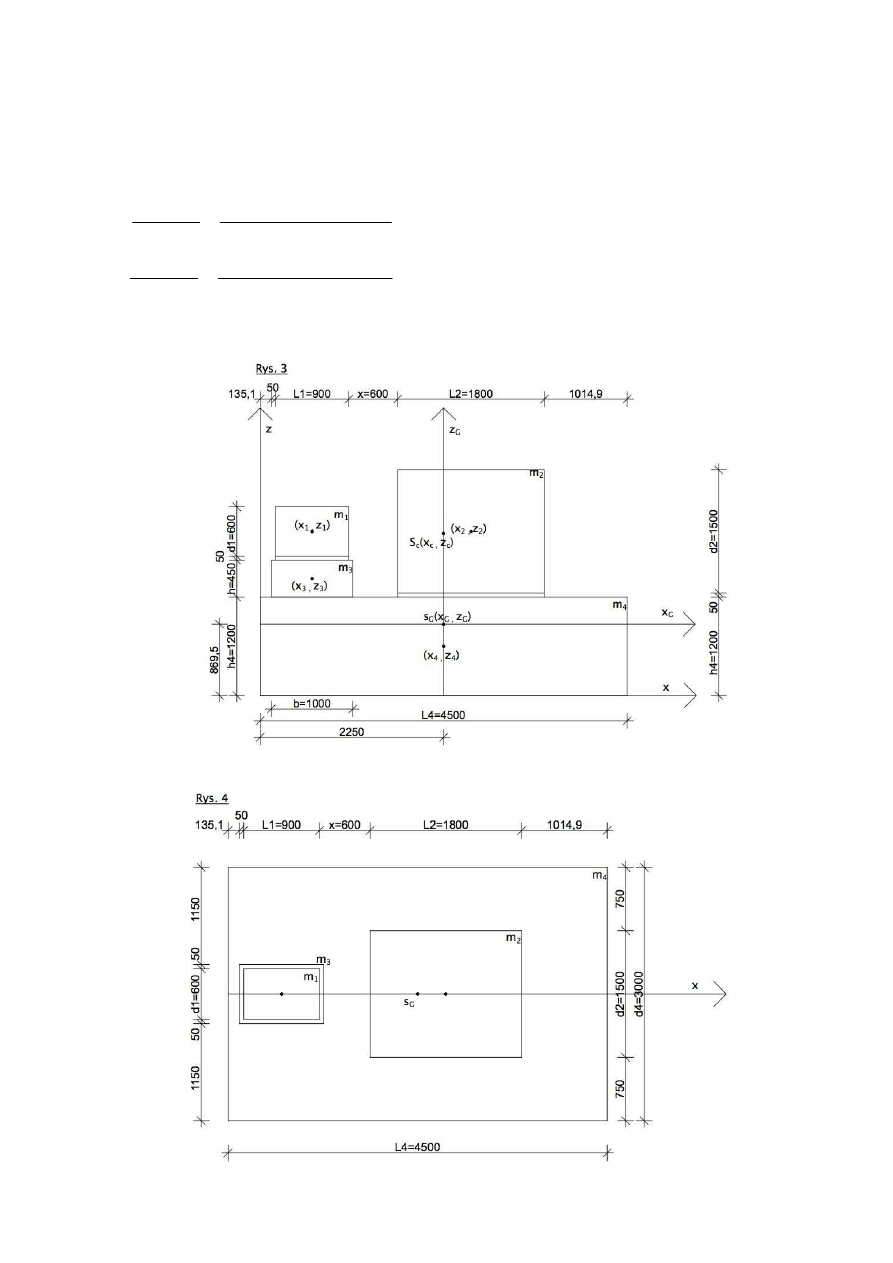
Przyjęcie wymiarów fundamentu:
m
4
= (4 ÷ 5) (m
1
+ m
2
)
(m
1
+ m
2
) = 0,9 + 8 = 8,9 Mg
35,6 Mg < m
4
< 44,5 Mg
Przyjęto:
d
4
= 3000mm
l
4
= 4500mm
h
4
= 1200mm
m
4
= d
4
·l
4
·h
4
·γ = 3,0·4,5·1,2·2,4 = 38,9 Mg
3
c)
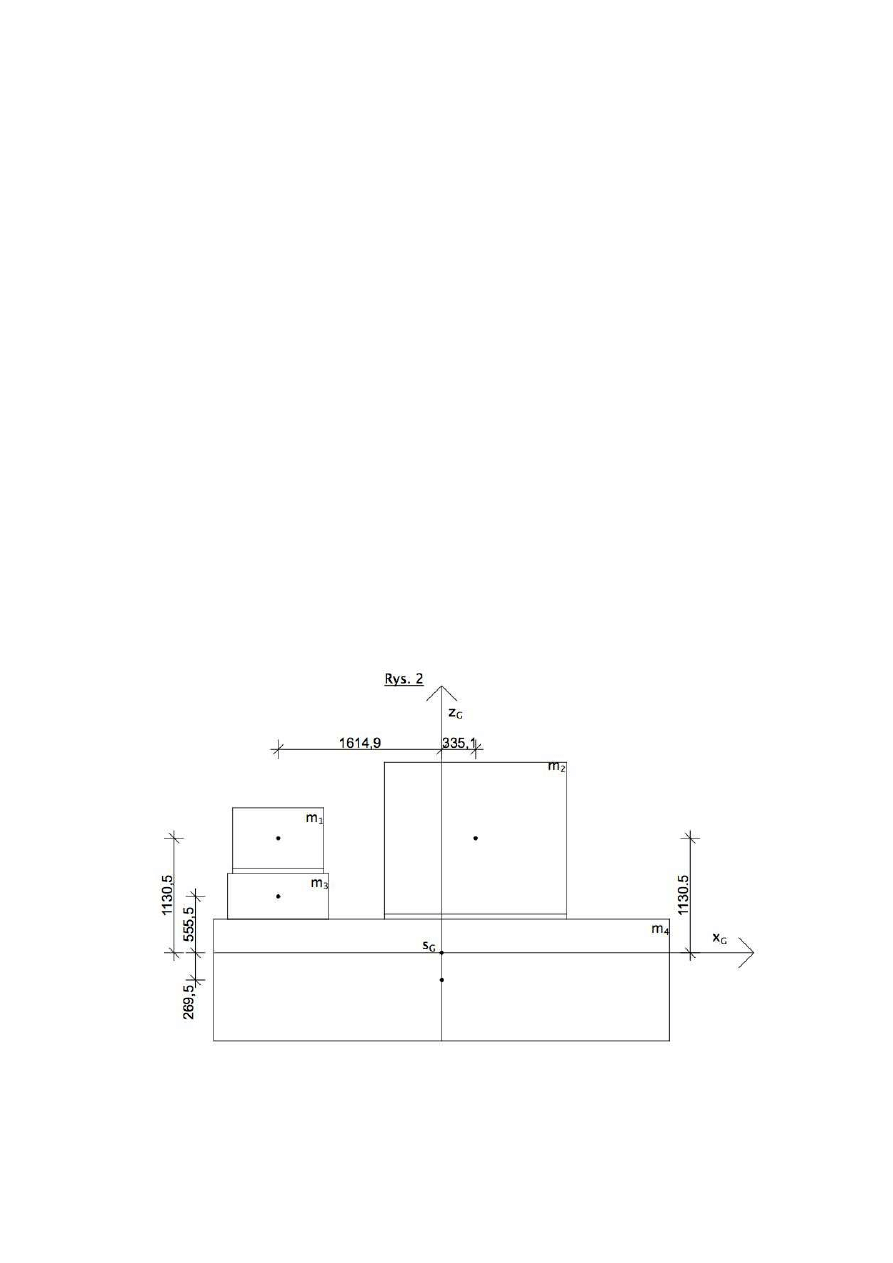
Wyznaczenie głównego środka ciężkości:
M
c
= 9,66 Mg m
4
= 38,9 Mg
mm
M
m
x
X
C
i
i
G
00
,
2250
56
,
48
9
,
38
2250
66
,
9
2250
=
⋅
+
⋅
=
⋅
=
∑
mm
M
m
z
Z
C
i
i
G
5
,
869
56
,
48
9
,
38
600
66
,
9
8
,
1954
=
⋅
+
⋅
=
⋅
=
∑
)
5
,
869
,
2250
(
)
,
(
G
G
G
G
S
Z
X
S
=
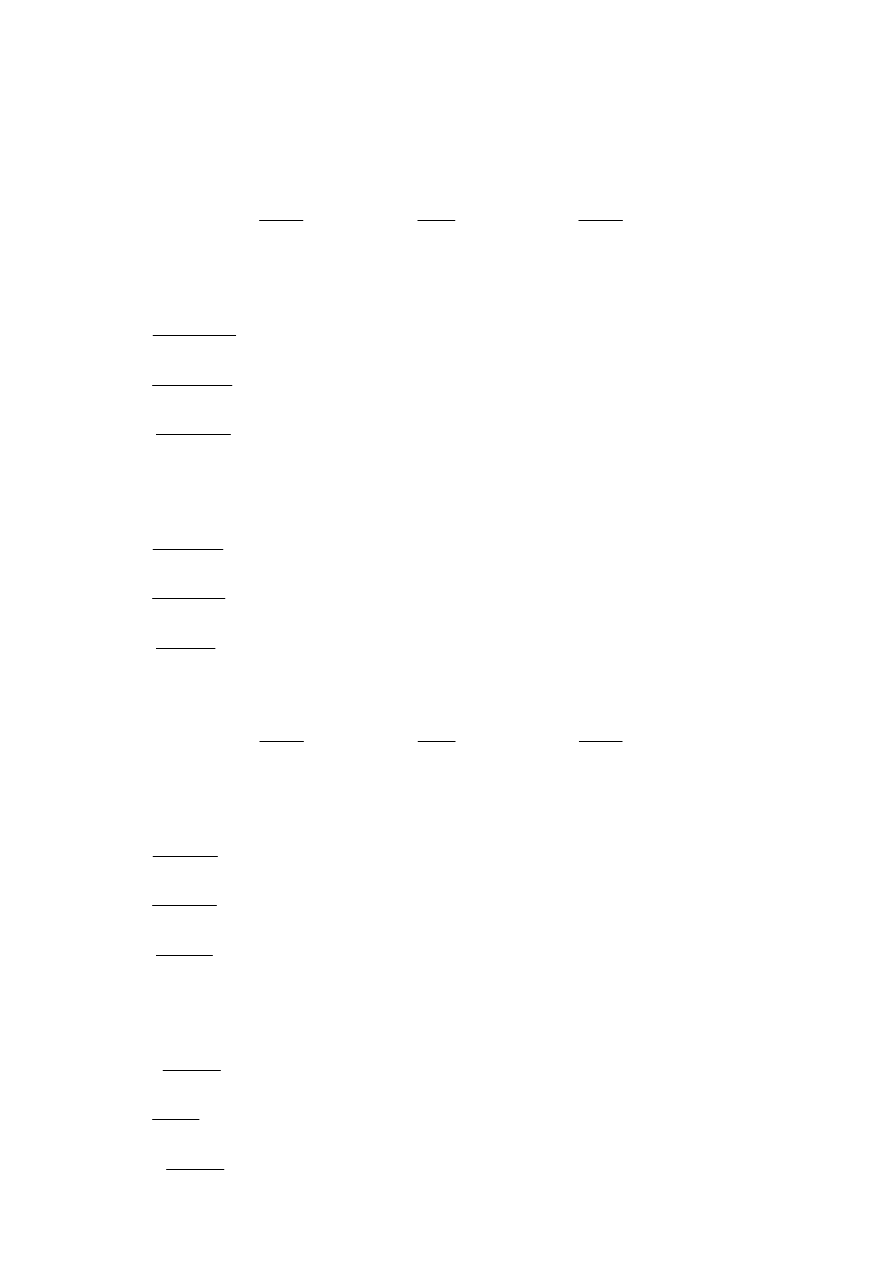
4
3.
Wyznaczenie momentów bezwładności mas układu względem płaszczyzn i osi
głównych.
3.1. Momenty bezwładności mas względem płaszczyzn głównych:
a)
Prostopadłościan o wymiarach w kierunku poszczególnych osi: l, b, h:
12
h
m
Y
X
2
1
1
⋅
=
Θ
12
l
m
Z
Y
2
1
1
⋅
=
Θ
12
b
m
Z
X
2
1
1
⋅
=
Θ
•
Cokół żelbetowy pod silnikiem:
a = 700 mm
b = 1000 mm
h = 450 mm
m
3
= 0,76 Mg
2
2
1
1
0128
,
0
12
45
,
0
76
,
0
m
Mg
Y
X
⋅
=
⋅
=
Θ
2
2
1
1
0633
,
0
12
0
,
1
762
,
0
m
Mg
Z
Y
⋅
=
⋅
=
Θ
2
2
1
1
031
,
0
12
7
,
0
76
,
0
m
Mg
Z
X
⋅
=
⋅
=
Θ
•
Fundament:
d
4
= 3000 mm
l
4
= 4500 mm
h
4
= 800 mm
m
4
= 38,9 Mg
2
2
1
1
668
,
4
12
2
,
1
9
,
38
m
Mg
Y
X
⋅
=
⋅
=
Θ
2
2
1
1
6438
,
65
12
5
,
4
9
,
38
m
Mg
Z
Y
⋅
=
⋅
=
Θ
2
2
1
1
0
,
1754
,
29
12
3
9
,
38
m
Mg
Z
X
⋅
=
⋅
=
Θ
b)
Walec o średnicy d i długości l usytuowany wzdłuż osi x
0
:
16
d
m
Y
X
2
1
1
⋅
=
Θ
12
l
m
Z
Y
2
1
1
⋅
=
Θ
16
d
m
Z
X
2
1
1
⋅
=
Θ
•
Silnik:
d
1
= 600 mm
l
1
= 900 mm
m
1
= 0,9 Mg
2
2
1
1
0202
,
0
16
6
,
0
9
,
0
m
Mg
Y
X
⋅
=
⋅
=
Θ
2
2
1
1
0608
,
0
12
9
,
0
9
,
0
m
Mg
Z
Y
⋅
=
⋅
=
Θ
2
2
1
1
0202
,
0
16
6
,
0
m
Mg
m
Z
X
⋅
=
⋅
=
Θ
•
Wentylator:
d
2
= 800mm
l
2
= 1000mm
m
2
= 1,50Mg
2
2
1
1
125
,
1
16
5
,
1
5
,
1
8
m
Mg
Y
X
⋅
=
⋅
=
Θ
2
2
1
1
16
,
2
12
8
,
1
8
m
Mg
Z
Y
⋅
=
⋅
=
Θ
2
2
1
1
125
,
1
16
5
,
1
5
,
1
8
m
Mg
Z
X
⋅
=
⋅
=
Θ
5
3.2
Momenty bezwładności mas względem płaszczyzn w układzie współrzędnych
przesuniętych o wektor [X, Y, Z]:
2
1
1
0
0
Z
m
Y
X
Y
X
⋅
+
Θ
=
Θ
2
1
1
0
0
X
m
Z
Y
Z
Y
⋅
+
Θ
=
Θ
2
1
1
0
0
Y
m
Z
X
Z
X
⋅
+
Θ
=
Θ
•
Silnik:
2
2
2
1
1
0
0
m
1,1704Mg
=
1,1305
9
,
0
0202
,
0
⋅
⋅
+
=
⋅
+
Θ
=
Θ
Z
m
Y
X
Y
X
2
2
2
1
1
0
0
4079
,
2
1,6149
0,9
+
0,0608
=
m
Mg
X
m
Z
Y
Z
Y
⋅
=
⋅
⋅
+
Θ
=
Θ
2
2
2
1
1
0
0
0202
,
0
0
9
,
0
0202
,
0
m
Mg
Y
m
Z
X
Z
X
⋅
=
⋅
+
=
⋅
+
Θ
=
Θ
•
Wentylator:
2
2
2
1
1
0
0
m
11,3492Mg
=
1205
,
1
8
125
,
1
⋅
⋅
+
=
⋅
+
Θ
=
Θ
Z
m
Y
X
Y
X
2
2
2
1
1
0
0
0583
,
3
3351
,
0
8
+
2,16
=
m
Mg
X
m
Z
Y
Z
Y
⋅
=
⋅
⋅
+
Θ
=
Θ
2
2
2
1
1
0
0
125
,
1
0
8
125
,
1
m
Mg
Y
m
Z
X
Z
X
⋅
=
⋅
+
=
⋅
+
Θ
=
Θ
•
Cokół:
2
2
2
1
1
0
0
m
0,2469Mg
=
5555
,
0
76
,
0
0128
,
0
⋅
⋅
+
=
⋅
+
Θ
=
Θ
Z
m
Y
X
Y
X
2
2
2
1
1
0
0
0453
,
02
6149
,
1
0,76
+
0,0633
=
m
Mg
X
m
Z
Y
Z
Y
⋅
=
⋅
⋅
+
Θ
=
Θ
2
2
2
1
1
0
0
031
,
0
0
76
,
0
031
,
0
m
Mg
Y
m
Z
X
Z
X
⋅
=
⋅
+
=
⋅
+
Θ
=
Θ
•
Fundament:
2
2
2
1
1
0
0
m
7,4933Mg
=
2695
,
0
9
,
38
668
,
4
⋅
⋅
+
=
⋅
+
Θ
=
Θ
Z
m
Y
X
Y
X
2
2
2
1
1
0
0
64
,
65
0
9
,
38
+
65,64
=
m
Mg
X
m
Z
Y
Z
Y
⋅
=
⋅
⋅
+
Θ
=
Θ
2
2
2
1
1
0
0
175
,
29
0
9
,
38
175
,
29
m
Mg
Y
m
Z
X
Z
X
⋅
=
⋅
+
=
⋅
+
Θ
=
Θ

6
3.3
Momenty bezwładności mas względem osi głównych:
∑
Θ
+
∑
Θ
=
Θ
0
0
0
0
0
Z
X
Y
X
X
∑
Θ
+
∑
Θ
=
Θ
0
0
0
0
0
Z
Y
Y
X
Y
0
0
0
0
0
Z
X
Z
Y
Z
∑
Θ
+
∑
Θ
=
Θ
2
0
611
,
50
)
175
,
29
031
,
0
125
,
1
0202
,
0
(
)
4933
,
7
2469
,
0
3492
,
11
1704
,
1
(
m
Mg
X
⋅
=
+
+
+
+
+
+
+
=
Θ
2
0
41
,
93
)
64
,
65
0453
,
2
0583
,
3
4079
,
2
(
)
4933
,
7
2469
,
0
3492
,
11
1704
,
1
(
m
Mg
Y
⋅
=
+
+
+
+
+
+
+
=
Θ
2
0
5
,
103
)
175
,
29
031
,
0
125
,
1
0202
,
0
(
)
64
,
65
0453
,
2
0583
,
3
4079
,
2
(
m
Mg
Z
⋅
=
+
+
+
+
+
+
+
=
Θ
4.
Dobór liczby sprężyn w wibroizolacji, rozmieszczenie i określenie sztywności
wibroizolacji.
A)
Dane sprężyny wibroizolacji:
•
średnica pręta: d = 20 mm
•
średnica podziałowa: D = 136 mm
•
wysokość: H
0
= 265 mm
•
liczba zwojów: i
0
= 6,5
B)
Dopuszczalne obliczeniowe obciążenie jednej sprężyny:
w
k
8
d
R
P
2
t
dop
⋅
⋅
⋅
π
⋅
=
R
t
– wytrzymałość obliczeniowa stali sprężynowej na skręcanie, R
t
= 730,0MPa
w – wskaźnik sprężyny, w = D/d
8
,
6
20
136
=
=
=
d
D
w
k – współczynnik poprawkowy uwzględniający nierównomierny stan naprężeń w przekroju
sprężyny
21
,
1
8
,
6
1
8
,
6
1
8
7
8
,
6
1
4
5
1
1
1
8
7
1
4
5
1
3
2
3
2
=
+
⋅
+
⋅
+
=
+
⋅
+
⋅
+
=
w
w
w
k
kN
P
dop
93
,
13
8
,
6
21
,
1
8
20
14
,
3
73
,
0
2
=
⋅
⋅
⋅
⋅
=

7
C)
Wymagana ilość sprężyn w układzie z uwzględnieniem 15% rezerwy obciążenia:
dop
min
P
85
,
0
Q
n
⋅
=
Q – ciężar całkowity układu
Q = M·g
M = m
1
+ m
2
+ m
3
+ m
4
= 0,9 + 8 + 0,76 + 38,9 = 48,56 Mg
2
s
m
81
,
9
g
=
Q = 48,56·9,81 = 476, 37 kN
40
23
,
40
93
,
13
85
,
0
37
,
476
min
≈
=
⋅
=
n
Przyjęto ilość sprężyn: n = 40 szt.
D)
Sztywność wibroizolacji:
•
sztywność pionowa:
3
Z
w
i
8
d
G
n
K
⋅
⋅
⋅
⋅
=
n – przyjęta całkowita ilość sprężyn w wibroizolacji układu,
G – moduł sprężystości poprzecznej stali sprężynowej, G = 78500MPa
d – średnica pręta sprężyny,
i – liczba pracujących zwojów sprężyny, i = i
0
– 1,5 = 6,5 – 1,5 = 5
w – wskaźnik sprężyny, w = D/d
m
kN
K
Z
13
,
4993
8
,
6
5
8
20
78500
40
3
=
⋅
⋅
⋅
⋅
=
•
sztywność pozioma:
K
x
= K
y
f
st
– ugięcie statyczne sprężyny,
mm
m
K
Q
f
Z
st
0
,
95
095
,
0
13
,
4993
37
,
476
=
=
=
=
H
st
– wysokość sprężyny obciążonej,
H
st
= H
0
– f
st
= 265 – 95,0 = 170 mm
D – średnica podziałowa sprężyny
56
,
0
0
,
170
0
,
95
=
=
st
st
H
f
oraz
25
,
1
136
0
,
170
=
=
D
H
st
Przyjęto na podstawie rysunku 19 normy PN-80/B-03040:
7
,
0
=
=
Z
Y
Z
X
K
K
K
K
m
kN
K
K
Z
X
19
,
3495
13
,
4993
7
,
0
95
,
0
=
⋅
=
⋅
=
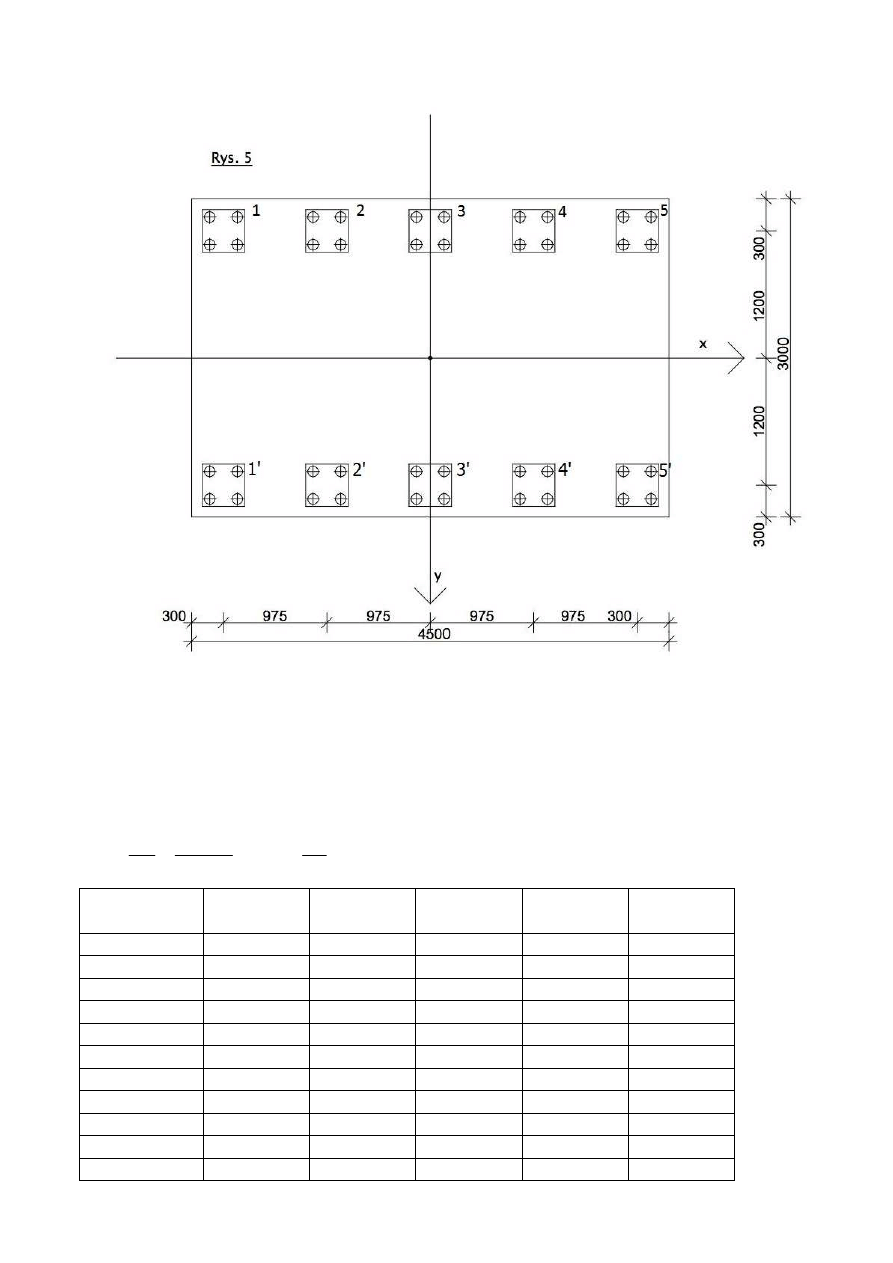
8
•
rozmieszczenie wibroizolacji:
•
sztywności wahadłowe:
K
ϕ
xz
= K
z
’
⋅
Σ
x
i
2
K
ϕ
yz
= K
z
’
⋅
Σ
y
i
2
K
z
’– sztywność pionowa jednego wibroizolatora [kN/m],
x
i
– współrzędna x wibroizolatora od osi ciężkości układu [m],
y
i
– współrzędna y wibroizolatora od osi ciężkości układu [m]
n – liczba wibroizolatorów
m
kN
n
K
K
Z
z
31
,
499
10
13
,
4993
'
=
=
=
Nr
wibroizolatora
x
ki
[m]
x
2
ki
[m
2
]
y
ki
[m]
y
2
ki
[m
2
]
x
ki
⋅
y
ki
[m
2
]
1
-1,950
3,8
-1,2
1,44
2,34
2
-0,975
0,95
-1,2
1,44
1,17
3
0
0
-1,2
1,44
0
4
0,975
0,95
-1,2
1,44
-1,17
5
1,950
3,8
-1,2
1,44
-2,34
1’
-1,950
3,8
1,2
1,44
-2,34
2’
-0,975
0,95
1,2
1,44
-1,17
3’
0
0
1,2
1,44
0
4’
0,975
0,95
1,2
1,44
1,17
5’
1,950
3,8
1,2
1,44
2,34
Σ
0
19
0
14,4
0
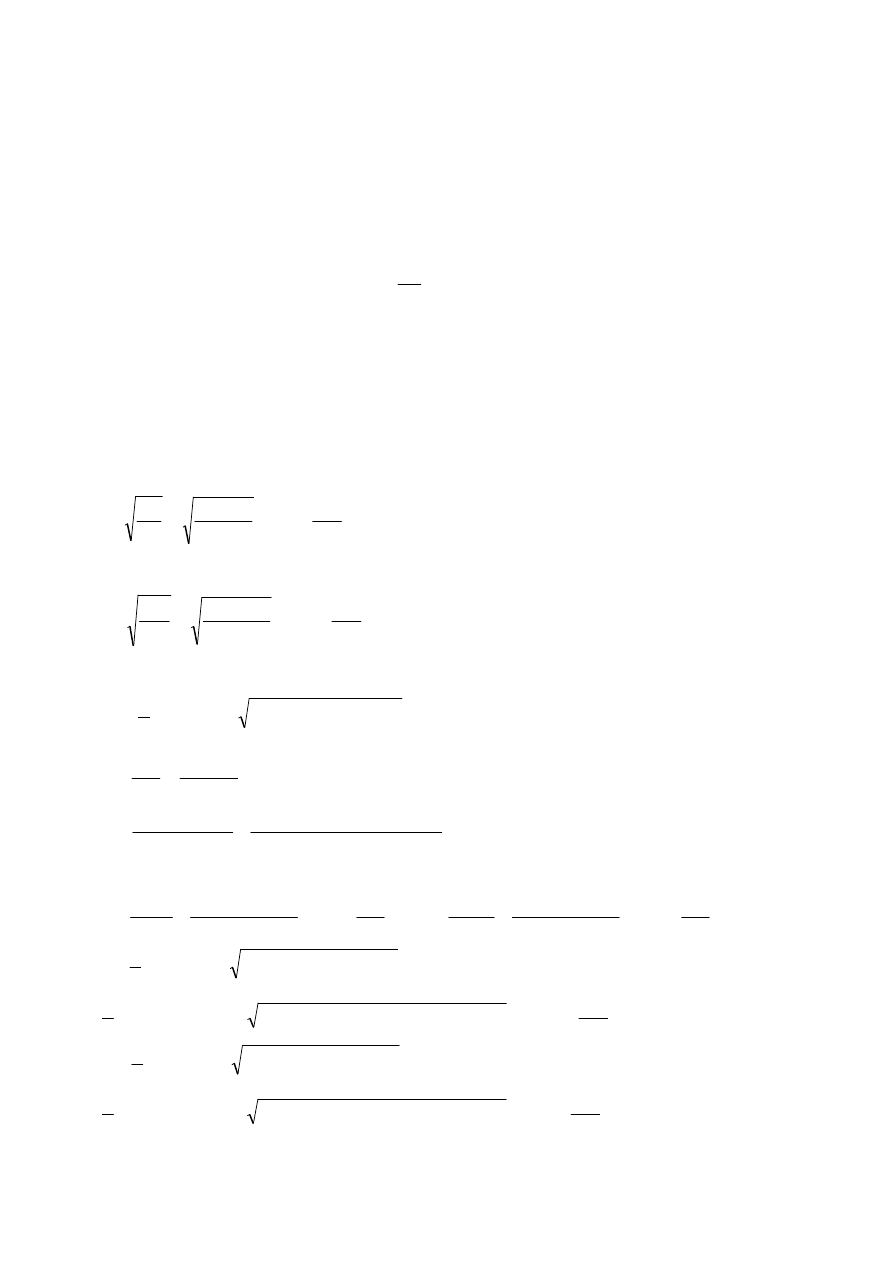
9
K
ϕ
xz
= 499,31
⋅
19 = 9486,95 kNm
K
ϕ
yz
= 499,31
⋅
14,4 = 7190,06 kNm
•
sztywność skrętna
K
ψ
= K
x
’
⋅
(
Σ
x
i
2
+
Σ
y
i
2
)
K
x’
– sztywność pozioma jednego wibroizolatora
K
x’
= 0,7 · K
z
’ = 0,7
⋅
499,31 = 349,52
m
kN
K
ψ
= 349,52
⋅
(19 + 14,4) = 11673,97 kNm
5.
Określenie częstotliwości drgań własnych układu
A)
Prędkości kątowe drgań własnych-scentrowanego bloku fundamentowego opartego
na sprężystym podłożu gruntowym wyznacza się w [rad/s] wg wzorów:
•
Prędkość kątowa drgań własnych pionowych:
s
rad
M
K
z
z
14
,
10
56
,
48
13
,
4993
=
=
=
λ
•
Prędkość kątowa drgań własnych skrętnych:
s
rad
K
z
62
,
10
5
,
103
97
,
11673
0
=
=
Θ
=
ψ
ψ
λ
•
Prędkości kątowe drgań własnych w płaszczyźnie podłużnej:
(
)
µ
⋅
µ
+
λ
−
λ
±
λ
+
λ
=
λ
b
a
2
2
xz
2
x
2
xz
2
x
2
2
,
1
4
2
1
98
,
71
56
,
48
19
,
3495
2
=
=
=
M
K
X
x
λ
06
,
137
41
,
93
19
,
3495
974
,
0
9486,95
2
0
2
2
=
⋅
+
=
Θ
⋅
+
=
Y
K
s
K
X
xz
xz
ϕ
λ
- prędkości kątowe drgań podukładów
s – odległość między środkiem ciężkości i środkiem sztywności układu
Mg
kN
M
K
s
x
a
11
,
70
56
,
48
19
,
3495
974
,
0
=
⋅
=
⋅
=
µ
Mg
kN
Y
K
s
X
b
44
,
36
41
,
93
19
,
3495
974
,
0
0
=
⋅
=
Θ
⋅
=
µ
(
)
[
]
s
rad
b
a
xz
x
xz
x
63
,
164
44
,
36
11
,
70
4
)
06
,
137
98
,
71
(
06
,
137
98
,
71
2
1
4
2
1
2
2
2
2
2
2
2
1
=
⋅
⋅
+
−
+
+
⋅
=
=
⋅
+
−
+
+
=
µ
µ
λ
λ
λ
λ
λ
(
)
[
]
s
rad
b
a
xz
x
xz
x
41
,
44
44
,
36
11
,
70
4
)
06
,
137
98
,
71
(
06
,
137
98
,
71
2
1
4
2
1
2
2
2
2
2
2
2
2
=
⋅
⋅
+
−
−
+
⋅
=
=
⋅
+
−
−
+
=
µ
µ
λ
λ
λ
λ
λ
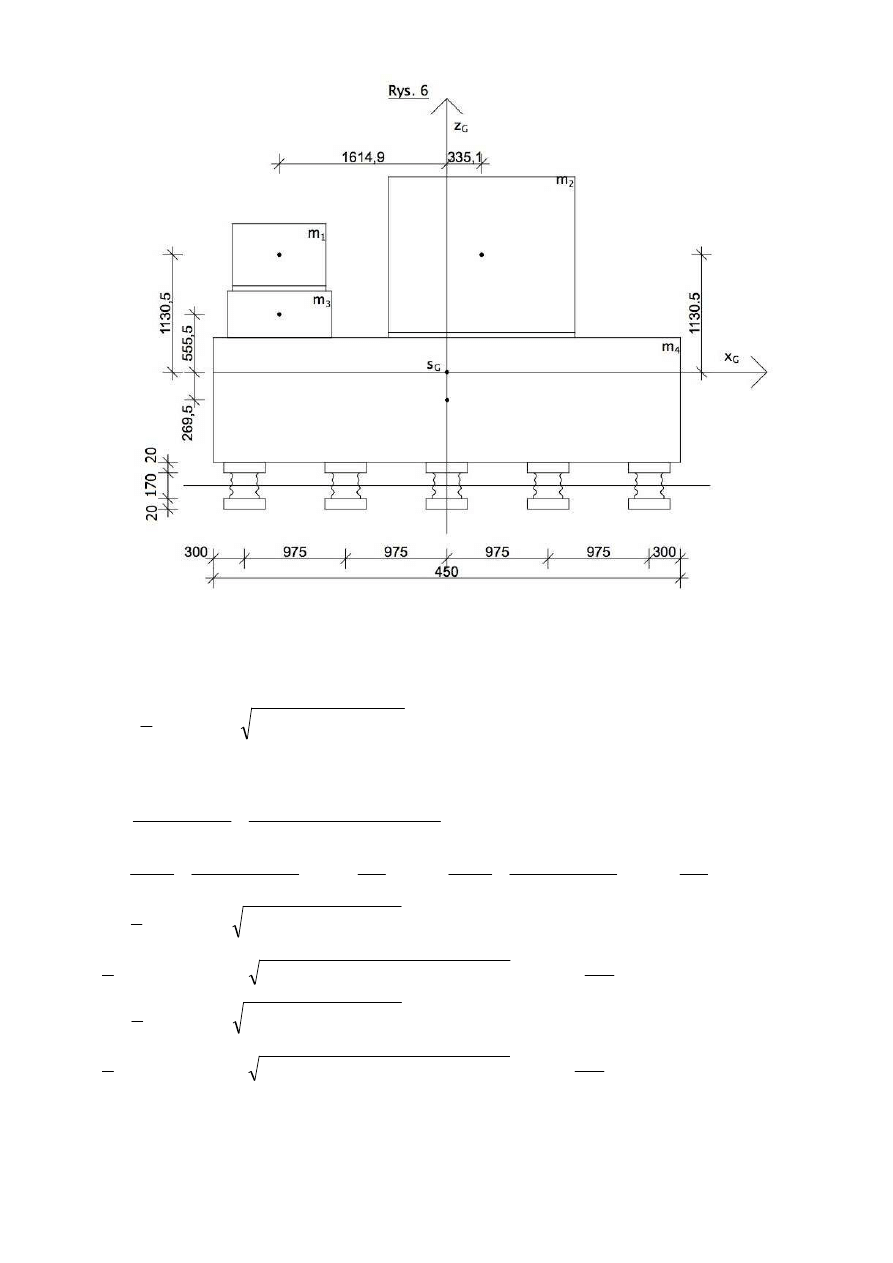
10
s = 600+269,5+20+85=974,5 mm
•
Prędkości kątowe drgań własnych w płaszczyźnie poprzecznej:
(
)
µ
⋅
µ
+
λ
−
λ
±
λ
+
λ
=
λ
b
a
2
2
yz
2
y
2
yz
2
y
2
4
,
3
4
2
1
98
,
71
2
2
=
=
x
y
λ
λ
58
,
207
61
,
50
19
,
3495
974
,
0
06
,
7190
2
0
2
2
=
⋅
+
=
Θ
⋅
+
=
x
K
s
K
Y
yz
yz
ϕ
λ
- prędkości kątowe drgań podukładów
Mg
kN
M
K
s
Y
a
11
,
70
56
,
48
19
,
3495
974
,
0
=
⋅
=
⋅
=
µ
Mg
kN
x
K
s
Y
b
27
,
67
61
,
50
19
,
3495
974
,
0
0
=
⋅
=
Θ
⋅
=
µ
(
)
[
]
s
rad
b
a
yz
y
yz
y
28
,
236
27
,
67
11
,
70
4
)
58
,
207
98
,
71
(
58
,
207
98
,
71
2
1
4
2
1
2
2
2
2
2
2
2
3
=
⋅
⋅
+
−
+
+
⋅
=
=
⋅
+
−
+
+
=
µ
µ
λ
λ
λ
λ
λ
(
)
[
]
s
rad
b
a
yz
y
yz
y
28
,
43
27
,
67
11
,
70
4
)
58
,
207
98
,
71
(
58
,
207
98
,
71
2
1
4
2
1
2
2
2
2
2
2
2
4
=
⋅
⋅
+
−
−
+
⋅
=
=
⋅
+
−
−
+
=
µ
µ
λ
λ
λ
λ
λ

11
6.
Wyznaczenie amplitud drgań.
n
m
- prędkość obrotowa maszyny, n
m
= 750 obr/min
f
m
– częstotliwość drgań własnych
5
,
12
60
750
60
=
=
=
m
m
n
f
Hz
s
rad
f
m
5
,
78
5
,
12
14
,
3
2
2
=
⋅
⋅
=
⋅
⋅
=
π
ω
Wyznaczanie sił wzbudzających:
w
d
G
P
⋅
=
15
,
0
- dla maszyn o prędkości obrotowej powyżej 750 obr/min
Silnik:
s
ws
G
5
,
0
G
⋅
=
kN
829
,
8
Mg
9
,
0
G
s
=
=
kN
415
,
4
Mg
45
,
0
9
,
0
5
,
0
G
ws
=
=
⋅
=
kN
Mg
P
ds
662
,
0
068
,
0
45
,
0
15
,
0
=
=
⋅
=
Wentylator:
w
ww
G
5
,
0
G
⋅
=
kN
Mg
G
w
48
,
78
8
=
=
kN
Mg
G
ww
24
,
39
4
8
5
,
0
=
=
⋅
=
kN
Mg
P
dw
89
,
5
6
,
0
4
15
,
0
=
=
⋅
=
Wyznaczenie amplitud drgań:
•
Schemat I
x
s
= 1,6149 m
x
w
= 0,3351 m
P
z max
= P
ds
+ P
dw
= 0,662 + 5,89 = 6,552 kN
M
y0
= P
ds
· x
s
- P
dw
· x
w
= 0,662 · 1,6149 – 5,89 · 0,3351 = -0,905 kNm
•
Schemat II
x
s
= 1,6149 m
x
w
= 0,3351 m
P
z
= P
ds
- P
dw
= 0,662 - 5,89 = -5,228 kN
M
y0 max
= P
ds
· x
s
+ P
dw
· x
w
= 0,662 · 1,6149 + 5,89 · 0,3351 = 3,043 kNm
•
Schemat III
x
s
= 1,6149 m
x
w
= 0,3351 m
z
s
= 1,1305 m
P
y
= P
ds
+ P
dw
= 0,662 + 5,89 = 6,552 kN
M
x0
= (P
ds
+ P
dw
) · z
s
= 6,552· 1,1305 = 7,407 kNm
M
z0
= P
ds
· x
s
- P
dw
· x
w
= 0,662 · 1,6149 – 5,89 · 0,3351 = -0,905 kNm
•
Schemat IV:
x
s
= 1,6149 m
x
w
= 0,3351 m
z
s
= 1,1305 m
P
y
= P
ds
- P
dw
= 0,662 - 5,89 = -5,228 kN
M
x0
= (P
ds
- P
dw
) · z
s
= (-5,228) · 1,1305 = -5,91 kNm
M
z0
= P
ds
· x
s
+ P
dw
· x
w
= 0,662 · 1,6149 + 5,89 · 0,3351 = 3,043 kNm
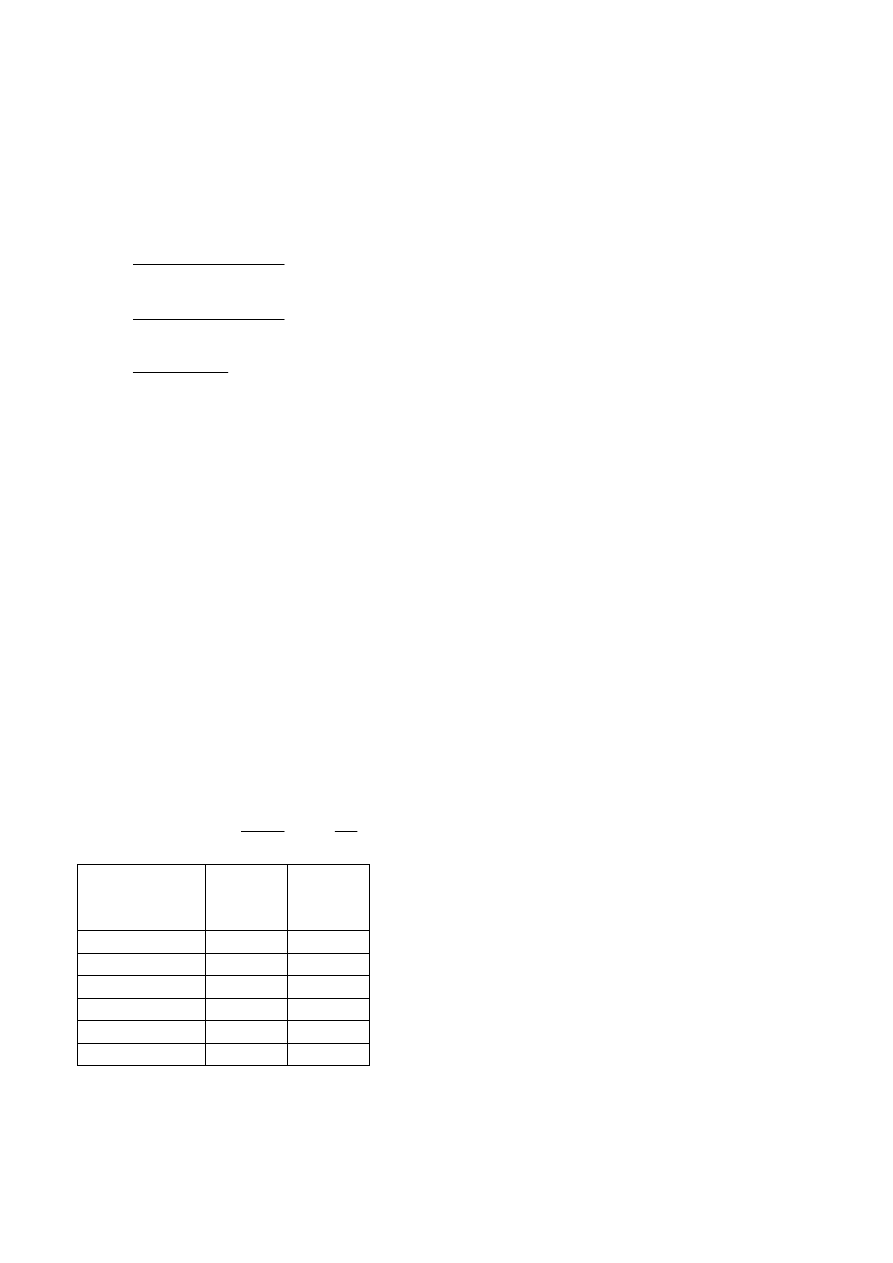
12
Wyznaczenie cząstkowych drgań wymuszonych wibroizolowanego układu, bez uwzględnienia
tłumienia, gdy środki ciężkości układu i sztywności wibroizolatorów nie znajdują się w jednym
punkcie:
Założono, że wszystkie obciążenia działają z funkcją sinus:
Amplitudy cząstkowe obrotowe względem osi:
•
Składowe sinusowe:
rad
,
s
K
'
P
B
'
M
'
x
x
y
y
0
y
x
0
x
0
ϕ
∆
⋅
⋅
+
⋅
=
ϕ
rad
,
s
K
'
P
B
'
M
'
y
y
x
x
0
x
y
0
y
0
ϕ
∆
⋅
⋅
+
⋅
=
ϕ
rad
,
)
1
(
K
'
M
'
2
z
z
0
z
0
ϕ
Ψ
η
−
⋅
=
ϕ
kNm
K
K
yz
x
06
,
7190
=
=
ϕ
ϕ
kNm
K
K
xz
y
95
,
9486
=
=
ϕ
ϕ
kNm
K
97
,
11673
=
Ψ
(
) (
)
2
8911716638
5
,
78
28
,
43
5
,
78
28
,
236
611
,
50
56
,
48
)
(
)
(
2
2
2
2
2
2
2
1
0
=
−
⋅
−
⋅
⋅
=
∆
−
⋅
−
⋅
Θ
=
∆
x
x
x
x
x
m
ϕ
ϕ
ϕ
ϕ
ω
λ
ω
λ
77
,
301271
5
,
78
611
,
50
974
,
0
19
,
3495
06
,
7190
2
2
2
0
2
−
=
⋅
−
⋅
+
=
⋅
Θ
−
⋅
+
=
ω
ϕ
ϕ
x
x
y
x
x
s
K
K
B
67
,
295743
5
,
78
56
,
48
19
,
3495
2
2
−
=
⋅
−
=
⋅
−
=
ω
m
K
B
x
x
(
) (
)
00
1664367056
5
,
78
41
,
44
5
,
78
63
,
164
41
,
93
56
,
48
)
(
)
(
2
2
2
2
2
2
2
1
0
=
−
⋅
−
⋅
⋅
=
∆
−
⋅
−
⋅
Θ
=
∆
y
y
y
y
y
m
ϕ
ϕ
ϕ
ϕ
ω
λ
ω
λ
02
,
562813
5
,
78
41
,
93
974
,
0
19
,
3495
95
,
9486
2
2
2
0
2
−
=
⋅
−
⋅
+
=
⋅
Θ
−
⋅
+
=
ω
ϕ
ϕ
y
y
x
y
y
s
K
K
B
67
,
295743
5
,
78
56
,
48
19
,
3495
2
2
−
=
⋅
−
=
⋅
−
=
ω
m
K
B
y
y
π
λ
⋅
=
i
i
30
n
60
n
f
i
i
=
λ
i
rad/s
n
i
drg/mi
n
f
i
Hz
λ
z
=10,14
96,88
1,61
λ
ψ
=10,62
101,46
1,69
λ
1
=12,83
122,58
2,04
λ
2
=6,66
63,63
1,06
λ
3
=15,37
146,85
2,45
λ
4
=6,58
62,87
1,05
13
•
Schemat I:
rad
B
M
y
x
y
y
6
0
0
10
61
,
1
00
1664367056
)
64
,
295743
(
905
,
0
'
'
−
⋅
=
−
⋅
−
=
∆
⋅
=
ϕ
ϕ
74
,
7
14
,
10
5
,
78
=
=
=
z
z
λ
ω
η
m
K
P
a
z
z
z
z
5
2
2
0
0
10
23
,
2
)
74
,
7
1
(
13
,
4993
552
,
6
)
1
(
'
'
−
⋅
−
=
−
⋅
=
−
⋅
=
η
rad
s
K
M
a
y
x
x
y
x
8
0
0
10
85
,
1
00
1664367056
974
,
0
19
,
3495
905
,
0
'
'
−
⋅
−
=
⋅
⋅
−
=
∆
⋅
⋅
=
ϕ
•
Schemat II:
rad
B
M
y
x
y
y
6
0
0
10
41
,
5
00
1664367056
)
67
,
295743
(
043
,
3
'
'
−
⋅
−
=
−
⋅
=
∆
⋅
=
ϕ
ϕ
74
,
7
14
,
10
5
,
78
=
=
=
z
z
λ
ω
η
m
K
P
a
z
z
z
z
5
2
2
0
0
10
78
,
1
)
74
,
7
1
(
13
,
4993
228
,
5
)
1
(
'
'
−
⋅
=
−
⋅
−
=
−
⋅
=
η
rad
s
K
M
a
y
x
x
y
x
8
0
0
10
22
,
6
00
1664367056
974
,
0
19
,
3495
043
,
3
'
'
−
⋅
=
⋅
⋅
=
∆
⋅
⋅
=
ϕ
•
Schemat III:
rad
s
K
P
B
M
x
x
y
y
y
x
x
5
0
0
0
10
43
,
2
2
8911716638
974
,
0
19
,
3495
552
,
6
)
67
,
295743
(
407
,
7
'
'
'
−
⋅
−
=
⋅
⋅
+
−
⋅
=
∆
⋅
⋅
+
⋅
=
ϕ
ϕ
rad
s
K
M
B
P
a
x
x
y
x
x
y
y
5
0
0
0
10
19
,
2
2
8911716638
974
,
0
19
,
3495
407
,
7
)
77
,
301271
(
552
,
6
'
'
'
−
⋅
−
=
⋅
⋅
+
−
⋅
=
∆
⋅
⋅
+
⋅
=
ϕ
ϕ
39
,
7
62
,
10
5
,
78
=
=
=
ψ
ϕ
λ
ω
η
z
m
K
M
z
z
z
6
2
2
0
0
10
45
,
1
)
39
,
7
1
(
97
,
11673
905
,
0
)
1
(
'
'
−
Ψ
⋅
=
−
⋅
−
=
−
⋅
=
ϕ
η
ϕ
•
Schemat IV:
rad
s
K
P
B
M
x
x
y
y
y
x
x
5
0
0
0
10
94
,
1
2
8911716638
974
,
0
19
,
3495
228
,
5
)
67
,
295743
(
91
,
5
'
'
'
−
⋅
=
⋅
⋅
−
−
⋅
−
=
∆
⋅
⋅
+
⋅
=
ϕ
ϕ
rad
s
K
M
B
P
a
x
x
y
x
x
y
y
4
0
0
0
10
74
,
1
2
8911716638
974
,
0
19
,
3495
91
,
5
)
77
,
301271
(
228
,
5
'
'
'
−
⋅
=
⋅
⋅
−
−
⋅
−
=
∆
⋅
⋅
+
⋅
=
ϕ
ϕ
39
,
7
62
,
10
5
,
78
=
=
=
ψ
ϕ
λ
ω
η
z
m
K
M
z
z
z
6
2
2
0
0
10
86
,
4
)
39
,
7
1
(
97
,
11673
043
,
3
)
1
(
'
'
−
Ψ
⋅
−
=
−
⋅
=
−
⋅
=
ϕ
η
ϕ

14
Wyznaczenie amplitud przesunięć dowolnego punktu i układu o współrzędnych x
0i
, y
0i
, z
0i
przy działaniu składowej sinusowej:
Współrzędne punktów skrajnych układu wibroizolowanego:
x
0i
= ±2250mm
y
0i
= ±1500mm
z
0i
= +330,5mm
z
0i
= -869,5mm
m
a
m
y
z
a
a
xi
i
z
i
y
x
xi
µ
ϕ
ϕ
06
,
12
10
2056
,
1
)
50
,
1
(
)
10
86
,
4
(
)
8695
,
0
(
)
10
41
,
5
(
10
22
,
6
'
'
'
5
6
6
8
0
0
0
0
0
=
⋅
=
−
⋅
⋅
−
−
−
⋅
⋅
−
+
⋅
=
=
−
+
=
−
−
−
−
m
a
m
z
x
a
a
yi
i
x
i
z
y
yi
µ
ϕ
ϕ
96
,
53
10
3963
,
5
)
8695
,
0
(
)
10
43
,
2
(
)
25
,
2
(
)
10
86
,
4
(
10
19
,
2
'
'
'
5
5
6
5
0
0
0
0
0
=
⋅
−
=
−
⋅
⋅
−
−
+
⋅
⋅
−
+
⋅
−
=
=
−
+
=
−
−
−
−
m
a
m
x
y
a
a
zi
i
y
i
x
z
zi
µ
ϕ
ϕ
92
,
70
10
0922
,
7
)
25
,
2
(
)
10
41
,
5
(
)
5
,
1
(
)
10
43
,
2
(
10
23
,
2
'
'
'
5
6
5
5
0
0
0
0
0
=
⋅
−
=
−
⋅
⋅
−
−
+
⋅
⋅
−
+
⋅
−
=
=
−
+
=
−
−
−
−
Wartości porównano z wartościami dopuszczalnymi (rys. 4 PN-80/B-03040), odczytano dla
częstości wzbudzającej 12,5Hz (750obr/min):
•
Dla drgań poziomych:
m
a
xi
µ
01
,
9
=
<
m
a
dop
µ
5
,
202
5
,
1
135
=
⋅
=
m
a
yi
µ
96
,
53
=
<
m
a
dop
µ
5
,
202
5
,
1
135
=
⋅
=
•
Dla drgań pionowych:
m
a
zi
µ
92
,
70
=
<
m
a
dop
µ
135
5
,
1
90
=
⋅
=
Warunki spełnione
Wyszukiwarka
Podobne podstrony:
Tomasz Marek Sobieraj GRA
Sobieradek 1, ZHP - przydatne dokumenty, Karty sprawności
sprawozdanie.sieci.6.marek, Politechnika Lubelska, Studia, Semestr 6, sem VI, VI-semestr, 05labsieci
SYLABUS Technologie informacyjne Ogrodnictwo SGGW dr Marek Wierzbicki, Ogrodnictwo 2011, INFORMATYKA
Hłasko - Dwaj mężczyźni, UMCS Filologia polska, Marek Hłasko
I.WYCHOWANIE OBYWATELSKIE, 6.Symbole narodowe, Marek Biesiada
III.CZAS W HISTORII, 12.IVB.Obliczanie czasu minionych wydarzeń, Marek Biesiada
II.WYCHOWANIE DO ŻYCIE W RODZINIE, 14.Potrzeba przyjaźni, Marek Biesiada
13, HOOKE, Marek Strzelczyk
REFERATY, Rola Zbigniewa Oleśnickiego w polityce polskiej XV wieku II, Marek Biesiada
I. EPOKA WIELKICH ODKRYĆ GEOGRAFICZNYCH,RENESANSU I REFORMACJI, 2.Przyczyny wielkich odkryć, Marek B
logika-testy, LogikaIIIgrupa2010czesc1, Zadania egzaminacyjne z logiki dla III grupy - egzaminator d
lab n10 Marek Marków 144105, Marek Marków 144105
Negocjacje w biznesie [ opracowanie z książki] [ wykłady dr Marek Datko], Negocjacje w biznesie - wy
II.CZŁOWIEK MIĘDZY WIARĄ A ROZUMEM.EUROPA W XVII STULECIU, 19.Kultura i sztuka baroku w Europie, Mar
IV.CZŁOWIEK WALCZĄCY O WOLNOŚĆ I PRAWA, 35.Obrady kongresu wiedeńskiego, Marek Biesiada
05 Konduktometria, naoh,nh3h2o,ch3cooh, Marek Mokrzycki IM sem
I. EPOKA WIELKICH ODKRYĆ GEOGRAFICZNYCH,RENESANSU I REFORMACJI, 12.Gospodarka i społeczeństwo, Marek
więcej podobnych podstron