3UDZGRSRGRELHVWZR L VWDW\VW\ND

18.01.1997 r.

___________________________________________________________________________

1

Zadanie 1.

5R]ZD*P\ ]GDU]HQLD ORVRZH

2

1

, A

A

oraz C

WDNLH *H

( )

3

1

Pr

1

=

A

C

,

( )

2

1

Pr

2

=

A

C

,

( )

( )

2

1

Pr

Pr

2

1

=

=

A

A

,

zdarzenia

1

A i

2

A

V QLH]DOH*QH RUD]

∅

=

∩

∩

C

A

A

2

1

.

= SRZ\*V]\FK GDQ\FK Z\QLND *H

(A)

(

)

3

2

Pr

2

1

=

∪

A

A

C

(B)

zdarzenia

2

1

, A

A

i C

V QLH]DOH*QH

(C)

(

)

9

5

Pr

2

1

=

∪

A

A

C

(D)

GDQH ]DZLHUDM VSU]HF]QRü WDND V\WXDFMD MHVW QLHPR*OLZD

(E)

(

)

12

5

Pr

2

1

=

∪

A

A

C

3UDZGRSRGRELHVWZR L VWDW\VW\ND

18.01.1997 r.

___________________________________________________________________________

2

Zadanie 2.

-HOL GOD ]PLHQQHM ORVRZHM R UR]NáDG]LH Poissona mamy

(

)

(

)

2

Pr

9

8

1

Pr

=

⋅

=

≤

N

N

, to:

(A)

( )

9

17

=

N

E

(B)

( )

3

=

N

E

(C)

( )

2

=

N

VAR

(D)

( )

3

2

=

N

E

(E)

( )

9

8

=

N

E

3UDZGRSRGRELHVWZR L VWDW\VW\ND

18.01.1997 r.

___________________________________________________________________________

3

Zadanie 3.

=Dáy*P\ *H ]PLHQQH ORVRZH

735

2

1

,

,

,

X

X

X

oraz

880

2

1

,

,

,

Y

Y

Y

V

QLH]DOH*QH R UR]NáDGDFK

(

)

7

3

0

Pr

=

=

i

X

,

(

)

7

4

1

Pr

=

=

i

X

,

(

)

(

)

2

1

1

Pr

0

Pr

=

=

=

=

i

i

Y

Y

.

3UDZGRSRGRELHVWZR WHJR *H

∑

∑

=

=

<

880

1

735

1

i

i

i

i

Y

X

,

SROLF]RQH Z SU]\EOL*HQLX SU]\ SRPRF\ DSURNV\PDFML UR]NáDGHP QRUPDOQ\P Z\QRVL

A)

0.01

(B)

0.99

(C)

0.16

(D)

0.50

(E)

0.84

3UDZGRSRGRELHVWZR L VWDW\VW\ND

18.01.1997 r.

___________________________________________________________________________

4

Zadanie 4. Zmienne losowe

1

X ,

2

X i

3

X

PDM áF]Q\ UR]NáDG QRUPDOQ\ JG]LH

( )

0

=

i

X

E

,

( )

1

=

i

X

VAR

dla

3

,

2

,

1

=

i

.

-HOL

(

)

(

)

(

)

0

,

,

,

3

2

2

1

3

2

2

1

=

+

+

=

=

X

X

X

X

COV

X

X

COV

X

X

COV

, to:

(A)

Z\QLND VWG *H

(

)

0

Pr

3

1

=

−

=

X

X

(B)

Z\QLND VWG *H

(

)

1

Pr

3

1

=

=

X

X

(C)

Z\QLND VWG *H

(

)

2

1

Pr

3

1

=

−

>

X

X

(D)

Z\QLND VWG *H

(

)

1

Pr

3

1

=

−

=

X

X

(E)

QLH PXVL VWG Z\QLNDü *DGQH ]H VWZLHUG]H $'

3UDZGRSRGRELHVWZR L VWDW\VW\ND

18.01.1997 r.

___________________________________________________________________________

5

Zadanie 5. Zmienne losowe X i Y

V QLH]DOH*QH

X

PD UR]NáDG R JVWRFL

( )







≤

≤

⋅

=

przypadku

przeciwnym

w

x

dla

x

x

f

0

1

0

2

Y

PD UR]NáDG R JVWRFL

( )







≤

=

−

przypadku

przeciwnym

w

y

dla

e

y

g

y

0

0

-HOL

Y

X

S

+

=

to









≤

2

1

X

S

E

wynosi:

(A)

2

(B)

2

3

(C)

3

4

(D)

3

1

(E)

12

13

3UDZGRSRGRELHVWZR L VWDW\VW\ND

18.01.1997 r.

___________________________________________________________________________

6

Zadanie 6.

10

2

1

,

,

,

x

x

x

MHVW SUyE ORVRZ ] UR]NáDGX

(

)

2

,

σ

µ

N

, gdzie

µ

i

2

σ

V

nieznanymi parametrami. Niech

[

]

U

L,

EG]LH SU]HG]LDáHP XIQRFL GOD SDUDPHWUX

µ

WDNLP *H

(

)

(

)

025

.

0

Pr

Pr

,

,

=

<

=

>

µ

µ

σ

µ

σ

µ

U

L

GOD ND*G\FK

µ

i

2

σ

.

Niech

(

]

W

,

∞

−

EG]LH MHGQRVWURQQ\P SU]HG]LDáHP XIQRFL GOD SDUDPHWUX

µ

WDNLP *H

(

)

01

.

0

Pr

,

=

<

µ

σ

µ

W

GOD ND*G\FK

µ

i

2

σ

.

2ED SU]HG]LDá\ ]EXGRZDQH V Z VWDQGDUGRZ\ VSRVyE Z RSDUFLX R UHGQL L ZDULDQFM ]
próbki x i

2

s

-H*HOL

262

.

0

−

=

L

i

262

.

4

=

U

WR ZDUWRü W wynosi:

(A)

4.262

(B)

4.821

(C)

5.169

(D)

3.833

(E)

QLH PR*QD SRGDü ZDUWRFL W na podstawie tych danych

3UDZGRSRGRELHVWZR L VWDW\VW\ND

18.01.1997 r.

___________________________________________________________________________

7

Zadanie 7. Niech

n

X

X

X

,

,

,

2

1

, gdzie

1

>

n

EG]LH SUyE ORVRZ ] UR]NáDGX

Z\NáDGQLF]HJR R JVWRFL

( )









≤

=

−

przypadku

przeciwnym

w

x

dla

e

x

f

x

0

0

1

µ

µ

5R]ZD*DP\ GZD HVW\PDWRU\ QLH]QDQHJR SDUDPHWUX

0

>

µ

:

∑

=

⋅

=

=

n

i

i

X

n

X

1

1

1

ˆ

µ

{

}

n

X

X

X

n

,

,

,

min

ˆ

2

1

2

⋅

=

µ

.

(A)

Estymator

1

ˆ

µ

MHVW QLHREFL*RQ\ ]D

2

ˆ

µ

MHVW REFL*RQ\

(B)

Estymator

1

ˆ

µ

MHVW REFL*RQ\ ]D

2

ˆ

µ

MHVW QLHREFL*RQ\

(C)

Oba

HVW\PDWRU\ V QLHREFL*RQH L PDM UyZQH ZDULDQFMH

(D)

2ED HVW\PDWRU\ V QLHREFL*RQH GOD SHZQ\FK ZDUWRFL

µ

estymator

1

ˆ

µ

ma

ZLNV] ZDULDQFM QL*

2

ˆ

µ

.

(E)

2ED HVW\PDWRU\ V QLHREFL*RQH

1

ˆ

µ

PD ]DZV]H PQLHMV] ZDULDQFM QL*

2

ˆ

µ

.

3UDZGRSRGRELHVWZR L VWDW\VW\ND

18.01.1997 r.

___________________________________________________________________________

8

Zadanie 8.

n

x

x

x

,

,

,

2

1

MHVW SUyE ORVRZ ] UR]NáDGX R G\VWU\EXDQFLH

( )

(

)

α

α

x

e

x

F

−

+

=

1

1

,

(

)

0

,

>

∞

<

<

∞

−

α

x

.

(VW\PDWRU QDMZLNV]HM ZLDU\JRGQRFL QLH]QDQHJR SDUDPHWUX

α

PD SRVWDü

(A)

( )

(

)

n

n

i

i

x

1

1

exp

1

ˆ

−

=

∏

−

+

=

α

(B)

( )

x

−

=

exp

ˆ

α

, gdzie

∑

=

⋅

=

n

i

i

x

n

x

1

1

(C)

( )

(

)









−

+

⋅

=

∑

=

−

n

i

i

x

n

1

1

exp

1

1

ln

ˆ

α

(D)

( )

(

)

∑

=

−

+

⋅

=

n

i

i

x

n

1

exp

1

ln

1

ˆ

α

(E)

( )

(

)

1

1

exp

1

ln

ˆ

−

=









−

+

⋅

=

∑

n

i

i

x

n

α

3UDZGRSRGRELHVWZR L VWDW\VW\ND

18.01.1997 r.

___________________________________________________________________________

9

Zadanie 9. Zmienna losowa X

PD JVWRü SUDZGRSRGRELHVWZD

( )

x

f

. Na podstawie

pojedynczej obserwacji X przeprowadzamy test hipotezy:

( )







≤

≤

=

przypadku

przeciwnym

w

x

dla

x

f

H

0

1

0

1

:

0

przeciwko alternatywie:

( )







≤

≤

⋅

=

przypadku

przeciwnym

w

x

dla

x

x

f

H

0

1

0

5

:

4

1

1DMPRFQLHMV]\ WHVW QD SR]LRPLH LVWRWQRFL

α

ma moc:

(A)

(

)

5

1

1

α

−

−

(B)

(

)

5

1

α

−

(C)

5

α

(D)

4

5

α

(E)

4

5

1

α

−

3UDZGRSRGRELHVWZR L VWDW\VW\ND

18.01.1997 r.

___________________________________________________________________________

10

Zadanie 10.

:\NRQDQR UD]\ U]XW GZLHPD NRüPL GR JU\ F]DUQ L ELDá

UD]\ QD ELDáHM NRFL Z\SDGáR ZLFHM RF]HN QL* QD F]DUQHM

UD]\ QD ELDáHM NRFL Z\SDGáR PQLHM RF]HN QL* QD F]DUQHM

UD]\ QD REX NRFLDFK Z\SDGáD WD VDPD OLF]ED RF]HN

5R]ZD*P\ KLSRWH]

0

H

ÄRELH NRFL V U]HWHOQH L Z\QLN U]XWX NRFL ELDá MHVW

QLH]DOH*Q\ RG Z\QLNX U]XWX NRFL F]DUQ´

&]\ RWU]\PDQH Z\QLNL GDM SRGVWDZ *HE\ RGU]XFLü KLSRWH]

0

H ? Przeprowadzono

test

2

χ

w oparciu o przytoczone dane.

(A)

1D SR]LRPLH LVWRWQRFL

01

.

0

=

α

test prowadzi do odrzucenia

0

H .

(B)

1D SR]LRPLH LVWRWQRFL

05

.

0

=

α

test prowadzi do odrzucenia

0

H , natomiast

dla

05

.

0

=

α

test nie prowadzi do odrzucenia

0

H .

(C)

1D SR]LRPLH LVWRWQRFL

1

.

0

=

α

test prowadzi do odrzucenia

0

H , natomiast dla

01

.

0

=

α

test nie prowadzi do odrzucenia

0

H .

(D)

1D SR]LRPLH LVWRWQRFL

1

.

0

=

α

test nie prowadzi do odrzucenia

0

H .

(E)

1D SR]LRPLH LVWRWQRFL

005

.

0

=

α

test prowadzi do odrzucenia

0

H .

3UDZGRSRGRELHVWZR L VWDW\VW\ND

18.01.1997 r.

___________________________________________________________________________

11

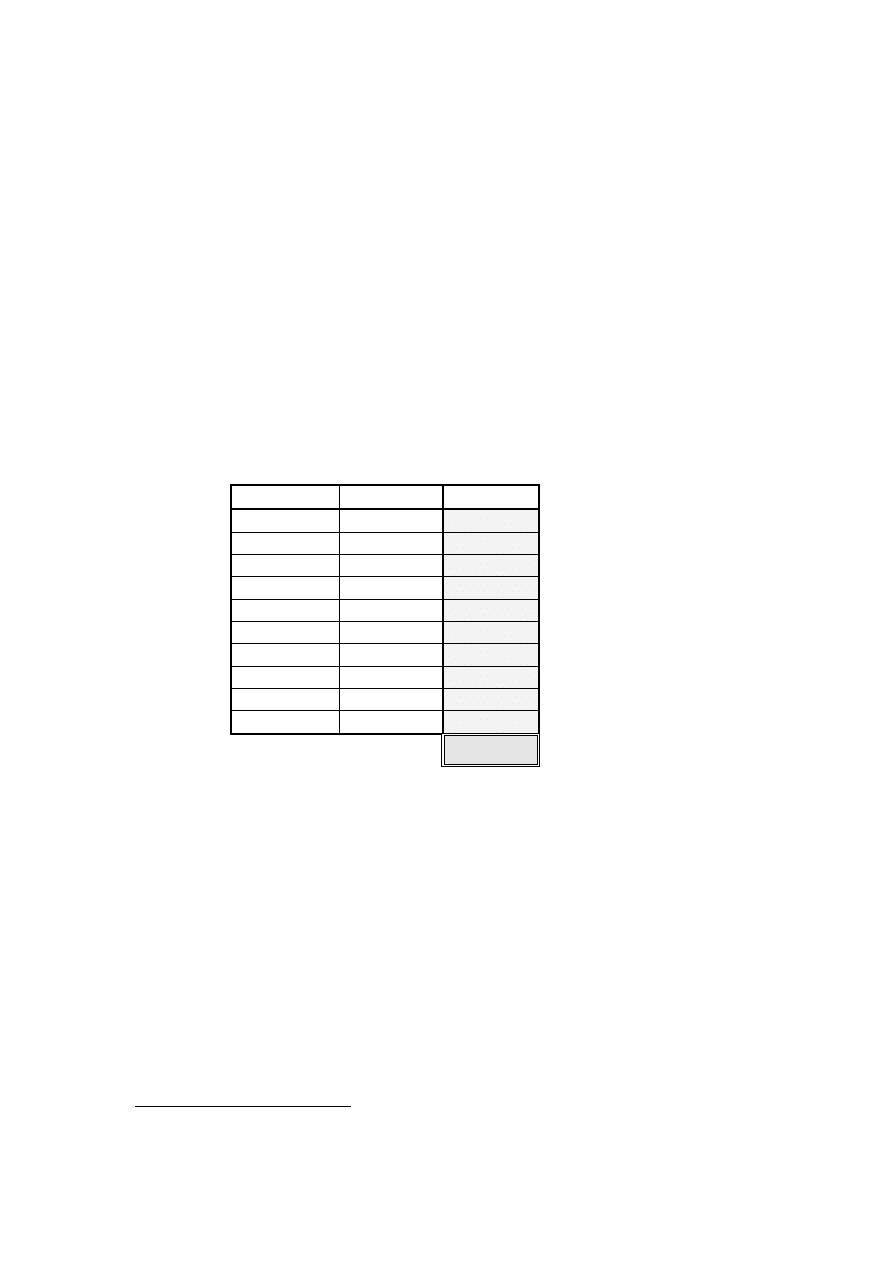
Egzamin dla Aktuariuszy z 18 stycznia 1997 r.

3UDZGRSRGRELHVWZR L VWDW\VW\ND

Arkusz odpowiedzi

*

,PL L QD]ZLVNR ./8&= 2'32:,('=,

Pesel ...........................................

Zadanie nr

2GSRZLHG( Punktacja

♦

1

C

2

B

3

E

4

D

5

C

6

B

7

E

8

E

9

A

10

D

*

2FHQLDQH V Z\áF]QLH RGSRZLHG]L XPLHV]F]RQH Z Arkuszu odpowiedzi.

♦

:\SHáQLD .RPLVMD (J]DPLQDF\MQD