PRZEGLĄD BUDOWLANY

6/2005

36

ZARZĄDZANIE–ORGANIZACJA

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

1. Wprowadzenie

Zagadnienie przedstawione w arty-

kule dotyczy problemów harmo-

nogramowania i jest przedmiotem

badań w wielu ośrodkach. W aktual-

nej literaturze zagranicznej dotyczą-

cej problematyki planowania robót

budowlanych proponowane są

np.: sposoby harmonogramowania

liniowego (LSM – Linear Scheduling

Model), wykresów cyklicznych

(LOB – Line of Balance), oraz pla-

nowanie sieciowe typu CPM/PERT,

z uwzględnieniami szeregu funkcji

celu: najmniejszego kosztu, czasu,

z ograniczonymi zasobami, priory-

tetami robót itp., zarówno w ujęciu

deterministycznym jak i probabi-

listycznym. Harmonogramowanie

procesów ciągłych liniowych przed-

stawiane było w wielu pracach: Arditi

(1986, 1986, 2001, 2002), Hegazy

(1993), Johston (1984), w któ-

rych opisano techniki planowania

graficznego. Rozwiązywane były

zagadnienia synchronizacji proce-

sów budowlanych wykonywane

na działkach (częściach budowli).

Line of Balance (LOB) umożliwiają

powiązanie różnych procesów, które

są wykonywane jako ciągłe na wielu

działkach roboczych. W innych

opracowaniach: Hamerlink (2003),

Hamerlink and Rowings (1998),

Rabhar and Rowings (1992), Harris

and Joannou (1998) proponowa-

ne są nowe sposoby planowa-

nia graficznego. Prezentowane

są rozwiązania wielu zagadnień

szczegółowych: Chrzanowski and

Johnson (1986) oraz wyboru opty-

malnych wariantów organizacyj-

nych z zastosowaniem wielu kryte-

riów: Zavadskas (2000). W artykule

prezentowany jest problem pla-

nowania robót z uwzględnieniem

buforów czasu oraz zachowaniem

ciągłości procesów. Przyjęto mini-

mum czasu jako podstawowe kry-

terium wyboru wariantu organiza-

cyjnego, Zavadskas, Kaklauskas,

Turkis (1997). Ponadto przedsta-

wiono sposoby ustalania kolejności

robót na działkach z wykorzysta-

niem sprężeń czasowych Afanasjev

(1994, 2000) Hejducki (1999, 2000,

2001), Mrozowicz (1997,1999, 2001).

Jest on rozwinięciem LSM (Linear

Scheduling Model), z uwzględnie-

niem zagadnienia kolejnościowe-

go (seguencing problem). Wśród

wielu czynników mających wpływ

na wielkość buforu przedsięwzię-

cia, można wymienić następujące

czynniki niepewności, np. zakłó-

cenia dostaw materiałów i urzą-

dzeń, nierównomierne finansowe,

błędy projektowe, zmienne czynniki

atmosferyczne, awarie sprzętu, nie-

sprawność wykonawców, zakłóce-

nia administracyjno-prawne i wiele

innych. W literaturze dotyczącej

metodyki CCS/BM, tj. łańcuchów

krytycznych proponuje się wprowa-

dzenie dodatkowych rezerw (bufo-

rów) znajdujących się zarówno

na końcu drogi krytycznej przedsię-

wzięcia PB (project buffer) jak i poza

nią FB (feeding buffer). Są to mini-

malne rezerwy związane z dostawa-

mi materiałów, maszyn oraz pracą

firm wykonawczych. Wykonawcy

negocjując terminy wykonania

zadań, uwzględniają swoje bezpie-

czeństwo dotrzymania umownego

terminu realizacji, poprzez intuicyj-

ne wprowadzenie rezerw czasu

(buforów) zarówno z uwzględnie-

niem swoich podwykonawców jak

i dostawców. Proponowane arbitral-

ne skracanie terminów dla poszcze-

gólnych uczestników procesu reali-

zacji (np. o 50%, Goldratt), wydaje

się podejściem bardzo subiektyw-

nym, co wymaga weryfikacji prak-

tycznej. Tak więc wielu autorów

próbuje sprowadzić zagadnienia

losowe do deterministycznych,

które następnie łatwo można wyko-

rzystać w praktyce. Rozwiązania

koncepcyjne i modelowe dla poje-

dynczych procesów są dość boga-

to przedstawione i analizowane. Dla

bardziej złożonych przedsięwzięć,

zagadnienie harmonogramu może

być zaliczone do grupy trudnych,

o dużej złożoności obliczeniowej.

Dotyczy to przede wszystkim uję-

cia zagadnienia kolejnościowego,

które ma charakter permutacyj-

ny z uwzględnieniem ograniczeń

technologicznych, organizacyj-

nych, funkcji celu o np. T®min.

Analizując przebieg przedsięwzięć

budowlanych, zauważyć można

sprzeczność podejścia do sza-

cowania czasu trwania procesów

przez wykonawców oraz inwesto-

rów (generalnego wykonawcy PM/

CM). Wykonawca chce najczęściej

zapewnić sobie ciągłość wykona-

nia swojego zadania, minimalizu-

jąc koszty, związane z przestojami

na placu budowy, zabezpieczenia

materiałów, urządzeń, konieczności

Zastosowanie buforów czasu

w harmonogramowaniu procesów

budowlanych

Dr inż. Magdalena Rogalska, Politechnika Lubelska

Dr hab. inż. Zdzisław Hejducki, Politechnika Wrocławska

PRZEGLĄD BUDOWLANY

6/2005

ZARZĄDZANIE–ORGANIZACJA

37

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

obniżenia wydajności, ze względu

na możliwość przerw w ich pracy.

Inwestor (generalny wykonawca

PM/CM) najczęściej stara się tak

sterować procesem budowy, aby

w momencie pojawienia się możli-

wości natychmiast rozpocząć kolej-

ny proces technologiczny na danym

fragmencie realizowanego obiektu.

Z uwagi na różne wielkości robót

i czasy ich wykonania, zapewniając

ciągłość różnym procesom (robo-

tom ziemnym, fundamentowym,

konstrukcyjnym, wykończeniowym

i innym), firmy realizujące te proce-

sy mogą mieć przestoje, oczeku-

jąc wykonania robót poprzedzają-

cych. W wyniku przeprowadzonych

obliczeń zauważyć można, że dla

kompleksu robót, zapewnienie cią-

głości wykonania robót przez firmy

zapewnia dłuższy czas realizacji

przedsięwzięcia niż w przypadku,

gdy pracują one z przerwami, lecz

zapewniona jest ciągłość kolejnych

technologicznie robót. Ponadto,

zmienna kolejność wykonywania

robót na wielu częściach obiektów

wpływa na zwiększenie lub zmniej-

szenie czasu trwania przedsięwzię-

cia w stosunku do dyrektywnie

ustalonego.

2. Modelowanie macierzowe

kompleksu procesów budowla-

nych (MM)

Stosując do obliczenia harmono-

gramów systemy komputerowe,

łatwym sposobem wprowadze-

nia danych jest zapis macierzo-

wy. Pozwala on na podzał procesu

budowy, zgodnie z zasadami tech-

nologii, na rodzaje robót np. wg

metodyki WBS (work breakdown

strucktures) oraz wyznaczyć zada-

nia związane z budową poszczegól-

nych elementów obiektu budowla-

nego. Można w modelu macierzo-

wym ująć kolejność technologiczną,

np. przez ustalenie kodu macierzy

oraz wydzielić niezależne (np. poje-

dyncze budynki mieszkalne, części

obiektów rozdzielone, np. przer-

wami dylatacyjnymi, kondygnacje

budynku, na których mogą być

prowadzone, równolegle, potoko-

wo lub sekwencyjnie, np. roboty

wykończeniowe itp.). Tak zbudowa-

ną macierz wykorzystującą wiedzę

inżyniera eksperta, w postaci ciągu

cyfr można wykorzystać w różnych

standardowych systemach kompu-

terowych, np. Mathematica, Matlab

lub indywidualnych, np. Organizator.

Modele macierzowe przedsięwzięć

budowlanych mogą być zastoso-

wane do obliczania parametrów

harmonogramów.

3. Podstawowe założenia

do obliczeń

Uwzględnienie przyjętych ograni-

czeń wymaga wykonania obliczeń

w celu ustalenia wartości kluczo-

wych harmonogramu, takich jak:

terminów rozpoczęcia i zakończe-

nia robót, wielkości sektorów, liczby

wykonawców, kolejności sektorów,

przebiegu ścieżki krytycznej, czasu

wykonania zadania. Dopuszczalne

są przestoje wykonawców oraz

sytuacje, kiedy w danym sektorze

nie są prowadzone prace w sposób

ciągły. Oczywiście ma to wpływ

na całkowity czas wykonania zada-

nia TT. Do obliczeń stosuje się pro-

gramy komputerowe, modyfikowa-

ne z wersji pierwotnej o nazwie

POTOKI. Modyfikacje następują

równolegle wraz z rozwojem meto-

dy (np. w związku z wprowadza-

niem nowych ograniczeń) i technik

komputerowych. Ostatnią wersją

jest ORGANIZATOR, ale już przy-

gotowywany jest do modyfikacji

w celu uwzględnienia zakłóceń

pogodowych w budownictwie dro-

gowym oraz TOC (Teorii Ograniczeń

Goldratta) poprzez wprowadzenie

buforów zasilających i skrócenie

czasu trwania procesów. Program

komputerowy ORGANIZATOR ge-

neruje cyklogramy i sieci zależ-

ności (układ procesów w sekto-

rach i zależności pomiędzy nimi),

a nie wykresy Gantta. Kluczowymi

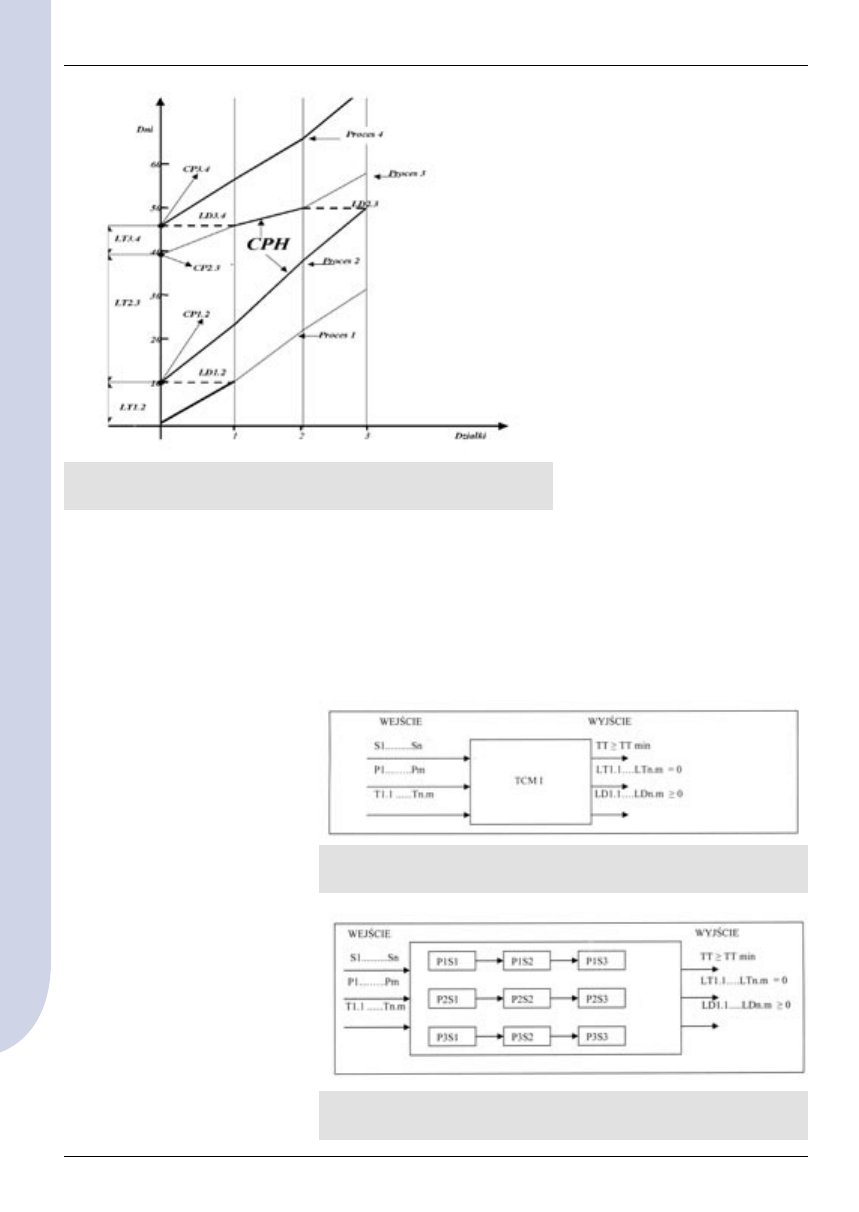
wartościami w cyklogramach są

czasy wykonania poszczególnych

procesów w sektorach oraz punk-

ty kontrolne CP. Wprowadza się

następujące oznaczenia stosowane

w publikacjach zagranicznych:

LT – (least time) najkrótszy czas

pomiędzy procesem w toku

a kolejnym procesem – najmniejszy

dystans czasowy,

LD – (least distance) najmniejsza

odległość miejsca pomiędzy proce-

sem w toku a kolejnym procesem,

CPH – (controling path) droga

krytyczna procesów budowlanych

[dni],

CL – (controling link) ścieżka

krytyczna – połączenie graficzne

pomiędzy kolejnymi procesami,

CP – (controling point) punkt kry-

tyczny odpowiadający rozpoczęciu

kolejnego procesu,

T – czas trwania procesu,

TT – (time total) całkowity czas

wykonania zadania,

m – liczba procesów,

n – liczba sektorów.

Uwzględniając wpływ czynników

niepewności, jako zasilające bufory

czasu FB i projektowe PB, przeana-

lizowano ich wpływ na całkowity

czas realizacji TT. Zastosowano pro-

gram komputerowy ORGANIZATOR

wykorzystujący algorytmy optymali-

zacji kombinatorycznej o charakte-

rze permutacyjnym. Jako funkcję

celu przyjęto minimalny czas reali-

zacji przedsięwzięcia

T ® T

min

Poniżej przedstawiono założenia

do obliczeń parametrów harmono-

gramów:

I Warunek ciągłości procesów

budowlanych dla każdego rodza-

ju (metoda sprzężeń czasowych

TCM I)

LT1.1….LTn.m = 0

II Warunek ciągłości procesów

budowlanych w kolejności tech-

nologicznej, w sektorach (metoda

sprzężeń czasowych TCM II)

LD1.1….LDn.m = 0

III Warunek utworzenia minimalnej

drogi krytycznej (metoda sprzężeń

czasowych TCM III, IV i V)

CPH = TTmin

Warunek I (metoda sprzężeń czaso-

wych TCM I) stosuje się w przypad-

ku, kiedy założeniem priorytetowym

jest zapewnienie ciągłości wykony-

wania procesów P1.....Pm w sek-

torach S1....Sn. Zwykle wiąże się

to z zapewnieniem ciągłości pracy

PRZEGLĄD BUDOWLANY

6/2005

38

ZARZĄDZANIE–ORGANIZACJA

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

wykonawcom lub pracy sprzętu.

Ze względu na przyjętą technolo-

gię zapewnienie ciągłości procesu

może stać się założeniem prioryte-

towym, np. w przypadku koniecz-

ności betonowania bez szwów tech-

nologicznych. Ta sama sytuacja ma

miejsce w odniesieniu do procesów

wiodących, czyli umożliwiających

rozpoczęcie wszystkich zależ-

nych od niego prac. Zdarza się,

że ze względów ekonomicznych

zatrudnienie określonego wyko-

nawcy lub sprzętu po uwzględnie-

niu postojów staje się nieopłacalne.

Nie przynosi również zysku wielo-

krotne podejmowanie pracy przez

tego samego wykonawcę ze wzglę-

du na transport i montaż sprzę-

tu oraz urządzeń. Niektóre firmy

wykonawcze szczególnie wysoko

wyspecjalizowane, stawiają jako

warunek podjęcia zadania zapew-

nienie ciągłości ich prac. Nadwyżka

popytu nad podażą niektórych

usług powoduje, że zapewnienie

ciągłości pracy pewnym wykonaw-

com staje się założeniem prioryte-

towym.

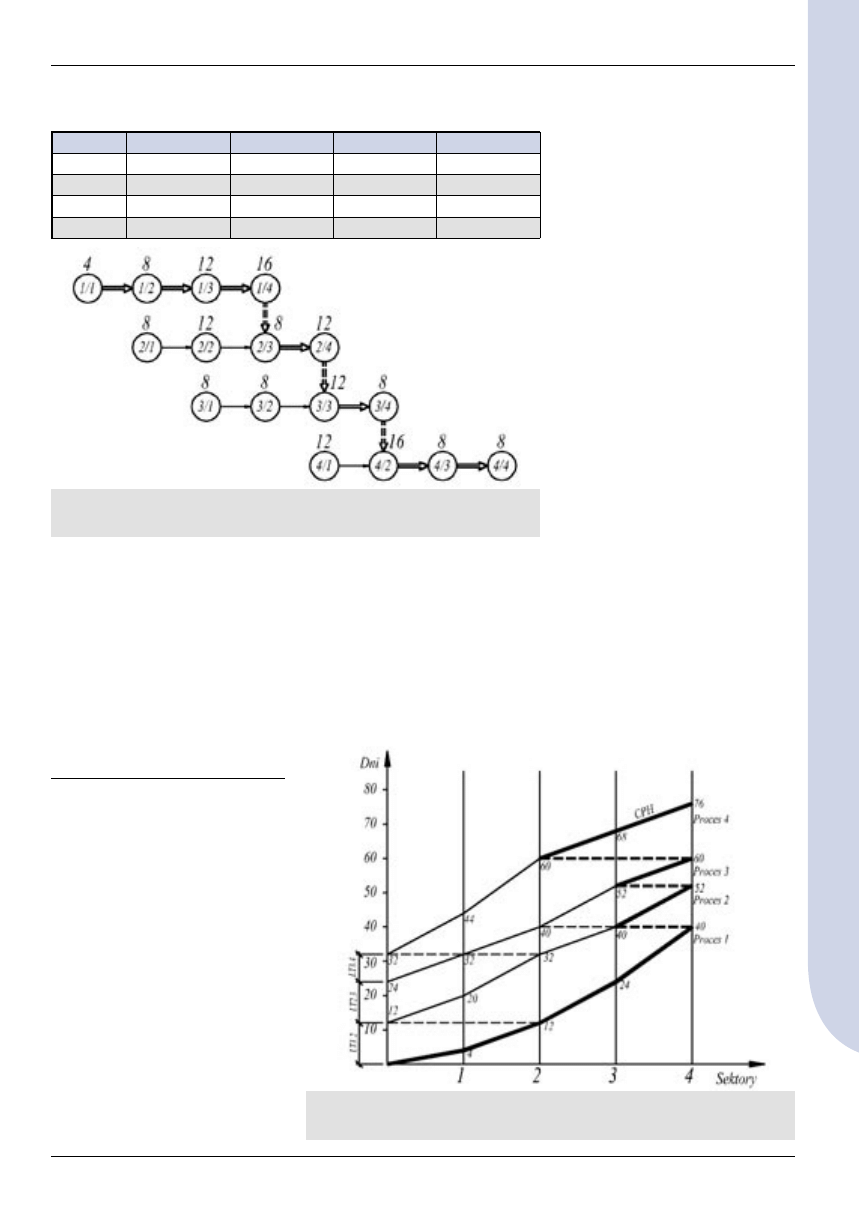
Na rysunku 2 określono dane wyj-

ściowe, które zostaną wygenero-

wane przez program komputerowy

ORGANIZATOR.

Do obliczeń przyjmujemy z góry

założone i obliczone w sposób

deterministyczny sektory S1....Sn,

procesy P1....Pm uszeregowane

w kolejności technologicznej oraz

czasy ich wykonania T1.1...Tn.m.

Zakłada się, że nie jest na tym eta-

pie ostatecznie ustalona kolejność

wykonywania prac w poszczegól-

nych sektorach. Będzie ona osta-

tecznie ustalona na etapie opty-

malizacji pierwszej, która następu-

je po dokonaniu podstawowych

obliczeń. Zatem należy przyjąć

pewną kolejność sektorów, jed-

nak nie będzie problemem zmiana

ich kolejności. Wystarczy jedynie

wywołać opcję OPTYMALIZACJA

i zostanie to wykonane w ciągu

kilku sekund bez konieczności

ponownego wpisywania danych

czy też wnikliwej analizy danych.

Zwykle najkorzystniejsze wyniki

obliczeń uzyskuje się, gdy czas

trwania procesów w ostatnim sek-

torze jest najkrótszy w odniesieniu

do pozostałych. Jako efekt obliczeń

otrzymamy całkowity czas wykona-

nia przedsięwzięcia TT, który będzie

dłuższy lub równy minimalnemu

czasowi trwania przedsięwzięcia

TTmin w odniesieniu do zastosowa-

nia wszystkich pięciu pozostałych

metod obliczeniowych programem

ORGANIZATOR. Natomiast dystan-

se czasowe LT1.1....LTn.m pomię-

dzy procesami w toku a kolejnymi

występującymi po nich zawsze są

równe zeru – czyli zagwarantowa-

na została ciągłość procesów P1...

Pm. Jednocześnie prawdopodob-

nie nie uzyskamy ciągłości pracy

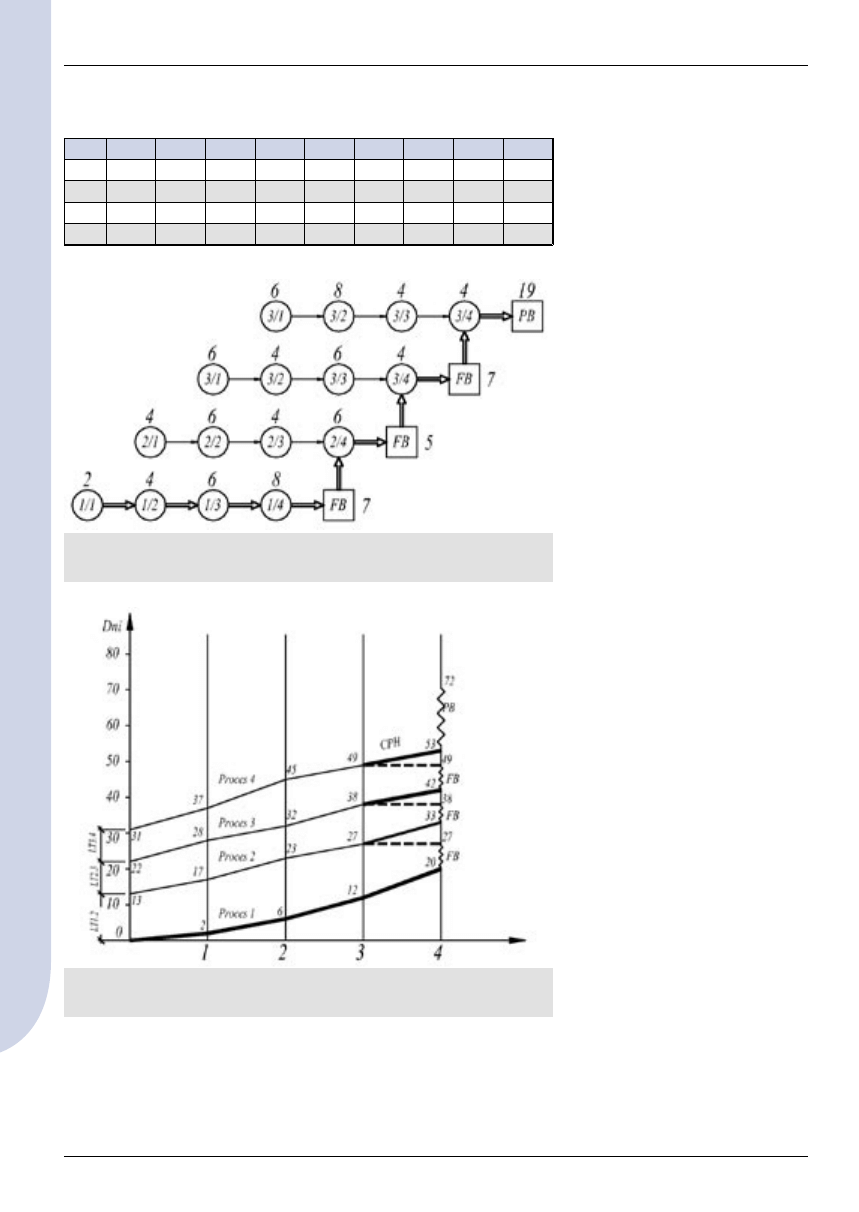
Rys. 2. Schemat obliczeń z uwzględnieniem warunku I

Rys. 3. Powiązania priorytetowe

Rys. 1. Procesy ciągłe, oznaczenia

PRZEGLĄD BUDOWLANY

6/2005

ZARZĄDZANIE–ORGANIZACJA

39

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

w sektorach, jakkolwiek czasem

może się to zdarzyć, nie jest to jed-

nak założenie priorytetowe.

Na rysunku 2 przedstawiono po-

wiązania priorytetowe, czyli takie,

dla których LT zawsze muszą być

równe zero i stanowić będą bazę

w tworzeniu harmonogramu.

4. Analiza buforów czasu

w LSM – Linear Scheduling

Model

Poniżej przedstawiono schematy

wybranych cyklogramów utworzo-

nych na podstawie przykładowych

danych liczbowych. Celem analizy

było określenie wpływu buforów

zasilających FB na czas trwania

przedsięwzięcia TT. Analizę prze-

prowadzono dla dwóch przypad-

ków usytuowania drogi krytycznej

na cyklogramie: z uwzględnieniem

skrajnych procesów początkowych

oraz skrajnych procesów końco-

wych. Wiąże się to ze zmianą poło-

żenia buforów zasilających FB oraz

przebiegu drogi krytycznej w nowym

łańcuchu CC. W tabelach podano

czasy trwania procesów w sekto-

rach, w tabeli 1 dane wejściowe,

w tabeli 2 oraz 3 zmodyfikowane

wartości, z uwzględnieniem zało-

żeń obliczania buforów czasu wg

metody E. Goldratta. Dla jasności

wywodu przedstawiono sieci zależ-

ności procesów z zaznaczeniem

klasycznej drogi krytycznej (rys. 4)

oraz łańcuchów krytycznych z bufo-

rami czasu FB i PB.

W wyniku przeprowadzonych,

z zastosowaniem programu ORGA-

NIZATOR, obliczeń uzyskano

czasy trwania poszczególnych

prac w sektorach, które pozwoli-

ły na zbudowanie cyklogramu wg

metodyki LSM. Na rysunku 5 oraz

7 pojawiły się dwie drogi krytyczne

łączące procesy początkowe oraz

końcowe. Uwzględnienie warunku

ciągłości procesów (TCM I) spo-

wodowało, że wielkości LT 1, LT 2,

LT 3 zapewniają maksymalne zbli-

żenie procesów 1, 2, 3. Analizując

przebieg procesów i tworząc drogę

krytyczną CPH, można zauważyć,

że minimalny czas realizacji przed-

sięwzięcia TT uzyskuje się w wyniku

sumowania odpowiednich czasów

trwania procesów w sektorach,

które mogą utworzyć dwie niezależ-

ne drogi krytyczne.

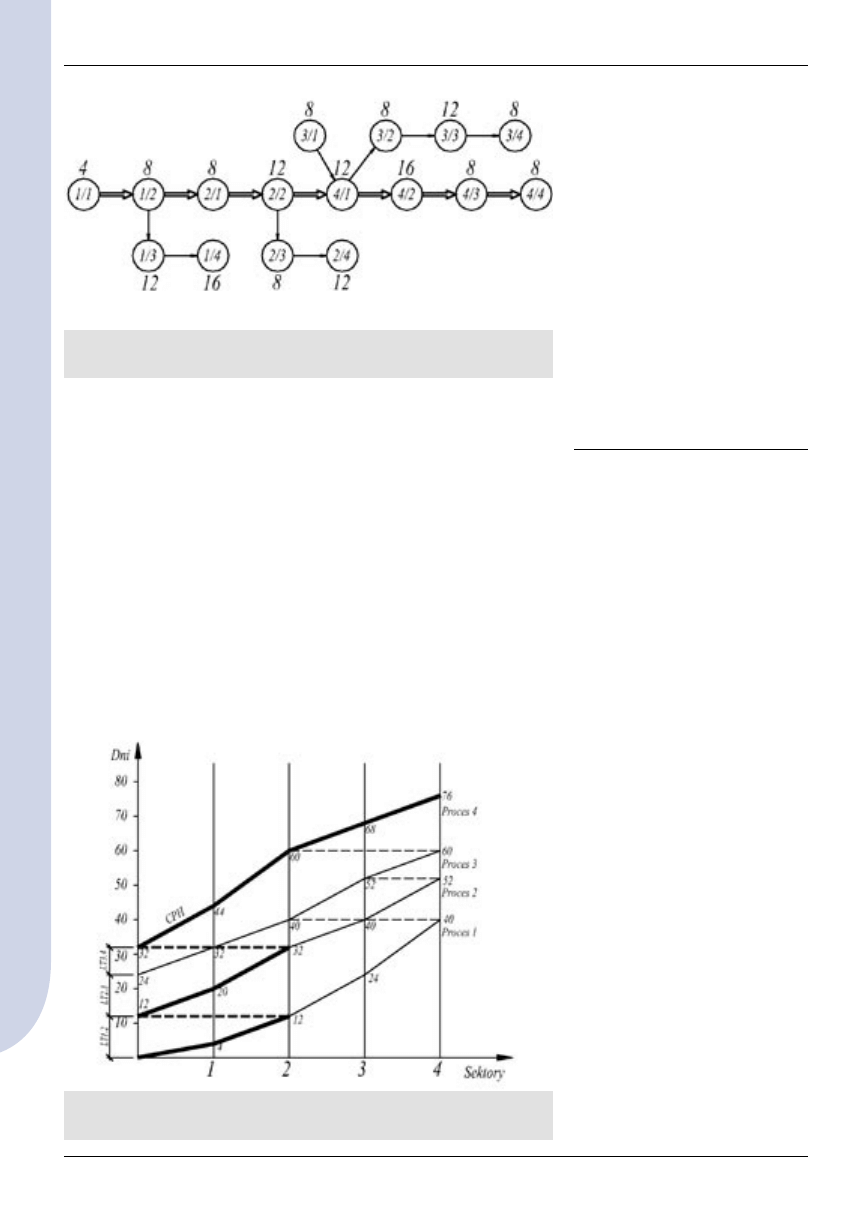
Schematy i przebieg dróg krytycz-

nych pokazano na rysunku 5 i 7.

Na rysunku 4 i 6 przedstawiono

w układzie sieci zależności drogi

krytycznej dla dwóch wariantów

ich przebiegu. Analizując układ pro-

cesów, zauważyć można, że wła-

ściwie z uwagi na przyjęte ograni-

czenia (warunek I, TCM I) wszystkie

procesy wykonywane w sektorach

mają charakter procesów krytycz-

nych, mimo że nie znajdują się

na drodze krytycznej. Uwzględniony

warunek ciągłości wykonania pro-

cesów(TCM I) powoduje, że wydłu-

Tab. 1. Dane wejściowe

Sektor

Proces 1

Proces 2

Proces 3

Proces 4

1

4

8

8

12

2

8

12

8

16

3

12

8

12

8

4

16

12

8

8

Rys. 4. Sieć zależności dla danych wejściowych z tabeli 1

Rys. 5. Cyklogram z wariantem drogi krytycznej

PRZEGLĄD BUDOWLANY

6/2005

40

ZARZĄDZANIE–ORGANIZACJA

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

żenie czasu trwania jakiegokolwiek

z nich wpływa na całkowity czas

realizacji TT.

W tabeli 2 przedstawiono zmodyfi-

kowane dane czasów trwania pro-

cesów z uwzględnieniem metody

Goldratta. Wprowadzono wartości

buforów zasilających FB i PB dla

ciągu procesów i drogi krytycznej.

Obliczenia przeprowadzono z zasto-

sowaniem programu komputerowe-

go, a uzyskane wyniki przedstawio-

no na rysunku 9. Analizując cyklo-

gram zauważyć można, że bufory

zasilające weszły w skład łańcucha

krytycznego, wpływając bezpośred-

nio na czas trwania przedsięwzięcia

TT. Uzyskano całkowity czas reali-

zacji TT = 74 jednostki, pomimo

skrócenia poszczególnych czasów

trwania procesów o połowę i zamia-

ny zredukowanych czasów bufo-

rem o wymiarze 25%. Nie spowo-

dowało to proporcjonalnego skró-

cenia całego przedsięwzięcia o tę

wartość. Czas całkowity TT uległ

nieznacznemu skróceniu z 76 jed-

nostek do 74.

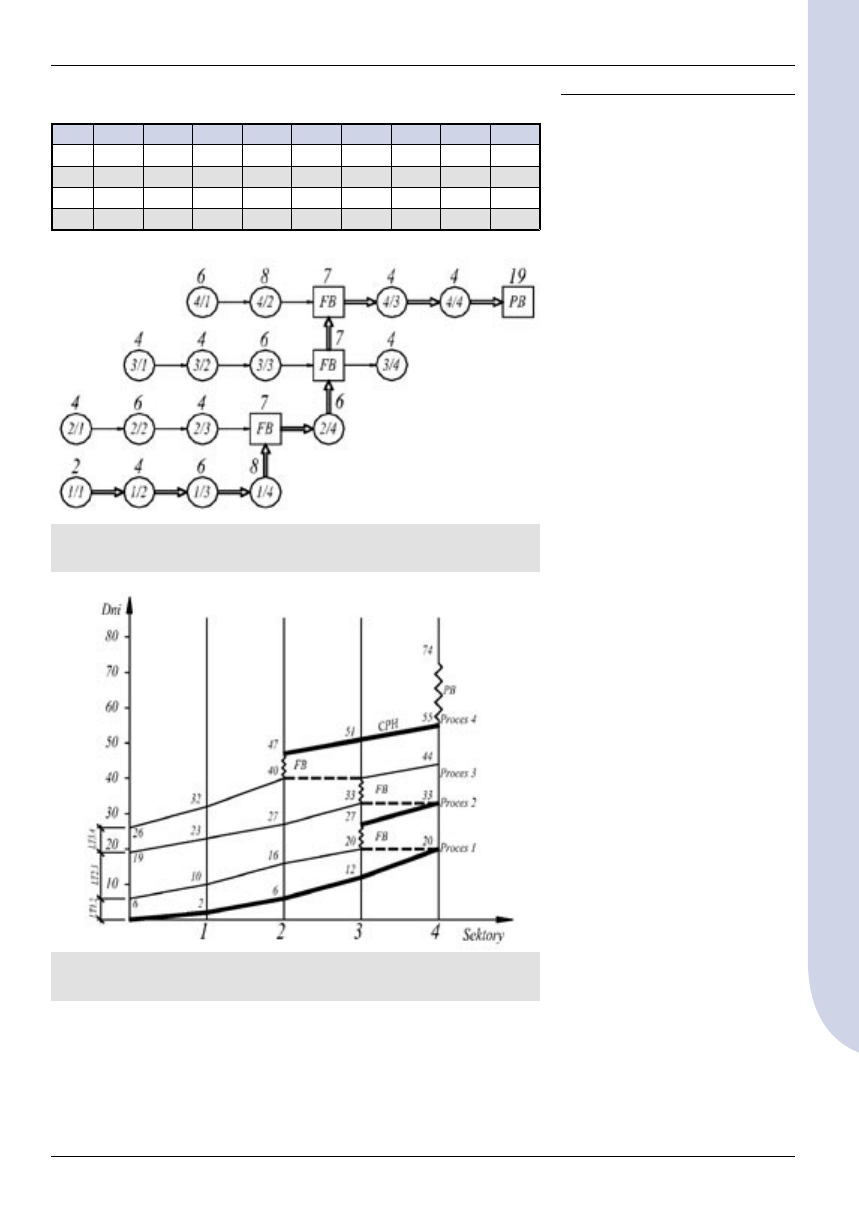
Na podstawie wariantu z drogą kry-

tyczną (rys. 5) utworzoną z proce-

sów końcowych sporządzono tabe-

lę 3, w której wprowadzono dane

liczbowe (czasy trwania procesów

w sektorach) zmodyfikowane wg

metody Goldratta. Wartości liczbo-

we buforów zasilających FB umiesz-

czono na końcach ciągów poszcze-

gólnych procesów. Na podstawie

analizy zbudowanego cyklogramu

(rys. 11), zawierającego wyniki obli-

czeń programu ORGANIZATOR

z zachowaniem ciągłości procesów

(TCM I) zauważyć można, że bufory

zasilające znalazły się w łańcuchu

krytycznym procesów i drodze kry-

tycznej, mając bezpośredni wpływ

na czas trwania przedsięwzięcia

TT=72 jednostki. Bufory zasilają-

ce FB mają charakter procesów

i tak są traktowane w obliczeniach.

Zmniejszenie ich wymiarów ma

wpływ na skrócenie czasu trwania

przedsięwzięcia.

5. Podsumowanie

Przeprowadzona analiza oraz

wykonane obliczenia potwierdzają

stwierdzenie, że skrócenie czasu

trwania poszczególnych procesów

nie powoduje skrócenia całkowite-

go czasu trwania przedsięwzięcia

z uwzględnieniem buforów o warto-

ści 25% T, jako uzyskanego zapasu

czasu. Jest to zbytnie uproszcze-

nie i być może słuszne dla proce-

sów sekwencyjnych. Czas trwa-

nia przedsięwzięcia zależny jest

od wyboru składowych łańcucha

krytycznego. Analizując mode-

le graficzne – cyklogramy budo-

wane wg metodyki LSM (Linear

Scheduling Model), można zauwa-

żyć, że przyjęcie łańcucha kry-

tycznego jak najbardziej zbliżone-

go do prawej krawędzi wykresu

powoduje skrócenie czasu trwania

przedsięwzięcia. W cyklogramach

istnieje ponadto konieczność trak-

towania buforów zasilających FB

jako osobnych procesów, ze wzglę-

du na warunek zachowania ciągło-

ści pracy grup roboczych i uniknię-

cia strat finansowych związanych

z niepotrzebnymi przestojami.

Stosując algorytmy szeregowania

zadań w opcji programu kompu-

terowego ORGANIZATOR, istnieje

możliwość skrócenia czasu trwa-

nia przedsięwzięcia poprzez zmia-

nę kolejności wykonywania prac

w poszczególnych sektorach, pod

warunkiem niezależności i dostęp-

Rys. 6. Sieć zależności dla danych wejściowych z tabeli 1

Rys. 7. Cyklogram z wariantem drogi krytycznej

PRZEGLĄD BUDOWLANY

6/2005

ZARZĄDZANIE–ORGANIZACJA

41

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

ności sektorów robót. W zależno-

ści od jednostkowego kwantyfiko-

wanego ryzyka danego procesu

istnieje możliwość przyjmowania

zróżnicowanych wielkości buforów

zasilających FB i projektowego PB.

Zapewnią one wówczas uwzględ-

nienie szczególnych uwarunko-

wań technicznych zróżnicowanych

procesów budowlanych, lokalnych

ograniczeń wykonawczych i czyn-

ników ryzyka.

BIBLIOGRAFIA

[1] Afanasjev V.A, Afanasjev A.V., Potocnaja

organizacja rabot v stroitelstwie, Sankt-

Petersburg, 2000.

[2] Arditi D., Tokdemir O.B.& Suh K.,

Scheduling system for repetitive unit

construction using line-of-balance

technology, Department of Civil and

Architectural Engineering, Illinois Institute

of Technology, Department of Civil

Engineering, Honan University, Honam,

South Korea, 2001.

[3] Arditi D., Tokdemir, O.B. & Suh, K.,

Effect of learning on line-of-balance

scheduling, International Journal of Project

Management, in press, 2001.

[4] Chrzanowski, Jr., E. N., and Johnston,

d. W., Application of linear construction,

J. Constr. Eng.,112(4), 476-491, 1986.

[5] Goldratt E.M. Critical Chain, Great

Barrington, MA: The North River Press, 1997.

[6] Goldratt E.M.,Fox R.E., The Race.

Croton-on-NY, North River Press, 1986.

[7] Goldratt E.M., The Haystack Syndrome.

Croton-on-Hud, North River Press, 1990.

[8] Goldratt E.M, It is no luck, Aldershot,

England, Gower, 1994.

[9] Goldratt E.M, The Goal, Great

Barrington, MA, The North River Press, 1 st

ed. 1984, 2nd revised ed. 1992.

[10] Herroelen W., Leus R., On the merits

and pitfalls of critical chain scheduling,

Journal of Operations Management 19

(2001) 559-577.

[11] Hamerlink D.J., Linear scheduling

model: The development of a linear

scheduling model with micro computer

application for highway construction control,

PhD tezis, Iowa State Univ., 1995.

[12] Hamerlink D.J., Rowings J.E.,

Linear scheduling model: Development

of controlling activity path, Journal of

Construction Engineering and Management,

124(4), 266–268, 1998.

[13] Harris R., B., Ionnou P.G., Scheduling

projects with repeating activities, Journal of

Construction Engineering and Management,

124(4), 269-278, 1998.

[14] Hegazy, T., Optimization of construction

time-cost trade-off analisys using genetic

algorithms, Canadian Journal of Civil

Engineering, 26: 685-697, 1999.

[15] Hegazy, T., Moselhi, O. & Fazio, P.,

BAL: an algorithm for scheduling and control

of linear projects, AACE Transactoins, C.8,

8.1 – 8.14, 1993.

[16] Hejducki Z., Sprzężenia czasowe

w metodach organizacji złożonych

procesów budowlanych, WPWr, 2000.

[17] Jaworski K.M., Metodologia

projektowania realizacji budowy, PWN,

Warszawa, 1999.

[18] Johnston, D.W., Linear scheduling

method for highway construction,

J. Constr. Div., Am. Soc. Civ. Eng, 107(2),

247-261, 1984.

[19] Kasprowicz T., Inżynieria przedsięwzięć

budowlanych, Warszawa, WAT, 2002.

Tab. 2. Dane liczbowe zmodyfikowane wg Metody Goldratta

Sektor

P1

FB1

P2

FB2

P3

FB3

P4

FB4

PB

1

2

0

4

0

4

0

6

0

0

2

4

0

6

0

4

0

8

7

0

3

6

0

4

7

6

7

4

0

0

4

8

0

6

0

4

0

4

0

19

Rys. 8. Sieć zależności z uwzględnieniem buforów czasu

Rys. 9. Cyklogram z łańcuchem krytycznym i buforami czasu

PRZEGLĄD BUDOWLANY

6/2005

42

ZARZĄDZANIE–ORGANIZACJA

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

[20] Marcinkowski R, Metody rozdziału

zasobów realizatora w działalności

inżynieryjno-budowlanej Warszawa, WAT,

2002.

[21] Mattila K.G., Acse A.M., Park A.,

Comparison of Linear Scheduling Model

and Repetitive Scheduling Method, J.Constr.

Eng. Manage., 129(1), 56-64, 2003.

[22] Mattila, K.G. & Abraham, D. M.,

Resource leveling of linear schedules using

integer linear programming, Journal of

Construction Engineering and Management,

ASCE, 120(4), 232 – 244, 1998.

[23] Moder,J.J., Philips, C.R., and Davis,

E.W., Project Management with CPM,

PERT and precedence diagramming, Van

Nostrand Reinhold, New York, 1983.

[24] Moselhi, O. & El-Rayes, K., Scheduling

of respective projects with cost optimization,

Journal of Construction Engineering and

Management, ASCE, 199, 681-697, 1993.

[25] Mrozowicz J., Metody organizacji

procesów budowlanych uwzględniające

sprzężenia czasowe, WPWr, 1997.

[26] O’Brien, J. J., Scheduling handbook,

McGraw-Hill, New York, 1969.

[27] Rahbar, F.F., and Rowings, J. E.,

Respective activity scheduling process,

Trans., Am. Assn. Cost Eng., 2,

O.5.1-O.5.8, 1992.

[28] Rowings, J.E. & Rahbar, f., Use of

linear scheduling in transportation projects,

In: Proceedings of the Transportation

Research Board 71st Annual Meeting. TRB,

Washington, D.C., 1992.

[29] Senouci, A.B. & Eldin, N.N., Dynamic

programming approach to scheduling

of nonserial linear project, Journal of

Computing in Civil Engineering, 10,

106-144, 1996.

[30] Stella, P. and Glavinich, T., Construction

planning and scheduling, 2nd Ed.,

Associated General Contractors of America,

Alexandria, Va, 1994.

[31] Stradel, O., and Cacha, J., Time space

scheduling method” J.Constr. Div., Am. Soc.

Civ. Eng., 108(3), 445-457, 1982.

[32] Suhail, S. A., and Neale, R. H,

CPM/LOB: New methodology to integrare

CPM and line of balance, J. Constr. Eng.

Manage., 120(3), 667-684, 1994.

[33] Thabet, W.Y. & Beliveau, Y.J.,

HVLS: horizontal and vertical logic

scheduling for multistory projects, Journal of

Construction Engineering and Management,

ASCE, 120, 875-892, 1994.

[34] Vorster, M. C., and Parvin, C. M.,

„Linear scheduling for highway constractors

and state DOT’s.” Videotapes, P&W

Publications, Richmond, Va, 1990.

[35] Vorster, M.C., and Bafna T., Discussion

of „Formal development of line-of-balance

technique” by Z. M. Al Sarraj, J. Constr.

Eng. Manage., 118(1), 210-211, 1992.

[36] Vorster, M.C., Beliveau, Y.J., and Bafna,

T., Linear scheduling and visualization,

Transp. Res. Rec. 1351, 32-39, 1992.

[37] Wang, C. & Huang, Y., Controling

activity interval times in LOB scheduling .”

Construction Management and Economics,

16, 5-16, 1998.

[38] Zavadskas E.K., Mehrkriterielle

Entscheidungen im Bauwesen, Vilnius,

Technika, 2000.

[39] Zawadskas E.K. Kaklauskas A.,

Turskis Z., Multikriteria decision-making

system for building refurbishment Statyba,

Vilnius, 1997.

Tab. 3. Dane liczbowe zmodyfikowane wg metody Goldratta – wartości FB

dla drogi krytycznej

Sektor

P1

FB1

P2

FB2

P3

FB3

P4

FB4

PB

1

2

0

4

0

4

2

6

0

4

0

6

0

4

0

8

0

3

6

0

4

0

6

0

4

0

4

8

7

6

5

4

7

4

0

19

Rys. 10. Sieć zależności z uwzględnieniem buforów czasu

Rys. 11. Cyklogram z łańcuchem krytycznym i buforami czasu