1
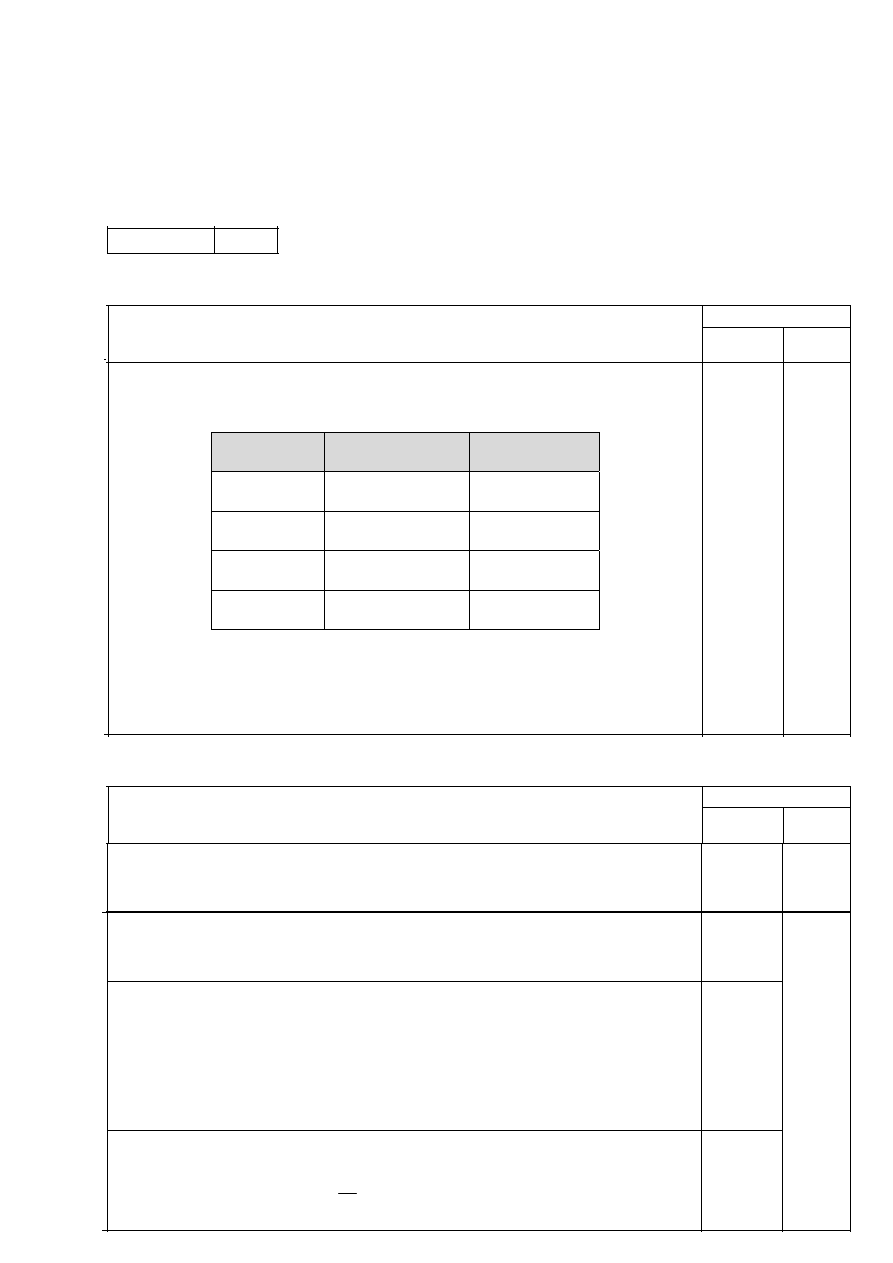
0,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
0
1,25
2,50
3,75
5,00
6,25
7,50
v v v
v
v
v
v
v
Termodynamika
– poziom podstawowy
KLUCZ ODPOWIEDZI
Zadanie 1. (1 pkt)
Źródło: CKE 2005 (PP), zad. 8.
Zadanie 2. (2 pkt)
Źródło: CKE 2005 (PP), zad. 17.
v v v
v
v
v
v
v
v v v
v
v
v
v
v
Zadanie 3. (3 pkt)
Źródło: CKE 2005 (PP), zad. 19.
0,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
0
1,25
2,50
3,75
5,00
6,25
7,50
Lub:
v v v
v
v
v
v
v
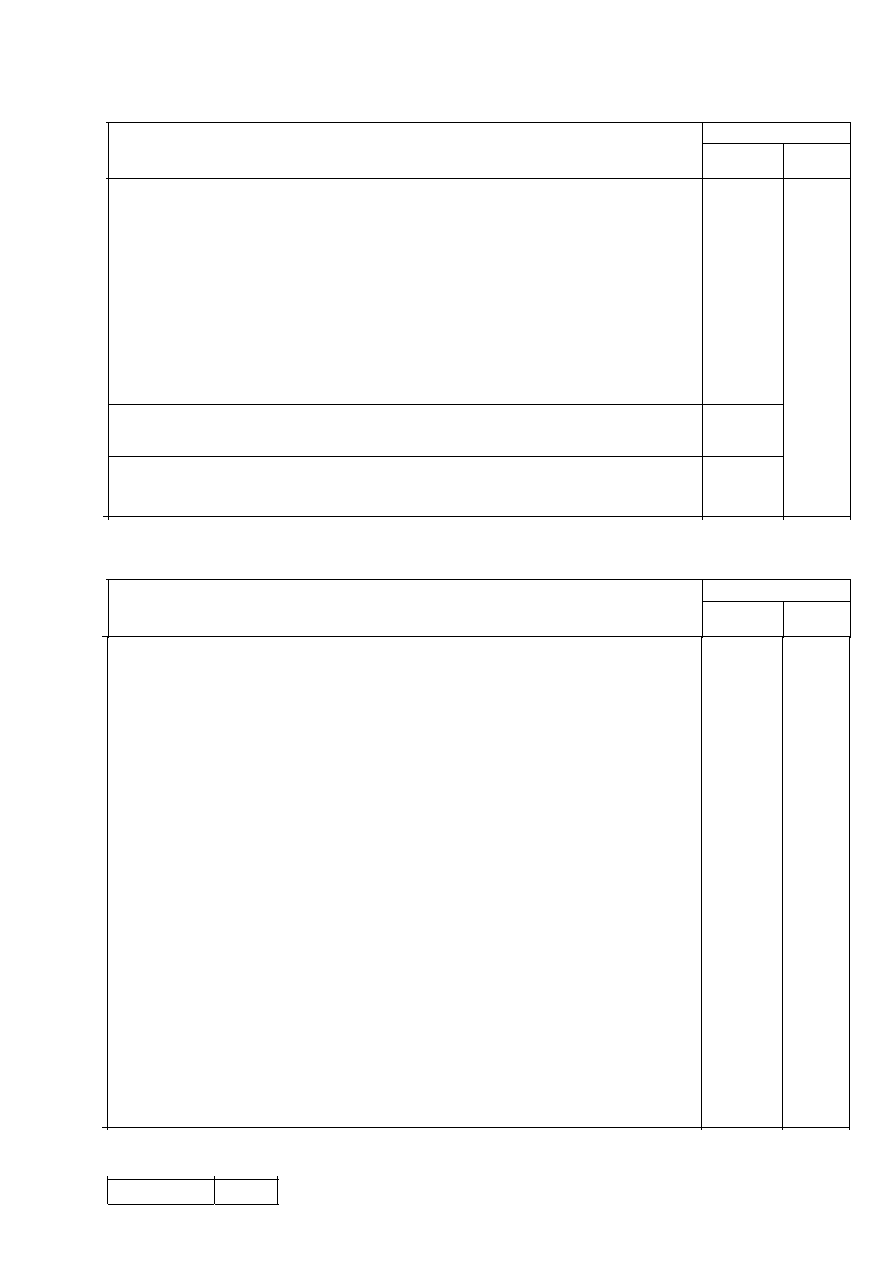
2
Lub:
v v v
v
v
v
v
v
Zadanie 4. (2 pkt)
Źródło: CKE 2005 (PP), zad. 21.
Zadanie 5. (2 pkt)
Źródło: CKE 2005 (PP), zad. 26.
v v v
v
v
v
v
v
Zadanie 6. (1 pkt)
Źródło: CKE 01.2006 (PP), zad. 5.
v v v
v
v
v
v
v
3
Zadanie 7. (2 pkt)
Źródło: CKE 01.2006 (PP), zad. 15.
Z równania stanu:
0
3
0
0
0
0
3
2
T
V
p
T
V
p
1
15
.
Gaz
OkreĞlenie objĊtoĞci gazu w stanie 3:
V
3
=
0
2
3
V
1
2
OkreĞlenie ciepáa pobranego:
Q
1
= W + Q
2
1
OkreĞlenie sprawnoĞci:
2
W
W Q
K
1
16
.
Si
ln
ik
Obliczenie sprawnoĞci:
0,25
K
(25%)
1
3
WyraĪenie masy równaniem:
2
c
E
m
'
1
17
.
M
as
a i
e
ne
rg
ia
.
Obliczenie wartoĞci masy:
'
m =
kg
10
4
,
4
9
1
2
Prawidáowy ksztaát wykresu mający początek w N
o
.
1
Prawidáowo zaznaczony na wykresie czas poáowicznego
rozpadu dla:
N = N
0
/2
1
18
.
W
Ċg
ie
l
OkreĞlenie wieku znalezionych szczątków:
t = 17100 lat
1
3
Wykres nie
moĪe byü linią
áamaną.
N
o
N
T
1/2
t
N
o
/2
3
MODEL ODPOWIEDZI I SCHEMAT OCENIANIA
ARKUSZA I
Zadania zamkniĊte
Numer zadania
1
2
3
4
5
6
7
8
Prawidáowa
odpowiedĨ
C
A
D
C
B
B
B
C
Liczba
punktów
1
1
1
1
1
1
1
1
Zadania otwarte
Zdający moĪe rozwiązaü zadania kaĪdą poprawną metodą. Otrzymuje
wtedy maksymalną liczbĊ punktów.
Numer
zadania
Proponowana odpowiedĨ
Punktacja
Uwagi
Porównanie energii wydzielonej podczas ocháadzania
z energią potencjalną:
E = mgh lub Q = mgh
1
OkreĞlenie wysokoĞci:
mg
Q
h
1
9. Samochód na podno
Ğniku
Obliczenie wysokoĞci:
6,72m
h |
1
3
10.1
1
10
. W
yz
na
cz
an
ie
p
rz
ys
pi
es
ze
ni
a
zi
em
sk
ie
go
10.2
NaleĪy zmierzyü okres (lub czĊstotliwoĞü) drgaĔ wahadáa
i jego dáugoĞü.
1
2
N
Q
1
Zadanie 8. (3 pkt)
Źródło: CKE 01.2006 (PP), zad. 16.
Z równania stanu:
0
3
0
0
0
0
3
2
T
V
p
T
V
p
1
15
.
Gaz
OkreĞlenie objĊtoĞci gazu w stanie 3:
V
3
=
0
2
3
V
1
2
OkreĞlenie ciepáa pobranego:
Q
1
= W + Q
2
1
OkreĞlenie sprawnoĞci:
2
W
W Q
K
1
16
.
Si
ln
ik
Obliczenie sprawnoĞci:
0,25
K
(25%)
1
3
WyraĪenie masy równaniem:
2
c
E
m
'
1
17
.
M
as
a i
e
ne
rg
ia
.
Obliczenie wartoĞci masy:
'
m =
kg
10
4
,
4
9
1
2
Prawidáowy ksztaát wykresu mający początek w N
o
.
1
Prawidáowo zaznaczony na wykresie czas poáowicznego
rozpadu dla:
N = N
0
/2
1
18
.
W
Ċg
ie
l
OkreĞlenie wieku znalezionych szczątków:
t = 17100 lat
1
3
Wykres nie
moĪe byü linią
áamaną.
N
o
N
T
1/2
t
N
o
/2
3
MODEL ODPOWIEDZI I SCHEMAT OCENIANIA
ARKUSZA I
Zadania zamkniĊte
Numer zadania
1
2
3
4
5
6
7
8
Prawidáowa
odpowiedĨ
C
A
D
C
B
B
B
C
Liczba
punktów
1
1
1
1
1
1
1
1
Zadania otwarte
Zdający moĪe rozwiązaü zadania kaĪdą poprawną metodą. Otrzymuje
wtedy maksymalną liczbĊ punktów.
Numer
zadania
Proponowana odpowiedĨ
Punktacja
Uwagi
Porównanie energii wydzielonej podczas ocháadzania
z energią potencjalną:
E = mgh lub Q = mgh
1
OkreĞlenie wysokoĞci:
mg
Q
h
1
9. Samochód na podno
Ğniku
Obliczenie wysokoĞci:
6,72m
h |
1
3
10.1
1
10
. W
yz
na
cz
an
ie
p
rz
ys
pi
es
ze
ni
a
zi
em
sk
ie
go
10.2
NaleĪy zmierzyü okres (lub czĊstotliwoĞü) drgaĔ wahadáa
i jego dáugoĞü.
1
2
N
Q
1
Zadanie 9. (3 pkt)
Źródło: CKE 05.2006 (PP), zad. 20.
Egzamin maturalny z fizyki i astronomii
11
Arkusz I
Zadanie 19. Echo (3 pkt)
JeĪeli dwa jednakowe dĨwiĊki docierają do ucha w odstĊpie czasu dáuĪszym niĪ 0,1 s są
sáyszane przez czáowieka oddzielnie (powstaje echo). JeĞli odstĊp czasu jest krótszy od 0,1 s
dwa dĨwiĊki odbieramy jako jeden o przedáuĪonym czasie trwania (powstaje pogáos). Oblicz,
w jakiej najmniejszej odlegáoĞci od sáuchacza powinna znajdowaü siĊ pionowa Ğciana
odbijająca dĨwiĊk, aby po klaĞniĊciu w dáonie sáuchacz usáyszaá echo. Przyjmij, Īe wartoĞü
prĊdkoĞci dĨwiĊku w powietrzu wynosi 340 m/s.
Zadanie 20. Zbiornik z azotem (3 pkt)
Stalowy zbiornik zawiera azot pod ciĞnieniem 1200 kPa. Temperatura gazu wynosi 27
o
C.
Zbiornik zabezpieczony jest zaworem bezpieczeĔstwa, który otwiera siĊ gdy ciĞnienie gazu
przekroczy 1500 kPa. Zbiornik wystawiono na dziaáanie promieni sáonecznych, w wyniku
czego temperatura gazu wzrosáa do 77
o
C. Podaj, czy w opisanej sytuacji nastąpi otwarcie
zaworu. OdpowiedĨ uzasadnij, wykonując niezbĊdne obliczenia. Przyjmij, Īe objĊtoĞü
zbiornika mimo ogrzania nie ulega zmianie.
Nr zadania
18.1 18.2
19
20
Maks. liczba pkt
1
2
3
3
Wypeánia
egzaminator! Uzyskana liczba pkt
Droga przebyta przez falĊ akustyczną
s = 2l
, gdzie
l
jest odlegáoĞcią od
Ğciany.
PoniewaĪ,
2l = vǻt
2
t
l
'
v
2
1,
0
340
s
s
m
l
m
l 17
Aby sáuchacz usáyszaá echo odlegáoĞü od Ğciany powinna byü wiĊksza niĪ
17 m.
2
2
2
1
1
1
T
V
p
T
V
p
,
poniewaĪ
1
2
V
V
kPa
p
K
K
kPa
p
T
T
p
p
T
p
T
p
1400
300
350
1200
2
2
1
2
1
2
2
2
1
1
Zawór bezpieczeĔstwa nie otworzy siĊ.
4
Zadanie 10. (1 pkt)
Źródło: CKE 11.2006 (PP), zad. 3.
Zadanie 11. (1 pkt)
Źródło: CKE 11.2006 (PP), zad. 4.
Zadanie 12. (1 pkt)
Źródło: CKE 11.2006 (PP), zad. 5.
v v v
v
v
v
v
v
v v v
v
v
v
v
v
v v v
v
v
v
v
v
v v v
v
v
v
v
v
v v v
v
v
v
v
v
Zadanie 13. (2 pkt)
Źródło: CKE 11.2006 (PP), zad. 16.
Próbny egzamin maturalny z fizyki i astronomii
Poziom podstawowy
2
Zadania zamkniĊte (punktacja 0 – 1)
Zadanie
1
2
3
4
5
6
7
8
9
10
OdpowiedĨ
A
B
B
A
C
A
B
D
B
A
Nr.
zadania
Punktowane elementy odpowiedzi
Liczba
punktów Razem
11.1
Wpisanie prawidáowych
okreĞleĔ pod rysunkami.
1
ZauwaĪenie, Īe droga jest równa poáowie dáugoĞci okrĊgu
1
11
11.2 Obliczenie drogi | 6,28m
s
.
1
3
Ustalenie przebytej drogi (10 m)
np. na podstawie wykresu.
1
12
Obliczenie wartoĞci prĊdkoĞci Ğredniej
m
= 2,5
s
sr
v
.
1
2
Ustalenie wartoĞci siáy napĊdowej F
nap
= 2500 N.
1
Ustalenie
wartoĞci siáy wypadkowej po ustaniu wiatru F
wyp
= 500 N.
1
13
Obliczenie wartoĞci przyspieszenia
2
m
= 0,5
s
a
.
1
3
Zastosowanie równaĔ opisujących drogĊ i prĊdkoĞü w ruchu
jednostajnie przyspieszonym i przeksztaácenie ich do postaci
umoĪliwiającej obliczenie przyspieszenia (
2
2
a
s
v
).
1
14
Obliczenie wartoĞci przyspieszenia a
= 1,2 m/s
2
.
1
2
15.1 Zaznaczenie prawidáowej odpowiedzi –
tylko elektrony.
1
15 15.2
Udzielenie prawidáowej odpowiedzi –
przewodnictwo
elektryczne metali pogarsza siĊ (zmniejsza siĊ) wraz
ze wzrostem temperatury.
Dopuszcza siĊ uzasadnienie opisujące zaleĪnoĞü oporu
przewodnika (metali) od temperatury.
1
2
16.1
Udzielenie prawidáowej odpowiedzi
– jednoczesna zmiana ciĞnienia, objĊtoĞci i temperatury
zachodzi w przemianie 1 – 2.
1
16
16.2 Udzielenie prawidáowej odpowiedzi – temperatura gazu jest
najwyĪsza w punkcie 2.
1
2
WyraĪenie wartoĞci siáy dziaáającej na gwóĨdĨ
p
F
t
'
'
.
1
17.1
Obliczenie wartoĞci siáy F
= 2,5 kN.
1
2
ZauwaĪenie, Īe
2
2
m
mgh
v
1
Zapisanie wyraĪenia
2
2
h
g
v
.
1
17
17.2
Obliczenie wysokoĞci h
= 5 m.
1
3
tor
przemieszenie
A
B
A
B
Próbny egzamin maturalny z fizyki i astronomii
Poziom podstawowy
2
Zadania zamkniĊte (punktacja 0 – 1)
Zadanie
1
2
3
4
5
6
7
8
9
10
OdpowiedĨ
A
B
B
A
C
A
B
D
B
A
Nr.
zadania
Punktowane elementy odpowiedzi
Liczba
punktów Razem
11.1
Wpisanie prawidáowych
okreĞleĔ pod rysunkami.
1
ZauwaĪenie, Īe droga jest równa poáowie dáugoĞci okrĊgu
1
11
11.2 Obliczenie drogi | 6,28m
s
.
1
3
Ustalenie przebytej drogi (10 m)
np. na podstawie wykresu.
1
12
Obliczenie wartoĞci prĊdkoĞci Ğredniej
m
= 2,5
s
sr
v
.
1
2
Ustalenie wartoĞci siáy napĊdowej F
nap
= 2500 N.
1
Ustalenie
wartoĞci siáy wypadkowej po ustaniu wiatru F
wyp
= 500 N.
1
13
Obliczenie wartoĞci przyspieszenia
2
m
= 0,5
s
a
.
1
3
Zastosowanie równaĔ opisujących drogĊ i prĊdkoĞü w ruchu
jednostajnie przyspieszonym i przeksztaácenie ich do postaci
umoĪliwiającej obliczenie przyspieszenia (
2
2
a
s
v
).
1
14
Obliczenie wartoĞci przyspieszenia a
= 1,2 m/s
2
.
1
2
15.1 Zaznaczenie prawidáowej odpowiedzi –
tylko elektrony.
1
15 15.2
Udzielenie prawidáowej odpowiedzi –
przewodnictwo
elektryczne metali pogarsza siĊ (zmniejsza siĊ) wraz
ze wzrostem temperatury.
Dopuszcza siĊ uzasadnienie opisujące zaleĪnoĞü oporu
przewodnika (metali) od temperatury.
1
2
16.1
Udzielenie prawidáowej odpowiedzi
– jednoczesna zmiana ciĞnienia, objĊtoĞci i temperatury
zachodzi w przemianie 1 – 2.
1
16
16.2 Udzielenie prawidáowej odpowiedzi – temperatura gazu jest
najwyĪsza w punkcie 2.
1
2
WyraĪenie wartoĞci siáy dziaáającej na gwóĨdĨ
p
F
t
'
'
.
1
17.1
Obliczenie wartoĞci siáy F
= 2,5 kN.
1
2
ZauwaĪenie, Īe
2
2
m
mgh
v
1
Zapisanie wyraĪenia
2
2
h
g
v
.
1
17
17.2
Obliczenie wysokoĞci h
= 5 m.
1
3
tor
przemieszenie
A
B
A
B
Zadanie 14. (1 pkt)
Źródło: CKE 2007 (PP), zad. 9.
Zadanie 15. (2 pkt)
Źródło: CKE 2007 (PP), zad. 19.
Egzamin maturalny z fizyki i astronomii
3
Poziom podstawowy
Zadanie 6. (1 pkt)
Wiązka dodatnio naáadowanych cząstek pochodzenia kosmicznego dociera do Ziemi
prostopadle do jej powierzchni w okolicach równika (rys.). W wyniku dziaáania ziemskiego
pola magnetycznego zostanie ona odchylona w kierunku
A. póánocnym.
B. poáudniowym.
C.
wschodnim.
D. zachodnim.
Zadanie 7. (1 pkt)
RozciągniĊcie sprĊĪyny o 1 cm z poáoĪenia równowagi wymaga wykonania pracy 2 J.
RozciągniĊcie tej samej sprĊĪyny o 3 cm, równieĪ z poáoĪenia równowagi, wymaga
wykonania pracy
A. 6 J.
B. 12 J.
C.
18 J.
D. 24 J.
Zadanie 8. (1 pkt)
Podczas przejĞcia wiązki Ğwiatáa z oĞrodka o wiĊkszym wspóáczynniku zaáamania do oĞrodka
o mniejszym wspóáczynniku zaáamania
dáugoĞü fali
prĊdkoĞü fali
A.
roĞnie,
roĞnie,
B.
roĞnie,
maleje,
C.
maleje,
roĞnie,
D.
maleje,
maleje,
Zadanie 9. (1 pkt)
SprawnoĞü silnika cieplnego wynosi 20%. W ciągu 1 godziny silnik oddaje do cháodnicy
20 kJ energii. W tym czasie pobiera on z grzejnika energiĊ cieplną o wartoĞci
A.
25 kJ.
B. 40 kJ.
C. 50 kJ.
D. 100 kJ.
Zadanie 10. (1 pkt)
Trzy czwarte początkowej liczby jąder pewnego izotopu promieniotwórczego ulega
rozpadowi w czasie 24 godzin. Okres poáowicznego rozpadu tego izotopu jest równy
A. 2 godziny.
B. 4 godziny.
C. 8 godzin.
D.
12 godzin.
oĞ obrotu Ziemi
Z
W
Pn
Pd
S
N
8
Egzamin maturalny z fizyki i astronomii
Poziom podstawowy
18.2. (4 pkt)
Przedstaw na wykresie zaleĪnoĞü wychylenia tego wahadáa od czasu. Na wykresie zaznacz
wartoĞci liczbowe amplitudy oraz okresu drgaĔ.
obliczenia
wykres
19. Gaz (2 pkt)
W cylindrze o objĊtoĞci 15 dm
3
znajduje siĊ wodór. CiĞnienie wodoru jest równe 1013,82 hPa,
a jego temperatura wynosi 27
o
C.
Oblicz liczbĊ moli wodoru znajdujących siĊ w cylindrze.
2
2 s ;
1,40s
20
T
T
T
S
Z
S
|
pV
pV nRT
n
RT
3 3
101 382 Pa 15 10 m
J
8,31
300K
mol K
0,61mola
n
n
|
x, m
t, s
1,4
– 0,02
0,7
2,8
2,1
0,02
0
5
Zadanie 16. (1 pkt)
Źródło: CKE 2008 (PP), zad. 4.
Zadanie 17. (1 pkt)
Źródło: CKE 2008 (PP), zad. 5.
Egzamin maturalny z fizyki i astronomii
Poziom podstawowy
2
ZADANIA ZAMKNIĉTE
W zadaniach od 1. do 10. wybierz i zaznacz na karcie odpowiedzi jedną
poprawną odpowiedĨ.
Zadanie 1. (1 pkt)
Ziemia pozostaje w spoczynku wzglĊdem
A. SáoĔca.
B. KsiĊĪyca.
C. Galaktyki.
D.
satelity geostacjonarnego.
Zadanie 2. (1 pkt)
JeĪeli podczas ruchu samochodu, na prostoliniowym odcinku autostrady energia kinetyczna
samochodu wzrosáa 4 razy, to wartoĞü prĊdkoĞci samochodu wzrosáa
A.
2
razy.
B.
2 razy.
C. 4 razy.
D. 16 razy.
Zadanie 3. (1 pkt)
ZaleĪnoĞü energii potencjalnej i kinetycznej od czasu podczas swobodnego spadania ciaáa
z pewnej wysokoĞci poprawnie przedstawiono na
A.
wykresie 1.
B. wykresie 2.
C. wykresie 3.
D. wykresie 4.
Zadanie 4. (1 pkt)
Promienie sáoneczne ogrzaáy szczelnie zamkniĊtą metalową butlĊ z gazem. JeĪeli pominiemy
rozszerzalnoĞü termiczną butli, to gaz w butli ulegá przemianie
A. izobarycznej.
B.
izochorycznej.
C. izotermicznej.
D. adiabatycznej.
t
E
p
, E
k
t
E
p
, E
k
E
p
E
k
wykres 1
wykres 2
t
E
p
, E
k
wykres 4
wykres 3
t
E
p
, E
k
Egzamin maturalny z fizyki i astronomii
Poziom podstawowy
3
Zadanie 5. (1 pkt)
Unoszenie siĊ w górĊ iskier nad páonącym ogniskiem w bezwietrzny dzieĔ jest spowodowane
zjawiskiem
A. dyfuzji.
B.
konwekcji.
C. przewodnictwa.
D. promieniowania.
Zadanie 6. (1 pkt)
Gdy w atomie wodoru elektron przejdzie z orbity pierwszej na drugą, to promieĔ orbity
wzrasta czterokrotnie. WartoĞü siáy przyciągania elektrostatycznego dziaáającej pomiĊdzy
jądrem i elektronem zmaleje w tej sytuacji
A. 2 razy.
B. 4 razy.
C. 8 razy.
D.
16 razy.
Zadanie 7. (1 pkt)
W cyklotronie do zakrzywiania torów naáadowanych cząstek wykorzystuje siĊ
A. staáe pole elektryczne.
B.
staáe pole magnetyczne.
C. zmienne pole elektryczne.
D. zmienne pole magnetyczne.
Zadanie 8. (1 pkt)
Ziemia krąĪy wokóá SáoĔca w odlegáoĞci w przybliĪeniu 4 razy wiĊkszej niĪ Merkury.
Korzystając z trzeciego prawa Keplera moĪna ustaliü, Īe okres obiegu Ziemi wokóá SáoĔca
jest w porównaniu z okresem obiegu Merkurego dáuĪszy
okoáo
A. 2 razy.
B. 4 razy.
C.
8 razy.
D. 16 razy.
Zadanie 9. (1 pkt)
Jądro izotopu ulegáo rozpadowi promieniotwórczemu. Powstaáo nowe jądro zawierające
o jeden proton wiĊcej i o jeden neutron mniej niĪ jądro wyjĞciowe. Przedstawiony powyĪej
opis dotyczy rozpadu
A. alfa.
B. gamma.
C. beta plus.
D.
beta minus.
Zadanie 10. (1 pkt)
Przyrząd sáuĪący do uzyskiwania i obserwacji widma promieniowania elektromagnetycznego
to
A. kineskop.
B. mikroskop.
C. oscyloskop.
D.
spektroskop.
Egzamin maturalny z fizyki i astronomii
Poziom podstawowy
9
Zadanie 18.1 (3 pkt)
Oblicz masĊ molową tego gazu.
p V n R T
gdzie
m
n
P
Zatem
m
p V
R T
P
ĺ
m R T
p
V
P
ĺ
R T
p d
P
d R T
p
P
Po podstawieniu danych liczbowych odczytanych z wykresu
3
kg
J
0,08
8,31
300K
m
mol K
100000Pa
P
ĺ
3
2 10 kg/mol
P
|
Zadanie 18.2
(2 pkt)
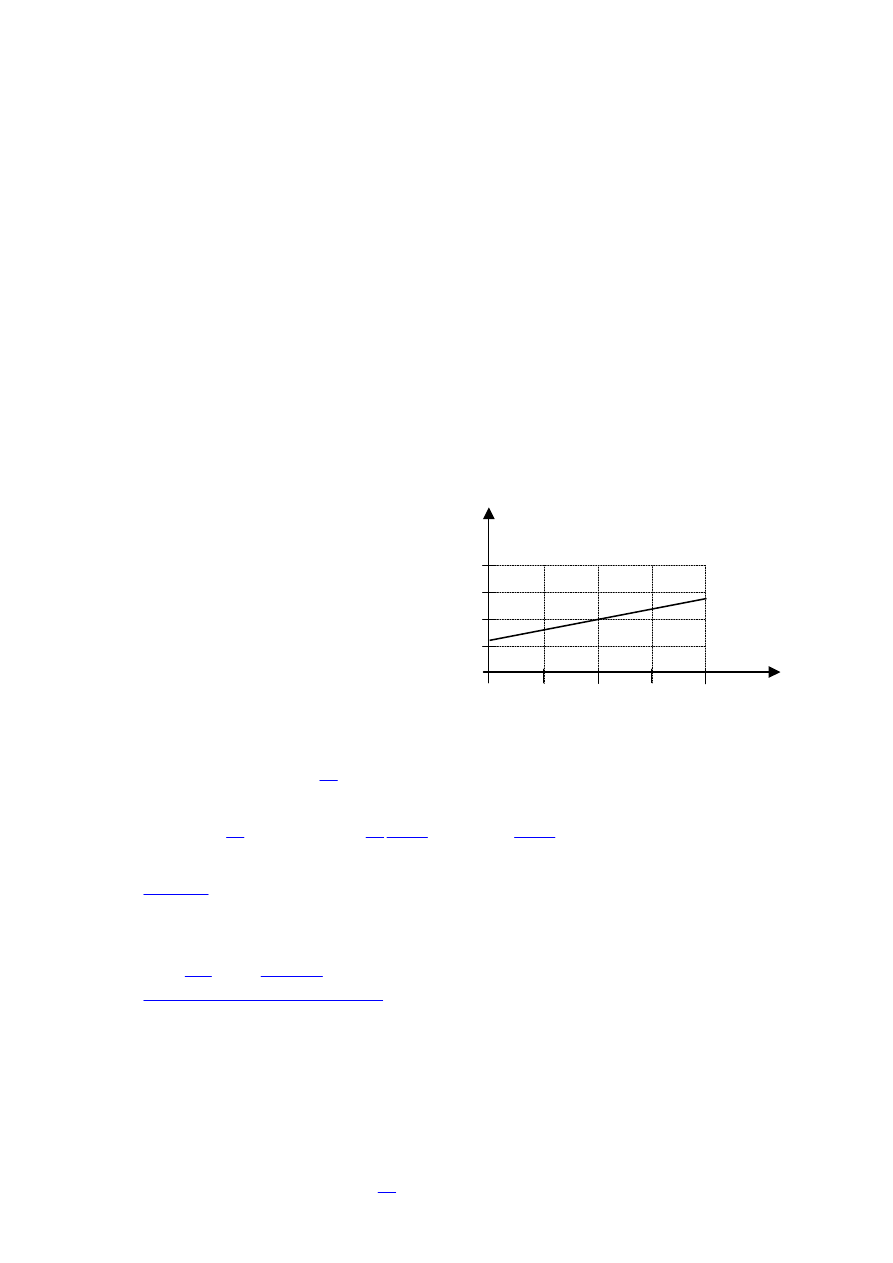
Podaj, czy w tej przemianie objĊtoĞü gazu rosáa, czy malaáa. OdpowiedĨ uzasadnij.
W tej przemianie objĊtoĞü gazu malaáa.
Z wykresu wynika, Īe podczas przemiany gĊstoĞü gazu rosáa. PoniewaĪ masa
gazu jest staáa, z zaleĪnoĞci
m
d
V
wynika, Īe objĊtoĞü gazu malaáa.
Zadanie 19. Soczewka (4 pkt)
ZdolnoĞü skupiająca soczewki páasko-wypukáej wykonanej z materiaáu o wspóáczynniku
zaáamania równym 2 i umieszczonej w powietrzu wynosi 2 dioptrie.
Zadanie 19.1
(3 pkt)
Oblicz promieĔ krzywizny wypukáej czĊĞci soczewki.
1
2
1
1
1
1
n
f
R
R
§
·
¨
¸
©
¹
gdzie
2
1 0
R
, zatem moĪna zapisaü:
1
1
n
f
R
poniewaĪ
1
Z
f
to
1
n
Z
R
skąd po przeksztaáceniu otrzymamy:
1
n
R
Z
czyli
2 1
1
2
m
R
ĺ R =
0,5m
Zadanie 19.2 (1 pkt)
Napisz, czy ta soczewka moĪe korygowaü wadĊ dalekowzrocznoĞci.
Opisana w zadaniu soczewka moĪe korygowaü wadĊ dalekowzrocznoĞci.
Nr zadania
16. 17. 18.1. 18.2. 19.1. 19.2.
Maks. liczba pkt
2
1
3
2
3
1
Wypeánia
egzaminator! Uzyskana liczba pkt
Zadanie 18.1 (3 pkt)
Zadanie 18. (5 pkt)
Źródło: CKE 2008 (PP), zad. 18.
Egzamin maturalny z fizyki i astronomii
Poziom podstawowy
8
Zadanie 16. Metalowa puszka (2 pkt)
Do pustej metalowej puszki po napoju, poáoĪonej tak, Īe moĪe siĊ toczyü po poziomej uziemionej
metalowej páycie, zbliĪamy z boku na niewielką odlegáoĞü dodatnio naelektryzowaną paáeczkĊ.
WyjaĞnij, dlaczego puszka zaczyna siĊ toczyü. OkreĞl, w którą stronĊ bĊdzie toczyü siĊ
puszka.
W wyniku zjawiska indukcji elektrostatycznej na metalowej puszce, od strony
paáeczki, pojawia siĊ áadunek elektryczny przeciwnego znaku.
Powoduje to przyciąganie puszki i paáeczki.
Puszka bĊdzie siĊ toczyü w stronĊ naelektryzowanej paáeczki.
Zadanie 17. Elektron (1 pkt)
Oblicz koĔcową, relatywistyczną wartoĞü pĊdu elektronu przyspieszanego w akceleratorze
do prĊdkoĞci 0,8 c. ZaáóĪ, Īe początkowa wartoĞü prĊdkoĞci przyspieszanego elektronu jest
znikomo maáa.
2
2
1
o
m
p
c
X
X
gdzie
v = 0,8
c
2
2
0,8
0,8
1
o
m
c
p
c
c
0,8
1 0,64
o
m c
p
0,8
0,6
o
m c
p
31
8
4 9,11 10 kg 3 10 m/s
3
p
p = 3,64·10
–22
kg·m/s
Zadanie 18. Przemiana izotermiczna (5 pkt)
Gaz o temperaturze
27
o
C poddano
przemianie izotermicznej. CiĞnienie
początkowe gazu wynosiáo 800 hPa.
Wykres przedstawia zaleĪnoĞü gĊstoĞci
gazu od jego ciĞnienia dla tej przemiany.
Podczas przemiany masa gazu nie
ulegaáa zmianie.
p, hPa
d, kg/m
3
800
1000 1100 1200
0,04
0,06
0,08
0,12
0,10
900
Zadanie 18.2 (2 pkt)
6
Zadanie 19. (1 pkt)
Źródło: CKE 2009 (PP), zad. 4.
Fizyka i astronomia – poziom podstawowy
Klucz punktowania odpowiedzi
3
Zadanie 1.
WiadomoĞci i rozumienie Wyznaczenie wartoĞci prĊdkoĞci i przyspieszenia ciaáa
wykorzystując równanie ruchu.
0–1
Poprawna odpowiedĨ:
WartoĞü prĊdkoĞci początkowej, m/s
WartoĞü przyspieszenia, m/s
2
C.
15
3
Zadanie 2.
WiadomoĞci i rozumienie
Wskazanie przyczyny wystĊpowania przyspieszenia
doĞrodkowego ciaáa poruszającego siĊ po okrĊgu
ruchem jednostajnym.
0–1
Poprawna odpowiedĨ:
B. zmiana kierunku prĊdkoĞci liniowej.
Zadanie 3.
WiadomoĞci i rozumienie Wyznaczenie wartoĞü zmiany prĊdkoĞci ciaáa
odbijającego siĊ od podáoĪa.
0–1
Poprawna odpowiedĨ:
D. 3,5 m/s.
Zadanie 4.
WiadomoĞci i rozumienie Dobranie wáaĞciwego wykresu do przedstawionej
przemiany gazowej.
0–1
Poprawna odpowiedĨ:
A. 1.
Zadanie 5.
WiadomoĞci i rozumienie Wybranie wáaĞciwego opisu dotyczącego przepáywu
prądu w miedzianym przewodniku.
0–1
Poprawna odpowiedĨ:
A. elektronów, a jego opór wraz ze wzrostem temperatury roĞnie.
T
p
Zadanie 20. (5 pkt)
Źródło: CKE 2009 (PP), zad. 14.
Fizyka i astronomia – poziom podstawowy
Klucz punktowania odpowiedzi
6
Zadanie 12.3
Korzystanie z informacji
Wykazanie, Īe w ukáadzie SI energia kinetyczna
protonu wyraĪona jest w dĪulach.
0–2
1 pkt – zapisanie, Īe
> @
kg
T
m
C
E
k
2
2
2
1 pkt – wykonanie przeksztaáceĔ i wykazanie, Īe [E
k
] =
2
2
s
m
kg
= J
Zadanie 13.1
Korzystanie z informacji
Obliczenie wspóáczynnika sprĊĪystoĞci sprĊĪyny
wykorzystując wykres zaleĪnoĞci siáy wprawiającej
ciaáo w drgania od jego przemieszczenia.
0–2
1 pkt – zapisanie zaleĪnoĞci
x
F
k i podstawienie wartoĞci liczbowych odczytanych
z wykresu
1 pkt – obliczenie wspóáczynnika sprĊĪystoĞci sprĊĪyny k = 80 N/m
Zadanie 13.2
Korzystanie z informacji
Wykazanie, Īe maksymalna wartoĞü przyspieszenia
drgającej kulki jest równa podanej wartoĞci.
0–1
1 pkt – zapisanie zaleĪnoĞci
m
F
a i obliczenie maksymalnej wartoĞci przyspieszenia
a
max
= 4 m/s
2
Zadanie 14.1
Tworzenie informacji
Ustalenie, jak zmieniáa siĊ gĊstoĞü gazu
w przedstawionej przemianie gazowej.
Uzasadnienie odpowiedzi, podając odpowiednie
zaleĪnoĞci.
0–2
1 pkt – zapisanie stwierdzenia:
gĊstoĞü gazu w przemianie rosáa
1 pkt – zapisanie uzasadnienia np.: wzrost ciĞnienia gazu byá trzykrotny, a temperatury
dwukrotny zatem objĊtoĞü
malaáa
lub
zapisanie
V
m
U
gdzie
p
T
R
n
V
i odpowiedni komentarz o zmianie objĊtoĞci
Zadanie 14.2
Korzystanie z informacji
Ustalenie, który z wymienionych w tabeli gazów
poddano opisanej przemianie gazowej.
0–3
1 pkt – zapisanie równania
T
R
n
V
p
i podstawienie
P
m
n
Zadanie 20.2 (3 pkt)
Zadanie 20.1 (2 pkt)
Fizyka i astronomia – poziom podstawowy
Klucz punktowania odpowiedzi
7
1pkt – obliczenie masy molowej gazu (
µ = 32 g)
Zdający moĪe obliczyü liczbĊ moli gazu (n § 1,5), a nastĊpne masĊ molową
g
g
32
5
1
48
,
P
1pkt – prawidáowy wybór gazu z podanej tabeli: tlen
Zadanie 15.
Korzystanie z informacji Obliczenie dáugoĞü fali Ğwiatáa emitowanego przez
laser.
0–3
1 pkt – skorzystanie z zaleĪnoĞci
P =
t
E
n
f
1pkt – uwzglĊdnienie, Īe
O
c
h
E
f
1pkt – obliczenie dáugoĞci fali Ȝ § 6,32·10
–7
m (Ȝ § 631,5 nm)
Zadanie 16.
Tworzenie informacji
Narysowanie dalszego biegu promieni Ğwietlnych
w sytuacjach przedstawionych na rysunkach.
0–3
Po 1 pkt za prawidáowy bieg promienia w kaĪdej z trzech przedstawionych sytuacji
(na pierwszym i drugim rysunku zdający moĪe równieĪ narysowaü promieĔ odbity)
Zadanie 17.1
WiadomoĞci i rozumienie Zapisanie reakcji rozpadu atomu záota.
0–1
1 pkt – poprawne zapisanie równania reakcji:
e
e
Hg
Au
Q
~
o
0
1
198
80
198
79
lub
e
Hg
Au
Q
E
~
o
0
1
198
80
198
79
Antyneutrino w zapisie równania nie jest wymagane.
Zadanie 17.2
Korzystanie z informacji
Obliczenie masy izotopu záota pozostaáego
po okreĞlonym czasie w preparacie
promieniotwórczym.
0–2
1 pkt – uwzglĊdnienie, Īe 8,1 dnia to trzy okresy poáowicznego rozpadu
1 pkt – obliczenie masy izotopu záota, która pozostaáa po tym czasie
m = 1,25 µg
7
Zadanie 21. (3 pkt)
Źródło: CKE 2010 (PP), zad. 14.
Egzamin maturalny z fizyki i astronomii
Klucz punktowania odpowiedzi – poziom podstawowy
5
Zadanie 13.2.
Tworzenie informacji
Obliczenie wspóáczynnika tarcia klocka o podáoĪe.
Wykazanie, Īe klocek i podáoĪe są wykonane
z drewna
0–2
1 p. – zastosowanie I zasady dynamiki Newtona w celu obliczenia wspóáczynnika tarcia
klocka o podáoĪe, np.:
T
zew
F
F
lub
g
m
F
zew
P
1 p. – obliczenie wspóáczynnika tarcia µ = 0,3 i porównanie z danymi przedstawionymi
w tabeli dla róĪnych materiaáów
Zadanie 14.1.
Tworzenie informacji
Zaznaczenie na wykresie pola powierzchni figury,
które liczbowo jest równe pracy wykonanej przez
silnik w jednym cyklu
0–1
1 p. – zaznaczenie pola figury A – B – C – D
Zadanie 14.2.
Tworzenie informacji
Zapisanie nazwy przemiany jakiej podlega gaz/para
dla przytoczonej przemiany
0–1
1 p. – zapisanie nazwy przemiany, np.: rozprĊĪanie przy staáym ciĞnieniu
(dopuszcza siĊ zapisanie, Īe jest to przemiana izobaryczna)
Zadanie 14.3.
Korzystanie z informacji
Obliczenie teoretycznej sprawnoĞci silnika Carnota
pracującego w warunkach opisanych w zadaniu
0–1
1 p. – obliczenie teoretycznej sprawnoĞci silnika Carnota Ș = 0,4
Zadanie 15.1.
Korzystanie z informacji
Zapisanie nazwy pola elektrostatycznego
wytworzonego przez áadunek punktowy
0–1
1 p. – poprawne uzupeánienie zdania:
... centralnym.
Zadanie 15.2.
Korzystanie z informacji
Obliczenie wartoĞci áadunku, który jest Ĩródáem pola
elektrostatycznego opisanego w treĞci zadania
0–3
1 p. – zastosowanie prawa Coulomba i definicji natĊĪenia pola, otrzymanie wzoru,
np.:
k
r
E
Q
2
1 p. – odczytanie z wykresu wartoĞci natĊĪenia pola dla jednej z wartoĞci 1/r
2
1 p. – obliczenie wartoĞci áadunku Q § 1·10
-12
C
Zadanie 21.1 (1 pkt)
Zadanie 21.3 (1 pkt)
Zadanie 21.2 (1 pkt)