1

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

Skraplanie

(kondensacja)

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

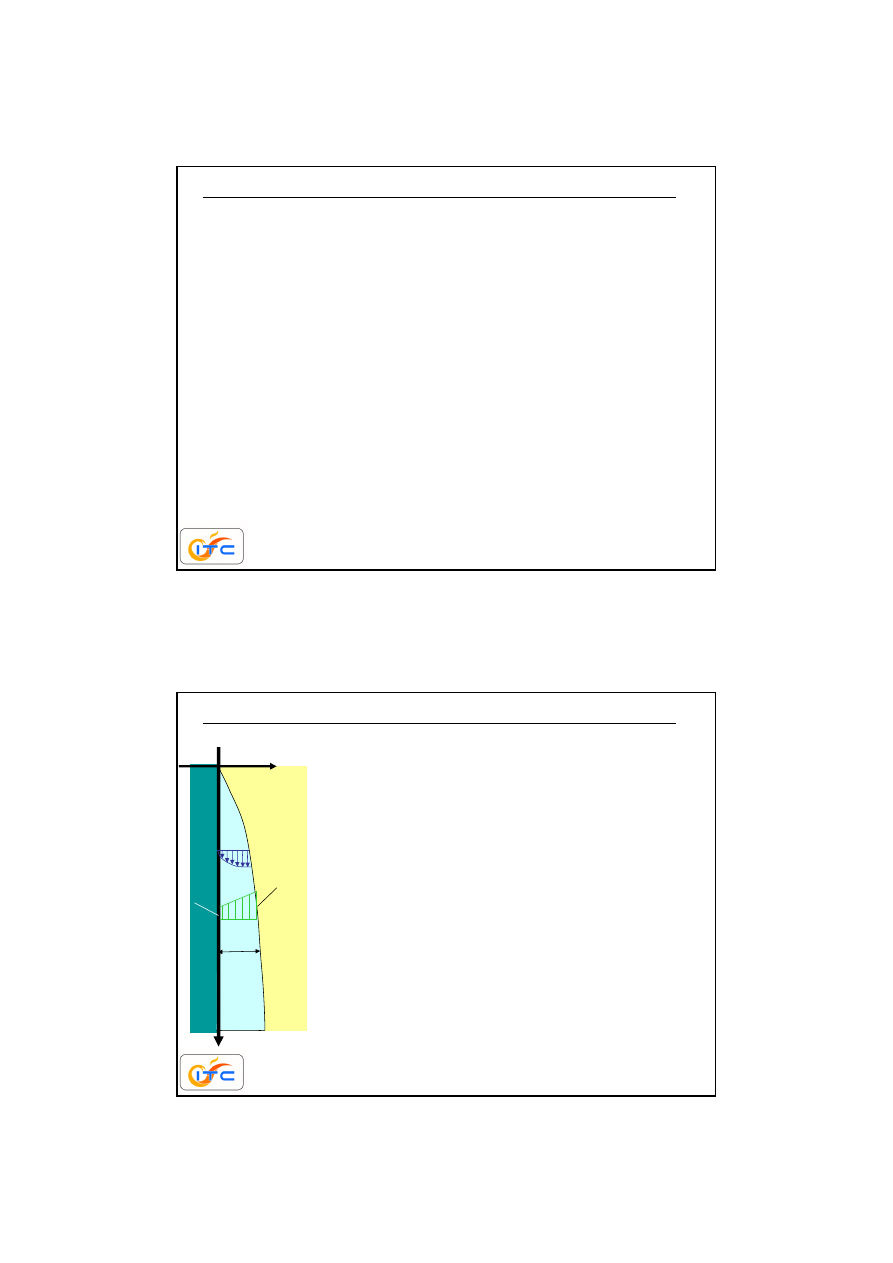
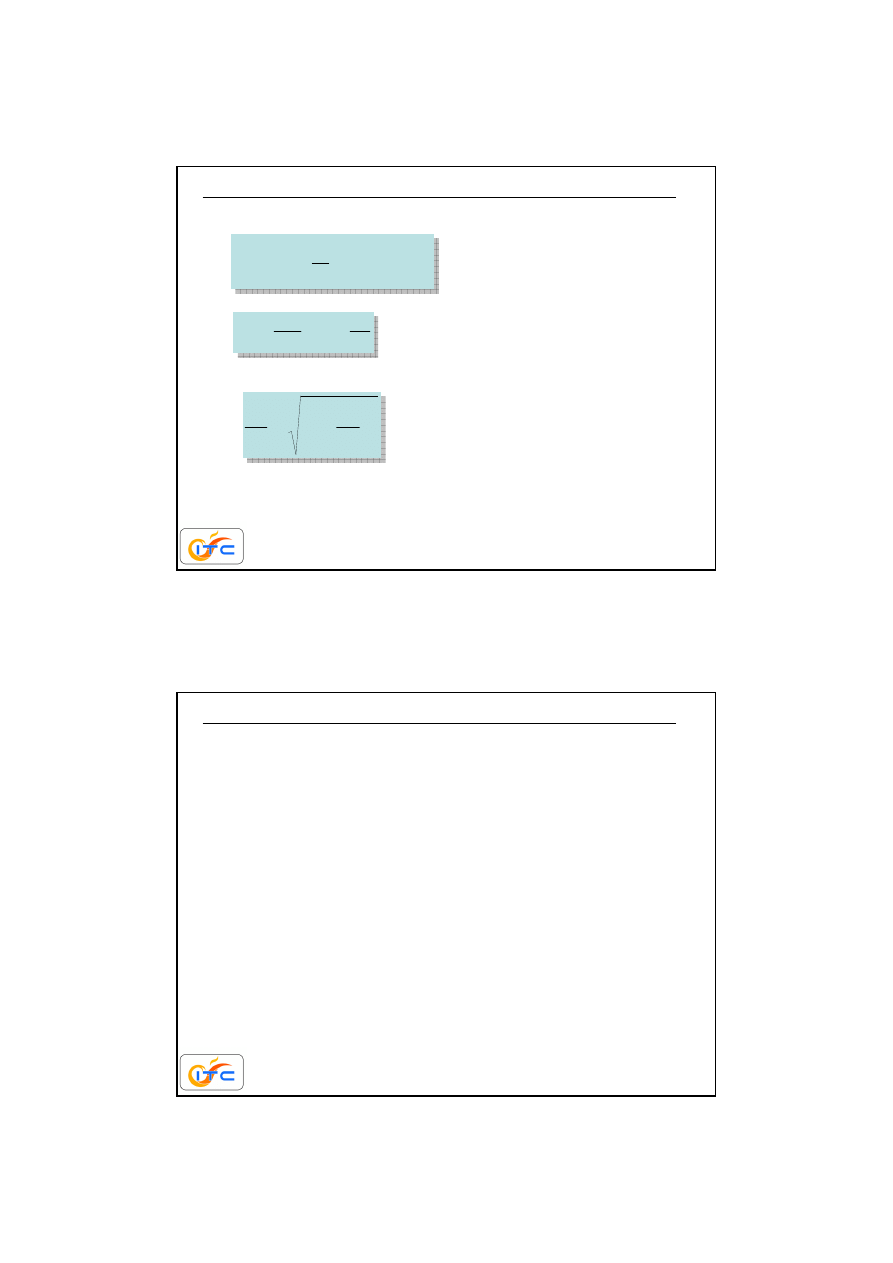
Przestrze

ń

wypełnion

ą

par

ą

nasycon

ą

such

ą

o

temperaturze

T

s

ogranicza

ś

cianka pionowa o

temperaturze

T

w

< T

s

.

Na

ś

ciance wykrapla si

ę

woda

spływaj

ą

c w dół.

• spływ kondensatu jest laminarny, nieistotne s

ą

efekty

bezwładno

ś

ciowe i napi

ę

cia powierzchniowego, pr

ę

dko

ś

ci

pary i gradienty ci

ś

nienia

• temperatura

ś

cianki jest stała i wynosi

T

w

• nie ma oporu dyfuzji mi

ę

dzy par

ą

a warstw

ą

kondensatu,

w zwi

ą

zku z czym temperatura zewn

ę

trznej warstwy

kondensatu jest równa temperaturze nasycenia

T

s

• opór przepływu ciepła od pary do

ś

cianki pochodzi od

przewodzenia przez warstw

ę

kondensatu

• wła

ś

ciwo

ś

ci mediów s

ą

stałe

• rozkład temperatury w warstwie kondensatu jest liniowy

skraplanie na pionowej

ś

ciance

y

w

a

rs

tw

a

k

o

n

d

e

n

s

a

tu

T(x)

T

w

T

s

w

x

(x)

δδδδ

(y)

x

zało

ż

enia

p

a

ra

ś

c

ia

n

k

a

2

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

Rozkład pr

ę

dko

ś

ci wynika z równania p

ę

du

p

c

ρ

ρ

,

g

ę

sto

ść

cieczy i pary

0

d

)

(

d

0

)

0

(

=

δ

=

=

=

y

y

w

y

w

x

x

c

η

lepko

ść

cieczy

g

przyspieszenie ziemskie

0

)

(

d

d

2

2

=

ρ

−

ρ

+

η

p

c

x

c

g

y

w

warunki brzegowe

x

d

Rozkład temperatury wynika z równania energii

na odcinku

dx

wykrapla si

ę

dm

kg/s kondensatu oddaj

ą

c ciepło kondensacji

r

.

Ciepło to jest odprowadzane przez

ś

ciank

ę

.

I

I

d

+

I

y

r

m

d

w

Q

d

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

r

entalpia kondensacji

r

m

Q

w

d

d

=

ciepło uwolnione na skutek kondensacji na powierzchni swobodnej, jest
przewodzone od tej powierzchni do

ś

cianki przez błon

ę

kondensatu. Ciepło

przewodzone oblicza si

ę

zakł

ą

daj

ą

c liniowy przebieg temperatury w poprzek

błony kondensatu

przyrost entalpii strumienia kondensatu jest pomijalny w porównaniu
z ciepłem kondensacji

)

(

/

)

(

)

(

x

y

T

T

T

y

T

w

s

w

δ

−

+

=

4

3

2

)

(

943

.

0

H

T

T

g

r

w

s

c

c

c

−

η

λ

ρ

=

α

ś

rednia warto

ść

współczynnika wnikania na

ś

ciance pionowej o wysoko

ś

ci

H

szczegółowe wyprowadzenie w dodatku

3

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

c

c

c

w

s

c

c

c

c

c

c

T

T

c

r

gH

gH

H

λ

η

=

−

=

ν

=

η

ρ

=

λ

α

=

Pr

)

(

K

;

Ga

;

Nu

2

3

2

2

3

gdzie:

Ga

– liczba Galileusza,

K

–

liczba kondensacji,

c

c

–

ciepło wła

ś

ciwe cieczy

0.25

K)

Pr

(Ga

1.13

Nu

=

z eksperymentów wynika,

ż

e stał

ą

0.943

trzeba zwi

ę

kszy

ć

o ok.

20%

(falowanie powierzchni kondensatu). wła

ś

ciwo

ś

ci oblicza

ć

dla

ś

redniej temperatury filmu

T

f

=(T

s

+T

w

)/2

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

Turbulentny spływ kondensatu

wyznaczenie liczba Reynoldsa

c

e

H

D

w

η

ρ

=

Re

S

m /

=

Γ

S

szeroko

ść ś

cianki

,

δδδδ

grubo

ść

warstwy kondensatu

S

H

T

r

S

Q

∆

α

=

Γ

=

r

H

T

/

∆

α

=

Γ

c

c

H

Hu

r

T

H

ν

=

η

∆

α

=

4

4

Re

c

r

T

u

ρ

∆

α

=

gdzie

odpowiednik

pr

ę

dko

ś

ci

δ

ρ

=

S

w

m

S

tak

ż

e obwód zwil

ż

ony

S

S

D

e

/

4

δ

=

c

c

c

H

S

m

S

m

η

Γ

=

η

=

δ

δη

=

4

4

4

Re

gdzie

jednostkowa g

ę

sto

ść

zraszania

nieznana jest pr

ę

dko

ść

.

Eliminuj

ą

c pr

ę

dko

ść

przez strumie

ń

masy

bilans ciepła

4

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

Liczba Nusselta definiowana jest na wielko

ść

proporcjonaln

ą

do grubo

ś

ci warstwy przy

ś

ciennej

3

/

1

2













ν

=

g

l

c

z

λ

α

=

z

z

l

Nu

1800

Re

Re

0077

.

0

Nu

4

.

0

>

=

H

H

z

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

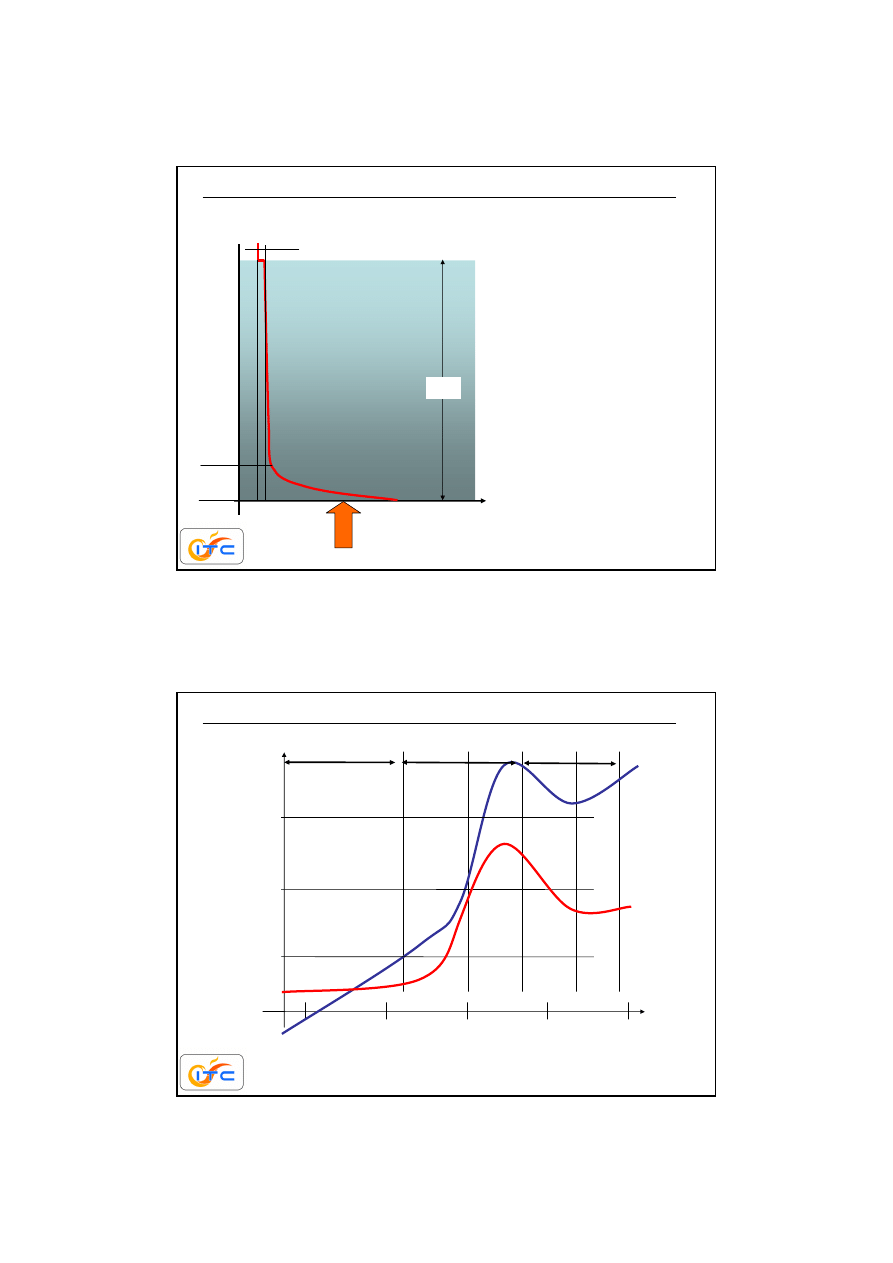
Wrzenie

5

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

6cm

100

o

C

temperatura w

o

C

0.4

o

C

109.1

o

C

3mm

rozkład temperatury we wrz

ą

cej wodzie

g

ę

sto

ść

strumienia ciepła 22.5kW/m

2

Wrzenie swobodne (pool boiling)

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

s

ta

b

il

n

e

w

rz

e

n

ie

b

ło

n

o

w

e

nadwy

ż

ka temperatury

ś

cianki

nad temperatur

ę

wrzenia w K

0.1

1.0

10.

100

1000

konwekcja
swobodna

wrzenie
p

ę

cherzykowe

wrzenie
błonowe

p

ę

c

h

e

rz

e

p

a

ry

k

o

n

d

e

n

s

u

j

ą

w

c

ie

c

z

y

p

ę

c

h

e

rz

e

p

a

ry

d

o

c

ie

ra

j

ą

d

o

z

w

ie

rc

ia

d

ła

w

rz

e

n

ie

p

ę

c

h

e

rz

y

k

o

w

e

i

c

z

ę

ś

c

io

w

o

n

ie

s

ta

b

il

n

e

b

ło

n

o

w

e

w

s

p

.

w

n

ik

a

n

ia

c

ie

p

ła

W

/m

2

K

10

6

10

5

10

4

10

3

10

2

αααα

q

g

ę

s

to

ś

ć

s

tr

u

m

ie

n

ia

c

ie

p

ła

W

/m

2

znaczny wpływ
promieniowani
a

6

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

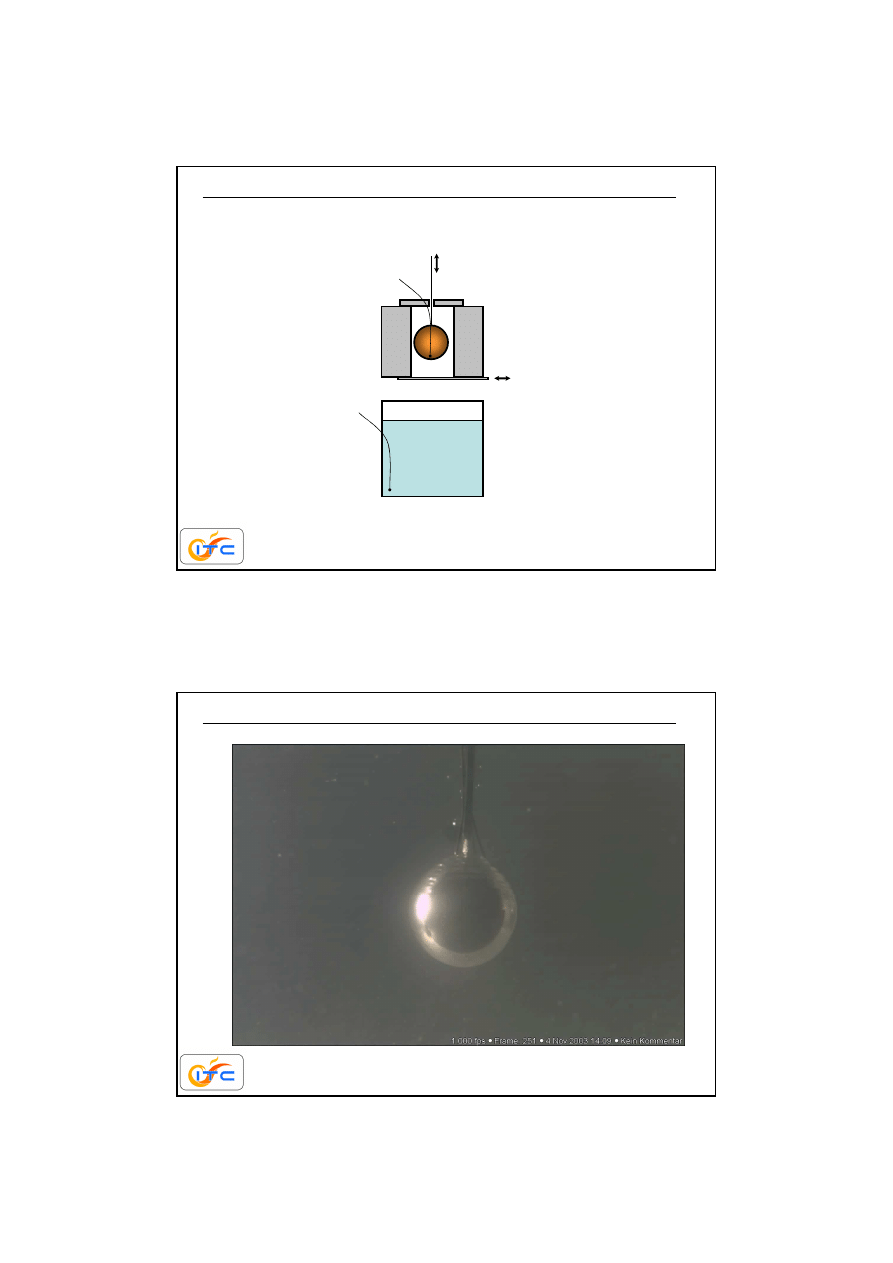
piec

okno

termopara

termopary

woda

eksperymentalne wyznaczanie współczynnika wynikania
przy wrzeniu. Wrzenie błonowe i pęcherzykowe

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

7

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

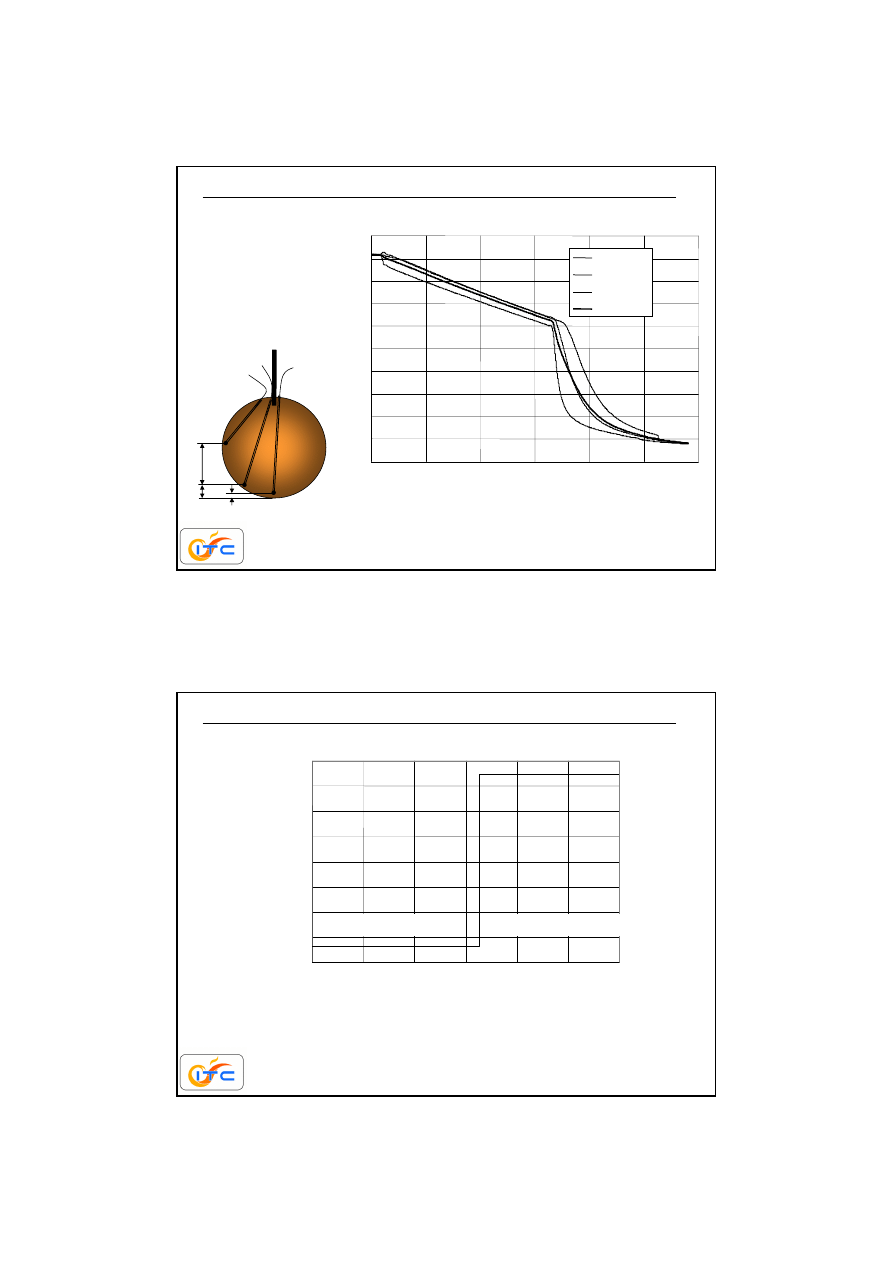
zmierzone przebiegi temperatury

1

5

m

m

2

m

m

0

100

200

300

400

500

600

700

800

900

1000

0

10

20

30

40

50

60

czas, s

te

m

p

e

ra

tu

ra

,

C

sensor #1

sensor #2

sensor #3

ś

rednia

1

0

m

m

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

0

500

1000

1500

2000

2500

3000

3500

4000

0

10

20

30

40

50

60

czas

s

w

s

p

ó

łc

z

y

n

n

ik

w

n

ik

a

n

ia

c

ie

p

ła

W

/(

m

2

-K

)

wyznaczony przebieg zmienno

ś

ci współczynnika wnikania

wrzenie błonowe

wrzenie p

ę

cherzykowe

8

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

'

"

Pr

Re

Nu

7

.

0

3

/

2

ρ

ρ

=

−

c

l

l

C

g

l

)

''

'

(

ρ

−

ρ

σ

=

charakterystyczny wymiar liniowy

c

pary

c

c

c

pary

l

c

l

r

Tl

l

w

l

η

ρ

ρ

∆

α

=

η

ρ

=

λ

α

=

Re

;

Nu

liczby bezwymiarowe

Rohsenow

C

liczba zale

ż

na od zestawu

ciecz-powierzchnia ogrzewana

ββββ

D

b

ś

rednica odrywaj

ą

cego si

ę

p

ę

cherzyka

(równowaga siły wyporu i przylegania do

ś

cianki)

g

D

b

)

''

'

(

02

.

0

ρ

−

ρ

σ

β

=

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

0.0058

Woda stal nierdzewna
pokryta teflonem

0.0080

Woda -stal nierdzewna
polerowana mechanicznie

0.0128

Woda -mied

ź

polerowana

0.0130

Woda- mied

ź

0.0130

Czterochlorek
w

ę

gla - mied

ź

0.0027

Alkohol etylowy-

chrom

0.0100

benzen -chrom

0.0060

Woda- mosi

ą

dz

przykładowe warto

ś

ci stałej

C

we wzorze Rohsenowa

Wzory wielko

ś

ciowe (tylko dla wody)

4

/

1

1

)]

"

'

(

[

"

ρ

−

ρ

σ

ρ

=

g

r

k

q

kr

krytyczny (maksymalny) strumie

ń

ciepła

K

m

W

p

T

K

m

W

p

q

2

5

.

0

33

.

2

2

15

.

0

7

.

0

/

;

122

.

0

/

;

53

.

0

∆

=

α

=

α

&

Kutateladze

k

1

=0.13-0.16

dla cieczy niemetalicznych

( )

2

/

1

4

/

1

2

'

"

1

"

)

"

'

(

"

24













ρ

ρ

−













ρ

ρ

−

ρ

σ

ρ

π

=

g

r

q

kr

Zuber

zmienne podstawia

ć

w

podstawowych jednostkach układu SI

W/m

2

N/m

2

9

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

Wrzenie p

ę

cherzykowe w rurkach, konwekcja wymuszona

2

1













α

α

+

=

α

α

k

w

k

c

x

d

d

mx

λ

α

=

η

π

=

Nu

4

Re

x

stopie

ń

sucho

ś

ci

d

ś

rednica wewn

ę

trzna rurki

4

.

0

87

.

0

28

.

0

Pr

Re

"

'

06

.

0

Nu

c

x













ρ

ρ

=

αααα

k

współczynnik wnikania obliczony dla konwekcji wymuszonej cieczy

αααα

ω

ωω

ω

współczynnik wnikania obliczony dla wrzenia swobodnego

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

DODATEK

laminarny spływ kondensatu

10

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

Rozkład pr

ę

dko

ś

ci wynika z równania p

ę

du

p

c

ρ

ρ

,

g

ę

sto

ść

cieczy i pary

0

d

)

(

d

0

)

0

(

=

δ

=

=

=

y

y

w

y

w

x

x

c

η

lepko

ść

cieczy

g

przyspieszenie ziemskie

0

)

(

d

d

2

2

=

ρ

−

ρ

+

η

p

c

x

c

g

y

w

warunki brzegowe

0

2

2

1

2

=

+

+

η

ρ

−

=

c

y

c

y

g

w

c

c

x

stałe całkowania z warunków brzegowych

pomija si

ę

g

ę

sto

ść

pary w porównaniu

z g

ę

sto

ś

ci

ą

cieczy

dwukrotne całkowanie

δ

η

ρ

=

=

c

c

g

c

c

1

2

;

0

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

)

(

3

d

)

(

)

(

1

0

2

x

g

y

y

w

x

w

y

c

c

x

x

∫

δ

=

δ

η

ρ

=

δ

=

)

(

)

(

)

(

x

w

x

S

x

m

x

c

ρ

δ

=

zawiera nieznan

ą

grubo

ść

warstwy kondensatu

δ

0

2

2

=

δ

η

ρ

+

η

ρ

−

=

y

g

y

g

w

c

c

x

ró

ż

niczkowy przyrost masy kondensatu ze wzrostem grubo

ś

ci warstwy

ś

rednia pr

ę

dko

ść

dla współrz

ę

dnej

x

strumie

ń

masy kondensatu kg/s

)

(

d

)

(

)]

(

3

d[

)]

(

)

(

d[

)

(

d

2

3

x

x

g

S

x

g

S

x

x

w

S

x

m

c

c

c

c

c

c

x

c

δ

δ

η

ρ

ρ

=

δ

η

ρ

ρ

=

δ

ρ

=

nieznan

ą

grubo

ść

warstwy kondensatu wyznacza si

ę

z bilansu masy i energii

S

szeroko

ść ś

cianki

wynikowy rozkład pr

ę

dko

ś

ci

11

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

x

d

r

entalpia kondensacji

Rozkład temperatury wynika z równania energii

na odcinku

dx

wykrapla si

ę

dm

kg/s kondensatu oddaj

ą

c ciepło kondensacji

r

.

Ciepło to jest odprowadzane przez

ś

ciank

ę

.

r

m

Q

w

d

d

=

przyrost entalpii strumienia skroplin jest mały w porównaniu
z ciepłem kondensacji

dI=0

I

I

d

+

I

y

Ciepło uwolnione na skutek kondensacji na powierzchni swobodnej, jest
przewodzone od tej powierzchni do

ś

cianki przez błon

ę

kondensatu

r

m

d

w

Q

d

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

x

T

T

x

S

x

y

T

S

Q

w

s

c

c

w

d

)

(

)

(

d

d

d

d

−

δ

λ

=

λ

=

)

(

d

)

(

d

)

(

)

(

2

x

x

g

rS

x

T

T

x

S

c

c

c

w

s

c

δ

δ

η

ρ

ρ

=

−

δ

λ

strumie

ń

przewodzonego ciepła

Zakłada si

ę

liniowy rozkład temperatury w błonie kondensatu

)

(

/

)

(

)

(

x

y

T

T

T

y

T

w

s

w

δ

−

+

=

st

ą

d pochodna temperatury

)

(

d

d

x

T

T

y

T

w

s

δ

−

=

pochodn

ą

temperatury zast

ą

piono

powy

ż

szym równaniem

równo

ść

strumieni ciepła przewodzonego i uwalnianego przez kondensacj

ę

r

m

Q

w

d

d

=

12

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

)

(

d

)

(

)

(

d

3

2

x

x

T

T

g

r

x

w

s

c

c

c

δ

δ

−

λ

η

ρ

=

po uproszczeniu

całkuj

ą

c powy

ż

sze otrzymuje si

ę

)

(

)

(

4

4

2

3

x

T

T

g

r

c

x

w

s

c

c

c

δ

−

λ

η

ρ

=

+

z warunku brzegowego

δ(

x=0)=0 c

3

=0

4

2

)

(

4

)

(

g

r

x

T

T

x

c

w

s

c

c

ρ

−

λ

η

=

δ

chcemy

ż

eby g

ę

sto

ść

strumienia ciepła wyra

ż

ała si

ę

przez prawo Newtona

)

(

)

(

w

s

w

T

T

x

q

−

α

=

z drugiej strony g

ę

sto

ść

strumienia ciepła wynika z przewodzenia

przez warstw

ę

kondensatu

)

(

)

(

d

d

)

(

w

s

c

c

w

T

T

x

y

T

x

q

−

δ

λ

=

λ

=

transport ciepła i masy

skraplanie i wrzenie

skraplanie i wrzenie

©Ryszard A. Białecki

porównuj

ą

c strumienie ciepła i podstawiaj

ą

c grubo

ść

warstwy kondensatu

4

3

2

)

(

4

)

(

x

T

T

g

r

x

w

s

c

c

c

−

η

λ

ρ

=

α

lokalna warto

ść

współczynnika wnikania

4

3

2

4

3

2

0

)

(

943

.

0

)

(

3

4

d

)

(

1

H

T

T

g

r

H

T

T

g

r

x

x

H

w

s

c

c

c

w

s

c

c

c

H

−

η

λ

ρ

=

−

η

λ

ρ

=

α

=

α

∫

wprowadzaj

ą

c liczby kryterialne

ś

rednia warto

ść

współczynnika wnikania na

ś

ciance pionowej o wysoko

ś

ci

H

c

c

c

w

s

c

c

c

c

c

c

T

T

c

r

gH

gH

H

λ

η

=

−

=

ν

=

η

ρ

=

λ

α

=

Pr

)

(

K

;

Ga

;

Nu

2

3

2

2

3

gdzie:

Ga

– liczba Galileusza,

K

–

liczba kondensacji,

c

c

–

ciepło wła

ś

ciwe cieczy

0.25

K)

Pr

(Ga

1.13

Nu

=

z eksperymentów wynika,

ż

e stał

ą

0.943

trzeba zwi

ę

kszy

ć

o ok.

20%

(falowanie powierzchni kondensatu). wła

ś

ciwo

ś

ci oblicza

ć

dla

ś

redniej temperatury filmu

T

f

=(T

s

+T

w

)/2