2801

OPTYKA GEOMETRYCZNA I FALOWA

Dział fizyki zajmujący się zagadnieniem rozchodzenia się światła w

różnych ośrodkach.

Promień świetlny

- kierunek prostopadły do powierzchni falowej, lub

- prosta, wzdłuż której rozchodzi się światło, lub

- tor rozchodzenia fotonów (wg. teorii korpuskularnej).

Źródła światła (to ciała emitujące światło):

a). same świecą gwiazdy, lampy...

b). planety, ściana, kartka "świecą" światłem odbitym - tylko gdy

są oświetlone, a same nie świecą.

Ciała mogą być:

- przeźroczyste lub

- nieprzeźroczyste.

- odbijające,

- przepuszczające światło,

- rozpraszające.

Na ogół promieniowanie padające na dane ciało jest:

częściowo odbijane, cz. absorbowane i cz. przepuszczane.

2802

PODSTAWOWE PRAWA OPTYKI GEOMETRYCZNEJ

I Pr. O.G.:

Światło rozchodzi się po liniach prostych

≡ płaskie czoło fali

II Pr. O.G. (PRAWO FERMATA, 1650 r. Pierre Fermat):

Światło biegnąc od p. A do B wybiera zawsze taką drogę aby

czas jej przebycia był ekstremalny (jak najkrótszy lub jak naj-

dłuższy). Tzn. droga optyczna musi być extremalna L

o

= l

g

· n

(L

o

- dr optyczna, l

g

- dr geometryczna, n - wsp. załamania).

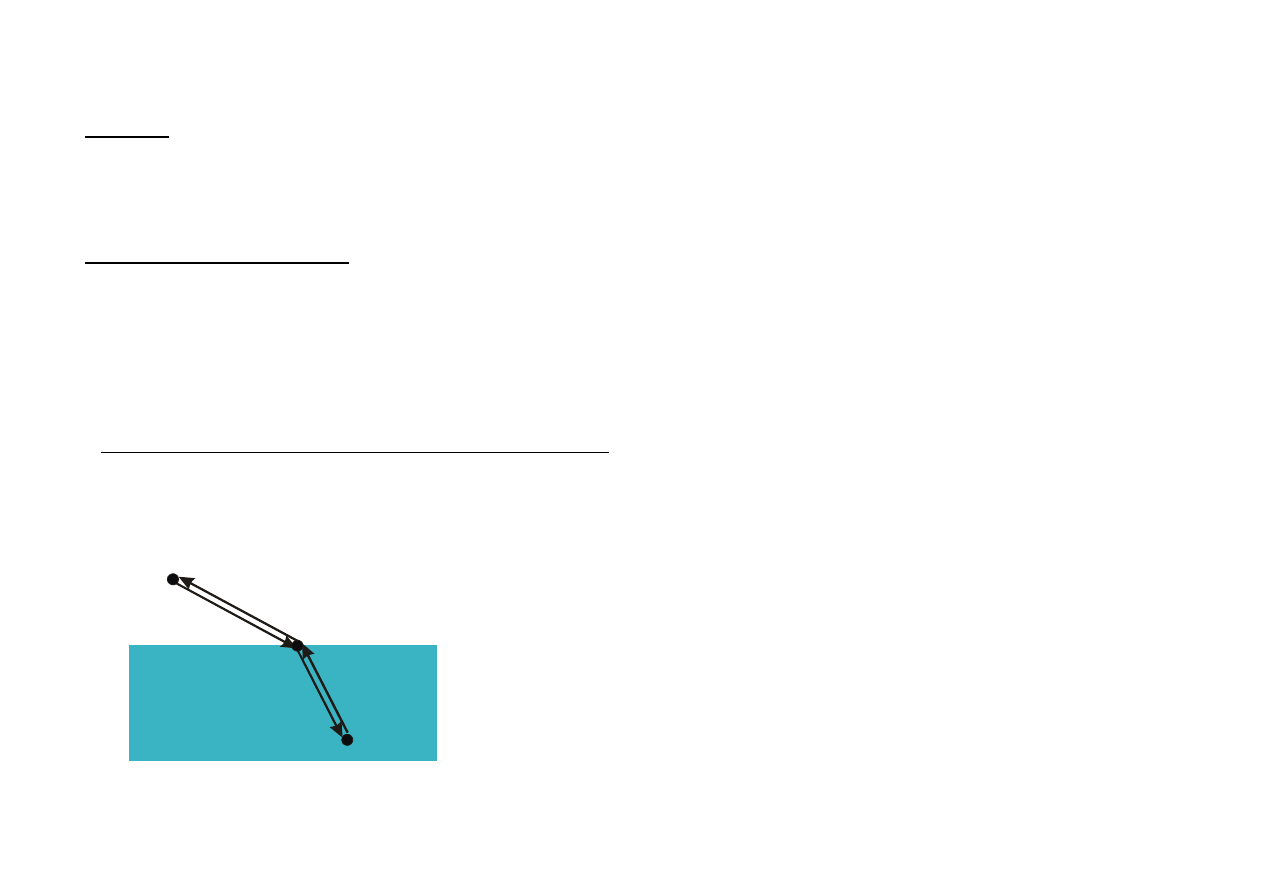
III Pr. O.G. ZASADA ODWRACALNOŚCI BIEGU PROMIENIA:

Jeżeli dowolny promień świetlny wysłany z A do C przebędzie

drogę AB w pierwszym ośrodku i BC w drugim, to inny wysła-

ny z C do A przebędzie dokładnie tę samą drogę.

I

II

A

B

C

2803

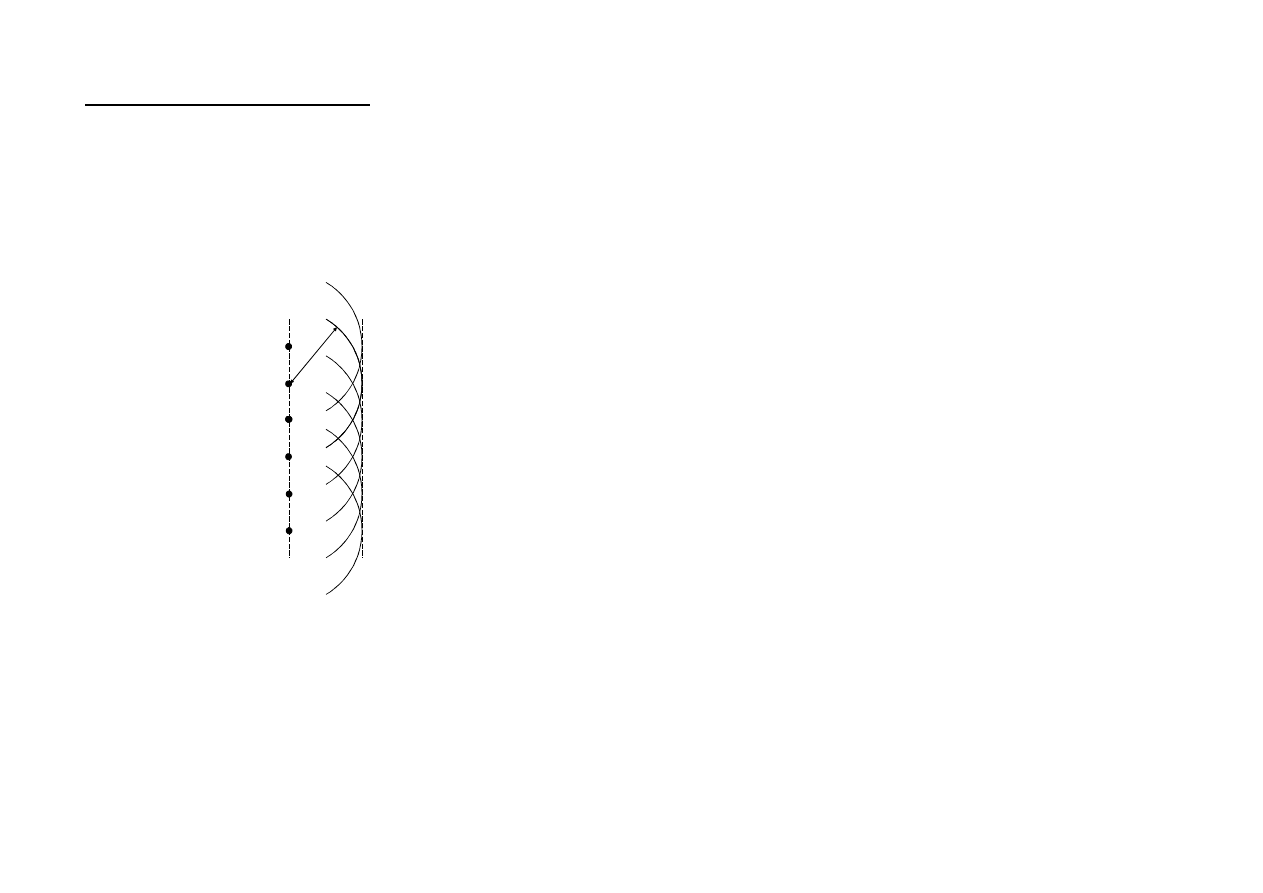
IV Pr. O.G. - ZASADA HUYGENSA

(oparta na konstrukcji geometrycznej):

wszystkie punkty ośrodka po dojściu do nich zaburzenia stają

się źródłami nowych fal kulistych, lub inaczej:

wszystkie punkty czoła fali można uważać za źródła nowych

fal kulistych.

ct

czoło fali
w chwili
t = 0

nowe położenie
czoła fali

Christian Huyghens (1678 r.) założył, że światło jest falą ( a nie

strumieniem cząstek).

Teoria nie wspomina o elektromagnetycznym charakterze świa-

tła ani nie wyjaśnia, że światło jest falą poprzeczną.

Pozwala przewidzieć gdzie znajdzie się czoło fali w dowolnej

chwili w przyszłości, jeżeli znamy jej obecne położenie.

2804

małe
źródło

duży
przedmiot

S

E

cień

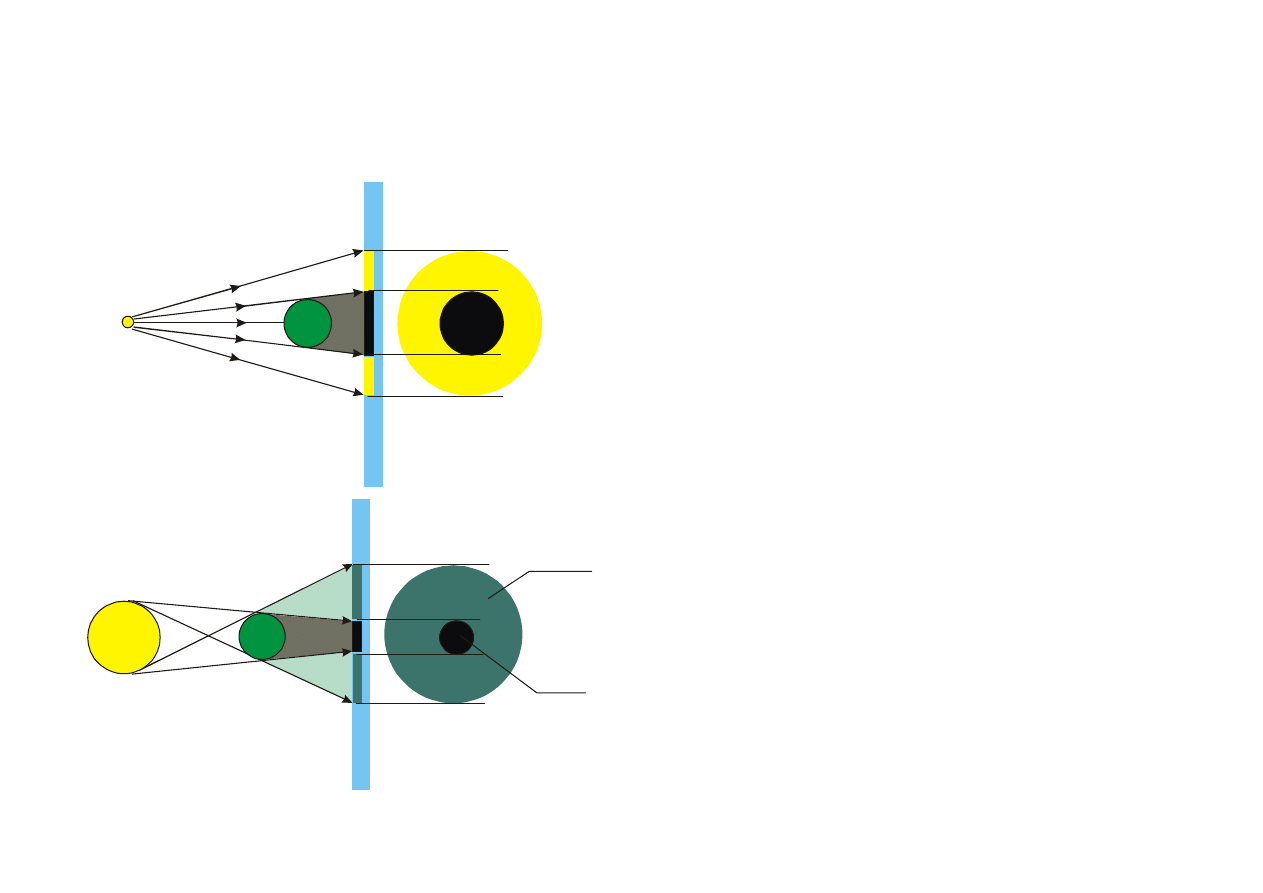
Przykład ilustrujący I Pr. Opt. Geom. (liniowe rozchodz się pro-

mieni)

Powstawanie cienia

Powstawanie półcienia

duże
źródło

mały
przedmiot

S

E

cień

półcień

P

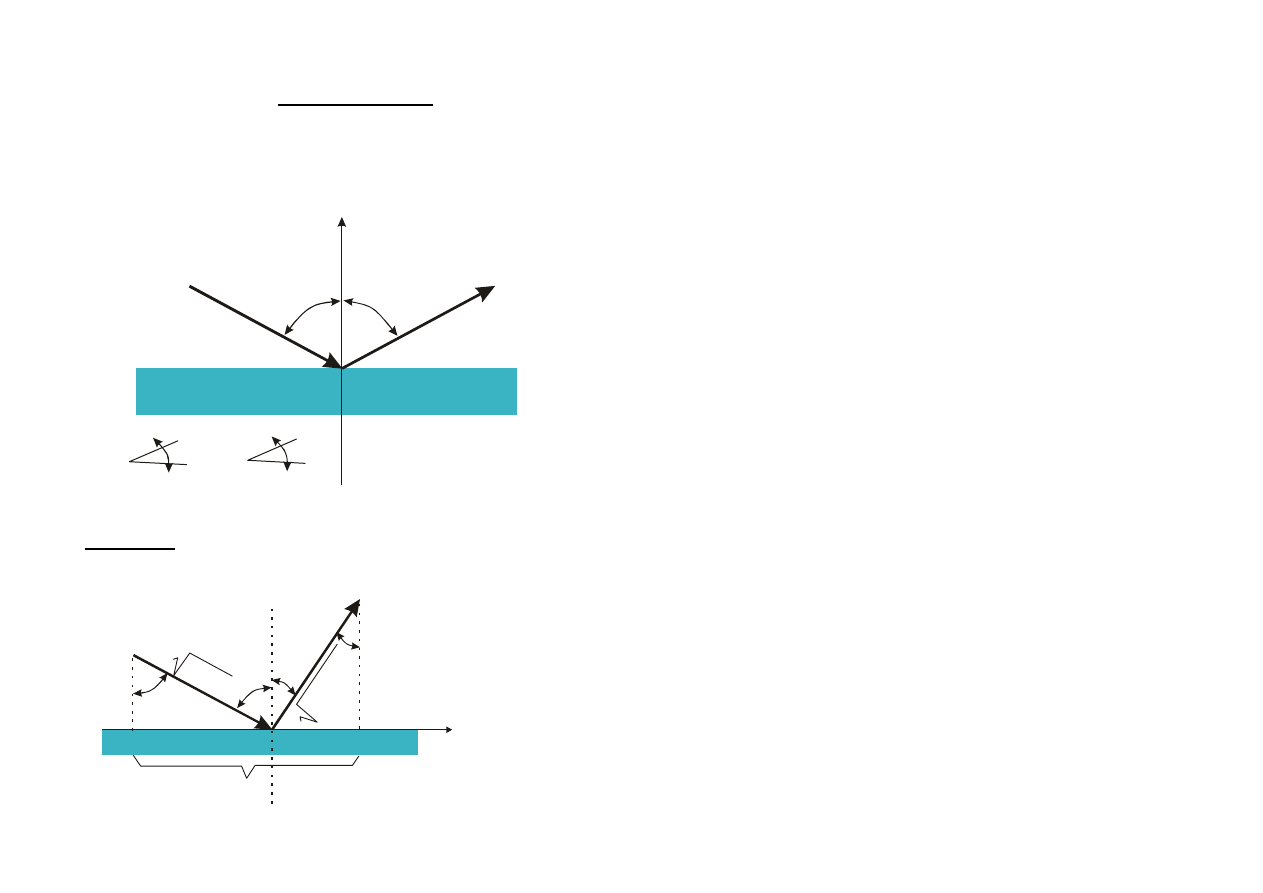
2805

PRAWO ODBICIA:

kąt padania jest równy kątowi odbicia, a promień padający,

odbity i normalna do powierzchni leżą w tej samej płaszczyź-

nie.

Przykład 1

Wyprowadzenie prawa odbicia z zasady Fermata:

szukamy położenia

punktu P takiego,

aby czas przebycia

drogi l był extre-

malny.

α

α

β

β

a

x

d-x

b

0

X

A

P

B

d

a +

x

2

2

(d

-x

)

+

b

2

2

n

pp

po

α

α =

β

β

2806

0

dx

dl =

,

(

)

2

2

2

2

x

d

b

x

a

l

−

+

+

+

=

,

(

)

(

)

[

]

(

) ( )

0

1

x

d

2

x

d

b

2

1

x

2

x

a

2

1

dx

dl

2

/

1

2

2

2

/

1

2

2

=

−

⋅

−

⋅

−

+

+

⋅

+

=

−

−

(

)

(

)

(

)

[

]

2

/

1

2

2

2

/

1

2

2

x

d

b

x

d

x

a

x

−

−

−

+

−

=

+

⋅

,

(

)

2

2

2

2

x

d

b

x

d

x

a

x

−

+

−

=

+

α

= sin

L

,

β

= sin

P

zatem:

β

=

α sin

sin

czyli

β

=

α

ROZPRASZANIE – odbicie we wszystkich kierunkach

Ciała porowate (ściany, drewno, papier, tzn takie których nierówno-

ści pow. są duże w porównaniu z λ) odbijają światło we wszystkich

kierunkach ≡ rozpraszają.

2807

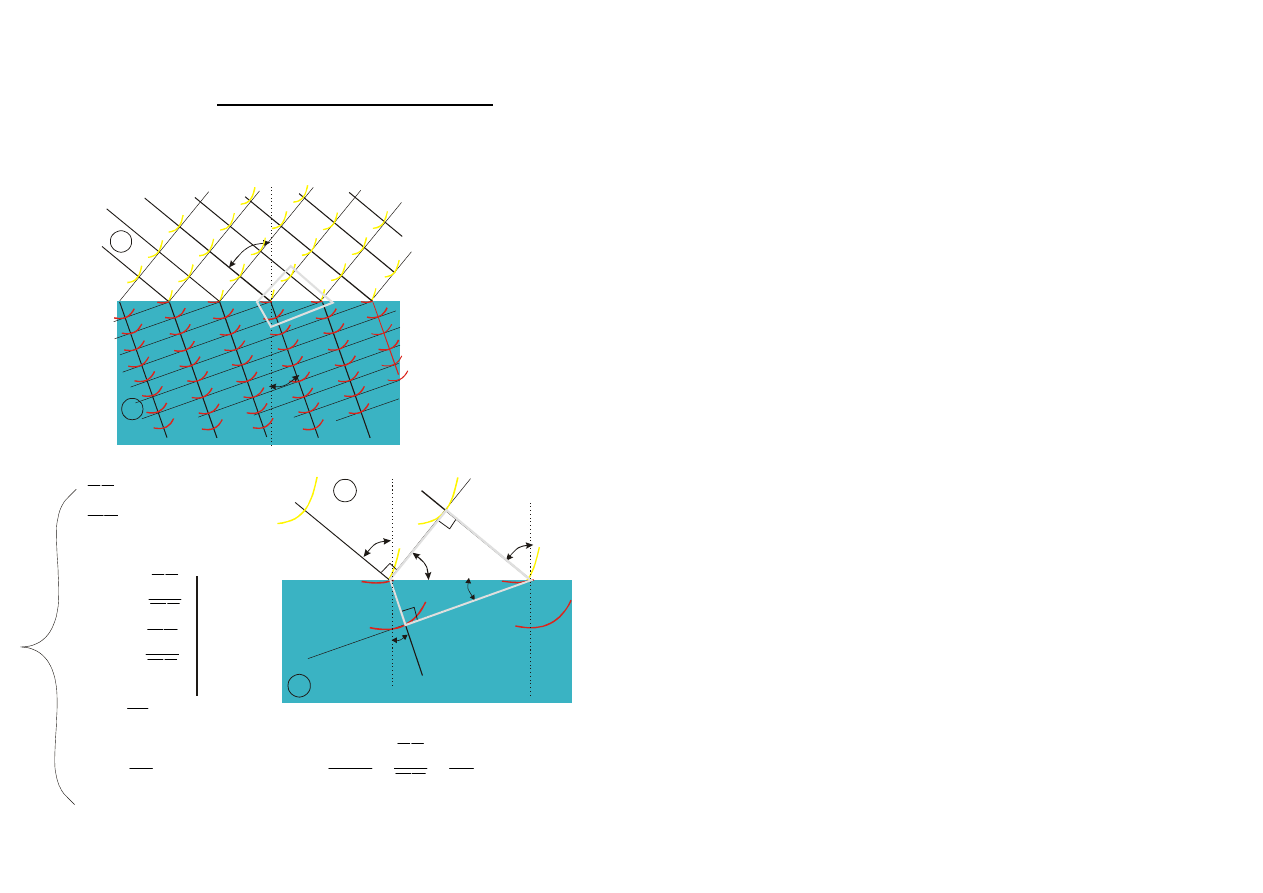
PRAWO ZAŁAMANIA (SNELLA)

Wyprowadźmy prawo załamania z zasady Huygensa:
Załóżmy, że promień o długości fali

λ

1

przechodzi z ośrodka 1 o

prędkości rozchodzenia światła v

1

, do ośrodka 2:

λ

2

i v

2

.

Odcinek OS wspólny

1

1

t

v

S

P

∆

⋅

=

,

2

2

t

v

T

O

∆

⋅

=

,

2

1

t

t

∆

=

∆

,

S

O

S

P

sin

=

α

,

S

O

T

O

sin =

β

,

1

1

v

c

n =

,

2

2

v

c

n =

, zatem

=

=

=

β

α

2

1

v

v

T

O

S

P

sin

sin

= Const

α

1

2

λ

λ

v

v

1

1

2

β

2

:

α

α

α

1

λ

λ

v

1

1

β

β

2

v

2

2

λ

T

S

P

O

n

n

1

2

2808

n

α

β

ρ

ρ

ν

ν

(pow.)

(szkło)

1

2

ośr.
opt. rzadki

gęsty

n

n

v

v

1

1

1

1

2

2

2

2

>

>

<

=

Const

v

v

sin

sin

2

1

=

=

β

α

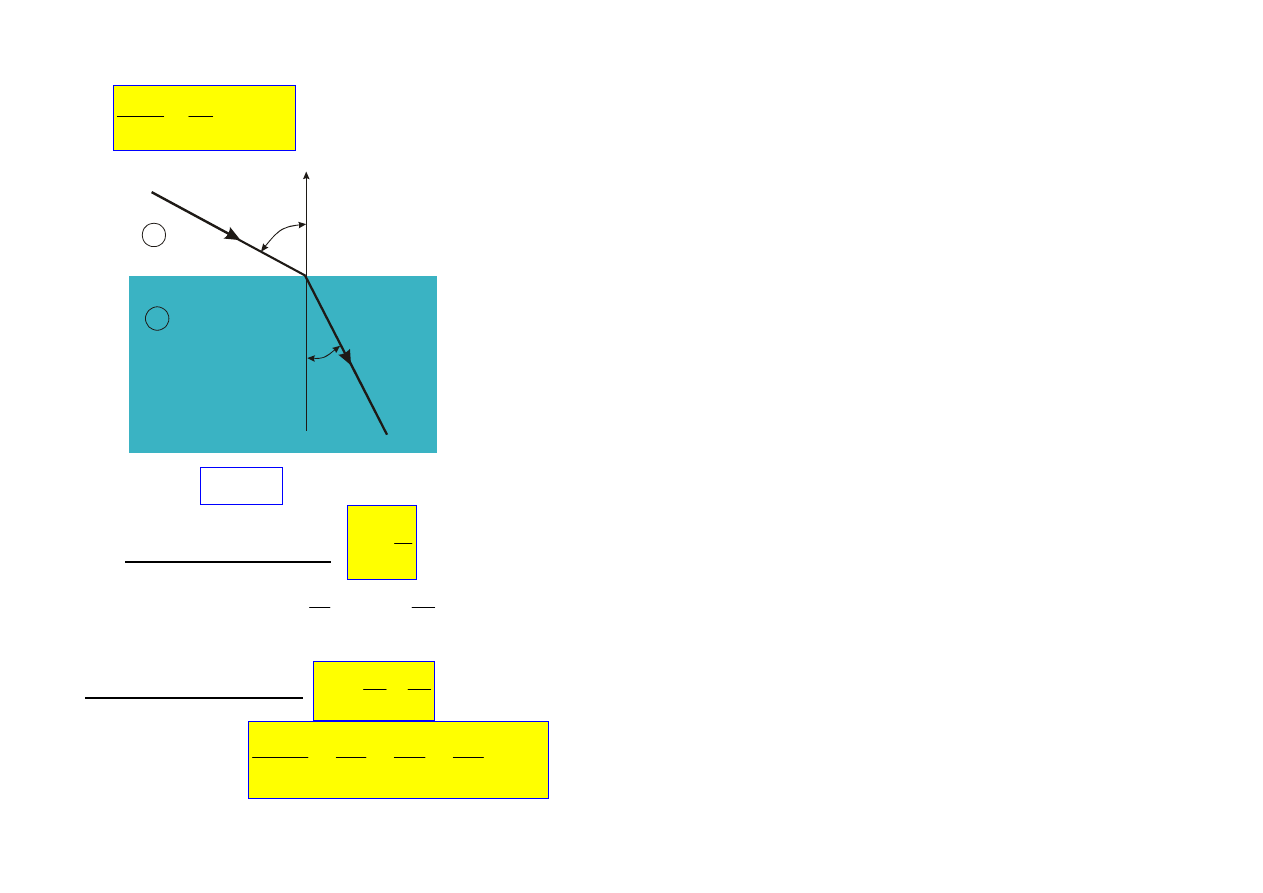
Prawo załamania

(SNELLA 1591 - 1626)

Zapamiętać:

2

1

ν

=

ν

- zawsze!!!

oraz bezwzgl wsp. załamania:

v

c

n =

,

1

1

v

c

n =

i

2

2

v

c

n =

,

podstawmy do ww wz Snella

ν

⋅

λ

=

c

,

względny wsp. załamania:

2

1

1

2

21

v

v

n

n

n

=

=

.

Pełne pr. Snella:

21

1

2

2

1

2

1

n

n

n

v

v

sin

sin

=

=

λ

λ

=

=

β

α

.

2809

CAŁKOWITE WEWNĘTRZNE ODBICIE

ρ

ρ

(pow.)

(szkło)

1

2

ośr.
opt. rzadki

gęsty

n

n

1

1

2

2

θ

gr

21

1

2

O

GR

n

n

n

90

sin

sin

=

=

θ

,

21

1

2

GR

n

n

n

sin

=

=

θ

,

Dla granicy szkło sodowe/powietrze

o

gr

8

,

41

=

θ

.

2810

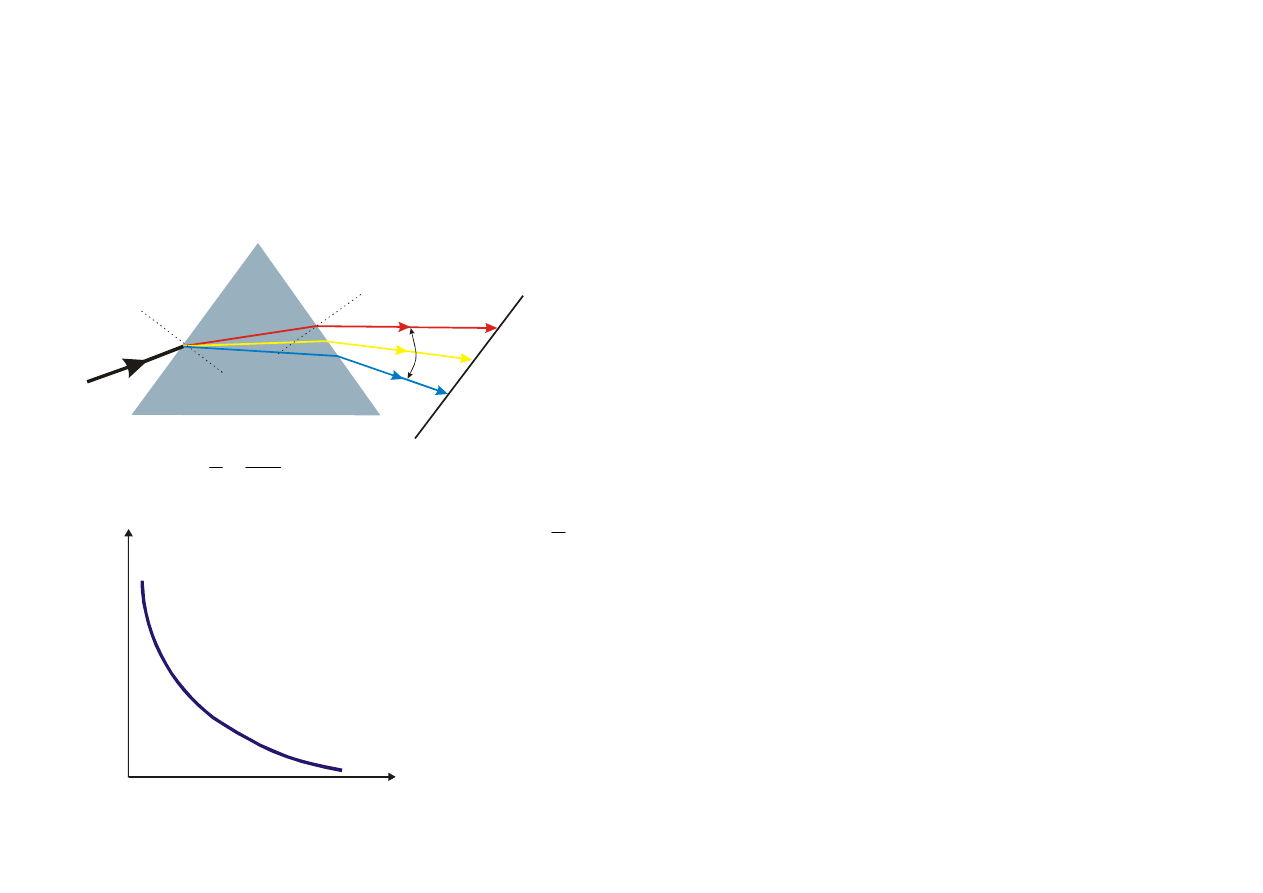
DYSPERSJA ŚWIATŁA

(rozszczepienie światła)

Zjawisko odkryte przez I. Newtona w 1666 r. –

– odkrył, że światło białe nie jest jednorodne (monochromatyczne).

Ponieważ

ν

⋅

λ

=

=

c

v

c

n

więc

( )

λ

= f

v

i

( )

λ

= f

n

,

zatem

λ

1

~

n

.

Zwykle:

Tę własność wykorzystuje

się w spektrometrach

św.

białe

czerwone 700nm

żółte

zielone

niebieskie

fiolet 360nm

miara
dyspersji

n

λ

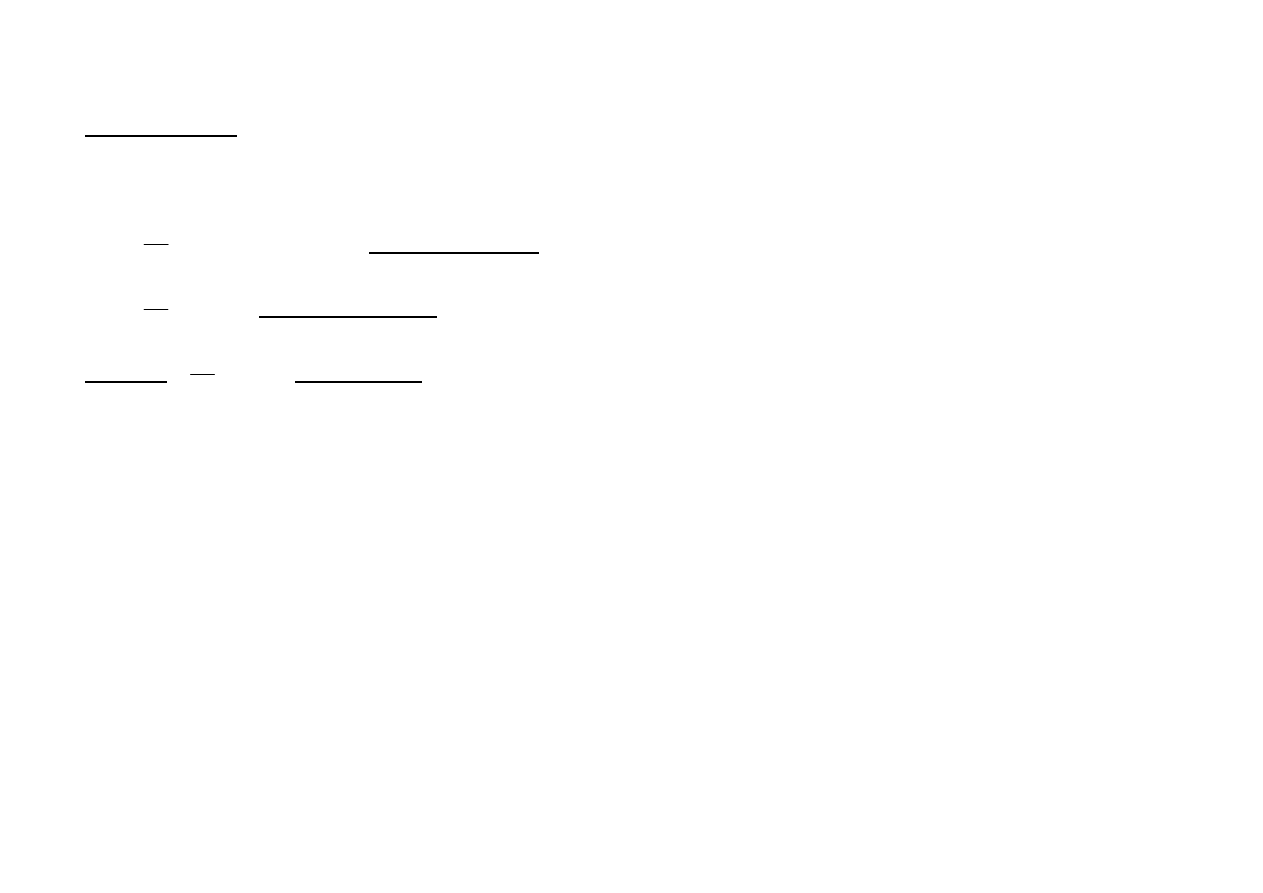
2811

Dyspersja światła to zależność prędkości fazowej v światła od

długości fali:

( )

λ

= f

v

,

jeżeli

0

d

dv >

λ

, to dla

λ

v

≡ dyspersja normalna

jeżeli

0

d

dv <

λ

, to ≡ dyspersja anomalna.

W próżni:

0

d

dv =

λ

≡ brak dyspersji.

2812

PRZYRZĄDY OPTYCZNE

ZWIERCIADŁA

Zwierciadło płaskie: we własnym zakresie;

Jaka powinna być wysokość zwierciadła płaskiego (lustra) aby

mężczyzna o wzroście 2 m obejrzał się w nim cały?

Zwierciadło kuliste

P

p

O

o

F f

r

f

1

o

1

p

1

=

+

, gdzie

r

2

1

f =

.

2813

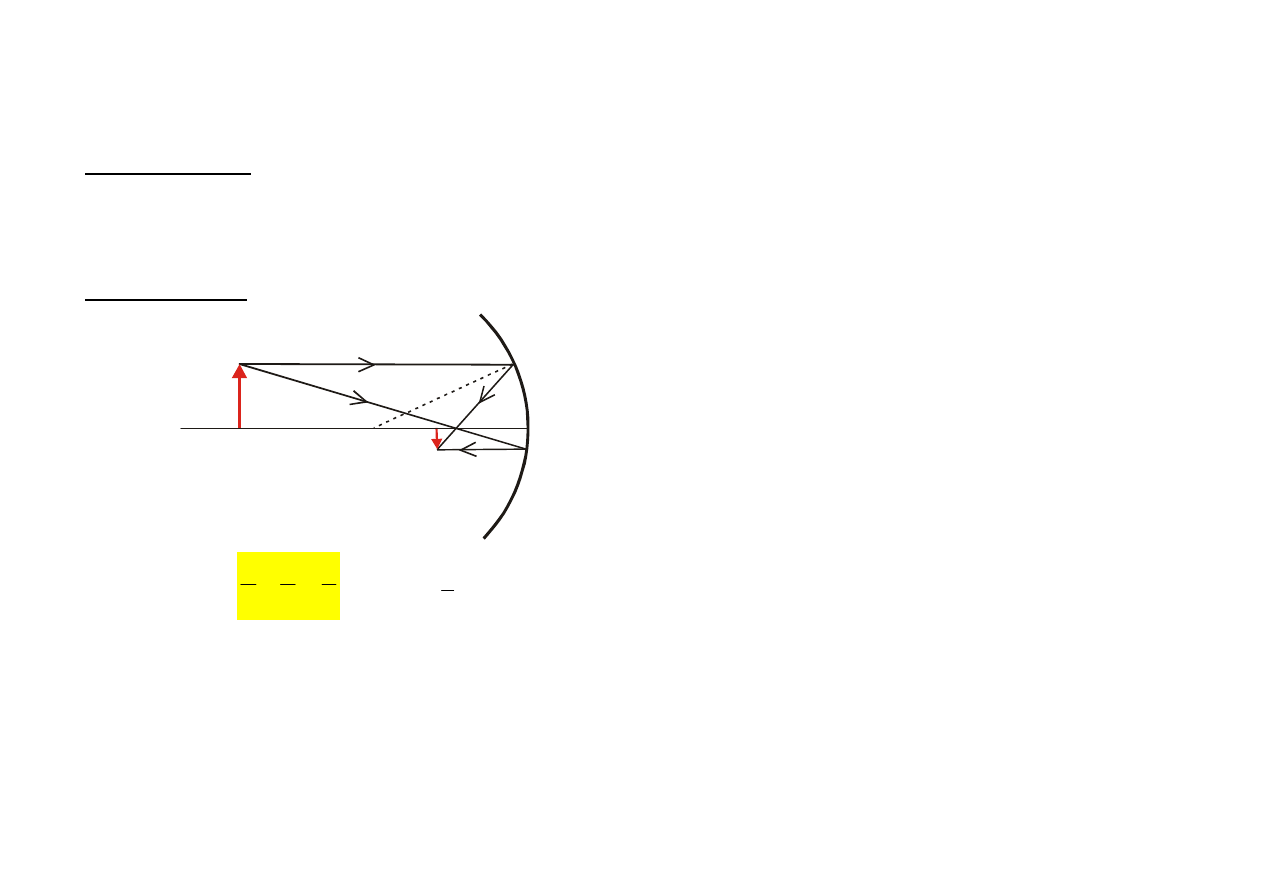
SOCZEWKI

Skupiająca
Def.: ognisko to punkt geometryczny, w którym skupiają się
wszystkie promienie padające, równoległe do osi optycznej so-
czewki.
Ogniskowa f to odległość ogniska od soczewki.













+

−

=

2

1

r

1

r

1

)

1

n

(

f

1

,

gdzie n - wsp. załamania soczewki, r

1

, r

2

- promienie krzywizn oby-

dwu stron soczewki.

r

r

1

2

oś optyczna

Notacja:

-

-

-

-

-

-

soczewka
skupiająca

soczewka
rozpraszająca

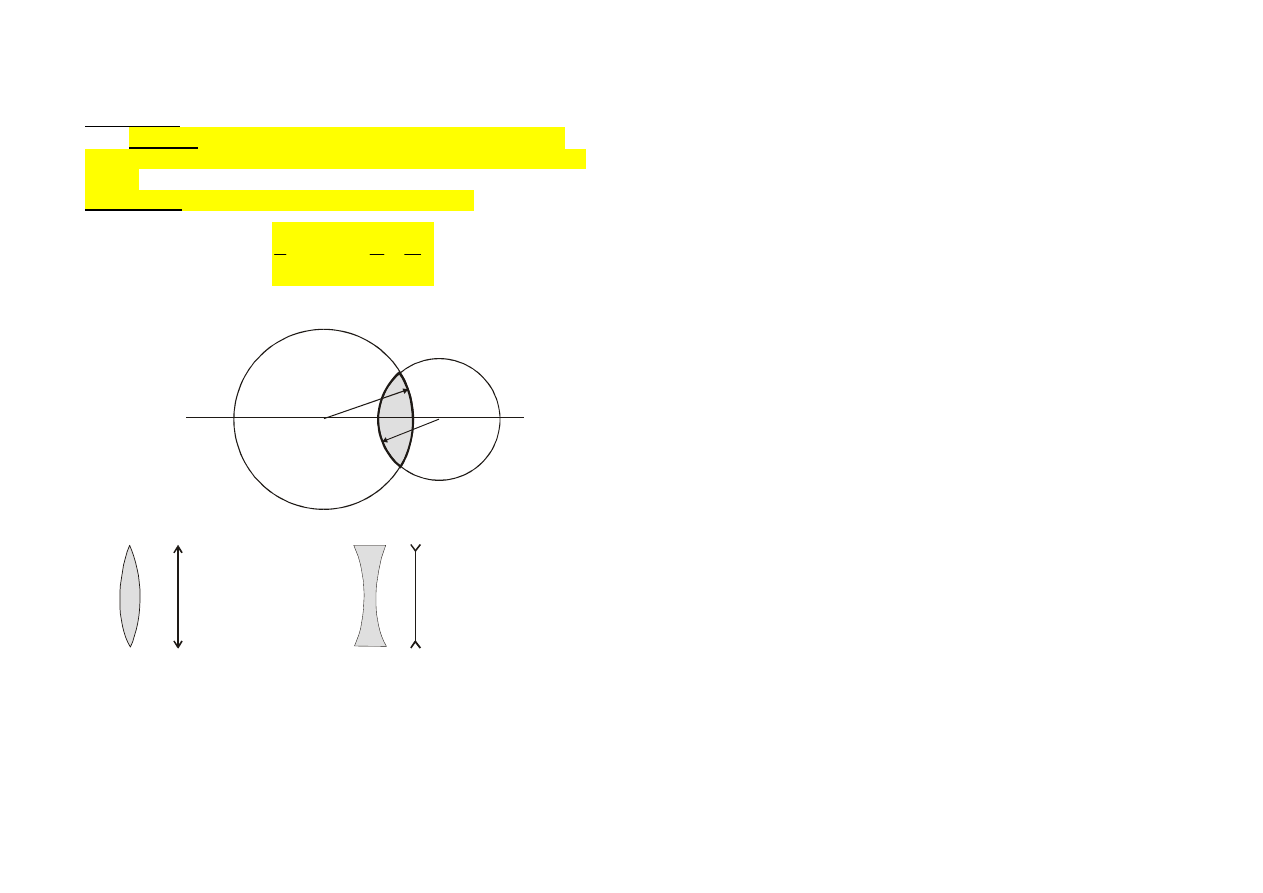
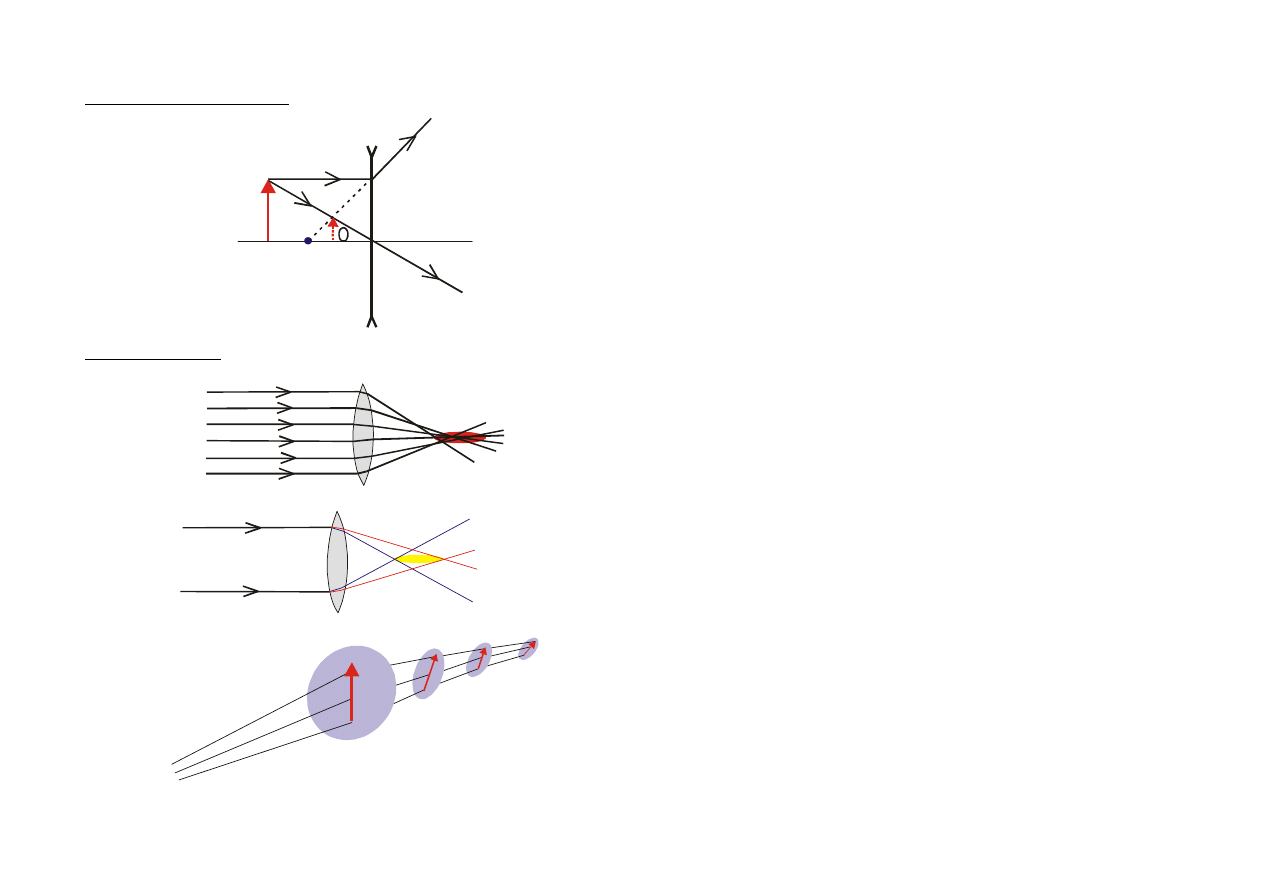
KONSTRUKCJA OBRAZU - wykorzystujemy dowolne dwa z
trzech promieni wychodzących z przedmiotu, a następnie:
1). przechodzących przez ognisko, a następnie załamanych II ro

osi optycznej,

2). przechodzących przez środek soczewki bez załamania,
3). padający równolegle do osi optycznej, załamany i przechodzący

przez ognisko.

2814

Soczewka skupiająca:

P

p

O

o

F

F

2F

2F

f

f

f

1

o

1

p

1

=

+

, oraz powiększenie:

p

o

P

O

m

=

=

Wzór soczewkowy jest słuszny przy założeniu:

1. soczewki są b. cienkie,
2. krzywizny soczewek są kuliste,
3. kąt padania promieni w stosunku do osi są małe,
4. światło jest monochromatyczne.

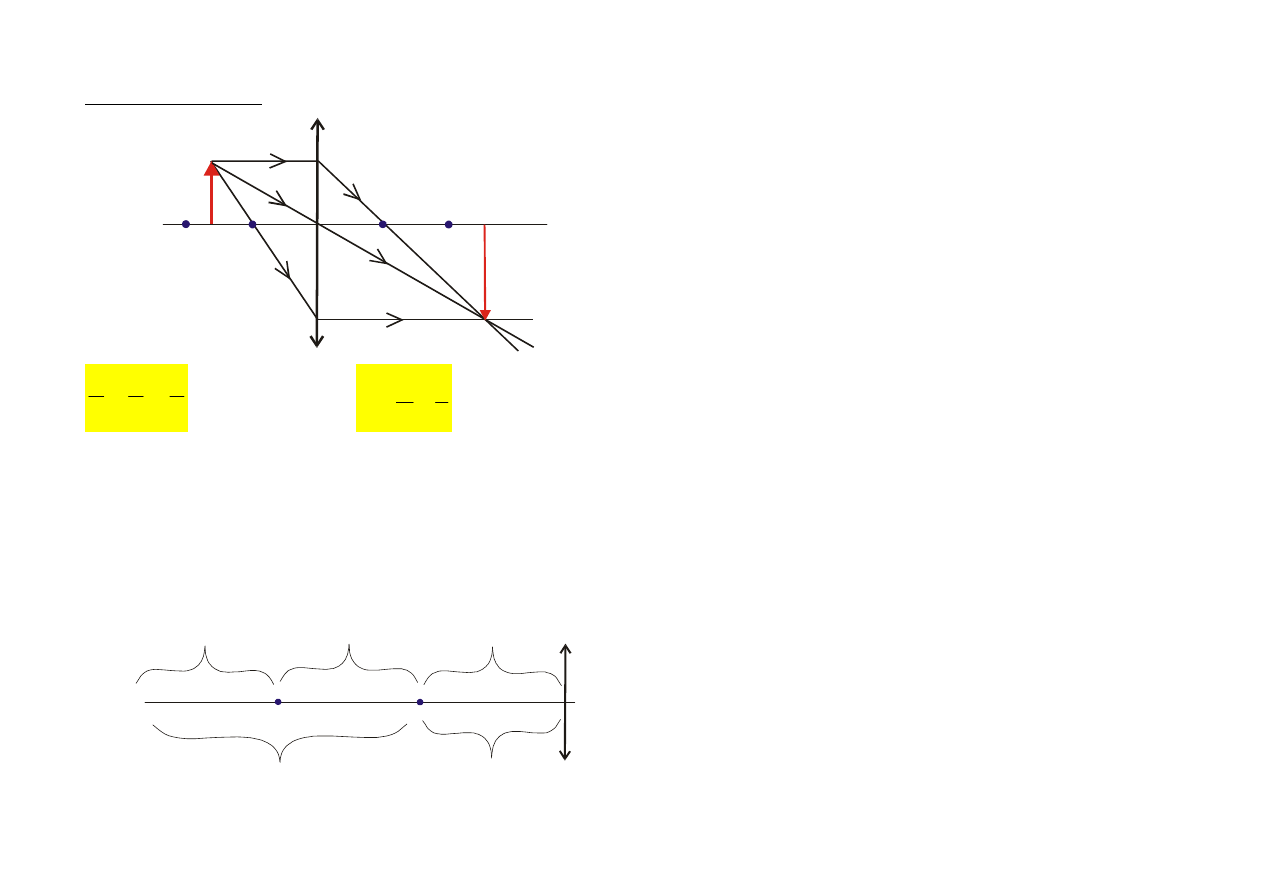
Analiza warunków powstawania obrazów:
np. przypadek szczególny: dla p=o=2f, p+o=4f i m=1

F

2F

m

=

1

m

<

1

m

>

1

pomniejszony powiększony

pozorny

b

ra

k

odwrócony

prosty

powiększony

2815

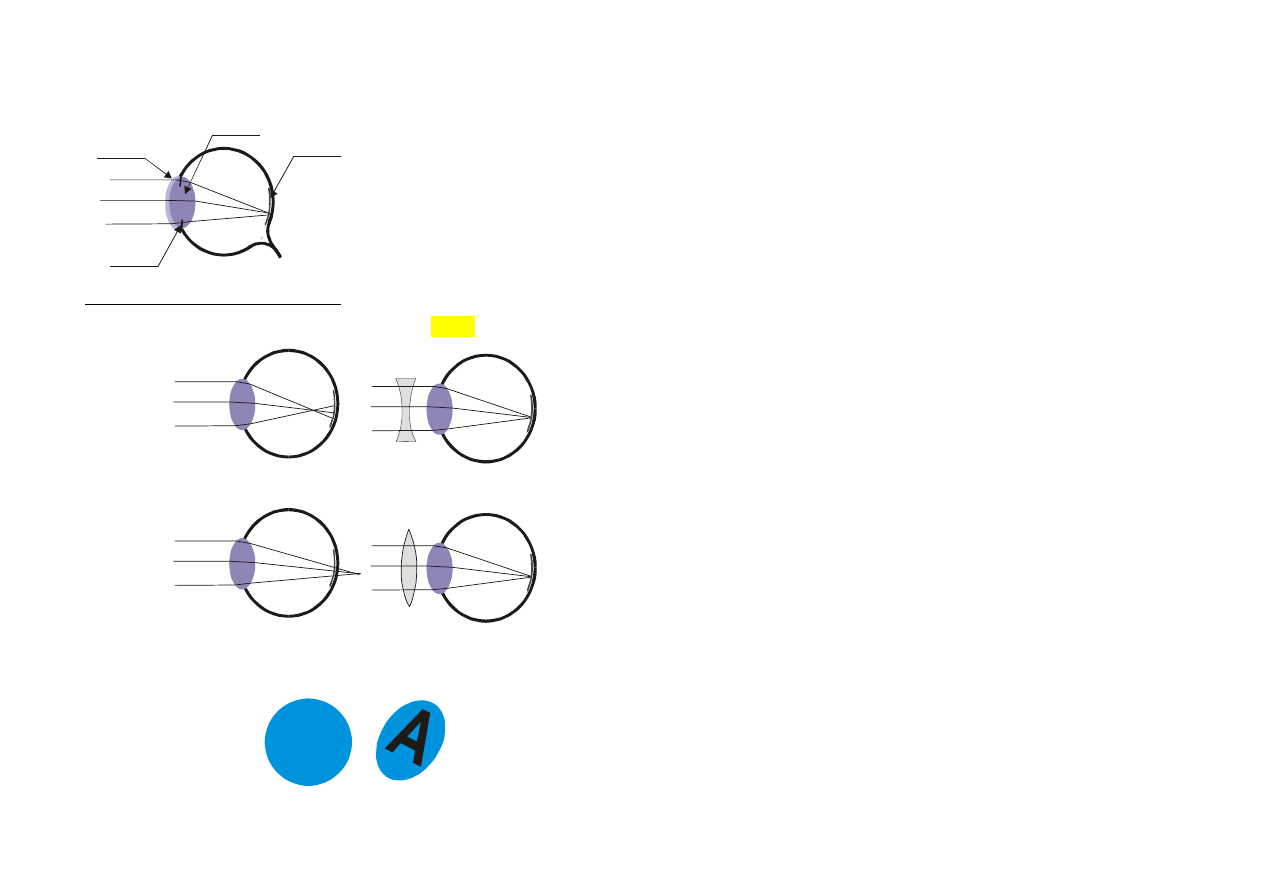
Soczewka rozpraszająca:

P

F

obraz
pozorny

Wady soczewek:
a) aberracja sferyczna – brak ogniska,

b) aberracja chromatyczna (dla światła niemonochromat.),

św. białe

fiolet

czerwień

c) astygmatyzm (błąd odwzorowania kątowego).

2816

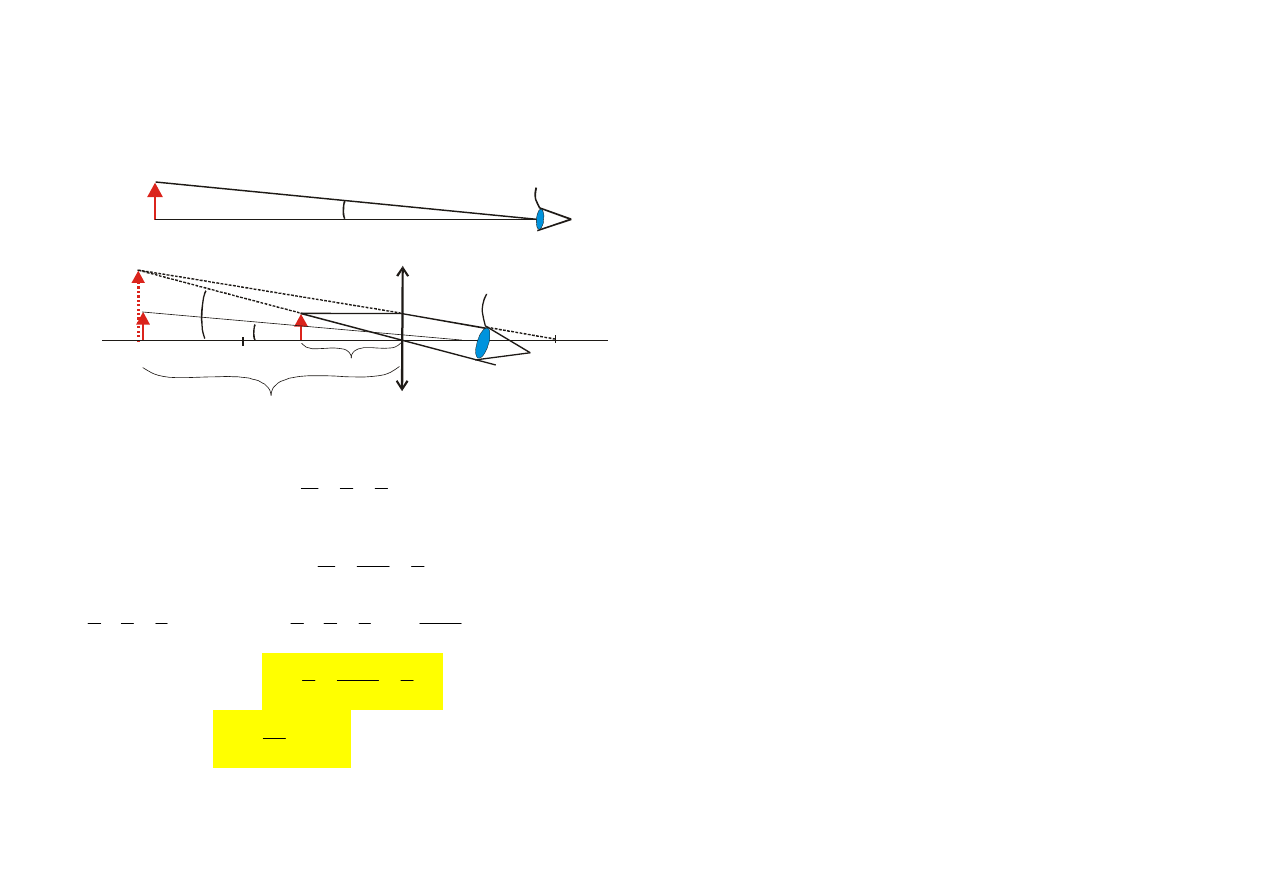
OKO – układ optyczny

rogówka

soczewka

źrenica

siatkówka

neurony

retinal

Wady wzroku (ukł. optycznego):

a) krótkowzroczność (zdolność skupiająca D=1/f [Dioptria=1/m]

z korektą

b) nadwzroczność ("plusy")

z korektą

c) astygmatyzm – brak kulistości soczewki oka, błąd odwzorowania

kątowego

A

2817

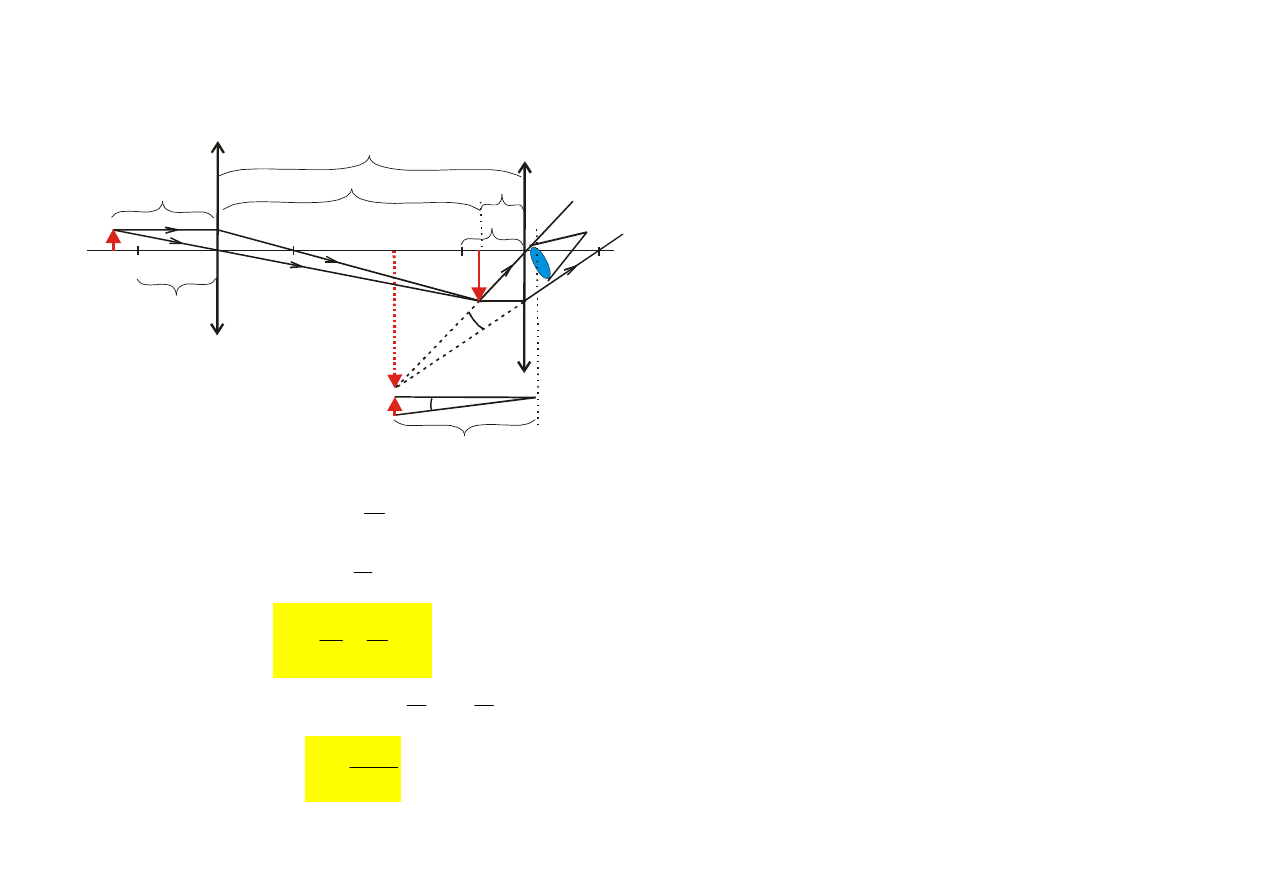
LUPA

– soczewka skupiająca o małej ogniskowej f służąca do odczyty-

wania drobnego druku lub oglądania małych przedmiotów.

P

α

odl. dobrego widzenia d ~25 cm

za mały kąt

P

α

φ

φ > α

O

F

F

p

o~d

~

Lupa zwiększa kąt widzenia małych przedmiotów do wielkości roz-
różnialnych przez oko.

Powiększenie:

p

d

p

o

P

O

m

≈

=

=

,

Powiększenie kątowe:

p

d

tg

tg

P

O

m

=

α

φ

=

=

,

f

1

o

1

p

1

=

+

, a dla

d

o ≈

f

1

d

1

p

1

=

+

,

f

d

fd

p

−

=

,

1

f

d

f

f

d

p

d

m

−

=

−

=

=

.

Dla d=+25 cm

cm

1

f

25

m













−

=

.

Np. dla f=5 cm, m=4 {oznacz. na lupie x4}.

2818

MIKROSKOP

– to złożenie 2-ch soczewek.

P

α

φ

F

F

F

F

1

1

1

1

2

2

1

1

1

2

2

2

2

O

O

f

f

p

o

p

l - dł. tubusa

o ~d

p

rz

e

d

m

io

t

O - obraz pośredni

2

1

m

m

m

⋅

=

,

1

1

1

p

o

m =

,

1

f

d

m

2

2

−

=

,













−

⋅

=

1

f

d

p

o

m

2

1

1

.

Załóżmy

l

o

1

≈

,

1

1

f

p ≈

,

2

f

d >>

, zatem

2

2

f

d

1

f

d

≈

−

:

2

1

f

f

d

l

m

⋅

⋅

=

.