
DZIAŁANIA NA MACIERZACH
Macierz - układ liczb rzeczywistych lub zespolonych, zapisanych w postaci dwuwymiarowej tablicy
Zapis: A
lub [a
ij
],
i = 1,2,...,m, j=1,2,...,n gdzie: a
ij
- wyrazy macierzy
i - pierwszy indeks - nr wiersza
j - drugi indeks - nr kolumny
Para liczb m x n nazywa się wymiarem macierzy
Macierz
Wektor
=
mn
m
n
a
a
a
a
a
a
A
L
L
M
L
L
M
M
L
L
L
1
21
1
12
11
=
m
X
X
X
M
M
1
Macierze jednakowego typu - jednakowa liczba kolumn i wierszy.
ZAPIS INDEKSOWY
[a
i
] - wektor
[a
ij
] - macierz - tablica, w której każda kolumna jest wektorem
[a
ijk
] - sześcian, w który każda warstwa jest macierzą
[a
ijkl
]- wektor, w którym każdy element jest sześcianem
a
4213
-
wyraz w 4-tym wierszu,
2-giej kolumnie,
1-szej warstwie,
3-cim sześcianie.
a
243
- wyraz w 2-gim wierszu,
4-tej kolumnie,
3-ciej warstwie
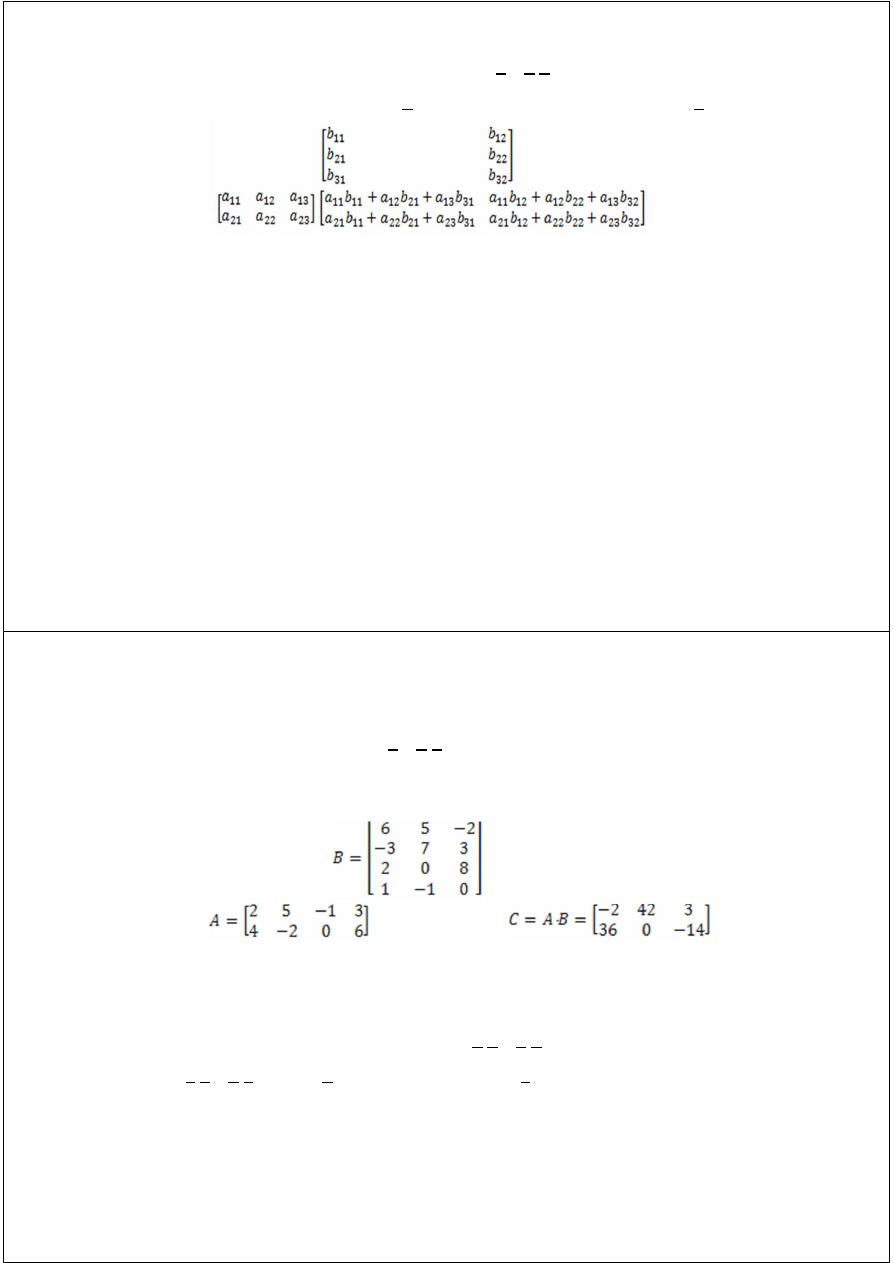
MNOŻENIE MACIERZY
C = A
⋅
B
c
ij
= a
ik
⋅
b
kj
Uwaga!!! Długość wiersza macierzy A równa wysokości kolumny macierzy B
Wyraz macierzy c
ij
= a
ik
⋅
b
kj
, k=1,2,3
i, j - indeksy żywe (określają pozycję wyrazu w macierzy wynikowej)
k - indeks niemy (powtórzony 2 razy określa sumę po wszystkich możliwych wyrazach)
c
ik
= a
ik
b
kj
- jest elementem macierzy 2-go rzędu, indeks niemy k powtórzony 3 razy
c
ij
= a
ik
b
kj
= a
i1
b
1j
+ a
i2
b
2j
+ a
i3
b
3j
, k=1,2,3
Przykład: a
ijkj
i, j, k = 1,2,3 - wyraz macierzy 3x3, której każdy wyraz jest sumą
a
ik
= a
ijkj
= a
i1k1
+ a
i2k2
+ a
i3k3
a
ikk
i, k = 1,2,3 - wyraz wektora 3x1, którego każdy wyraz jest sumą
a
i
= a
ikk
= a
i11
+ a
i22
+ a
i33
ZADANIE 1. Wykonaj mnożenie C = A
⋅
B
Mnożenie macierzy nie jest przemienne
A
⋅
B
≠
B
⋅
A
ale E
⋅
A = A
⋅
E , gdzie A - macierz kwadratowa, E - macierz jednostkowa

Macierz osobliwa det A = 0
Macierz transponowana A
T
, [a
ik
]
T
= [a
ki
]
Macierz symetryczna A
A = A
T
, [a
ik
] = [a
ki
]
Macierz antysymetryczna (skośnie symetryczna) A , A =- A
T
[a
ik
] = -[a
ki
]
MACIERZE KWADRATOWE
– liczba kolumn jest równa liczbie wierszy
Macierz
Macierz
diagonalna
jednostkowa
=
nn
a
a
a
A
0
0
0
0
0
0
0
0
0
0
0
0
21
11
O
E
A
A
E
E
⋅
=
⋅
=
,
1
0
0
0
0
0
0
0
0
1
0
0
0
0
1
O
WYZNACZNIK MACIERZY KWADRATOWEJ
A
jest pewną liczbą przypisaną tej macierzy.
Oznaczenie wyznacznika symbolem
Wyznacznikiem n-tego stopnia nazywamy liczbę, która układowi n
2
liczb a
ik
przypisuje wartość
lub det A
lub det A
Stopień wyznacznika jest określony przez wymiar macierzy kwadratowej
- wyznacznik 2-go stopnia - wyznacznik macierzy 2x2
- wyznacznik 3-go stopnia - wyznacznik macierzy 3x3

Wyznacznik drugiego stopnia oblicza się według wzoru:
Wyznacznik trzeciego stopnia oblicza sie według tzw.
reguły Sarrusa
:
ZADANIE 2.
Oblicz wyznacznik macierzy
700
48
72
805
96
84
45
9
6
3
8
5
2
7
4
1
=
−
−
−
+
+
=
=
A
0
48
72
105
96
84
45
9
8
7
6
5
4
3
2
1
=
−
−
−
+
+
=
=
A
Wyznacznik n-tego stopnia oblicza się wg twierdzenia Laplace'a :
a) wyznacznik rozwinięty wg k-tego wiersza
b) wyznacznik rozwinięty wg k-tej kolumny
A
ik
dopełnieniem algebraicznym wyrazu a
ik
macierzy A -->
gdzie W
ik
jest podwyznacznikiem oraz
PODWYZNACZNIK (MINOR) W
ik
wyznacznika n -tego stopnia
nazywamy wyznacznik (n-1)-tego stopnia, który powstaje z wyznacznika W
po opuszczeniu w nim i-tego wiersza i k-tej kolumny.
Nazywamy go minorem wyrazu a
ik
.
∑
=
=
+
+
+
=
n
J
kj
kj
kn
kn
k
k
k
k
A
a
A
a
...
A
a
A
a
A
1
2
2
1
1
det
∑
=
=
+
+
+
=
n
i
ik
ik
nk
nk
k
k
k
k
A
a
A
a
...
A
a
A
a
A
1
2
2
1
1
det
( )
ik
k
i
ik
W
A
⋅
−
=
+
1
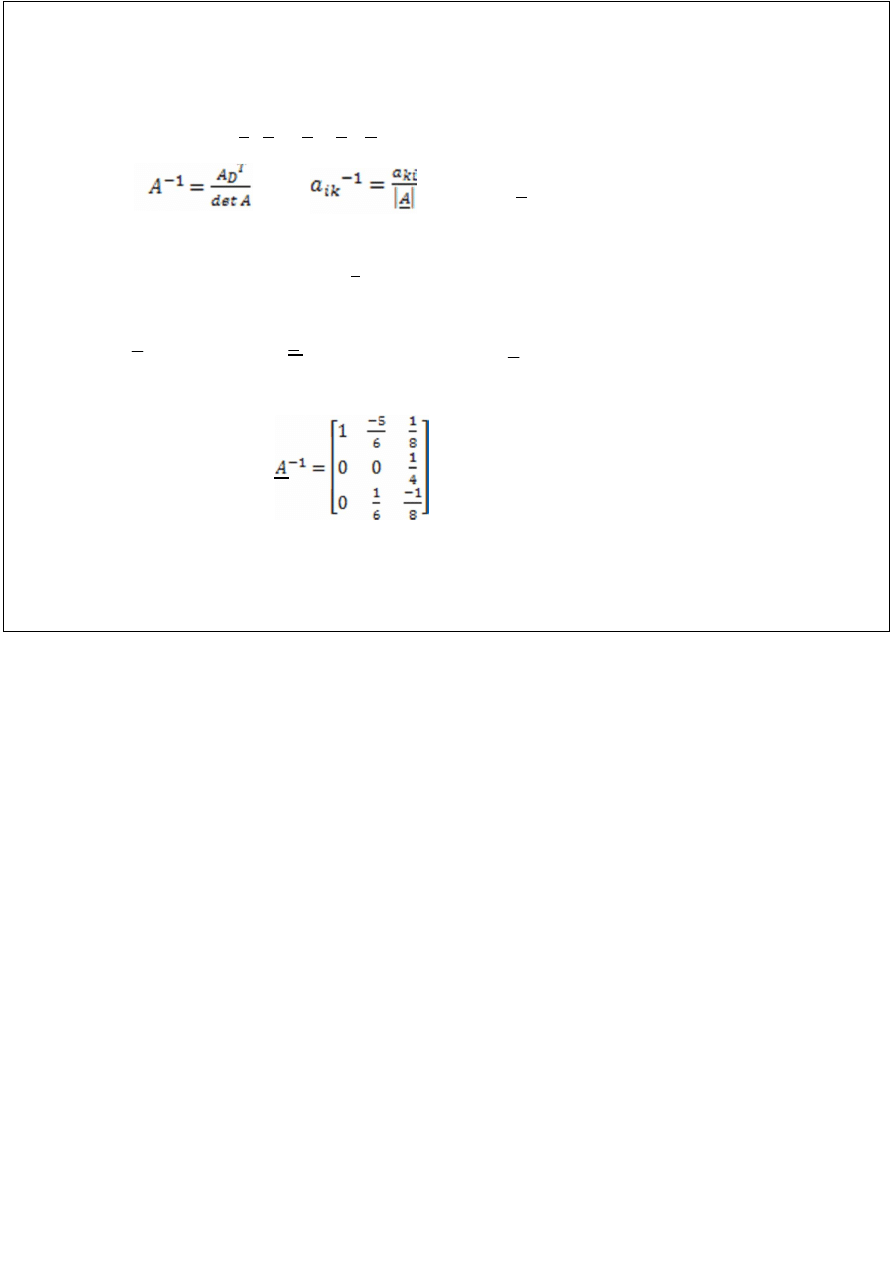
Macierz odwrotna
A · A
-1
= A
-1
· A = E
def.:
, gdzie A
D
– macierz dopełnie
ń
algebraicznych
MACIERZ ODWROTNA (macierzy kwadratowej)
ZADANIE 3. Wyznacz macierz odwrotną A
-1
=
0
4
0
6
3
0
5
2
1
A
−−−−
−−−−
−−−−
−−−−
====
3
6
3
4
0
20
0
0
24
Α
D
−
−
−
−
=
3
4
0
6
0
0
3
20
24
T
D
A
Det A = -24
Wyszukiwarka
Podobne podstrony:
3 Zadania do wykladu Dzialania na macierzach rzad macierzy
3.Zadania do wykladu Dzialania na macierzach rzad macierzy
Matematyjka Dzialania na macierzach
dzialania na macierzach [ www potrzebujegotowki pl ]
podstawowe dzialania na macierzach
,algebra liniowa z geometrią analityczną, działania na macierzach
Dzialania Na Macierzach
3 Zadania do wykladu Dzialania na macierzach rzad macierzy
,algebra 1, Macierz i działanie na macierzach
Zestaw 11 Działania na wektorach i macierzach
Zestaw 11- Działania na wektorach i macierzach
Prawa działań na zbiorach
dzialania na wielomianach
Leki dzialajace na uklad oddechowy 2
PSYCHOLOGIA W DZIAŁANIACH NA RZECZ BEZPIECZEŃSTWA
06 LEKI DZIAŁAJĄCE NA ZWOJE UKLADU AUTONOMICZNEGO
więcej podobnych podstron