3UDZGRSRGRELHVWZR L VWDW\VW\ND
14.10.2000
r.
___________________________________________________________________________
1
Zadanie 1.
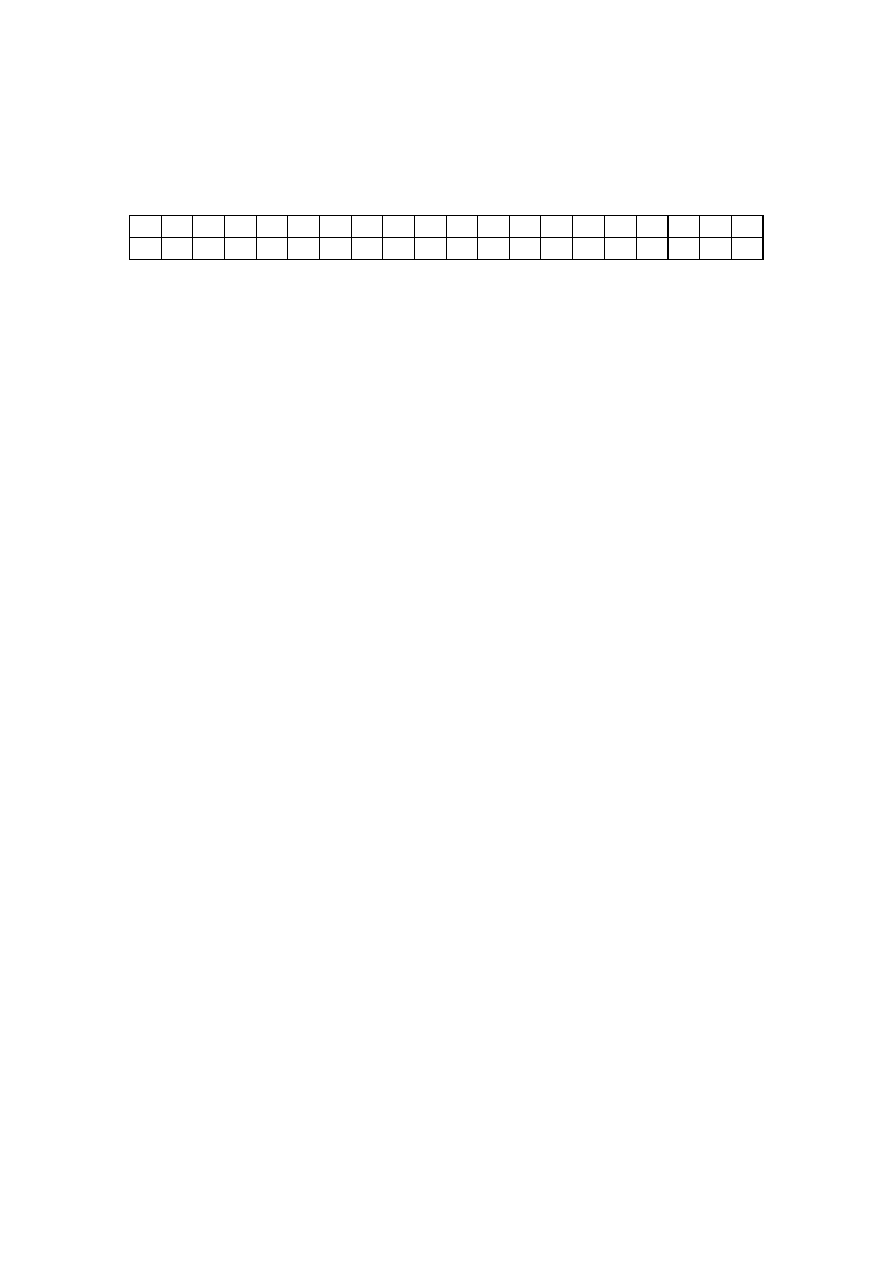
: FLJX U]XWyZ PRQHW OLF]\P\ VHULH RUáyZ .D*G\ FLJ VVLDGXMF\FK ]H VRE
RUáyZ X]QDMHP\ ]D VHUL 3U]\MPXMHP\ ]DWHP *H VHULH PRJ Ä]DFKRG]Lü QD VLHELH´ QD
SU]\NáDG Z FLJX
R O O O O O O O R O O O R O O O O O R R
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
PDP\ VHULH ]DF]\QDMFH VL RG PLHMVF L
2EOLF] ZDUWRü RF]HNLZDQ OLF]E\ VHULL RUáyZ Z U]XWDFK
(A) 2
(B) 20/32
(C) 1
(D) 20/16
(E) 1/2

3UDZGRSRGRELHVWZR L VWDW\VW\ND
14.10.2000
r.
___________________________________________________________________________
2
Zadanie 2.
1D RNUJX R REZRG]LH Z\ELHUDP\ SXQNW
0
X
D QDVWSQLH ORVRZR L QLH]DOH*QLH
wybieramy punkty
n
X
X ,...,
1
. Niech Y
R]QDF]D RGOHJáRü RG
0
X
GR QDMEOL*V]HJR
VSRUyG SXQNWyZ
n
X
X ,...,
1
OLF]RQ Z]GáX* RNUJX 2EOLF]\ü
[ ]
Y
E
.
(A)
[ ]
1
1
+
=
n
Y
E
.
(B)
[ ]
n
Y
E
1
4
1
=
.
(C )
[ ]
1
1
2
1
+
=
n
Y
E
.
(D)
[ ]
(
)
2
1
1
+
=
n
Y
E
.
(E)
[ ]
n
Y
E
4
1
=
.

3UDZGRSRGRELHVWZR L VWDW\VW\ND
14.10.2000
r.
___________________________________________________________________________
3
Zadanie 3.
Niech X i Y
EG ]PLHQQ\PL ORVRZ\PL R áF]Q\P UR]NáDG]LH QRUPDOQ\P WDNLP
*H
,
0
]
[
]
[
=
=
Y
E
X
E
1
]
[
=
X
Var
,
5
]
[
=
Y
Var
,
2
]
,
[
−
=
Y
X
Cov
. Oblic
]\ü
]
|
[
2
x
X
Y
E
=
.
(A)
2
2
4
5
]
|
[
x
x
X
Y
E
+
=
=
.
(B)
2
2
4
1
]
|
[
x
x
X
Y
E
+
=
=
.
(C) 1
]
|
[
2
=
=
x
X
Y
E
.
(D) 5
]
|
[
2
=
=
x
X
Y
E
.
(E)
2
2
4
]
|
[
x
x
X
Y
E
+
=
=
.
Wskazówka:
5R]SDWU] ]PLHQQ ORVRZ
X
Y
Z
2
+
=
.

3UDZGRSRGRELHVWZR L VWDW\VW\ND
14.10.2000
r.
___________________________________________________________________________
4
Zadanie 4.
Niech ,...
,...,
,
2
1
n
X
X
X
EG QLH]DOH*Q\PL ]PLHQQ\PL ORVRZ\PL R UR]NáDG]LH
jednostajnym na przedziale
[ ]
2
,
0
. Niech
.
...
2
1
n
n
X
X
X
Y
⋅
⋅
⋅
=
.WyUD ] QDVWSXMF\FK UyZQRFL MHVW SUDZG]LZD"
(A)
(
)
0
1
Pr
lim
=
≤
∞
→
n
n
Y
.
(B)
(
)
2
/
1
1
Pr
lim
=
≤
∞
→
n
n
Y
.
(C)
(
)
0
)
/
2
(
Pr
lim
=
≤
∞
→
n
n
n
e
Y
.
(D)
(
)
2
/
1
)
/
2
(
Pr
lim
=
≤
∞
→
n
n
n
e
Y
.
(E)
(
)
1
)
/
2
(
Pr
lim
=
≤
∞
→
n
n
n
e
Y
.
Wskazówka: Wykorzystaj Centralne Twierdzenie Graniczne.

3UDZGRSRGRELHVWZR L VWDW\VW\ND
14.10.2000
r.
___________________________________________________________________________
5
Zadanie 5.
=Dáy*P\ *H
Y
X ,
i Z
V QLH]DOH*Q\PL ]PLHQQ\PL ORVRZ\PL R VWDQGDUGRZ\P
UR]NáDG]LH QRUPalnym
( )
1
,
0
N
=QDOH(ü OLF]E a WDN *H
.
6
.
0
|
|
Pr
2
2
2
=
≤
+
+
a
Z
Y
X
X
(A)
9785
.
0
=
a
.
(B)
6
.
0
=
a
.
(C)
565
.
0
=
a
.
(D)
750
.
0
=
a
.
(E)
825
.
0
=
a
.
Wskazówka 1: Wykorzystaj pr
RVW\ Z]yU Z\UD*DMF\
(
)
t
Z
Y
>
+
2
2
Pr
.
Wskazówka 2:
:\NRU]\VWDM JHRPHWU\F]Q LQWHUSUHWDFM ZHWRUD
2
2
2
)
,
,
(
Z
Y
X
Z
Y
X
+
+
.

3UDZGRSRGRELHVWZR L VWDW\VW\ND
14.10.2000
r.
___________________________________________________________________________
6
Zadanie 6.
Niech
20
11
10
1
,
,
,
,
X
X
X
X
EG QLH]DOH*Q\PL ]PLHQQ\PL ORVRZ\PL SU]\ W\P
10
1
,
X
X
PDM UR]NáDG QRUmalny
(
)
2
1
,
σ
µ
N
]D
20
11
,
,
X
X
PDM UR]NáDG
normalny
(
)
2
2
,
σ
µ
N
. Niech
∑
∑
∑
=
=
=
=
=
=
20
1
20
11
2
10
1
1
.
20
1
,
10
1
,
10
1
i
i
i
i
i
i
X
X
X
X
X
X
'REUDü OLF]E\
α
i
β
WDN *HE\ VWDW\VW\ND
(
)
(
)
2
2
1
20
1
2
2
ˆ
X
X
X
X
i
i
−
+
−
=
∑
=
β
α
σ
E\áD QLHREFL*RQ\P HVW\PDWRUHm parametru
2
σ
.
(A) 19
/
1
;
19
/
1
−
=
=
β
α
.
(B) 19
/
5
;
19
/
1
−
=
=
β
α
.
(C) 18
/
2
;
18
/
1
−
=
=
β
α
.
(D) 18
/
5
;
18
/
1
−
=
=
β
α
.
(E) 0
;
18
/
1
=
=
β
α
.

3UDZGRSRGRELHVWZR L VWDW\VW\ND
14.10.2000
r.
___________________________________________________________________________
7
Zadanie 7.
n
X
X ,...,
1
MHVW SUyEN ] UR]NáDGX R JVWRFL SUDZGRSRGRELHVWZD
<
<
=
−
.
0
,
1
0
)
(
1
1
1
przypadku
przeciwnym
w
x
dla
x
x
f
θ
θ
θ
Niech
θ
ˆ EG]LH HVW\PDWRUHP QDMZLNV]HM ZLDURJRGQRFL QLH]QDQHJR SDUDPHWUX
θ
.
2EOLF]\ü IXQNFM U\]\ND WHJR HVW\PDWRUD W]Q
(
)
2
)
ˆ
(
)
(
θ
θ
θ
θ
−
=
E
R
.
(A)
)
2
(
1
)
(
2
θ
θ
θ
+
=
n
R
(B)
2
1
)
(
θ
θ
n
R
=
(C)
θ
θ
n
R
1
)
(
=
(D)
θ
θ
n
R
1
)
(
=
(E)
2
1
)
(
θ
θ
n
R
=
Wskazówka:
0R*QD REOLF]\ü UR]NáDG SUDZGRSRGRELHVWZD ]PLHQQ\FK ORVRZ\FK
i
i
X
Y
ln
−
=
.

3UDZGRSRGRELHVWZR L VWDW\VW\ND
14.10.2000
r.
___________________________________________________________________________
8
Zadanie 8.
Niech
5
4
3
2
1
,
,
,
,
X
X
X
X
X
EG]LH SUyEN ] UR]NáDGX Z\NDGQLF]HJR R JVWRFL
SUDZGRSRGRELHVWZD
>
=
−
.
0
,
0
)
(
przypadku
przeciwnym
w
x
dla
e
x
f
x
θ
θ
θ
Parametr
θ
MHVW QLH]QDQ\ :LDGRPR *H HVW\PDWRUHP QDMZLNV]HM ZLDURJRGQRFL WHJR
parametru jest
5
/
5
ˆ
S
=
θ
, gdzie
5
4
3
2
1
5
X
X
X
X
X
S
+
+
+
+
=
1DOH*\ ]EXGRZDü
SU]HG]LDá XIQRFL GOD SDUDPHWUX
θ
postaci
[ ] [
]
.
/
,
/
,
5
5
S
a
S
a
=
θ
θ
)GDP\ *HE\ WHQ SU]HG]LDá E\á V\PHWU\F]Q\ Z W\P VHQVLH *H
(
)
( )
θ
θ
θ
θ
>
=
<
Pr
Pr
.
:\]QDF]\ü VWDáe a i a WDN *HE\ RWU]\PDü SU]HG]LDá QD SR]LRPLH XIQRFL
95
.
0
1
=
−
α
.
(A)
30
.
18
;
94
.
3
=
=
a
a
.
(B)
025
.
0
log
5
;
975
.
0
log
5
−
=
−
=
a
a
.
(C)
83
.
12
;
83
.
0
=
=
a
a
.
(D)
24
.
10
;
62
.
1
=
=
a
a
.
(E)
48
.
20
;
24
.
3
=
=
a
a
.
Wskazówka: Zmienna losowa
5
S
PD UR]NáDG *DPPD

3UDZGRSRGRELHVWZR L VWDW\VW\ND
14.10.2000
r.
___________________________________________________________________________
9
Zadanie 9.
Urna zawiera r kul ponumerowanych liczbami
r
,
,
2
,
1
. Liczba kul r jest nieznanym
param
HWUHP R NWyUP ZLHP\ *H MHVW ZLNV]\ RG :\ELHUDP\ ] XUQ\ NXO ORVXMF MH
bez zwracania.
1D SRGVWDZLH QXPHUyZ Z\ORVRZDQ\FK NXO WHVWXMHP\ KLSRWH] ]HURZ
25
:
0
=
r
H
przeciwko alternatywie
48
:
1
=
r
H
.
2EOLF]\ü PRF QDMPRFQLHMV]HJR WHVWX QD SR]LRPLH LVWRWQRFL
2
.
0
=
α
= GRNáDGQRFL GR
WU]HFK F\IU SR NURSFH G]LHVLWQHM PRF MHVW UyZQD
(A) 0.800
(B) 0.873
(C) 0.900
(D) 0.995
(E) 0.975
Wskazówka:
0R*QD VNRQVWUXRZDü WHVW QDMPRFQLHMV]\ QD SRGDQ\P SR]LRPLH LVWRWQRFL
który wykorzystuje tylko
QDMZ*V]\ numer wylosowanej kuli.

3UDZGRSRGRELHVWZR L VWDW\VW\ND
14.10.2000
r.
___________________________________________________________________________
10
Zadanie 10.
Zmienna losowa X
SU]\MPXMH ZDUWRFL OXE ] MHGQDNRZ\P SUDZGRSRGRELHVWZHP
½. Zmienna losowa Y
SU]\MPXMH ZDUWRFL
k
,
,
2
,
1
'\VSRQXMHP\ SUyEN ] áF]QHJR
UR]NáDGX SUDZGRSRGRELHVWZD ]PLHQQ\FK ORVRZ\FK X i Y ]áR*RQ ] n par
obserwacji. Niech
j
i
n
R]QDF]D OLF]E WDNLFK SDU GOD NWyU\FK ]PLHnna X SU]\MáD
ZDUWRü i ]D Y - ZDUWRü j (
k
j
i
,
,
2
,
1
;
2
,
1
=
=
). W celu weryfikacji hipotezy o
QLH]DOH*QRFL ]PLHQQ\FK X i Y , czyli hipotezy
(
)
(
)
j
Y
j
Y
i
X
H
=
=
=
=
Pr
2
1
,
Pr
:
0
dla
k
j
i
,
,
2
,
1
;
2
,
1
=
=
,
X*\ZDP\ VWDW\VW\NL
(
)
∑∑
=
=
−
=
2
1
1
2
2
2
/
ˆ
2
/
ˆ
i
k
j
j
j
j
i
p
n
p
n
n
χ
, gdzie
n
n
n
p
j
j
j
2
1
ˆ
+
=
.
Przy
∞
→
n
UR]NáDG WHM VWDW\VW\NL ]PLHU]D GR UR]NáDGX FKL-kwadrat ] OLF]E VWRSQL
VZRERG\ UyZQ
(A)
1
2
−
k
(B)
1
−
k
(C) k
(D) k
2
(E)
)
1
(
2
−
k
3UDZGRSRGRELHVWZR L VWDW\VW\ND
14.10.2000
r.
___________________________________________________________________________
11
(J]DPLQ GOD $NWXDULXV]\ ] SD(G]LHrnika 2000 r.
3UDZGRSRGRELHVWZR L VWDW\VW\ND
Arkusz odpowiedzi
*
,PL L QD]ZLVNR
Pesel ...........................................
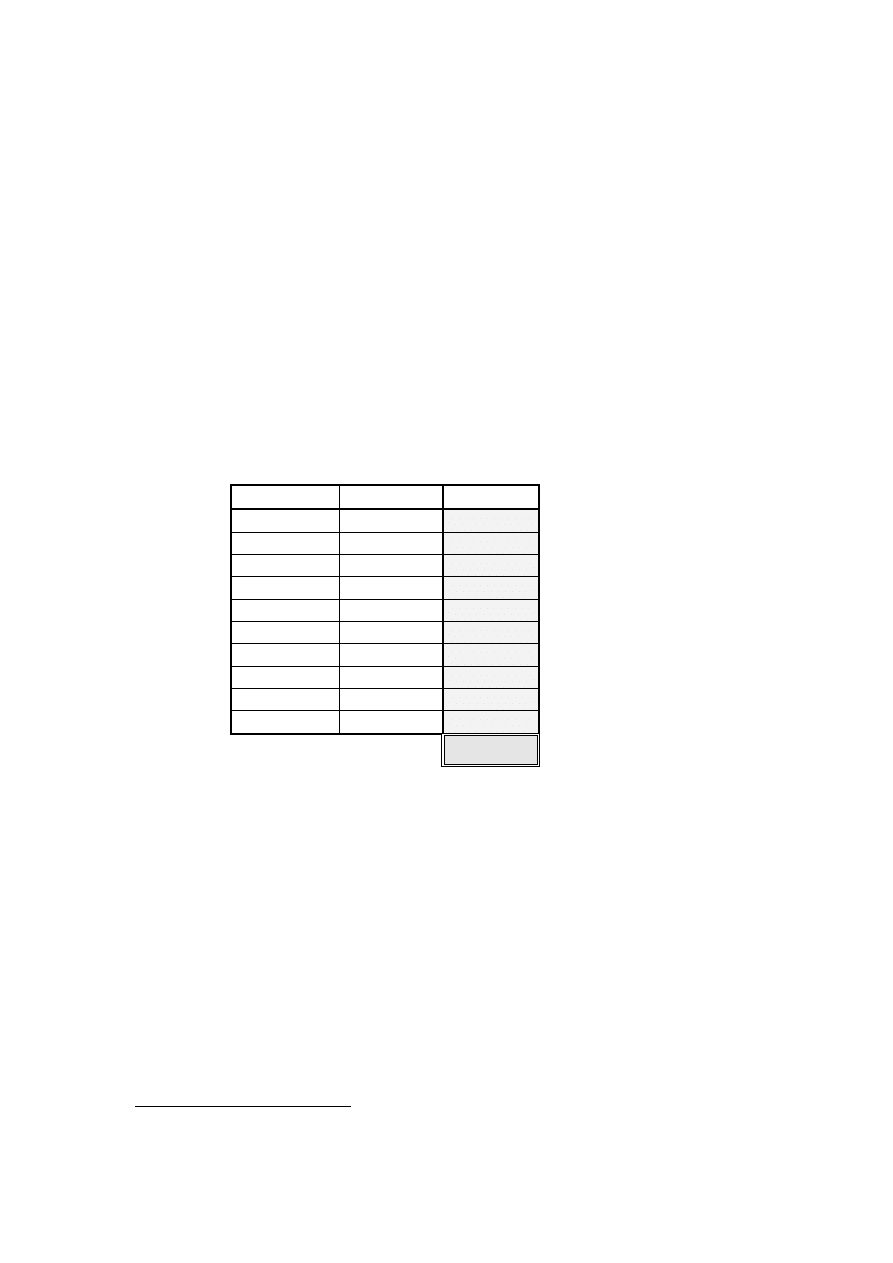
Zadanie
nr Od
SRZLHG( Punktacja
♦
1 E
2 C
3 B
4 D
5 B
6 D
7 E
8 D
9 E
10 C
*
2FHQLDQH V Z\áF]QLH RGSRZLHG]L XPLHV]F]RQH Z Arkuszu odpowiedzi.
♦
:\SHáQLD .RPLVMD (J]DPLQDF\MQD
Wyszukiwarka
Podobne podstrony:
2000 10 14 praid 21577 Nieznany
2000.10.14 prawdopodobie stwo i statystyka
2000 10 14 prawdopodobie stwo i statystykaid 21578
2002 10 12 pra
Cwiczenia nr 10 (z 14) id 98678 Nieznany
Harmonogram ćwiczeń s5 2014 TABL 03 (08 10 14 )
Matematyka Wykład 1 10 14
10 14
10 14 Analiza FOR Konstytucyjne konsekwencje zmian w ofe
odejmowanie do 10 14
IMiUE, 7 10 14 rys 2
10 14 86
Mikroekonomia Wykład 7 10 14
10 10 14
pieleg chirurg 10 14
10 14
2004 10 14 Optymalizacja wyklady
czasowniki 10-14, Archeo, JĘZYK ŁACIŃSKI
więcej podobnych podstron