RADY GENIALNYCH MATEMATYKÓW cz. 1

Autor: dr Stanisław Domoradzki

W 2012 roku będziemy obchodzić 120 rocznicę urodzin genialnego matematyka Stefana Banacha
(1892–1945). Stefan Banach to twórca analizy funkcjonalnej, a jednocześnie jeden z najbarwniejszych
matematyków XX wieku. Był zdania, że tylko te państwa mogą być silne, które pielęgnują matema-
tykę. Mniej znana jest jego działalność związana z pisaniem podręczników do szkoły powszechnej i
gimnazjum. Wspólnie z Banachem podręczniki pisali Wacław Sierpiński i Włodzimierz Stożek.

1

Na

przykładach zaczerpniętych z podręczników dla klas V i VII pokażę jeden ze sposobów, jak można
przeciwdziałać trudnościom w uczeniu się matematyki poprzez oglądanie świata przez matematykę.
Czytelnik zechce się zastanowić, czy używany przez niego podręcznik pozwala na takie oglądanie
świata, a tym samym zwiększa motywację ucznia. W opracowaniu odnoszę się do następujących
podręczników:

•

S. Banach, W. Sierpiński, W. Stożek, Arytmetyka i geometrja dla V klasy szkoły podstawowej, Lwów
– Warszawa 1933.

•

S. Banach, W. Sierpiński, W. Stożek, Arytmetyka i geometrja dla klasy VII szkoły powszechnej, Lwów
– Warszawa 1935.

Pierwszy z podręczników ma 192 strony i składa się z 13 następujących rozdziałów: Układ dziesiętny,
Dodawanie, Odejmowanie, Odcinki i kąty, Wielokąty, Mnożenie, Dzielenie, Skala, Pola, Objętości,
Własności liczb całkowitych, Ułamki, Liczby dziesiętne. Każdy rozdział składa się z kilku podroz-
działów, posiada krótką częścią teoretyczną i obszerną część zadaniową. Podręcznik ten napisany
jest językiem prostym i konkretnym, wyróżnia go prostota i rzeczowość, pozbawiony jest wszelkiej
pretensjonalności. Wszystkie rozumowania są zwięzłe, nie pozostawiają niedomówień ani wątpli-
wości. Tekstów matematycznych jest mało, za to dużo jest zadań, najczęściej zadań łatwych. Au-
torzy dbali o to, aby treści nauczania były dostosowane do możliwości poznawczych ucznia i stale
zachęcali uczniów do samodzielnych wysiłków, dbali też o stopniowanie trudności. Ważną rolę we
wszystkich podręcznikach napisanych przez zespół autorów odgrywał rachunek pamięciowy, gdyż
bez umiejętności rachowania w pamięci uczeń nie będzie miał sukcesów w matematyce. Podobnie
wysoko autorzy podkreślają umiejętność szacowania.

Przykład 1
Rachunek pamięciowy i ułatwienia

a) Do liczb: 16, 45, 87, 92, 245, 567, 5234, 11127 dodawaj po kolei: 8, 9, 11, 12, 38, 88, 101, 102, 998,

999.

b) Podziel przez 5 następujące liczby: 25, 57, 73, 92, 265, 520, 600, 880. Uwaga: Mnóż przez 2,

a wynik dziel przez 10.

1

Wacław Sierpiński (1882–1969), współtwórca Polskiej Szkoły Matematycznej, wybitny specjalista w teorii liczb,

teorii mnogości i topologii, profesor Uniwersytetów we Lwowie i Warszawie, członek Paryskiej Akademii Nauk;
Włodzimierz Stożek (1883–1941), profesor matematyki Politechniki Lwowskiej.

Jak pomóc w przezwyciężaniu trudności w uczeniu się matematyki

RADY GENIALNYCH MATEMATYKÓW cz. 1

Autor: dr Stanisław Domoradzki

1. Znajdź w używanym przez Ciebie podręczniku przykłady takich ułatwień.
2. Do jakich sytuacji dydaktycznych prezentowanych w książce E. Gruszczyk-
Kolczyńskiej

2

zaliczyć by można ułatwienia prezentowane przez Banacha?

Przykład 2
Po podaniu niezbędnych określeń dotyczących trójkątów w podręczniku do V klasy są zaprezentowa-
ne następujące zadania:
1. Narysuj kilka trójkątów i oznacz je.
2. Narysuj dowolny trójkąt i porównaj: a) sumę, b) różnicę dwóch boków z trzecim bokiem.
3. Narysuj trójkąt prostokątny i oznacz jego przyprostokątne i przeciwprostokątną.
4. Jedna przyprostokątna ma 6 cm, druga 8 cm. Ile ma przeciwprostokątna? Odczytaj z rysunku (ry-

sunek ma narysować uczeń).

5. Narysuj trójkąt prostokątny, znając jego przyprostokątne:

a) 3 cm, 4 cm,
b) 2 cm, 5 cm,
c) 2cm, 4 cm.

6. Z 4 trójkątów prostokątnych o przyprostokątnych 3 cm, i 5 cm złóż trójkąt prostokątny.
7. Podziel prostokąt o bokach 9 cm i 6 cm na 6 równych trójkątów prostokątnych o przyprostokąt-

nych 6 cm i 3 cm.

8. Narysuj kąt i na jego ramionach (od wierzchołka) odetnij równe odcinki. Łącząc końce tych od-

cinków, otrzymasz trójkąt równoramienny. Wskaż ramiona, podstawę i wierzchołek. Zmierz kąty
przy podstawie.

9. Narysuj trójkąt równoramienny, a zarazem prostokątny. Zmierz kąty przy podstawie.

Podaj różnicę w dzisiejszym podejściu do nauczania geometrii do podejścia
prezentowanego powyżej. Podaj pięć powodów, które pozwolą uczniowi prze-
zwyciężać trudności przy zastosowaniu powyższych ćwiczeń.

2

E. Gruszczyk-Kolczyńska, Wspomaganie rozwoju umysłowego oraz edukacja matematyczna dzieci w ostatnim roku

wychowania przedszkolnego i pierwszym roku edukacji szkolnej, Warszawa 2009.

SPRAWDŹ SIĘ

SPRAWDŹ SIĘ

RADY GENIALNYCH MATEMATYKÓW cz. 1

Autor: dr Stanisław Domoradzki

Przykład 3
Działania na liczbach całkowitych

1. Przeczytaj liczby: 18 023 146, 4 280 612 532 i odpowiedz na następujące pytania: które z cyfr

stoją na miejscu setek, dziesiątek tysięcy, jednostek milionów, setek milionów, dziesiątek mi-
liardów, jednostek bilionów.

2. Zapisz liczby (podane są w postaci słownej): trzynaście bilionów dwa miliardy osiemnaście mi-

lionów sto cztery tysiące dwadzieścia sześć – 13 002 018 104 026. Przykłady przemyślane, które
równocześnie diagnozują wiedzę ucznia.

Przykład 4
Działania na ułamkach

1. Narysuj odcinek o długości 6 cm, a obok niego tego odcinka.

2. Przedstaw w postaci ilorazu ułamki:

3. Ilorazy typu 5 : 6, 11 : 4, 28 : 6, 4 : 17 przedstaw w postaci ułamków.

Przykład 5
Weryfikowanie wiedzy teoretycznej z praktyką dnia codziennego

1. Ile to jest gramów

2. Ile centymetrów stanowi

3. Wyraź w ułamkach metry, które stanowią 10 cm, 50 cm, 64 cm, 71 cm.
4. Wyraź w ułamkach kilogramy, które stanowią: 30 g, 125 g, 850 g, 4 g.

Zadania, które wiążą wiadomości dnia codziennego i wiadomości szkolne są pięknym przykładem za-
dań problemowych. Autorzy nie instruują nauczyciela, zachęcają do stawiania różnorodnych pytań.

Zmodyfikuj ostatni z prezentowanych przykładów dla uczniów zróżnicowanych
wiekowo.

3

4

kg, kg, kg, kg

5

8

9

25

3

50

2

5

m, m, m, m

3

4

19

20

13

50

1

3 ,

,

, , ,

, ,

1

4

1

3

3

8

2

3

5

8

7

10

2

7 ,

,

, , .

13

18

1

3

9

18

126

3

ZAPLANUJ

RADY GENIALNYCH MATEMATYKÓW cz. 1

Autor: dr Stanisław Domoradzki

Przykład 6
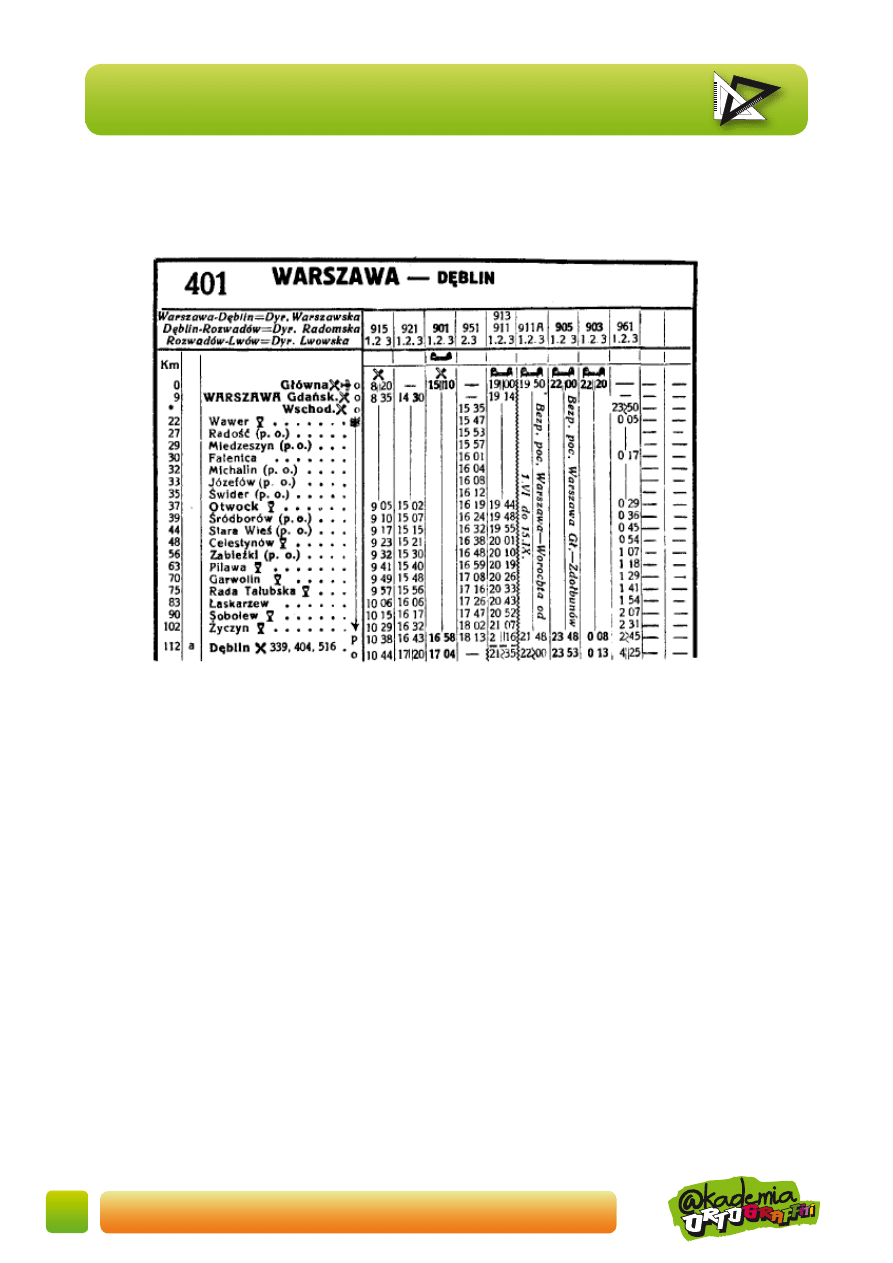
Wykorzystanie informacji zawartych w rozkładzie jazdy pociągów

1. Ile czasu na przebycie drogi z Otwocka do Dęblina potrzebuje pociąg

a) nr 915,
b) nr 921,
c) nr 951?

Jaka jest przeciętna prędkość w minutach każdego z tych pociągów?
2. Jaka jest przeciętna prędkość w minutach na drodze Warszawa – Dęblin pociągu

a) nr 901,
b) nr 913?

3. Ile czasu na przebycie 10 km przeciętnie potrzebuje pociąg

a) nr 901,
b) nr 915?

4. Porównaj przeciętne prędkości na drodze Warszawa – Dęblin w minutach pociągów

a) nr. 915,
b) nr 901,
c) 911A.

RADY GENIALNYCH MATEMATYKÓW cz. 1

Autor: dr Stanisław Domoradzki

Wykorzystując powyższy pomysł, ułóż z uczniem serię podobnych zdań.

ZAPLANUJ