2101
POTENCJAŁ ELEKTRYCZNY
POTENCJAŁ ELEKTRYCZNY
POTENCJAŁ ELEKTRYCZNY
POTENCJAŁ ELEKTRYCZNY
E
r
charakteryzowało pole z punktu widzenia oddziaływań,
czyli miało sens taki, że znając wartość
)
r
(
E
r
można było
obliczyć
)
r
(
E
q
)
r
(
F
0
r
r
⋅
=
. E
r
jest wektorem.
Z punktu widzenia możliwości wykonania pracy w polu
el. wielkością fiz. charakteryzującą tę możliwość jest V.
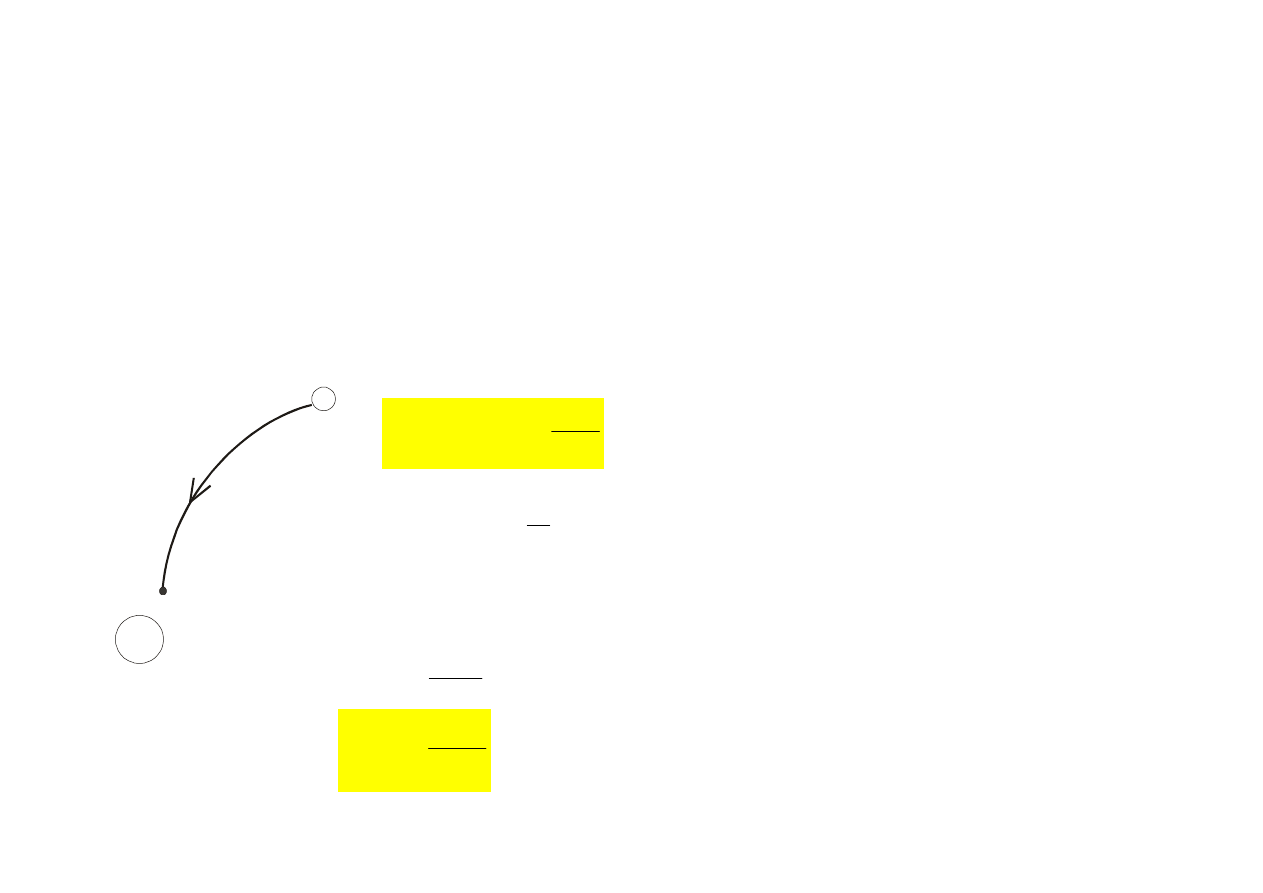
Aby wyznaczyć różnicę potencjałów elektrycznych po-
między punktami pola A i B przesuwamy ładunek próbny
q
0
z A do B mierząc jednocześnie pracę W
AB
, którą w tym
celu trzeba wykonać (lub wykonuje pole).
Def. różnicy potencjał.:
0
AB
A
B
q
W
V
V
V
=
−
=
∆
,
gdzie
B
A
AB
W
W
→
≡
.
C
1
J
1
V
1
]
V
[
=
=
.
A jak zdefiniować V?
Umowa: A wybiera się w
∞
czyli V
A
=0, a więc:
0
B
B
q
W
V
→
∞
=
, lub ogólniej:
DEF:
0
r
.
q
W
)
r
(
V
∞
=
r
+
++
+
A
B
A
V
B
V
q
0
q
ładunek
wytwarzający
pole
2102
Potencjał
)
r
(
V
r
w danym punkcie jest równoważny
pracy, jaką należy wykonać, aby ładunek próbny q
0
przesunąć z
∞
do danego punktu pola
r
r
.
Potencjał jest skalarem!!
Notacja: potencjał ładunku dodatniego jest dodatni V>0,
potencjał ładunku ujemnego jest ujemny V<0.
POTENCJAŁ ŁADUNKU PUNKTOWEGO
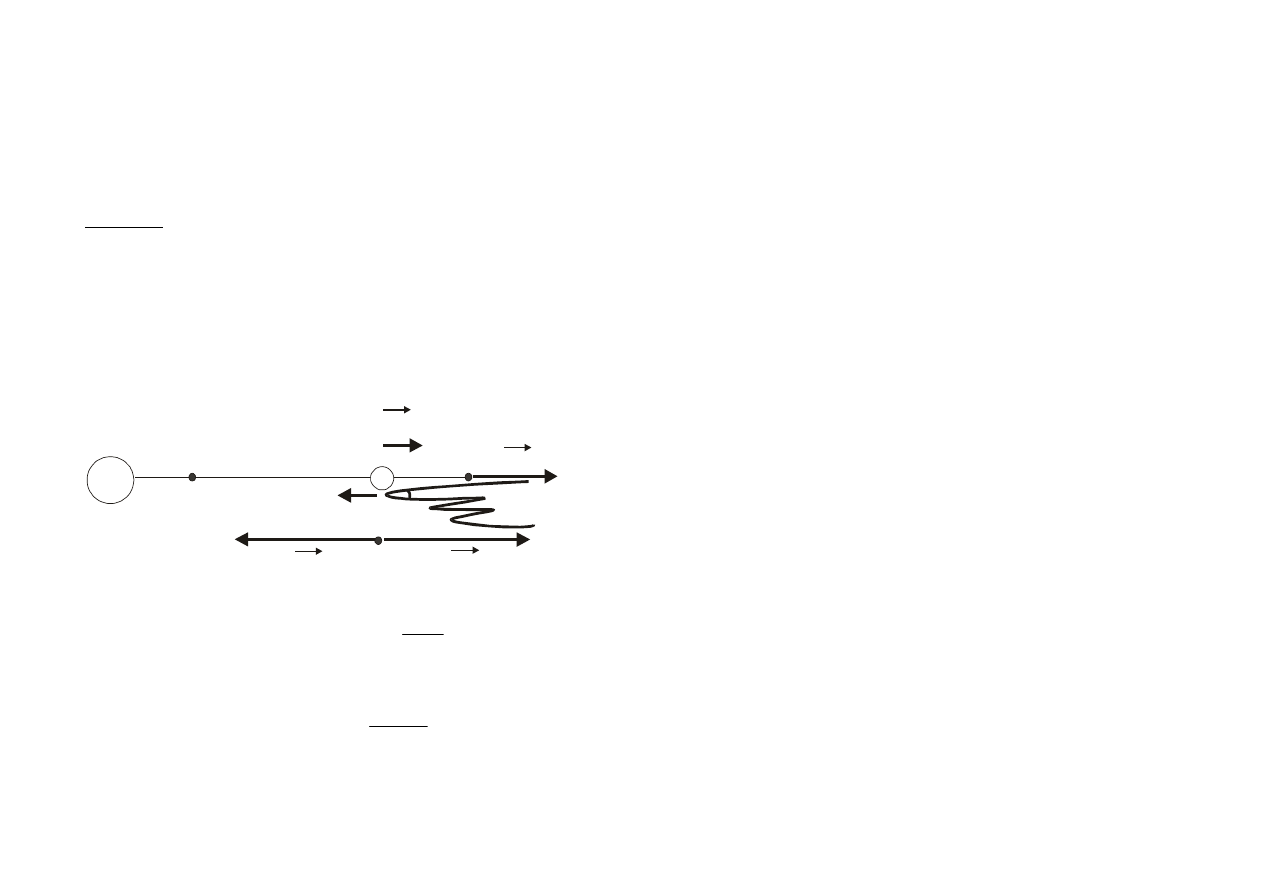
Przesuwajmy ładunek q
0
z punktu A do B w polu el. wy-
tworzonym przez ładunek punktowy q.
+
++
+
A
B
A
V
B
V
q
0
q
r
dr
F
q E
0
AB
A
B
q
W
V
V
V
=
−
=
∆
,
0
B
A
A
B
q
r
d
F
V
V
∫
⋅
=
−
r
r
,
E
q
F
0
r
r
⋅
−
=
,
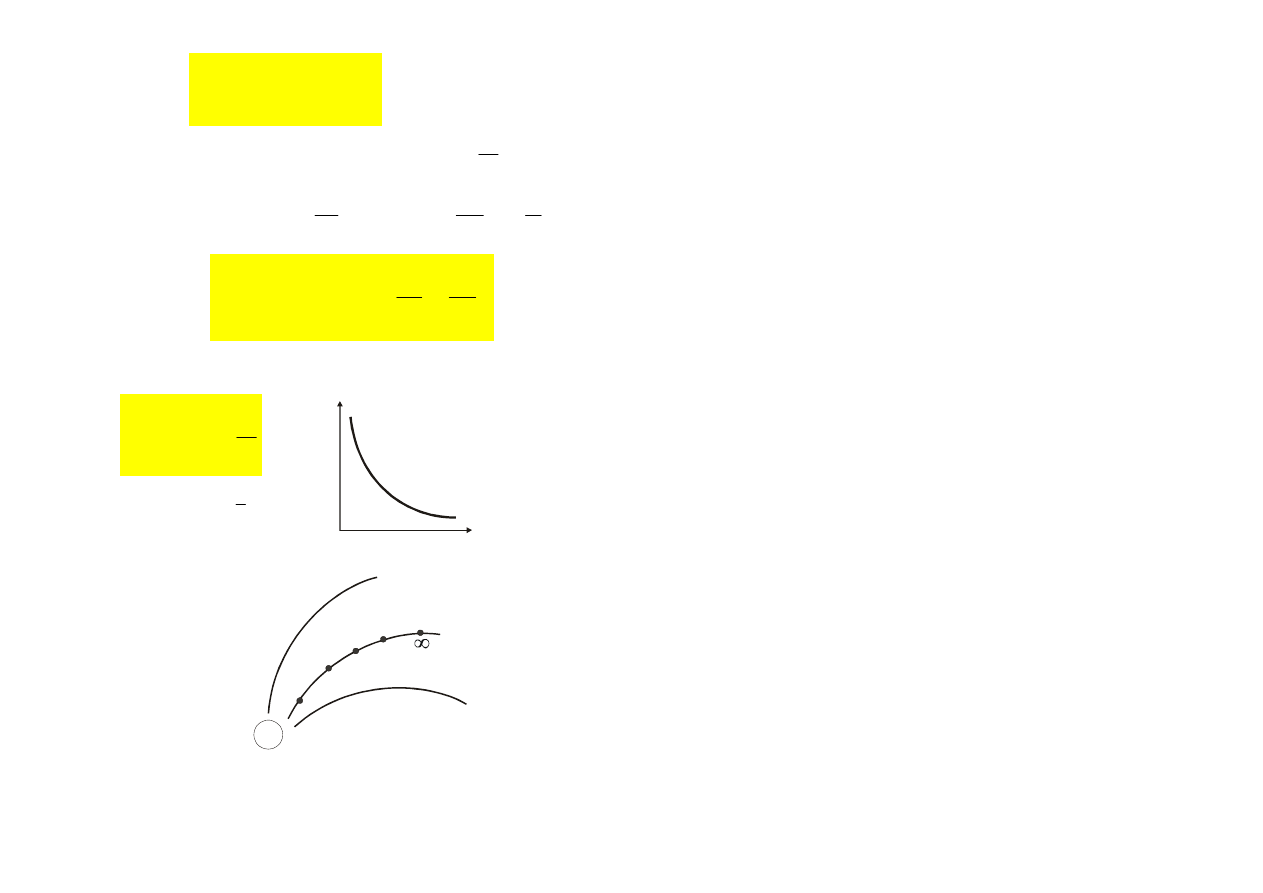
2103
∫
⋅
−
=
−
B
A
A
B
r
d
E
V
V
r
r
(zapamiętaj!).
Dla ładunku punktowego
rˆ
r
q
k
E
2
=
r
,
∫
−
=
−
B
A
r
r
2
A
B
r
dr
kq
V
V
, {
x
1
x
dx
2
−
=
∫
},
−
−
=
−
A
B
A
B
r
1
r
1
kq
V
V
.
Gdy
∞
→
A
r
to
0
V
A
→ ;
)
r
(
V
V
V
r
B
=
=
Dla ładunku punktowego:
r
q
k
)
r
(
V
=
.
q
~
V
, oraz
r
1
~
V
,
++
+
V
V
V
V
V
+q
ładunek
wytwarzający
pole
V=0
r
1
~
V
r
1
~
V
V
r

2104
POTENCJAŁ UKŁADU ŁADUNKÓW PUNKTOWYCH
Potencjał jest skalarną wielkością addytywną:
∑
∑
=
=
=
=
n
1
i
i
i
n
1
i
i
r
q
k
V
V
.
POTENCJAŁ ŁADUNKU ROZCIĄGŁEGO
∫
∫
=
=
r
dq
k
dV
V
.
POTENCJAŁ DIPOLA
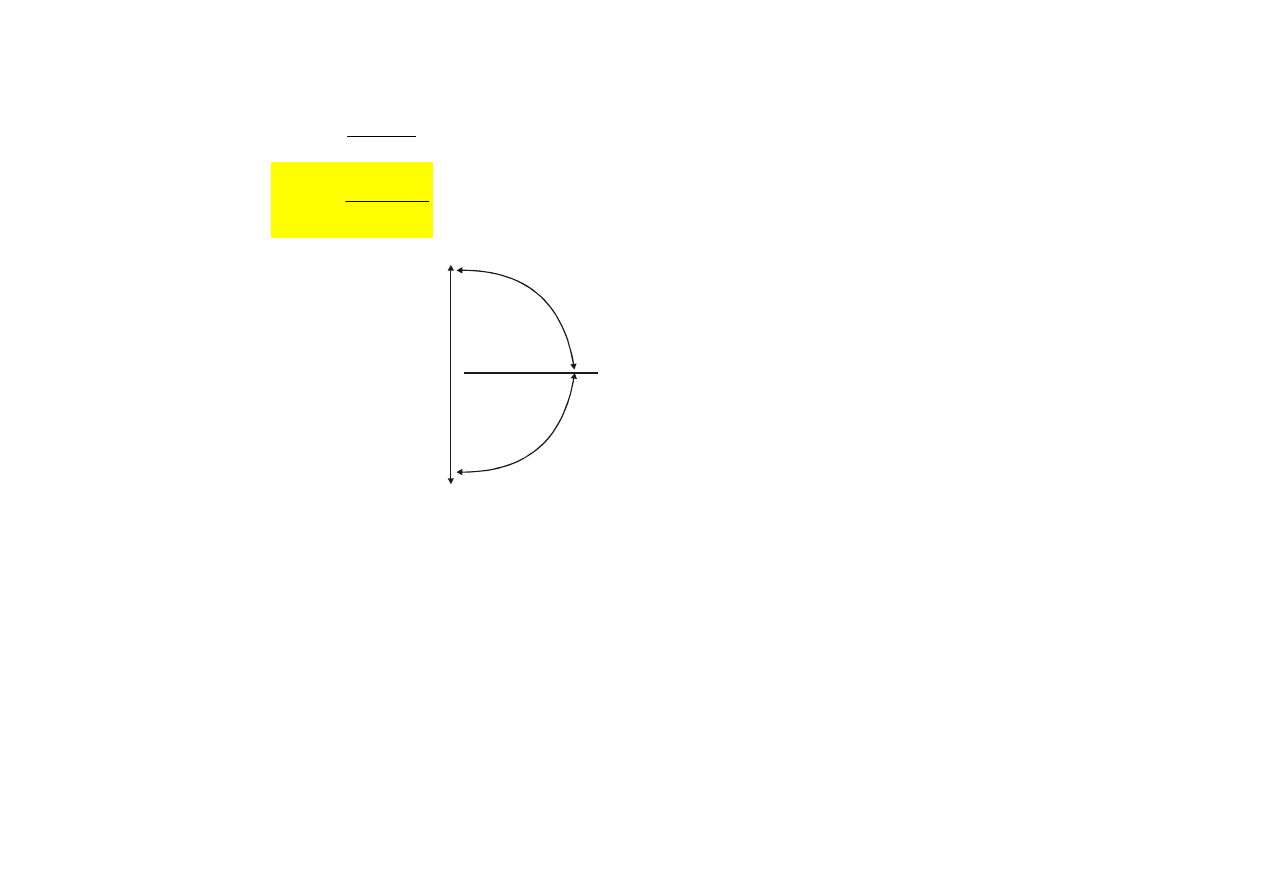
Przykład
Obliczyć potencjał V w odległości r od dipola ustawio-
nego pod kątem α do osi obserwacji (r>>2a, p = 2aq).
Z
r
r
r
P
+q
-q
a
a
α
α
1
2
'
2
1
i
i
V
V
V
V
+
=
=
∑
,
2
1
1
2
2
1
r
r
r
r
kq
r
q
r
q
k
V
⋅
−
=
−
+
=
,
2105
dla r>>2a i α'≈ α
α
≈
−
cos
a
2
r
r
1
2
, oraz
2
1
2
r
r
r
≈
⋅
,
2
r
cos
a
2
kq
V
α
=
,
2
r
cos
p
k
V
α
=
.
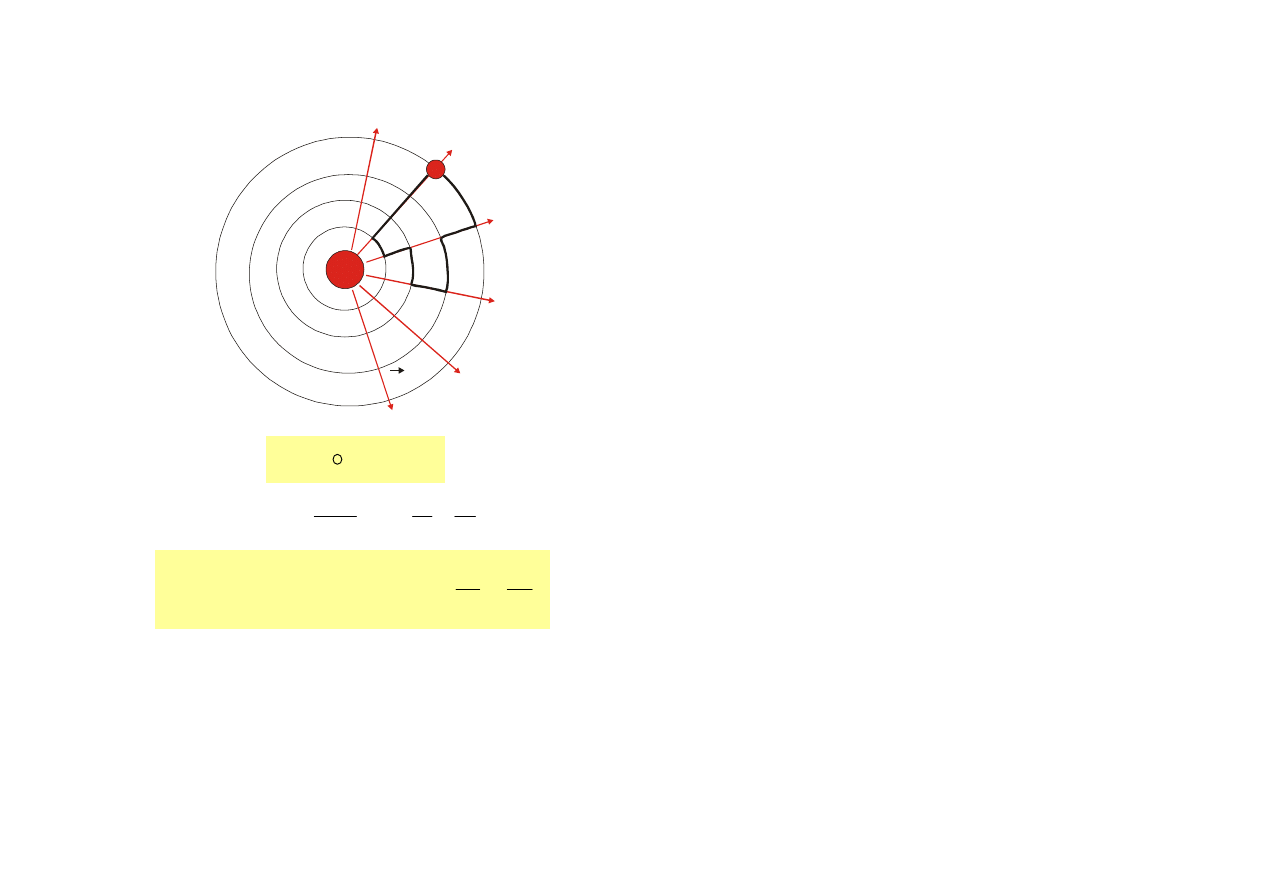
Przeanalizujmy warunki kąto-
we:
dla α: (0
o
– 90
o
) V>0,
α = 0
o
V = V
max
oraz V>0
α: (90
o
– 180
o
) V<0,
α: (0
o
– 90
o
) V>0,
α = 90
o
V = 0,
α = 180
o
V = V
max
oraz
V<0.
V >0
V <0
V = 0
V > 0
V < 0
max
max
α=90
o
α=180
o
α=0
o
2106
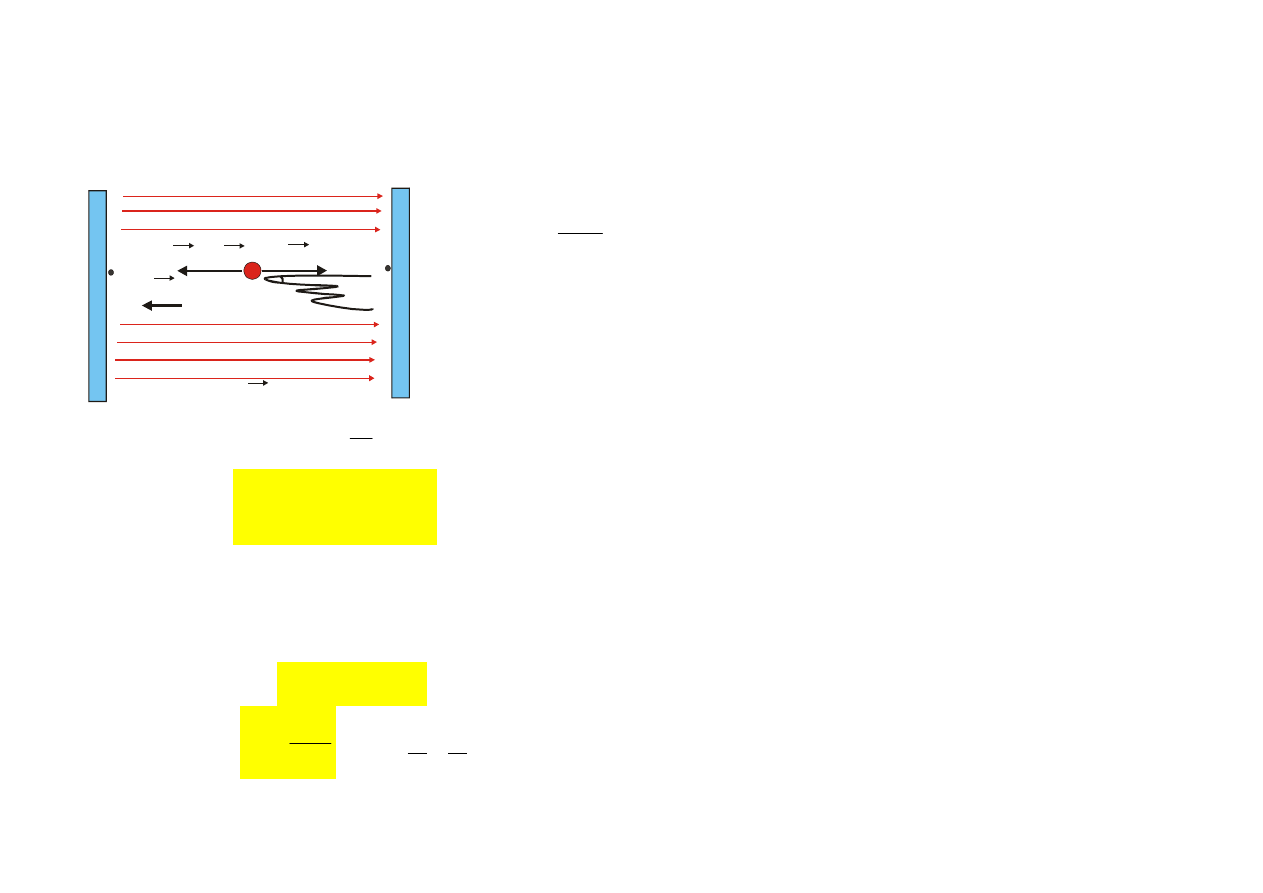
ZACHOWAWCZOŚĆ POLA EL
Pole el. (podobnie jak pole grawitacyjne) jest polem za-
chowawczym.
+
q
0
q
E
+
Praca po drodze zamkniętej jest równa zeru.
0
r
d
F
W
o
=
⋅
=
∫
r
r
−
=
=
−
A
B
0
AB
A
B
r
1
r
1
kq
q
W
V
V
,
(
)
−
=
−
=
A
B
0
A
B
0
AB
r
1
r
1
kqq
V
V
q
W
.
Powierzchnia każdego przewodnika jest powierzchnią
stałego potencjału (
powierzchnią ekwipotencjalną
).
Praca nie zależy od wyboru drogi, a zależy od różnicy po-
tencjałów.
2107
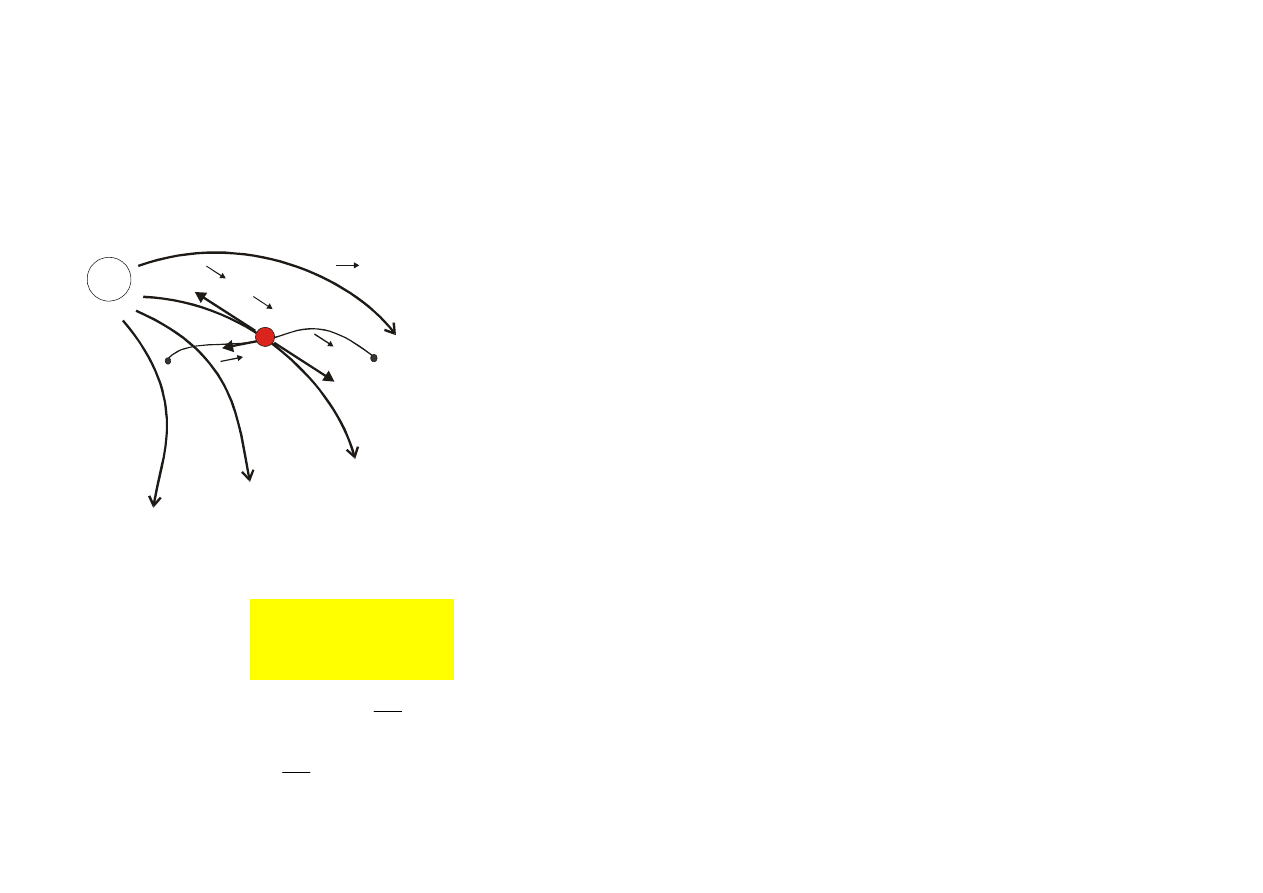
POTENCJAŁ POLA EL. JEDNORODNEGO
Przesuwajmy ładunek q
0
ruchem jednostajnym na drodze
d od A
→
→
→
→ B w jednorodnym polu el. E. Obl. ∆V = ?
z def.:
0
AB
A
B
q
W
V
V
=
−
∫
⋅
=
B
A
AB
r
d
F
W
r
r
,
E
q
F
0
r
r
⋅
−
=
,
∫
⋅
⋅
−
=
−
B
A
0
0
A
B
r
d
E
q
q
1
V
V
r
r
∫
⋅
−
=
−
B
A
A
B
r
d
E
V
V
r
r
, warto zapamiętać!
↑
↓
r
d
...
a
.
E
r
r
,
dr
E
r
d
E
⋅
−
=
⋅
r
r
,
Const
E =
r
,
∫
=
−
B
A
A
B
dr
E
V
V
,
d
dr
B
A
=
∫
,
d
E
V
V
A
B
⋅
=
−
,
Ed
V =
∆
.
d
V
E
∆
=
,
C
N
m
V
]
E
[
=
=
A
B
E
dr
q E
+
+
+
+
+
+
-
-
-
-
-
-
+
F=-q E
0
0
2108
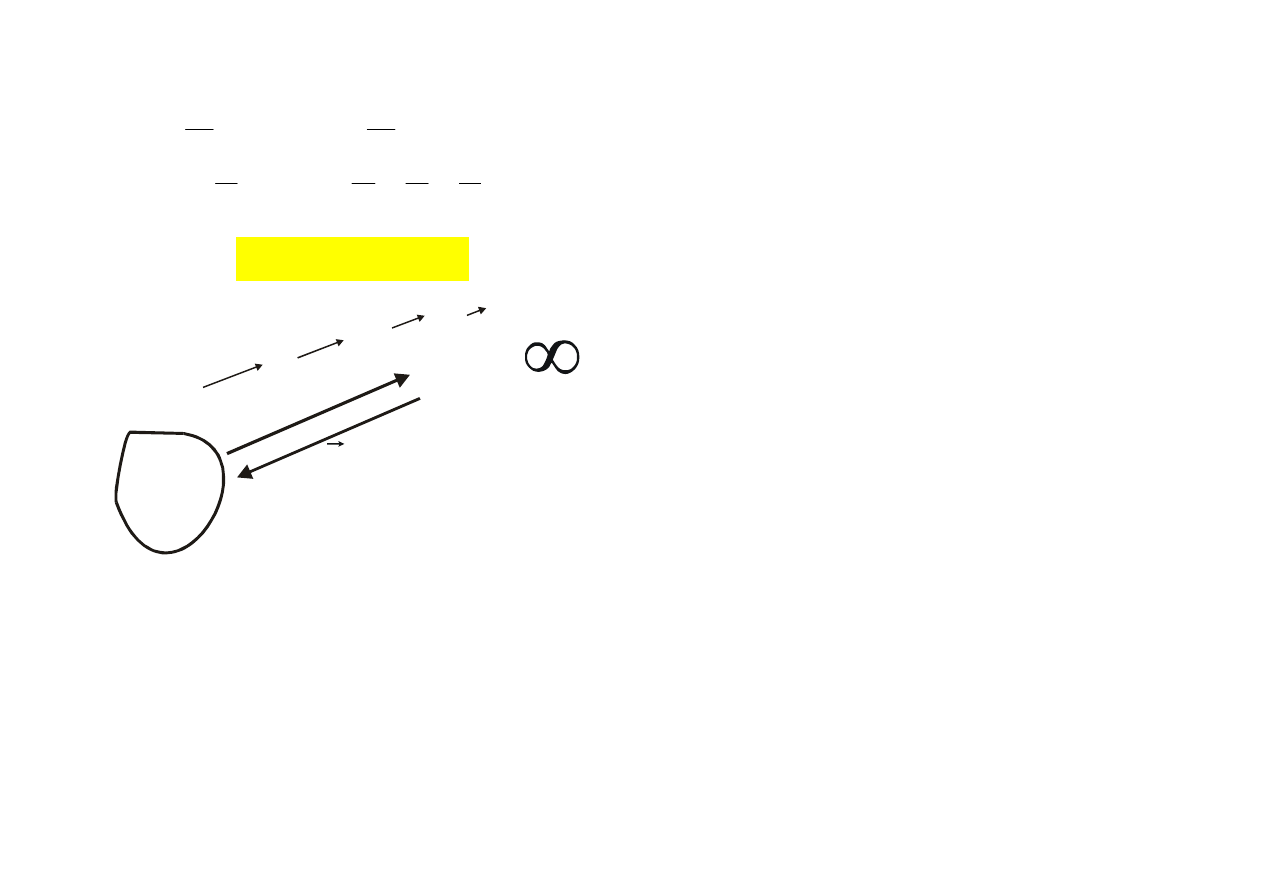
POTENCJAŁ POLA EL. NIEJEDNORODNEGO
(Związek pomiędzy E a V)
Przesuwajmy ładunek q
0
ruchem jednostajnym od A
→
→
→
→ B
w niejednorodnym polu el. E. Obl. ∆V = ?
Z poprzedniego:
∫
⋅
−
=
−
B
A
A
B
r
d
E
V
V
r
r
,
Tym razem E nie jest
jednorodne,
Const
E ≠
r
a zatem nie możemy
wyłączyć E przed cał-
kę.
Jeśli równocześnie:
∞
→
A
to
0
V
V
A
=
=
∞
:
∫
∞
⋅
−
=
=
B
B
r
d
E
)
r
(
V
V
r
r
,
∫
∞
⋅
−
=
r
r
d
)
r
(
E
)
r
(
V
r
r
.
∫
∫
∞
⋅
=
=
r
V
0
r
d
r
d
dV
dV
V
r
r
,
∫
∫
∞
∞
⋅
−
=
⋅
r
r
r
d
E
r
d
r
d
dV
r
r
r
r
.
++
+
+q
B
A
E
dr
q E
+
F=
-q E
0
0
2109
Identyczne zmienne i granice całkowania, więc
wyrażenia podcałkowe są sobie równe:
E
r
d
dV
r
r
−
=
, a
V
gradV
r
d
dV
∇
=
=
r
r
.
{
kˆ
z
jˆ
y
iˆ
x
grad
r
d
d
∂
∂
+
∂
∂
+
∂
∂
=
∇
=
=
r
r
}
V
gradV
E
∇
−
=
−
=
r
r
.
+
+
+
+
+
+
+
+
+
+
+
E
V
V
V
V
E
E
E
V
∇
V
∇
r
wskazuje kierunek wzrostu V. Ma zwrot przeciwny
do E.
2110
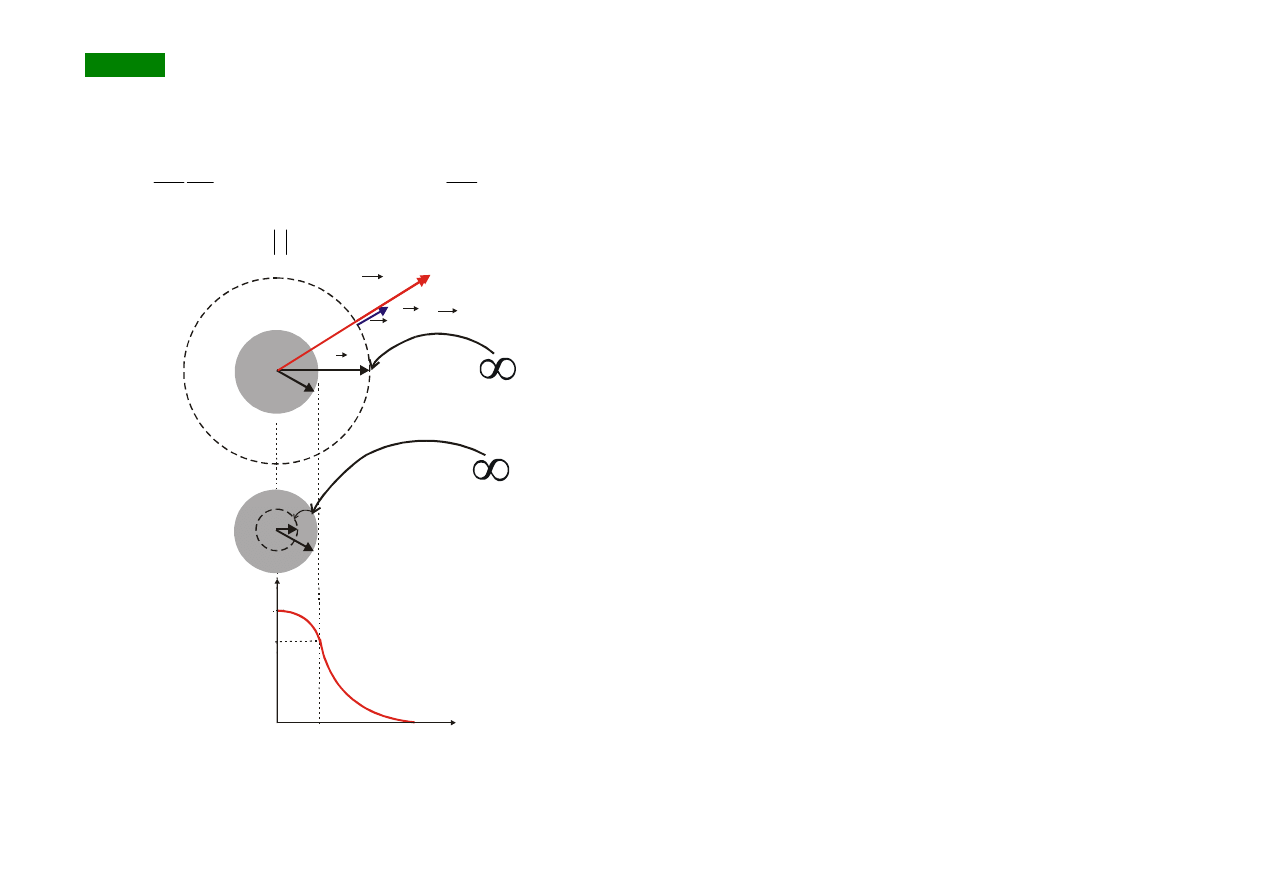
Przykład
Obl. V na zewnątrz i wewnątrz kulistej chmury ładunku o
promieniu R naładowanej ładunkiem o gęstości obj. ρ, je-
żeli znane są zależności E(r):
2
3
0
z
r
R
3
)
r
(
E
ε
ρ
=
dla r>R, oraz
r
3
)
r
(
E
0
w
ε
ρ
=
dla r<R.
∫
∞
⋅
−
=
r
r
d
)
r
(
E
)
r
(
V
r
r
,
r
d
E
r
r
.
E
E
dr
dr
II
r
R
R
+
+
+
+
+
+
+
+
+
+
ρ
ρ
V
r
R
~
r
1
r
I
2
0
R
2ε
ρ
2
0
R
3
ε
ρ
2
r
a
~ −
E
E
z
w

2111
Dla r>R (na zewn.):
∫
∞
⋅
−
=
r
z
r
d
)
r
(
E
)
r
(
V
r
r
∫
∫
∞
∞
ε
ρ
−
=
⋅
ε
ρ
−
=
r
2
0
3
r
2
3
0
r
dr
3
R
dr
r
R
3
)
r
(
V
, {
x
1
x
dx
2
−
=
∫
}
r
R
3
)
r
(
V
3
0
ε
ρ
=
Dla r<R (wewn.):
⋅
+
⋅
−
=
⋅
−
=
∫
∫
∫
∞
∞
r
R
w
R
z
r
r
d
)
r
(
E
r
d
)
r
(
E
r
d
)
r
(
E
)
r
(
V
r
r
r
r
r
r
.
Z powyższego (
dla r>R
) mamy
2
0
R
3
0
R
z
R
3
r
R
3
r
d
)
r
(
E
ε
ρ
=
ε
ρ
=
⋅
−
∞
∞
∫
r
r
.
z kolei
∫
∫
∫
⋅
ε
ρ
=
⋅
ε
ρ
=
⋅
r
R
0
r
R
0
r
R
w
dr
r
3
dr
r
3
r
d
)
r
(
E
r
r
2
x
xdx
2
=
∫
−
ε
ρ
=
ε
ρ
=
⋅
∫
2
R
2
r
3
2
r
3
r
d
)
r
(
E
2
2
0
r
R
2
0
r
R
w
r
r
.
+
−
ε
ρ
=
−
−
ε
ρ
=
2
R
2
r
2
R
2
3
2
R
2
r
R
3
)
r
(
V
2
2
2
0
2
2
2
0
,
2112
(
)
2
2
0
r
R
3
6
)
r
(
V
−
ε
ρ
=
.
dla r=0
(
)
2
0
2
2
0
R
2
0
R
3
6
V
ε
ρ
=
−
ε
ρ
=
,
dla r<R
2
r
a
~
)
r
(
V
−
dla r=R
(
)
2
0
2
2
0
R
3
R
R
3
6
V
ε
ρ
=
−
ε
ρ
=
,
dla r>R
r
1
~
)
r
(
V
,
dla
∞
→
r
0
V →
.
2113
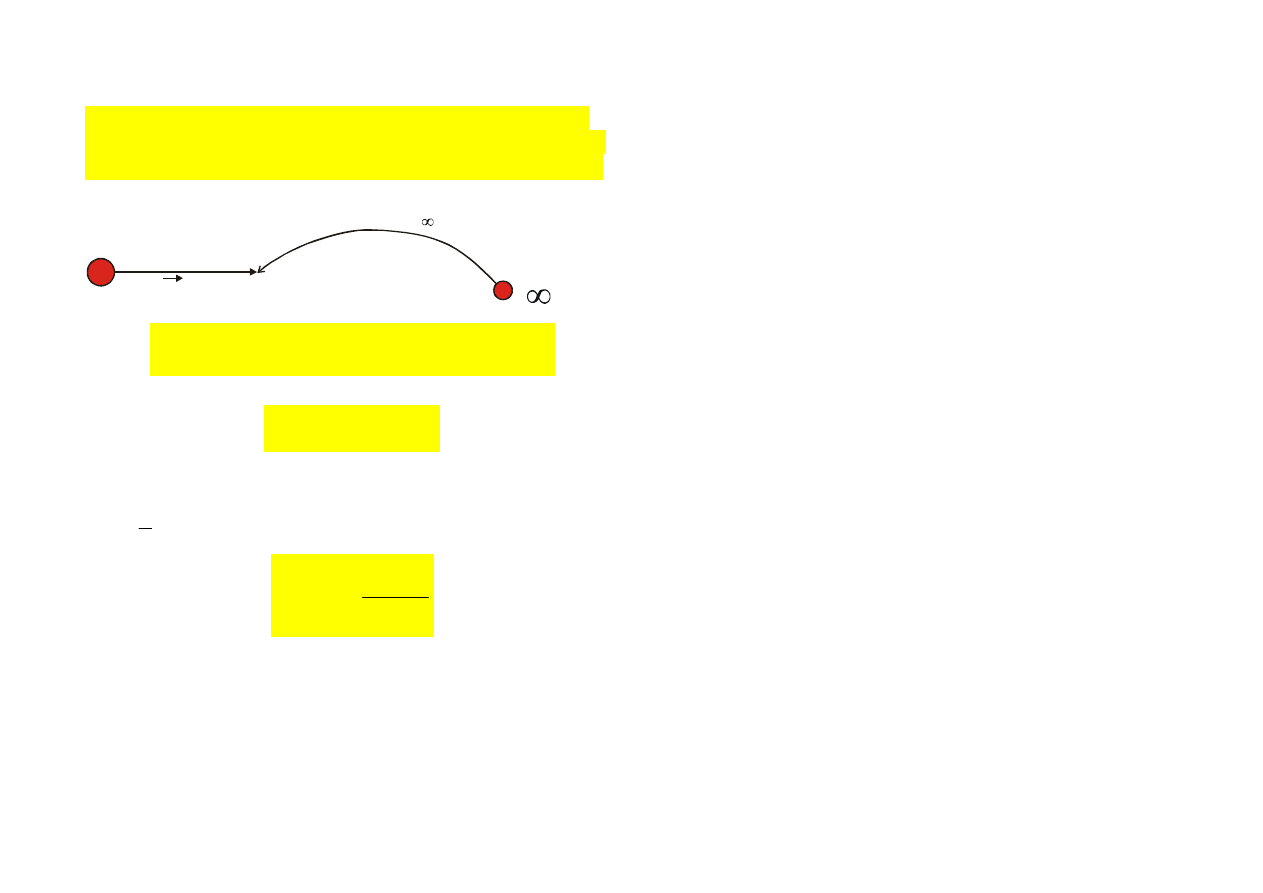
POTENCJALNA ENENRGIA EL.
Def.:
Potencjalna En. El. układu ładunków jest równoważna
pracy, jaka jest potrzebna do utworzenia tego układu ła-
dunków przemieszczając je z
∞
do danego punktu pola.
q
r
V(r)
W
q
0
r
+
+
(
)
∞
∞
−
≡
≡
V
V
q
W
E
r
0
r
p
,
0
V
=
∞
,
0
p
q
)
r
(
V
E
⋅
=
.
Dla układu dwóch ładunków punktowych
q i q
0
:
r
q
k
V
=
r
q
q
k
E
0
p
⋅
=
.
2114
ZESTAWIENIE:
2
0
r
q
q
~
F
⋅
,
0
q
F
E
r
r
=
r
q
q
~
E
W
0
p
r
⋅
≡
∞
,
0
r
q
W
V
∞
≡
2
r
q
~
E
r
q
~
V
2115
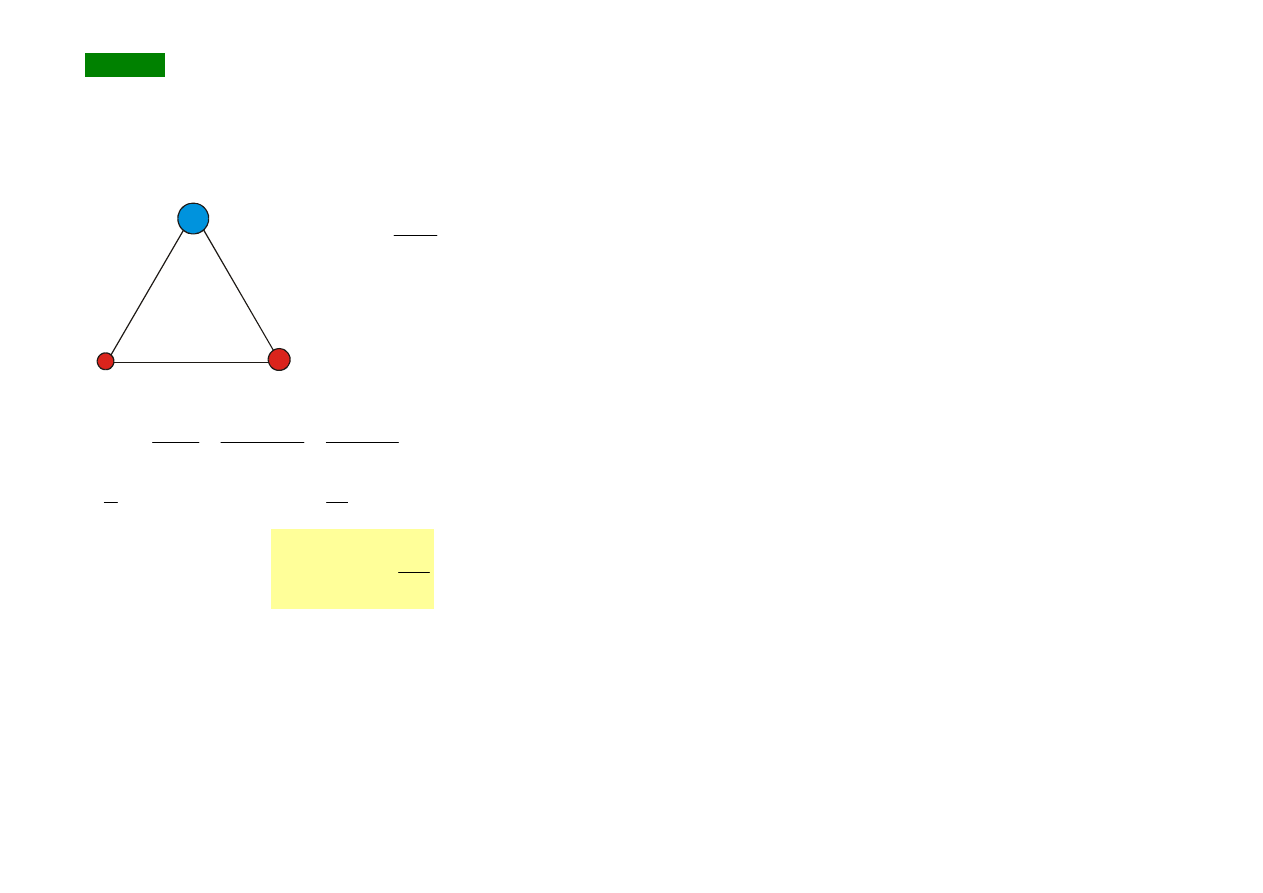
Przykład
Obl. potencjalną enenrgię el
E
p
układu trzech ładunków
punktowych
+q, +2q, -4q znajdujących się w narożach
trójkąta równobocznego o boku
a.
r
p
W
E
∞
≡
,
r
q
q
k
E
0
pqq
0
⋅
=
,
31
p
23
p
12
p
p
E
E
E
E
+
+
=
,
=
⋅
−
+
−
⋅
+
⋅
=
a
q
)
q
4
(
a
)
q
4
(
q
2
a
q
2
q
k
E
p
(
)
a
q
k
10
q
4
q
8
q
2
a
k
2
2
2
2
−
=
−
−
=
,
a
q
k
10
E
2
p
−
=
.
E
p
<0 tzn. wykonaliśmy pracę ujemną przy konstruowaniu
układu tych ładunków (praca wykonana przez układ),
E
p
<0 odpowiada siłom przyciągającycm (ładunki uwolnio-
ne zaczną się do siebie zbliżać).
a
a
a
+q
+2q
-4q
1
2
3
2116
RÓWNANIE LAPLACE'A
V
E
∇
−
=
r
r
/
∇
r
,
0
E
ε
ρ
=
⋅
∇
r
r
,
V
E
∇
⋅
∇
−
=
⋅
∇
r
r
r
r
,
0
E
ε
ρ
=
⋅
∇
r
r
∂
∂
+
∂
∂
+
∂
∂
=
∆
=
∇
=
∇
⋅
∇
2
2
2
2
2
2
2
z
y
x
r
r
0
V
ε
ρ
−
=
∆
Potencjał el. V powstaje dzięki rozkładowi ładunków
w próżni ρ=0 (brak ładunków
0
V =
∆
.
2117
NAPIĘCIE I POTENCJAŁ
BA
A
B
U
V
V
V
=
−
=
∆
,
Def: Napięcie pomiędzy punktami A i B równa się różni-
cy potencjałów tych punktów.
0
AB
A
B
q
W
V
V
=
−
,
0
AB
BA
q
W
U
=
.
Def:
Napięciem U
BA
punktu B względem punktu A nazywamy
iloraz pracy W
AB
wykonanej przy przemieszczeniu ładun-
ku q
0
z punktu A do B i wielkości tego ładunku.
Potencjał el. określonego punktu przedstawia napięcie
tego punktu względem
0 (punktu w nieskończoności).
∫
∞
∞
∞
⋅
−
=
−
=
−
=
=
=
B
B
B
B
B
r
d
E
0
V
V
V
V
V
V
r
r
.
Np. napięcie
220V jest równoważne różnicy potencjałów
220V - 0V.
Wyszukiwarka
Podobne podstrony:
całki, szeregi zadania z kolosa wykład 21 03 2009
BPZ Wykład 21, I rok, BPZ
3 wykład (21 10 2010)
6 wyklad 4 (z 21 01 2012)
8 wyklad 4 (z 21 01 2012)
Wykład 9 (21.11.07), toxycologia
ekonomia wykład 21 04 2011, moje dokumenty, ekonomia wykład
wyklad 21.02.2010
Teoria sterowania wykład 4 (21 03 2003)
PMP Wykłady 1-21, studia prawnicze, 4 rok, prawo miedzynarodowe publiczne
Biologia wykład 21 11 2006
WYKŁAD 3, WYKŁAD 3 21
7 wyklad 4 (z 21 01 2012)
MSP wyklady, MSP wykład(21
Patofizjologia wyklad 21.02.08, Patofizjologia wykład
POZ wyklady 7 21 28 X 2012, skala Barthel, Wysokość kapitacyjnych stawek rocznych
analiza wyklad 21 05 2010
(21 Potencjał zakłócający i anomalie)
więcej podobnych podstron