wiczenie 45
Polarymetr
Wst¦p teoretyczny: Krzysztof R¦bilas
∗
WIATO
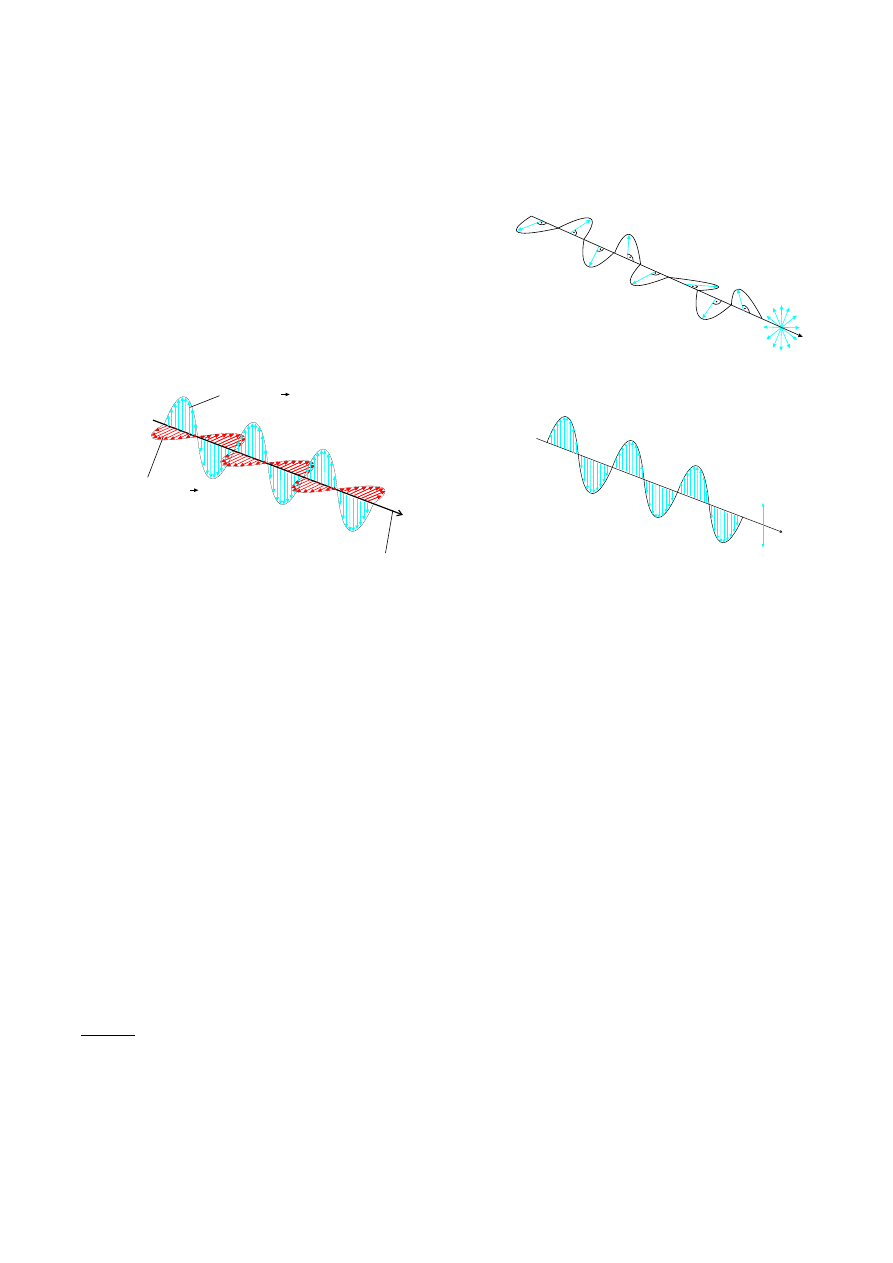
W uj¦ciu zyki klasycznej opieraj¡cej si¦ na teorii Ma-
xwella ±wiatªo widzialne to fala elektromagnetyczna o
dªugo±ci w zakresie ok. 400-700 nm. W fali elektroma-
gnetycznej wektory nat¦»enia pola elektrycznego ~
E
i in-
dukcji pola magnetycznego ~
B
ustawione s¡ prostopadle
do kierunku biegu fali (Rys. 1). Ponadto wektory ~
E
i
Wektory indukcji
pola magnetycznego B
Wektory natê¿enia pola
elektrycznego E
Kierunek rozchodzenia siê fali
Rysunek 1: Fala elektromagnetyczna.
~
B
ustawione s¡ prostopadle wzgl¦dem siebie, zatem in-
formacja o kierunku wektora ~
E
pozwala automatycznie
ustali¢ kierunek wektora ~
B
. Z tego wzgl¦du zwyczajowo
rozpatruje si¦ jedynie wektor nat¦»enia pola elektryczne-
go ~
E
, który nosi te» nazw¦ wektora ±wietlnego.
Poniewa» drgania wektora pola elektrycznego ~
E
od-
bywaj¡ si¦ w pªaszczy¹nie prostopadªej do kierunku roz-
chodzenia si¦ fali, fala elektromagnetyczna jest fal¡ po-
przeczn¡ i jako taka mo»e by¢ niespolaryzowana lub
spolaryzowana.
Fala elektromagnetyczna jest fal¡ niespolaryzowan¡
je±li wektory ±wietlne ~
E
ustawione s¡ w fali chaotycz-
nie we wszystkich kierunkach (ale zawsze prostopadle do
wektora pr¦dko±ci fali) z jednakowym prawdopodobie«-
stwem (Rys. 2).
Fala elektromagnetyczna jest fal¡ spolaryzowan¡ li-
niowo je±li wektory ±wietlne ~
E
ustawione s¡ w fali rów-
nolegle wzgl¦dem siebie i tworz¡ wraz z kierunkiem roz-
chodzenia si¦ fali tzw. pªaszczyzn¦ polaryzacji (Rys.
3).
Najogólniejszym stanem polaryzacji jest tzw. polaryza-
∗
Autorem ¢wiczenia w Pracowni Fizycznej Zakªadu Fizyki Akade-
mii Rolniczej w Krakowie jest Józef Mazurkiewicz.
Rysunek 2: Fala elektromagnetyczna niespolaryzowana.
Rysunek 3: Fala elektromagnetyczna spolaryzowana liniowo.
cja eliptyczna, w której wektory ~
E
i ~
B
zakre±laj¡ w miej-
scu, przez które przechodzi fala, linie w ksztaªcie elipsy.
Mo»liwa jest te» polaryzacja koªowa, przy której wektory
~
E
i ~
B
zakre±laj¡ lini¦ w ksztaªcie koªa.
Zwykªe ±wiatªo skªada si¦ z wielu fal emitowanych
przez pojedyncze atomy lub molekuªy. Ka»dy atom wysy-
ªa fal¦ o okre±lonej polaryzacji. Przy du»ej liczbie atomów
¹ródªa, kierunki wektora ~
E
s¡ jednakowo prawdopodob-
ne i wypadkowa fala b¦d¡ca sum¡ fal emitowanych przez
poszczególne atomy jest fal¡ niespolaryzowan¡.
METODY POLARYZACJI WIATA
Aby otrzyma¢ fal¦ spolaryzowan¡ liniowo, nale»y z
wi¡zki ±wiatªa niespolaryzowanego usun¡¢ wszystkie fale
oprócz tych, których wektor pola elektrycznego ~
E
drga
w jednej pªaszczy¹nie.
Selektywna absorpcja
Pewne substancje anizotropowe zªo»one ze zorientowa-
nych molekuª przepuszczaj¡ tylko te fale, których wek-
tor pola elektrycznego ~
E
ustawiony jest w okre±lonym
kierunku równolegªym do tzw. osi transmisji. Przykªa-
2
dem takiej substancji jest turmalin, szpat islandzki lub
sztucznie wytwarzany materiaª zwany polaroidem. Okre-
±lona orientacja powi¡zanych ze sob¡ molekuª wi¡»e si¦
z istnieniem wyró»nionego kierunku przewodnictwa elek-
trycznego w tych substancjach. W rezultacie molekuªy
absorbuj¡ fale ±wietle, których wektor pola elektrycznego
~
E
jest zgodny z kierunkiem przewodnictwa, a przepusz-
czaj¡ fale maj¡ce wektor elektryczny ~
E
ustawiony pro-
stopadle do kierunku przewodnictwa elektrycznego (tj.
zgodnie z osi¡ transmisji).
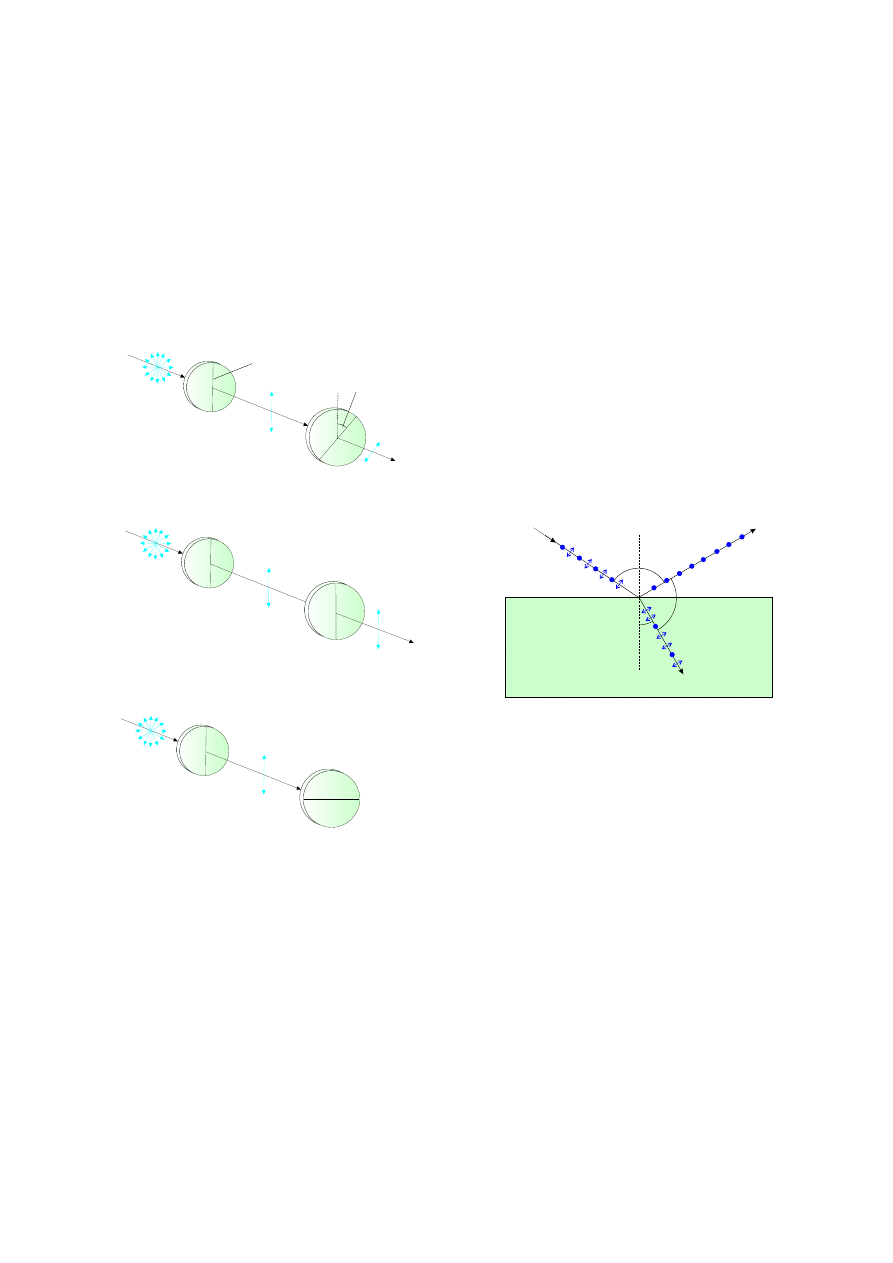
Na Rys. 4a przedstawiono przej±cie ±wiatªa niespolary-
zowanego przez dwie pªytki polaryzuj¡ce, tzw. polaryza-
tory, których osie transmisji tworz¡ k¡t θ. Pierwszy po-
q
E cos
E
0
0
q
Oœ transmisji
a)
b)
c)
Polaryzator
Analizator
E
0
E
0
E
0
Rysunek 4: Dziaªanie ukªadu polaryzator-analizator, gdy: a)
ich osie transmisji tworz¡ k¡t θ, b) osie transmisji s¡ do siebie
równolegªe, c) osie transmisji s¡ do siebie prostopadªe.
laryzator przepuszcza ±wiatªo o wektorze pola elektrycz-
nego ~
E
0
zgodnym z jego osi¡ transmisji. Drugi polaryza-
tor, zwany analizatorem, przepuszcza jedynie skªadow¡
pola ~
E
0
zgodn¡ ze swoj¡ osi¡ transmisji, czyli wektory o
dªugo±ci E
0
cos θ
. Nat¦»enie ±wiatªa jest proporcjonalne
do kwadratu wektora pola elektrycznego, zatem nat¦»e-
nie ±wiatªa po przej±ciu przez analizator wynosi (prawo
Malusa):
I = I
0
cos
2
θ,
(1)
gdzie I
0
to nat¦»enie ±wiatªa padaj¡cego na analiza-
tor. Maksimum przepuszczanego ±wiatªa przez ukªad
polaryzator-analizator nast¦puje, gdy osie transmisji obu
pªytek s¡ zgodne (θ = 0
o
lub 180
o
) - Rys. 4b. Przy pro-
stopadªym ustawieniu osi (θ = 90
o
lub 270
o
) nast¦puje
caªkowite wygaszenie ±wiatªa - Rys. 4c.
Odbicie ±wiatªa
wiatªo ulega caªkowitej lub cz¦±ciowej polaryzacji
podczas odbicia od powierzchni dielektryka. Wi¡zka
±wiatªa podaj¡ca z pró»ni na powierzchni¦ jakiego±
o±rodka cz¦±ciowo si¦ odbija i cz¦±ciowo wchodzi do
o±rodka w formie wi¡zki zaªamanej (Rys. 5). Przy do-
wolnym k¡cie padania 0
o
< α < 90
o
, promie« zaªamany
i odbity s¡ cz¦±ciowo spolaryzowane. Promie« zaªamany
polaryzuje si¦ w kierunku zgodnym z pªaszczyzn¡ pada-
nia, a promie« odbity w kierunku prostopadªym do pªasz-
czyzny padania. Je±li promie« odbity i zaªamany tworz¡
k¡t prosty, wówczas promie« odbity jest spolaryzowany
caªkowicie. Dzieje si¦ to przy k¡cie padania wi¡zki zwa-
90
œwiat³o
niespolaryzowane
o
a
a
b
B
B
ca³kowicie spolaryzowany
promieñ odbity
Rysunek 5: Polaryzacja ±wiatªa przez odbicie od powierzchni
dielektryka.
nym k¡tem Brewstera α
B
. Z prawa zaªamania ±wiatªa
wynika, »e tan α
B
= n
, gdzie n to wspóªczynnik zaªama-
nia o±rodka.
Podwójne zaªamanie
W o±rodkach jednorodnych ±wiatªo porusza si¦ we
wszystkich kierunkach z jednakow¡ pr¦dko±ci¡. Istniej¡
jednak materiaªy krystaliczne, takie jak kalcyt lub kwarc,
w których pr¦dko±¢ ±wiatªa zale»y od kierunku. Gdy pro-
mie« ±wiatªa niespolaryzowanego pada na tak¡ substan-
cj¦, nast¦puje tzw. zjawisko podwójnego zaªamania:
na granicy o±rodka nast¦puje rozszczepienie promienia
na dwa zaªamane pod ró»nym k¡tem promienie, promie«
zwyczajny O i promie« nadzwyczajny E. Ka»dy z za-
ªamanych promieni jest liniowo spolaryzowany (w kie-
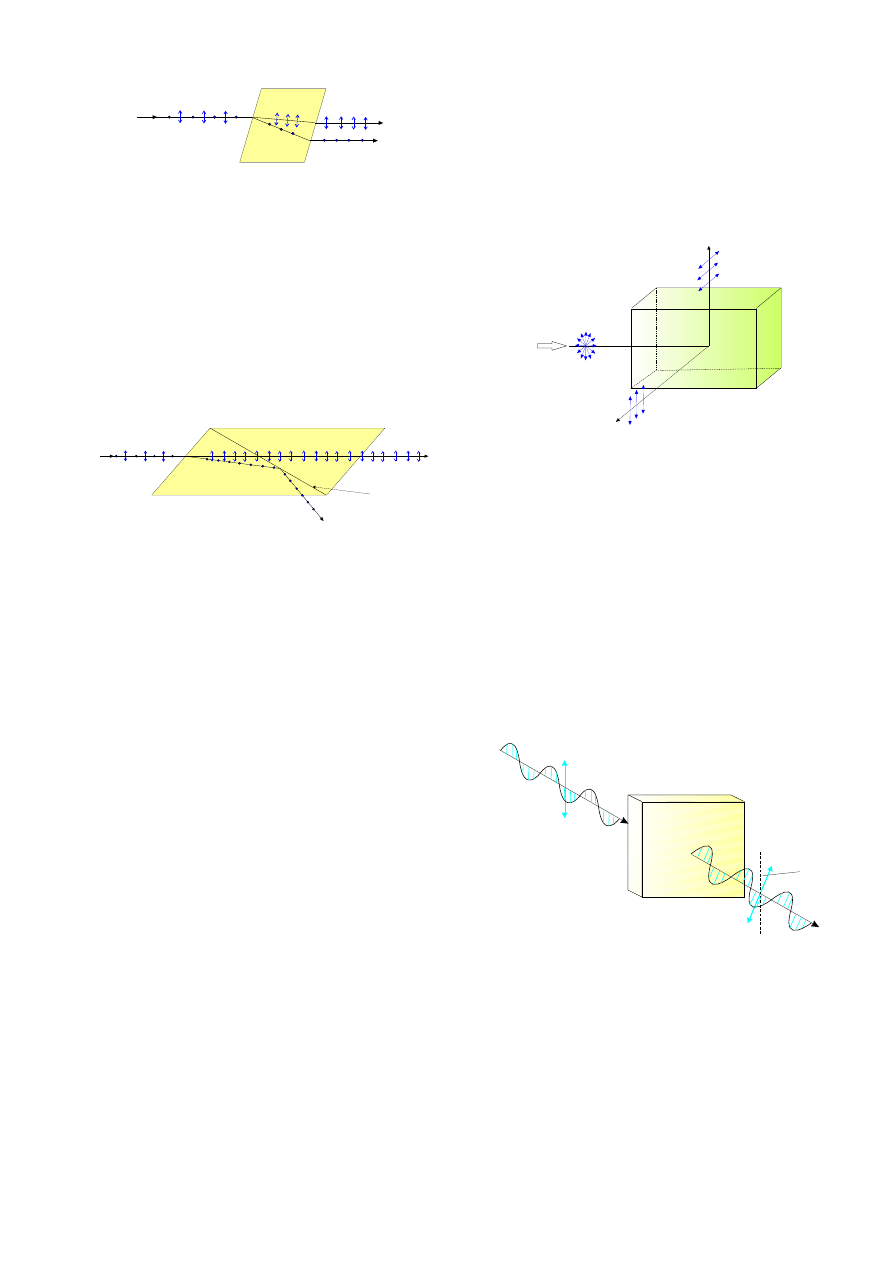
3
œwiat³o
niespolaryzowane
promieñ
nadzwyczajny (E)
promieñ
zwyczajny (O)
Rysunek 6: Bieg promieni ±witlnych przez krysztaª dwójªom-
ny.
runkach wzajemnie prostopadªych). Substancje, w któ-
rych zachodzi zjawisko podwójnego zaªamania nazywamy
krysztaªami dwójªomnymi.
W celu uzyskania ±wiatªa spolaryzowanego liniowo wy-
starczy zastosowa¢ krysztaª dwójªomny i wyeliminowa¢
jeden z promieni. Na tej zasadzie dziaªa polaryzator li-
niowy zwany pryzmatem Nicola lub po prostu niko-
lem (Rys. 7). Skªada si¦ on z dwóch kawaªków krysztaªu
(O)
(E)
balsam
kanadyjski
90
22
68
o
o
o
Rysunek 7: Bieg promieni w pryzmacie Nicola.
dwójªomnego (szpatu islandzkiego) poª¡czonych ze sob¡
balsamem kanadyjskim. Krysztaª dwójªomny powoduje
rozszczepienie wi¡zki na dwa liniowo spolaryzowane pro-
mienie. Obecno±¢ balsamu kanadyjskiego o wspóªczyn-
niku zaªamania mniejszym ni» wspóªczynnik zaªamania
szpatu islandzkiego sprawia, »e promie« zwyczajny O ule-
ga caªkowitemu wewn¦trznemu odbiciu, a przez ukªad
przechodzi jedynie jeden liniowo spolaryzowany promie«
E
.
Rozpraszanie ±wiatªa
wiatªo ulega polaryzacji równie» przy rozproszeniu.
Zjawisko rozproszenia ±wiatªa polega na absorpcji i pra-
wie natychmiastowej reemisji ±wiatªa przez atomy lub
cz¡steczki o±rodka, przez które przechodzi ±wiatªo. Roz-
proszenie ±wiatªa na cz¡steczkach powietrza sprawia, »e
docieraj¡ce do nas ±wiatªo sªoneczne jest cz¦±ciowo spo-
laryzowane. Z rozpraszaniem ±wiatªa na cz¡steczkach po-
wietrza wi¡»e si¦ równie» obserwowany kolor nieba, bo-
wiem najªatwiej rozpraszane jest ±wiatªo o maªej dªugo±ci
fali czyli wªa±nie o barwie niebieskiej.
Polaryzacj¦ ±wiatªa przez rozproszenie tªumaczy si¦
tym, »e ±wiatªo indukuje w cz¡steczkach drgania ªadun-
ków w kierunku prostopadªym do swego kierunku rozcho-
dzenia si¦. Drgaj¡ce ªadunki reemituj¡ ±wiatªo (±wiatªo
rozproszone) o wektorze pola elektrycznego ~
E
zgodnym
z kierunkiem ich drga«. Poniewa» fale ±wietlne s¡ po-
przeczne, wobec tego o±rodek mo»e wysyªa¢ fale tylko w
kierunkach prostopadªych do kierunku wªasnych drga«.
Tak wi¦c wi¡zka rozproszona pod k¡tem prostym wzgl¦-
dem wi¡zki padaj¡cej b¦dzie zawsze spolaryzowana w
pªaszczy¹nie prostopadªej do kierunku wi¡zki padaj¡cej
(Rys. 8).
Rysunek 8: Polaryzacja ±wiatªa przez rozproszenie.
SKRCENIE PASZCZYZNY POLARYZACJI
WIATA
W 1811 roku Dominique Arago stwierdziª, »e pªytka
kwarcowa powoduje skr¦canie pªaszczyzny polary-
zacji ±wiatªa przechodz¡cego przez t¡ pªytk¦. To znaczy,
±wiatªo liniowo spolaryzowane w pewnej pªaszczy¹nie po
przej±ciu przez pªytk¦ kwarcow¡ wci¡» byªo spolaryzowa-
ne liniowo ale w innej pªaszczy¹nie, obróconej (skr¦conej)
o pewien k¡t φ wzgl¦dem pªaszczyzny pierwotnej (Rys.
9).
f
p³ytka kwarcowa
Rysunek 9: Pªaszczyzna polaryzacji ±wiatªa ulega skr¦ceniu o
k¡t φ po przej±ciu przez pªytk¦ kwarcow¡.
W 1815 roku Jean Baptist Biot odkryª, »e naturalnie
wyst¦puj¡ce zwi¡zki organiczne takie jak cukier, terpen-
tyna, i kwas winny s¡ aktywne (czynne) optycznie
tj. skr¦caj¡ pªaszczyzn¦ polaryzacji ±wiatªa. Pªaszczyzna
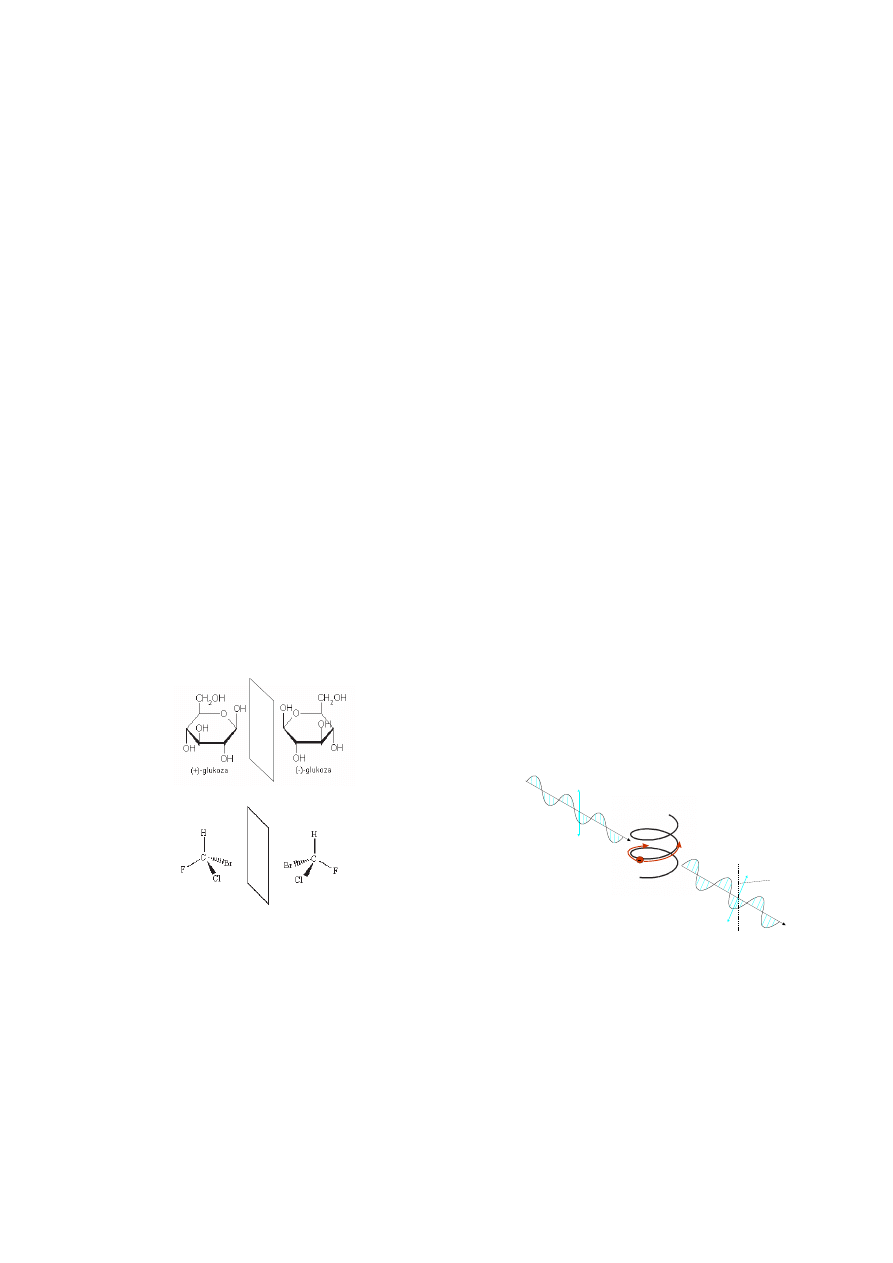
4
polaryzacji ±wiatªa ulega skr¦ceniu przy przej±ciu ±wiatªa
przez o±rodki optycznie czynne takie jak: glukoza, fruk-
toza, sacharoza, wi¦kszo±¢ olejków eterycznych, biaªka,
alkaloidy. Istniej¡ substancje, które s¡ optycznie czynne
w stanie krystalicznym, a roztwory tych substancji nie
wykazuj¡ tej wªa±ciwo±ci, oraz substancje, które w stanie
ciekªym i gazowym, a tak»e w roztworach s¡ optycznie
czynne.
W 1848 roku Louis Pasteur badaj¡c sól kwasu winowe-
go stwierdziª, »e winian sodowo-amonowy wyst¦puje jako
mieszanina dwóch rodzajów krysztaªów b¦d¡cych wza-
jemnymi lustrzanymi odbiciami. Rozdzieliwszy te dwa ro-
dzaje krysztaªów, sporz¡dziª z nich dwa rodzaje roztwo-
rów. Okazaªo si¦, »e jeden roztwór wykazywaª aktywno±¢
optyczn¡ prawoskr¦tn¡, a drugi lewoskr¦tn¡. Poniewa»
rozpuszczona substancja nie posiada okre±lonej struktury
krystalicznej, Pasteur wywnioskowaª st¡d, »e przyczyn¡
aktywno±ci optycznej winianu sodowo-amonowy s¡ dwa
rodzaje cz¡steczek ró»ni¡cych si¦ aktywno±ci¡ optyczn¡.
Rzeczywi±cie, okazuje si¦, »e zwi¡zki o takim sa-
mym wzorze sumarycznym mog¡ ró»ni¢ si¦ wªa±ciwo-
±ciami zyko-chemicznymi. Zwi¡zki takie nazywamy izo-
merami. Izomery ró»ni¡ce si¦ rozmieszczeniem atomów
w przestrzeni, nazywa si¦ stereoizomerami. Stereo-
izomery b¦d¡ce swoim lustrzanym odbiciem nazywane
s¡ enancjomerami, pozostaªe diastereoizomerami.
Cz¡steczki danego zwi¡zku nazywamy chiralnymi, je±li
istniej¡ w formie dwóch nienakªadalnych na siebie enan-
cjomerów (tak jak r¦ka lewa i prawa albo spr¦»yna lewo-
i prawoskr¦tna, b¦d¡c swymi zwierciadlanymi odbiciami,
s¡ nienakªadalne na siebie). Przykªady zwi¡zków chiral-
nych przedstawiono na Rys. 10.
bromochlorofluorometan
Rysunek 10: Zwi¡zki chiralne wyst¦puj¡ w postaci dwóch nie-
nakªadalnych na siebie odbi¢ lustrzanych (enancjomerów).
Generalnie, warunkiem koniecznym wyst¦powania
czynno±ci optycznej cz¡steczek jest ich chiralno±¢. Jeden
z enancjomerów cz¡stek chiralnych wykazuje aktywno±¢
optyczn¡ prawo- a drugi lewoskr¦tn¡. Je±li roztwór za-
wiera enancjomery prawo- i lewoskr¦tne w tej samej ilo-
±ci (jest to tzw. roztwór racemiczny), nie jest on czynny
optycznie. Aktywno±¢ optyczn¡ wykazuj¡ roztwory za-
wieraj¡ce tylko jeden z enancjomerów cz¡stek chiralnych
lub oba rodzaje, ale w ró»nych proporcjach. Aktywno±¢
optyczna substancji naturalnych (szczególnie aminokwa-
sów) spowodowana jest tym, »e wyst¦puj¡ one w przy-
rodzie w przewa»aj¡cej cz¦±ci w formie cz¡steczek lewo-
skr¦tnych.
Aktywno±¢ optyczna kwarcu zwi¡zana jest nie tyle
z budow¡ cz¡steczek ale z jego struktur¡ krystaliczn¡
(±wiadczy o tym to, »e zmielony lub ciekªy kwarc nie wy-
kazuje aktywno±ci optycznej). Kwarc wyst¦puje w dwóch
formach krystalicznych wykazuj¡cych prawo- i lewoskr¦t-
n¡ aktywno±¢ optyczn¡. Mówimy, »e s¡ to struktury
enancjomorczne.
Okazuje sie, »e dla niektórych substancji aktywnych
optycznie (sacharydów) b¦d¡cych w formie roztworów k¡t
skr¦cenia pªaszczyzny polaryzacji mo»e zmienia¢ si¦ w
czasie. Zjawisko to nazywamy mutarotacj¡. Przyczyn¡
mutarotacji jest zmiana wzgl¦dnej liczby enancjomerów
prawo- i lewoskr¦tnych w roztworze (jeden rodzaj izome-
ru przeksztaªca sie w drugi). Proces ten trwa a» do usta-
lenia si¦ równowagi chemicznej mi¦dzy izomerami. Na
przykªad w stanie równowagi roztwór wodny D-glukozy
zawiera 35,5% formy α i 64,5% formy β.
WYJANIENIE ZJAWISKA AKTYWNOCI
OPTYCZNEJ
Nienakªadalne na siebie enancjomery cz¡stek chiral-
nych mo»na porówna¢ do obiektów w ksztaªcie ±ruby
prawo- lub lewoskr¦tnej. Zaªó»my, »e roztwór skªada si¦
tylko z jednego rodzaju enacjomeru, np. prawoskr¦tne-
go. Je±li ±wiatªo spolaryzowane pada na cz¡stk¦ ±rubow¡,
wówczas pobudza do drga« znajduj¡ce si¦ w cz¡steczce
elektrony, które w takiej cz¡steczce musz¡ porusza¢ si¦
po drodze spiralnej - Rys. 11. Z powodu ruchu ±rubo-
df
Rysunek 11: Model cz¡stki chiralnej. Elektron pobudzany do
drga« przez fal¦ spolaryzowan¡ liniowo drga wzdªu» linii ±ru-
bowej. Reemitowana przez drgaj¡cy elektron fala ma wekto-
ry ±wietlne uªo»one w pªaszczy¹nie obróconej o maªy k¡t δφ
wzgl¦dem pªaszczyzny polaryzacji ±wiatªa padaj¡cego.
wego elektronu reemitowana przez niego fala elektroma-
gnetyczna ma wektory ±wietlne o kierunku niezgodnym z
5
kierunkiem wektorów ±wietlnych padaj¡cej fali, a zatem
b¦dzie spolaryzowana w innej pªaszczy¹nie ni» fala pa-
daj¡ca. Mo»na pokaza¢, »e efekt ten zachodzi niezale»nie
od orientacji cz¡steczki i zawsze obrót wektora ±wietl-
nego zachodzi w t¦ sam¡ stron¦. Przej±ciu fali spolary-
zowanej przez cz¡steczki spiralne o jednakowej skr¦tno-
±ci towarzyszy zatem zmiana pªaszczyzny polaryzacji fali
(aktywno±¢ optyczna).
K¡t skr¦cenia pªaszczyzny polaryzacji φ jest propor-
cjonalny do liczby cz¡steczek, na które traa fala pod-
czas przechodzenia przez roztwór. Oznacza to, »e φ jest
proporcjonalne do st¦»enia roztworu c (wyra»onego w
g/cm
3
) oraz do dªugo±ci drogi ±wiatªa w roztworze l (pra-
wo Biota):
φ = [α] c l.
(2)
Wspóªczynnik proporcjonalno±ci [α] zwany jest skr¦ce-
niem wªa±ciwym i zale»y on od rodzaju substancji roz-
puszczonej, temperatury, rozpuszczalnika i dªugo±ci fali
±wiatªa. Znaj¡c wspóªczynnik [α] i mierz¡c k¡t skr¦cenia
pªaszczyzny polaryzacji φ mo»na na podstawie wzoru (2)
wyznaczy¢ nieznane st¦»enie roztworu.
POLARYMETR
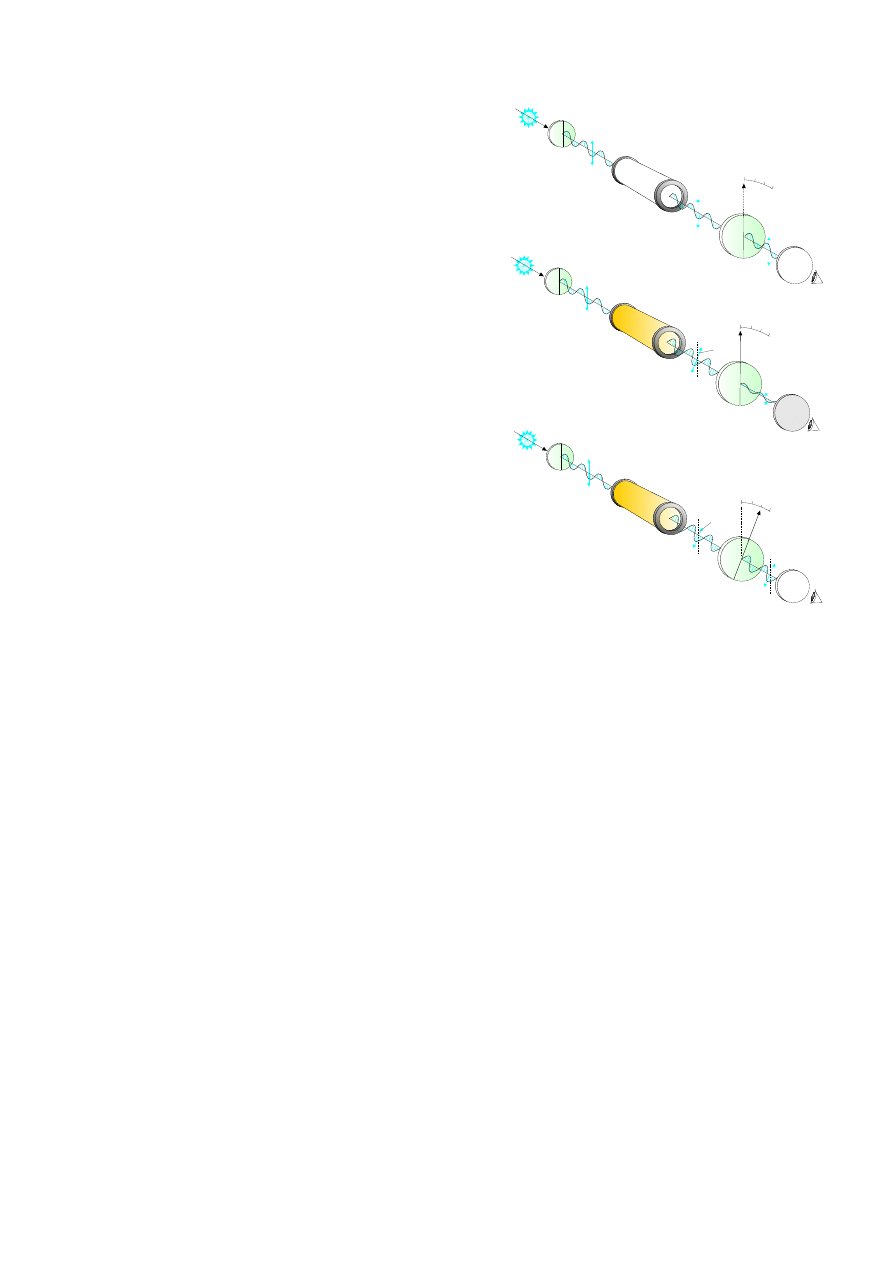
Zasada dziaªania
Do pomiaru kata skr¦cenia pªaszczyzny polaryzacji
sªu»y polarymetr. Ide¦ dziaªania polarymetru przedsta-
wiono na Rys. 12. wiatªo niespolaryzowane przechodzi
przez polaryzator P1 ulegaj¡c polaryzacji. Spolaryzowa-
na wi¡zka przechodzi przez rurk¦ R, w której umieszcza
si¦ badane roztwory. Je±li rurka zawiera wod¦ lub inn¡
substancje nieczynn¡ optycznie (Rys. 12a)), ±wiatªo wy-
chodzi z niej spolaryzowane w tej samej pªaszczy¹nie, w
jakiej byªo spolaryzowane przed wej±ciem do rurki. Na-
st¦pnie traa na drugi polaryzator P2 (analizator). Je±li
o± transmisji polaryzatora P2 jest zgodna z osi¡ transmi-
sji polaryzatora P1 (a wi¦c i kierunkiem polaryzacji ±wia-
tªa), otrzymujemy jasno o±wietlone pole widzenia. Je±li
w rurce umie±cimy substancj¦ czynna optycznie (Rys.
12b)), wówczas ±wiatªo po wyj±ciu z rurki jest spolaryzo-
wane liniowo w innej pªaszczy¹nie ni» przed wej±ciem do
rurki. Pªaszczyzna polaryzacji ±wiatªa zostaje obrócona
o k¡t φ. Je»eli o± transmisji analizatora P2 pozostawi-
my zgodn¡ z osi¡ polaryzatora P1, wtedy pole widzenia
ulegnie przyciemnieniu, bowiem analizator przepu±ci je-
dynie skªadow¡ pola elektrycznego fali padaj¡cej równ¡
E
0
cos φ
. Aby odzyska¢ pierwotn¡ maksymaln¡ jasno±¢
pola widzenia, nale»y analizator obróci¢ o k¡t skr¦cenia
pªaszczyzny polaryzacji φ. Wtedy bowiem ponownie caªe
pole elektryczne zostaje przepuszczone przez analizator.
Ze skali doª¡czonej do analizatora mo»na odczyta¢ k¡t φ.
0
0
0
f
f
f
P1
P2
R
a)
b)
c)
Rysunek 12: Zasada dziaªania polarymetru (opis w tek±cie).
Polarymetr póªcieniowy
W opisanej powy»ej metodzie pomiar kata skr¦cenia
polaryzacji ±wiatªa wymaga ustawienia analizatora w ta-
kiej pozycji, by uzyskiwa¢ maksymalne o±wietlenie po-
la widzenia. Poniewa» do±¢ trudno ocenia si¦ maksimum
jasno±ci, w praktyce u»ywa si¦ polarymetrów z dodatko-
wym elementem, tzw. pªytk¡ póªcieniow¡ PP (Rys. 13).
Jest to pªytka kwarcowa, która przesªania poªow¦ pola
widzenia. Zaªó»my, »e w rurce R jest woda lub inna sub-
stancja nieczynna optycznie. Z powodu tego, »e w póªcie-
niowej pªytce kwarcowej zachodzi skr¦cenie pªaszczyzny
polaryzacji o pewien maªy k¡t β, przy zgodnych osiach
transmisji polaryzatora P1 i analizatora P2, poªowa pola
widzenia b¦dzie przyciemniona (Rys. 13a). W tej sytuacji
nale»y ustawi¢ analizator w takiej pozycji, by obie po-
ªówki pola widzenia byªy jednakowo zaciemnione. atwo
dostrzec, »e aby to osi¡gn¡¢ o± transmisji analizatora po-
winna pokrywa¢ si¦ z dwusieczn¡ kata β. Wtedy bowiem
w obu poªówkach pola widzenia przepuszczona zostanie
przez analizator skªadowa pola elektrycznego o tej samej
warto±ci E
0
cos(β/2)
. Na skali k¡towej polarymetru po-
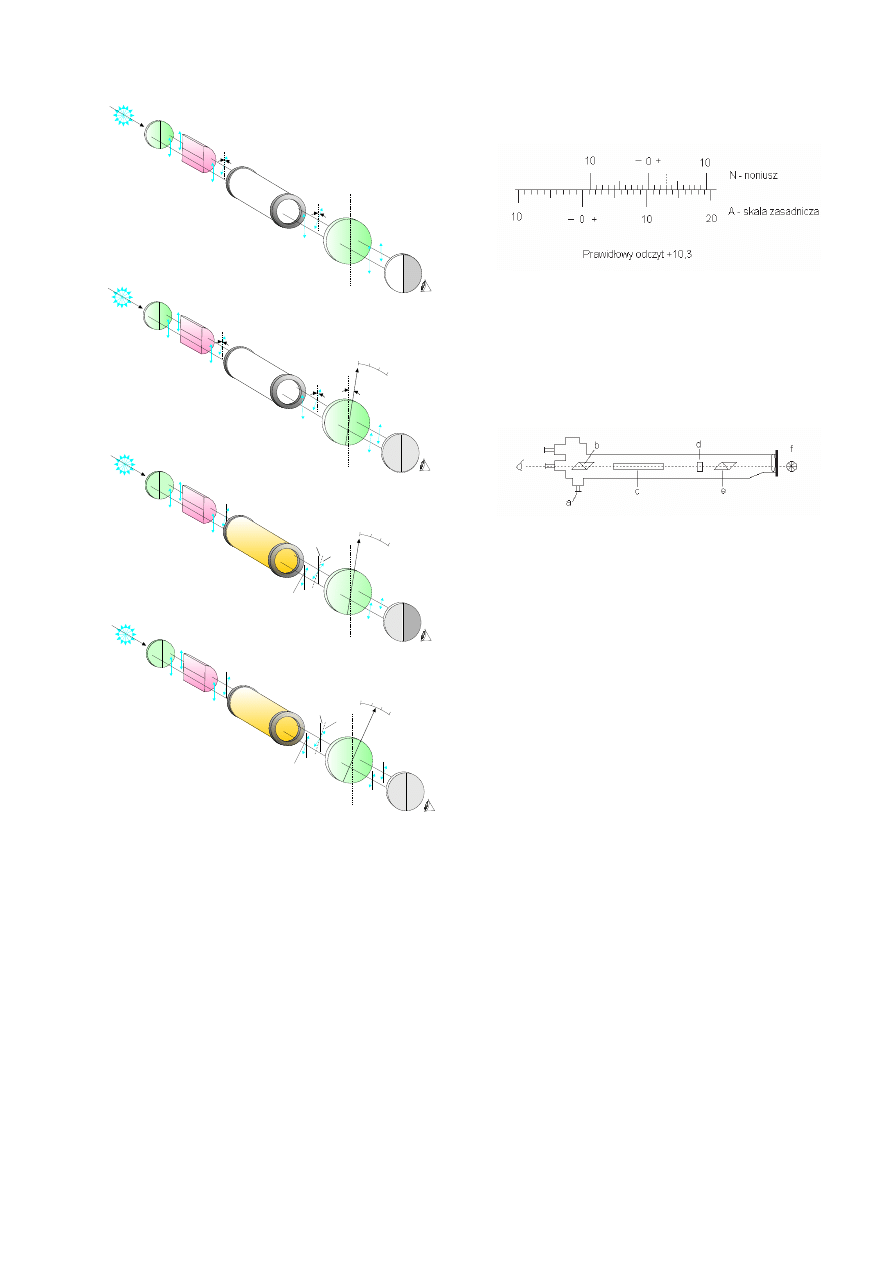
6
0
f
f
0
a)
b)
c)
0
f
f
f
d)
b
b
b
b/2
b
PP
P1
P2
R
b
b
Rysunek 13: Zasada dziaªania polarymetru póªcieniowego
(opis w tek±cie).
winni±my mie¢ wtedy warto±¢ 0 (Rys. 13b).
Je±li w rurce R umie±cimy ciecz optycznie czynn¡, to
pªaszczyzna polaryzacji ±wiatªa po wyj±ciu z rurki ule-
gnie skr¦ceniu o taki sam k¡t φ w caªym polu widzenia,
co spowoduje ró»nice o±wietlenia poszczególnych jego po-
ªówek (Rys. 13c). Przywrócenie równego o±wietlenia do-
konuje si¦ przez obrót analizatora P2 dokªadnie o k¡t
φ
równy skr¦ceniu pªaszczyzny polaryzacji przez badan¡
ciecz (Rys. 13d). Analizator zaopatrzony jest w podziaª-
k¦ k¡tow¡ z noniuszem, co pozwala na odczyt kata φ
z dokªadno±ci¡ do dziesi¡tych cz¦±ci stopnia - Rys. 14.
Szczegóªowy schemat polarymetru Laurenta u»ywanego
Rysunek 14: Zasada posªugiwania si¦ skal¡ z noniuszem: Kre-
ska 0 noniusza jest wskazówk¡ dla skali zasadniczej. Kre-
ska noniusza pokrywaj¡ca si¦ z któr¡± kresk¡ skali zasadniczej
wskazuje liczb¦ dzi¦si¡tych cz¦±ci k¡ta.
na pracowni przedstawiono na Rys. 15.
Rysunek 15: Polarymetr Laurenta: a - ±ruba reguluj¡ca poªo-
»enie analizatora, b - analizator (nikol), c - rurka pomiarowa z
roztworem, d - póªcieniowa pªytka kwarcowa, e - polaryzator
(nikol), f - ¹ródªo ±wiatªa.
WYKONANIE WICZENIA
1. Ustawi¢ lamp¦ naprzeciw polaryzatora tak, aby
pole widzenia byªo dostatecznie o±wietlone.
2. Obracaj¡c analizator ustawi¢ go w takiej pozycji,
aby obie poªówki pola widzenia byªy jednakowo o±wie-
tlone. Odczyta¢ wynik ustawienia na skali z noniuszem
i zapisa¢ wynik pomiaru. Powtórzy¢ pomiar 10 razy i
wyniki zapisa¢ jako φ
0
.
3. Napeªni¢ rurk¦ pomiarow¡ wod¡ destylowan¡ i
wstawi¢ j¡ do polarymetru. Sprawdzi¢ czy zmieniªa
si¦ warto±¢ φ
0
. (Je»eli tak, wymy¢ dokªadnie rurk¦ i
powtórzy¢ punkt 2 i 3).
4. Napeªni¢ nim rurk¦ pomiarow¡ roztworem cukru o
st¦»eniu c = (10 g cukru) /100 cm
3
. Uwaga: W rurce nie
mog¡ pozosta¢ p¦cherzyki powietrza.
5. Wªo»y¢ rurk¦ z roztworem do polarymetru i zmie-
rzy¢ k¡t skr¦cenia (10 razy) oznaczy¢ t¡ warto±¢ jako φ
1
.

7
6. Podobnie wykona¢ pomiary k¡ta skr¦cenia (tak»e 10
razy ) dla roztworu o st¦»eniu c
A
(roztwór A) i st¦»eniu
c
B
(roztwór B). Wyniki oznaczy¢ odpowiednio jako φ
A
i
φ
B
.
OPRACOWANIE WYNIKÓW
1. Wyliczy¢ warto±ci ±rednie φ
0
´
sr
, φ
1
´
sr
, φ
A
´
sr
, φ
B
´
sr
.
2. Obliczy¢ skr¦cenie wªa±ciwe cukru korzystaj¡c ze
wzoru:
[α] =
φ
1
− φ
0
c · l
,
(3)
gdzie:
c
- st¦»enie roztworu = 10 g / 100 cm
3
l
- dªugo±¢ rurki pomiarowej = 14,8 cm,
a za warto±ci φ
0
i φ
1
wstawi¢ uzyskane w p. 1 wyniki dla
φ
0
´
sr
i φ
1
´
sr
. Wyniki nale»y poda¢ w jednostkach cm
2
/g
.
3. Obliczy¢ st¦»enie roztworu A korzystaj¡c z zale»no-
±ci:
c
A
=
φ
A
− φ
0
[α] · l
,
(4)
wstawiaj¡c za φ
A
otrzyman¡ w p. 1 warto±¢ φ
A
´
sr
.
4. Podobnie jak dla roztworu A obliczy¢ st¦»enie
roztworu B.
5. Dla roztworów A i B obliczy¢ skªady procentowe
tych roztworów wedªug wzoru:
p = c/d,
przy czym: c - st¦»enie roztworu,
d
- g¦sto±¢ roztworu, któr¡ nale»y odczyta¢ z zaª¡czonej
tabeli.
Tabela:
Zale»no±¢ g¦sto±ci roztworów cukru od jego st¦»enia.
c [g/100cm
3
]
d [g/cm
3
]
1
1,0021
5
1,0177
10
1,0367
15
1,0558
20
1,0748
25
1,0942
30
1,1136
DYSKUSJA BDU
1. Ze wzgl¦du na 10-cio krotne powtarzanie pomiarów
obliczy¢ bª¡d ±redni kwadratowy ±rednich φ
0
´
sr
, φ
1
´
sr
,
φ
A
´
sr
, φ
B
´
sr
zgodnie ze wzorem 2, strona 13 (Opracowanie
i prezentacja wyników pomiarów).
2. Za bª¡d maksymalny pomiaru ±rednich φ
0
´
sr
, φ
1
´
sr
,
φ
A
´
sr
, φ
B
´
sr
przyj¡¢ trzykrotn¡ warto±¢ ich bª¦du ±rednie-
go kwadratowego.
3. Metod¡ ró»niczki zupeªnej policzy¢ maksymalny
bª¡d pomiaru [α]:
∆[α] =
¯
¯
¯
¯
∂[α]
∂φ
0
¯
¯
¯
¯ ∆φ
0
+
¯
¯
¯
¯
∂[α]
∂φ
1
¯
¯
¯
¯ ∆φ
1
,
(5)
a nast¦pnie bª¡d maksymalny pomiaru st¦»enia c
A
i c
B
wedªug schematu:
∆c
A
=
¯
¯
¯
¯
∂c
A
∂[α]
¯
¯
¯
¯ ∆[α] +
¯
¯
¯
¯
∂c
A
∂φ
0
¯
¯
¯
¯ ∆φ
0
+
¯
¯
¯
¯
∂c
A
∂φ
A
¯
¯
¯
¯ ∆φ
A
.
(6)
LITERATURA UZUPENIAJCA
1. Sz. Szczeniowski, Fizyka do±wiadczalna, cz¦±¢ IV,
s. 359-465.
2. Szyszko, Instrumentalne metody analityczne, PZWL
1982, s. 66-91.
3. Shurcli i S. S. Ballard, wiatªo spolaryzowane, PWN
1968.
4. Zbigniew Kami«ski, Fizyka (dla kandydatów na
wy»sze uczelnie techniczne, WNT 1965, s. 328-332.
5. Pigo« i Z. Zruzewicz, Chemia zyczna, cz. 2.
6. D. Hollyday, R. Resnick, Fizyka T. 2, s. 561-579.
7. Feynman, Feynmana wykªady z zyki, T. 1, cz¦±¢ 2,
s. 106-120.
8. M. Massalska, J. Masalski, Fizyka kl. IV, s. 110-121.
9. S. Przestalski, Fizyka z elementami biozyki i agro-
zyki, PWN, 19977, s. 183-193.
10. R. T. Morrison, R. N. Boyd, Chemia organiczna,
PWN, T1, s. 154-179.
11. Cz. Bobrowski Fizyka (krótki kurs dla in»ynierów),
WNT, 1981, s. 291-297.
Wyszukiwarka
Podobne podstrony:
cw 45
Nowy folder, cw 45 Marcin Mis, 1
cw 45
cw 45, Fizyka
Ćw. 45, BIOTECHNOLOGIA POLITECHNIKA ŁÓDZKA, CHEMIA FIZYCZNA
cw 45 lim
ćw 45 doc
cw 1(45)
cw 45
fizyczna ćw 45
cw 45
cw 45 limian
cw 1(45)
Ćw nr 45, 45, Imie Nazwisko
Ćw nr 45, 45 - prawa Malusa2, Politechnika Rzeszowska
Ćw nr 45, 45 - prawa Malusa2, Politechnika Rzeszowska
Ćw nr 45, wykres 45
Ćw nr 45, 45,,, Imie Nazwisko
Ćw nr 45, FIZ45, Imie Nazwisko
więcej podobnych podstron