WPROWADZENIE

DO SZTUCZNEJ INTELIGENCJI

POLITECHNIKA WARSZAWSKA

WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA

MEL

MEL

NS 586

Dr in

ż

. Franciszek Dul

© F.A. Dul 2007

6. GRY

−

POSZUKIWANIA

W OBECNOŚCI PRZECIWNIKA

© F.A. Dul 2007

W OBECNOŚCI PRZECIWNIKA

Gry

Poka

ż

emy, w jaki sposób agent mo

ż

e

osi

ą

gn

ąć

zamierzony cel je

ż

eli musi

kooperowa

ć

lub konkurowa

ć

albo nawet

walczy

ć

z innymi agentami.

© F.A. Dul 2007

walczy

ć

z innymi agentami.

• Czym s

ą

gry?

• Decyzje optymalne w grach.
• Przycinanie

α

–

β

.

• Gry z elementami hazardu.
• Nieidealne decyzje podejmowane w czasie

rzeczywistym.

Plan rozdziału

© F.A. Dul 2007

6.1. Czym s

ą

gry?

Istota gier: s

ą

to zadania z wieloma agentami działaj

ą

cymi

(konkuruj

ą

cymi) w tym samym

ś

rodowisku.

• Co robi

ą

inni agencji i w jaki sposób wpływaj

ą

na działania naszego agenta?

•

Ś

rodowiska wieloagentowe mog

ą

by

ć

kooperatywne

lub konkurencyjne;

• Konkurencyjne

ś

rodowiska wieloagentowe prowadz

ą

do zada

ń

poszukiwania z przeciwnikiem, czyli gier.

© F.A. Dul 2007

do zada

ń

poszukiwania z przeciwnikiem, czyli gier.

Jaki jest cel analizy gier?

• Zabawa, hazard;
• S

ą

to zagadnienia interesuj

ą

ce, ale cz

ę

sto bardzo

trudne;

• S

ą

łatwe do sformułowania; agenci mog

ą

zwykle

wykonywa

ć

niewiele działa

ń

;

• Słu

ż

y budowie robotów które maj

ą

działa

ć

w

ś

rodowisku

nieprzyjaznym;

Relacja gier i poszukiwa

ń

Poszukiwania – nie ma przeciwnika.

• Rozwi

ą

zanie jest heurystyczn

ą

metod

ą

osi

ą

gni

ę

cia celu.

• Heurystyki i CSP mog

ą

znale

źć

rozwi

ą

zanie optymalne.

• Funkcja szacuj

ą

ca - oszacowanie kosztu przej

ś

cia

od startu do celu poprzez dany w

ę

zeł.

• Przykłady: planowanie dróg, opracowywanie

harmonogramów.

6.1. Gry

© F.A. Dul 2007

Gry – s

ą

przeciwnicy.

• Rozwi

ą

zanie jest

strategi

ą

gry

, czyli odpowiedzi

ą

na ka

ż

de działanie przeciwnika;

• Ograniczenia czasowe gry wymuszaj

ą

znajdywanie

rozwi

ą

za

ń

przybli

ż

onych.

• Funkcja szacuj

ą

ca - oszacowanie „dobroci” sytuacji.

• Przykłady: szachy, warcaby, Trik-trak (backgammon),

kółko i krzy

ż

yk (Tic-Tac-Toe), Othello, Go.

Klasyfikacja gier

6.1. Gry

Deterministyczne

Hazardowe

Informacja
pełna

Szachy,
Warcaby,
Go,
Othello,
Kółko i krzy

ż

yk

Trik-trak
(backgammon),
Monopoly

© F.A. Dul 2007

Kółko i krzy

ż

yk

Informacja
niepełna

Bryd

ż

,

Poker,
Scrabble,
wojna atomowa

6.2. Definicja gry

W grze uczestnicz

ą

dwaj gracze: MAX i MIN.

Gra jako poszukiwanie

• Stan pocz

ą

tkowy: np. ustawienie szachów

na szachownicy;

• gr

ę

rozpoczyna MAX;

• ruchy wykonuj

ą

naprzemian a

ż

do zako

ń

czenia gry;

• zwyci

ę

zca otrzymuje nagrod

ę

, przegrany ponosi kar

ę

.

© F.A. Dul 2007

na szachownicy;

• Funkcja nast

ę

pnika: lista ruchów (stanów) spełniaj

ą

cych

reguły gry;

• Test ko

ń

ca - czy gra si

ę

zako

ń

czyła?

• Funkcja u

ż

yteczno

ś

ci - definiuje warto

ś

ci stanów

ko

ń

cowych, np. zwyci

ę

zca (+1), przegrany (-1)

oraz remis(0) w grze kółko i krzy

ż

yk (tic-tac-toe).

Gracz MAX u

ż

ywa algorytmu przeszukiwania drzewa

do wyznaczenia nast

ę

pnego ruchu.

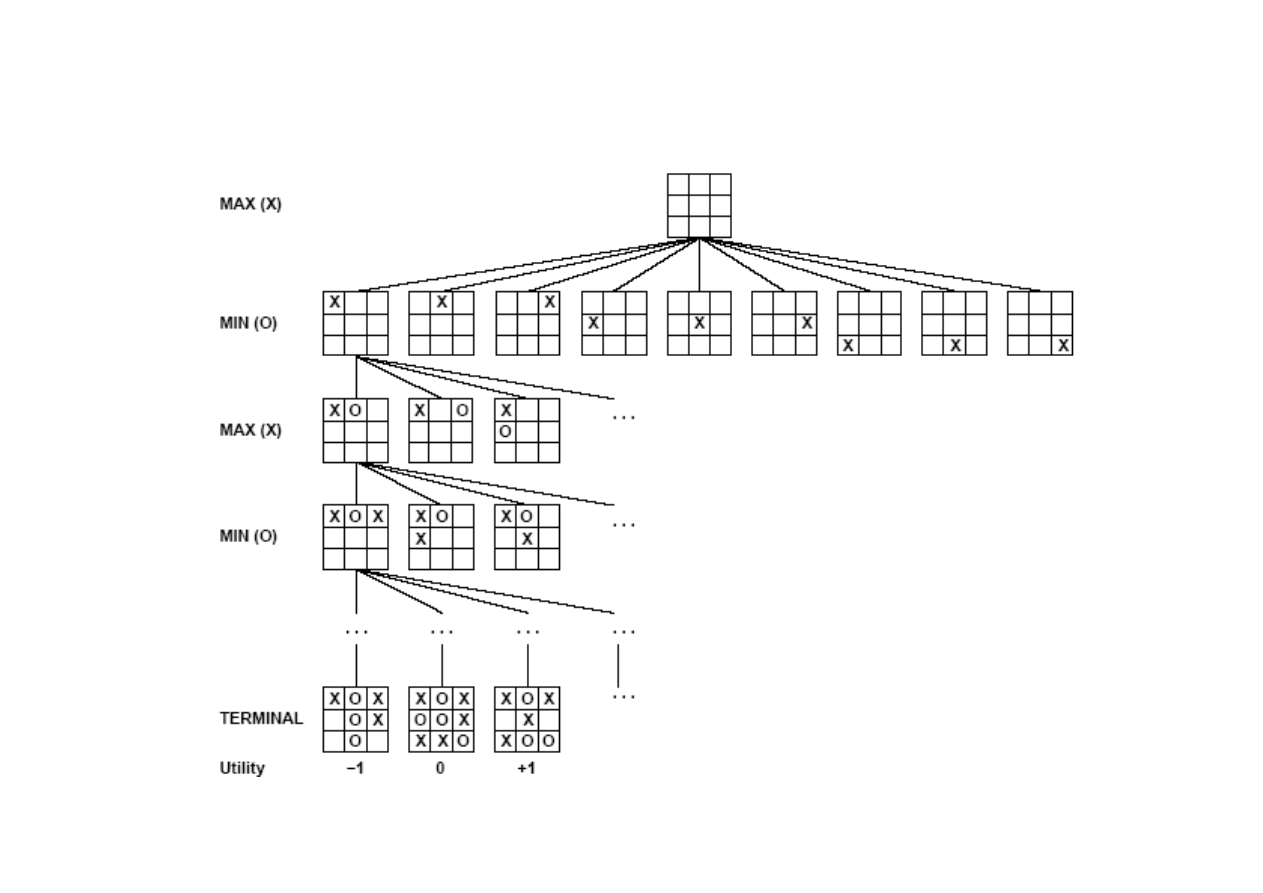
Drzewo gry w kółko i krzy

ż

yk

6.2. Definicja gry

© F.A. Dul 2007

Strategie optymalne

Znale

źć

strategi

ę

warunkow

ą

dla gracza MAX przy zało

ż

eniu,

ż

e MIN jest przeciwnikiem nieomylnym.

Znaj

ą

c drzewo gry strategi

ę

optymaln

ą

mo

ż

na wyznaczy

ć

na podstawie warto

ś

ci minimax dla ka

ż

dego w

ę

zła.

6.2. Definicja gry

Zało

ż

enie - obaj gracze graj

ą

optymalnie.

Nale

ż

y wybra

ć

ruch do w

ę

zła który ma najwi

ę

ksz

ą

warto

ść

minimax:

© F.A. Dul 2007

Odpowiada to uzyskaniu najkorzystniejszego wyniku przy
najlepszej grze.

minimax:

MINIMAX-VALUE(n) =

UTILITY(n)

If n is a terminal

max

s

∈

successors(n)

MINIMAX-VALUE(s)

If n is a max node

min

s

∈

successors(n)

MINIMAX-VALUE(s)

If n is a min node

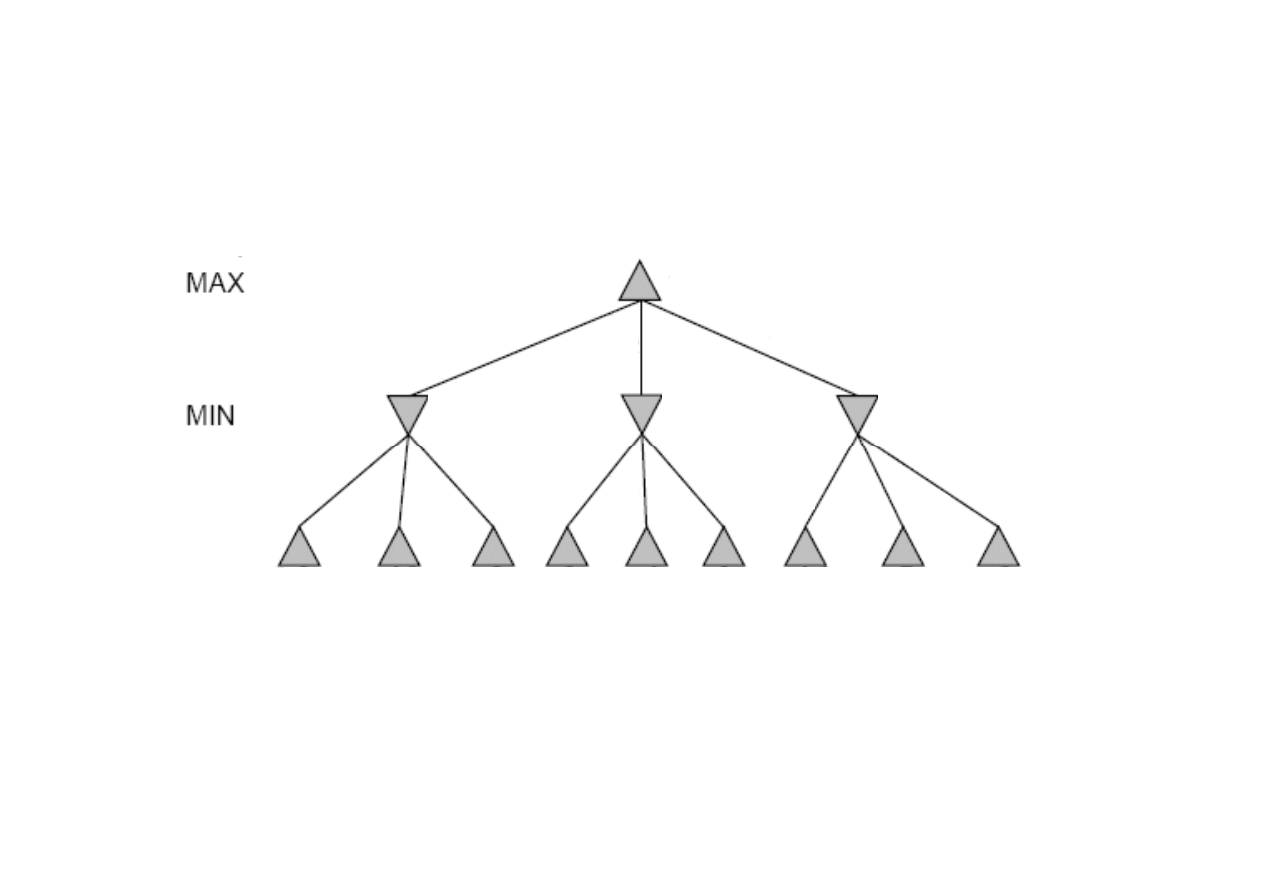
Algorytm MINIMAX

6.2. Definicja gry

Zasada algorytmu minimax dla dwóch graczy MAX i MIN

© F.A. Dul 2007

Drzewo gry dla dwóch przeciwników.

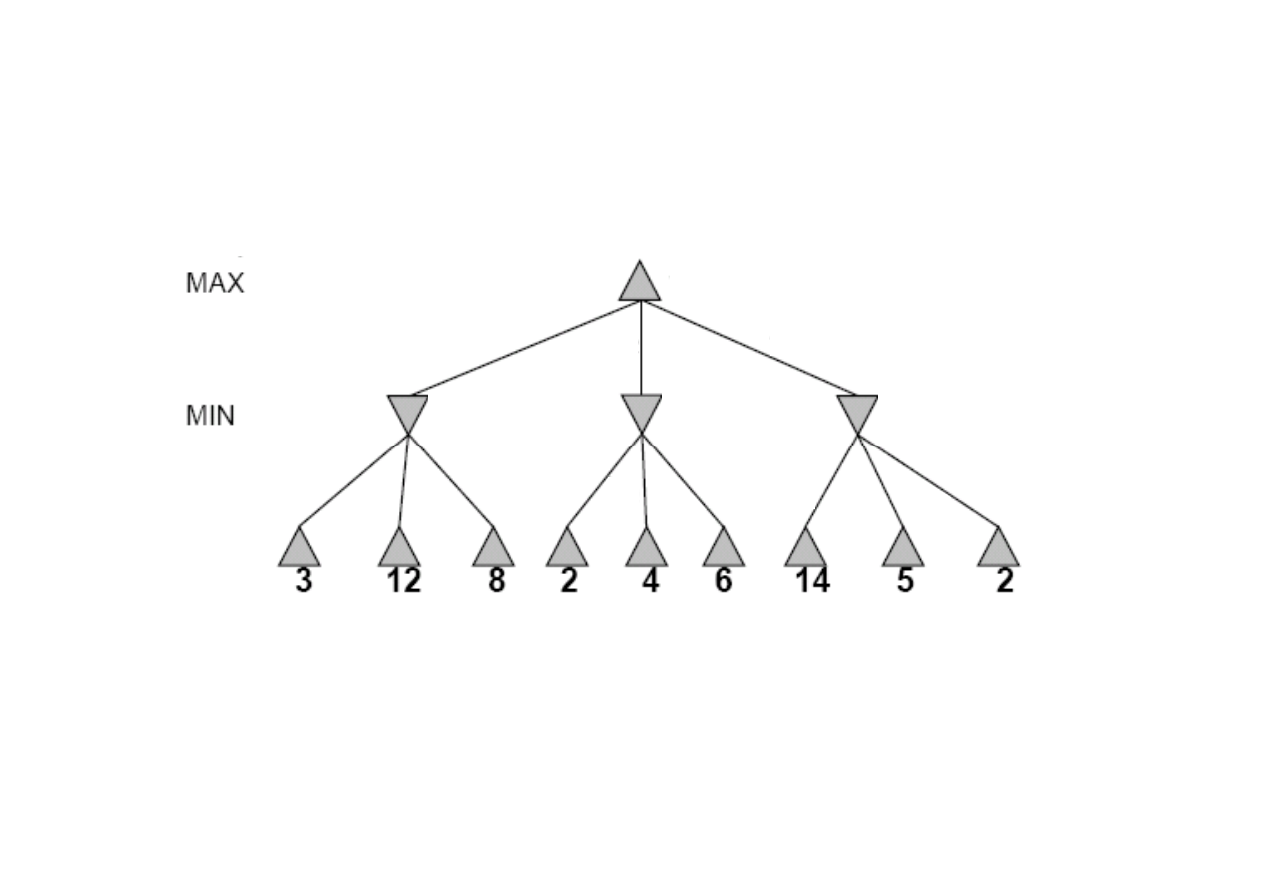
Algorytm MINIMAX

6.2. Definicja gry

Zasada algorytmu minimax dla dwóch graczy MAX i MIN

© F.A. Dul 2007

Warto

ś

ci funkcji kosztu dla w

ę

złów ko

ń

cowych.

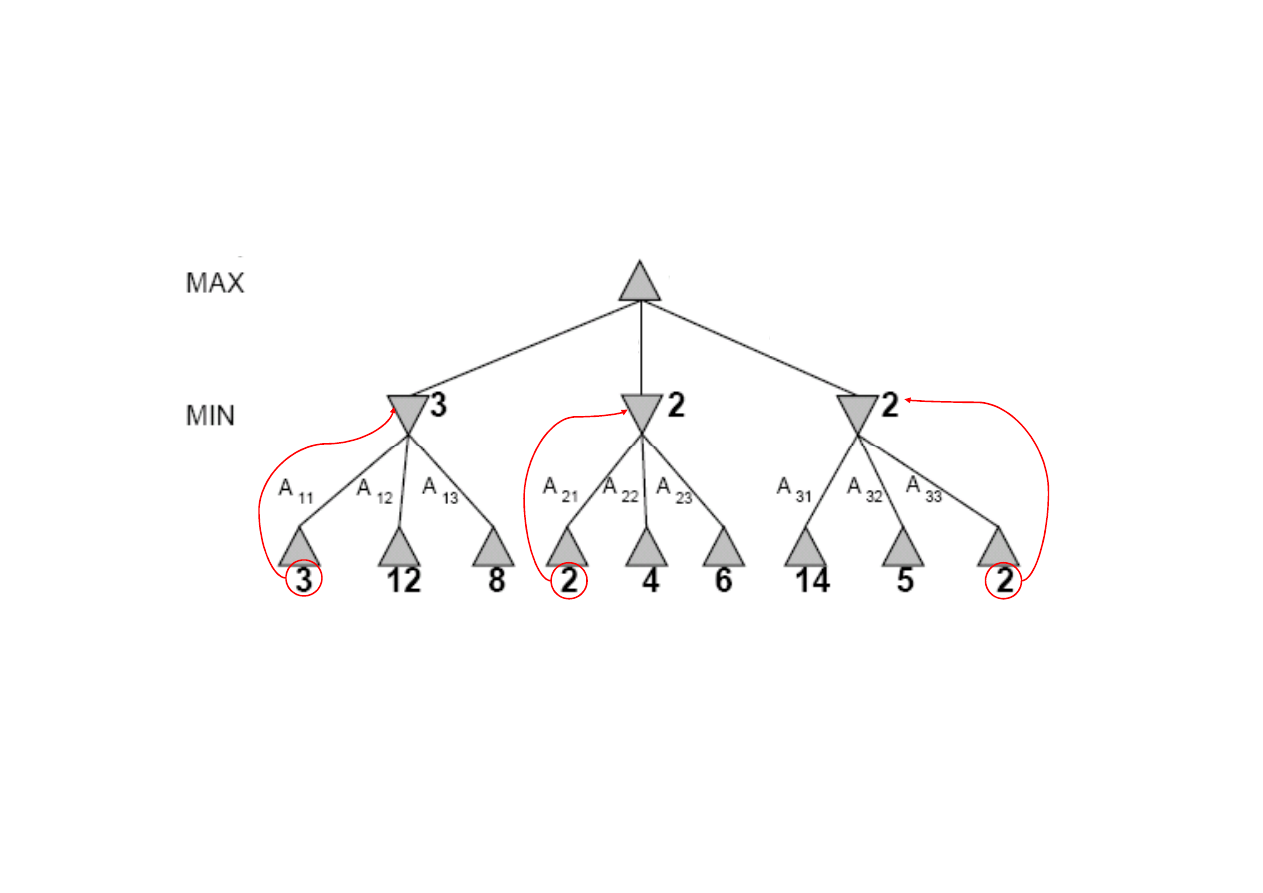
Algorytm MINIMAX

6.2. Definicja gry

Zasada algorytmu minimax dla dwóch graczy MAX i MIN

© F.A. Dul 2007

MIN wybiera posuni

ę

cia odpowiadaj

ą

ce warto

ś

ciom

najmniejszym...

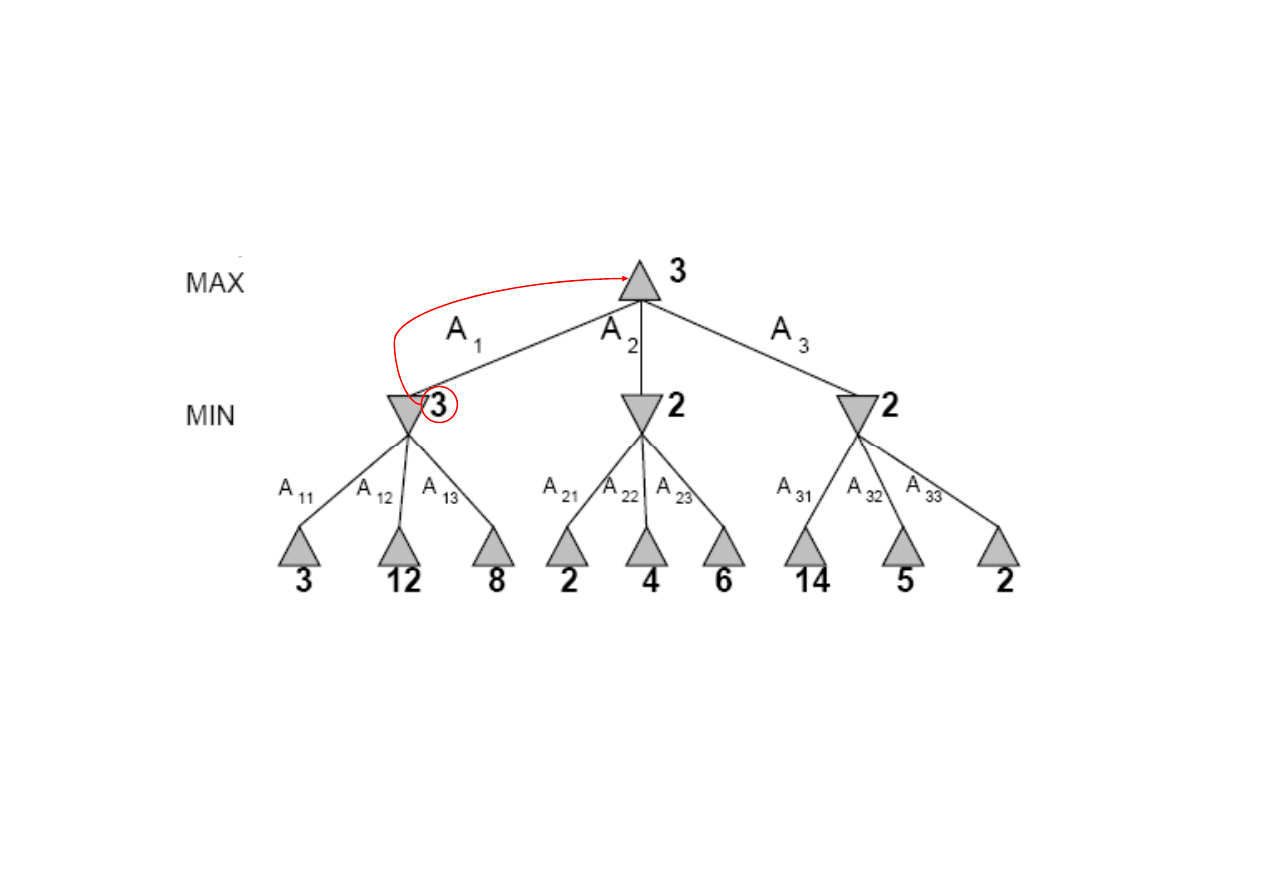
Algorytm MINIMAX

6.2. Definicja gry

Wybór minimax

Zasada algorytmu minimax dla dwóch graczy MAX i MIN

© F.A. Dul 2007

Algorytm minimax maksymalizuje wi

ę

c najgorszy wynik gracza

MAX.

…za

ś

MAX – posuni

ę

cia odpowiadaj

ą

ce warto

ś

ciom

najwi

ę

kszym.

Algorytm MINIMAX

6.2. Definicja gry

function MINIMAX-DECISION(state) returns an action

inputs: state, current state in game
v

←

MAX-VALUE(state)

return the action in SUCCESSORS(state) with value v

function MAX-VALUE(state) returns a utility value

if TERMINAL-TEST(state) then return UTILITY(state)
v

←

-

∞

© F.A. Dul 2007

function MIN-VALUE(state) returns a utility value

if TERMINAL-TEST(state) then return UTILITY(state)
v

← ∞

for a,s in SUCCESSORS(state) do

v

←

MIN(v,MAX-VALUE(s))

return v

v

←

-

∞

for a,s in SUCCESSORS(state) do

v

←

MAX(v,MIN-VALUE(s))

return v

Własno

ś

ci algorytmu MINIMAX

6.2. Definicja gry

• Zupełno

ść

Tak, je

ż

eli drzewo jest sko

ń

czone.

• Czas

O(b

m

)

• Pami

ęć

O(bm) (poszukiwanie w gł

ą

b)

• Optymalno

ść

Tak (przeciwko graj

ą

cemu optymalnie

przeciwnikowi)

Dla typowej partii szachów: b ~ 35, m ~ 100 co oznacza,

© F.A. Dul 2007

Dla typowej partii szachów: b ~ 35, m ~ 100 co oznacza,

ż

e rozwi

ą

zanie

ś

cisłe jest zupełnie nieosi

ą

galne.

Najwi

ę

ksz

ą

wad

ą

algorytmu MINIMAX jest wykładniczy wzrost

czasu wyznaczania rozwi

ą

zania ze wzrostem liczby ruchów.

Rozwi

ą

zaniem problemu jest zastosowanie algorytmów

obcinania gał

ę

zi drzewa poszukiwa

ń

.

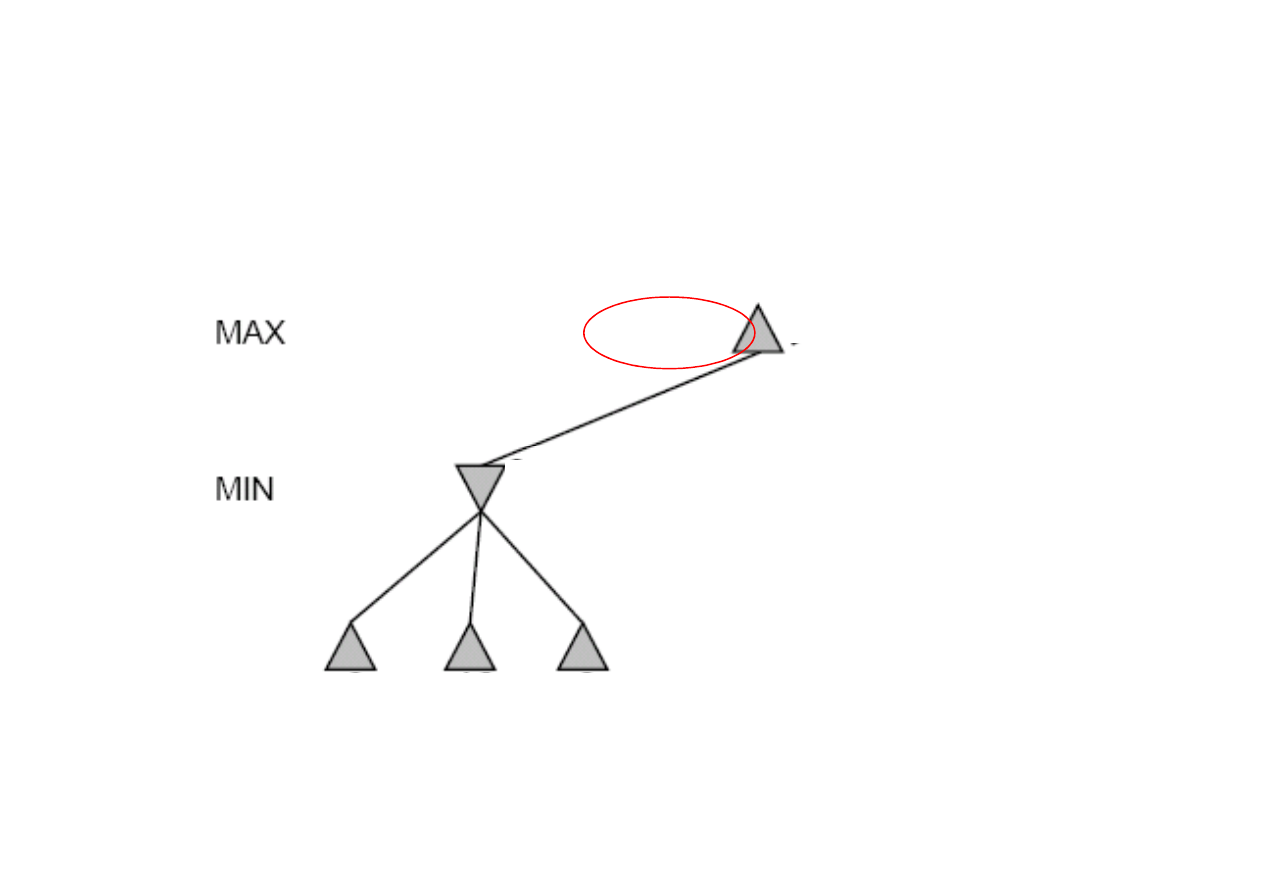
Idea: odrzcanie (przycinanie) tych gał

ę

zi drzewa poszukiwa

ń

,

które s

ą

nieperspektywiczne.

[-

∞

,+

∞

]

Zakres mo

ż

liwych warto

ś

ci

6.3. Algorytm przycinania

αααα

–

ββββ

© F.A. Dul 2007

[-

∞

, +

∞

]

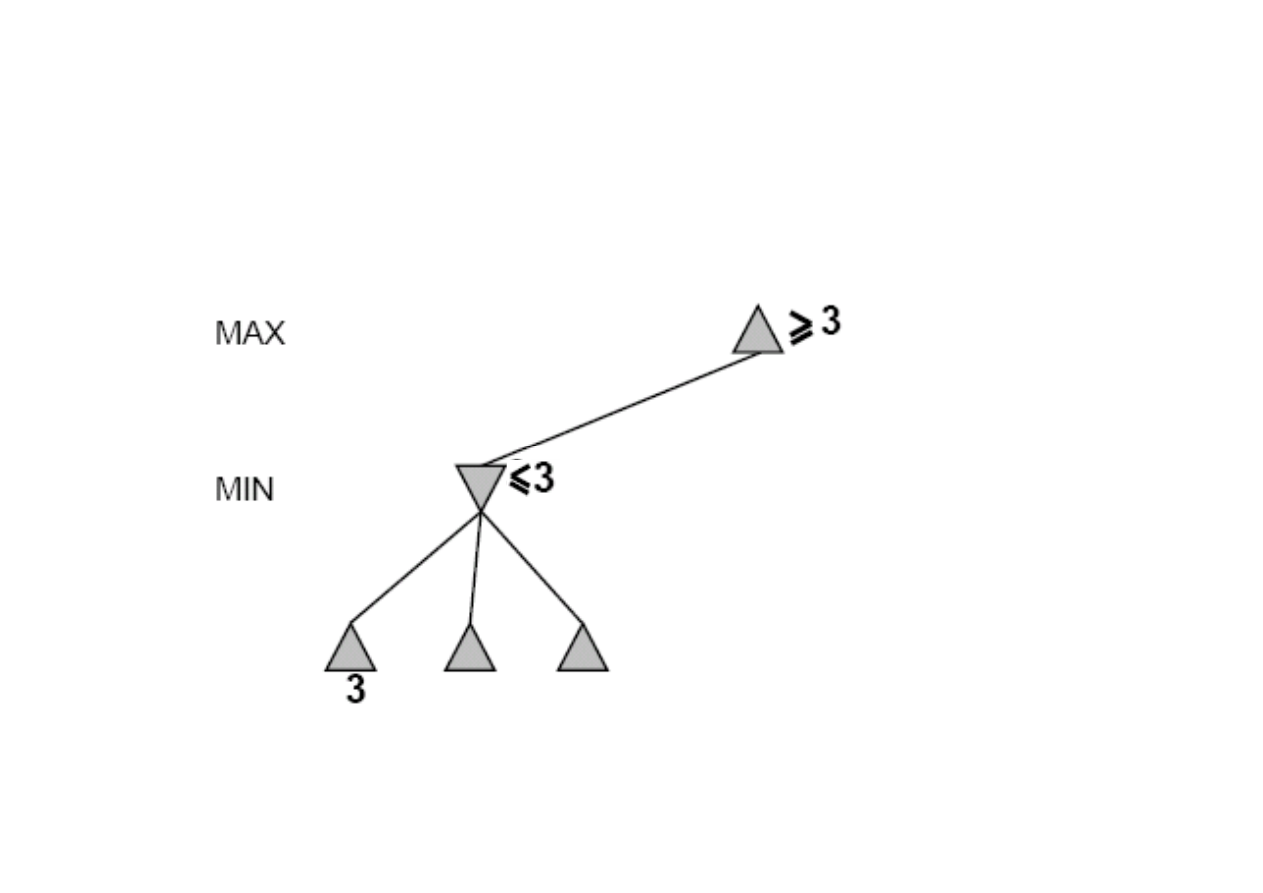
Idea: odrzcanie (przycinanie) tych gał

ę

zi drzewa poszukiwa

ń

,

które s

ą

nieperspektywiczne.

[-

∞

,+

∞

]

6.3. Algorytm przycinania

αααα

–

ββββ

© F.A. Dul 2007

[-

∞

,3]

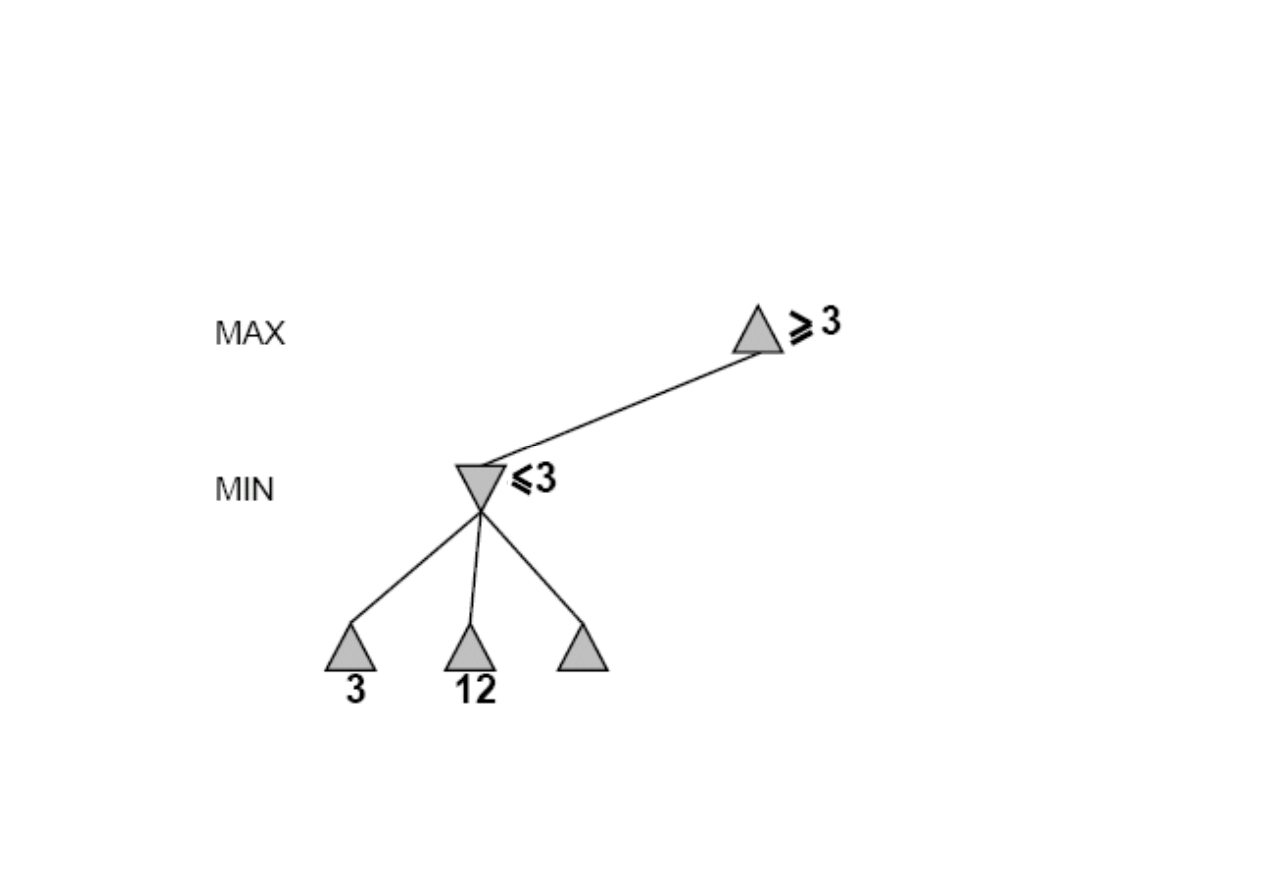
6.3. Algorytm przycinania

αααα

–

ββββ

Idea: odrzcanie (przycinanie) tych gał

ę

zi drzewa poszukiwa

ń

,

które s

ą

nieperspektywiczne.

[-

∞

,+

∞

]

© F.A. Dul 2007

[-

∞

,3]

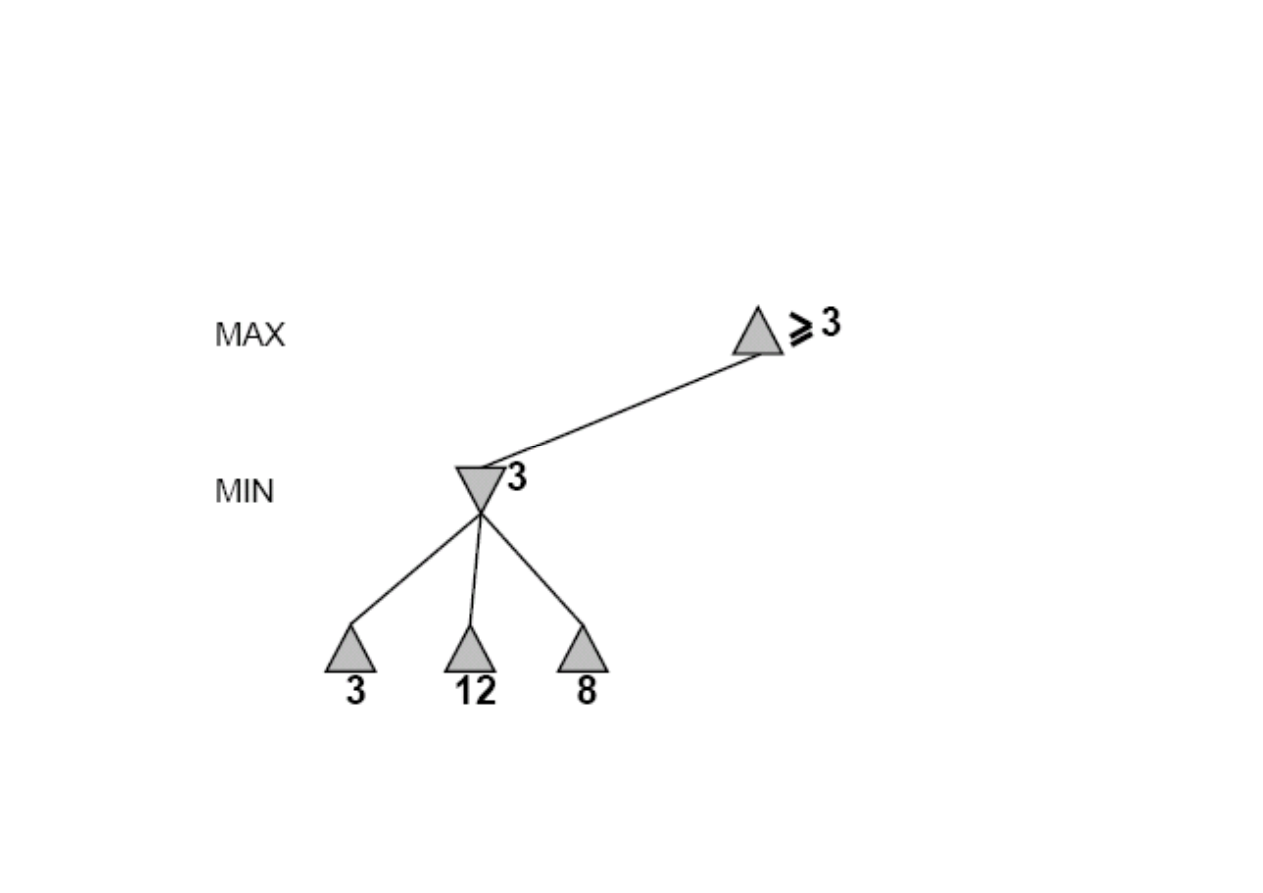
Idea: odrzcanie (przycinanie) tych gał

ę

zi drzewa poszukiwa

ń

,

które s

ą

nieperspektywiczne.

[3,+

∞

]

6.3. Algorytm przycinania

αααα

–

ββββ

© F.A. Dul 2007

[3,3]

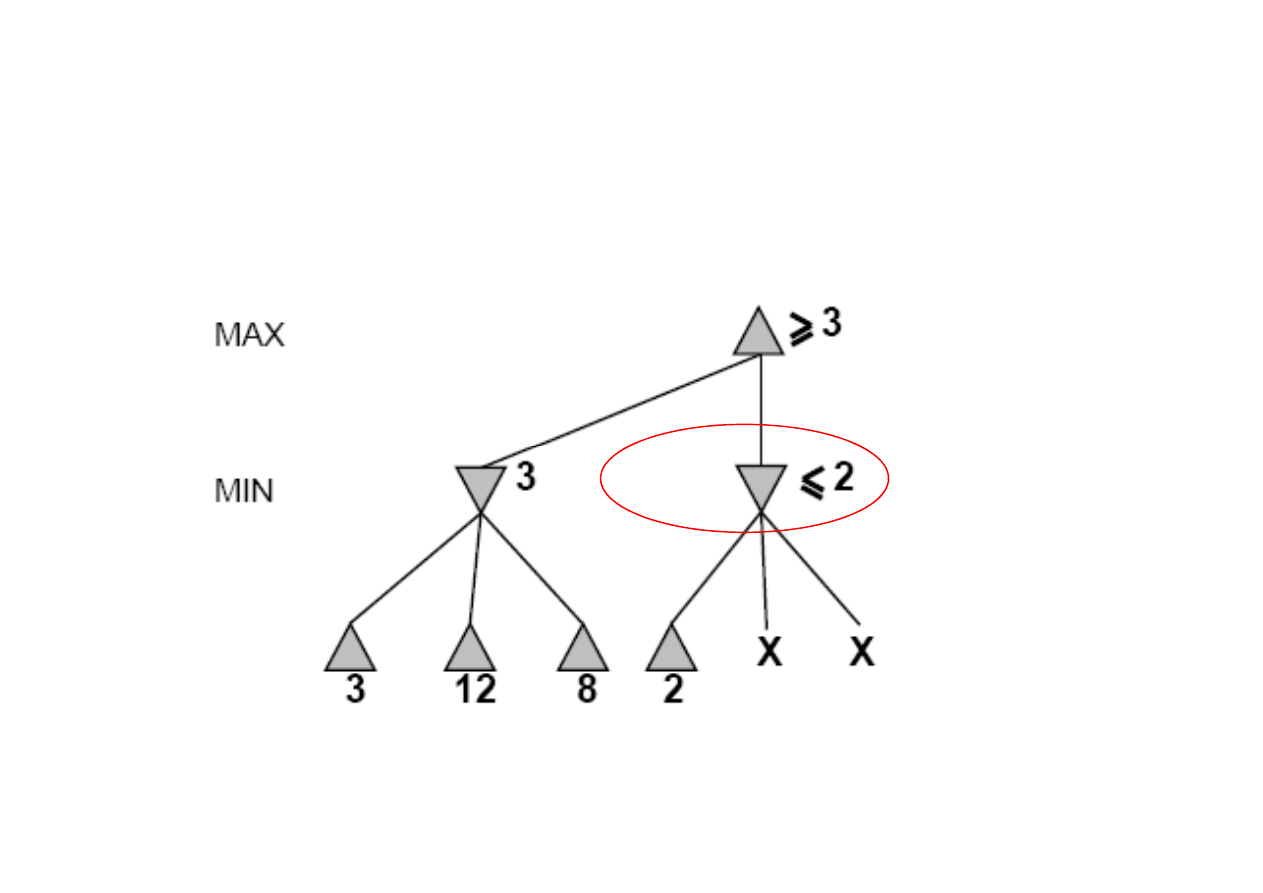
Idea: odrzcanie (przycinanie) tych gał

ę

zi drzewa poszukiwa

ń

,

które s

ą

nieperspektywiczne.

[3,+

∞

]

Ten w

ę

zeł jest

gorszy dla MAX

6.3. Algorytm przycinania

αααα

–

ββββ

© F.A. Dul 2007

[-

∞

,2]

[3,3]

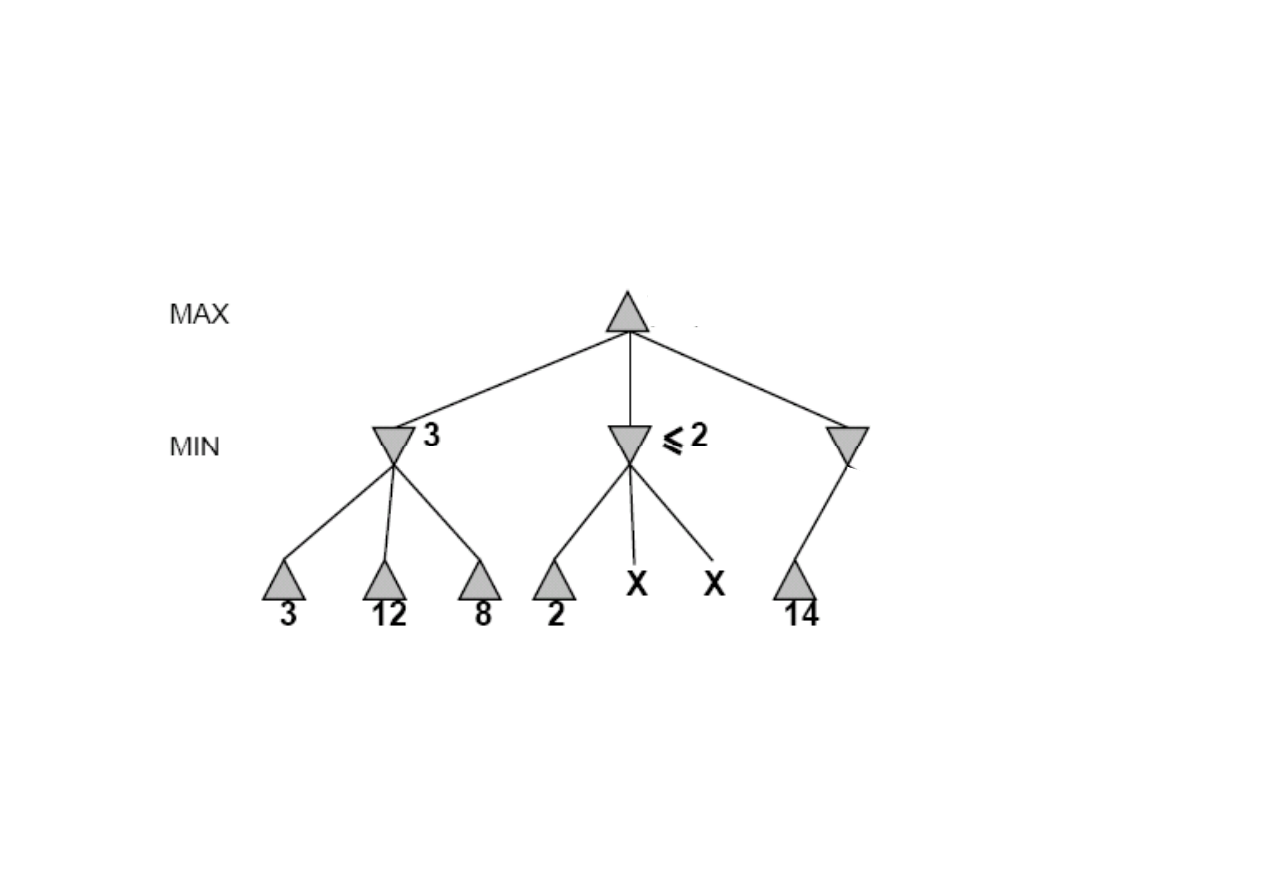
Idea: odrzcanie (przycinanie) tych gał

ę

zi drzewa poszukiwa

ń

,

które s

ą

nieperspektywiczne.

[-

∞

,14]

[-

∞

,2]

[3,14]

[3,3]

≥≥≥≥

3

,

≤≤≤≤

14

≤≤≤≤

14

6.3. Algorytm przycinania

αααα

–

ββββ

© F.A. Dul 2007

[-

∞

,14]

[-

∞

,2]

[3,3]

≤≤≤≤

14

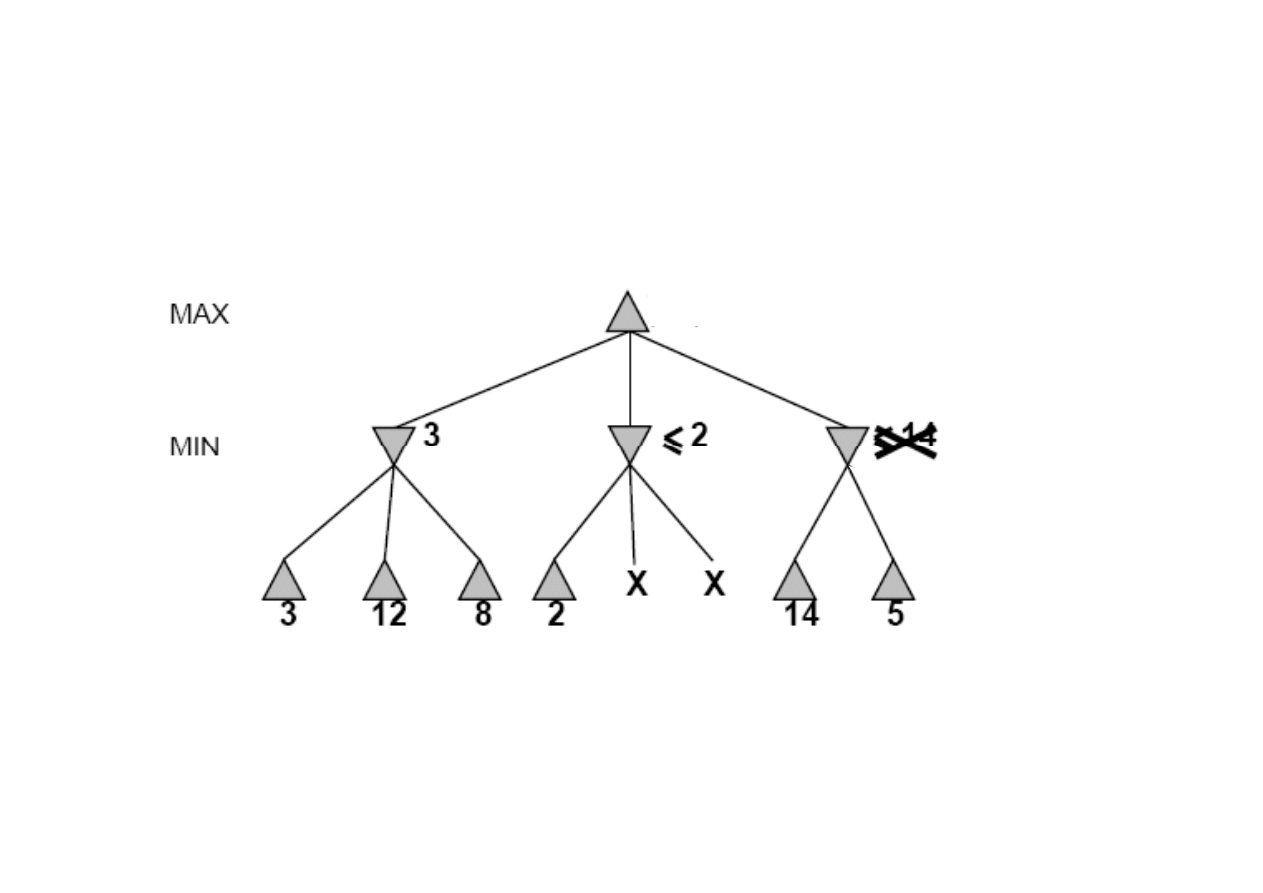
Idea: odrzcanie (przycinanie) tych gał

ę

zi drzewa poszukiwa

ń

,

które s

ą

nieperspektywiczne.

[-

∞

,5]

[-

∞

,2]

[3,5]

[3,3]

≥≥≥≥

3

,

≤≤≤≤

5

≤≤≤≤

5

6.3. Algorytm przycinania

αααα

–

ββββ

© F.A. Dul 2007

[-

∞

,5]

[-

∞

,2]

[3,3]

≤≤≤≤

5

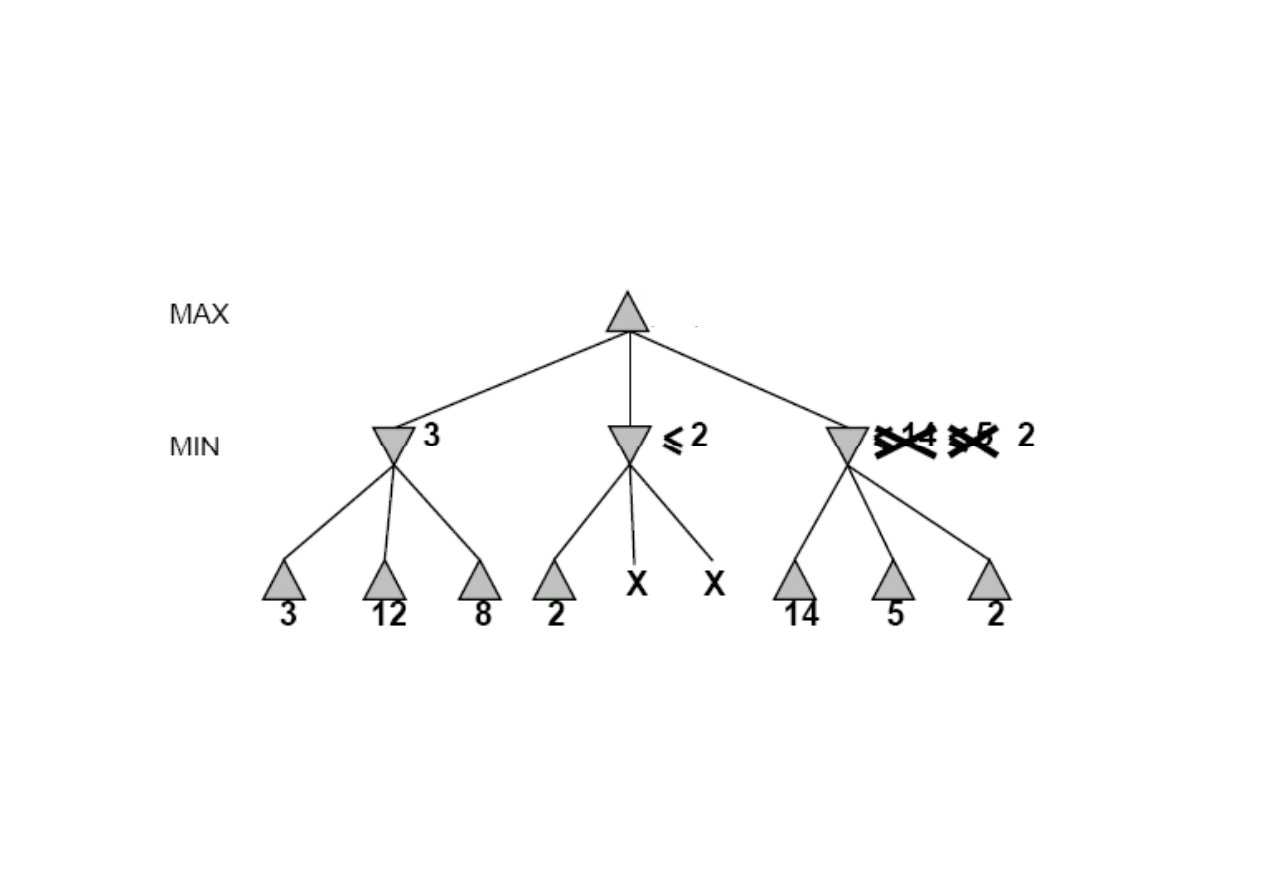
Idea: odrzcanie (przycinanie) tych gał

ę

zi drzewa poszukiwa

ń

,

które s

ą

nieperspektywiczne.

[2,2]

[-

∞

,2]

[3,3]

[3,3]

6.3. Algorytm przycinania

αααα

–

ββββ

© F.A. Dul 2007

[2,2]

[-

∞

,2]

[3,3]

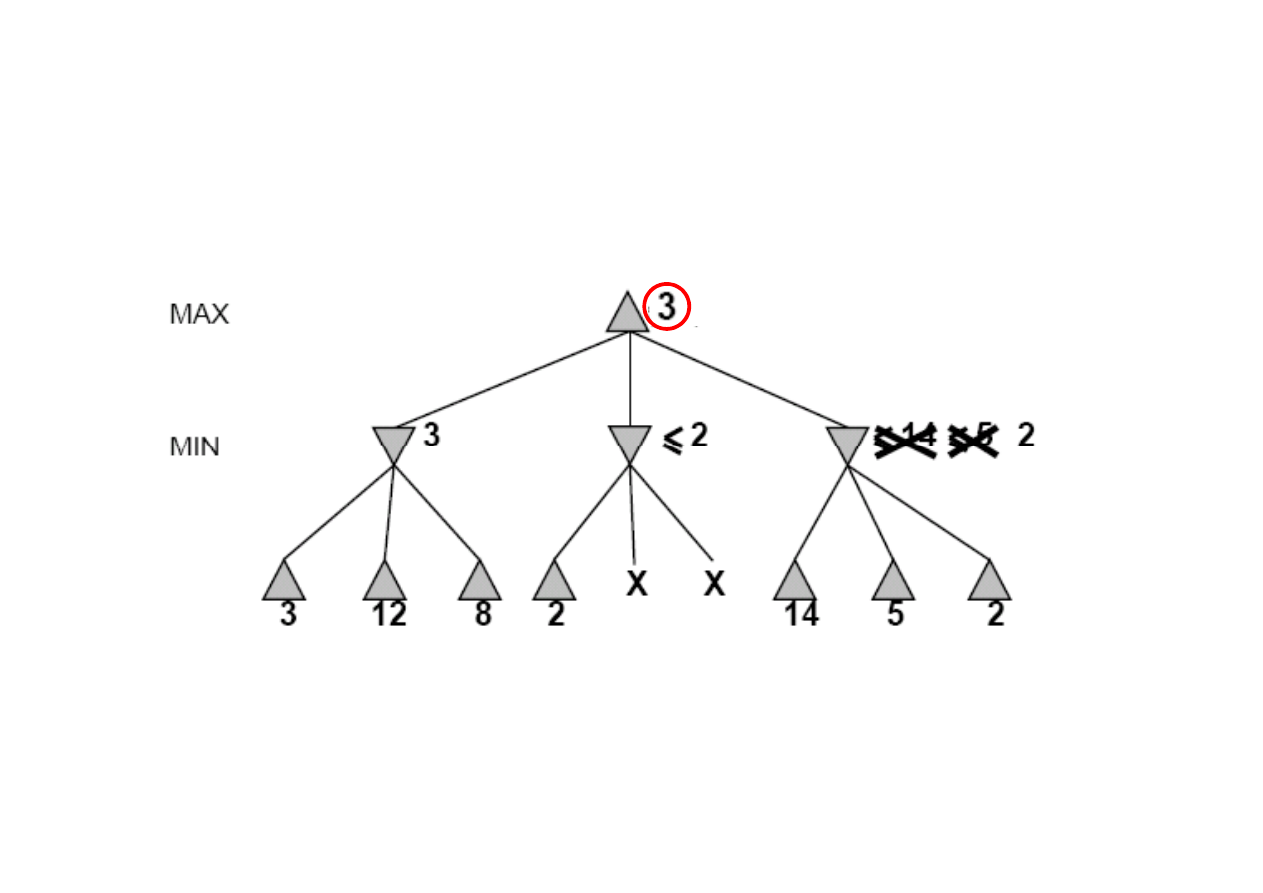
Idea: odrzcanie (przycinanie) tych gał

ę

zi drzewa poszukiwa

ń

,

które s

ą

nieperspektywiczne.

[2,2]

[-

∞

,2]

[3,3]

[3,3]

6.3. Algorytm przycinania

αααα

–

ββββ

© F.A. Dul 2007

[2,2]

[-

∞

,2]

[3,3]

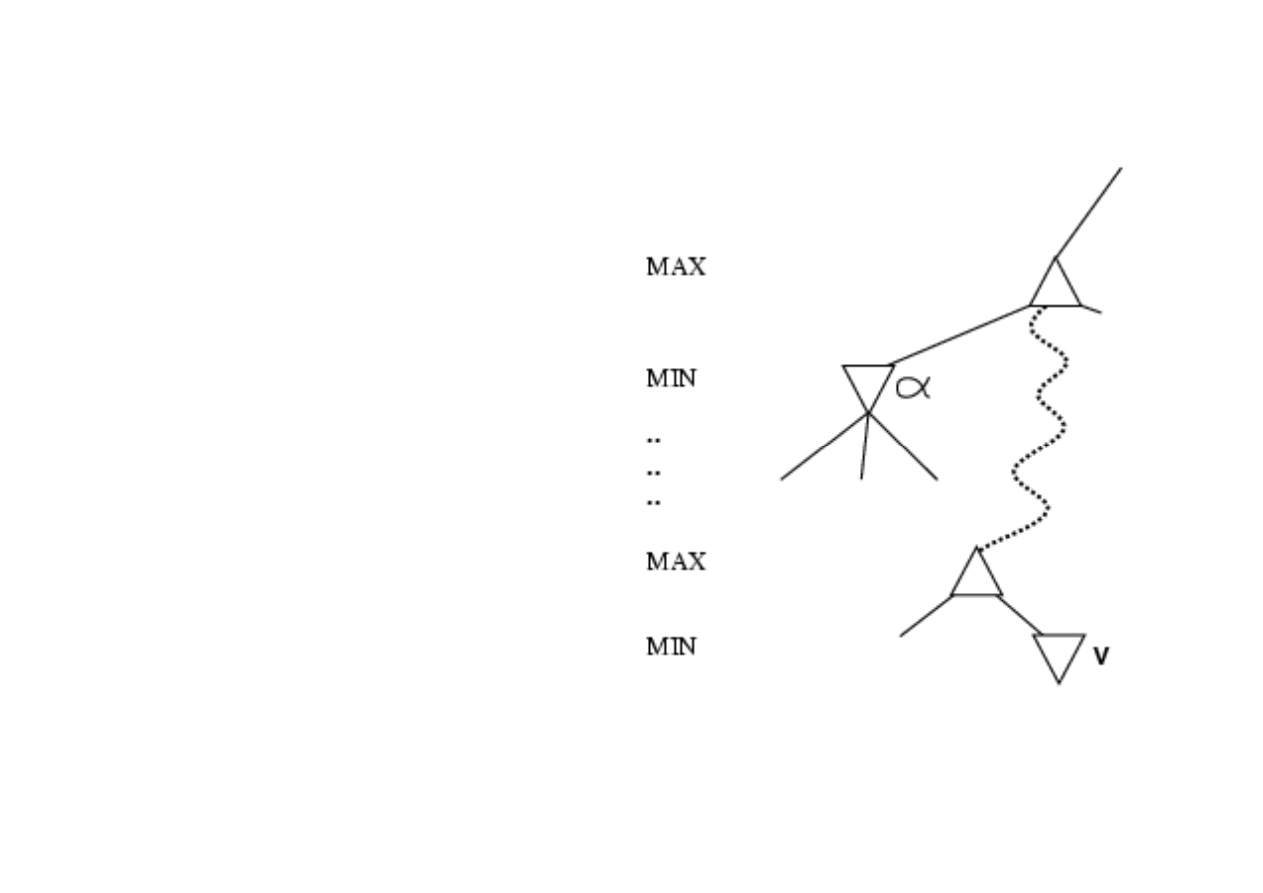
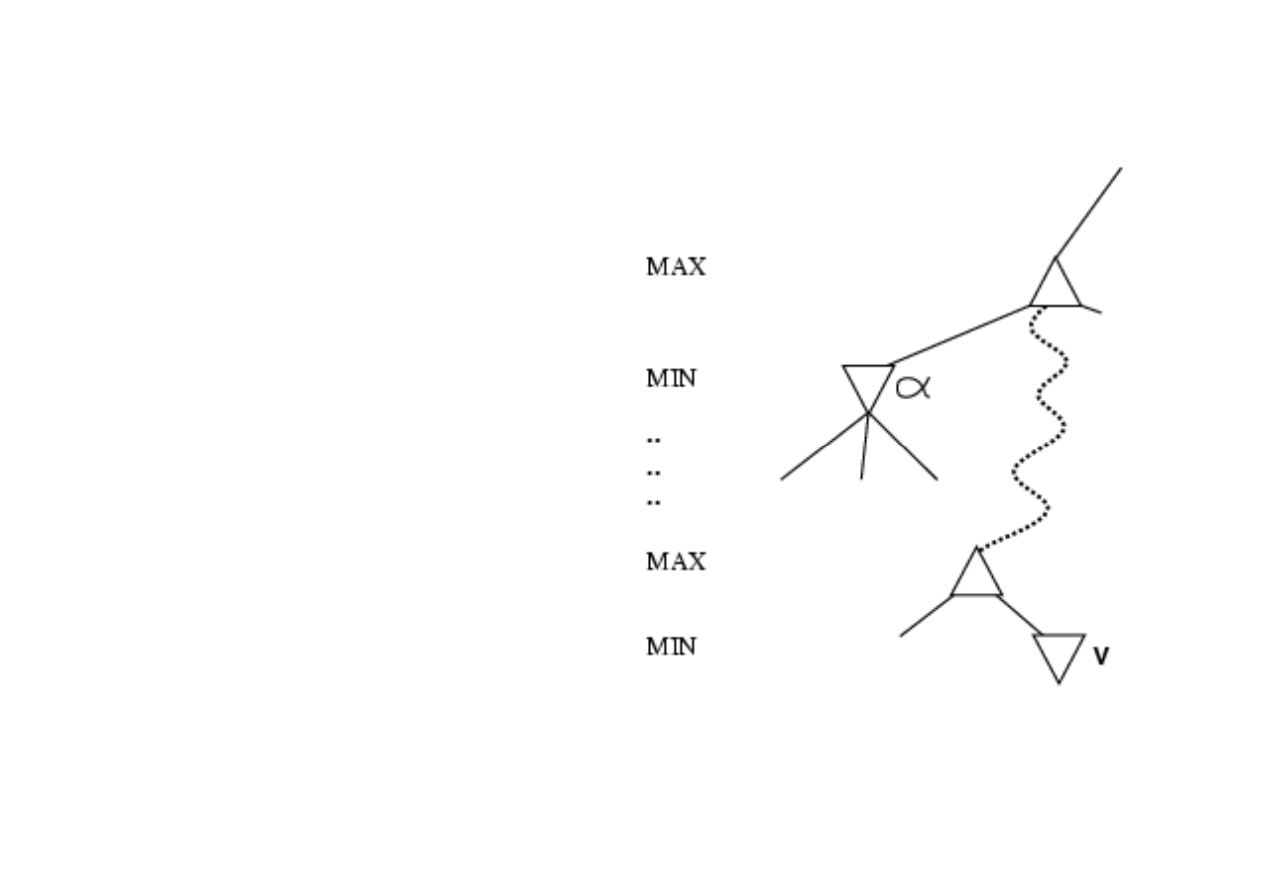
Zasada ogólna przycinania

αααα

-

ββββ

• Rozwa

ż

my w

ę

zeł v le

żą

cy

gdzie

ś

na drzewie.

• Je

ż

eli gracz MAX mo

ż

e

dokona

ć

lepszego wyboru

w w

ęź

le rodzica lub

gdziekolwiek wy

ż

ej (

αααα

)

w

ę

zeł v nigdy nie bi

ę

dzie

6.3. Algorytm przycinania

αααα

–

ββββ

© F.A. Dul 2007

w

ę

zeł v nigdy nie bi

ę

dzie

osi

ą

gni

ę

ty.

• Gał

ąź

z w

ę

złem v mo

ż

e

by

ć

przyci

ę

ta.

Dlaczego algorytm nosi nazw

ę

„przycinanie

αααα

-

ββββ

” ?

• Niech

αααα

b

ę

dzie najlepsz

ą

(najwi

ę

ksz

ą

) warto

ś

ci

ą

na

gał

ę

zi gracza MAX.

• Je

ż

eli v jest gorsze ni

ż

αααα

,

gracz MAX ominie gał

ąź

na której znajduje si

ę

v

– Mo

ż

na przyci

ąć

t

ę

gał

ąź

.

6.3. Algorytm przycinania

αααα

–

ββββ

© F.A. Dul 2007

– Mo

ż

na przyci

ąć

t

ę

gał

ąź

.

•

ββββ

definiuje si

ę

podobnie

dla gracza MIN.

Algorytm przycinania

αααα

-

ββββ

function ALPHA-BETA-SEARCH(state) returns an action

inputs: state, current state in game
v

←

MAX-VALUE(state, -

∞

, +

∞

)

return the action in SUCCESSORS(state) with value v

function MAX-VALUE(state,

α

,

β

) returns a utility value

if TERMINAL-TEST(state) then return UTILITY(state)
v

←

-

∞

for a,s in SUCCESSORS(state) do

v

←

MAX( v, MIN-VALUE(s,

α

,

β

) )

≥

β

6.3. Algorytm przycinania

αααα

–

ββββ

© F.A. Dul 2007

v

←

MAX( v, MIN-VALUE(s,

α

,

β

) )

if v

≥

β

then return v

α

←

MAX(

α

,v)

return v

function MIN-VALUE(state,

α

,

β

) returns a utility value

if TERMINAL-TEST(state) then return UTILITY(state)
v

←

+

∞

for a,s in SUCCESSORS(state) do

v

←

MIN( v, MAX-VALUE(s,

α

,

β

) )

if v

≤

α

then return v

β

←

MIN(

β

,v)

return v

Własno

ś

ci algorytmu przycinania

αααα

-

ββββ

• Przycinanie nie wpływa na ko

ń

cowy wynik gry.

• Przycina

ć

mo

ż

na całe gał

ę

zie (poddrzewa).

• Wła

ś

ciwe uporz

ą

dkowanie (kolejno

ść

) ruchów

zwi

ę

ksza efektywno

ść

przycinania.

• Czas oblicze

ń

przy idealnym uporz

ą

dkowaniu ruchów

~O(b

m/2

). Pozwala to podwoi

ć

gł

ę

boko

ść

poszukiwa

ń

.

6.3. Algorytm przycinania

αααα

–

ββββ

© F.A. Dul 2007

6.4. Gry z niepełn

ą

informacj

ą

Algorytmy MINMAX i przycinania

α

-

β

wymagaj

ą

zbyt wielu

oszacowa

ń

warto

ś

ci na gał

ę

ziach, co zaj

ę

łoby za du

ż

o czasu

w grach rzeczywistych.

Poprawa efektywno

ś

ci algorytmów gier (Shannon, 1950)

• Wprowadzenie ustalonej gł

ę

boko

ś

ci poszukiwa

ń

tak, aby

nie przekroczy

ć

limitu czasu ustalonego w danej grze;

• Zast

ą

pienie TERMINAL-TEST przez CUTOFF-TEST;

© F.A. Dul 2007

• Zast

ą

pienie TERMINAL-TEST przez CUTOFF-TEST;

• Zastosowanie heurystycznej funkcji EVAL zamiast funkcji

u

ż

yteczno

ś

ci w przycinaniu

α

-

β

:

if TERMINAL-TEST(state) then return UTILITY(state

)

if CUTOFF-TEST(state,depth) then return EVAL(state)

Funkcja heurystyczna EVAL

Idea: oszacowanie przewidywanego wyniku gry pocz

ą

wszy

od aktualnego stanu.

Efektywno

ść

gry zale

ż

y od jako

ś

ci funkcji EVAL:

• funkcja EVAL powinna porz

ą

dkowa

ć

w

ę

zły ko

ń

cz

ą

ce gr

ę

w taki sam sposób jak funkcja UTILITY,

• obliczenia nie mog

ą

trwa

ć

zbyt długo,

• dla stanów nieko

ń

cowych funkcja EVAL powinna by

ć

6.4. Gry z niepełn

ą

informacj

ą

© F.A. Dul 2007

• dla stanów nieko

ń

cowych funkcja EVAL powinna by

ć

silnie skorelowana z aktualn

ą

szans

ą

wygranej.

W szachach EVAL jest zazwyczaj

liniow

ą

sum

ą

wa

ż

on

ą

starsze

ń

stwa

figur

Eval(s) = w

1

f

1

(s) + w

2

f

2

(s) + … + w

n

f

n

(s)

Np. w

1

= 9 dla

f

1

(s) = (liczba białych królowych) – (liczba czarnych królowych)

Addytywno

ść

funkcji EVAL zakłada niezale

ż

no

ść

sytuacji

szachowych.

Efekt wyj

ś

cia poza horyzont

Poszukiwania o ustalonej
gł

ę

boko

ś

ci nie zauwa

żą

mo

ż

liwej

zmiany pionka na królow

ą

6.4. Gry z niepełn

ą

informacj

ą

Funkcja EVAL w postaci kombinacji liniowej sytuacji jest
jednak u

ż

yteczna tylko dla stanów zmieniaj

ą

cych si

ę

umiarkowanie.

© F.A. Dul 2007

Jak to działa w praktyce?

Załó

ż

my,

ż

e na jeden ruch mamy 100 sekund, a mo

ż

emy

sprawdza

ć

10

4

w

ę

złów/s.

Mo

ż

emy zatem sprawdza

ć

10

6

w

ę

złów na jeden ruch.

b

m

= 10

6

, b=35

m = 4 posuni

ę

cia naprzód

Analiza mniej ni

ż

czterech posuni

ęć

naprzód cechuje gracza

beznadziejnego!

6.4. Gry z niepełn

ą

informacj

ą

© F.A. Dul 2007

beznadziejnego!

• 4 ruchy - nowicjusz,
• 8 ruchów - mistrz, komputer PC,
• 12 ruchów - arcymistrz Kasparow, komputer Deep Blue.

6.5. Gry z losowo

ś

ci

ą

W wielu grach wyst

ę

puj

ą

elementy losowe, odzwierciedlaj

ą

ce

nieprzewidywalno

ść

rzeczywisto

ś

ci.

Gra Trik-Trak (Backgammon) zawiera losowo

ść

w postaci

rzutów kostk

ą

.

0 1 2 3 4 5 6 7 8 9 10 11 12

13

© F.A. Dul 2007

Mo

ż

liwe ruchy: (5-10,5-11), (5-11,19-24),(5-10,10-16)

oraz (5-11,11-16)

25 24 23 22 21 20 19 18 17 16 15 14 13

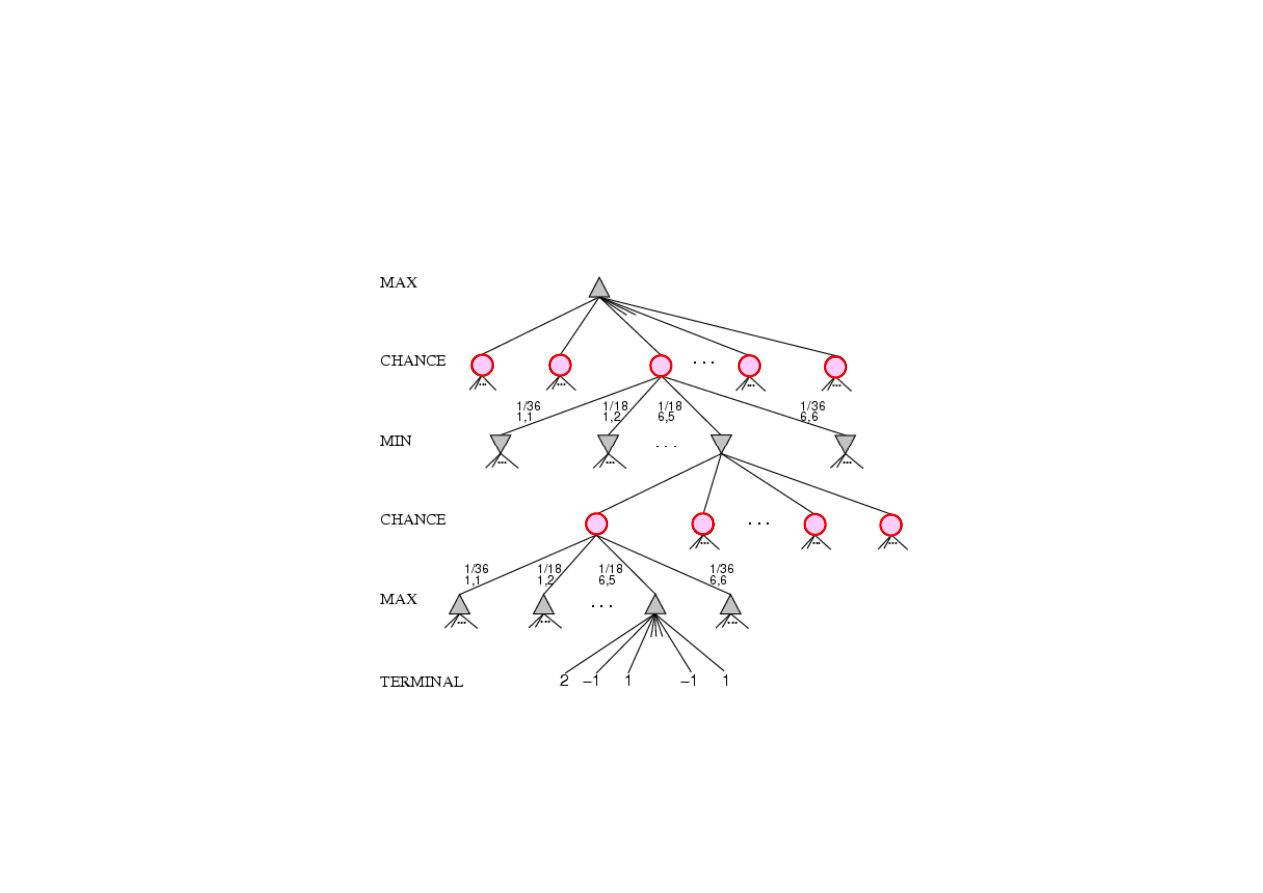
6.5. Gry z losowo

ś

ci

ą

Do analizy gier losowych nie wystarcza drzewo dla ruchów
MAX – MIN.
Nale

ż

y je uzupełni

ć

w

ę

złami losowymi

(chance nodes).

© F.A. Dul 2007

C

W w

ę

złach losowych wyboru gał

ę

zi dokonuje si

ę

na

podstawie prawdopodobie

ń

stw poszczególnych mo

ż

liwo

ś

ci.

6.5. Gry z losowo

ś

ci

ą

Algorytmy M

INMAX

dla gier losowych wykorzystuje warto

ść

oczekiwan

ą

obliczan

ą

wzgl

ę

dem wszystkich mo

ż

liwych

zdarze

ń

.

E

XPECTIMINIMAX(n) =

U

TILITY(n)

If n is a terminal

Uogólnienie algorytmu M

INMAX

dla gier losowych w postaci

algorytmu E

XPECTIMINMAX

© F.A. Dul 2007

U

TILITY(n)

If n is a terminal

max

s

∈

successors(n)

E

XPECTIMINIMAX(s)

If n is a MAX node

min

s

∈

successors(n)

E

XPECTIMINIMAX(s)

If n is a MIN node

∑

s

∈

successors(n)

P

(s)

·

E

XPECTIMINIMAX(s) If n is a CHANCE node

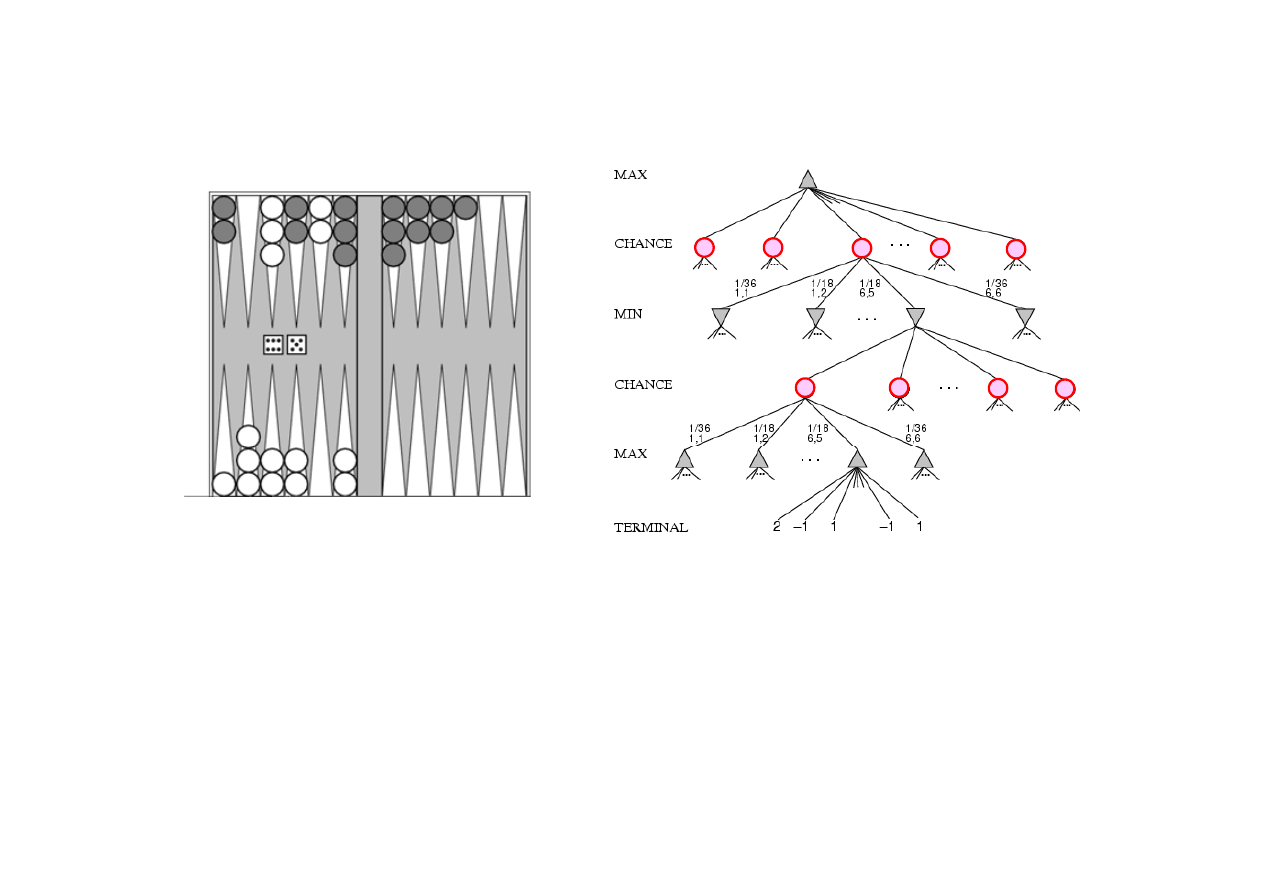
6.5. Gry z losowo

ś

ci

ą

Przykład działania algorytmu E

XPECTIMINMAX

dla gry Trik-Trak.

0 1 2 3 4 5 6 7 8 9 10 11 12

13

C

© F.A. Dul 2007

Mo

ż

liwe ruchy: (5-10,5-11), (5-11,19-24),(5-10,10-16)

oraz (5-11,11-16)

25 24 23 22 21 20 19 18 17 16 15 14 13

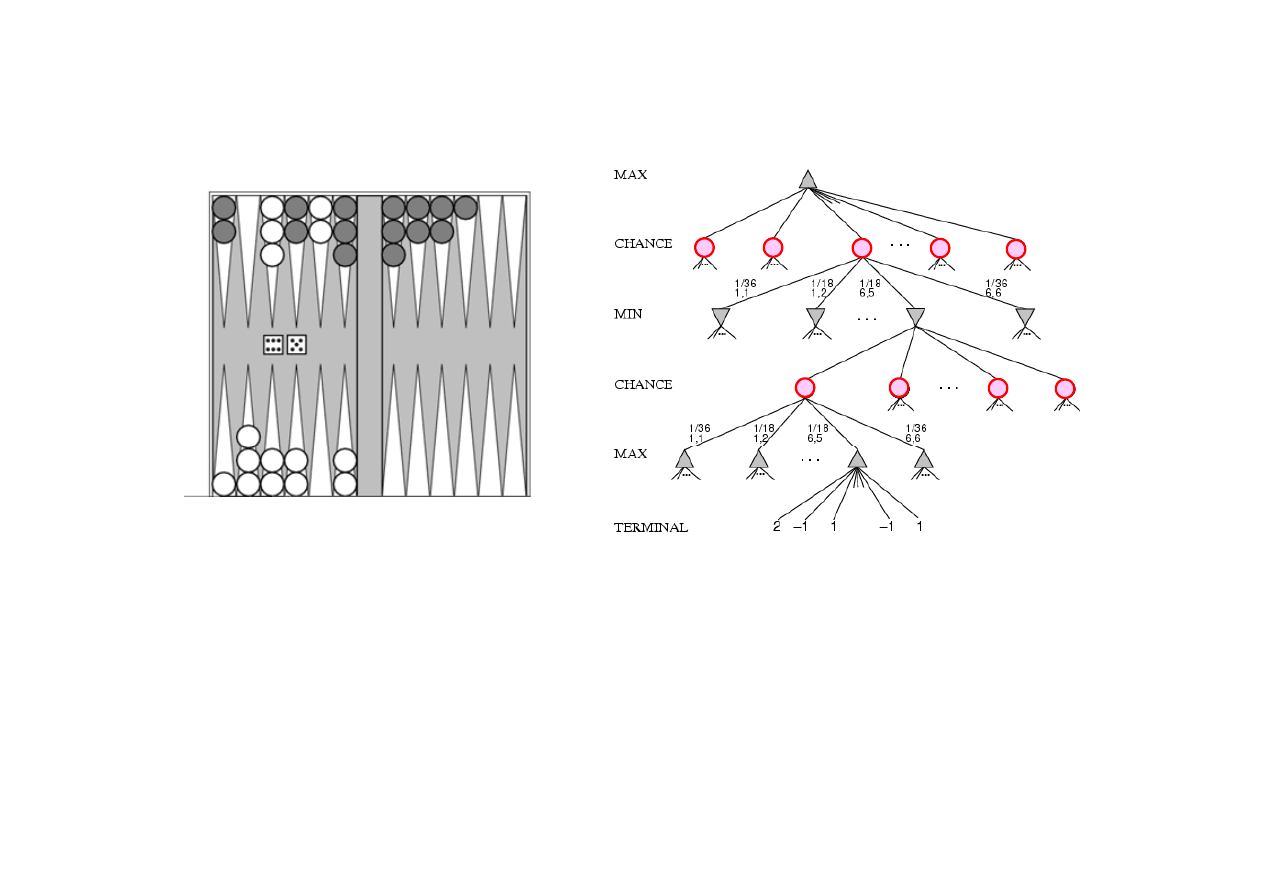
6.5. Gry z losowo

ś

ci

ą

Przykład działania algorytmu E

XPECTIMINMAX

dla gry Trik-Trak.

0 1 2 3 4 5 6 7 8 9 10 11 12

13

C

© F.A. Dul 2007

Mo

ż

liwe ruchy: (5-10,5-11), (5-11,19-24),(5-10,10-16)

oraz (5-11,11-16)

25 24 23 22 21 20 19 18 17 16 15 14 13

Prawdopodobie

ń

stwa par [1,1] , ... , [6,6] wynosz

ą

1/36.

Prawdopodobie

ń

stwa pozostałych rzutów – 1/18.

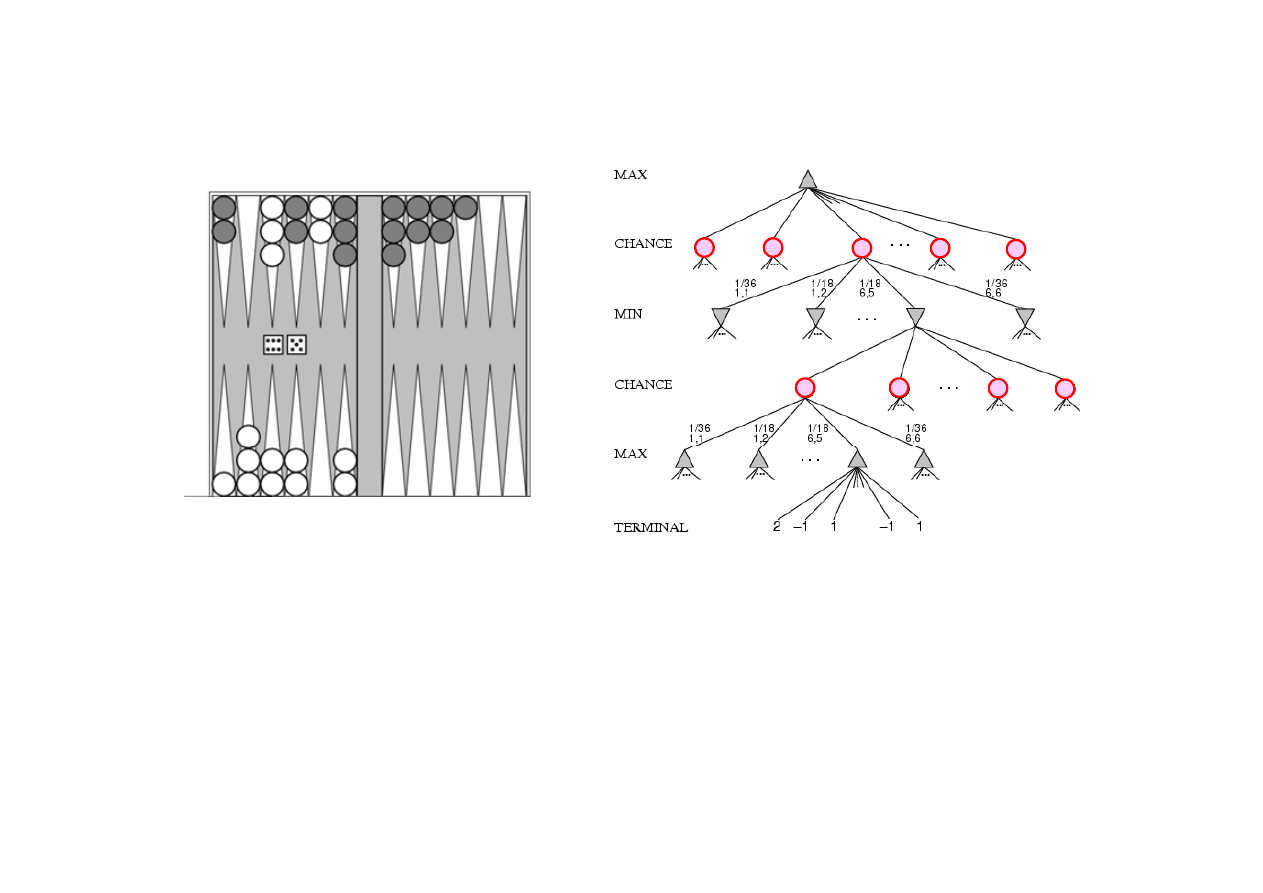
6.5. Gry z losowo

ś

ci

ą

Przykład działania algorytmu E

XPECTIMINMAX

dla gry Trik-Trak.

0 1 2 3 4 5 6 7 8 9 10 11 12

13

C

© F.A. Dul 2007

Mo

ż

liwe ruchy: (5-10,5-11), (5-11,19-24),(5-10,10-16)

oraz (5-11,11-16)

25 24 23 22 21 20 19 18 17 16 15 14 13

Prawdopodobie

ń

stwa par [1,1] , ... , [6,6] wynosz

ą

1/36.

Prawdopodobie

ń

stwa pozostałych rzutów – 1/18.

Obliczenie warto

ś

ci oczekiwanej pozwala wybra

ć

gał

ąź

poszukiwa

ń

.

Karty − gry losowe z niepełn

ą

informacj

ą

Gry w karty s

ą

interesuj

ą

ce, gdy

ż

wyst

ę

puj

ą

w nich zarówno

losowo

ść

jak i niepewno

ś

ci informacji:

• pocz

ą

tkowy rozkład kart jest losowy,

• gracze nie znaj

ą

rozkładu kart przeciwników.

6.5. Gry z losowo

ś

ci

ą

Losowo

ść

wyst

ę

puje tylko na pocz

ą

tku gry.

Poniewa

ż

brak jest pełnej informacji o rozkładzie kart,

to mo

ż

na wykorzystywa

ć

tylko t

ę

informacj

ę

, która jest

dost

ę

pna w danej chwili.

© F.A. Dul 2007

to mo

ż

na wykorzystywa

ć

tylko t

ę

informacj

ę

, która jest

dost

ę

pna w danej chwili.

Do analizy gier w karty mo

ż

na u

ż

y

ć

algorytmu MINIMAX.

Idea

: obliczy

ć

warto

ś

ci MINIMAX dla ka

ż

dego ruchu

w ka

ż

dym rozdaniu i wybra

ć

ruchy z najwi

ę

kszymi

warto

ś

ciami oczekiwanymi.

Program GIB do gry w bryd

ż

a działa nast

ę

puj

ą

co:

• generuje sto rozda

ń

zgodnych z licytacj

ą

,

• wybiera te ruchy, które wygraj

ą

wi

ę

cej lew.

•

Szachy

W roku 1997 komputer Deep Blue pokonał arcymistrza

ś

wiata Garego Kasparowa w sze

ś

ciu partiach.

6.6. Osi

ą

gni

ę

cia programów AI dla gier

© F.A. Dul 2007

DeepBlue analizował sze

ść

milionów pozycji w ci

ą

gu

sekundy u

ż

ywaj

ą

c bardzo wyszukanego szacowania oraz

pewnych metod nieujawnionych, co umo

ż

liwiło przedłu

ż

anie

ś

cie

ż

ek poszukiwa

ń

nawet do 40 ruchów do przodu.

•

Warcaby

W roku 1994 program Chinook zako

ń

czył czterdziestoletnie

panowanie geniusza warcabów, wielokrotnego mistrza

ś

wiata, dr Mariona Tinsleya.

6.6. Osi

ą

gni

ę

cia programów AI dla gier

© F.A. Dul 2007

Chinook u

ż

ywał w tym celu bazy danych zawieraj

ą

cej

wst

ę

pnie obliczone ko

ń

cówki gry opisuj

ą

ce 444,000,000,000

pozycje dla o

ś

miu lub mniejszej liczby pionków.

•

Othello (Reversi)

Mistrzowie odrzucaj

ą

gr

ę

z komputerami, gdy

ż

s

ą

one zbyt

dobre. Program Logistello wygrał mistrzostwa

ś

wiata w roku

1997 wynikiem 6:0.

•

Go

Mistrzowie odrzucaj

ą

gr

ę

z komputerami, gdy

ż

s

ą

one

za słabe. W tej grze b > 361 wi

ę

c wi

ę

kszo

ść

programów

u

ż

ywa baz wiedzy które sugeruj

ą

mo

ż

liwe ruchy.

Najlepsze programy: Goemate i Go4++, osi

ą

gaj

ą

zaledwie

6.6. Osi

ą

gni

ę

cia programów AI dla gier

© F.A. Dul 2007

Najlepsze programy: Goemate i Go4++, osi

ą

gaj

ą

zaledwie

poziom słabych amatorów.

•

Bryd

ż

Program Bridge Baron™ wygrał po raz pierwszy mistrzostwa

ś

wiata w roku 1997, a ogółem - pi

ę

ciokrotnie.

Program GIB wygrał mistrzostwa

ś

wiata w roku 2000.

•

Trik-Trak (Backgammon)

Program TD-G

AMMON

uwa

ż

any jest za jednego z trzech

najlepszych graczy na

ś

wiecie.

Podsumowanie

• Gry s

ą

przyjemne (ale czasami niebezpieczne...)

• W grach dwóch graczy o sumie zerowej z pełn

ą

informacj

ą

algorytm M

INIMAX

pozwala wyznaczy

ć

ruchy optymalne.

• Niemo

ż

no

ść

analizy całego drzewa zmusza do u

ż

ycia

funkcji szacuj

ą

cych u

ż

yteczno

ś

ci stanów w grze.

• Gry ilustruj

ą

wiele wa

ż

nych kwestii dotycz

ą

cych AI:

• gra perfekcyjna jest nieosi

ą

galna, konieczna jest

© F.A. Dul 2007

• gra perfekcyjna jest nieosi

ą

galna, konieczna jest

aproksymacja;

• niepewno

ść

wymaga u

ż

ycia metod statystycznych.

• Gry dorównuj

ą

mistrzom w wielu przypadkach:

szachach, warcabach, Othello, Trik-Traku i innych.

• Uwa

ż

a si

ę

,

ż

e gry s

ą

tym dla sztucznej inteligencji,

czym wy

ś

cigi Grand Prix Formuły I s

ą

dla rozwoju

automobilizmu.

Podsumowanie

W

ą

tpliwo

ść

Wprawdzie programy AI s

ą

w stanie pokona

ć

nawet

arcymistrzów, ale musz

ą

one korzysta

ć

z heurystyk

wymy

ś

lonych przez człowieka.

Czy zatem mo

ż

na uwa

ż

a

ć

,

ż

e s

ą

to rzeczywi

ś

cie byty

cechuj

ą

ce si

ę

sztuczn

ą

inteligencj

ą

?

© F.A. Dul 2007