Wykªad 11

Fizyka (Informatyka - EEIiA 2008/09)

16 12 2008

c

Mariusz Krasi«ski 2008

Spis tre±ci

1 Interferencja

1

1.1 Dodawanie fal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1

1.2 Nakªadanie si¦ fal z dwóch ¹ródeª . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2

1.3 Warunki interferencji . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3

1.4 Dwa ¹ródªa punktowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4

UWAGA! Wi¦kszo±¢ rysunków wymaga wªasnor¦cznego dopisania oznacze«! Wyliczenia zamieszczone w

ramkach stanowi¡ materiaª uzupeªniaj¡cy.

Lektura uzupeªniaj¡ca:
M. Krasi«ski, Fale rozdziaª 11 (strony 267-300) w skrypcie pt. Wst¦p do analizy matematycznej i wybranych

dziaªów zyki, red. A. Just, Wyd. Polit. Šódzkiej, Šód¹ 2007.

1 Interferencja

1.1 Dodawanie fal

Wynik naªo»enia si¦ dwóch fal o jednakowych cz¦sto±ciach (w jakim± punkcie) zale»y od ró»nicy faz pomi¦dzy

falami w tym punkcie.

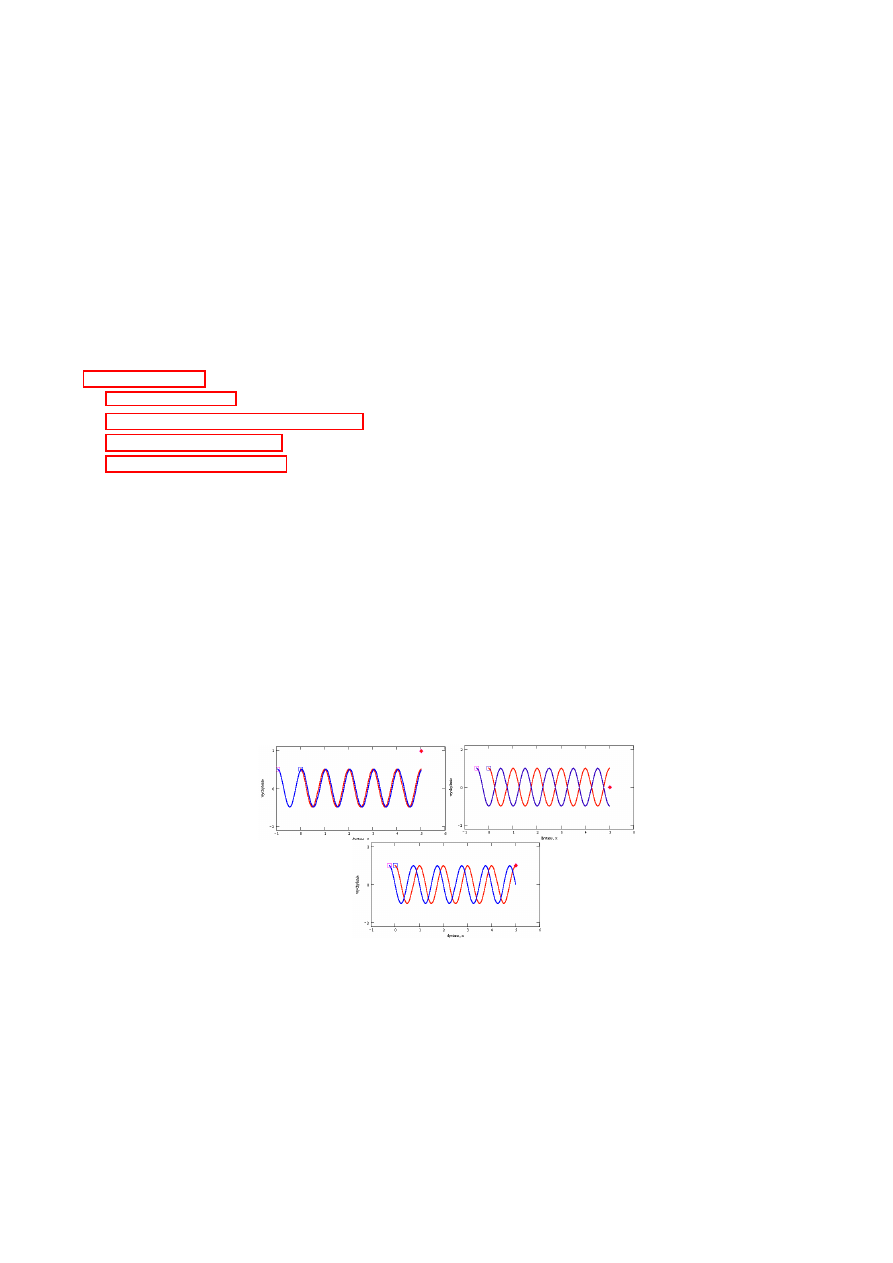
Rysunek 1: Kolejno: wzmocnienie, wygaszenie oraz po±redni rezultat naªo»enia na siebie dwóch fal o jed-

nakowych cz¦sto±ciach. Pami¦taj, »e poza wygaszeniem i wzmocnieniem mamy caª¡ gam¦ innych rezultatów.

Patrz²c na rysunki powy»ej mo»emy zauwa»y¢, »e je±li w pewnym punkcie obserwujemy nakªadanie si¦ na siebie

dwóch fal o jednakowych cz¦sto±ciach to:

•

Je»eli ró»nica faz dwóch fal w tym punkcie jest 0, 2π, 4π, 6π...... (ogólnie ∆φ = 2Nπ) to amplituda

wypadkowa jest równa sumie amplitud fal skªadowych (cz¦sto mówimy wtedy o wzmocnieniu). Je±li

amplitudy fal skªadowych byªy sobie równe wtedy Ψ

wypadkowe

= Ψ

1

+ Ψ

2

= 2Ψ

1

.

•

Je»eli ró»nica faz dwóch fal w tym punkcie jest 0, π, 3π, 5π...... (ogólnie ∆φ = (2N + 1)π) to amplituda

wypadkowa jest równa ró»nicy amplitud fal skªadowych (cz¦sto mówimy wtedy o wygaszeniu). Je±li

amplitudy fal skªadowych byªy sobie równe wtedy Ψ

wypadkowe

= Ψ

1

− Ψ

2

= 0

1

1.2 Nakªadanie si¦ fal z dwóch ¹ródeª

1 INTERFERENCJA

1.2 Nakªadanie si¦ fal z dwóch ¹ródeª

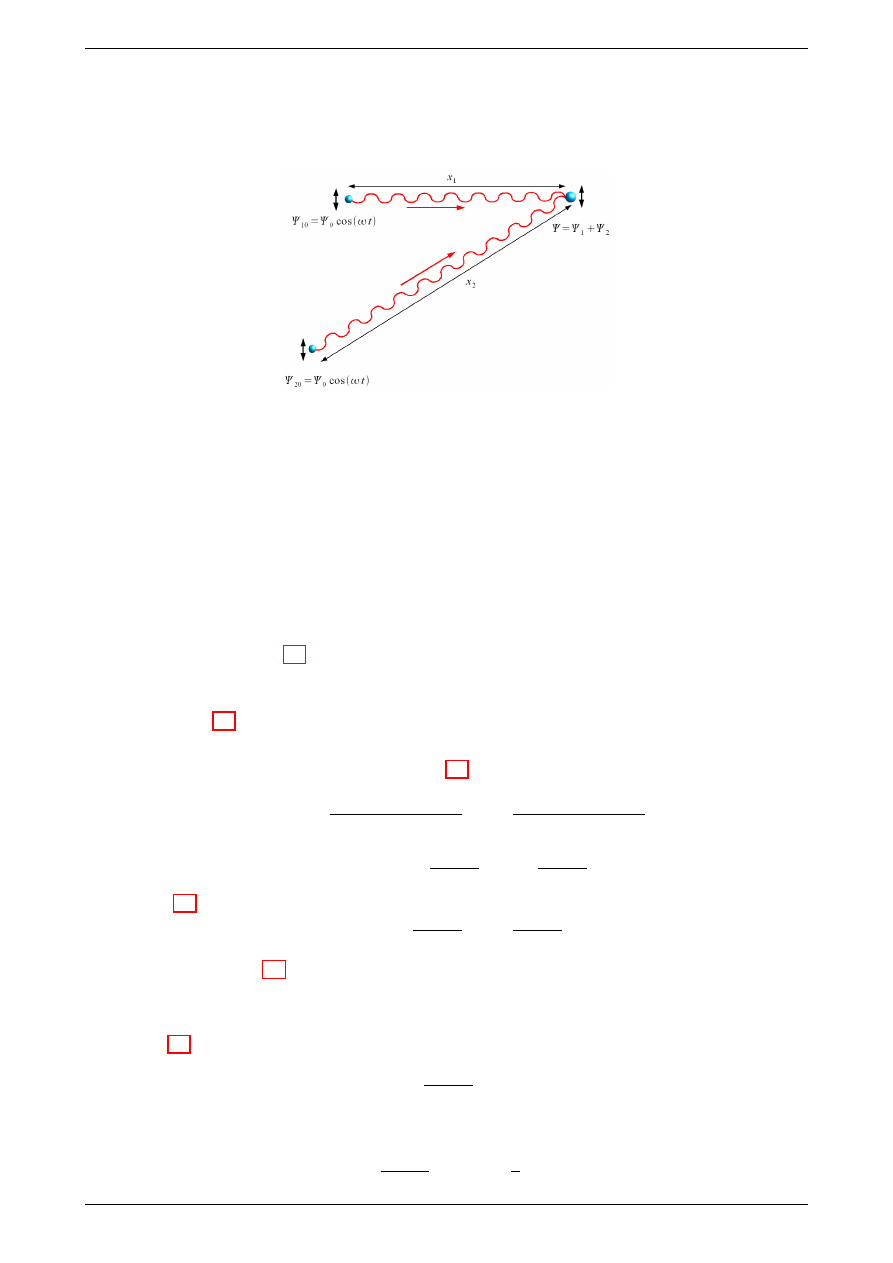
Wyobra¹my sobie, »e do pewnego punktu docieraj¡ fale z dwóch ¹ródeª. Zaªó»my, i» fazy fal emitowanych z

tych ¹ródeª s¡ jednakowe. Jednakowe niech b¦d¡ te» cz¦sto±ci tych fal oraz ich amplitudy.

Rysunek 2: Nakªadanie si¦ fal pochodz¡cych z dwóch identycznych ¹ródeª. Oba ¹ródªa drgaj¡ w tej samej fazie!

Uwaga! Rysunek jest trójwymiarowy, fale maj¡ t¦ sam¡ polaryzacj¦.

Fazy fal docieraj¡cych do miejsca obserwacji wynosz¡

φ

1

= ωt − kx

1

φ

2

= ωt − kx

2

(1.1)

gdzie x

1

i x

2

s¡ odlegªo±ciami punktu obserwacji od odpowiednich ¹ródeª.

Wychylenie w punkcie obserwacji pochodz¡ce od ka»dej z fal wynosi

Ψ

1

= Ψ

0

cos(ωt − kx

1

)

Ψ

2

= Ψ

0

cos(ωt − kx

2

)

(1.2)

W takim razie wychylenie wypadkowe w punkcie obserwacji, pochodz¡ce od obu fal, b¦dzie algebraiczn¡ sum¡

obu wychyle«. Korzystaj¡c z (1.2) otrzymamy

Ψ = Ψ

1

+ Ψ

2

= Ψ

0

cos(ωt − kx

1

) + Ψ

0

cos(ωt − kx

2

)

(1.3)

albo na podstawie (1.1)

Ψ = Ψ

1

+ Ψ

2

= Ψ

0

cos(φ

1

) + Ψ

0

cos(φ

2

)

(1.4)

Korzystaj¡c z wzoru na sum¦ cosinusów otrzymamy z (1.3)

Ψ = 2Ψ

0

cos

ωt − kx

1

+ ωt − kx

2

2

cos

ωt − kx

1

− ωt + kx

2

2

Ψ = 2Ψ

0

cos

ωt − k

x

1

+ x

2

2

cos

k

x

2

− x

1

2

(1.5)

Natomiast z (1.4) otrzymamy

Ψ = 2Ψ

0

cos

φ

1

+ φ

2

2

cos

φ

2

− φ

1

2

(1.6)

Drugi nawias w równaniu (1.5) nie zawiera czasu!

1.2.1 Wygaszanie

Z równania (1.5) wynika, »e wypadkowa amplituda wynosi zero Ψ = 0 , niezale»nie od czasu, wtedy gdy

cos

k

x

2

− x

1

2

= 0

Warunek ten jest speªniony gdy

k

x

2

− x

1

2

= (2N + 1)

π

2

c

Mariusz Krasi«ski 2008

2

1.3 Warunki interferencji

1 INTERFERENCJA

Pami¦taj¡c, »e k = (2π)/λ otrzymamy

x

2

− x

1

= (2N + 1)

λ

2

(1.7)

Post¦puj¡c analogicznie z równaniem (1.6) otrzymamy warunek

cos

φ

2

− φ

1

2

= 0

czyli

φ

2

− φ

1

2

= (2N + 1)

π

2

φ

2

− φ

1

= (2N + 1)π

(1.8)

1.2.2 Wzmacnianie

Z równania (1.5) wynika, »e wypadkowa amplituda jest maksymalna Ψ = max , niezale»nie od czasu, wtedy

gdy

cos

k

x

2

− x

1

2

= ±1

Warunek ten jest speªniony gdy

k

x

2

− x

1

2

= N π

Pami¦taj¡c, »e k = (2π)/λotrzymamy

x

2

− x

1

= N λ

(1.9)

Post¦puj¡c analogicznie z równaniem (1.6) otrzymamy warunek

cos

φ

2

− φ

1

2

= ±1

czyli

φ

2

− φ

1

2

= N π

φ

2

− φ

1

= 2N π

(1.10)

UWAGA! S¡ te» przypadki po±rednie.

1.3 Warunki interferencji

Aby zaszªa interferencja fale musz¡

•

mie¢ t¦ sam¡ cz¦sto±¢

•

mie¢ t¦ sam¡ polaryzacj¦ (aby zaobserwowa¢ jakie± efekty interferencyjne wystarczy, »e pªaszczyzny

polaryzacji fal nie b¦d¡ prostopadªe)

•

¹ródªa musz¡ by¢ spójne (™ródªa spójne to takie, dla których ró»nica faz jest staªa w czasie albo bardzo

wolno zmienna)

c

Mariusz Krasi«ski 2008

3

1.4 Dwa ¹ródªa punktowe

1 INTERFERENCJA

1.4 Dwa ¹ródªa punktowe

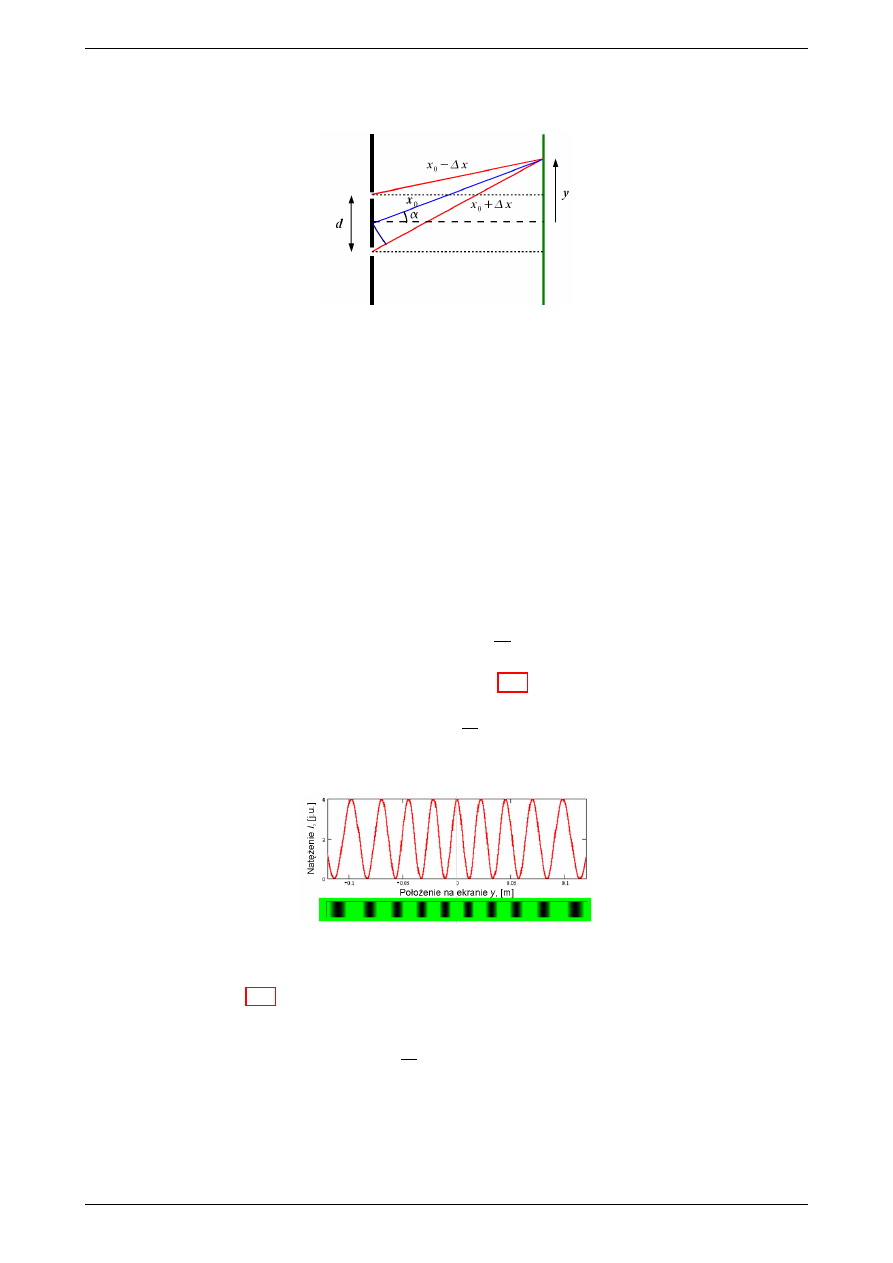
Rysunek 3: Dwa punktowe ¹ródªa (do±wiadczenie Younga)

Zaªo»enia modelu:

•

jednakowe nat¦»enia obu ¹ródeª

•

spadek nat¦»enia z odlegªo±ci¡ jest pomijalnie maªy

•

ekran daleko

Nat¦»enie pola elektrycznego w okre±lonym punkcie ekranu jest sum¡ algebraiczn¡ nat¦»e« pochodz¡cych od

obu ¹ródeª

E = E

1

e

i[ωt−k(x

0

−∆x)]

+ E

2

e

i[ωt−k(x

0

+∆x)]

Mo»na pokaza¢, »e nat¦»enie wypadkowe speªnia zale»no±¢

E = E

0

e

i(ωt−kx

0

)

2 cos

πd

λ

sin α

(1.11)

Pami¦taj¡c, »e I ∝ |E

o

|

2

otrzymujemy ostatecznie z równania (1.11) zale»no±¢

I = 4I

0

cos

2

πd

λ

sin α

(1.12)

Obraz (na ekranie!) powinien wygl¡da¢ jak na rysunku poni»ej.

Rysunek 4: Obraz na ekranie uzyskany od ukªadu dwóch punktowych szczelin. Przypadek idealny.

Korzystaj¡c z równania (1.12) mo»emy znale¹¢ poªo»enia punktów o najwi¦kszej jasno±ci. Maksimum nat¦»enia

otrzymujemy dla cos(...) = ±1 czyli:

πd

λ

sin α = mπ

d sin α = mλ

(1.13)

gdzie m jest liczb¡ caªkowit¡.

c

Mariusz Krasi«ski 2008

4