1

JERZY CZ. OSSOWSKI

Politechnika Gda ska

Katedra Ekonomii i Zarz dzania Przedsi biorstwem

II Ogólnopolska Konferencja Naukowa

pt. „MODELOWANIE I PROGNOZOWANIE GOSPODARKI NARODOWEJ ”,

Katedra Ekonometrii, Wydział Zarz dzania, Uniwersytet Gda ski,

Jastrz bia Góra, 28-30 maj 2007 r.

POMIAR I INTERPRETACJA EFEKTÓW SEZONOWYCH

W PRZYCZYNOWO-SKUTKOWYCH MODELACH DYNAMICZNYCH

NA PRZYKŁADZIE MODELU PŁAC W POLSCE

1. Sformułowanie problemu

Rozwa my przyczynowo-skutkowy dynamiczny model z jedno okresowym opó nieniem

zmiennej endogenicznej. Załó my ponadto, e zmienna endogeniczna podlega wahaniom sezonowym.

Model ten zapisa mo emy nast puj co:

t

1

m

1

j

tj

j

k

1

i

ti

i

1

t

0

t

u

v

c

x

b

aY

b

Y

++++

++++

++++

++++

====

−−−−

====

====

−−−−

,

(0<a<1)

(1)

gdzie:

t = 1,2,3,...,n - numer okresu obserwacji (okresu: półrocznego, kwartalnego lub

miesi cznego)

Y

t

- zmienna endogeniczna w okresie

t,

x

ti

-

i-ta zmienna egzogeniczna w okresie t (i = 1,2,...,k),

j = 1,2,...,m

- numer sezonu: półrocznego (

m=2), kwartalnego (m=4)

lub miesi cznego (

m=12),

v

tj

= s

tj

– s

t1

- centrowana zmienna sezonowa, gdzie s

tj

jest to zmienna zero-jedynkowa:

a, b

i

, c

j

- parametry strukturalne modelu,

u

t

- składnik zakłócaj cy modelu maj cy charakter losowy.

Na podstawie modelu (1), wykorzystuj c parametry

b

i

oraz parametr a, potrafimy okre li

krótkookresowe oraz długookresowe efekty oddziaływania zmiennych

x

ti

na zmienn

Y

t

. Wyłania si

jednak problemem zwi zany z interpretacj efektów sezonowych. Zauwa my bowiem, i

bezpo rednia interpretacja tych efektów na podstawie jedynie parametrów

c

j

mo e by myl ca. Efekty

te w dowolnym sezonie

j-tym skorygowane powinny by przez efekty z poprzedzaj cych go sezonów.

Wynika to z faktu, i w zbiorze zmiennych obja niaj cych wyst puje zmienna endogeniczna

opó niona w czasie, która w okresie wcze niejszym podlegała zmianom sezonowym. Oznacza to, e

wcze niejsze efekty sezonowe, przeniesione na zmienn

Y

t

, znajduj swoje odzwierciedlenie w

parametrze

c

j

. W zarysowanej sytuacji postawi mo emy nast puj ce pytania:

• co stanowi poziom odniesienia dla zmian sezonowych w modelach dynamicznych?

• w jaki sposób zmierzy i zinterpretowa efekty sezonowe w modelu dynamicznym?

• jaki charakter, z punktu widzenia czynnika czasu, maj efekty sezonowe w modelach

dynamicznych?

2. Sezonowo i jej pomiar w przypadku prostych modeli autoregresyjnych

1 w ka dym j-tym sezonie,

0 w pozostałych sezonach

s

tj

=

2

Uznajmy, e za pomoc symbolu

y

t

okre lamy oczyszczon z zakłóce losowych zmienn

endogeniczn

Y

t

. Oznacza to, e y

t

jest składnikiem deterministycznym (systematycznym) modelu (1).

Wst pnie załó my, i w okresach

t=1,2,3,...,n zmienne x

ti

nie wykazuj zmienno ci (tzn.

x

ti

= const.)

Umówmy si ponadto, e w zarysowanych warunkach

t

jest warto ci , jak przyjmuje w okresie

t

funkcja trendu

t

(t) zmiennej y

t

. W zarysowanych warunkach funkcja trendu ma nast puj c posta :

),

y~

y~

(

a

y~

y~

e

o

t

e

t

−−−−

++++

====

(0<a<1)

(2)

Zauwa my, e

e

t

0

t

y~

y~

t

y~

y~

0

t

→

→

→

→

∞

∞

∞

∞

→

→

→

→

→

→

→

→

→

→

→

→

(3)

Z (3) wynika, e:

• parametr

0

jest warto ci inicjuj c trendu

t,

tzn. warto ci trendu dla

t=0,

• parametr

e

jest warto ci graniczn do której zmierza trend

t,

tzn. gdy

t

.

Zauwa my, e:

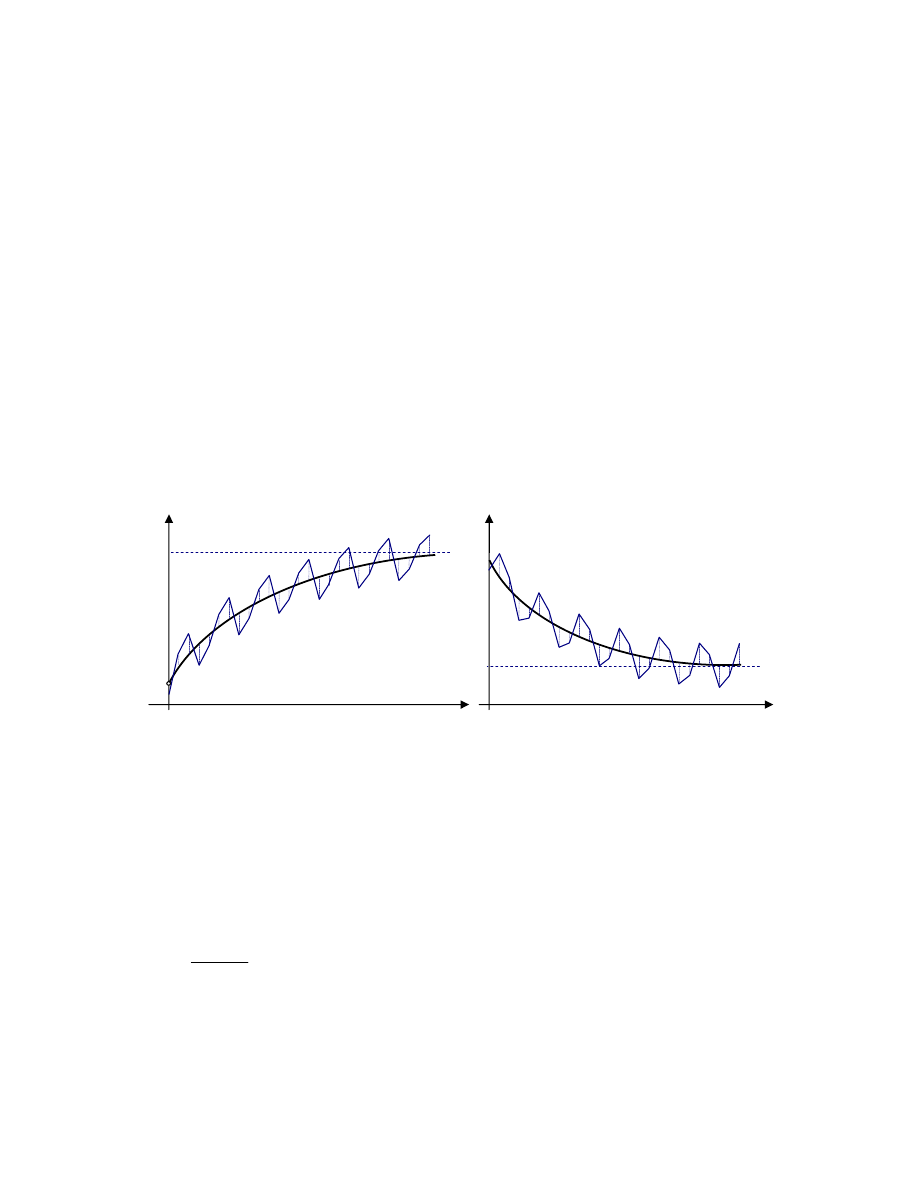
• w sytuacji, gdy warto graniczna trendu

e

jest wi ksza od warto ci inicjuj cej

0

, funkcja trendu

t

(t) jest funkcj rosn c (rys.1, przypadek A),

• w sytuacji, gdy warto graniczna trendu

e

jest mniejsza od warto ci inicjuj cej

0

, funkcja trendu

t

(t) jest funkcj malej c (rys.1, przypadek B),

Funkcj (2) przekształci mo na do nast puj cej postaci:

),

y~

y~

(

a

y~

y~

e

o

t

e

t

−−−−

====

−−−−

(4)

Oznacza to, e dla okresu wcze niejszego powy sze wyra enie zapiszemy nast puj co:

),

y~

y~

(

a

y~

y~

e

o

1

t

e

1

t

−−−−

====

−−−−

−−−−

−−−−

(5)

Dziel c obustronnie (4) przez (5) otrzymujemy:

a

y~

y~

y~

y~

e

1

t

e

t

====

−−−−

−−−−

−−−−

(6)

Oznacza to, e:

),

y~

y~

(

a

y~

y~

e

1

t

e

t

−−−−

====

−−−−

−−−−

(7)

y

t

t

(t)

y

t

(t)

t

0

0

e

Rys. 1 Funkcja składnika systematycznego

y

t

(t) i funkcja jego trendu

t

(t) w warunkach sezonowo ci

kwartalnej w przypadkach wzrostu (przypadek

A) i spadku zmiennej obja nianej (przypadek B).

e

y

t

0

0

t

Przypadek

A:

0

<

e

Przypadek

B:

0

>

e

t

(t)

y

t

(t)

gdzie:

t

(t):

t

=

0

+a

t

(

0

-

e

)

y

t

(t): y

t

=

t

+ e

1

v

t1

+e

2

v

t2

+e

3

v

t3

3

Z powy szego wynika, e:

,

y~

a

y~

)

a

1

(

y~

1

t

e

t

−−−−

++++

−−−−

====

(8)

co mo emy zapisa nast puj co:

,

y~

a

B

y~

1

t

t

−−−−

++++

====

(9)

gdzie:

a

1

B

y~

y~

)

a

1

(

B

e

e

−−−−

====

−−−−

====

(10)

Wykorzystuj c (9), jedno-okresowy przyrost trendu zapiszemy w nast puj cy sposób:

1

t

1

t

1

t

t

y

y~

a

B

y~

y~

−−−−

−−−−

−−−−

−−−−

++++

====

−−−−

,

(11)

co ostatecznie przyjmie nast puj c posta :

1

t

1

t

t

y~

)

1

a

(

B

y~

y~

−−−−

−−−−

−−−−

++++

====

−−−−

,

(12)

Z przyj tych zało e wynika, e zmienna

y

t

charakteryzuje si zmienno ci sezonow .

Umówmy si , e parametr

e

j

w kolejnych sezonach

j = 1,2,3,...,m okre lonego roku wyznacza

odchylenie składnika systematycznego modelu (

yt) od jego trendu (

t

). Odchylenia te nazwa mo emy

czystymi efektami sezonowymi. W ka dym kolejnym roku efekty te przyjm nast puj ce warto ci:

1

m

t

1

m

t

m

2

t

2

t

3

1

t

1

t

2

t

t

1

y~

y

e

..........

..........

y~

y

e

y~

y

e

y~

y

e

−−−−

++++

−−−−

++++

++++

++++

++++

++++

−−−−

====

−−−−

====

−−−−

====

−−−−

====

(13)

Uznajemy jednocze nie, e suma odchyle składnika systematycznego od jego trendu jest równa zero,

tzn.:

0

e

....

e

e

e

m

3

2

1

====

++++

++++

++++

++++

(14)

Z (13) wynika, e w okresie

t-1 efekt sezonowy powinien by równy efektowi sezonowemu z okresu

t+m-1, tzn.:

1

t

1

t

m

y~

y

e

−−−−

−−−−

−−−−

====

(15)

Na podstawie (13) i (15) powiemy, e:

1

t

t

m

1

t

1

t

e

y~

y

e

y~

y

++++

====

++++

====

−−−−

−−−−

(16)

Oznacza to, e:

m

1

1

t

t

1

t

t

e

e

y~

y~

y

y

−−−−

++++

−−−−

====

−−−−

−−−−

−−−−

.

(17)

Wykorzystuj c (12) powy sze wyra enie zapisa mo emy nast puj co:

m

1

1

t

1

t

t

e

e

y~

)

1

a

(

B

y

y

−−−−

++++

−−−−

++++

====

−−−−

−−−−

−−−−

,

(18)

co przekształcaj c otrzymujemy:

4

1

t

m

1

1

t

t

y

e

e

y~

)

1

a

(

B

y

−−−−

−−−−

++++

−−−−

++++

−−−−

++++

====

.

(19)

Z (15) wynika, e:

m

1

t

1

t

e

y

y~

−−−−

====

−−−−

−−−−

(20)

Wprowadzaj c (20) do (19) otrzymujemy:

1

t

m

1

m

1

t

t

y

e

e

)

e

y

)(

1

a

(

B

y

−−−−

−−−−

++++

−−−−

++++

−−−−

−−−−

++++

====

,

(21)

co po uporz dkowaniu zapiszemy ostatecznie w postaci nast puj cego modelu dynamicznego:

m

1

1

t

t

e

a

e

ay

B

y

⋅⋅⋅⋅

−−−−

++++

++++

====

−−−−

(22)

Powy sze wyra enie, po rozpisaniu go dla wszystkich sezonów danego roku, przyjmie nast puj c

posta :

1

m

m

1

m

t

1

m

t

2

3

1

t

2

t

1

2

t

1

t

m

1

1

t

t

e

a

e

y

a

B

y

..

..........

..........

..........

..........

..........

e

a

e

y

a

B

y

e

a

e

y

a

B

y

e

a

e

y

a

B

y

−−−−

−−−−

++++

−−−−

++++

++++

++++

++++

−−−−

⋅⋅⋅⋅

−−−−

++++

⋅⋅⋅⋅

++++

====

⋅⋅⋅⋅

−−−−

++++

⋅⋅⋅⋅

++++

====

⋅⋅⋅⋅

−−−−

++++

⋅⋅⋅⋅

++++

====

⋅⋅⋅⋅

−−−−

++++

⋅⋅⋅⋅

++++

====

(23)

Uznajmy, e parametry

c

j

dla

j =1,2,3,...,m s składnikami sezonowymi rozwa anego powy ej modelu

dynamicznego. Oznacza to, e:

1

m

m

m

2

3

3

1

2

2

m

1

1

e

a

e

c

......

..........

..........

e

a

e

c

e

a

e

c

e

a

e

c

−−−−

⋅⋅⋅⋅

−−−−

====

⋅⋅⋅⋅

−−−−

====

⋅⋅⋅⋅

−−−−

====

⋅⋅⋅⋅

−−−−

====

(24)

Z uwagi na (14) stwierdzamy, i :

====

====

====

====

++++

====

m

1

j

j

m

1

j

m

1

j

j

j

0

e

a

e

c

(25)

Oznacza to, e model (22) mo emy zapisa , wykorzystuj c zdefiniowane dla (1) centrowane zmienne

sezonowe (

v

tj

), w nast puj cej postaci:

−−−−

====

−−−−

++++

⋅⋅⋅⋅

++++

====

1

m

1

j

tj

j

1

t

t

v

c

y

a

B

y

(26)

Rozwa my mo liwo zidentyfikowania parametrów

e

j

- charakteryzuj cych sezonowo

powtarzaj ce si odchylenia zmiennej

y

t

od jej trendu

t

- na podstawie parametrów

a oraz c

j

-

charakteryzuj cych struktur

modelu dynamicznego (26). W tym celu nale y układ równa (24)

przekształci do nast puj cej postaci rekurencyjnej:

)

m

.

27

(

e

a

c

e

......

..........

..........

)

3

.

27

(

e

a

c

e

)

2

.

27

(

e

a

c

e

)

1

.

27

(

e

a

c

e

1

m

m

m

2

3

3

1

2

2

m

1

1

−−−−

⋅⋅⋅⋅

++++

====

⋅⋅⋅⋅

++++

====

⋅⋅⋅⋅

++++

====

⋅⋅⋅⋅

++++

====

(27)

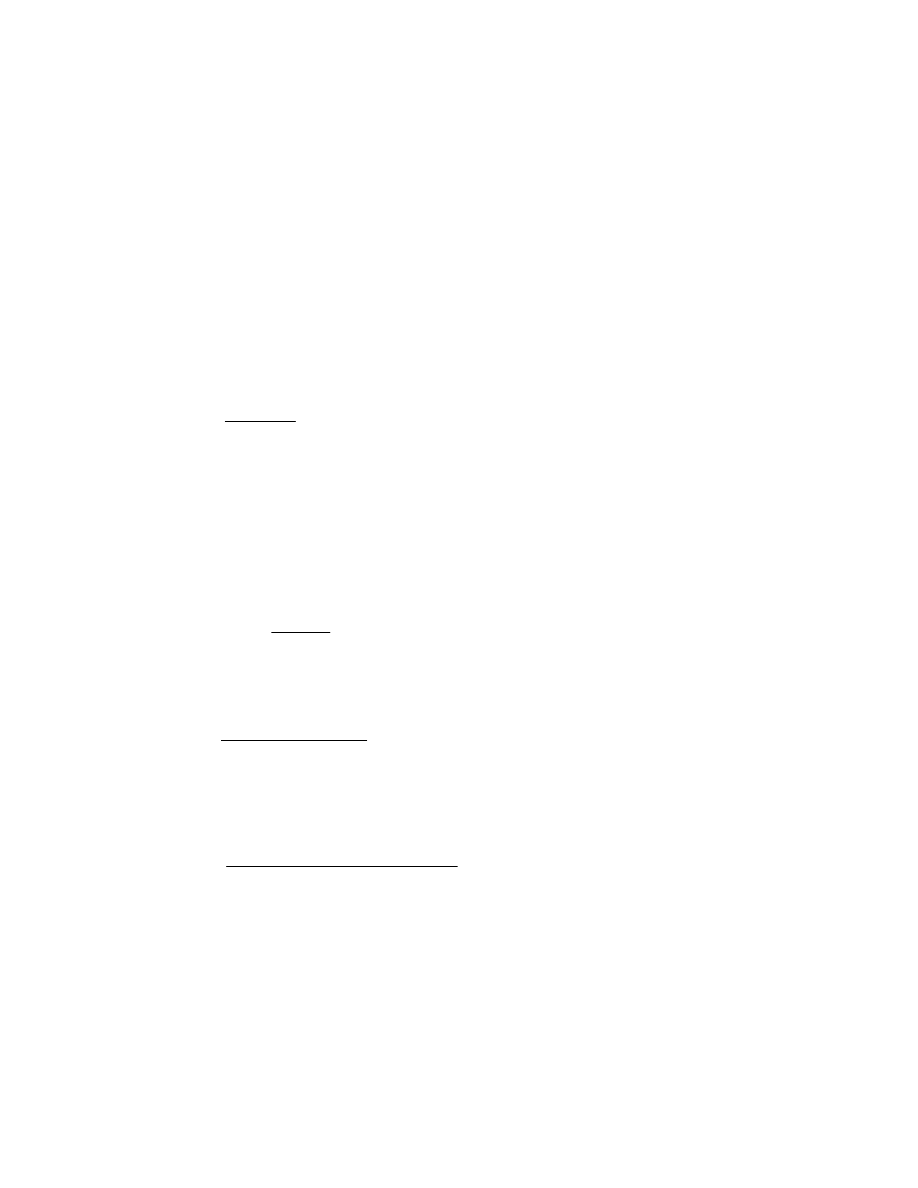
5

Traktuj c parametry

e

j

jako niewiadome, celem rozwi zania powy szego układu równa , w

pierwszym kroku nale y wprowadzi zdefiniowany w (27.1) parametr

e

1

do (27.2). W wyniku tego

otrzymujemy nast puj ce zdefiniowanie parametru

e

2

:

m

2

1

2

2

e

a

c

a

c

e

++++

⋅⋅⋅⋅

++++

====

(27.2.a)

Wprowadzaj c obecnie (27.2a) do (27.3) otrzymujemy:

m

3

1

2

2

3

3

e

a

c

a

c

a

c

e

++++

++++

⋅⋅⋅⋅

++++

====

(27.3.a)

W wyniku kolejnych podstawie ostatecznie dochodzimy do nast puj cej postaci:

m

m

1

1

m

2

m

2

1

m

m

m

e

a

c

a

...

c

a

c

a

c

e

++++

++++

++++

++++

⋅⋅⋅⋅

++++

====

−−−−

−−−−

−−−−

(27.m.a)

Na podstawie powy szego równania wyznaczamy warto

e

m

według nast puj cej zasady:

m

m

1

j

j

j

m

m

a

1

c

a

e

−−−−

⋅⋅⋅⋅

====

====

−−−−

(28)

Jest to zapis ogólny dla sezonowo ci półrocznej, kwartalnej oraz miesi cznej. Zauwa my, e

wprowadzaj c do równania (27.1) warto parametru

e

m

wyznaczamy warto parametru

e

1

, która

charakteryzuje efekt sezonowy w sezonie pierwszym. To z kolei pozwala obliczy parametr

e

2

na

podstawie (27.2). Kolejno podstawiaj c warto ci parametrów

e

j

w sposób rekurencyjny wyznaczymy

wszystkie poszukiwane efekty sezonowe. Na podstawie wzoru (28) okre li mo emy przypadki

szczegółowe.

W przypadku sezonowo ci półrocznej (m=2) posta (27) sprowadza si do układu dwu

równa dla którego wyra enie (28) przyjmie nast puj c posta :

2

2

1

2

a

1

c

c

a

e

−−−−

++++

⋅⋅⋅⋅

====

.

(29)

W przypadku sezonowo ci kwartalnej (m=4) posta (27) sprowadza si do układu czterech

równa dla którego wyra enie (28) przyjmie nast puj c posta :

4

4

3

2

2

1

3

4

a

1

c

c

a

c

a

c

a

e

−−−−

++++

⋅⋅⋅⋅

++++

++++

====

.

(30)

Z kolei

w przypadku sezonowo ci miesi cznej (m=12) posta (27) zawiera b dzie 12

równa z dwunastu niewiadomymi wielko ciami

e

j

. W układzie tym wyra enie (28) przyjmie

nast puj c posta :

12

12

11

3

9

2

10

1

11

12

a

1

c

c

a

...

c

a

c

a

c

a

e

−−−−

++++

⋅⋅⋅⋅

++++

++++

++++

++++

====

.

(31)

Oznacza to, e sezonowy model dynamiczny (26) wyrazi mo na alternatywnie w postaci

modelu tendencji z efektami sezonowymi. Wykorzystuj c zdefiniowania scentrowanych zmiennych

zero-jedynkowych (

v

tj

) model ten zapiszemy nast puj co:

−−−−

====

−−−−

====

++++

====

++++

−−−−

++++

====

1

m

1

j

tj

j

t

1

m

1

j

tj

j

e

o

t

e

t

v

e

)

t

(

y~

v

e

)

y~

y~

(

a

y~

y

(32)

Obraz graficzny powy szego modelu, ograniczony do sezonowo ci kwartalnej, przedstawiono na

rysunku 1.

6

3. Przyczynowo-skutkowy model dynamiczny a posta jego trendu

Uznajmy, e zmienna

x

t

reprezentuje zmienne egzogeniczne

x

ti

uj te w modelu (1). Je li

obecnie zało ymy, e zmienna ta w dowolnym okresie

t=1,2,3,...,n podlega zmianom, wówczas posta

autoregresyjn zmiennej

t

, okre lon w (9), zapisa mo emy w nast puj cy sposób:

,

y~

a

B

y~

:

)

x

,t

(

y~

1

t

t

t

t

t

−−−−

++++

====

(33)

gdzie:

t

1

0

t

x

b

b

B

++++

====

(34)

Oznacza to, e model (33) zapisa mo emy w nast puj cej postaci:

t

1

1

t

0

t

x

b

y~

a

b

y~

++++

++++

====

−−−−

(35)

Z powy szego wynika, e zdefiniowana w (10) warto graniczna trendu (

t

) podlega przemieszczeniu

wraz ze zmian zmiennej

x

t

, jako e granic wyznacza nast puj co zdefiniowana funkcja:

t

1

0

t

et

x

a

1

b

a

1

b

a

1

B

y~

−−−−

++++

−−−−

====

−−−−

====

(36)

Na podstawie (35) i zwi zanej z ni funkcj (36) okre li mo emy efekty krótkookresowego i

długookresowego oddziaływania zmiennej

x

t

na zmienn

t

.

Efekt krótkookresowy (natychmiastowy) definiujemy w nast puj cy sposób:

t

1

t

t

k

t

1

t

t

k

t

x

b

y~

:

)

x

(

Ef

b

x

y~

Ef

∆∆∆∆

====

∆∆∆∆

∆∆∆∆

====

∆∆∆∆

∆∆∆∆

====

(37)

Na podstawie powy szego powiemy, e

je eli zmienna x

t

w okresie t wzro nie o jednostk to w

tym samym okresie zmienna

t

zmieni si o b

1

jednostek. Oznacza to e całkowity efekt

krótkookresowy, wynikaj cy z przyrostu zmiennej o wielko

x

t

wyniesie

b

1

· x

t

. Efekty tych zmian

przedstawiono na rysunkach 2 i 3. Z analizy rysunków wynika, ze efekt krótkookresowy oznacza

przesuni cie w dowolnym okresie

t = h trendu w gór lub w dół.

Efekt długookresowy definiujemy nast puj co:

t

1

et

t

d

t

1

t

et

d

t

x

a

1

b

y~

:

)

x

(

Ef

a

1

b

x

y~

Ef

∆∆∆∆

−−−−

====

∆∆∆∆

∆∆∆∆

−−−−

====

∆∆∆∆

∆∆∆∆

====

(38)

Na podstawie powy szego powiemy, e

je eli zmienna x

t

w okresie t wzro nie o jednostk i

utrzyma si na nowym poziomie to zmienna

t

zmieni si ostatecznie o (b

1

/1-a) jednostek..

Oznacza to e całkowity efekt długookresowy, wynikaj cy z przyrostu zmiennej o wielko

x

t

wyniesie

[(b

1

/1-a)· x

t

]. Wielko ta równa jest przesuni ciu granicy do której zmierza b dzie,

przesuni ty w okresie

t = h, trend. Efekty tych zmian przedstawiono na rysunkach 2 i 3.

Z analizy rysunków 2 i 3 wynika, e wraz ze zmian poło enia trendów i granic do których

zmierzaj trendy nast puje jednoczesne przemieszczenie poło enia tzw. warto ci inicjuj cych

0t

, a

wi c warto ci wyznaczaj cych poło enie trendu na osi rz dnych w sytuacji, gdy zmienna

t przyjmie

warto zero. Warto zauwa y , aby funkcj (35) sprowadzi do modelu trendu, nale y zdefiniowa nie

tylko funkcj granicy trendu, tak jak przedstawiono to w (36). Nale y bowiem okre li dodatkowo

funkcj zmiany poło enia tzw. warto ci inicjuj cych.

Na wst pie zauwa my, e wykorzystuj c (36) zdefiniowany w (2) trend przeł cznikowy,

wynikaj cy z funkcji autoregresyjnej (35), zapiszemy nast puj co:

t

1

t

0

t

t

0

t

t

1

0

t

t

t

x

a

1

b

a

a

1

b

a

y~

a

x

a

1

b

a

1

b

y~

:

)

x

,t

(

y~

−−−−

−−−−

−−−−

−−−−

++++

−−−−

++++

−−−−

====

(39)

7

Je li obecnie zało ymy, e zmienna

x

t

w dowolnym okresie

t wzro nie o x

t

, to musimy uzna e

nast pi natychmiastowy przyrost zmiennej

t

o wielko

t

i jednoczesne przesuni cie warto ci

inicjuj cej

0t

o wielko

0t

. W tych warunkach powy szy model przyjmie nast puj c posta :

)

x

x

(

a

1

b

a

a

1

b

a

)

y~

y~

(

a

)

x

x

(

a

1

b

a

1

b

y~

y~

t

t

1

t

0

t

t

0

t

0

t

t

t

1

0

t

t

∆∆∆∆

++++

−−−−

−−−−

−−−−

−−−−

∆∆∆∆

++++

++++

∆∆∆∆

++++

−−−−

++++

−−−−

====

∆∆∆∆

++++

(40)

Je li odejmiemy stronami od równania (40) równanie (39) to otrzymamy:

t

1

t

t

0

t

t

1

t

x

a

1

b

a

y~

a

x

a

1

b

y~

∆∆∆∆

−−−−

−−−−

∆∆∆∆

++++

∆∆∆∆

−−−−

====

∆∆∆∆

(41)

Zauwa my, e zgodnie z (37) przyrost

t

zdefiniowany powy ej jest efektem krótkookresowym

wywołanym przez przyrost zmiennej

x

t

, co oznacza, e (41) zapisa mo na w nast puj cy sposób:

t

1

t

t

0

t

t

1

t

1

x

a

1

b

a

y~

a

x

a

1

b

x

b

∆∆∆∆

−−−−

−−−−

∆∆∆∆

++++

∆∆∆∆

−−−−

====

∆∆∆∆

(42)

y

t

t

(t,x

t

)

y

t

(t,x

t

)

t

0

01

e1

Rys. 2 Funkcja składnika systematycznego

y

t

(t,x

t

) i funkcja jego trendu przeł cznikowego

t

(t,x

t

)

w warunkach sezonowo ci i przyrostu zmiennej

x

t

(przypadek wzrostu wielko ci granicznej trendu)

e2

02

h

0t

Ef

t

d

:

et

Ef

t

k

:

t

)

gdzie:

Efekt długookresowy

Ef

t

d

( x

t

):

et

= (b

1

/1-a)· x

t

Efekt krótkookresowy

Ef

t

k

( x

t

):

t

) = b

1

x

t

Efekt zmian inicjuj cych:

0t

y

t

t

(t,x

t

)

y

t

(t,x

t

)

t

0

01

e1

Rys. 3 Funkcja składnika systematycznego

y

t

(t,x

t

) i funkcja jego trendu przeł cznikowego

t

(t,x

t

)

w warunkach sezonowo ci i przyrostu zmiennej

x

t

(przypadek spadku wielko ci granicznej trendu)

e2

02

h

0t

Ef

t

d

:

et

)

Ef

t

k

:

t

gdzie:

Efekt długookresowy

Ef

t

d

( x

t

):

et

= (b

1

/1-a)· x

t

Efekt krótkookresowy

Ef

t

k

( x

t

):

t

= b

1

· x

t

Efekt zmian inicjuj cych:

0t

8

Przekształcaj c powy sze wyra enie, w sposób umo liwiaj cy wyznaczenie przyrostu warto ci

inicjuj cej dla trendu z dowolnego okresu

t, otrzymujemy ostatecznie:

t

1

t

1

t

0

x

a

1

b

)

a

1

(

y~

∆∆∆∆

−−−−

−−−−

====

∆∆∆∆

−−−−

(43)

Je li uznamy, e

x

t

= x

t

– x

t-1

wówczas przyrost składnika inicjuj cego zapiszemy w nast puj cej

postaci:

0t

=

0t

-

0,t-1

W tej sytuacji

powy sze wyra enie zapiszemy nast puj co:

t

1

t

1

1

t,

0

t

0

x

a

1

b

)

a

1

(

y~

y~

∆∆∆∆

−−−−

−−−−

++++

====

−−−−

−−−−

(44)

Z (44) wynika, e warto inicjuj ca dla trendu przeł cznikowego w ka dym z okresów

t jest równa

skorygowanej warto ci inicjuj cej tego trendu z okresu poprzedniego (

t-1). Korekta ta jest zale na od

przyrostu zmiennej

x

t

. Z drugiej strony zauwa my, e warto inicjuj ca dla trendu z okresu

t=1 jest

równa

0

. Oznacza to, e wykorzystuj c (44) warto inicjuj c trendu przeł cznikowego w

dowolnym okresie

t w relacji do jej warto ci inicjuj cej z okresu t=1, tzn. wtedy gdy warto

inicjuj ca jest równa

0

, okre limy za pomoc nast puj cej funkcji:

====

−−−−

∆∆∆∆

−−−−

−−−−

++++

====

n

1

t

t

1

t

1

0

t

0

x

a

1

b

)

a

1

(

y~

y~

(45)

Obecnie wprowadzaj c (45) do trendu przeł cznikowego, zdefiniowanego w (39), otrzymujemy:

−−−−

++++

−−−−

∆∆∆∆

−−−−

−−−−

++++

++++

−−−−

++++

====

====

−−−−

n

1

t

t

1

0

t

1

t

1

0

t

t

1

0

t

t

t

a

1

x

b

b

x

a

1

b

)

a

1

(

y~

a

a

1

x

b

b

y~

:

)

x

,t

(

y~

(46)

Z powy szego wynika, e w warunkach znajomo ci parametrów

a, b

i

oraz warto ci inicjuj cej

0

, dla

okre lonych warto ci zmiennej

x

t

potrafimy wyznaczy trend przeł cznikowy. Trend ten w sposób

jednoznaczny daje si przekształci do przyczynowo-skutkowego modelu dynamicznego

zdefiniowanego w (35). Tym samym, je li obecnie zało ymy, e funkcja składnika systematycznego

y

t

(t,x

t

) charakteryzuje si stałymi sezonowymi odchyleniami od trendu przeł cznikowego

t

(t,x

t

),

model tego procesu zapisa mo emy nast puj co:

−−−−

====

++++

====

1

m

1

j

tj

j

t

t

t

t

t

v

e

)

x

,t

(

y~

y

:

)

x

,t

(

y

(47)

W wietle powy szych rozwa a wynika, e model (47) daje si sprowadzi jednoznacznie do

przyczynowo skutkowego modelu dynamicznego o nast puj cej postaci:

−−−−

====

−−−−

++++

++++

++++

====

1

m

1

j

tj

j

t

1

1

t

0

t

v

c

x

b

ay

b

y

(48)

Oznacza to, e na podstawie znajomo ci parametrów

c

j

z równania (48) mo emy wyznaczy

parametry

e

j

z równania (47). Przy identyfikacji parametrów

e

j

mamy prawo zastosowa zasady

sformułowane dla rozwi zania układu równa (27). Reasumuj c powiemy, e na podstawie

znajomo ci parametrów

a, b

0

, b

1

oraz

c

j

potrafimy w sposób jednoznaczny okre li i zinterpretowa :

• efekt krótkookresowy oddziaływania zmiennej x

t

na zmienn

y

t

(patrz: (37)),

• efekt długookresowy oddziaływania zmiennej x

t

na zmienn

y

t

(patrz: (38)),

• warunkowe graniczne poziomy wzrostu zmiennej y

t

(patrz: (36)),

• efekty sezonowe zmian zmiennej y

t.

(patrz: (27) i (28))

Z powy szych rozwa a wynika, e

parametr e

j

dla j=1,2,3,...,m, wskazuje na sezonowo

powtarzaj ce si odchylenie zmiennej y

t

od poziomu wyznaczonego przez czynnik x

t

. Przy czym

poziom ten jest okre lony przez poziom trendu przeł cznikowego, który został zdefiniowany

równaniem (46).

9

4. Kwartalny, multiplikatywny dynamiczny model płac – problemy interpretacji i estymacji

Konstruuj c przyczynowo-skutkowy model poziomu płac zało ono, zgodnie z zasadniczymi

pogl dami sformułowanymi literaturze przedmiotu, e w warunkach stało ci pozostałych zmiennych

poziom płac nominalnych (

WN):

• wzrasta wraz ze wzrostem wydajno ci pracy (APL),

• maleje wraz ze wzrostem stopy bezrobocia (SU), jako e siła negocjacyjna pracobiorców w

zakresie wzrostu płac (

WN) jest tym mniejsza, im wi ksza jest stopa bezrobocia (SU),

• wzrasta wraz ze wzrostem poziomu cen (ICK), jako e w negocjacjach płacowych pracobiorcy

d

do zapobie enia spadkowi płac realnych.

Ponadto - ustalaj c posta analityczn modelu - uznano, e:

• wzrost stopy bezrobocia prowadzi do obni enia wydajno ciowej elastyczno ci płac, tym samym

do spadku poziomu płac przy danym poziomie wydajno ci,

• dostosowywanie si płac do poziomu wydajno ci, stopy bezrobocia oraz poziomu cen jest

rozło one w czasie,

• oddziaływanie stopy bezrobocia na poziom płac nast puje z opó nieniem czasowym rz du i.

Wskazuje to na dynamiczne zmiany elastyczno ci płac wzgl dem wyró nionych czynników.

Celem sprawdzenia poprawno ci funkcjonowania powy szej prawidłowo ci i zweryfikowania jej dla

warunków Polski z lat 1995-2005 oraz uwzgl dniaj c fakt, posługiwania si danymi kwartalnymi,

wst pnie rozwa ono nast puj cy multiplikatywny, przyczynowo-skutkowy model płac:

t

u

3

t

v

3

c

2

t

v

2

c

1

t

v

1

c

3

b

t

i

t

SU

2

b

1

b

t

a

1

t

0

t

e

e

ICK

APL

WN

B

WN

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

−−−−

++++

−−−−

(49)

Po obustronnym zlogarytmowaniu modelu (49) zapiszemy go w nast puj cej postaci:

,

u

v

c

v

c

v

c

ICK

ln

b

SU

APL

ln

b

APL

ln

b

WN

ln

a

b

WN

ln

t

3

t

3

2

t

2

1

t

1

t

3

i

t

t

2

t

1

1

t

0

t

++++

++++

++++

++++

++++

++++

++++

++++

++++

====

−−−−

−−−−

(50)

W przypadku analizy kwartalnej wyniki oszacowa metod najmniejszych kwadratów (MNK)

modelu (50) mog by wypaczone na skutek sezonowego, wzajemnego skorelowania zmiennych

obja niaj cych. Aby unikn tego rodzaju niekorzystnej sytuacji, model (50) zmodyfikowano poprzez

wprowadzenie w miejsce zmiennych obja niaj cych ich czterookresowych rednich ruchomych. W

rezultacie model ten zapisa mo emy w nast puj cy sposób:

t

3

t

3

2

t

2

1

t

1

t

3

i

t

t

2

t

1

1

t

0

t

u

v

c

v

c

v

c

ICK

ln

A

b

ASU

APL

ln

A

b

APL

ln

A

b

WN

ln

a

b

WN

ln

++++

++++

++++

++++

++++

++++

++++

++++

++++

====

−−−−

−−−−

(51)

gdzie:

4

/

)

APL

ln

APL

ln

APL

ln

APL

(ln

APL

ln

A

3

t

2

t

1

t

t

t

−−−−

−−−−

−−−−

++++

++++

++++

====

(52.1)

4

/

)

SU

SU

SU

SU

(

ASU

3

t

2

t

1

t

t

t

−−−−

−−−−

−−−−

++++

++++

++++

====

(52.2)

4

/

)

ICK

ln

ICK

ln

ICK

ln

ICK

(ln

ICK

ln

A

3

t

2

t

1

t

t

t

−−−−

−−−−

−−−−

++++

++++

++++

====

(53.3)

Na podstawie modelu (51) okre li mo emy:
A1. Krótkookresow elastyczno płacy ze wzgl du na wydajno :

i

t

2

1

t

t

)

APL

(

WN

K

SU

b

b

APL

ln

A

/

WN

ln

E

−−−−

⋅⋅⋅⋅

++++

====

∆∆∆∆

∆∆∆∆

====

(53)

A2. Długookresow elastyczno płacy ze wzgl du na wydajno pracy:

)

a

1

/(

)

ASU

b

b

(

APL

ln

A

/

WN

ln

E

i

t

2

1

t

e

t

)

APL

(

WN

D

−−−−

⋅⋅⋅⋅

++++

====

∆∆∆∆

∆∆∆∆

====

−−−−

(54)

B1. Krótkookresow elastyczno płacy ze wzgl du na poziom cen:

10

3

t

t

)

ICK

(

WN

K

b

ICK

ln

A

/

WN

ln

E

====

∆∆∆∆

∆∆∆∆

====

(55)

B2. Długookresow elastyczno płacy ze wzgl du na poziom cen:

a

1

/

b

ICK

ln

A

/

WN

ln

E

3

t

e

t

)

ICK

(

WN

D

−−−−

====

∆∆∆∆

∆∆∆∆

====

(56)

W przypadku modelu dynamicznego, aby okre li efekty sezonowych odchyle płac od

poziomu wyznaczonego przez wyró nione czynniki, zgodnie z (27), musimy rozwi za nast puj cy

układ równa :

4

3

4

3

2

3

2

1

2

1

4

1

c

e

a

e

c

e

a

e

c

e

a

e

c

e

a

e

++++

⋅⋅⋅⋅

====

++++

⋅⋅⋅⋅

====

++++

⋅⋅⋅⋅

====

++++

⋅⋅⋅⋅

====

(57)

gdzie

e

j

jest poszukiwanym efektem sezonowym w j-tym kwartale. Rozwi zuj c powy szy układ w

pierwszej kolejno ci, zgodnie z (30) wyznaczamy, wielko

e

4

według nast puj cej zasady:

)

a

1

/(

)

c

c

a

c

a

c

a

(

e

4

4

3

2

2

1

3

4

−−−−

++++

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

====

(58)

Z uwagi na multiplikatywny charakter rozwa anego modelu na podstawie parametrów

e

j

okre lamy

powtarzaj ce si sezonowo wzgl dne odchylenie poziomu płac od poziomu wyznaczonego przez

czynniki uwzgl dnione w modelu.

Odchylenie to dla dowolnego kwartału j-tego, w uj ciu procentowym, obliczmy według nast puj cej

reguły:

%

100

)

1

e

(

%

100

)

X

,t

(

TrWN

)

X

,t

(

TrWN

WN

Efs

j

e

t

t

tj

j

⋅⋅⋅⋅

−−−−

====

⋅⋅⋅⋅

−−−−

====

(59)

Na podstawie (59) powiemy

o ile procent w ka dym j-tym kwartale odchylaj płace WN

tj

od

poziomu wyznaczonego przez czynniki uwzgl dnione w modelu. Zauwa my, e czynniki te

wyznaczaj poziom trendu przeł cznikowego

TrWN(t,X)

t

, w stosunku do którego odnosimy poziom

płac ukształtowany w kolejnych kwartałach.

5. Wyniki oszacowa kwartalnego, multiplikatywnego dynamicznego model płac

Dokonuj c oszacowa modelu (51) sprawdzono mi dzy innymi rz d opó nienia przy stopie

bezrobocia. Najlepsze wyniki oszacowa otrzymano zakładaj c przy zmiennej

ASU opó nienie

pierwszego rz du. Wyniki oszacowa modelu (51) dla aktualizowanej próby statystycznej z lat 1995 –

2005 przedstawiono w tabeli 1. Porównuj c wyniki tych oszacowa mo na uzna , e aktualizacja,

polegaj ca na nieuwzgl dnianiu najstarszych informacji w trakcie procesu szacowania modelu,

jedynie nieznacznie zmieniała warto ci oszacowa .

Na podstawie (53) i (54), wykorzystuj c zamieszczone w tabeli 1 wyniki oszacowa

parametrów strukturalnych modeli, wyznaczono krótkookresowe i długookresowe elastyczno ci płac

zakładaj c stopy bezrobocia z przedziału od 5% do 25%. Wyniki przedstawiono w tabelach 2A i 2B.

Z kolei na podstawie (55) i (56) okre li mo emy krótkookresow i długookresow

elastyczno płacy ze wzgl du na poziom cen. Warto zauwa y , e oszacowania efektów

długookresowych zamieszczono w nawiasach kwadratowych przy oszacowanych parametrach

b

3

. Na

ich podstawie powiemy:

• w warunkach stało ci pozostałych zmiennych, wzrost poziomu cen w okresie t o 1% prowadził do

przeci tnego przyrostu poziomu płac w tym samym okresie o około 0,65% (od 0,672% do

0,595%)od (efekt krótkookresowy),

• w warunkach stało ci pozostałych zmiennych, wzrost poziomu cen w okresie t o 1% i utrzymania

si ich na nowym poziomie prowadzi do granicznego (ostatecznego) przyrostu poziomu płac o

około 0,95% (od 1,04% do 0,868%) (efekt długookresowy).

11

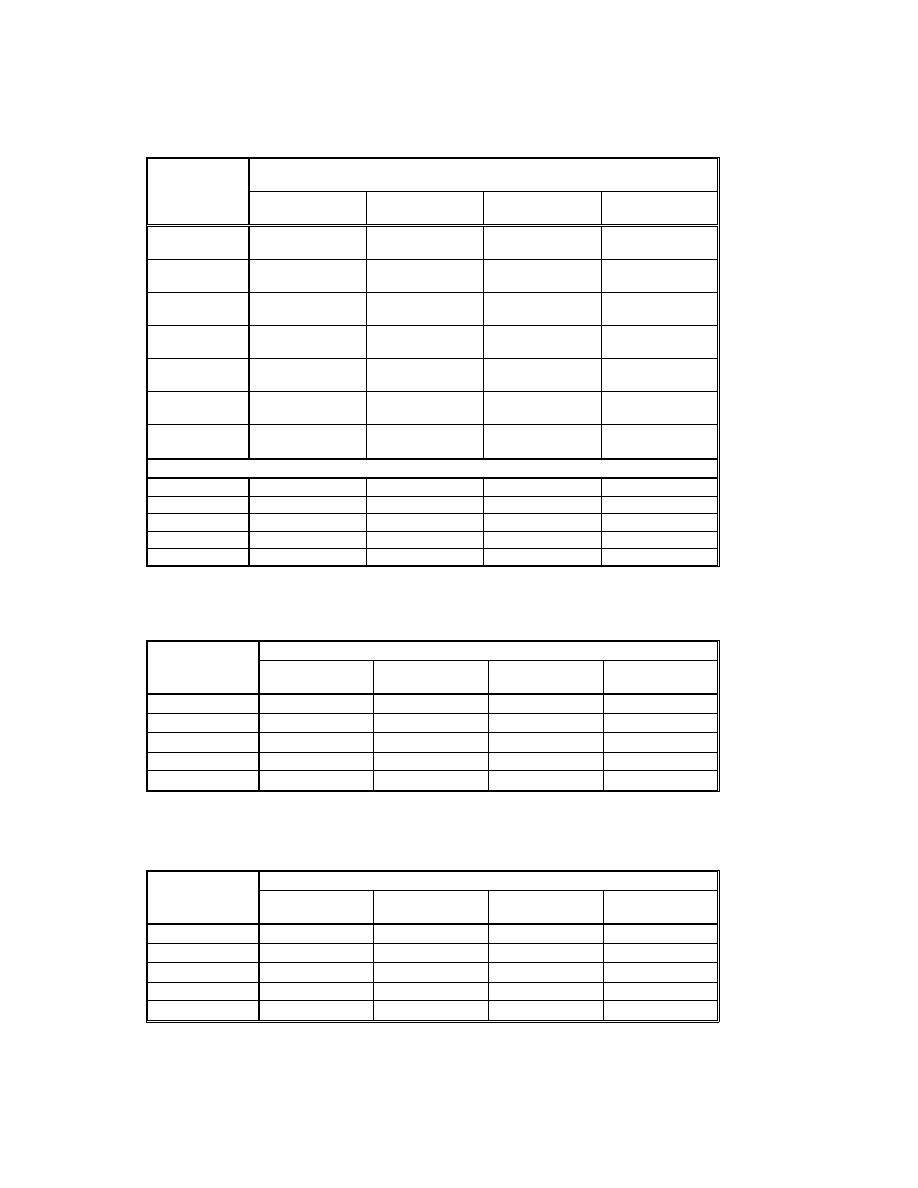
Tabela 1 Wyniki oszacowa MNK dynamicznego wydajno ciowego modelu płac (16)

(przypadek rocznych rednich ruchomych zmiennych obja nianych)

Oszacowane warto ci parametrów strukturalnych oraz warto ci

statystyk t-studenta dla próby z okresów:

Parametr

i

symbol

zmiennej

1996 kw.I

2005 kw.II

1996 kw.III

2005 kw.II

1997 kw.I

2005 kw.II

1997 kw.III

2005 kw.II

b

0

4,542

(6,894)

4,558

(5,596)

4,674

(5,492)

4,407

(4,925)

a

AlnWN

t-1

0,3340

(3,419)

0,3314

(2,731)

0,3155

(2,494)

0,3556

(2,678)

b

1

AlnAPL

t

0,7082

(2,462)

0,7127

(2,370)

0,7229

(2,351)

0,6878

(2,190)

b

2

ASU

t-1

AlnAPL

t

-0,0204

(-2,227)

-0,0207

(-2,146)

-0,0201

(-2,031)

-0,0188

(-1,819)

b

3

AlnICK

t

0,6483 [0,973]

(5,485)

0,6543 [0,979]

(4,322)

0,6521 [0,953]

(4,196)

0,6012 [0,933]

(3,697)

c

2

v

t2

-0,0235

(-5,734)

-0,0237

(-5,215)

-0,0240

(-5,156)

-0,0257

(-5,053)

c

3

v

t3

-0,0123

(-3,253)

-0,0122

(-3,052)

-0,0118

(-2,754)

-0,0110

(-2,462)

Charakterystyka próby statystycznej oraz miary jako ci oszacowa modelu

n

38

36

34

32

R

2

0,9975

0,9966

0,9954

0,9939

Se

0,0136

0,0140

0,0143

0,0144

DW

2,1192

2,0910

2,1199

2,1392

D-h[prob]

-0,4603[0,645]

-0,3980[0,691]

-0,5178[0,605]

-0,5967[0,551]

ródło: Obliczenia własne na podstawie danych GUS

Tabela 2A Krótkookresowe symulowane warunkowe

elastyczno ci płac ze wzgl du na wydajno pracy

Oszacowane elastyczno ci dla okresów:

Zało ony poziom

stopy bezrobocia

(ASU

t-1

)

1996 kw.I

2005 kw.II

1996 kw.III

2005 kw.II

1997 kw.I

2005 kw.II

1997 kw.III

2005 kw.II

5%

0,6062

0,6092

0,6224

0,5938

10%

0,5042

0,5057

0,5219

0,4998

15%

0,4022

0,4022

0,4214

0,4058

20%

0,3002

0,2987

0,3209

0,3118

25%

0,1982

0,1952

0,2204

0,2178

ródło: Obliczenia własne

Tabela 2B Długookresowe symulowane warunkowe

elastyczno ci płac ze wzgl du na wydajno pracy

Oszacowane elastyczno ci dla okresów:

Zało ony poziom

stopy bezrobocia

(ASU

t-1

)

1996 kw.I

2005 kw.II

1996 kw.III

2005 kw.II

1997 kw.I

2005 kw.II

1997 kw.III

2005 kw.II

5%

0,9102

0,9116

0,9093

0,9215

10%

0,7571

0,7564

0,7625

0,7756

15%

0,6039

0,6016

0,6156

0,6297

20%

0,4508

0,4467

0,4688

0,4839

25%

0,2976

0,2920

0,3220

0,3380

ródło: Obliczenia własne

12

Na podstawie (57) i (58 ), wykorzystuj c oszacowania parametrów c

j

, oszacowano parametry

okre laj ce efekty sezonowe. Szacuj c te efekty, na przykład dla oszacowa obejmuj cej prób

statystyczn z lat 1996kwI – 2005kwII, rozwi zywano nast puj cy układ równa :

0358

,

0

cˆ

:

e

,

jako

0358

,

0

eˆ

334

,

0

eˆ

0123

,

0

cˆ

:

e

,

jako

0123

,

0

eˆ

334

,

0

eˆ

0235

,

0

cˆ

:

e

,

jako

0235

,

0

eˆ

334

,

0

eˆ

0

,

0

cˆ

:

e

,

jako

0

,

0

eˆ

334

,

0

eˆ

4

3

4

3

2

3

1

1

2

0

4

1

====

++++

====

−−−−

====

−−−−

====

−−−−

====

−−−−

====

====

++++

====

Z (58) wynika, e:

0294

,

0

)

334

,

0

1

/(

)

0358

,

0

0123

,

0

334

,

0

0235

,

0

334

,

0

0

,

0

334

,

0

(

eˆ

4

2

3

4

====

−−−−

++++

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

====

Wprowadzaj c oszacowanie parametru e

4

do rekurencyjnego układu równa ostatecznie otrzymujemy:

0294

,

0

eˆ

,

0191

,

0

eˆ

,

0202

,

0

eˆ

,

0098

,

0

eˆ

4

3

2

1

====

−−−−

====

−−−−

====

====

Wykorzystuj c powy sze oszacowania wyznaczamy na podstawie (59)

powtarzaj ce si sezonowo

wzgl dne odchylenie poziomu płac od poziomu wyznaczonego przez czynniki uwzgl dnione w

modelu:

%

98

,

2

%

100

)

1

e

(

Efs

%

89

,

1

%

100

)

1

e

(

Efs

%

00

,

2

%

100

)

1

e

(

Efs

%

99

,

0

%

100

)

1

e

(

Efs

0294

,

0

4

0191

,

0

3

0202

,

0

2

0098

,

0

1

====

⋅⋅⋅⋅

−−−−

====

−−−−

====

⋅⋅⋅⋅

−−−−

====

−−−−

====

⋅⋅⋅⋅

−−−−

====

====

⋅⋅⋅⋅

−−−−

====

−−−−

−−−−

Efekty sezonowe wyra one procentowymi odchyleniami płac od poziomu wyznaczonego przez

czynniki kształtuj ce poziom cen, dla poozostałych podokresów obliczono na podobnej zasadzie.

Wyniki tych oblicze przedstawiono w tabeli 3.

Tabela 3 Efekty sezonowe procentowych odchyle wysoko ci płac od ich poziomu wyznaczonego

poziomem wydajno ci, stop bezrobocia oraz poziomem cen

Oszacowane elastyczno ci dla okresów:

Numer kwartału

1996 kw.I

2005 kw.II

1996 kw.III

2005 kw.II

1997 kw.I

2005 kw.II

1997 kw.III

2005 kw.II

kwartał I

0,99%

0,99%

0,95%

1,08%

kwartał II

-2,00%

-2,02%

-2,08%

-2,17%

kwartał III

-1,89%

-1,88%

-1,82%

-1,86%

kwartał IV

2,99%

3,01%

3,04%

3,05%

ródło: Obliczenia własne

Wykorzystuj c wyniki oszacowa rozpatrywanych wersji przyczynowo-skutkowych modeli płac

oraz na podstawie przeprowadzonych symulacji sformułowa mo emy nast puj ce wnioski generalne:

• w latach 1996-2005 wyst powała cisła współzale no pomi dzy poziomem płac nominalnych a

wydajno ci pracy, stop bezrobocia i poziomem cen,

• zwi zki pomi dzy wysoko ci płac a wydajno ci pracy, stop bezrobocia i poziomem cen miały

charakter dynamiczny,

• Elastyczno płac ze wzgl du na wydajno pracy zmniejszała si wraz ze spadkiem stopy

bezrobocia oraz zwi kszała si wraz ze wzrostem tej stopy i wynosiła odpowiednio około:

przy stopie bezrobocia 10% w krótkim okresie 0,50% a w długim okresie 0,75%,

przy stopie bezrobocia 15% w krótkim okresie 0,40% a w długim okresie 0,60%,

przy stopie bezrobocia 20% w krótkim okresie 0,30% a w długim okresie 0,45%.

• w warunkach stało ci pozostałych czynników wzrost poziomu cen o 1% prowadził do

natychmiastowego przyrostu płac w granicach 0,65% oraz granicznego przyrostu wynosz cego

około 0,95%

13

• W zakresie odchyle płacy nominalnej od poziomu wyznaczonego przez wydajno pracy, stop

bezrobocia oraz poziom cen wyst powały efekty sezonowe. Odchylenia te wynosiły odpowiednio

około:

1,00 % w I kwartale,

-2,05% w II kwartale,

-1,85% w III kwartale,

3,00% w IV kwartale.

W cz ci teoretycznej referatu wykazano:

• sposób wyznaczania poziomu odniesienia dla zmian sezonowych w modelach dynamicznych,

• sposób pomiaru i interpretacji efektów sezonowych w modelu dynamicznym,

BIBLIOGRAFIA

[1] Barro R.: Makroekonomia, PWE, Warszawa 1997.

[2] Burda M., Wyplosz Ch.: Makroekonomia, Podr cznik europejski, PWE, Warszawa 1995.

[3] Chow G.: Ekonometria, Wydawnictwo Naukowe PWN, Warszawa 1995.

[4] Dornbusch R., Fischer S., Sparks G. R.: Macroeconomics, Third Canadian Edition, McGraw-Hill

Ryerson Limited, Toronto 1989.

[5] Maddala G.,S.: Introduction to Econometrics, John Wiley & Sons LTD, New York 2001.

[6] Hall R., E., Taylor J., B.: Makroekonomia, Teoria, funkcjonowanie i polityka, Wydawnictwo

Naukowe PWN, Warszawa 1995.

[7] Ossowski J., Cz.: Wybrane zagadnienia z makroekonomii, Poj cia, problemy, przykłady i zadania,

WSFiR, Sopot 2004.

[8] Ossowski J.,Cz.:Sezonowo w modelach dynamicznych - problemy interpretacyjne,

w „Dynamiczne modele ekonometryczne”, Katedra Ekonometrii i Statystyki, Uniwersytet

M.Kopernika, Toru 1997, s.51-56

[9] Ossowski J. Cz.: Problemy specyfikacji i estymacji przyczynowo-skutkowego modelu płac, XI

Seminarium Naukowe Katedry Ekonomii i Zarz dzania Przedsi biorstwem Politechniki Gda skiej

nt.: „GOSPODARKA POLSKI W OKRESIE TRANSFORMACJI”, 25-21 wrzesie 2006 r.

Wdzydze Kiszewskie,

[10] Romer D.: Makroekonomia dla zaawansowanych, Wydawnictwo Naukowe PWN, Warszawa

2000.

[11] Stewart M.B., Wallis K.F, (1981), Introductory Econometrics, Basil Blackwel, Oxford.

[12] Strzała K., (1994), Ekonometria inaczej, Wydawnictwo UG, Gda sk.

[13] Tu P.N.V., (1992), Dynamical systems, Springer-Verlag , Berlin -Heidelberg.

[14] Zieli ski Z., (1979), Metody analizy dynamiki i rytmiczno ci zjawisk gospodarczych, PWN,

Warszawa.

[15] Poland Quarterly Statistics, GUS, Warszawa, lata:1996-2005

14

Zał cznik A

Symulacyjny model dynamiczny z sezonowo ci kwartaln

Zało enia do modelu symulacyjnego:

Funkcja trendu przeł cznikowego

t

1

t

0

t

t

0

t

t

1

0

t

t

t

x

a

1

b

a

a

1

b

a

y~

a

x

a

1

b

a

1

b

y~

:

)

x

,t

(

y~

−−−−

−−−−

−−−−

−−−−

++++

−−−−

++++

−−−−

====

gdzie:

====

−−−−

∆∆∆∆

−−−−

−−−−

++++

====

n

1

t

t

1

t

1

0

t

0

x

a

1

b

)

a

1

(

y~

y~

Przyj te warto ci parametrów:

a = 0,9

b

0

= 10

b

1

= 5

0

= 200

Zało one warto ci zmiennej

x

t

warto ci dla okresów:

od t=1 do t= 8 : x

t

= 5...

od t= 9 do t= 16: x

t

=10

od t= 17 do t=24: x

t

=15

od t= 25 do t= 32: x

t

=20

od t=33 do t= 40: x

t

= 5...

Przyj ty system oznacze do MICROFIT:

Trend przeł cznikowy zmiennej obja nianej:

t

(t,x

t

) = Y

Składnik systematyczny modelu:

y

t

(t,x) =

SY

Wyliczenia w MICROFICIE:

Funkcja trendu przeł cznikowego:

Y = 100+50*x-100*0.9^t-50*x*0.9^t+y0*0.9^t

gdzie:

CSUMPOMDX : csum(pomdx)

POM : 1-0.9^(1-t)

POMDX : pom*dx

Y0 : 200+50*csumpomdx

Funkcja składnika systematycznego(trend+ funkcja składnika sezonowego):

SY = y+50*v1-50*v2-40*v3

15

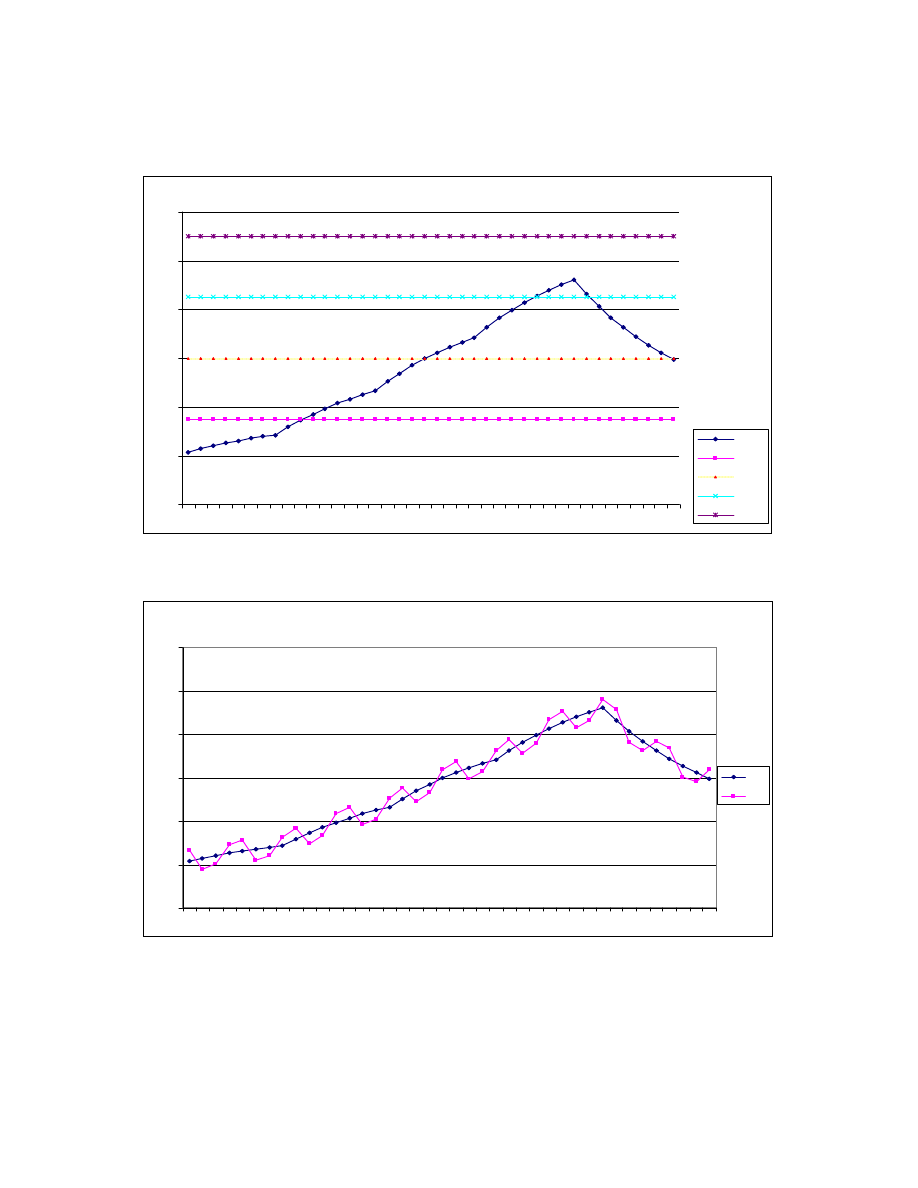
Wykres 1. Trend przeł cznikowy (Y) i jego granice (YEx)

0

200

400

600

800

1000

1200

1

3

5

7

9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39

Y
YE5
YE10
YE15
YE20

Wykres 2 Składnik systematyczny (SY) i jego trend przeł cznikowy

w warunkach sezonowo ci kwartalnej

0

200

400

600

800

1000

1200

1

3

5

7

9

11 13 15 17 19 21 23 25 27 29 31 33 35 37 39

Y
SY

16

Wyniki oszacowa modelu dynamicznego na podstawie symulowanego trendu

przeł cznikowego

Ordinary Least Squares Estimation

*******************************************************************************

Dependent variable is Y

39 observations used for estimation from 2000Q2 to 2009Q4

*******************************************************************************

Regressor Coefficient Standard Error T-Ratio[Prob]

C 10.0000 0.00 *NONE*

Y(-1) .90000 0.00 *NONE*

X 5.0000 0.00 *NONE*

*******************************************************************************

R-Squared 1.0000 R-Bar-Squared 1.0000

S.E. of Regression .0000 F-stat. F( 2, 36) *NONE*

Mean of Dependent Variable 569.8195 S.D. of Dependent Variable 216.9486

Residual Sum of Squares .0000 Equation Log-likelihood *NONE*

Akaike Info. Criterion *NONE* Schwarz Bayesian Criterion *NONE*

DW-statistic *NONE* Durbin's h-statistic *NONE*

*******************************************************************************

Wyniki oszacowa modelu dynamicznego na podstawie symulowanego trendu

przeł cznikowego z sezonowo ci kwartaln

Ordinary Least Squares Estimation

*******************************************************************************

Dependent variable is SY

39 observations used for estimation from 2000Q2 to 2009Q4

*******************************************************************************

Regressor Coefficient Standard Error T-Ratio[Prob]

C 10.0000 0.00 *NONE*

SY(-1) .90000 0.00 *NONE*

X 5.0000 0.00 *NONE*

V1 14.0000 0.00 *NONE*

V2 -95.0000 0.00 *NONE*

V3 5.0000 0.00 *NONE*

*******************************************************************************

R-Squared 1.0000 R-Bar-Squared 1.0000

S.E. of Regression .0000 F-stat. F( 5, 33) *NONE*

Mean of Dependent Variable 568.5375 S.D. of Dependent Variable 223.5954

Residual Sum of Squares .0000 Equation Log-likelihood *NONE*

Akaike Info. Criterion *NONE* Schwarz Bayesian Criterion *NONE*

DW-statistic *NONE* Durbin's h-statistic *NONE*

*******************************************************************************

17