MECHANIKA

UKŁADÓW WIELOCZŁONOWYCH

Prowadzący: dr inż. Paweł Ostapkowicz
WM-324

Wykład 2
Temat:

Wykreślne metody wyznaczania prędkości i przyspieszeń

mechanizmów płaskich

1. Wstęp

Kinematyka: (od greckiego słowa „kinema” - ruch) – dział mechaniki, który zajmuje się
badaniem ruchu mechanizmów w oderwaniu od przyczyn (sił), które ten ruch powodują.
Stąd uzasadnia to często stosowaną zamiennie ze słowem kinematyka nazwę geometria
ruchu.

Badanie ruchu polega na określeniu położeń, prędkości i przyspieszeń punktów (danego
mechanizmu).
W kinematyce występują dwie jednostki:
- długości (przemieszczenia),
- czasu.

Kinematyka dzieli się na dwa podstawowe działy:
1)

analiza – dotyczy badania ruchu istniejących mechanizmów,

2)

synteza – dotyczy projektowania mechanizmów wykonujących określony ruch.

Metody stosowane w kinematyce można podzielić na trzy grupy:
- metody wykreślne – są szczególnie przydatne dla konstruktorów mechanizmów
i maszyn. Pozwalają prosto i szybko wyznaczyć położenia, prędkości i przyśpieszenia
w złożonych mechanizmach;
- metody analityczne – zapewniają większą dokładność wyników;
- metody numeryczne – zapewniają większą dokładność wyników i szybkość obliczeń.


Metody analizy powinny być dobierane w zależności od żądanej dokładności i rodzaju
mechanizmu. W mechanizmach prostych metody analityczne są dość proste,
w mechanizmach złożonych stają się one mocno skomplikowane.

2. Przypomnienie wiadomości o wektorach

Wektor jest to wielkość posiadająca:
- kierunek,
- zwrot,
- punkt przyłożenia,
- wartość.

Działania na wektorach:
- mnożenie skalarne,
- dodawanie skalarne,
- dodawanie graficzne.

3. Metody wykreślne kinematyki

Podstawowym zagadnieniem przy stosowaniu metod wykreślnych jest przyjęcie
odpowiedniej podziałki.
Podziałka

χ

jest to skalar określający stosunek wielkości rzeczywistej do rysunkowej

i mający taki wymiar, aby na rysunku otrzymać długość w milimetrach.

)

(

)

(

X

X

X

X

=

=

→

→

χ

→

X

- wektor rzeczywisty,

X

- moduł wektora,

)

(

→

X

- wektor rysunkowy,

)

(X

- moduł wektora,

v

χ

- podziałka prędkości (m/s / mm)

ε

χ

- podziałka dla przyspieszenia kątowego (1/s

2

/ mm)

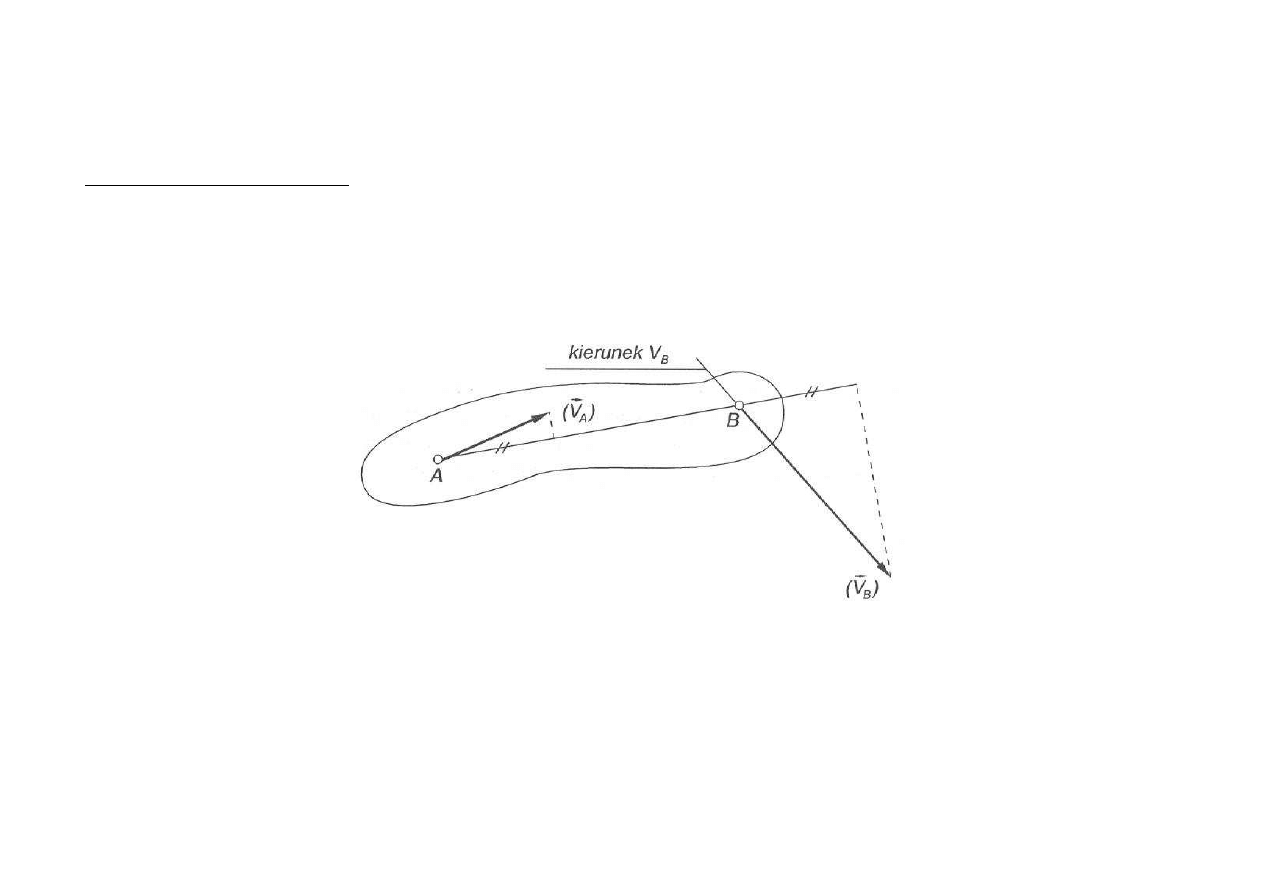
3.1. Wyznaczanie prędkości

METODA RZUTÓW

Twierdzenie: Rzuty prędkości dwóch punktów A i B członu sztywnego (nie powinien się
rozciągać lub kurczyć) na prostą AB są sobie równe.

Rys. Ilustracja metody rzutów

Dane konieczne do zastosowania metody to:
1)

prędkość jednego punktu,

2)

kierunek prędkości drugiego punktu.

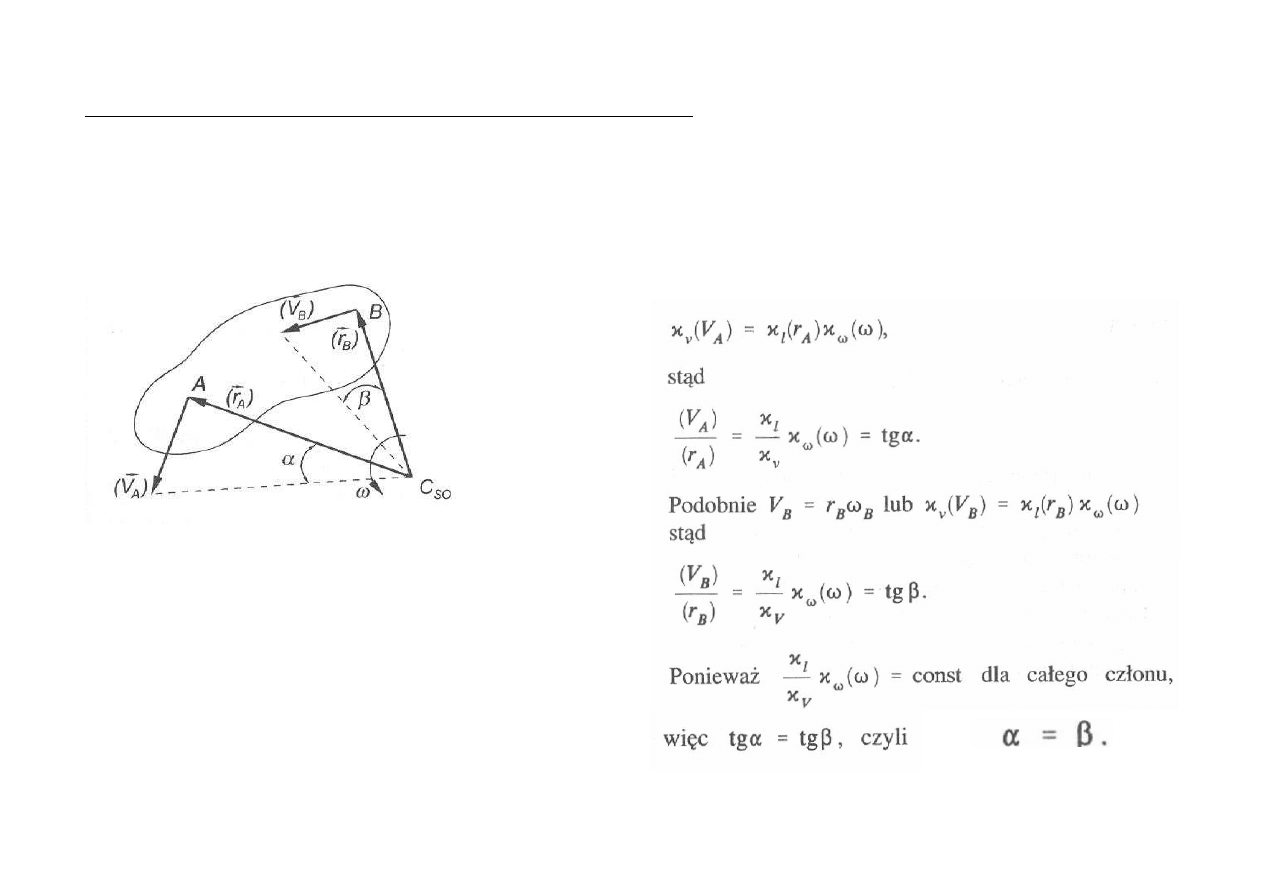
METODA CHWILOWEGO ŚRODKA OBROTU

Twierdzenie: Ze środka chwilowego obrotu członu widać prędkości wszystkich punktów
członu pod jednakowym kątem.

Zawsze można napisać, że

A

A

A

r

V

ω

=

Rys.

Ilustracja metody chwilowego

ś

rodka obrotu

Dane konieczne do zastosowania metody to:
1)

prędkość jednego punktu ciała,

2)

położenie chwilowego środka obrotu.

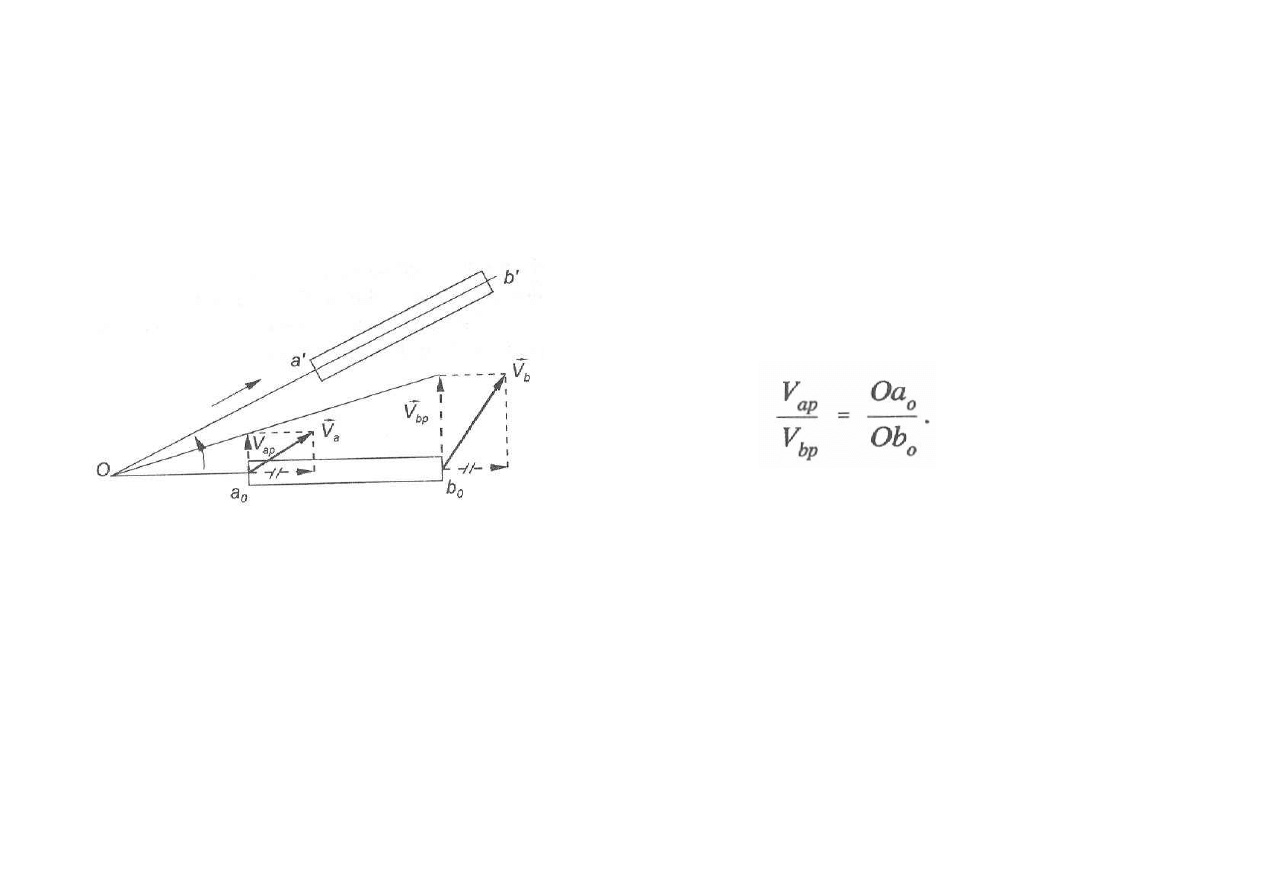
Co zrobić, gdy położenie chwilowego środka obrotu nie mieści się na rysunku?

Twierdzenie: Każdy ruch złożony może być rozpatrywany jako chwilowy ruch postępowy
i obrotowy.

Składowe chwilowego ruchu obrotowego są
prostopadłe do a

0

b

0

i są proporcjonalne do

odległości od punktu O.

To prawo proporcjonalności pozwala określić
prędkość dowolnego punktu członu sztywnego,

w przypadku gdy nie znany jest kierunek jego
prędkości,

a

ś

rodek

prędkości

leży

poza

rysunkiem.

Dane konieczne do zastosowania metody to:
1) prędkość jednego punktu ciała,
2) kierunek prędkości drugiego punktu.

Rys. Ilustracja zasady, że każdy
ruch złożony składa się z ruchu
obrotowego i postępowego

Do wyznaczenia chwilowego środka obrotu (środka prędkości) trzeba mieć dane kierunki
prędkości dwóch punktów ciała sztywnego i punkty przyłożenia tych prędkości. Środek
prędkości leży na przecięciu prostopadłych do kierunków prędkości, wyprowadzonych z
punktów przyłożenia prędkości.

Jak wyznaczyć chwilowe środki obrotu trzech układów płaskich poruszających się
względem siebie?

Twierdzenie: Trzy chwilowe środki obrotu względnego dowolnych trzech członów
mechanizmu płaskiego leżą na jednej prostej.

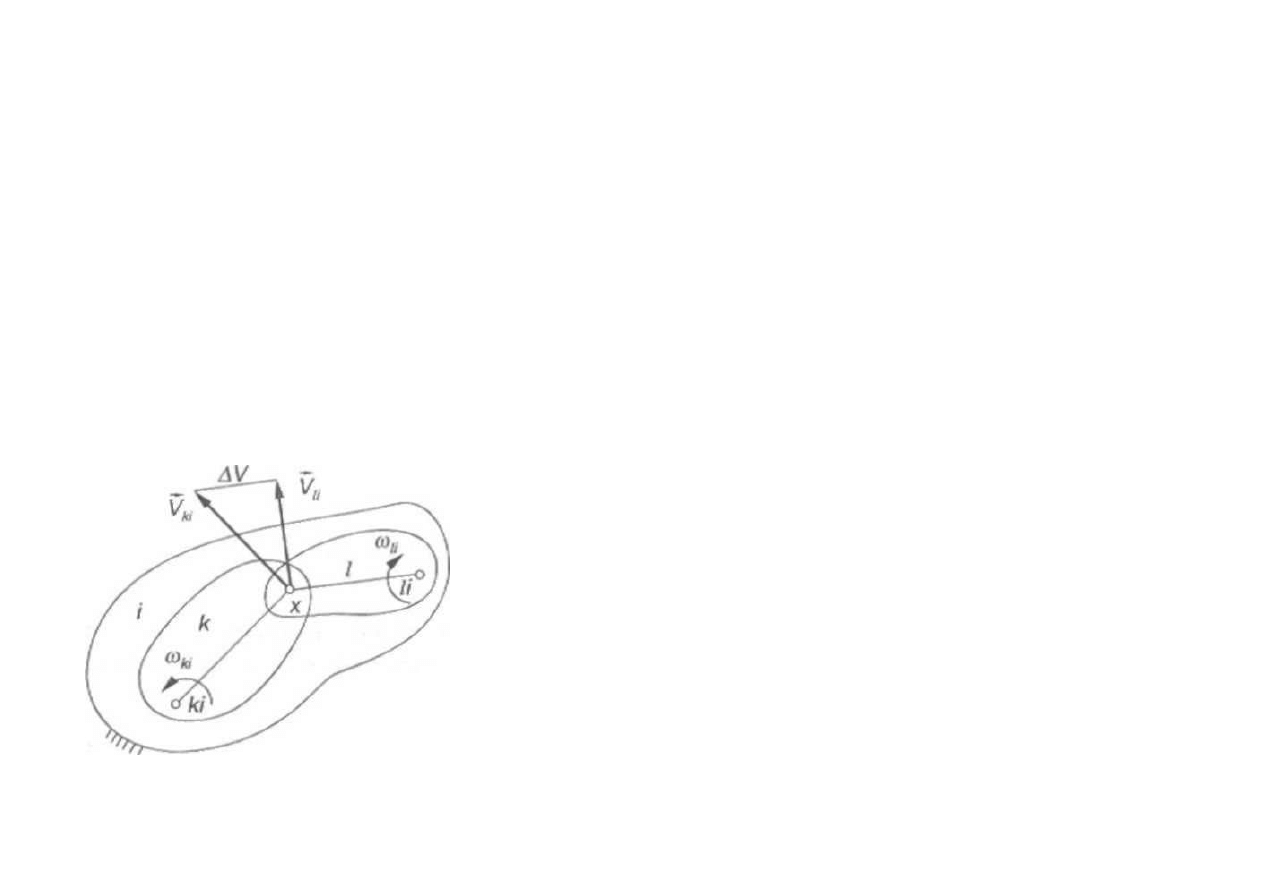
Rys. Trzy układy płaskie poruszające się względem siebie

trzy układy płaskie: i, k , l; dane środki obrotu: ki, li, kl;
przy czym poszukiwany jest środek obrotu kl

Punkt x będzie chwilowym środkiem obrotu członów k i l
wtedy i tylko wtedy, jeśli ∆V = 0, a to wymaga aby x leżał
na prostej kl.

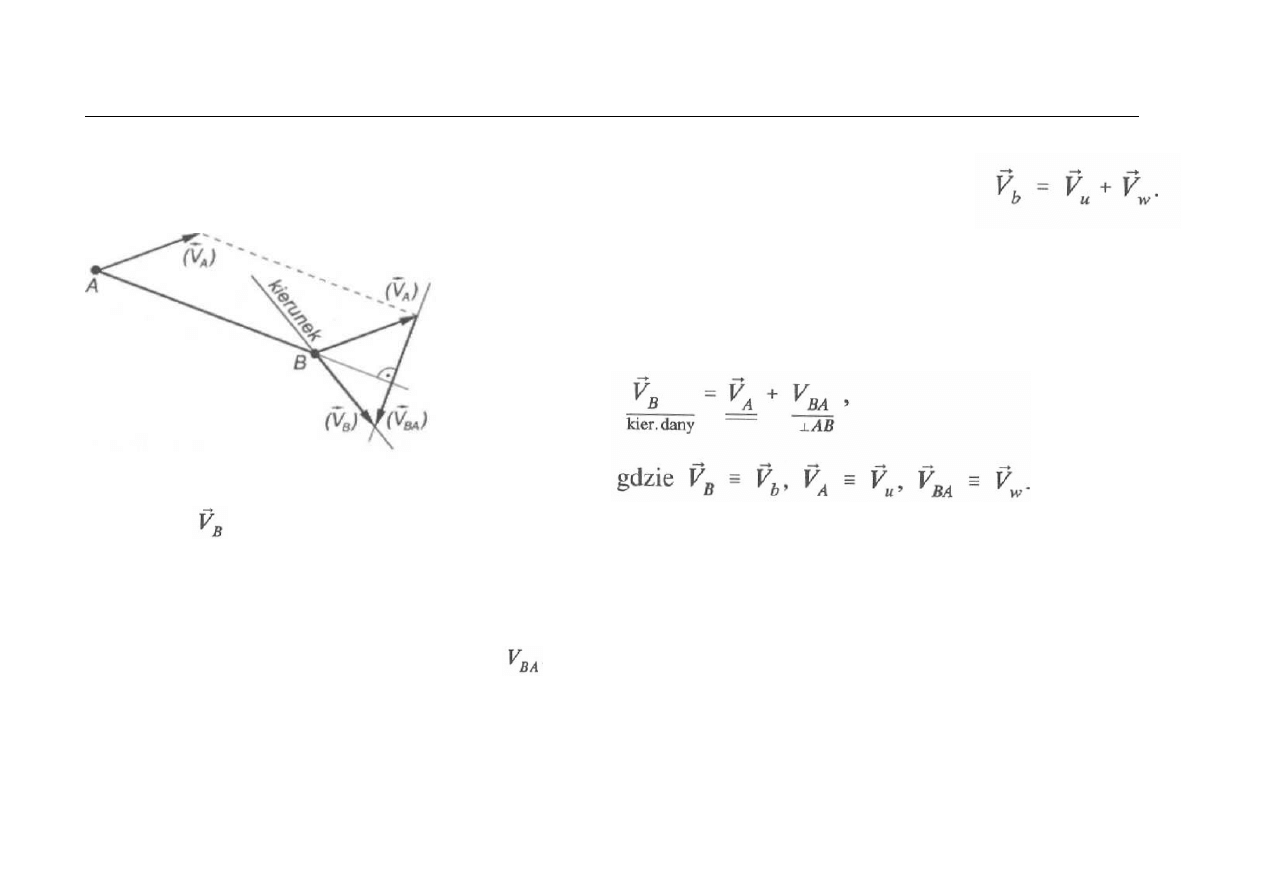
METODA ROZKŁADU NA PRĘDKOŚĆ UNOSZENIA I PRĘDKOŚĆ WZGLĘDNĄ

Twierdzenie: Prędkość bezwzględna dowolnego punktu ciała sztywnego
jest sumą wektorową prędkości unoszenia i prędkości względnej.

Ruch względny jednego punktu członu sztywnego
względem drugiego punktu tego członu może być tylko
ruchem obrotowym, prędkość względna musi być zawsze
prostopadła do prostej łączącej punkty członu.

Rys. Ilustracja metody
Wektor będąc sumą ma zwrot przeciwny do składowych. Należy również
przestrzegać kolejności indeksów. Nie wolno ich zmieniać, szczególnie dla prędkości
względnej. Kreski pod oznaczeniami prędkości informują o ilości danych. Dwie kreski
oznaczają, że znany jest moduł i kierunek, jedna kreska, że znana jest tylko jedna z tych
wielkości np. kierunek prędkości

. Kierunki pisze się zwykle pod kreską.

Dane konieczne do zastosowania metody to:
1) prędkość jednego punktu ciała,
2) kierunek prędkości drugiego punktu.

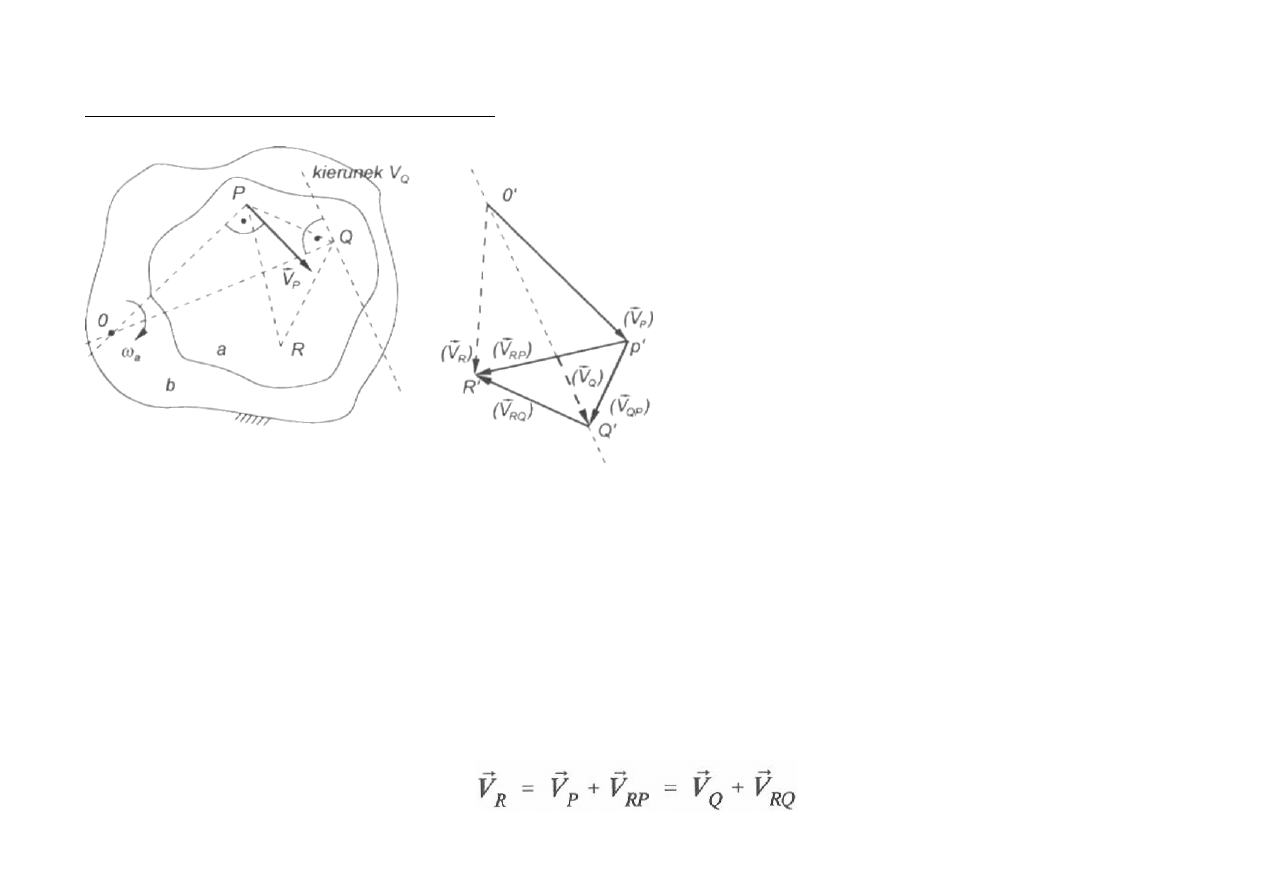
METODA PLANU PRĘDKOŚCI

Zadanie: Obliczyć prędkości punktów
Q i R członu a poruszającego się
względem nieruchomego członu b.

Dane: prędkość punktu P i kierunek
prędkości punktu Q.


Rys. Ilustracja metody

Obiera się dowolny punkt O' i w wybranej podziałce kreśli wektor prędkości

→

P

V

.

Z punktu P' kreśli się prostopadłą do PQ. Na kierunku tym będzie leżał wektor prędkości
względnej

QP

V

. Przez punkt O' kreśli się równoległą do kierunku V

Q

. Punkt Q' jako

przecięcie kierunków V

Q

i V

QP

daje wielkości tych prędkości. Odcinek O'Q' reprezentuje

w wybranej podziałce wektor

→

Q

V

, a odcinek P'Q' wektor

→

QP

V

. Przez punkt P' kreśli się

prostopadłą do PR. Jest to kierunek prędkości V

RP

. Kierunek prędkości V

RQ

otrzymuje się

kreśląc prostopadłą do QR przez punkt Q'. Przecięcie się kierunków V

RP

i V

RQ

daje wektor

→

R

V

zgodnie z sumą wektorową:

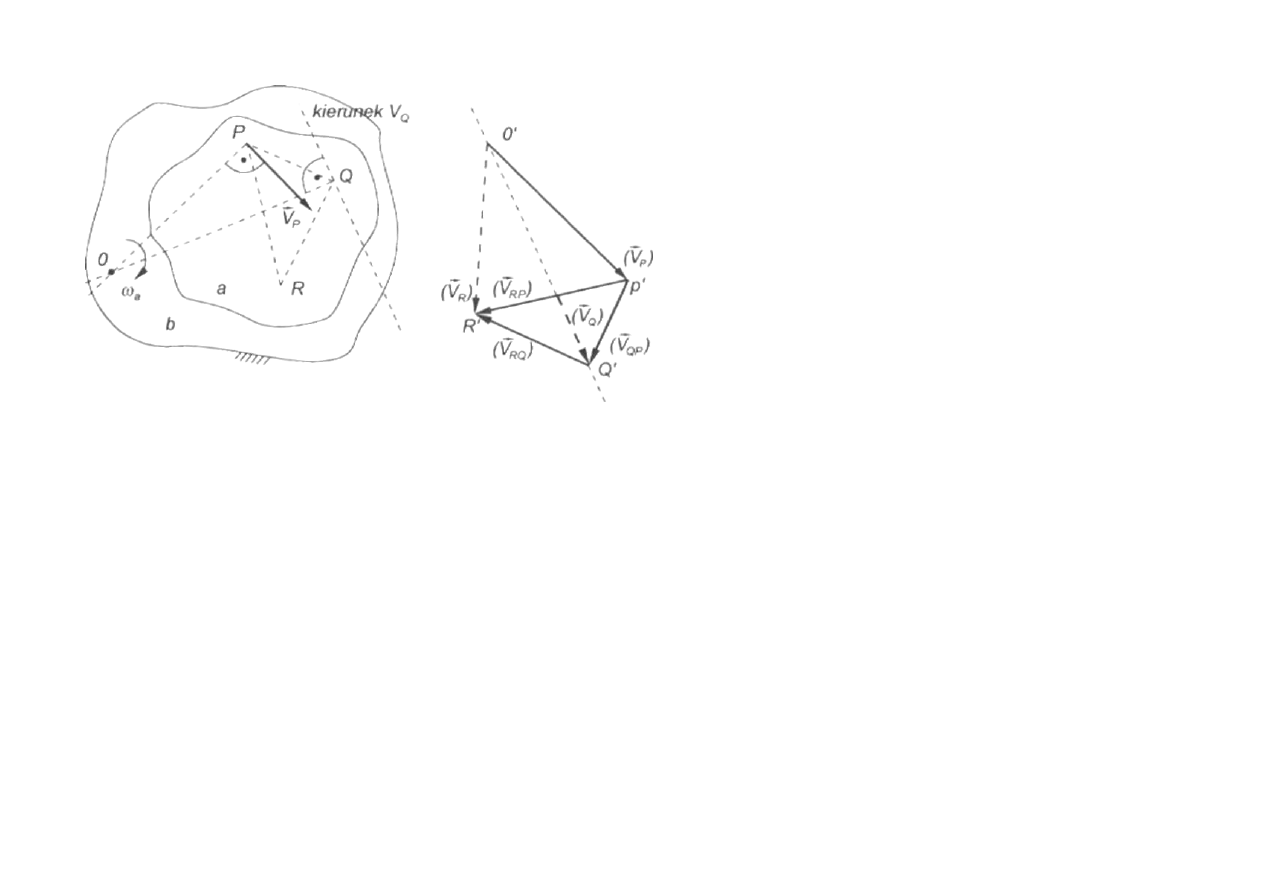
Obliczono prędkości punktów Q i R.
Trójkąt P'Q'R' jest podobny do trójkąta
PQR, tylko obrócony względem niego o
90°

w

stronę

obrotu

chwilowego.

Odpowiadające sobie boki są prostopadłe.
Trójkąt P'Q'R' nazywa się planem
prędkości.

Definicja: Figurę geometryczną będącą miejscem geometrycznym końców wektorów
prędkości figury płaskiej a, poruszającej się ruchem płaskim, wykreślonych z dowolnie
obranego punktu, nazywa się planem prędkości figury a w danym położeniu.

Własności planu prędkości:
1. Plan prędkości jest figurą podobną do badanej.
2. Jest obrócony względem figury badanej o kąt 90° w stronę obrotu chwilowego.

3. Wektory

→

)

'

'

( Q

P

,

→

)

'

'

(

R

P

... są prędkościami rysunkowymi względnymi.

4. Twierdzenie o planie prędkości jest prawdziwe dla jednego członu mechanizmu.

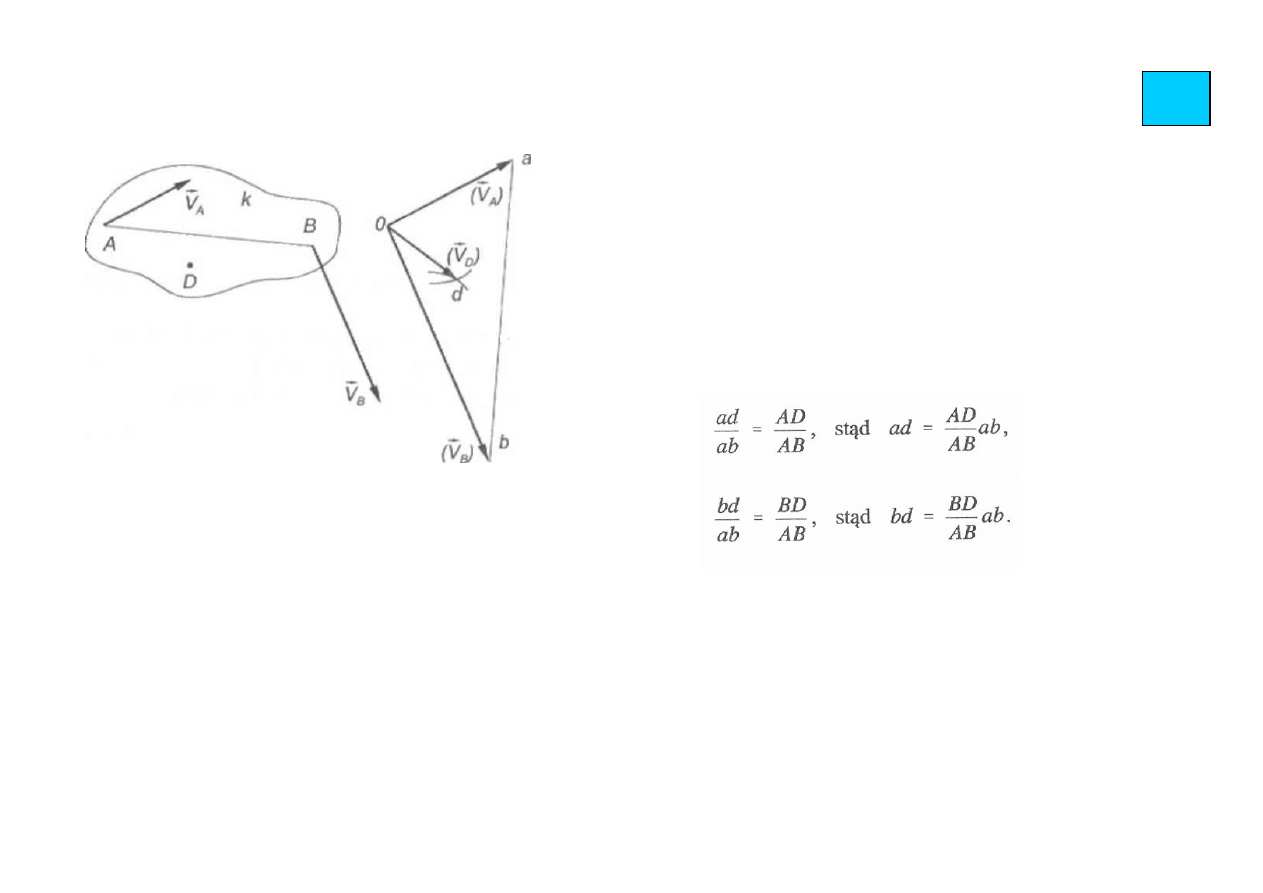
ćw.

Zadanie: Znaleźć prędkość punktu D, mając prędkości V

A

i V

B

i geometrię członu k

1) Z dowolnego punktu O należy wykreślić w
wybranej podziałce wektory V

A

i V

B

, otrzymując

plan prędkości prostej AB w postaci prostej ab.

2) Teraz należy znaleźć na planie prędkości punkt d
odpowiadający punktowi D.
Ponieważ plan prędkości jest figurą podobną do
danej, można napisać następujące proporcje:

Prawe strony równań są znane, zaś ab jest znane z planu prędkości. Należy obliczyć
odcinki ad i bd określające położenie punktu d na planie prędkości. Wiedząc, że plan
prędkości jest obrócony o kąt 90° w stronę obrotu chwilowego, położenie punktu d jest
całkowicie określone.

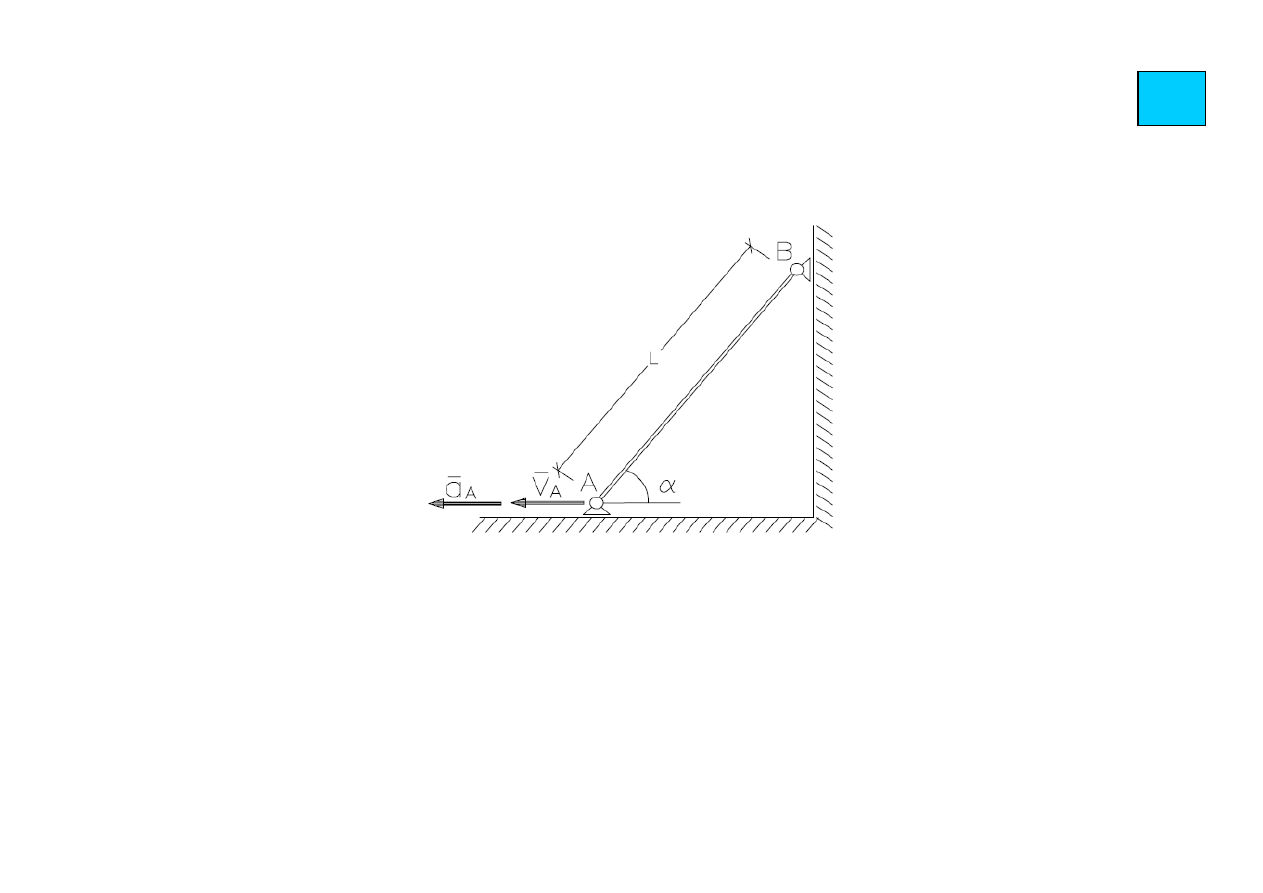
ćw.

Zadanie: Prędkość chwilowa i przyśpieszenie chwilowe punktu A pręta wynoszą:
V

0

i a

0

. Znaleźć prędkość punktu B pręta w danej chwili.

Obliczenie prędkości przeprowadzić trzema metodami:
a) z wykorzystaniem metody rzutów,
b) z wykorzystaniem planu chwilowych środków prędkości.

3.2. Wyznaczanie przyspieszenia

Aby wyznaczyć przyspieszenia punktów członu sztywnego, należy przedtem znać
prędkości tych punktów. Wygodnie jest wyznaczać przyspieszenia w takiej kolejności,
w jakiej wyznaczano prędkości. Są trzy metody wyznaczania przyspieszeń.

METODA ROZKŁADU PRZYSPIESZEŃ

Twierdzenie: przyspieszenie bezwzględne dowolnego punktu członu sztywnego jest sumą
wektorową przyspieszenia unoszenia, przyspieszenia względnego i przyspieszenia
Coriolisa.

Gdy rozpatruje się człon sztywny, wtedy ruch unoszenia jest

ruchem postępowym. Dla członu AB

→

→

=

A

u

p

p

i wtedy

zawsze

0

=

→

c

p

. Dla członu sztywnego ruch względny jest

ruchem obrotowym i wtedy:

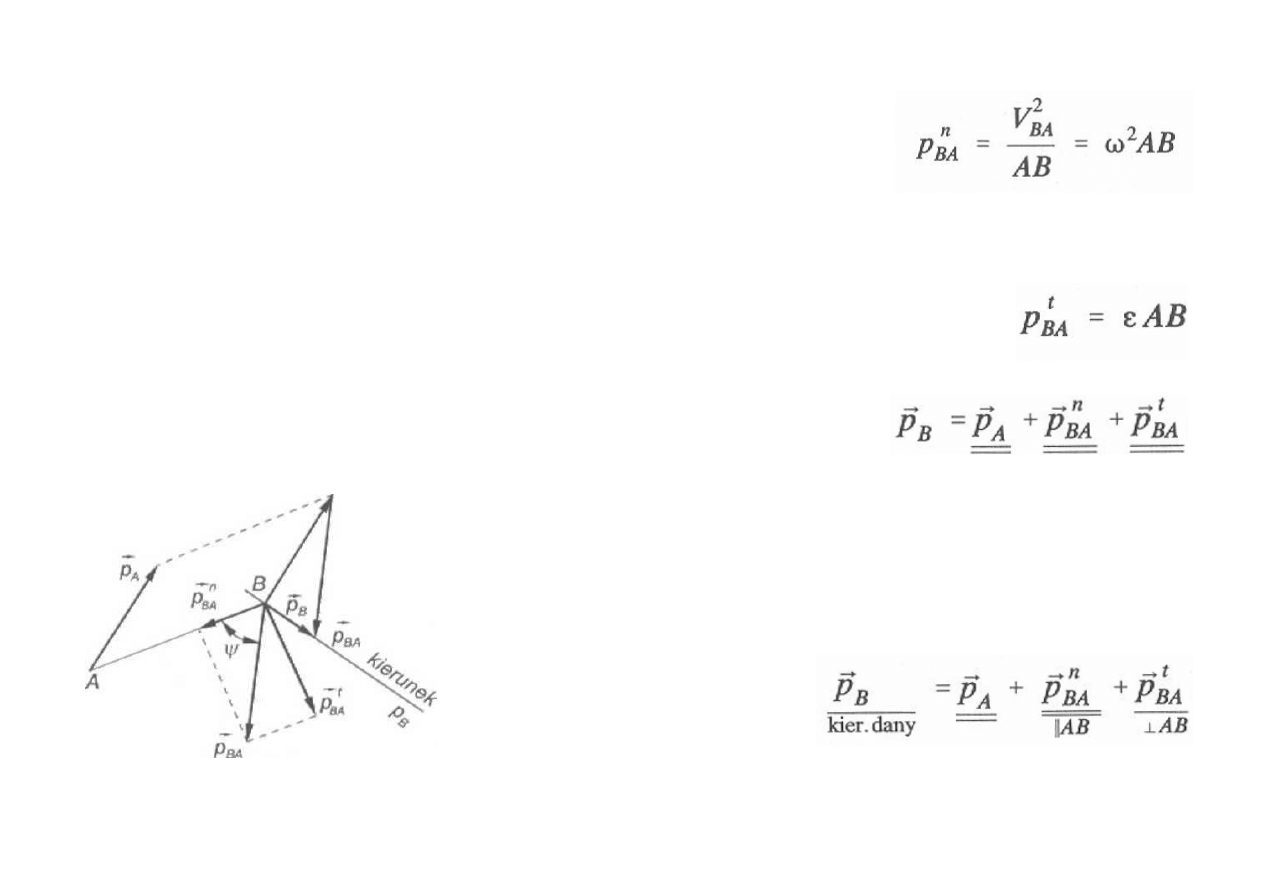
Gdy zostały uprzednio obliczone prędkości punktów, wektor

przyspieszenia normalnego

→

n

BA

p

jest zawsze znany, bo jego moduł

wyraża się równaniem:
a zwrot jest zawsze skierowany w stronę środka obrotu względnego.

Moduł względnego przyspieszenia stycznego

→

t

BA

p

, które jest prostopadłe do

względnego przyspieszenia normalnego, wyraża się równaniem:

Jeśli znane jest ε i przyspieszenie punktu A, można obliczyć
przyspieszenie punktu B za pomocą równania:

Jeśli nie jest znane ε, to w celu zastosowania metody należy
mieć

dane:

przyspieszenie

punktu

A

i

kierunek

przyspieszenia punktu B. Wtedy przyspieszenie punktu B
oblicza się za pomocą równania: