Opracował: dr in
ż
. Mariusz Leus
- 1 -
T: Wyznaczanie odkształce
ń
belek zginanych. Równanie ró
ż
niczkowe linii ugi
ę
cia
belki – metoda Clebscha
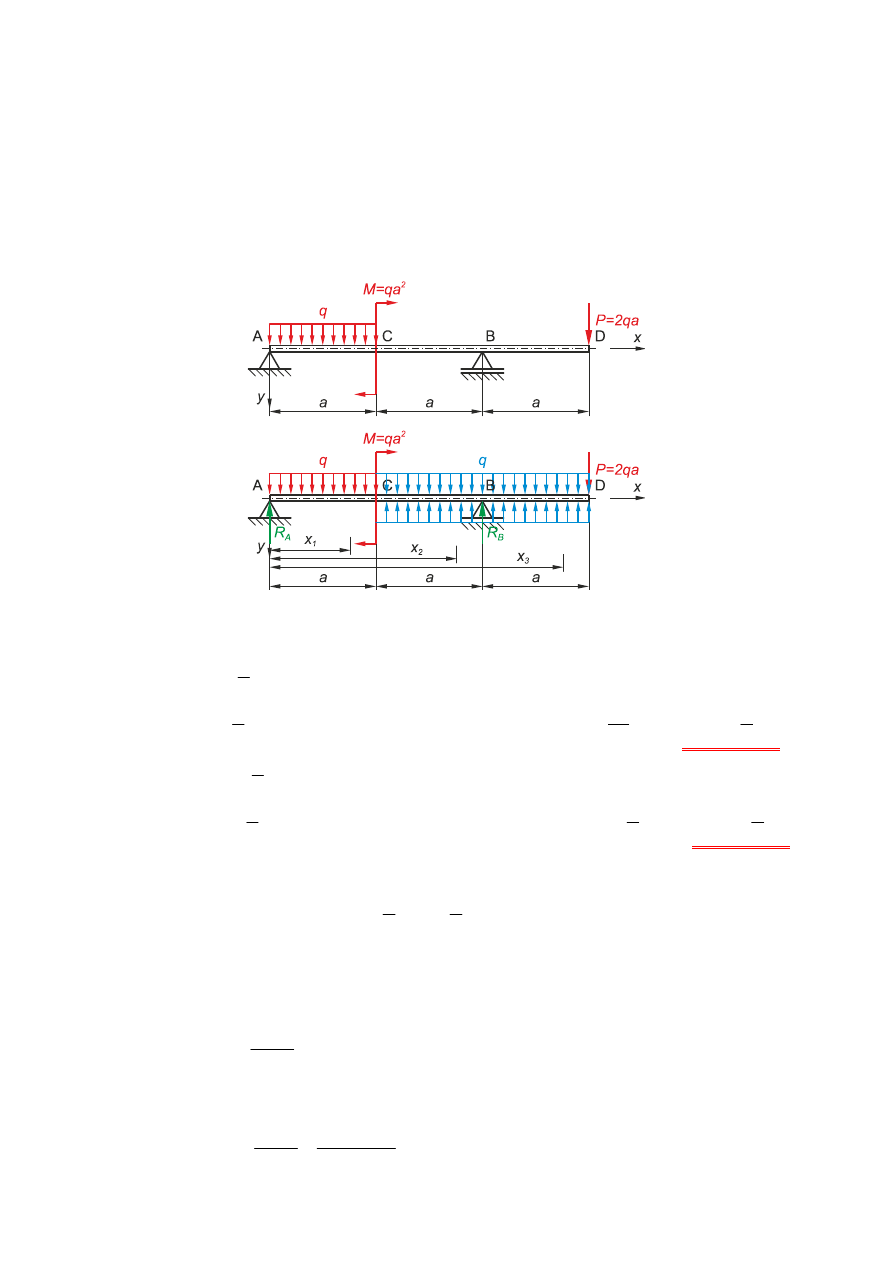
Zadanie 1.
Dla belki podpartej i obci
ąż
onej jak na rys. wyznaczy
ć
ugi
ę
cie w punkcie C i k
ą
t obrotu w punkcie D.
Dane: a, q, M = qa
2
, P = 2qa, EJ = const
Szukane:
?
=
C
y
;
?
=
Θ
D
1. Równania równowagi
1)
0
=
∑
A
M
;
0
3
2
2
1
2
=
⋅
+
⋅
−
+
a
P
a
R
M
qa
B
;
0
3
2
2
2
1
2
2
=
⋅
+
⋅
−
+
a
qa
a
R
qa
qa
B
;
2
2
15
2
qa
a
R
B
=
⋅
;
qa
R
B
4
3
3
=
2)
0
=
∑
B
M
;
0
2
2
3
2
=
⋅
+
⋅
+
+
−
a
P
a
R
M
qa
A
;
0
2
2
2
3
2
2
=
⋅
+
⋅
+
+
−
a
qa
a
R
qa
qa
A
;
2
2
3
2
qa
a
R
A
−
=
⋅
;
qa
R
A
4
3
−
=
Sprawdzenie:
0
2
4
3
3
4
3
=
−
−
+
−
=
−
−
+
=
∑
qa
qa
qa
qa
P
qa
R
R
F
B
A
y
2. Momenty gn
ą
ce w poszczególnych przedziałach
1) Przedział I:
a
x
≤
≤
1
0
( )
2
2
1
1
1
x
q
x
R
M
A
x
g
⋅
−
⋅
=
2) Przedział II:
a
x
a
2
2
≤
≤
( )
(
)
(
)
0
2
2
2
2
2
2
2
2
2
a
x
M
a
x
q
x
q
x
R
M
A
x
g
−
+
−
+
⋅
−
⋅
=
Opracował: dr in
ż
. Mariusz Leus
- 2 -
3) Przedział III:
a
x
a
3
2
3
≤
≤
( )
(
)
(
)
(
)
a
x
R
a
x
M
a
x
q
x
q
x
R
M
B
A
x
g
2
2
2
3
0
3
2
3
2
3
3
3
−
+
−
+
−
+
⋅
−
⋅
=
3. Równania ró
ż
niczkowe dla poszczególnych przedziałów
Przedział I:
1)
2
2
1
1
2
1
1
2
x
q
x
R
EJ
dx
y
d
A
⋅
+
⋅
−
=
⋅
2)
C
x
q
x
R
EJ
dx
dy
A
+
⋅
+
⋅
−
=
⋅
6
2
3
1
2
1
1
1
3)
D
x
C
x
q
x
R
EJ
y
A
+
⋅
+
⋅
+
⋅
−
=
⋅
1
4
1
3
1
24
6
1
Przedział II:
4)
(
)
(
)
0
2
2
2
2
2
2
2
2
2
2
2
2
a
x
M
a
x
q
x
q
x
R
EJ
dx
y
d
A
−
−
−
−
⋅
+
⋅
−
=
⋅
5)
(
)
(
)
C
a
x
M
a
x
q
x
q
x
R
EJ
dx
dy
A
+
−
−
−
−
⋅
+
⋅
−
=
⋅
2
3
2
3
2
2
2
2
2
6
6
2
6)
(
)
(
)
D
x
C
a
x
M
a
x
q
x
q
x
R
EJ
y
A
+
⋅
+
−
−
−
−
⋅
+
⋅
−
=
⋅
2
2
2
4
2
4
2
3
2
2
2
24
24
6
Przedział II:
7)
(
)
(
)
(
)
a
x
R
a
x
M
a
x
q
x
q
x
R
EJ
dx
y
d
B
A
2
2
2
3
0
3
2
3
2
3
3
2
3
3
2
−
−
−
−
−
−
⋅
+
⋅
−
=
⋅
8)
(
)
(
)
(
)
C
a
x
R
a
x
M
a
x
q
x
q
x
R
EJ
dx
dy
B
A
+
−
−
−
−
−
−
⋅
+
⋅
−
=
⋅
2
2
6
6
2
2
3
3
3
3
3
3
2
3
3
3
9)
(
)
(
)
(
)
D
x
C
a
x
R
a
x
M
a
x
q
x
q
x
R
EJ
y
B
A
+
⋅
+
−
−
−
−
−
−
⋅
+
⋅
−
=
⋅
3
3
3
2
3
4
3
4
3
3
3
3
6
2
2
24
24
6
4. Wyznaczenie stałych całkowania
dla x
1
= 0
→
y
1
= 0 z równania nr 3 otrzymujemy: D = 0
dla x
2
= 2a
→
y
2
= 0 z równania nr 6 otrzymujemy
( )
( )
(
)
(
)
0
2
2
2
24
2
24
2
6
2
4
3
0
2
2
4
4
3
+
⋅
+
−
−
−
−
+
⋅
−
−
=
a
C
a
a
qa
a
a
q
a
q
a
qa
a
C
qa
qa
qa
qa
2
2
1
24
1
24
16
24
24
0
4
4
4
4
⋅
+
−
−
+
=
4
24
27
2
qa
a
C
−
=
⋅
3
16
9
qa
C
−
=
5. Wyznaczenie ugi
ę
cia w punkcie C (y
C
)
dla x
1
= a
→
z równania nr 3 otrzymujemy
1
y
y
C
=
D
x
C
x
q
x
R
EJ
y
A
C
+
⋅
+
⋅
+
⋅
−
=
⋅
1
4
1
3
24
6
1
Opracował: dr in
ż
. Mariusz Leus
- 3 -
0
16
9
24
6
4
3
3
4
3
+
⋅
−
+
⋅
+
⋅
−
−
=
⋅
a
qa
a
q
a
qa
EJ
y
C
4
4
4
16
9
24
1
24
3
qa
qa
qa
EJ
y
C
−
+
=
⋅
4
4
4
48
27
48
2
48
6
qa
qa
qa
EJ
y
C
−
+
=
⋅
EJ
qa
y
C
48
19
4
−
=
6. Wyznaczenie k
ą
ta obrotu w punkcie D (
D
Θ
)
dla x
3
= 3a
→
z równania nr 8 otrzymujemy
3
3
dx
dy
D
=
Θ
(
)
(
)
(
)
C
a
x
R
a
x
M
a
x
q
x
q
x
R
EJ
C
A
D
+
−
−
−
−
−
−
⋅
+
⋅
−
=
⋅
Θ
2
2
6
6
2
2
3
3
3
3
3
3
2
3
( )
( )
(
)
(
)
(
)
3
2
2
3
3
2
16
9
2
2
3
4
3
3
3
6
3
6
3
2
3
4
3
qa
a
a
qa
a
a
qa
a
a
q
a
q
a
qa
EJ
D
−
−
⋅
−
−
⋅
−
−
−
⋅
+
⋅
−
−
=
⋅
Θ
3
3
2
3
3
3
16
9
8
15
2
6
8
6
27
8
27
qa
qa
qa
qa
qa
qa
EJ
D
−
−
−
−
+
=
⋅
Θ
3
3
2
3
3
3
48
27
48
90
2
48
64
48
216
48
162
qa
qa
qa
qa
qa
qa
EJ
D
−
−
−
−
+
=
⋅
Θ
EJ
qa
D
48
101
3
=
Θ