
Struktury niezawodnościowe
statków powietrznych
statków powietrznych
Dr inż. Robert Jakubowski

Niezawodność SP
•
Niezawodność statku powietrznego zależy od jego
struktury oraz niezawodności elementów
wchodzących w jego skład
•
Statek powietrzny może składać się z wielu
struktur. Klasycznie rozróżnia się struktury:
struktur. Klasycznie rozróżnia się struktury:
–
Płatowiec
–
Zespół napędowy
–
Systemy awioniczne
–
Wyposażenie dodatkowe np. uzbrojenie
Które dalej mogą się dzielić na mniejsze struktury

Np. zespół napędowy ogólnie można
podzielić na:
•
Wlot
•
Sprężarkę
•
Komorę spalania
•
Zespół turbin
•
Dyszę wylotową
•
Dyszę wylotową
•
Instalacje silnikowe
–
Paliwowa
–
Olejowe
–
Elektryczna
–
Przeciwpożarowa
–
Rozruchowa
W kompleksowej ocenie niezawodności struktury należy dokonać dalszej dekompozycji
tych elementów dochodząc do ich elementarnych części jednakże decydujących o
niezawodności całego statku powietrznego

Kryteria oceny niezawodności
struktury niezawodnościowej
•
Niezawodnościowa struktura progowa typu k z n
elementów charakteryzuje się tym, że system jest
w stanie zdatności jeśli co najmniej k z jego n
elementów jest w stanie zdatności. Przykład ilość
poprawnie działających nitów w połączeniu
poprawnie działających nitów w połączeniu
nitowanym.
•
Niezawodnościowa struktura szeregowa
charakteryzuje się tym, że system jest w stanie
zdatności jeżeli wszystkie jego elementy są w
stanie zdatności.

Kryteria oceny niezawodności
struktury niezawodnościowej c.d.
•
Niezawodnościowa struktura równoległa
charakteryzuje się tym, że system jest w stanie
zdatności, jeżeli co najmniej jeden z jego
elementów jest w stanie zdatności
elementów jest w stanie zdatności
•
Niezawodnościowa struktura mieszana
oznacza różne kombinacje struktur
szeregowych i równoległych (najlepiej
opisująca SP)
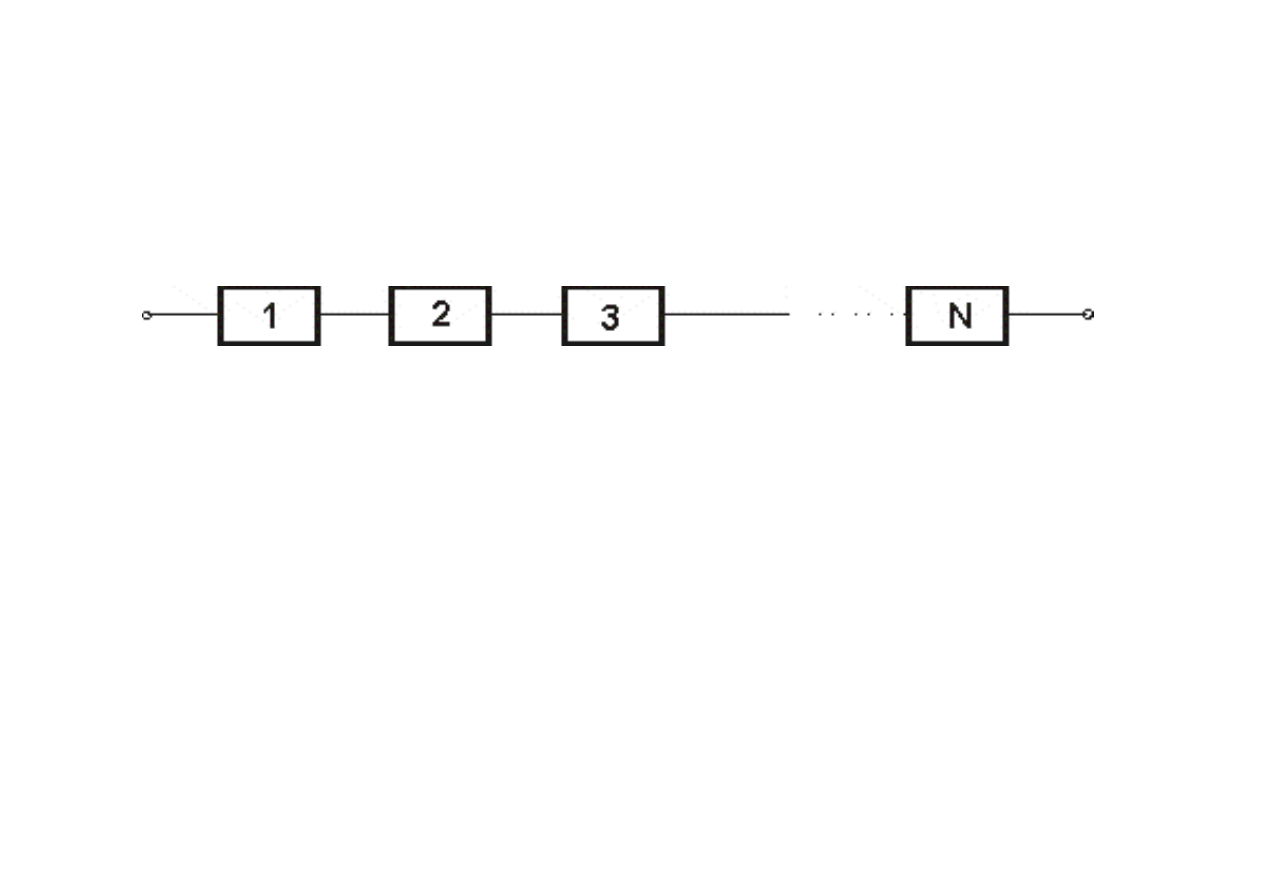
Szeregowa struktura
niezawodnościowa
Układ szeregowy występuje w stanie zdatności
gdy wszystkie jego elementy są w stanie
gdy wszystkie jego elementy są w stanie
zdatności oraz jest niezdatny gdy przynajmniej
jedne z jego elementów jest w stanie
niezdatności
( )
1
( )
N
i
i
R t
R t
=
=
∏
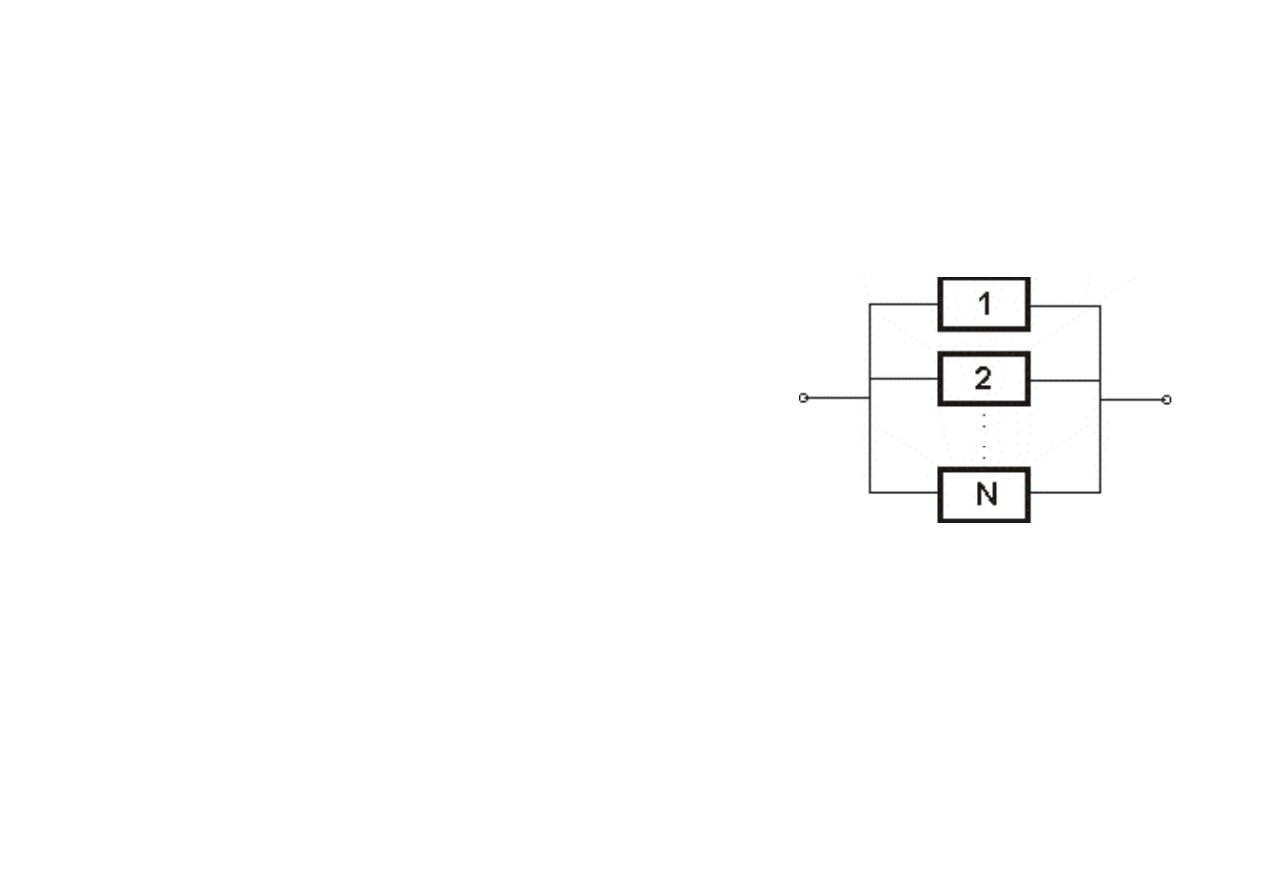
Równoległa struktura
niezawodnościowa
Układ równoległy występuje w
stanie zdatności gdy
przynajmniej jeden jego
element jest w stanie
element jest w stanie
zdatności oraz jest niezdatny
gdy wszystkie elementy
wchodzące w jego skład są
niezdatne
( )
(
)
1
( )
1
1
N
i
i
R t
R t
=
= −
−
∏
Niezawodność układu o strukturze równoległej wzrasta, gdy
wzrasta liczba jego elementów
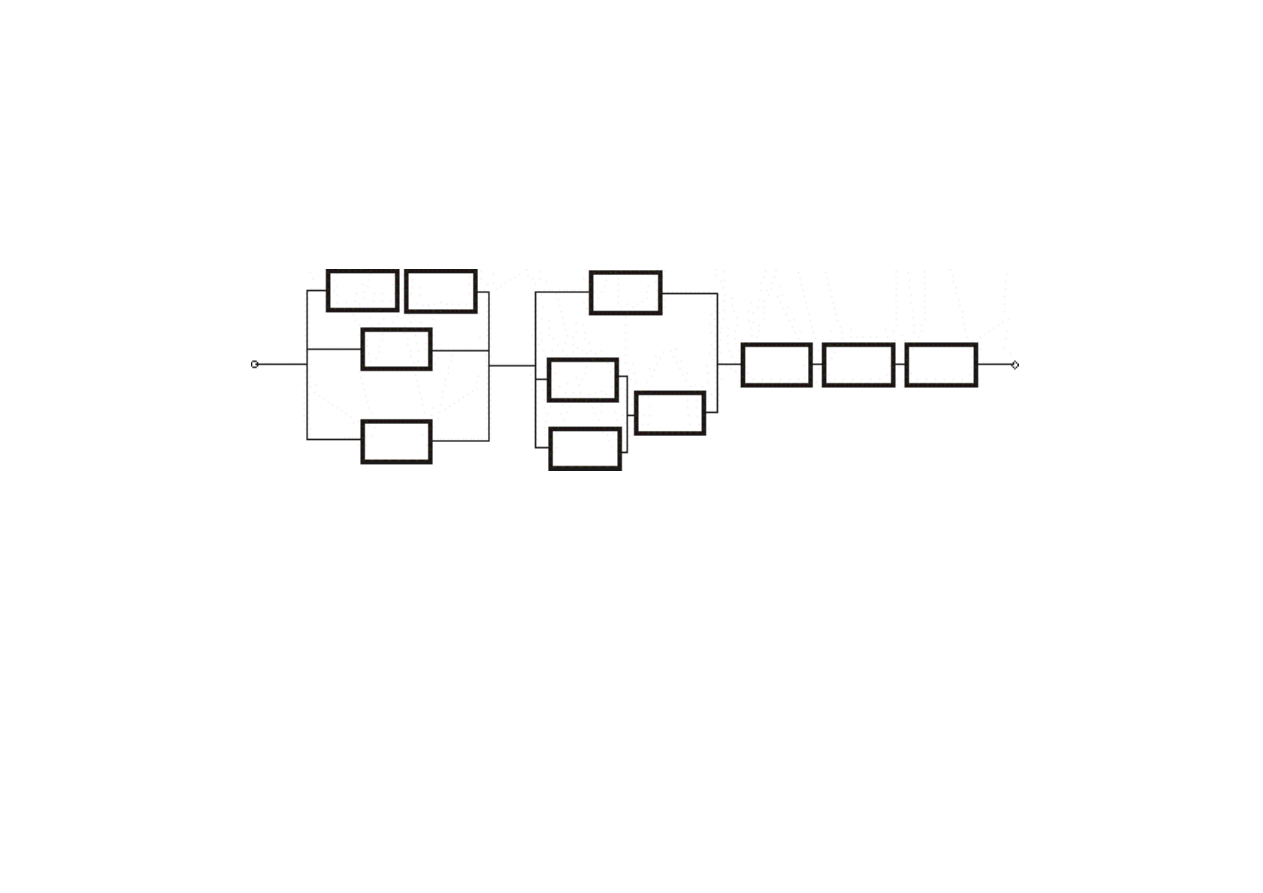
Mieszana struktura
niezawodnościowa
•
Układ posiada strukturę mieszaną, gdy
elementy wchodzące w jego skład można
podzielić na rozłączne podzbiory o strukturze
szeregowej lub równoległej
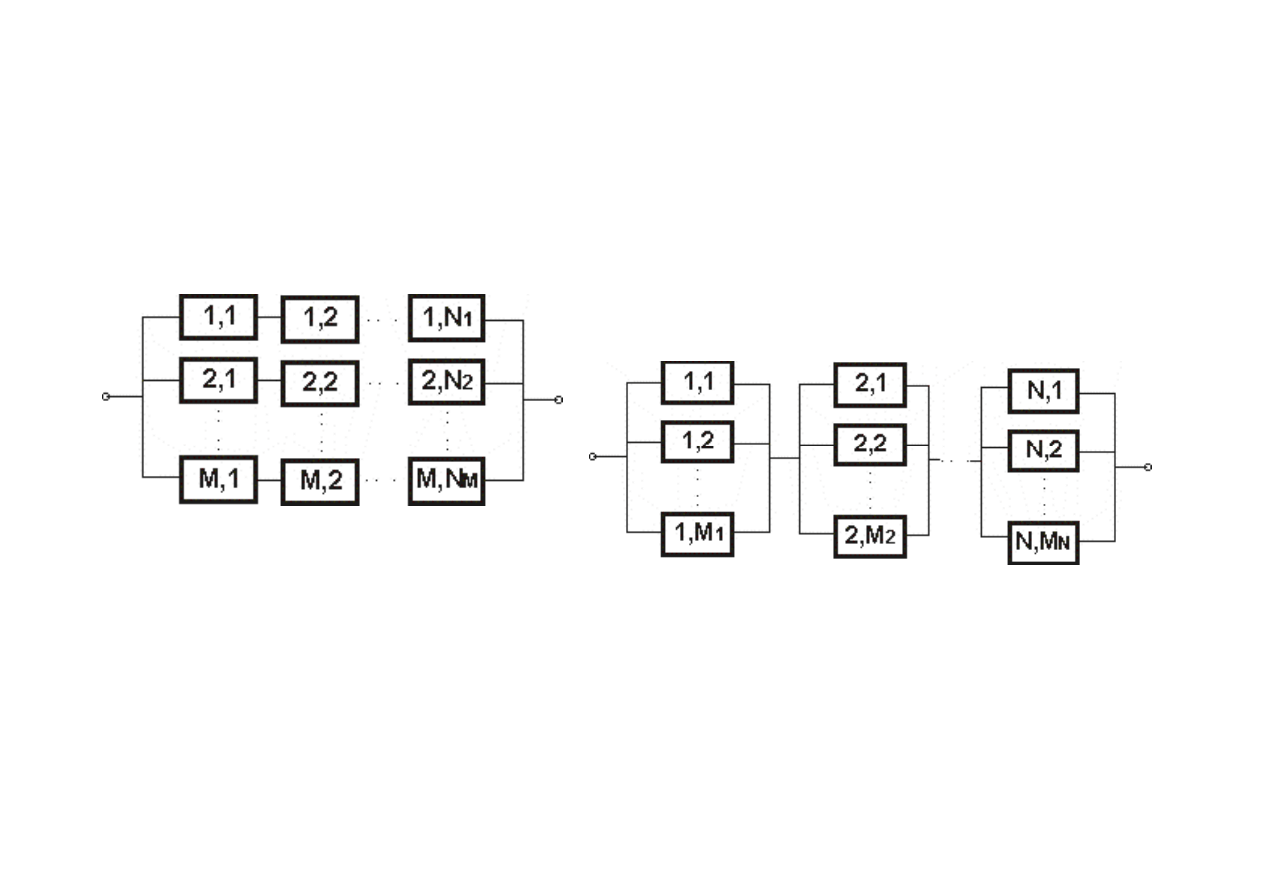
Ostateczna struktura układu
mieszanego
( )
1
1
( )
1
1
i
N
M
ij
i
j
R t
R
t
=
=
= −
−
∏ ∏
( )
(
)
1
1
( )
1
1
i
M
N
ij
i
j
R t
R
t
=
=
=
−
−
∏ ∏
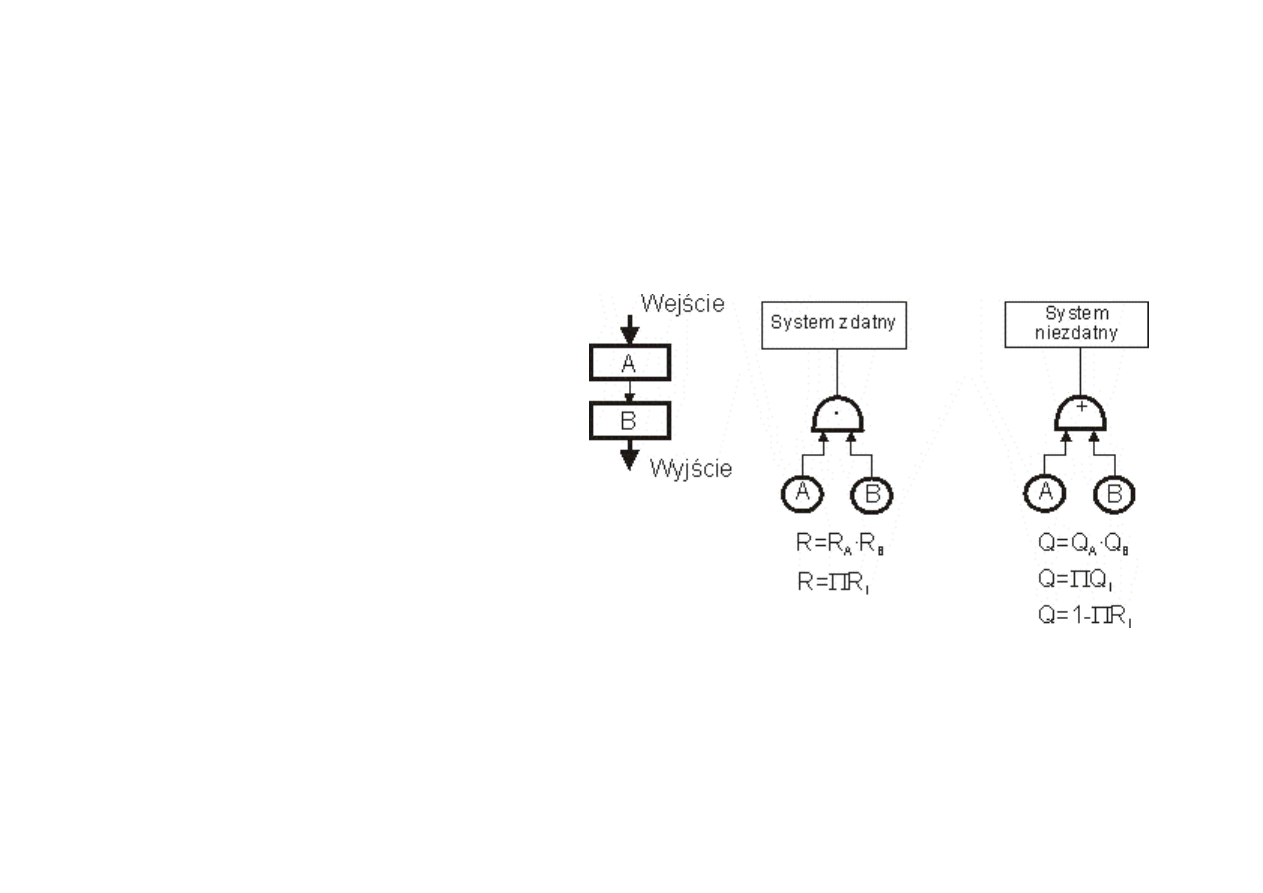
Tworzenie drzew zdarzeń struktur
niezawodnościowych
Struktura szeregowa
( )
( )
0
exp
t
i
i
R t
t dt
λλλλ
=
−
∫
Rozwiązania dla szczególnych przypadków
( )
( )
exp
t
n
R t
t dt
λλλλ
=
−
∑ ∫
( )
( )
1
2
( )
( )
...
n
t
t
t
t
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
=
= =
=
( )
( )
1
0
exp
i
i
R t
t dt
λλλλ
=
=
−
∑ ∫
Gdy:
( )
( )
0
exp
t
i
R t
n
t dt
λλλλ
=
−
∫
( )
1..
i
i
t
dla i
n
λ
λ
λ
λ
λ
λ
λ
λ
=
=
Gdy:
( )
1
exp
n
i
i
R t
t
λλλλ
=
=
−
∑
( )
1..
i
t
dla i
n
λ
λ
λ
λ
λ
λ
λ
λ
=
=
Gdy:
( )
(
)
exp
R t
tn
λλλλ
=
−
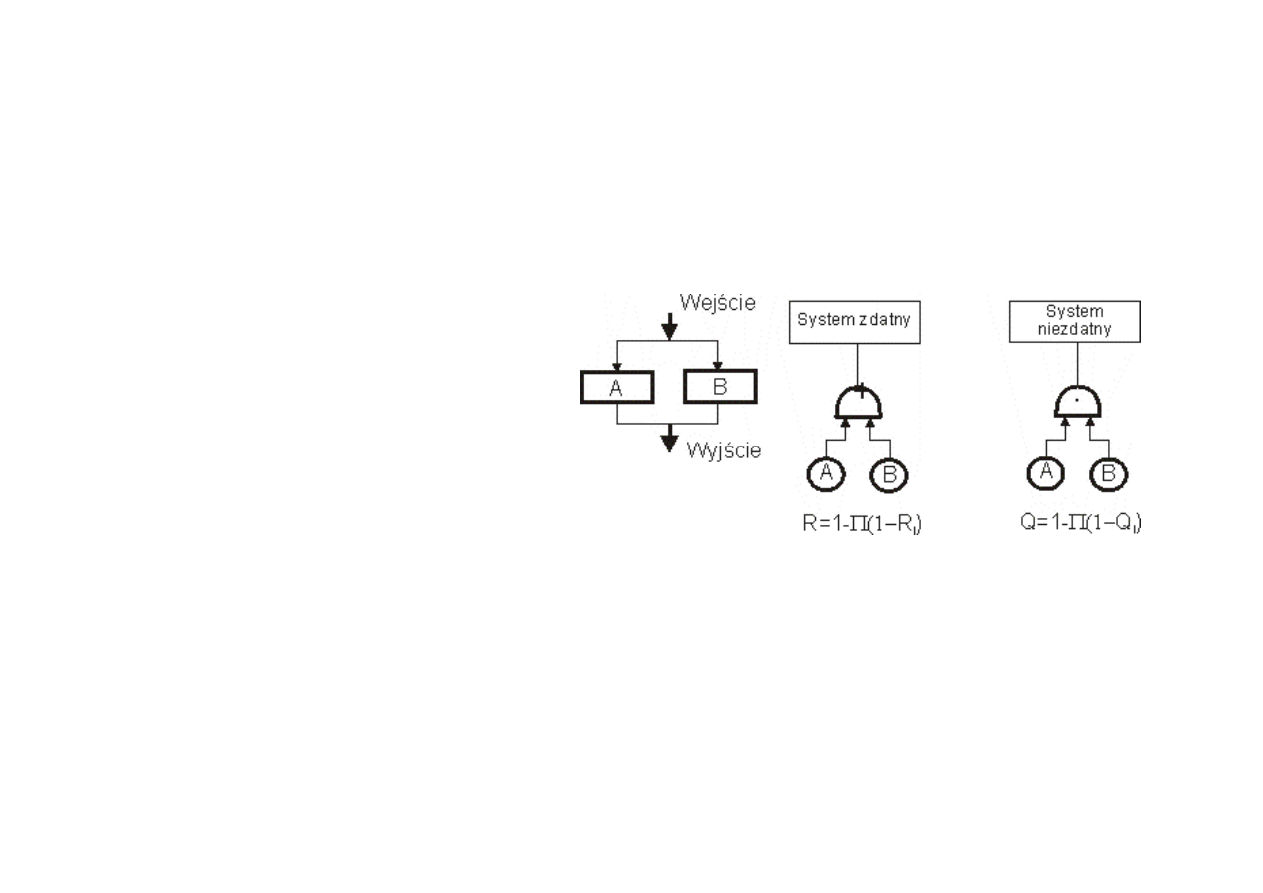
Tworzenie drzew zdarzeń struktur
niezawodnościowych
Struktura równoległa
( )
( )
0
exp
t
i
i
R t
t dt
λλλλ
=
−
∫
Rozwiązania dla szczególnych przypadków
( )
( )
1
1 exp
t
n
R t
t dt
λλλλ
= −
−
∏
∫
( )
( )
1
2
( )
( )
...
n
t
t
t
t
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
=
= =
=
( )
( )
1
0
1
1 exp
i
i
R t
t dt
λλλλ
=
= −
−
∏
∫
Gdy:
( )
( )
0
1
1 exp
n
t
R t
t dt
λλλλ
= − −
−
∫
( )
1..
i
i
t
dla i
n
λ
λ
λ
λ
λ
λ
λ
λ
=
=
Gdy:
( )
1..
i
t
dla i
n
λ
λ
λ
λ
λ
λ
λ
λ
=
=
Gdy:
( )
( )
(
)
1
1 exp
n
R t
t
λλλλ
= − −
−
( )
( )
(
)
1
1
1 exp
n
i
i
R t
t
λλλλ
=
= −
−
∏
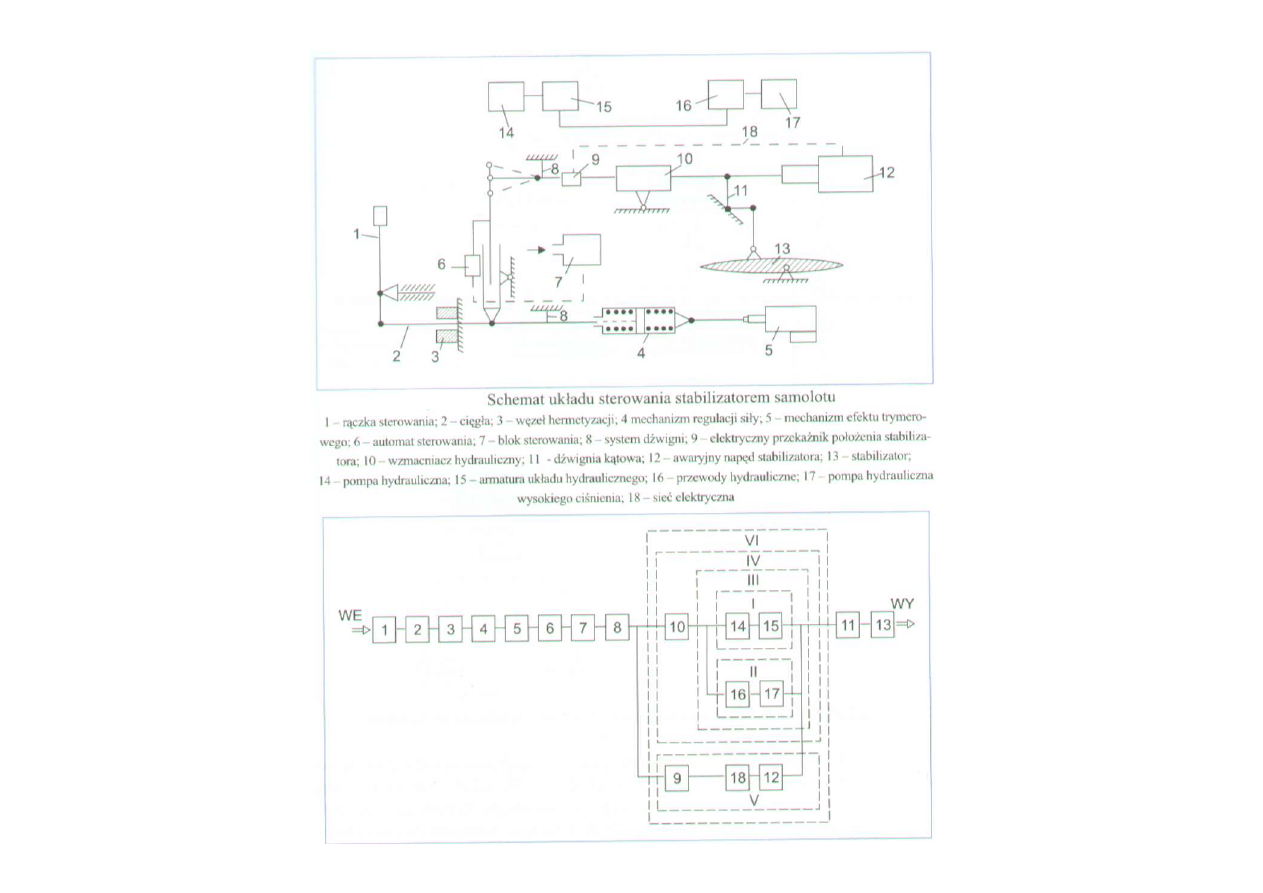
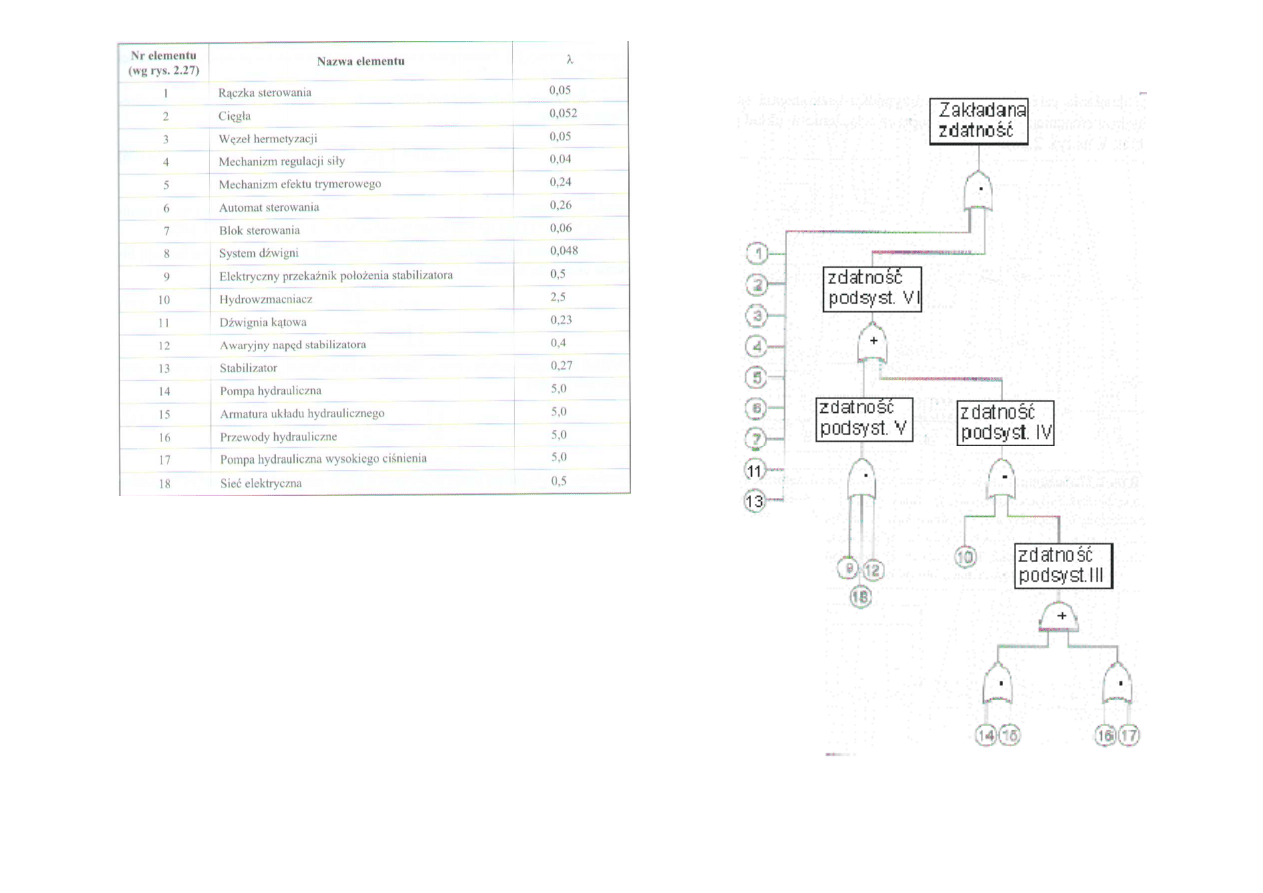
Źródło: Lewitowicz, Kustroń: Podstawy
eksploatacji statków powietrznych T II
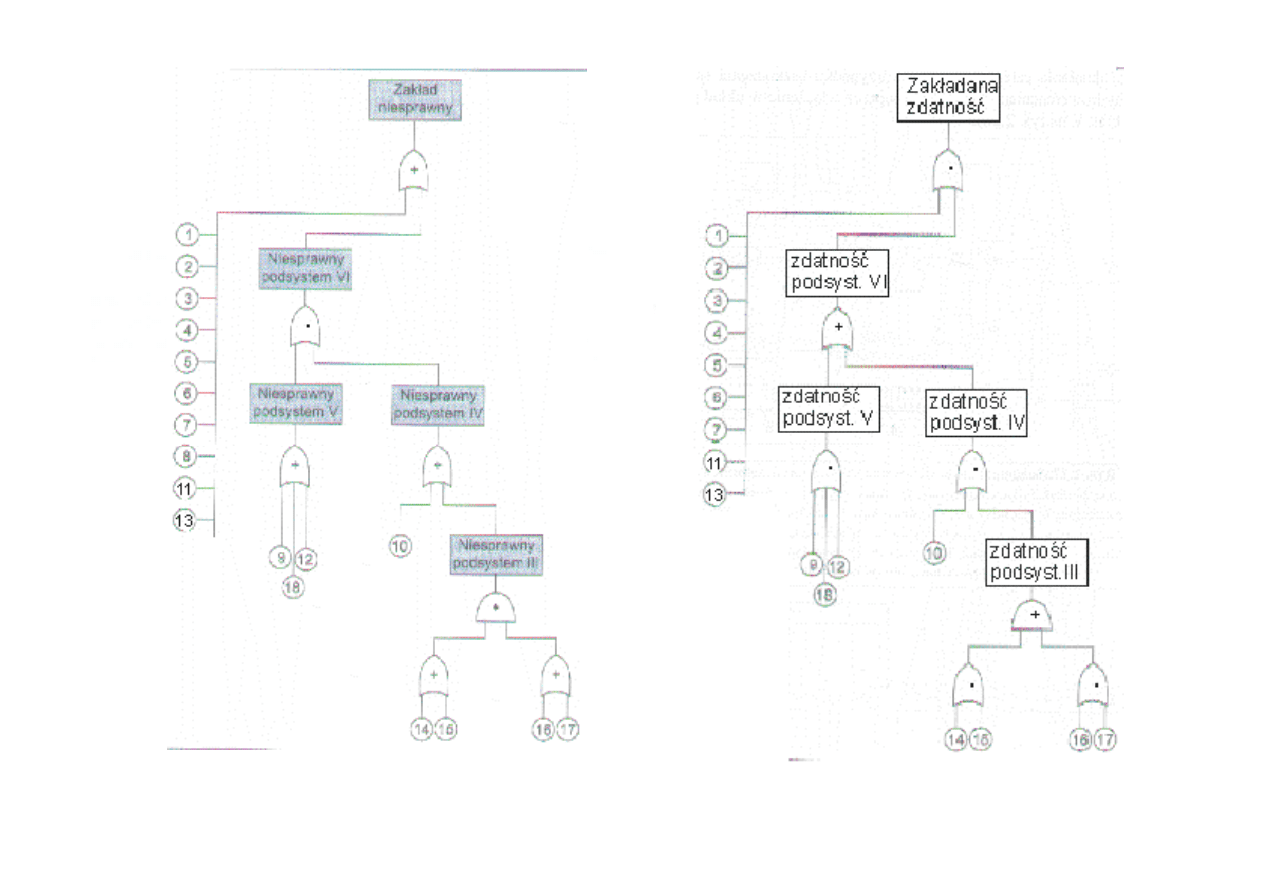
Drzewo niezawności dla systemu
sterowania stabilizatorem samolotu
Źródło: Lewitowicz, Kustroń: Podstawy
eksploatacji statków powietrznych T II
[%]
( )
(
)
(
)
0,1
1
exp
exp
0, 05 0, 05
n
t
I
i
i
R t
t
t
e
λλλλ
−
=
=
−
=
− ⋅
+
=
∑
( )
(
)
(
)
0,1
exp
0, 05 0, 05
t
II
R
t
t
e
−
=
− ⋅
+
=
( )
(
)
(
)(
)
( )
2
2
0,1
0,1
0,1
0,1
0,2
1
1
1
1
1
1
2
t
t
t
t
t
III
i
I
II
i
R
t
R
R
R
e
e
e
e
e
−
−
−
−
−
=
= −
−
= − −
−
=
+
−
=
−
∏
( )
(
)
0,1
0,2
0,025
0,125
0,225
10
2
2
t
t
t
t
t
IV
III
R
t
R R
e
e
e
e
e
−
−
−
−
−
=
=
−
=
−
( )
(
)
(
)
(0,005 0,004 ,005)
0,014
9
12
18
exp
t
t
V
R
t
t
e
e
λ λ
λ
λ λ
λ
λ λ
λ
λ λ
λ
−
+
+
−
=
−
+
+
=
=
( )
(
)(
)
(
)(
)
0,014
0,125
0,225
0,014
1
1
1
2
1
t
t
t
t
VI
IV
V
R
t
R
R
e
e
e
e
−
−
−
−
= − −
−
=
+
−
−
( )
0,02652
0,13752
0,23752
0,15152
0,25152
2
2
t
t
t
t
t
bt
R t
e
e
e
e
e
ae
−
−
−
−
−
−
=
+
−
−
+
=
∑
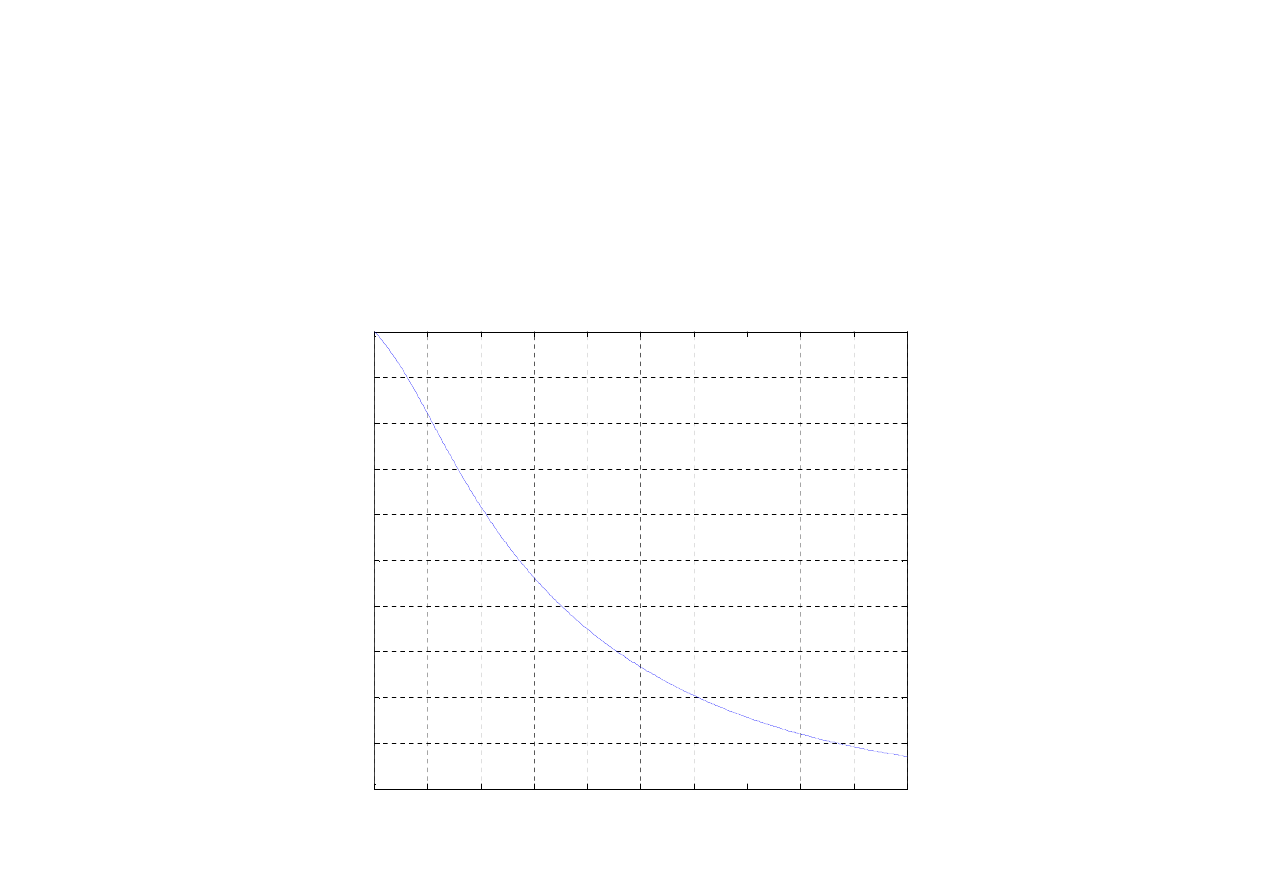
Obliczenia niezawodności układu dla
dowolnej chwili czasu t
R
0.8
0.9
1
( )
0,02652
0,13752
0,23752
0,15152
0,25152
2
2
t
t
t
t
t
R t
e
e
e
e
e
−
−
−
−
−
=
+
−
−
+
0
10
20
30
40
50
60
70
80
90
100
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
T

Obliczenie gęstości
prawdopodobieństwa uszkodzeń
układu
( )
( )
dR t
f t
dt
= −
0.02
0.025
f(t)
0
10
20
30
40
50
60
70
80
90
100
0
0.005
0.01
0.015
T
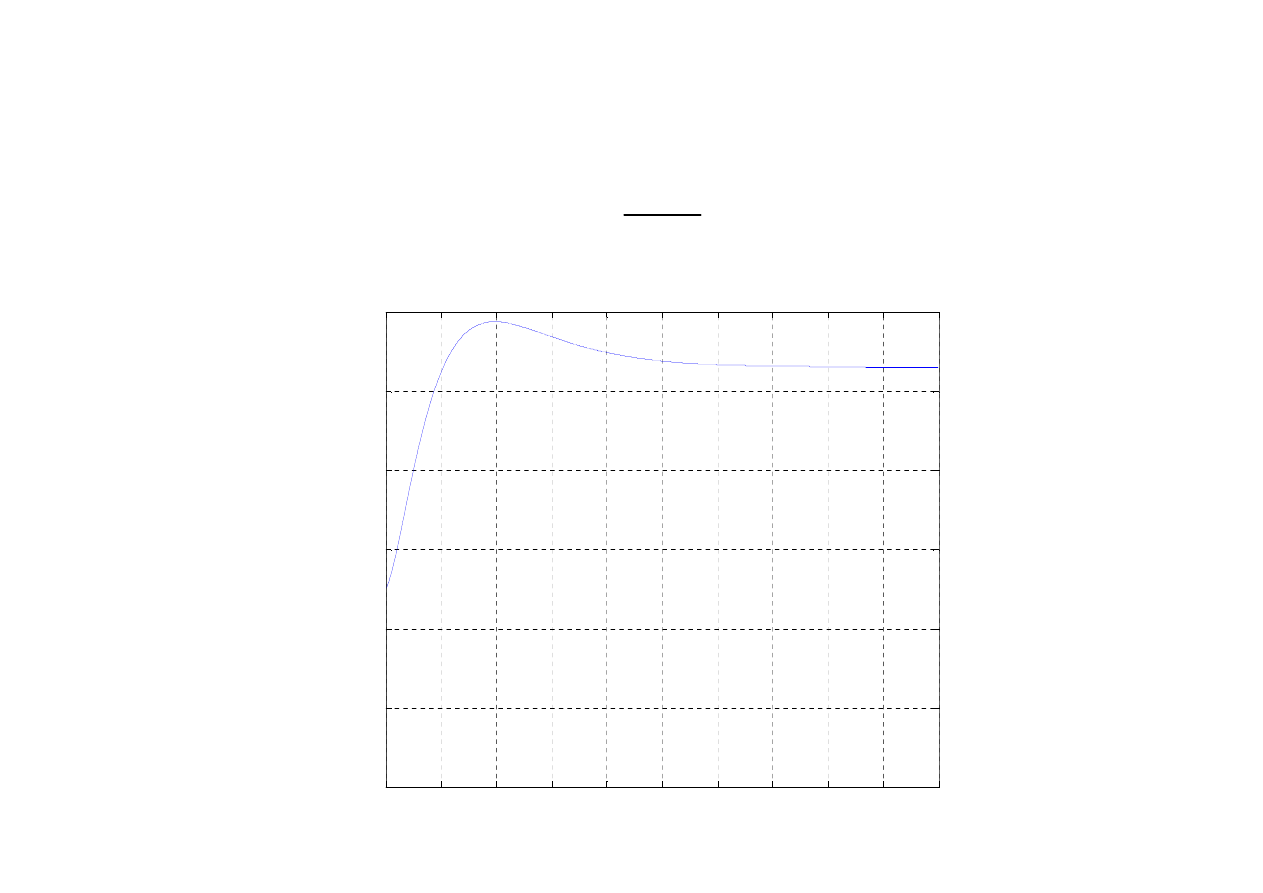
Funkcja rozkładu uszkodzeń układu
λ
(t)
( )
( )
( )
f t
t
R t
λλλλ
=
0.025
0.03
0
10
20
30
40
50
60
70
80
90
100
0
0.005
0.01
0.015
0.02
T
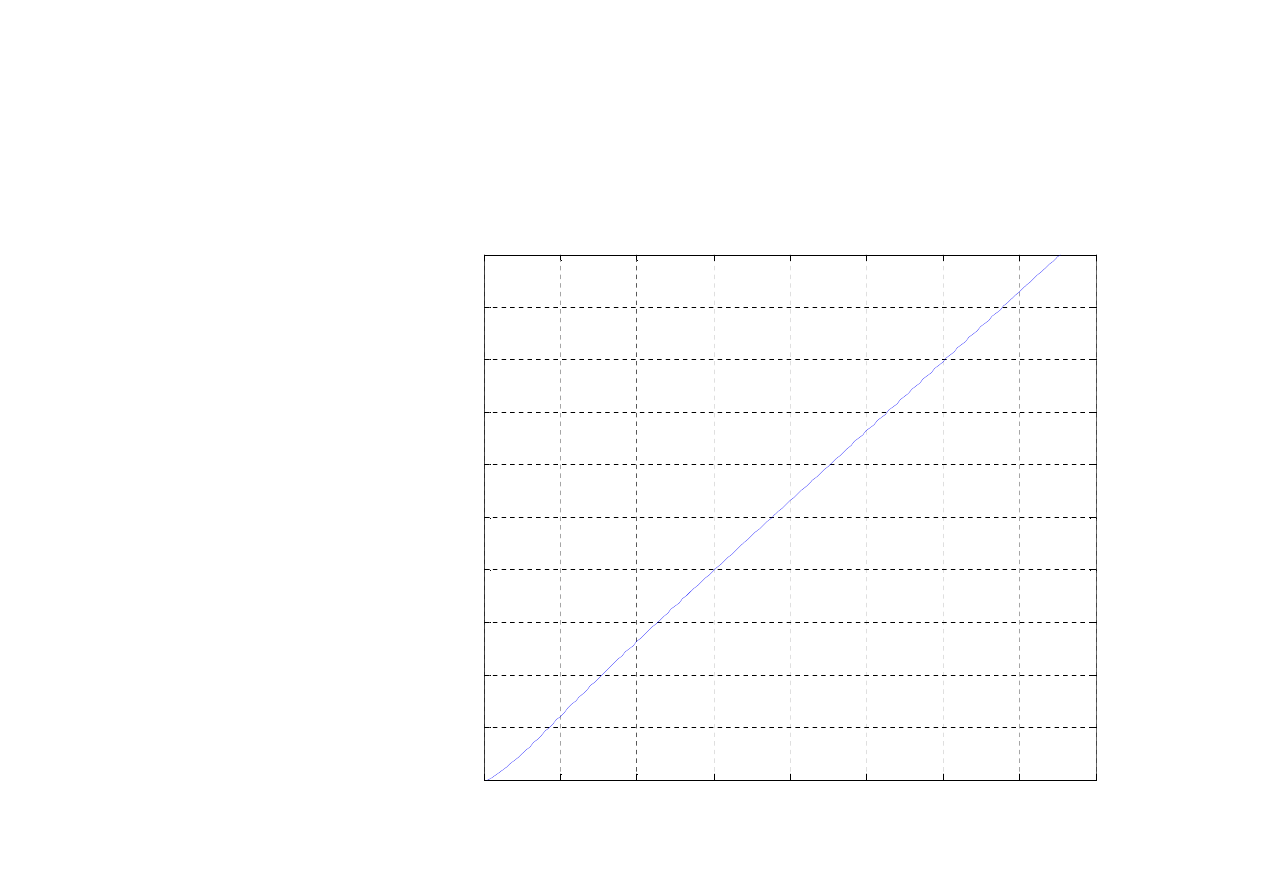
Skumulowana funkcja ryzyka i
oczekiwany czas pracy
1.4
1.6
1.8
2
Λ(
t)
0
10
20
30
40
50
60
70
80
0
0.2
0.4
0.6
0.8
1
1.2
T
( )
0
38,8
sr
t
R t dt
∞
=
=
∫
Wyszukiwarka
Podobne podstrony:
Klasyfikacja statków latających
10 niezawodnosc eksploatacyjna statkow powietrznych
Wyklad 2 Eksploatacja przepisy szczegolowe
Użytkowanie, Obsługiwanie i Kierowanie Eksploatacją
EKSPLORACJA DANYCH 9
Eksploatacja 3
eksploatacja
Wykład II Analiza podstawowych pojęć eksploatacyjnych i użytkowanie obiektów ED
OCENA ZAGROŻEŃ PRZY EKSPLOATACJI URZĄDZEŃ POD CIŚNIENIEM
Eksploatowanie częstościomierzy, generatorów pomiarowych, mostków i mierników RLC
eksploracja lab03, Lista sprawozdaniowych bazy danych
3 2 LN Energetyka ECiJ EgzaminDyplomowy OpracowaneZagadnienia eksploatacyjne WentylatorIPompy(1)
Eksploatowanie oscyloskopów
więcej podobnych podstron