- 11 -

Energia potencjalna

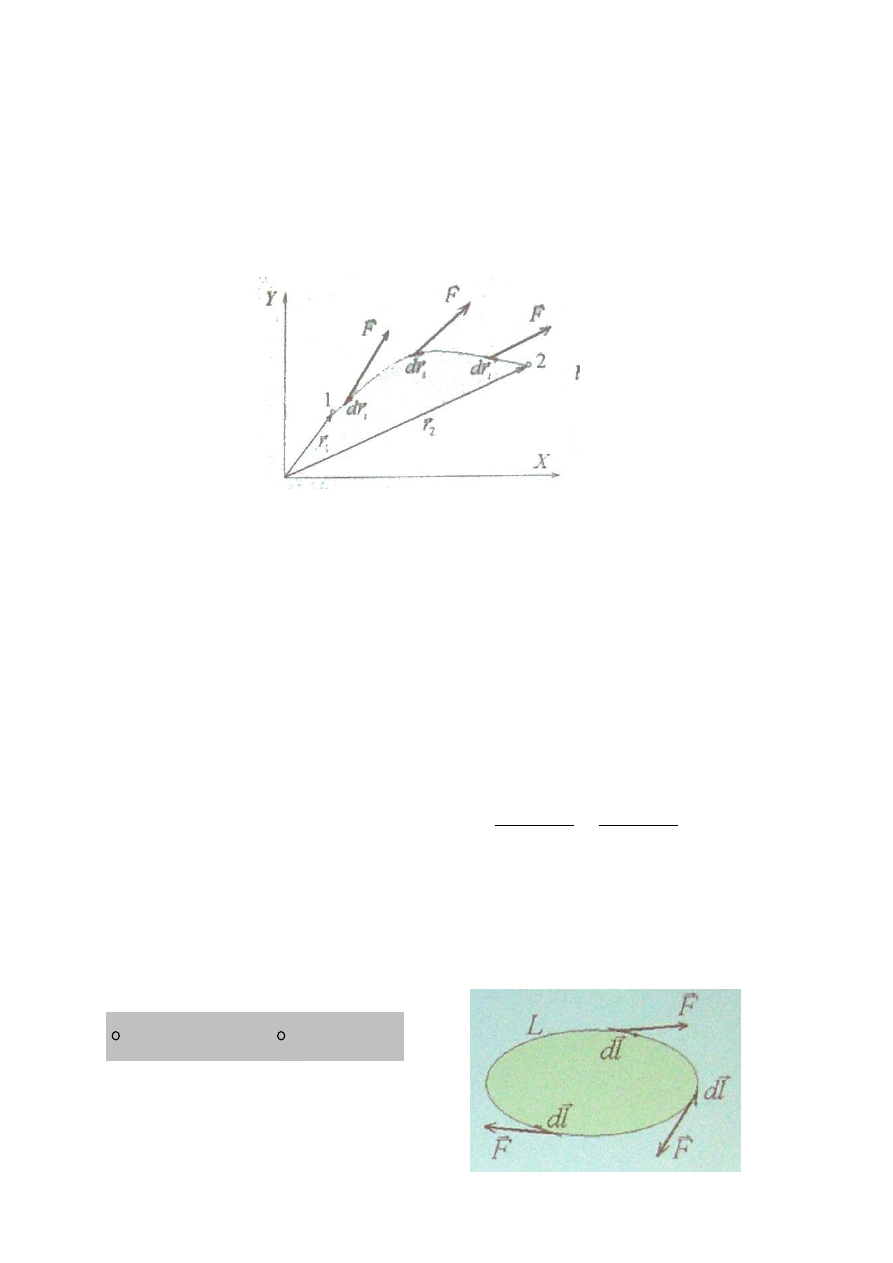
Pole elektryczne jest polem zachowawczym – praca w tym polu nie zalezy od

drogi, a tylko od położenia początkowego i końcowego.

Przemieszczając ładunek z pkt. R1 do pkt. r2 siła pola elektrycznego wykonują

pracę:

)

(

)

(

2

1

2

1

2

1

r

U

r

U

r

d

E

q

r

d

F

W

r

r

r

r





































Możemy na tej podstawie zdefiniować energię potencjalną jako pracę, którą muszą
wykonać siły zewnętrzne, aby przenieś ładunek z odległego obszaru w którym
energia potencjalna równa jest zero (

∞

), do danego pkt. pola.















r

r

z

r

d

E

q

r

d

F

r

U















)

(

Dla ładunku pkt. Q:



















r

r

Q

q

r

dr

Q

q

r

U

2

0

2

0

4

4

)

(







Gdy q, Q róznoimienne energia U(r) jest ujemna – pracę wykonują siły pola
elektrostatycznego.

Obliczamy pracę po zamkniętej drodze L:











0

0

l

d

E

l

d

F













- 12 -

Pole wektorowe spełniające taką właściwość nosi nazwę pola bezwirowego – pole
elektrostatyczne jest polem bezwirowym.

Potencjał pola elektrostatycznego

Stosunek energii potencjalnej ładunku q do wartości do wartości tego ładunku

nazywany jest potencjałem pola elektrostatycznego.







 





C

J

V

q

r

U

r

V

)

(

)

(









)

(

)

(

2

1

r

V

r

V

q

W











Dla ładunku pkt. Q:

r

Q

r

V





0

4

)

(





Dla układu ładunków pkt.:









i

i

r

r

q

r

V

2

1

0

4

)

(









Związek pomiędzy potencjałem a natężeniem pola elektrycznego:

)

(

)

(

r

V

q

r

d

E

q

r

U

r

































r

r

d

E

r

V









)

(

Różnica potencjałów pomiędzy pkt. 1 i 2 wynosi zatem:









































2

1

2

)

(

)

(

1

2

r

r

r

r

d

E

r

d

E

r

d

E

r

V

r

V























- 13 -

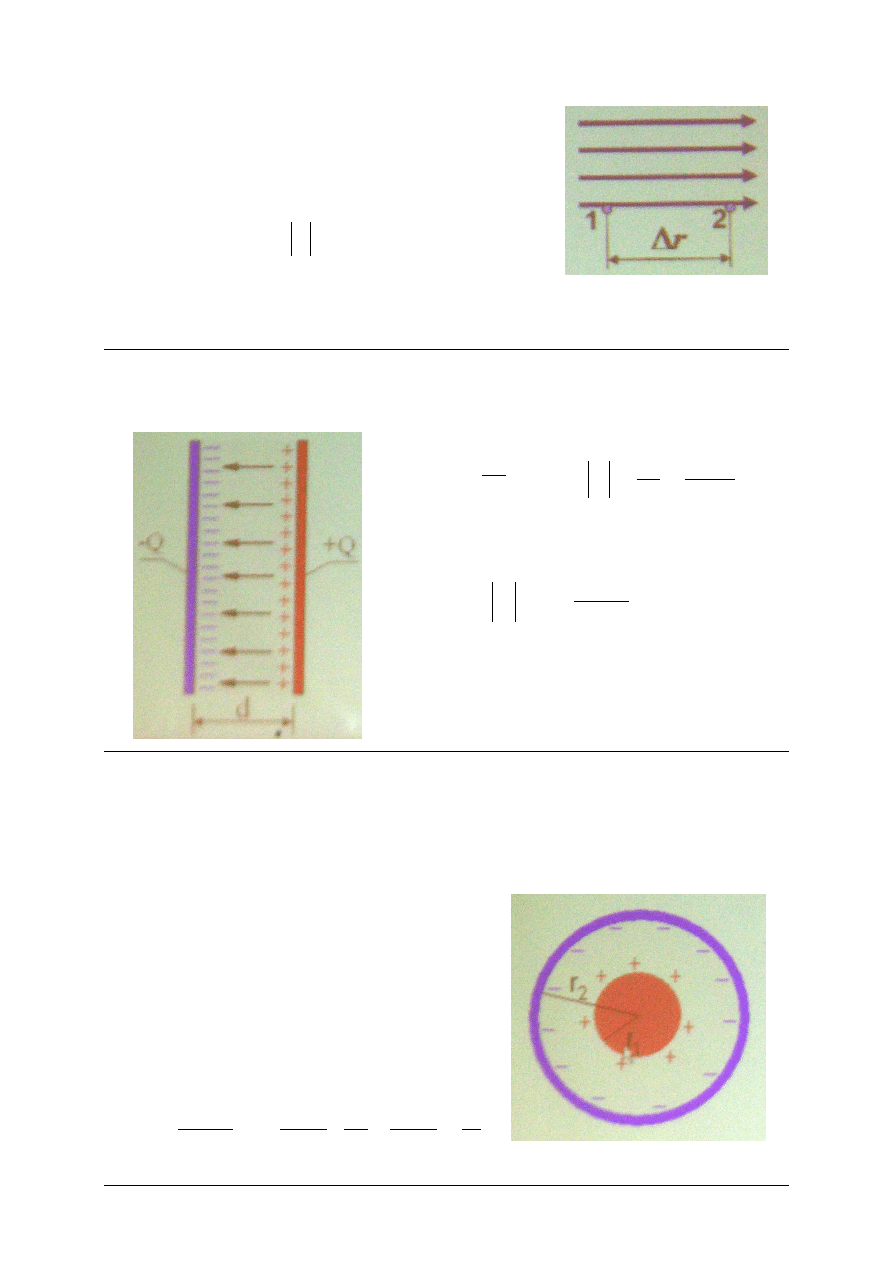
Dla pola jednorodnego:















2

)

(

)

(

1

2

r

r

d

E

r

V

r

V

V











r

E

r

r

E

V























)

(

1

2

Pole elektryczne skierowane jest w stronę niższego potencjału.

Przykład (1)

Obliczmy różnicę potencjałów dka dwuch płyt o powierzchni s,

znajdujących się w odległości d od siebie, naładowanych przeciwnie ładunkami Q.

S

Q





S

Q

E







0

0









S

d

Q

d

E

V













0





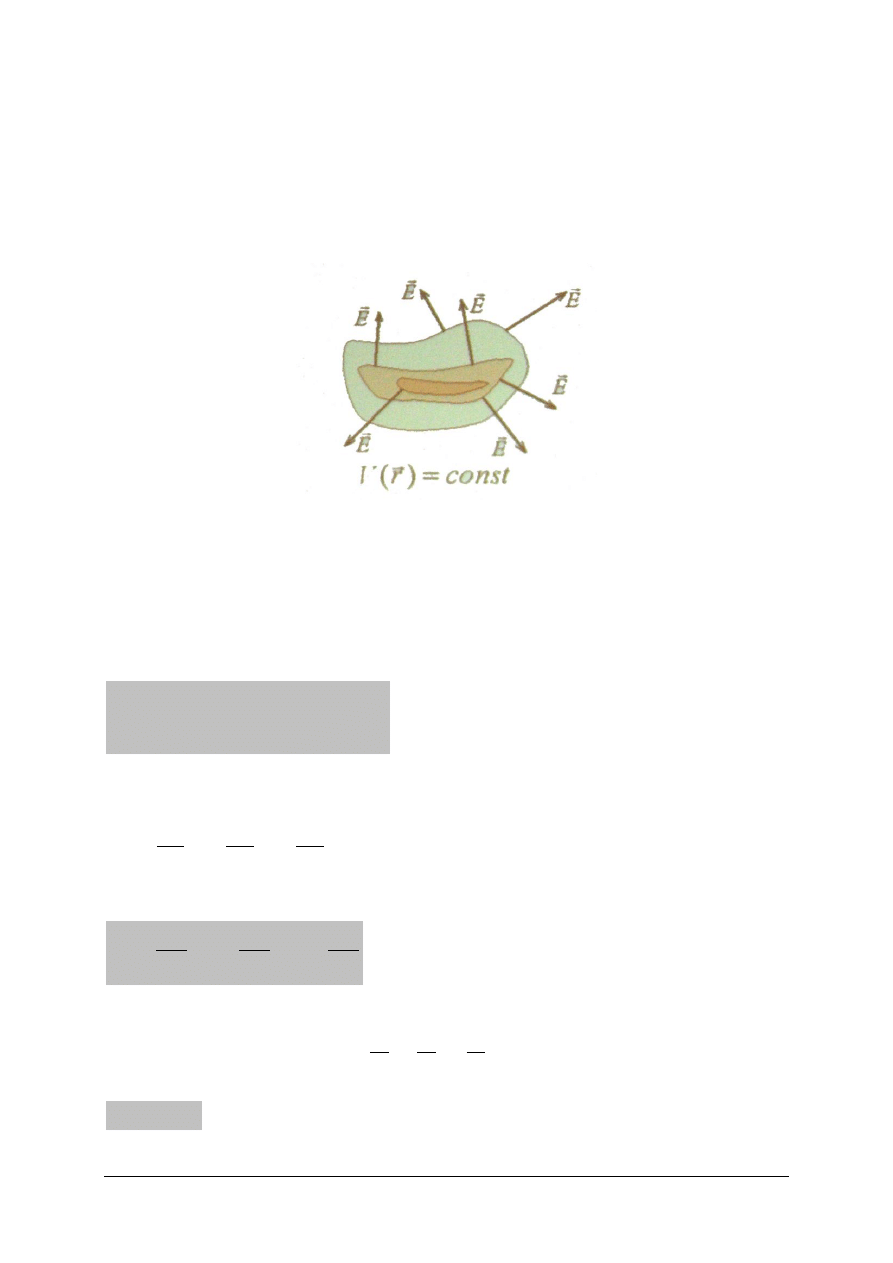
Przykład (2)

Kabel koncentryczny (współosiowy) składa się z drutu o promieniu r1

otoczonego wydrążonym przewodnikiem walcowym o promienu r2. Liniowe gęstości
ładunku na tych przewodnikach są ruwne n i –n. Znaleźć różnicę potencjałów między

tymi dwoma przewodnikami

Ponieważ pole ma kierunek radialny:









2

1

r

r

dr

E

V

Podstawiając wynik z omówionego przykładu:

1

2

0

0

0

ln

2

2

2

2

1

2

1

r

r

r

dr

dr

r

V

r

r

r

r

























- 14 -

Powierzchnia stałego potencjału

Powierzchnia stałego potencjału wyznacza równanie:

const

r

V



)

(





0



dV



0



r

d

E







r

d

E







Warunek ten oznacza, ze wektor pola jest w każdym punkcie prostopadły do
powierzchni stałego potencjału.

Związek potencjału z natężeniem pola

Mamy:

r

d

E

dV

r

d

E

V

r

r































2

1

Rozpisując te wyrażenie dla składowych pola:

dz

z

V

dy

y

V

dx

x

V

dV



















dz

E

dy

E

dx

E

r

d

E

z

y

x



















Porównując stronami otrzymujemy:

z

V

E

y

V

E

x

V

E

z

y

x



















;

;

Znajomość potencjału daje nam równocześnie trzy składowe wektora natężenia pola.
Wprowadzając operator :

k

z

j

y

i

x

grad

























równanie te możemy zapisać w

zwartej postaci wektorowej:

gradV

E







- 15 -

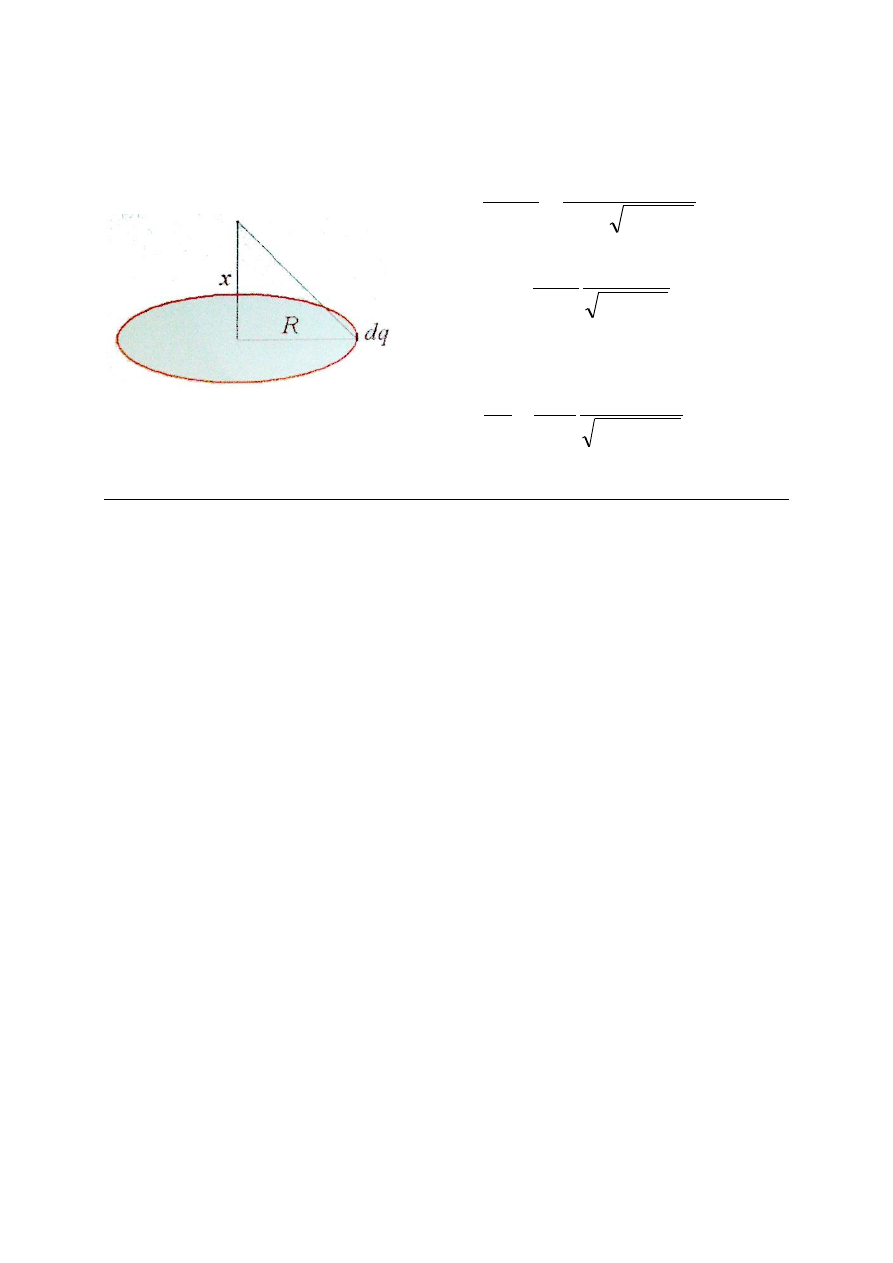
Przykład

Znaleźć potencjał i natężenie pola elektrycznego wytworzonego przez

ładunek Q rozmieszczony równomiernie na pierścieniu o promieniu R na osi
pierścienia w odległości x od jego środka

2

2

0

0

4

4

x

R

dq

r

dq

dV











2

2

0

4

1

x

R

Q

dV

V











3

2

2

0

)

(

4

1

x

R

x

Q

x

V

E

x















