EGZAMIN PISEMNY Z WYTRZYMAŁOŚCI MATERIAŁÓW II

ZESTAW 2005/B

studia zaoczne
IMIĘ I NAZWISKO STUDENTA (DRUKOWANE LITERY !) ...............................................................

Warunkiem dopuszczenia do części ustnej egzaminu jest uzyskanie co najmniej 50 punktów

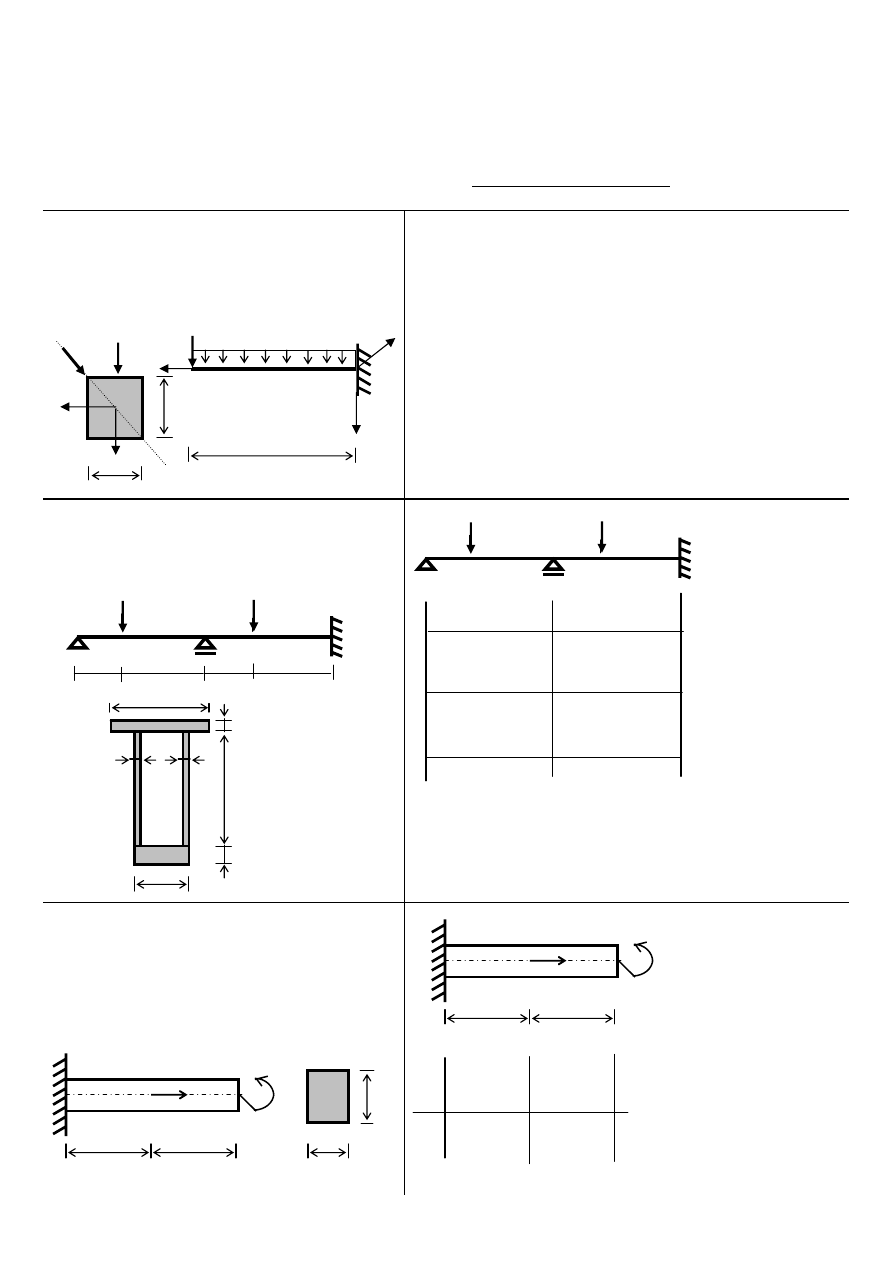
ZADANIE 1 15 pkt

P=............................kN

ZADANIE 2 20 pkt

Wpl = ................. cm

3

Mn = ......................... kNm

Pn = ................. kN

ZADANIE 3 15 pkt

a = ..................... cm

Proszę wpisać (narysować) wyniki końcowe zadań (wartości liczbowe, wykresy) w pola znajdujące się po prawej
stronie tego arkusza.
Po zakończeniu egzaminu należy oddać niniejszy arkusz wraz z rozwiązaniami szczegółowymi.

L

L

P

a=?

A

P=?

b

b

z

x

y

z

y

P

q

q=3kN/m

a

a

2a

C

2a

P

3P

16

10

1

2

4

[cm]

10

Wyznaczyć wartość obciążenia granicznego dla
belki pokazanej na rys.
Przyjąć: Rpl=160[MPa], a=1[m].

Dla pręta o przekroju prostokątnym, obciążonego
jak na rys., określić minimalny wymiar przekroju "a"
tak, aby ekstremalne naprężenia zastępcze wg
hipotezy Coulomba-Treski nie przekroczyły wartości
180 [MPa]. Przyjąć: L=1m, P=100 kN

B

C

P

3P

A

Wyznaczyć wartość siły P tak, aby oś obojętna w
przekroju A (utwierdzenie), pokrywała się z
kierunkiem tej siły (patrz rys.).
b= 8 [cm], E=10 [GPa]

a =1 m

1

M=PL

2a

L

L

P

M=PL

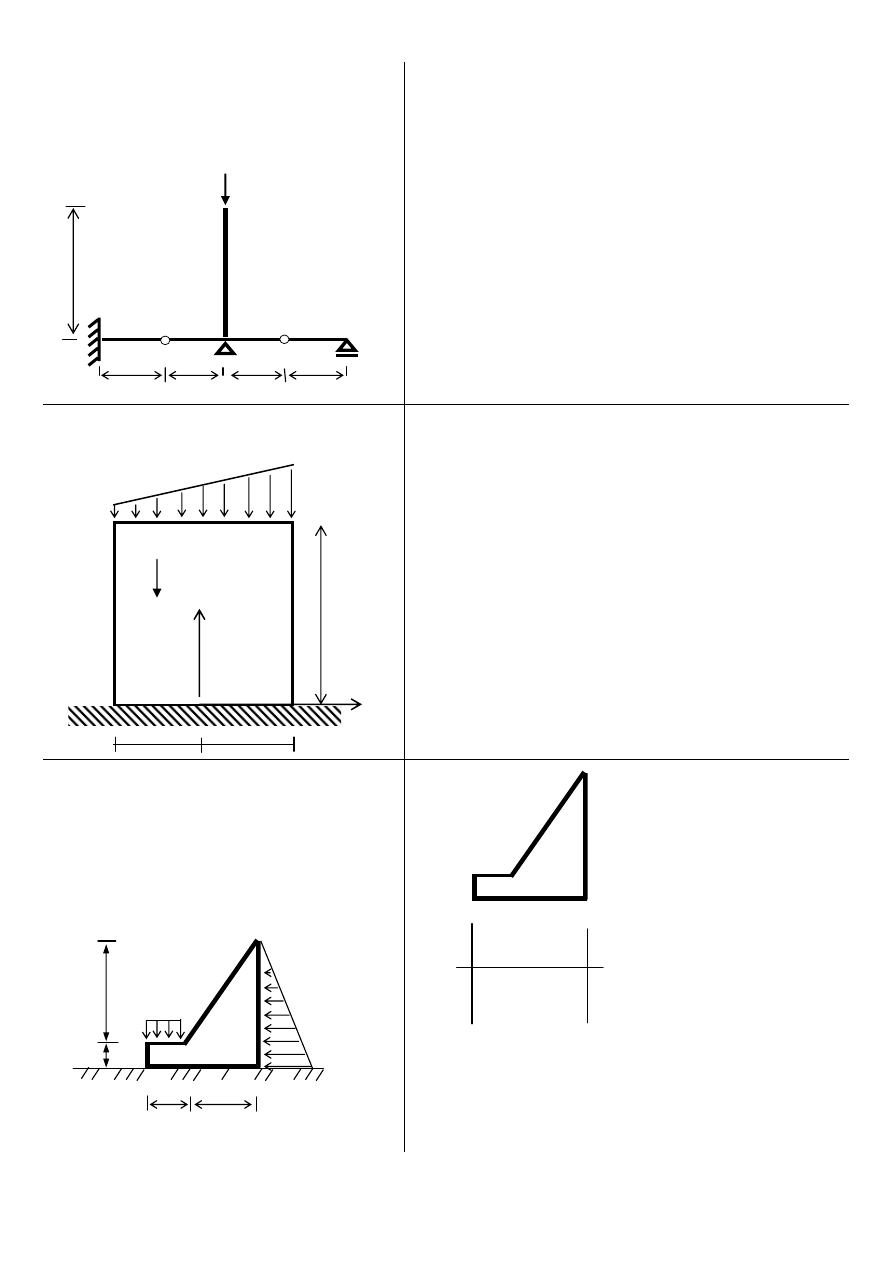
ZADANIE 4 15 pkt

P

kr

=

......................

ZADANIE 5 15 pkt

p - ciężar własny tarczy

σ

xx

(x,y)=

σ

yy

(x,y)=

σ

xy

(x,y)=

ZADANIE 6 20 pkt

σ

A

= .........................

σ

B

= .......................

Wyznaczyć stan naprężenia w tarczy przedstawionej
na rys.

Wyznaczyć wartość obciążenia krytycznego
dla układu pokazanego na rys.

P

EJ=∞

a

a

3a

EJ

2EJ

y

x

a

a

q

3q

2a

3

6 m

8

2

Sporządzić wykres naprężeń normalnych

σ w

gruncie (brak rozciągania) pod murem
oporowym. Ciężar właściwy

γ

m

=20 kN/m

3

A

B

a

a

EJ

2EJ

p

q=100 kN/m

2

p=50 kN/m

2