Numer zestawu 32.

Dane:

a = 2,96 [m]

b = 2,61 [m]

c = 3,19 [m]

d = 4,27 [m]

e = 6,47 [m]

x₁ = 0,17 [m]

x₂ = 3,21 [m]

x₃ = 5,8 [m]

M₁ = 20 [m*N]

M₂ = 0 [m*N]

M₃ = 45 [m*N]

P₁ = 0 [N]

P₂=40 [kN]

P₃ = 0 [kN]

q = 3 [kN/m]

rodzaj przekroju: dwuteowik

1. Schema rozpatrywanej belki.

2. Wyznaczenie reakcji podpór.

W celu wyznaczenia rekcji belkę podzielono na dwie części w przegubie B tak jak na przedstawionym schemacie.

∑ F_ix = RAx – RBx = 0 (1)

∑ F_iy= RAy – RBy = 0 (2)

∑ M_iA= MA + M1 – RBy*a = 0 (3)

∑ Fix = RBx = 0 (4)

∑ Fiy = RBy – P2 + RC –q*(e-d) = 0 (5)

∑ MiB = -P2*(x2 –a) + RC*b +M3 – q*(e –d)*[e – a – 0,5*(e – d)] = 0

∑Mib = M2 + RC*b – P3(x3-a) – q(e-d)*(e-a-0.5*(e-d))

(6)

Z równania (6) otrzymujemy:

RC = P2(x2-a)+q(e-d)*(e-a-0,5(e-d))-M3 MA być -7,32 [kN]

RC = - 10763,98 [N]

Z równania (2) otrzymujemy:

Ray = RBy

Z równania (5) otrzymujemy:

Ray = 35836,98 [N] MA być -53,92 [kN]

Z równania (3) otrzymujemy:

MA = 86075 [N]

3. Wzory na siły wewnętrzne w poszczególnych przedziałach.

x1 (0, x1)

T(x1) = Ray

Mg(x1) =Ray * x1 – MA

X2 (0,a)

T(x2) = Ray

Mg(x2) = Ray * x2 – MA – M1

X3 (0,d)

T(x3) = Ray – P2

Mg(x3) = Ray * x3 – P2 * [x3 – (d – x2)] – MA – M1

X4 (0, a + b + c – e)

T(x4) = 0

Mg(x4) = 0

X5(0, a + b + c – x3)

T(x5) = q * [x5 – (a + b + c – e)]

Mg(x5) = - q * [x5 – (a + b + c – e)] * [x5 – 0,5 * (e - x3)]

X6 (0,c)

T(x6) = q * [x6 – (a + b + c – e)]

Mg(x6) = - q * {x6 – [(a + b + c) – e]} * [x6 – 0,5 * (e - a - b)] – M3

X7 (0, a + b + c –d )

T(x7) = q * [x7 - (a + b + c – e)] + RC

Mg(x7) = RC * [x7 – (a +b – d)] – q * [x7 – (a + b + c – e)] * [x7 – 0,5 * (e – d)] – M3

4. Wartości uzyskane ze wzorów na siły wewnętrzne dla punktów charakterystycznych.

	(0;0)
T [N]	35836,02
Mg [N*m]	-86074,6
	x1
T [N]	35836,02
Mg [N*m]	-79982,5
	x2
T [N]	35836,02
Mg [N*m]	-0,0008
	x3
T [N]	-4163,98
Mg [N*m]	-81454,8
	x4
T [N]	0
Mg [N*m]	0
	x5
T [N]	2010
Mg [N*m]	-5276,25
	x6
T [N]	2700
Mg [N*m]	-52398
	x7
T [N]	-4163,98
Mg [N*m]	-101711

Wyznaczono wierzchołki parabol ze wzrów :

Mg(x5) = - q * [x5 – (a + b + c – e)] * [x5 – 0,5 * (e - x3)] (I)

Mg(x6) = - q * {x6 – [(a + b + c) – e]} * [x6 – 0,5 * (e - a - b)] – M3 (II)

Mg(x7) = RC * [x7 – (a +b – d)] – q * [x7 – (a + b + c – e)] * [x7 – 0,5 * (e – d)] – M3 (III)

W celu narysowania wykresu I określenia czy w danym przedziale funkcja ta osiąga maksimu, którym w tych przypadkach jest wierzchołek paraboli W.

X – wartość Mg [N*m]

Y – wartości odległości od początku przedziału [m]

Dla (I):

Mg(x5) = - 3000x² + 7875x – 2301,45

Parametr W (1,31 ; 2866,52)

Ponieważ długość przedziału od końca x4 do x5 zawiera się w (2,29 ; 2,96) więc wierzchołek paraboli nie leży w dany przedziale.

Dla (II):

Mg(x6) = -3000x² + 8220x – 3091,5

Parametr W( 1,37 ; 2539,2)

Ponieważ długość przedziału od końca x5 do x6 zawiera się w(2,96 ; 3,19) więc wierzchołek paraboli nie leży w dany przedziale.

Dla (III):

Mg(x7) = -3000x² -3206,98x – 38563,83

Parametr W (0,53 ; -37706,76)

Ponieważ długość przedziału od końca x6 do x7 zawiera się w(3,19 ; 4,49) więc wierzchołek paraboli nie leży w dany przedziale.

5. Zaprojektowanie przekroju belki.

Dane:

|Mzg|= 101711 [N*m]

δdop= 120 [MPa]

Wzór:

Po przekształceniu:

P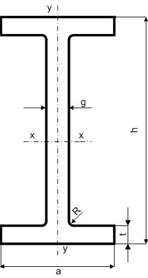 odstawiając do wzoru otrzymujemy:

Dwuteownikiem spełniającym powyższe warunki jest dwuteownik I 330PE.

Parametry teownika:

	h	a	g	t	r	A	G
	mm	mm	mm	mm	mm	cm^2	kg/m
I 330PE	330	160	7,5	11,5	18	62,6	49,1

Ix	Wx	ix	Iy	Wy	iy	I0
cm^4	cm^3	cm	cm^4	cm^3	cm	cm^4
11770	713	13,7	788	98,5	3,55	28,8