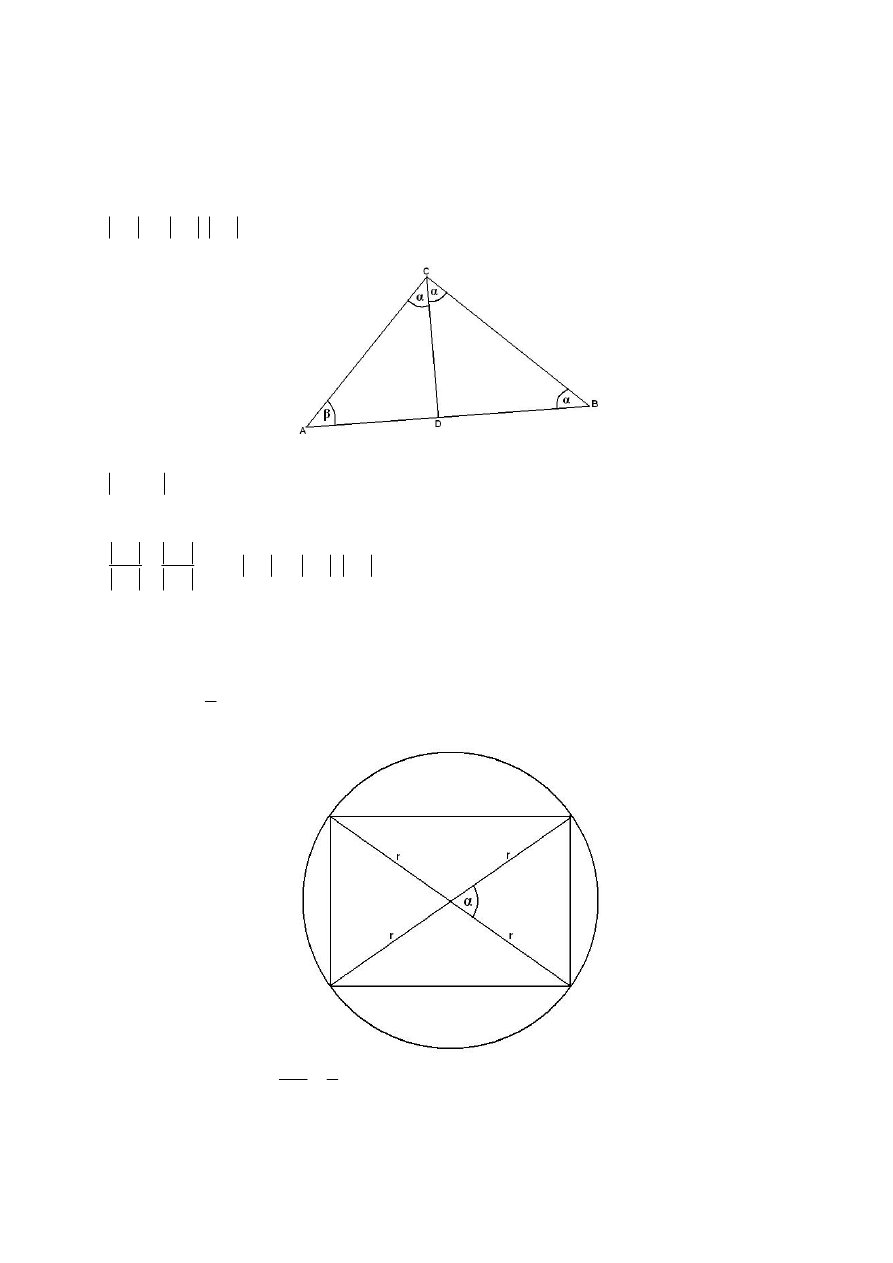
Cztery zadania nadesłane przez internautów

Zadanie 1.

W trójkącie ABC kąt przy wierzchołku C jest dwa razy większy od kąta przy
wierzchołku B. Dwusieczna kąta przecina bok AB w punkcie D. Wykazać, że

AB

AD

AC

2

⋅⋅⋅⋅

====

.

Rozwiązanie

αααα

====

αααα

−−−−

++++

αααα

−−−−

====

ββββ

++++

αααα

−−−−

====

∠

∠

∠

∠

αααα

−−−−

====

ββββ

2

)

3

180

(

180

)

(

180

ADC

3

180

o

o

o

o

Wobec tego trójkąty ABC i ACD są podobne, bo mają takie same kąty.
Korzystając z podobieństwa tych trójkątów, otrzymujemy:

AB

AD

AC

AD

AC

AC

AB

2

⋅⋅⋅⋅

====

⇔

⇔

⇔

⇔

====

, co należało udowodnić.

***************************************************************************
***************************************************************************

Zadanie 2.

Udowodnić, że stosunek pola prostokąta wpisanego w koło do pola tego koła jest

mniejszy od

3

2

.

Rozwiązanie

Należy udowodnić, że

3

2

r

S

2

<<<<

ππππ

, gdzie S – pole prostokąta.

Pole każdego czworokąta wypukłego można obliczyć jako połowę iloczynu długości
przekątnych przez sinus kąta między przekątnymi, dlatego:

αααα

====

αααα

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

sin

r

2

sin

r

2

r

2

2

1

S

2

Mamy:

ππππ

≤≤≤≤

ππππ

αααα

====

ππππ

αααα

====

ππππ

2

sin

2

r

sin

r

2

r

S

2

2

2

bo

1

sin

≤≤≤≤

αααα

i dalej:

3

2

2

<<<<

ππππ

, bo

3

>>>>

ππππ

.

Wynika stąd, że

3

2

r

S

2

<<<<

ππππ

, co należało udowodnić.

***************************************************************************
***************************************************************************

Zadanie 3.

Obliczyć sumę

n

3

2

n

nx

...

x

3

x

2

x

S

++++

++++

++++

++++

====

.

Rozwiązanie

((((

)))) ((((

))))

n

n

3

2

n

n

n

3

2

n

3

2

1

n

4

3

2

n

n

1

n

4

3

2

n

n

3

2

n

nx

x

...

x

x

x

)

1

x

(

S

:

mamy

nx

x

...

x

x

x

nx

...

x

3

x

2

x

nx

...

x

3

x

2

x

S

S

x

nx

...

x

3

x

2

x

S

x

nx

...

x

3

x

2

x

S

++++

−−−−

−−−−

−−−−

−−−−

−−−−

====

−−−−

⋅⋅⋅⋅

++++

−−−−

−−−−

−−−−

−−−−

−−−−

====

====

++++

++++

++++

++++

−−−−

++++

++++

++++

++++

====

−−−−

⋅⋅⋅⋅

++++

++++

++++

++++

====

⋅⋅⋅⋅

++++

++++

++++

++++

====

++++

++++

Jeżeli

1

x

====

, to

n

2

n

1

n

...

3

2

1

1

n

...

1

3

1

2

1

S

n

3

2

n

⋅⋅⋅⋅

++++

====

++++

++++

++++

++++

====

⋅⋅⋅⋅

++++

++++

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

++++

====

Jeżeli

1

x

≠≠≠≠

, to

1

x

nx

x

...

x

x

x

S

n

n

3

2

n

−−−−

++++

−−−−

−−−−

−−−−

−−−−

−−−−

====

((((

))))

1

x

)

1

x

(

x

x

1

x

1

x

x

...

x

x

x

x

...

x

x

x

n

n

n

3

2

n

3

2

−−−−

−−−−

−−−−

====

−−−−

−−−−

⋅⋅⋅⋅

−−−−

====

++++

++++

++++

++++

−−−−

====

−−−−

−−−−

−−−−

−−−−

−−−−

Stąd:

2

n

n

n

n

n

n

n

n

3

2

n

)

1

x

(

)

1

x

(

x

x

)

1

x

(

n

1

x

1

x

)

1

x

(

x

x

)

1

x

(

n

1

x

nx

1

x

)

1

x

(

x

1

x

nx

x

...

x

x

x

S

−−−−

−−−−

−−−−

−−−−

====

====

−−−−

−−−−

−−−−

−−−−

−−−−

====

−−−−

++++

−−−−

−−−−

−−−−

====

−−−−

++++

−−−−

−−−−

−−−−

−−−−

−−−−

====

***************************************************************************
***************************************************************************

Zadanie 4.

Rozwiązać równanie z niewiadomą x:

)

a

1

)(

a

1

)(

a

1

(

a

...

a

a

1

4

2

x

2

++++

++++

++++

====

++++

++++

++++

++++

.

Rozwiązanie

Lewa strona równania jest sumą

)

1

x

(

++++

wyrazów ciągu geometrycznego.

Jeżeli

1

a

====

, to lewa strona wynosi

1

x

++++

.

W tym przypadku:

1

)

a

1

)(

a

1

)(

a

1

(

x

4

2

−−−−

++++

++++

++++

====

.

Jeżeli

1

a

≠≠≠≠

, to równanie przyjmuje postać:

8

1

x

8

1

x

4

4

1

x

4

2

2

1

x

4

2

1

x

4

2

1

x

a

a

a

1

a

1

)

a

1

)(

a

1

(

a

1

)

a

1

)(

a

1

)(

a

1

(

a

1

)

a

1

)(

a

1

)(

a

1

)(

a

1

(

a

1

)

a

1

)(

a

1

)(

a

1

(

a

1

a

1

1

====

−−−−

====

−−−−

++++

−−−−

====

−−−−

++++

++++

−−−−

====

−−−−

++++

++++

++++

−−−−

====

−−−−

++++

++++

++++

====

−−−−

−−−−

⋅⋅⋅⋅

++++

++++

++++

++++

++++

++++

)

Dla

1

a

≠≠≠≠

otrzymujemy ostatecznie:

7

x

8

1

x

====

⇔

⇔

⇔

⇔

====

++++